引用本文
苏启航, 钱烨强, 袁伟, 杨明, 王春香. 基于自动修补策略的网络剪枝. 模式识别与人工智能, 2022,35(1): 62-70
SU Qihang, QIAN Yeqiang, YUAN Wei, YANG Ming, WANG Chunxiang. Network Pruning via Automatic Mending Strategy. PATTERN RECOGNITION AND ARTIFICIAL INTELLIGENCE, 2022,35(1): 62-70.  
Doi: 10.16451/j.cnki.issn1003-6059.202201006
Permissions
Copyright©2022, 《模式识别与人工智能》编辑部
《模式识别与人工智能》编辑部
基于自动修补策略的网络剪枝
苏启航1,2, 钱烨强3, 袁伟3, 杨明1,2, 王春香1,2
1.上海交通大学 自动化系 上海 200240
2.上海交通大学 系统控制与信息处理教育部重点实验室 上海 200240
3.上海交通大学 密西根学院 上海 200240
通讯作者:

王春香,博士,副教授,主要研究方向为移动机器人、自动驾驶、高级辅助驾驶.E-mail:wangcx@sjtu.edu.cn.

作者简介:

苏启航,硕士研究生,主要研究方向为计算机视觉、网络压缩.E-mail:sqh87898160@sjtu.edu.cn.

钱烨强,博士,主要研究方向为计算机视觉、模式识别、机器学习及智能交通中的应用.E-mail:qianyeqiang@sjtu.edu.cn.

袁 伟,博士,主要研究方向为自动驾驶系统、计算机视觉、深度学习、车辆控制.E-mail:weiy1991@sjtu.edu.cn.

杨 明,博士,教授,主要研究方向为低速无人驾驶中定位与导航技术.E-mail:MingYang@sjtu.edu.cn.

收稿日期: 2021-06-28 接受日期: 2021-10-28
资助项目: 国家自然科学基金项目(No.U1764264,62103261)资助
摘要

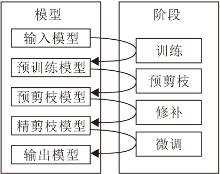
为有效缓解深度神经网络因其庞大的计算资源消耗而产生的实际应用受限的问题,研究人员设计包括剪枝在内的多种压缩策略.基于贪心思想的网络剪枝算法大都包含训练、剪枝、微调三部分,无法求得最优的剪枝结构.因此,文中结合人工规则和自动搜索方法,提出基于自动修补策略的网络剪枝.整体剪枝流程包括训练、预剪枝、修补和微调四个阶段,增加的修补阶段可调整预剪枝模型的结构.具体方法是使用神经架构搜索实现修补操作,设计搜索空间和搜索策略,并基于预剪枝阶段的卷积核排序加速评估过程.实验表明文中方法在剪枝率较高时仍能保持网络的准确率.

关键词: 深度神经网络; 网络剪枝; 神经架构搜索; 网络修补
中图分类号:TP 183
Network Pruning via Automatic Mending Strategy
SU Qihang1,2, QIAN Yeqiang3, YUAN Wei3, YANG Ming1,2, WANG Chunxiang1,2
1. Department of Automation, Shanghai Jiao Tong University, Shanghai 200240
2. Key Laboratory of System Control and Information Processing, Ministry of Education, Shanghai Jiao Tong University, Shanghai 200240
3. UM-SJTU Joint Institute, Shanghai Jiao Tong University, Shanghai 200240
Corresponding author:
WANG Chunxiang, Ph.D., associate professor. Her research interests mobile robots, autonomous driving and assistant driving.

About Author:
SU Qihang, master student. His research interests include computer vision and network compression.
QIAN Yeqiang, Ph.D. His research inte-rests include computer vision, pattern recognition, machine learning, and their applications in intelligent transportation systems.
YUAN Wei, Ph.D. His research interests include autonomous driving system, computer vision, deep learning and vehicle control.
YANG Ming, Ph.D., professor. His research interests include positioning and navigation in the low speed intelligent vehicles.

Fund:National Natural Science Foundation of China(No.U1764264,62103261)
Abstract

To alleviate the problem of the application of deep neural network being restricted owing to the massive computation resources, many network compression strategies including network pruning are put forward. Most of the network pruning methods based on greedy algorithm include training, pruning and fine-tuning, and therefore the optimal pruned structure cannot be obtained. In this paper, combining the rule-based method and the automatic search method, a network pruning method via automatic mending strategy is proposed. The whole pruning process is comprised of four stages: training, pre-pruning, mending and fine-tuning. The structure of the pre-pruned model is improved in the additional mending stage. Particularly, the neural architecture search is utilized to implement network mending. The search space and an efficient search strategy are designed. The estimation process is accelerated based on the filter ranking of the pre-pruning stage. Experiments show that the proposed method can guarantee the network accuracy in the case of high pruning rate.

Key words: Deep Neural Network; Network Pruning; Neural Architecture Search; Network Mending

本文责任编委 陶 卿

Recommended by Associate Editor TAO Qing

深度神经网络(Deep Neural Network, DNN)已广泛应用于计算机视觉任务中, 如图像分类[1]、目标检测[2]、语义分割[3]等.但是, DNN计算资源需求较大、功耗较高, 导致其在智能驾驶系统、移动设备处理等场景中应用受限.为了减少内存占用和加快推理时间, 研究者们提出许多压缩策略, 主要分为权值量化[4]、知识蒸馏[5]、低秩分解[6]、剪枝[7].

剪枝作为一种加速预训练较大模型的方法, 可进一步分为非结构化剪枝[8]和结构化剪枝[9].结构化剪枝可简化为2个问题:1)如何判断是否应该剪去一个指定的卷积核; 2)确定每层中应该剪去多少个卷积核.现有的剪枝方法试图最大限度地压缩网络而不造成太大的精度损失, 大多数遵循相同流程:训练、剪枝、微调.

对于问题1), 通常使用人工规则选择不重要的卷积核并将其剪去, 剪枝过程方便快捷.一个典型的剪枝思想是:如果网络中某个对象的值足够小, 就可对其进行剪枝.这里的对象可是卷积核的L1范数[10]、批量归一化层(Batch Normalization, BN)的比例因子[7]、输出特征图的重构误差[11] 、网络掩膜的值[12, 13]、下一层输出特征图的变化[14]等.同时, 也有一些关于“ 越小越不重要” 思想的正确性讨论[15, 16].另一个思想是删减冗余的卷积核.冗余卷积核中包含的信息或知识可被其它卷积核替代.例如, 一层中两个权重完全相同的卷积核可被认为是冗余的.在此基础上, Ding等[17]研究卷积核之间的相似性评价方法.更进一步, He等[15]利用几何中值选择冗余卷积核, Lin等[18]将低秩特征图定义为冗余通道.实际上, 不论“ 小” 思想和“ 冗余” 思想, 都是一种选择网络保留参数的策略.

对于问题2), 其目标等价于寻找最佳剪枝网络子结构.最简单的方法是使用预定义的剪枝率, 直接确定每层中应剪去多少个卷积核[11, 14, 15, 18, 19].常用方法是以相同比率修剪每层.然而, 剪枝得到的网络可能不是最佳的子结构.方法2)是使用迭代剪枝[10]逐层确定最优剪枝率.这种策略通常耗时较长, 并未充分研究外层间的剪枝顺序.方法3)是使用全局阈值[7, 20], 可自动确定每层中剪去的卷积核数量.该策略的问题是全局阈值对每层是否公平.方法4)是给网络添加一个附属掩膜[12, 13], 通过掩膜值确定待剪的卷积核.在训练时, 这些掩膜通常与网络参数一起学习.Lin等[12]交替更新掩膜和网络参数, 获得近似解.Huang等[13]利用正则化方法, 使掩膜的某些值趋于0.然而, 这种策略存在掩膜参数和网络参数数量不平衡的问题.方法5)是使用网络架构搜索[9, 21].受Liu等[22]工作的影响, 减少剪枝任务与神经架构搜索(Neural Architecture Search, NAS)任务之间的差异.利用基于遗传算法[23]和强化学习[24]的搜索策略, NAS可更公平地确定每层的通道数.Liu等[21]通过元学习为剪枝子网络分配权重, 通过遗传算法进行搜索.Lin等[9]使用人工蜂群算法寻找最优的剪枝结构.

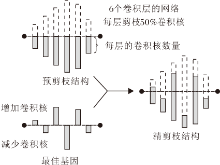
为了解决结构化剪枝的问题, 本文提出基于自动修补策略的网络剪枝(Network Pruning via Auto-matic Mending Strategy, PAM).不同于传统的三阶段网络剪枝流程, 本文方法在剪枝后增加一个修补阶段, 即流程包括训练、预剪枝、修补、微调.对于预先训练好的模型, 以相同的剪枝率对每层进行剪枝, 称为预剪枝阶段.该阶段用于判断不同卷积核的重要性, 主要解决问题1).然而, 在给定的剪枝率下, 预剪枝模型通常不是最优结构.因此, 在保持整体剪枝率不变的前提下, 在预剪枝网络的每层添加或删除卷积核, 称为修补阶段.这个阶段用于寻找最佳剪枝结构, 主要解决问题2).此外本文还研究预训练较大模型中权重的价值.实验表明, 使用这些权重可使性能估计策略更快、更可靠.

1 基于自动修补策略的网络剪枝
1.1 符号和说明

假设一个有L个卷积层的网络.第l层的所有卷积核权重表示为W(l)∈ RNl×Nl-1×Kl×Kl, 1≤ l≤ L, Nl表示该层的卷积核数量, Kl表示长宽尺寸(不妨设长宽尺寸相同).使用 Wi(l)∈ RNl-1×Kl×Kl表示第l个卷积层中的第i个卷积核.另外, 将剪枝后的第l层权重表示为 W︿(l)∈ RN︿l×N︿l-1×Kl×Kl, 1≤ N︿l≤ Nl, N︿l表示该层保留的卷积核数量.

1.2. 预剪枝

将同层中的相同卷积核视为冗余是一种常见的剪枝方法.Ding等[17]在训练过程中使用向心随机梯度下降法(Centripetal Stochastic Gradient Descent, Centripetal SGD)和K-means, 得到更多相同的卷积核.一般地, 在一个卷积层中剪去相同的卷积核可使下一层的输出特征图在微调后变化不大.这类似于Luo等[14]提出的剪枝目标.以此为原理, 常使用2个卷积核的向量差值的L2范数计算它们之间的相似度.本文进一步扩展卷积核冗余的定义.具体地, 如果第l层的卷积核 Wi(l)和 Wj(l)间的关系满足

Wi(l)=k Wj(l), abs(k)> 1,

认为 Wj(l)是冗余的, 其中, Wi(l)、 Wj(l)可视为向量.因此, 本文使用额外的角度信息计算卷积核的相似性:

dist( Wi(l), Wj(l))= ‖γi(l)Wi(l)-γj(l)Wj(l)‖2sinθ, (1)

其中, θ表示卷积核 Wi(l)、 Wj(l)间的角度, γi(l)表示与 Wi(l)对应的BN层尺度因子, ‖·‖2表示L2范数操作.由于BN层的尺度因子γ 为可训练的参数, 可对特征图的值进行再次缩放, 且BN层可与卷积层进行融合.因此, 如果网络使用BN层, 会考虑γ 的影响, 否则令γ =1.He等[15]提出, 如果一层中卷积核的最小范数不小, 范数偏差较大, 则“ 小范数不重要” 的原理将不再适用.由于本文的相似性度量包含角度信息, 当一层中的卷积核范数相似时, 距离将由它们的角度决定, 可自动解决范数偏差较小的问题.

卷积核相似性度量常和聚类算法一起用于剪枝[17].一般来说, 簇的数目等于保留卷积核的总数, 并且每簇中只保留一个卷积核.与此不同的是, 本文使用式(1)和凝聚聚类算法对每层中的卷积核进行重要性排序.卷积核的排序不仅可在预剪枝阶段作为剪枝标准, 还对修补阶段的设计起到重要作用.

在某一卷积层实现聚类算法时, 在同簇内可认为模长最大的卷积核最重要[10, 17], 因此令每个簇中模长最大的卷积核作为簇的聚类中心, 此外, 聚合一层的卷积核直到只形成唯一一个簇, 并记录聚类过程.若卷积核或簇越早聚合, 则簇的聚类中心卷积核越不重要, 以此得到各层卷积核的重要性排序.以一层有A、B、C、D四个卷积核为例, 初始集合

I=[[A], [B], [C], [D]],

首先划分为4个簇, 每个卷积核作为本簇的聚类中心.2个簇的距离等于聚类中心间的距离, 2个聚类中心(2个卷积核)的距离按照式(1)计算.计算距离最近的2个簇, 假设[A]、[B]之间距离最小且A的模长大于B, 则A和B聚合成一个簇,

I=[[A, B], [C], [D]],

A为新簇的聚类中心, B放入排序队列中.然后, 假设簇[A, B]、[C]的距离最小, C的模长大于A, 则

I=[[C, A, B], [D]],

C为新簇的聚类中心, A放入排序队列中.最后聚合仅剩2个簇, 假设C的模长大于D, 则C为最终的簇的聚类中心, D放入排序队列中.最终得到的卷积核重要性排序为B< A< D< C.

综上所述, 本文按如下过程执行预剪枝阶段.首先, 计算第l层的卷积核重要性排序F(l), 并使F(l)按照降序排列.然后, 基于设定的剪枝率和Nl计算保留的卷积核数量 N︿l, 并将集合F(l)划分为2个子集Z(l)和U(l), Z(l)为F(l)中前 N︿l的元素, 即保留重要的卷积核索引, U(l)为剩余的待剪去的卷积核索引.最后, 剪去U(l)中对应的卷积核和相关参数, 得到预剪枝模型.

1.3 修补

在修补阶段, 本文使用NAS调整预剪枝模型中每层的卷积核数量, 并保持网络的卷积核总数不变, 即本文的目标是在保持剪枝率不变的条件下得到一个更好的剪枝结构.这里的剪枝率为被剪的数量除以总数.由于不同层中卷积核的大小可能不同, 导致不同子网络在剪枝率相同的情况下依然可能具有不同的浮点运算次数(Floating-Point Operations per Second, FLOPs).

NAS设计的要素一般包括搜索空间、搜索策略和性能估计策略[25].搜索策略在搜索空间中发现一个新的结构, 并利用性能估计策略对结构进行评估.

本文采用基于遗传算法的NAS进行搜索, 将剪枝子网络结构编码为基因.具体地, 将预剪枝的网络结构编码为0号基因:

G0=[0, 0, …, 0], len(G0)=L.

基因G0给变异操作提供一个初始基因, 性能也可作为参考基线.显然, 如果想给第l层增加2个卷积核, 则只需将G0, l从0更改为2, 其中G0, l表示G0的第l个值.

值得注意的是:1)网络的编码基因只能代表一个子网络的结构, 即只能得到每层中卷积核的数量, 而不能得到权重.2)不同剪枝率下的G0是相同的.只有同时根据预剪枝结构和基因, 才能得到目标结构.

图1为修补阶段使用基因和预剪枝结构解码出目标结构的一个例子.修补阶段的任务是寻找最佳基因, 以获得最优的精剪枝结构.

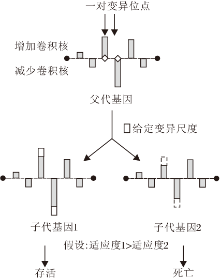
图1 修补预剪枝网络示意图Fig.1 Sketch map of mending pre-pruned network

在NAS领域, 利用遗传算法寻找最优结构[23, 26].变异操作是促进种群适应度不断提高的重要操作.然而, 在本文的搜索空间中使用变异操作会存在一个问题:典型的变异只发生在基因的一个位置, 无论增加或减少卷积核的数量, 都会引起整体剪枝率的变化.因此, 本文设计新的变异方法, 称为成对变异.“ 对” 意味着选择一对位置同时变异, 并产生一对后代.

以基因Gk进行成对变异操作为例:首先选择2个互不相同的随机变异位点i、 j, 1≤ i≤ L, 1≤ j≤ L.然后, 根据一个给定的变异尺度S, 使父代基因产生2个子代基因, 即

Gchild1=[…, Gk, i+S, …, Gk, j-S, …],

Gchild2=[…, Gk, i-S, …, Gk, j+S, …].

成对变异操作的示意图如图2所示, S表示增加或减少的卷积核数量.最后, 根据性能评估策略计算2个基因的适合度, 将较好的一个基因加入群体中, 直接丢弃另一个表现较差的基因.以这种变异方式, 一个基因向量中所有值的和可始终保持为0, 即整体剪枝率保持不变.此外, 作为一种直观的设计, 如果第i、 j层中的一层需要更多的卷积核以提高子网络的性能, 并且减少另一层的卷积核数量, 不会造成更多的性能损失, 在两个子代中将会有一个具有更好的性能.

图2 成对变异操作的示意图Fig.2 Sketch map of pair-mutation operation

本文采用锦标赛选择法对当前种群进行采样.在每个周期中, 删除群体中最老的基因[26].这种删除策略在NAS领域被证明可防止高适应度基因永远留在群体中, 从而产生大量后代.此外, 本文采用逐步变小的变异尺度S实现从粗到精的搜索.特别地, 如果变异操作导致第l层中的卷积核数量超过[1, Nl]的限制范围, 则限制此次循环中使用的变异尺度, 使卷积核数量控制在合法范围内.具体地:如果变异操作得到的结果小于1, 将该层的卷积核数量置为1; 如果结果大于Nl, 将该层的卷积核数量置为Nl.

本文还为搜索策略设计一个可选步骤— — 交叉操作.上述成对变异操作可在保持剪枝率不变的前提下快速提高种群适应度, 但本文还希望能寻找剪枝率更高但性能更优的子网络, 称为幸运子网络.此目标类似于Chin等[20]的目标, 旨在生成一组具有不同精度和延迟权衡的子网络.在本文的网络编码模式中, 更高的剪枝率意味着基因向量所有值的和小于0.具体地, 在候选基因中选择2个不同的基因作为父代基因, 随机选择一个位置交叉的2个基因, 产生2个子代Gchild3和Gchild4.若2个父代基因向量的所有值的和都是0, 不妨假设2个子代基因

sum(Gchild3)≤ sum(Gchild4),

则一定可推导出

sum(Gchild3)≤ 0, sum(Gchild4)≥ 0.

本文直接丢弃Gchild4, 计算Gchild3的适应度, 并放入种群中.在特殊情况下, 如果将交叉操作产生的基因用作父代基因, 则可能导致sum(Gchild3)和sum(Gchild4)同时小于0.假设

sum(Gchild3)> sum(Gchild4),

则直接舍弃Gchild4, 保留和设定剪枝率更接近的子代, 确保交叉操作只需要计算一个子代的适合度.

性能评估策略用于计算基因的适应度.评估网络结构性能的一种简单方法是从头开始训练网络, 并在验证集上评估准确率, 但耗时较大.因此, NAS领域中已研究一些加速估计策略[27], 或称为代理度量, 只需计算不同结构的相对性能, 即可对比好坏.Zhou等[28]综合不同的加速方法, 设计不同的代理度量, 并通过基于网络性能排名计算的Spearman系数评价不同代理度量的优劣.

本文的代理度量包括:1)只使用少量的训练轮数微调子网络以计算它们的适合度, 但会引入评估偏差.2)利用预剪枝阶段的卷积核排序快速初始化新结构.使用卷积核排序对保留的卷积核进行初始化相当于剪枝操作, 即保留排序中重要的卷积核, 删掉不重要的结构.本文通过实验证实这种初始化方法可减少评估偏差, 提高评估策略的稳定性.对于由基因产生的目标结构, 可将其看作是对原大网络进行剪枝得到的子结构, 不同于预剪枝的操作, 每层卷积核的数量不再由剪枝率决定, 而由基因决定.

最终本文方法框图如图3所示.

图3 本文方法框图Fig.3 Flow chart of the proposed method

2 实验及结果分析
2.1 实验设置

为了验证本文方法(PAM)的有效性, 在CIFAR-10[29]、CUB-200[30]数据集上进行对比实验.本文研究剪枝算法在卷积神经网络(Convolutional Neural Network, CNN)上的性能, 包括单分支网络(V-GG)[1]和残差网络(Residual Network, ResNet)[31].

本文选择如下对比方法:Slim(Network Slim-ming)[7], Soft(Soft Pruning)[19], FPGM(Filter Pru-ning via Geometric Median)[15], HRank(High-Rank Feature)[18].Slim使用BN层比例因子和一个全局阈值.在高压缩比的情况下, 这种剪枝策略有可能剪掉一层中所有卷积核, 导致网络无法正确推理.在此次实验中, 保证剪枝后网络的每层至少保留一个卷积核.Soft和FPGM在每层都使用相同的剪枝率.HRank使用特征图的秩判断卷积核的重要性, 在每层中使用一个预定义但各层不同的剪枝率.本文控制不同剪枝方法的压缩情况(参数量和FLOPs)彼此之间相差不至过大, 实现更公平的对比.

本文采用动量为0.9、权重衰减为0.000 1的随机梯度下降法(Stochastic Gradient Descent, SGD)[32]作为优化器.在修补阶段, 设置种群大小为50, 候选集大小为15, 迭代次数为200.此外, 初始变异尺度为16, 变异尺度在第80轮调整为8, 在第160轮调整为4.在计算基因适合度时, 将代理度量的微调轮数设置为5.在最后的微调阶段, 训练160轮.在种群演化的每轮中, 首先进行成对变异操作, 种群增加一个由变异得到的子代基因, 删除最老的一个基因.再执行交叉操作, 种群增加一个由交叉得到的子代基因, 删除最老的一个基因.

2.2 实验结果对比

对于VGG网络, 使用深度为19的结构, 基础剪枝率为90%.除了Soft和FPGM以外, 其它方法得到的网络结构各不相同.因此, 剪枝模型的FLOPs和参数量存在差异.在CIFAR-10数据集上, 各方法在VGG19网络上的剪枝结果如表1所示, 表中baseline表示原始的预训练模型.由表可知, PAM得到的网络具有最高的精度、最少的FLOPs和最少的参数量.

表1 各方法在VGG19网络上的剪枝结果 Table 1 Pruning results of different methods in VGG19 network

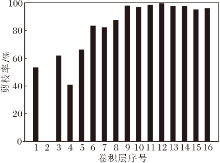
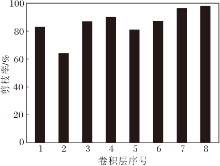
为了更清晰地展示预剪枝和修补的作用, 各阶段模型的准确率如下:预训练模型为93.76%, 预剪枝模型为56.89%, 精剪枝模型为85.96%, 输出模型为92.02%.PAM得到的剪枝网络各层的剪枝情况如图4所示.由图可看出, 网络输入端和输出端卷积层的剪枝率存在较大差异, VGG19是一个不同层卷积核冗余度差异较大的网络.实验证实PAM对其搜索最佳剪枝结构的有效性.

图4 VGG19网络各层的剪枝率Fig.4 Pruning rate of each layer in VGG19 network

在实验中, ResNet网络的深度为18, 基础剪枝率为90%.因为在残差块的输出部分有一个加法运算, 所以必须保持输入输出通道的对应关系.如同大多数剪枝策略, PAM不剪枝残差块最后的卷积层和跨连分支.在CIFAR-10数据集上, 各方法在ResNet-18网络上的剪枝结果如表2所示.由表可见, PAM的综合性能最好.

表2 各方法在ResNet18在网络上的剪枝结果 Table 2 Pruning results of different methods in ResNet18 network

ResNet网络各层的剪枝情况如图5所示, 图中只展示可剪的卷积层.从网络不同层的剪枝率差异可看出, ResNet18各层的冗余度差异小于VGG19, 这可能是因为残差结构具有恢复剪枝造成的信息丢失的能力.

图5 ResNet18网络各层的剪枝率Fig.5 Pruning rate of each layer in ResNet18 network

对VGG19、ResNet18网络通过交叉操作可获得“ 幸运子网络” 的结果.在搜索过程中增加交叉操作, 可得到许多不同剪枝率的剪枝子网络.本文选择几种不同的剪枝率, 并给出在每个选定的剪枝率下的最佳剪枝网络.结果见表3和表4.正如假设可见, 在搜索过程中有一些幸运的子网络.例如, 剪枝率为90.83%的ResNet18比基础剪枝率为90.00%的ResNet18性能更优.

表3 对VGG19进行交叉操作的结果 Table 3 Crossover operation results of VGG19
表4 对ResNet18进行交叉操作的结果 Table 4 Crossover operation results of ResNet18

此外, 针对VGG19修补的种群, 演化过程如图6所示.图中横坐标是从初始化种群开始计数的基因数目, 纵坐标是使用性能评估策略得到的基因适应度, 水平虚线是0号基因, 即预剪枝模型的适应度.由图可见变异操作和交叉操作对修补VGG19预剪枝网络的影响, 上述操作使种群适应度逐步上升最后趋于收敛.

图6 修补阶段的种群演化过程Fig.6 Evolutionary process of population in mending stage

本文分析剪枝的ResNet18网络在迁移学习中的性能.由于NAS技术资源消耗较大, 在大数据集上搜索会耗时较多.所以一些工作[24, 28]会将CIFAR-10数据集上搜索到的结构迁移到较大数据集上, 如ImageNet、CUB-200数据集, 以间接证实有效性.本文采取类似的实验方法.针对已在CIFAR-10数据集上剪枝和微调的网络, 改变第一个卷积层和最后一个全连接层, 其它部分不变.基线网络(baseline)训练160轮.使用相同的迁移学习超参数设置, PAM与baseline的剪枝结果如表5所示, PAM-TL表示PAM的迁移学习结果, PAM-scratch表示剪枝过的网络从头开始训练, Top-1准确率(Top-1 Accuracy)指预测的最大概率类别与真实类别相同的样本所占的比率.因为基线和剪枝模型的训练计算量差异较大, 本文参考文献[22]的工作, 对剪枝模型使用与baseline相同的计算量进行训练, 表示为PAM-TL-B.表5说明PAM的剪枝模型可较好地转移到其它数据集.从PAM-TL-B的结果可知, 当剪枝率较高时, 最好使用更多的训练轮数, 提高模型的准确率.

表5 ResNet18剪枝网络的迁移学习结果 Table 5 Transfer learning results of pruned ResNet18 network
2.3 代理度量分析

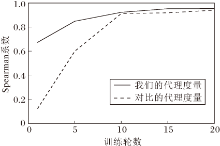
本节讨论剪枝后保留参数的价值, 并说明本文性能估计策略的有效性.受Zhou等[28]的启发, 本文使用Spearman系数评估代理度量.首先, 随机生成50个VGG19的剪枝子网结构(剪枝率均为90%), 并进行充分训练(在CIFAR-10数据集上训练160轮), 称为原始设置.然后, 对这50个子网络结构, 使用性能评估策略中的代理度量进行训练微调, 并将这个简化的设置表示为“ 我们的代理度量” .为了对比, 还使用随机权值初始化子网络, 再进行训练微调, 即这些网络结构不再使用保留参数, 将此简化设置称为“ 对比的代理度量” .最后, 利用Spearman系数计算原始设置和每个简化设置之间的相关性, 结果如图7所示, Spearman系数越高, 说明代理度量越可靠.

图7 代理度量的有效性分析Fig.7 Effectiveness analysis of proxy metrics

实验表明, 相比随机初始化方法, 本文的代理度量方法能更好地保持不同子网络精度的排序.在剪枝算法中, 保留权重的一般作用是加速剪枝后的微调过程.该实验还说明保留权重的另一个作用, 即当使用少量的训练轮数评价不同子网的相对性能时, 可提高评价的可靠性.

从实验结果可得出另一个结论:估计策略中使用的训练轮数越多, 可靠性越强.这对于调整搜索过程成本具有重要意义, 可通过调整代理度量中使用的轮数控制整个算法的耗时.

3 结束语

本文结合人工规则和自动搜索方法, 提出基于自动修补策略的网络剪枝.在预剪枝阶段, 基于角度和范数信息, 识别冗余的卷积核, 并在预剪枝后设计基于神经架构搜索实现的修补阶段.相比基于贪心思想的经典网络剪枝算法, 本文方法可求解更佳的网络剪枝结构, 获得更高的网络性能.同时, 基于预剪枝结构的基因编码策略及策略中的成对变异, 结合预剪枝阶段的先验知识都可提高本文方法的搜索效率.实验表明, 本文方法能较好地剪枝分类任务的网络.

从算法的搜索和评估策略的角度分析, 还可进一步改进本文方法.在修补阶段种群演化的初期, 得到的剪枝网络之间性能差距较大, 因此在评估策略中只需设置少量的训练轮数就可区分不同剪枝网络的优劣.而在演化的后期, 得到剪枝网络之间性能差距较小, 需要更多的训练轮数, 可考虑在种群演化过程中动态调整评估策略使用的训练轮数, 更合理地分配计算资源, 提高搜索效率.此外, 相比本文实验部分的分类网络, 目标检测、语义分割任务的网络结构更复杂, 需要进一步验证剪枝算法的有效性.将本文方法应用于更多的视觉任务是下一步研究的重点.

参考文献
[1] SIMONYAN K, ZISSERMAN A. Very Deep Convolutional Networks for Large-Scale Image Recognition[C/OL]. [2021-06-20]. https://arxiv.org/pdf/1409.1556.pdf. [本文引用:2]
[2] REN S Q, HE K M, GIRSHICK R, et al. Faster R-CNN: Towards Real-Time Object Detection with Region Proposal Networks. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2017, 39(6): 1137-1149. [本文引用:1]
[3] LONG J, SHELHAMER E, DARRELL T. Fully Convolutional Networks for Semantic Segmentation // Proc of the IEEE Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2015: 3431-3440. [本文引用:1]
[4] RASTEGARI M, ORDONEZ V, REDMON J, et al. XNOR-Net: ImageNet Classification Using Binary Convolutional Neural Networks // Proc of the European Conference on Computer Vision. Berlin, Germany: Springer, 2016: 525-542. [本文引用:1]
[5] HINTON G, VINYALS O, DEAN J. Distilling the Knowledge in a Neural Network[C/OL]. [2021-06-20]. https://arxiv.org/pdf/1503.02531.pdf. [本文引用:1]
[6] DENTON E, ZAREMBA W, BRUNA J, et al. Exploiting Linear Structure within Convolutional Networks for Efficient Evaluation [C/OL]. [2021-06-20]. https://arxiv.org/pdf/1404.0736.pdf. [本文引用:1]
[7] LIU Z, LI J G, SHEN Z Q, et al. Learning Efficient Convolutional Networks through Network Slimming // Proc of the IEEE International Conference on Computer Vision. Washington, USA: IEEE, 2017: 2755-2763. [本文引用:4]
[8] GUO Y W, YAO A B, CHEN Y R. Dynamic Network Surgery for Efficient DNNs // Proc of the 30th International Conference on Neural Information Processing Systems. Cambridge, USA: The MIT Press, 2016: 1387-1395. [本文引用:1]
[9] LIN M B, JI R R, ZHANG Y X, et al. Channel Pruning via Automatic Structure Search // Proc of the 29th International Joint Confe-rence on Artificial Intelligence. New York, USA: ACM, 2020: 673-679. [本文引用:3]
[10] LI H, KADAV A, DURDANOVIC I, et al. Pruning Filters for Efficient ConvNets[C/OL]. [2021-06-20]. https://arxiv.org/pdf/1608.08710.pdf. [本文引用:3]
[11] HE Y H, ZHANG X Y, SUN J. Channel Pruning for Accelerating very Deep Neural Networks // Proc of the IEEE International Conference on Computer Vision. Washington, USA: IEEE, 2017: 1389-1397. [本文引用:2]
[12] LIN S H, JI R R, LI Y C, et al. Accelerating Convolutional Networks via Global & Dynamic Filter Pruning // Proc of the 27th International Joint Conference on Artificial Intelligence. New York, USA: ACM, 2018: 2425-2432. [本文引用:3]
[13] HUANG Z H, WANG N Y. Data-Driven Sparse Structure Selection for Deep Neural Networks // Proc of the European Conference on Computer Vision. Berlin, Germany: Springer, 2018: 317-334. [本文引用:3]
[14] LUO J H, WU J X, LIN W Y. ThiNet: A Filter Level Pruning Method for Deep Neural Network Compression // Proc of the IEEE International Conference on Computer Vision. Washington, USA: IEEE, 2017: 5068-5076. [本文引用:3]
[15] HE Y, LIU P, WANG Z W, et al. Filter Pruning via Geometric Median for Deep Convolutional Neural Networks Acceleration // Proc of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2019: 4340-4349. [本文引用:5]
[16] YE J B, LU X, LIN Z, et al. Rethinking the Smaller-Norm-Less-Informative Assumption in Channel Pruning of Convolution Layers[C/OL]. [2021-06-20]. https://arxiv.org/pdf/1802.00124.pdf. [本文引用:1]
[17] DING X H, DING G G, GUO Y C, et al. Centripetal SGD for Pruning Very Deep Convolutional Networks with Complicated Structure // Proc of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2019: 4938-4948. [本文引用:4]
[18] LIN M B, JI R R, WANG Y, et al. HRank: Filter Pruning Using High-Rank Feature Map // Proc of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2020: 1526-1535. [本文引用:3]
[19] HE Y, KANG G L, DONG X Y, et al. Soft Filter Pruning for Accelerating Deep Convolutional Neural Networks // Proc of the 27th International Joint Conference on Artificial Intelligence. New York, USA: ACM, 2018: 2234-2240. [本文引用:2]
[20] CHIN T W, DING R Z, ZHANG C, et al. Towards Efficient Mo-del Compression via Learned Global Ranking // Proc of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2020: 1515-1525. [本文引用:2]
[21] LIU Z C, MU H Y, ZHANG X Y, et al. MetaPruning: Meta Learning for Automatic Neural Network Channel Pruning // Proc of the IEEE/CVF International Conference on Computer Vision. Washington, USA: IEEE, 2019: 3295-3304. [本文引用:2]
[22] LIU Z, SUN M J, ZHOU T H, et al. Rethinking the Value of Network Pruning[C/OL]. [2021-06-20]. https://arxiv.org/pdf/1810.05270.pdf. [本文引用:2]
[23] REAL E, MOORE S, SELLE A, et al. Large-Scale Evolution of Image Classifiers // Proc of the 34th International Conference on Machine Learning. New York, USA: ACM, 2017: 2902-2911. [本文引用:2]
[24] ZOPH B, LE Q V. Neural Architecture Search with Reinforcement Learning[C/OL]. [2021-06-20]. https://arxiv.org/pdf/1611.01578.pdf. [本文引用:2]
[25] ELSKEN T, METZEN J H, HUTTER F. Neural Architecture Search: A Survey. Journal of Machine Learning Research, 2019, 20: 1-21. [本文引用:1]
[26] REAL E, AGGARWAL A, HUANG Y P, et al. Regularized Evolution for Image Classifier Architecture Search[C/OL]. [2021-06-20]. https://arxiv.org/pdf/1802.01548.pdf. [本文引用:2]
[27] ZOPH B, VASUDEVAN V, SHLENS J, et al. Learning Transferable Architectures for Scalable Image Recognition // Proc of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2018: 8697-8710. [本文引用:1]
[28] ZHOU D Z, ZHOU X C, ZHANG W W, et al. EcoNAS: Finding Proxies for Economical Neural Architecture Search // Proc of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2020: 11393-11401. [本文引用:3]
[29] KRIZHEVSKY A. Learning Multiple Layers of Features from Tiny Images[C/OL]. [2021-06-20]. http://www.cs.toronto.edu/~kriz/learning-features-2009-TR.pdf. [本文引用:1]
[30] WAH C, BRANSON S, WELINDER P, et al. The Caltech-UCSD Birds-200-2011 Dataset[C/OL]. [2021-06-20]. http://www.vision.caltech.edu/visipedia/papers/CUB_200_2011.pdf. [本文引用:1]
[31] HE K M, ZHANG X Y, REN S Q, et al. Deep Residual Learning for Image Recognition // Proc of the IEEE Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2016: 770-778. [本文引用:1]
[32] SUTSKEVER I, MARTENS J, DAHL G, et al. On the Importance of Initialization and Momentum in Deep Learning. Journal of the Machine Learning Research, 2013, 28(3): 1139-1147. [本文引用:1]