赵建伟,博士,教授,主要研究方向为智能计算、图像处理等.E-mail:zhaojw@amss.ac.cn.
作者简介:

李养晓,硕士研究生,主要研究方向为智能计算、图像处理等.E-mail:1124755525@qq.com. 
卫福源,硕士研究生,主要研究方向为智能计算、图像处理等.E-mail:1224349166@qq.com. 
周正华,博士,副教授,主要研究方向为智能计算、图像处理等.E-mail:zzhzjw2003@163.com.
基于相关滤波设计鲁棒的追踪算法是目标追踪领域的一个重要研究方向.背景、空间信息和时间信息对提高算法的追踪性能具有重要意义.在背景感知追踪算法的基础上,融合空间信息和时间信息,考虑空间权值矩阵的自适应性,文中提出基于加速自适应时空背景感知相关滤波的目标追踪算法.运用加速的交替方向乘子法求解空间权值矩阵和滤波器,实现目标自适应追踪.利用背景信息、空间信息及空间权值的自适应性,增强追踪器对背景和目标的鉴别能力.运用时间正则项,缓解追踪器在目标遮挡下的追踪漂移问题.应用加速的交替方向乘子法,提高求解速度.实验表明,文中算法在目标遮挡、背景干扰等情况下的追踪性能较优.
ZHAO Jianwei, Ph.D., professor. Her research interests include intelligent computing and image processing.
About Author:
LI Yangxiao, master student. His research interests include intelligent computing and image processing.WEI Fuyuan, master student. His research interests include intelligent computing and image processing.
ZHOU Zhenghua, Ph.D., associate professor. His research interests include intelligent computing and image processing.
Designing a robust tracking algorithm based on correlation filters is an important research direction in the target tracking. The information of background, space and time is significant for improving the tracking performance of the algorithm. Grounded on the background-aware tracking algorithm, an object tracking algorithm based on accelerated adaptive spatial-temporal background aware correlation filter is proposed by fusing the spatial information, temporal information and the adaptability of the spatial weight matrix. Then,the appearance optimization model is solved by the accelerated alternating direction method of multipliers to obtain the spatial weight matrix and the correlation filter to realize the adaptive tracking. The proposed tracking algorithm enhances the discrimination of the tracker for the object from the background with the background information, spatial information and the adaptive spatial weight. The problem of tracking drifting for the case of target occlusion is alleviated by the temporal-regularization term, and the solving process is speeded up by the accelerated alternating direction method of multipliers. Experiments illustrate that the proposed algorithm produces better tracking results in the cases of target occlusion and background interference.
本文责任编委 徐 勇
Recommended by Associate Editor XU Yong
目标追踪是计算机视觉研究的热点之一, 在智能监控、机器人视觉、虚拟现实、军事成像等领域具有广泛应用.目标追踪的任务是根据视频序列第一帧中目标的初始位置, 设计追踪算法, 确定目标在下一帧中的位置.因为目标追踪过程中存在光线变化、快速移动、运动模糊、目标遮挡或目标变形等因素的干扰, 所以设计高效、鲁棒的追踪算法仍是一项具有挑战性的任务.
近年来, 基于相关滤波的追踪算法由于高效的追踪性能而受到人们的广泛关注[1, 2].这类追踪算法基于信号处理中“ 相似的信号具有相似的响应图” 的原理建立优化模型.Bolme等[3]将上述原理引入目标追踪领域中, 提出最小平方误差(Minimum Output Sum of Squared Error, MOSSE)追踪算法, 首先利用快速傅里叶变换提取训练样本, 再利用最小平方误差设计学习相关滤波的优化模型, 最后利用该模型求解的相关滤波, 确定下一帧目标的位置.在此基础上, 学者们提出许多改进的基于相关滤波的追踪算法.Henriques等[4]通过循环位移对图像进行密集采样, 增加训练样本的数量, 提出高效的核化相关滤波(Kernelized Correlation Filter, KCF)追踪算法.同时, Danelljan等[5]在MOSSE的外观模型中引入尺度正则化项, 提出判别尺度空间追踪算法(Discriminative Scale Space Tracker, DSST).为了缓解不必要的边界效应对追踪算法的影响, Danelljan等[6]在DSST的外观优化模型的尺度正则项中又引入空间权值矩阵, 提出基于空间正则化相关滤波(Spatially Regularized Discriminative Correlation Filters, SRD-CF)追踪算法.Li等[7]在SRDCF的外观模型中引入时间正则项, 学习前后帧相关滤波之间的联系, 提出基于时空正则化相关滤波(Spatial Temporal Regula-rized Correlation Filters, STRCF)追踪算法.
上述追踪算法主要是针对正训练样本在相关滤波的框架下进行外观优化模型的改进, 例如, 在MOSSE的外观优化模型中引入尺度正则项、空间正则项和时间正则项等.为了消除边界效应和增强背景和前景的区分度, Galoogahi等[8]提取负样本, 提出基于背景感知相关滤波(Background-Aware Corre-lation Filters, BACF)追踪算法.考虑到BACF空间正则项中的权值矩阵是固定的, 而实际应用中视频序列的空间信息是改变的, Dai等[9]在BACF的优化模型中引入时空正则项和自适应权值矩阵, 提出自适应空间正则化相关滤波(Adaptive Spatially-Re-gularized Correlation Filter, ASRCF)追踪算法.值得注意的是, 对于上述追踪算法的外观优化模型, 学者们主要利用交替方向乘子法(Alternating Direction Method of Multipliers, ADMM)[10]进行迭代求解.由于该类求解方法需要对变量进行遍历平均, 会破坏求解的稀疏性, 导致算法的收敛速度不是最优的.Ouyang等[11]在ADMM的基础上提出加速交替方向乘子法(Accelerated ADMM, A-ADMM), 提高算法求解速度的最优性.
本文在BACF的基础上, 结合时空正则化、ASRCF中的自适应权值和A-ADMM, 提出基于加速自适应时空背景感知相关滤波(Background-Aware Spatial Temporal Regularized Correlation Filter, BAST-RCF)的目标追踪算法.不同于ASRCF, 本文算法不仅考虑前后帧相关滤波之间的关系, 同时采用简单的自适应权值正则项, 并利用A-ADMM加快优化模型的求解速度.因此, 本文算法不仅可充分利用背景信息、空间信息、前后帧相关滤波间的关系, 提高算法的追踪性能, 而且通过自适应权值反映追踪过程中目标的外观变化.
考虑到现有的ASRCF未充分利用前后帧相关滤波之间的关系及求解优化模型的速度问题, 本文结合时间正则化和简单的自适应权值矩阵, 提出自适应时空背景感知外观优化模型, 并利用加速交替方向乘子法给出模型的迭代解.
设It为第t帧图像, 目标位置信息已知.为了预测下一帧目标位置, 需要学习第t帧图像的相关滤波ht.在建立外观优化模型进行相关滤波训练之前, 需要采集训练样本.为了减少目标周围的一些背景信息及相似目标的干扰, 本文采用循环位移操作进行训练样本的提取.传统的循环位移方法仅在一个小的图像块上操作, 不能产生足够多的训练样本.为了得到丰富的训练样本, 本文首先在每帧图像上进行循环位移操作, 然后裁取所需的图像块.
设
[
令yi∈ RM×M为相应的目标响应图.为了方便计算, 对
由于ASRCF未充分利用前后帧相关滤波之间的关系, 并且自适应空间权值矩阵需要参考权重wr, 因此本文简化自适应权值矩阵的约束形式, 并在外观优化模型中引入时间正则项, 提出自适应时空背景感知外观模型, 数学公式描述如下:
arg
其中,
y=[y1, y2, …, yK], xk=[
P为对角二进制矩阵, w为自适应权值矩阵, ht-1为根据上一帧学习得到的相关滤波, λ1、λ2、λ3分别为各项对应的正则项参数.
上述模型(1)中, 第1项是使用背景信息的脊回归项, 第2项强调前景信息, 第3项是规避模型退化的空间权值矩阵范数, 最后一项体现目标运动连续的时间正则项.值得注意的是, 模型(1)中的权值矩阵也是自适应的, 但不像ASRCF中需要参考权重wr, 因此较简便.
综上所述, 本文模型不仅可自适应地利用背景信息和前景信息, 而且可充分利用前后帧相关滤波之间的关系, 从而缓解目标快速移动导致的漂移问题.
本节对模型(1)进行求解.一般地, 基于相关滤波的目标追踪算法主要利用ADMM对优化模型进行求解.为了加快追踪速度, 本文采用A-ADMM[11]对外观模型进行求解.
为了便于计算, 首先利用傅里叶变换将式(1)从空间域转换到频域, 转换后形式如下:
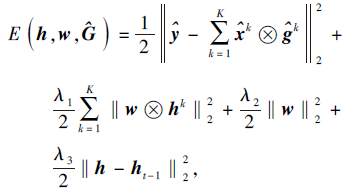
使得
其中,
为辅助变量矩阵, F∈
式(2)中的优化模型是双凸的, 因此可通过最小化获得局部最优解.优化模型(2)的增广拉格朗日函数为
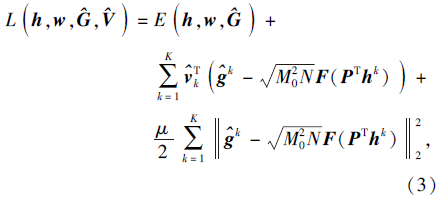
其中,
V=[v1, v2, …, vK]∈
为拉格朗日参数,
为相应的傅里叶变换.
令
uk=
则式(3)可转化为
L(h, w,
其中
对于式(4), 通过运用A-ADMM, 可转换为如下3个子问题:
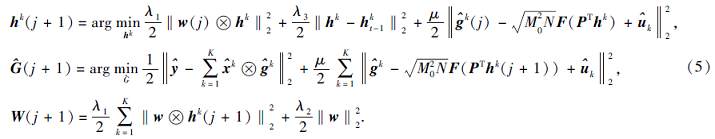
下面给出上述子问题具体解的形式.
求解h.对于第k个通道hk的求解, 由于
hk(j+1)=arg
[λ1W(j)TW(j)+μ
[μ
其中,
W(j)=diag(w(j))∈
为对角化矩阵, I为单位矩阵.式(6)仅需逐个元素
乘法和快速逆傅里叶变换, 因此计算复杂度为O(K
求解
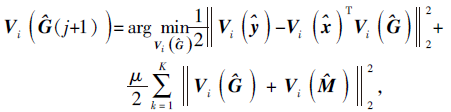
使得
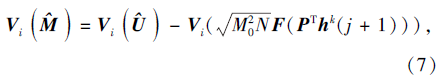
其中Vi(
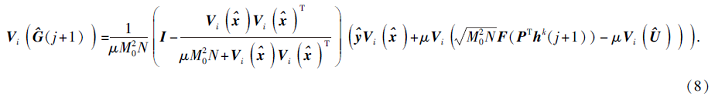
求解w.根据上述子问题得到的解可得到h, 则w的求解可表示为
w(j+1)=arg
再更新拉格朗日参数
其中
μ(j+1)=min{μmax, β μ(j)}.
综上所述, 外观优化模型可通过如下步骤进行迭代求解:利用式(6)更新h、式(7)更新
最后, 在傅里叶域上进行检测:
其中
本文选择在OTB50[12]、OTB100[13]、DTB70[14]、VOT2016[15]、TC128[16]数据集上进行实验.对比方法如下:KCF[4]、SRDCF[6]、STRCF[7]、BACF[8]、ASRC-F[9]、尺度自适应多维特征法(Scale Adaptive Multiple Features, SAMF)[17]、分层卷积特征法(Hierarchical Convolutional Features, HCF)[18]、时间正则背景感知相关滤波法(Temporal Regularized Background-Aware Correlation Filter, TRBACF)[19]、空间可靠性约束时间正则相关滤波法(Spatial Reliable Constraint Temporal Regularized Correlation Filter, SRCTRCF)[20].下文通过对比实验说明本文算法的良好性能.
实验中对本文算法作如下参数设置:尺度个数为5, 尺度步长为1.01, λ1=0.5, λ2=1.5, λ3=0.01, β =10, 学习率η=0.02, A-ADMM循环次数为2.
所有实验都是在配置为Intel Xeon CPU E5-1620 v3 @3.50 GHz的电脑上进行, 编程软件为MatlabR-2015b.
本节通过消融实验说明BASTRCF设计的合理性.表1为BASTRCF在OTB100数据集上的消融实验结果.
| 表1 在OTB100数据集上的消融实验结果 Table 1 Results of ablation experiment on OTB100 dataset % |
在表1中, BACF作为基准, BACF+SR表示在BACF的正则项中添加空间权值, BACF+SR+AW表示在BACF+SR的基础上考虑自适应权值矩阵, BASTRCF表示在BACF+SR+AW的基础上添加时间正则项.由表可看出, 随着外观模型中正则项的增加, 追踪算法的精确值和成功率都有不同程度的上升.这说明外观模型的每项对追踪结果都有一定的改进.特别地, 时间正则项和自适应空间权值对追踪结果的提升具有明显作用.
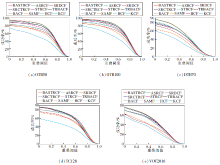
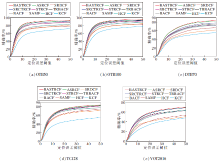
各算法在5个数据集上的成功率和精确度的结果如表2所示.同时, 图1、图2给出各算法在5个数据集上相应的成功率图和精确度图.
| 表2 各算法在5个数据集上的成功率和精确度的对比 Table 2 Comparison of success rate and precision of different algorithms on 5 datasets % |
从表2和图1、图2可知, BASTRCF在5个数据集上的成功率和精确度都达到最优效果.在OTB50数据集上, BASTRCF成功率为67.0%, 比第二名ASRCF提高0.4%, 比第三名SRCTRCF提高3.2%.同时, 在精确度方面, BASTRCF达到82.4%, 依然保持领先地位, 比第二名ASRCF提高1.3%, 比第三名SRCTRCF提高3.1%.
造成上述结果的主要原因是BASTRCF的时间正则项和自适应权重项可自适应地利用空间信息、背景信息和前后帧相关滤波的信息, 提高追踪算法的性能.
本节对比各算法在背景干扰、快速运动、目标遮挡上的追踪性能.
BASTRCF、ASRCF、STRCF、BACF在OTB50数据集中具有背景干扰属性的2个视频序列上的追踪结果如图3所示.由图可看出, 在英式足球视频序列中, 很多场景出现相似背景干扰的情况(如第309帧、第325帧、第350帧).两位足球运动员身穿相似的运动服、头戴相似的头盔, 这些干扰容易导致追踪目标发生漂移.但是, BASTRCF(红色框)可准确定位目标, 而其它3种追踪算法都发生漂移.针对足球比赛获奖视频序列, 背景对追踪目标干扰非常严重(如第93帧、第123帧、135帧), 容易导致追踪目标发生漂移.ASRCF(绿色框)和BACF(黑色框)都未准确追踪到目标, STRCF(蓝色框)在后面两帧中也发生漂移.但是, BASTRCF(红色框)仍可准确追踪目标.
 | 图3 各算法在OTB50数据集视频序列上的追踪结果对比Fig.3 Tracking result comparison of different algorithms on video sequences of OTB50 dataset |
BASTRCF、ASRCF、STRCF、BACF在OTB100数据集中具有快速运动属性的2个视频序列上的追踪结果如图4所示.
 | 图4 各算法在OTB100数据集视频序列上的追踪结果对比Fig.4 Tracking result comparison of different algorithms on video sequences of OTB100 dataset |
由图4可看出, 在对打的场景中, 两个人动作移动十分迅速(如第17帧、第22帧、第44帧), 因此目标的快速移动容易引起追踪器发生漂移, 导致追踪精确度降低.但是, BASTRCF(红色框)可准确定位目标, 而其它3种追踪算法都发生漂移.在羚羊运动的视频中, 羚羊运动十分迅速(如第27帧、第35帧、第52帧), 容易导致追踪目标漂移.但是, BASTRCF(红色框)一直准确定位目标, 而其它算法一开始就发生漂移.
BASTRCF、ASRCF、STRCF、BACF在DTB70数据集中具有目标遮挡属性的2个视频序列上的追踪结果如图5所示.
 | 图5 各算法在DTB70数据集视频序列上的追踪结果对比Fig.5 Tracking result comparison of different algorithms on video sequences of DTB70 dataset |
由图5可看出, 在飞鸟视频序列中, 小鸟飞进云朵里出现遮挡(如第63帧、102帧、第126帧), 会严重影响追踪算法的精确性.然而, BAST-RCF依然可准确定位目标, 其它算法都发生漂移.在瓶子视频序列中, 第782帧、867帧、第1 219帧出现瓶子被遮挡的情况, 严重干扰追踪算法的性能, 导致追踪算法转而追踪其它小瓶子.但是, BASTRCF(红色框)和ASRCF(绿色框)能准确定位目标, 而其它算法发生漂移.
BASTRCF、ASRCF、STRCF、BACF在TC128数据集中具有目标遮挡和快速运动属性的2个视频序列上的追踪结果如图6所示.由图可看出, 对于篮球视频序列, 穿绿色球服的运动员在防守穿白色球服的运动员时产生遮挡(见第10帧), 容易导致追踪目标发生漂移.然而, BASTRCF依然可准确定位目标, 其它算法都发生漂移.对于足球视频序列, 第10帧中足球发生快速移动, 严重影响追踪算法的追踪性能.然而, BASTRCF(红色框)仍能准确定位追踪目标, 其它算法都发生漂移.
 | 图6 各算法在TC128数据集视频序列上的追踪结果对比Fig.6 Tracking result comparison of different algorithms on video sequences of TC128 dataset |
BASTRCF、ASRCF、STRCF、BACF在VOT2016数据集中具有目标遮挡和快速运动属性的2个视频序列上的追踪结果如图7所示.由图可看出, 对于袋子视频序列, 白色袋子在没有规律地上下飘动, 这将影响追踪算法的追踪精度.BASTRCF仍可准确定位目标, 而其它算法都出现偏差.对于袋鼠视频序列, 第131帧中出现袋鼠被黑猫遮挡的情况, 严重影响算法的追踪性能, 导致追踪结果出现偏差.由图可看出, BASTRCF(红色框)和STRCF(蓝色框)都能准确定位目标, 而其它算法都发生漂移.
各算法在DTB70数据集上的追踪速度对比如下:KCF为171帧/秒, SAMF为22帧/秒, SRDCF为5帧/秒, BACF为35.3帧/秒, HCF为11.0帧/秒, STRCF为5.3帧/秒, TRBACF为27.6帧/秒, SRCTRCF为3.7帧/秒, ASRCF为28帧/秒, 本文算法(ADMM)为27帧/秒, 本文算法(A-ADMM)为30帧/秒.其中, 本文算法(ADMM)表示本文的自适应背景感知外观优化模型, 用ADMM求解优化模型.本文算法(A-ADMM)表示自适应背景感知外观优化模型, 用A-ADMM求解优化模型.
由于KCF结构简单, 因此追踪速度最快.BACF排名第二, 本文算法(A-ADMM)排名第三, 可达到30帧/秒, 快于ASRCF和本文算法(ADMM).这说明使用A-ADMM确实可提高追踪速度.
本文在背景感知追踪算法的基础上, 提出基于加速自适应时空背景感知相关滤波的目标追踪算法.在背景感知追踪算法的基础上, 融合空间信息和时间信息, 考虑空间权值矩阵的自适应性, 提出自适应时空背景感知外观优化模型, 运用加速交替方向乘子法求解空间权值矩阵和滤波器, 实现目标自适应追踪.不同于ASRCF, 本文算法不仅考虑前后帧相关滤波之间的关系, 同时使用更简单的自适应权值正则项, 并利用A-ADMM代替ADMM加速优化模型的求解.因此, 本文算法不仅可充分利用背景信息、空间信息、前后帧相关滤波间的关系, 提高追踪算法的性能, 而且通过自适应权值反映追踪过程中目标的外观变化.实验表明本文算法具有较好的追踪性能.未来可在此基础上, 考虑将相关滤波与深度学习结合, 利用深度网络提取不同层次的样本特征, 训练相关滤波器, 从而提高追踪器的追踪性能.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|
| [19] |
|
| [20] |
|