引用本文
张琳, 叶海良, 杨冰, 曹飞龙. 基于截断核范数的图像去噪展开网络. 模式识别与人工智能, 2022,35(10): 881-892
ZHANG Lin, YE Hailiang, YANG Bing, CAO Feilong. Truncated Nuclear Norm Based Unfolding Network for Image Denoising. PATTERN RECOGNITION AND ARTIFICIAL INTELLIGENCE, 2022,35(10): 881-892.  
Doi: 10.16451/j.cnki.issn1003-6059.202210002
Permissions
Copyright©2022, 《模式识别与人工智能》编辑部
《模式识别与人工智能》编辑部
基于截断核范数的图像去噪展开网络
张琳1, 叶海良1, 杨冰1, 曹飞龙1
1.中国计量大学 理学院 杭州 310018
通讯作者：

曹飞龙,博士,教授,主要研究方向为深度学习、图像处理等.E-mail:feilongcao@gmail.com.

作者简介:

张 琳,硕士研究生,主要研究方向为深度学习、图像处理等.E-mail:zhanglin2354@163.com.

叶海良,博士,讲师,主要研究方向为深度学习、图像处理.E-mail:yhl575@163.com.

杨 冰,博士,讲师,主要研究方向为深度学习、图像处理.E-mail:bingyang0517@163.com.

收稿日期: 2022-07-20 接受日期: 2022-10-08
资助项目: 国家自然科学基金项目(No.62176244, 62006215)、浙江省属高校基本科研业务费专项资金(No.2022YW65)资助
摘要

基于模型驱动的图像去噪通常需要先构造先验正则项,在求解优化模型时计算成本较高.基于数据驱动的方法得益于神经网络灵活的架构和强大的学习能力,具有较优越的性能和较高的效率,但往往缺乏足够的可解释性.为此,文中提出基于截断核范数的图像去噪展开网络,结合低秩矩阵恢复中基于截断核范数的模型驱动方法和图像去噪,并将每次迭代看作展开网络的一个阶段,把每个阶段进行连接,形成一个端到端的可训练展开网络.在上述每个阶段中,借助神经网络学习奇异值算子,解决奇异值分解在传统迭代算法中计算代价较高的问题.在多组去噪数据集上的实验验证文中网络的有效性.

关键词: 图像去噪; 深度学习; 截断核范数(TNN); 矩阵恢复
中图分类号:TP 391
Truncated Nuclear Norm Based Unfolding Network for Image Denoising
ZHANG Lin1, YE Hailiang1, YANG Bing1, CAO Feilong1
1. College of Sciences, China Jiliang University, Hangzhou 310018
Corresponding author：
CAO Feilong, Ph.D., professor. His research interests include deep learning and image processing.

About Author:
ZHANG Lin, master student. Her research interests include deep learning and image processing.
YE Hailiang, Ph.D., lecturer. His research interests include deep learning and image processing.
YANG Bing, Ph.D., lecturer. His research interests include deep learning and image processing.

Fund:National Natural Science Foundation of China(No.62176244,62006215), Fundamental Research Funds for the Provincial Universities of Zhejiang(No.2022YW65)
Abstract

In model-driven image denoising, prior regularization terms are required to be constructed in advance, resulting in high computational cost of dealing with optimization models. Data-driven methods possess superior performance and high efficiency due to the flexible architecture and powerful learning capability of neural networks, but their interpretability is insufficient. Therefore, truncated nuclear norm based unfolding network for image denoising is proposed and combined with the model-driven method based on truncated nuclear norm and image denoising in low-rank matrix recovery. Each iteration is regarded as a stage of the unfolding network. Singular value operators are learned with the help of neural networks to solve the problem of expensive computation of singular value decomposition in traditional iterative algorithms. Each of the stages is connected to form an end-to-end trainable unfolding network. The effectiveness of the proposed network is verified by the experiments on multiple datasets of image denoising.

Key words: Image Denoising; Deep Learning; Truncated Nuclear Norm(TNN); Matrix Recovery

图像去噪是计算机视觉领域的一个基本问题, 其目的是将含有噪声的数字图像恢复成干净图像.人们在采集、数字化和传输图像的过程中, 不可避免地受到成像设备和外部环境噪声干扰等影响, 从而降低图像的视觉效果, 导致获取的信息不准确甚至错误.因为图像去噪可从观测值中分离噪声并保留干净图像, 所以受到学者们的广泛关注, 如医学图像[1]、图像压缩[2]、视频去噪[3]、图像分割[4]、目标检测[5]、卫星成像[6]、遥感图像[7]等.

近年来, 学者们主要使用基于模型驱动的方法进行图像去噪[8, 9].由于传统的迭代算法都是根据反映任务本质的数学原理设计的, 因此具有高度的可解释性, 但基于模型驱动的方法也存在较明显的弊端.除了需要人为设置参数以获得最优结果之外, 较简单的优化方法往往降噪效果不佳.

之后, 学者们提出越来越多的基于数据驱动的图像去噪模型, 并逐渐成为图像去噪的主流方法, 尤其是卷积神经网络(Convolutional Neural Network, CNN).但是, CNN结构复杂多样, 并且依赖大量的训练数据, 因此, 常作为黑箱使用.例如, Zhang等[10]提出DnCNNs(Denoising Convolutional Neural Networks), 在分别处理图像去噪任务和单幅图像超分辨率任务时, 很难通过网络参数分析网络的运行机制及清楚观察它分别学到什么知识.因此神经网络的弊端在于底层结构的可解释性较弱.

算法展开方法可避免神经网络方法缺乏可解释性这一严重制约, 结合传统迭代算法和神经网络的优势, 同时避免各自的缺陷.具体地说, 网络在执行有限次循环过程中, 通过反向传播更新参数, 代替传统算法中难以明确设计的复杂映射, 而算法展开方法使网络模块和算法操作符之间具有精准的一一对应关系, 因此可继承传统迭代算法的可解释性.

表征自然图像的数据矩阵通常是低秩或近似低秩的, 可在几乎不损失原有信息的基础上, 只使用其中几个重要的特征表示图像, 如可使用奇异值分解(Singular Value Decomposition, SVD)达到压缩原图像的目的.因此, 利用SVD将图像去噪问题转化成低秩矩阵逼近问题是合理的, 这却是一个NP难问题[11].针对这一问题, Candè s等[12]提出使用矩阵的核范数作为秩函数的凸近似, 但核范数并不是秩函数最好的逼近.因为核范数对所有奇异值求和, 在最小化过程中, 所有的奇异值都会同时被最小化.针对这一问题, Hu等[13]提出截断核范数(Truncated Nu-clear Norm, TNN), 但在求TNN过程中SVD计算代价太高, 很难在现实生活中被真正实施运用.

因此, 本文考虑结合基于数据驱动的方法和基于模型驱动的方法, 相当于在网络中给噪声添加一个具有约束性的先验信息, 网络在该先验信息的指导下, 不仅具备较强的可解释性, 而且还在性能上体现较强的竞争力.由此提出基于截断核范数的图像去噪展开网络(TNN Based Unfolding Network for Image Denoising, TNNUNet).结合基于TNN的低秩稀疏矩阵恢复方法与图像去噪, 使用加性高斯白噪声(Additive White Gaussian Noise, AWGN)[14]拟合待消除的噪声.从训练数据集中学习奇异值矩阵, 避免SVD操作计算量过大的问题.将TNNUNet用于图像去噪任务, 实验表明, TNNUNet性能较优.

1 相关工作
1.1 基于截断核范数的图像去噪

近年来, 矩阵低秩稀疏分解(Low Rank and Spar- se Decomposition, LRSD)问题在许多领域都备受关注, 如:多视图聚类[15]、深度压缩[16]、图像分类[17]、高光谱异常检测[18]等.

对于给定的观测值X, 它对应的数据矩阵通常是低秩或近似低秩的.当加入具有稀疏性的噪声N后, 会破坏原数据矩阵的低秩性.Wright等[19]将该问题描述为

minC, Nrank(C)+λ ‖ N‖ 0, s.t. X=C+N.(1)

但由于秩函数和l0范数的不连续性和非凸性, 式(1)是一个NP难问题, 可使用核范数近似秩函数[20, 21].

同样地, 具有稀疏性的l1或l2, 1范数可作为l0范数的凸近似.于是式(1)可改写为

minC, N‖ C‖ * +λ ‖ N‖ p, s.t. X=C+N, (2)

其中‖ · ‖ * 为矩阵的核范数, 可选择l1或l2, 1范数, 分别被定义为

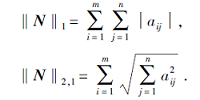
尽管使用核范数代替秩函数可将式(1)转化为凸函数, 但核范数也并不是秩函数最好的逼近.这是因为秩函数的值只与非零奇异值的个数有关, 而核范数是对矩阵的非零奇异值求和, 它的值与非零奇异值的大小有关, 而与非零奇异值的个数无关.因此, 核范数在最小化过程中, 所有奇异值无差异地一起被最小化.

为了解决这一问题, Gu等[22]提出WNNM (Wei- ghted Nuclear Norm Minimization), 通过对不同奇异值赋予不同的权重以区别对待奇异值的贡献, 但WNNM通常是非凸的.Hu等[13]提出TNN, 因为奇异值在奇异值矩阵中是从大到小排列的, 而且减少得特别快, 那么任意一个矩阵都可用前r个最大的奇异值近似描述.因此在最小化过程中, 只需要最小化最后min(m, n)-r个奇异值.于是式(2)可改写为

minC, N‖ C‖ r, * +λ ‖ N‖ p, s.t. X=C+N.(3)

通常使用核范数减去几个最大奇异值之和表示TNN.同时, 式(3)中的lp范数简单地选择l1范数.于是式(3)可转化为

minC, N(‖ C‖ * - ∑i=1rβ i(C)+λ ‖ N‖ 1), s.t. X=C+N.(4)

为了求解式(4), 对C进行SVD分解, 可得

U=(u1, u2, …, um)∈ Rm× m, V=(v1, v2, …, vn)∈ Rn× n,

截断至前r项, 得

A= (u1, u2, …, ur)T∈ Rr× m, B= (v1, v2, …, vr)TRr× n,

其中A和B分别满足AAT=Ir× r和BBT=Ir× r.根据Ye等[23]的工作, 有

maxAAT=Ir×rBBT=Ir×rtr(ACBT)= ∑i=1rβ i(C),

于是式(4)等价于

minC, N(‖ C‖ * - maxA, Btr(ACBT)+λ ‖ N‖ 1), s.t. X=C+N, AAT=Ir× r, BBT=Ir× r.(5)

在式(5)的基础上, Cao等[24]提出LRSD-TNN(Low-Rank and Sparse Decomposition Based on the TNN), 并应用于背景分离及去除面部图像阴影特征.这是因为将图像去噪问题转化成低秩矩阵逼近问题具有合理性, 并且容易展开到网络.

1.2 基于数据驱动的图像去噪

得益于灵活多变的网络结构和强大的学习能力, 神经网络成为图像去噪的主流方法.Zhang等[10]提出DnCNNs, 使用17层卷积堆叠的网络预测噪声, 强调残差学习和批归一化(Batch Normalization, BN)[25]相辅相成的作用.之后, Zhang等[26]提出FFDNet(Fast and Flexible Denoising CNN), 在原深层CNN的基础上添加全图的噪声水平估计, 更适用于真实场景的降噪.Tian等[27]提出DudeNet(Dual Denoising Network), 其中一支子网络将DnCNNs中的一部分普通卷积替换成空洞卷积, 称为“ 稀疏机制” , DudeNet融合两个子网络提取的特征, 达到特征增强的目的.

这种基于空洞卷积的稀疏机制可在网络深度与宽度之间进行权衡, 在减少网络复杂度的同时, 达到提升去噪性能的目的.Tian等[28]提出BRDNet(Batch-Renormalization Denoising Network), 在Dude-Net的基础上, 改变稀疏机制的内部结构, 即改变空洞卷积与普通卷积的个数和排列顺序, 并将两个子网络都更改为残差结构的形式.Tian等[29]提出ADNet(Attention-Guided Denoising CNN), 结合稀疏机制和注意力机制, 精细提取隐藏在背景中的噪声信息.

根据上述描述可看出, 在CNN中融入空洞卷积可在提升网络性能的同时保证效率.

1.3 基于算法展开的图像去噪

算法展开是避免神经网络黑盒性质的一种方法, 可通过算法展开生成可解释性网络.Zhang等[30]提出USRNet(Deep Unfolding Super-Resolution Net-work), 使用3个子网络分别作为数据模块、先验模块和超参模块, 代替算法中计算代价大和难以明确设计的映射.Wang等[31]提出RCDNet(Rain Con-volutional Dictionary Network), 使用网络代替算法中的两个近端算子.Zhang等[32]提出AMP-Net, 将AMP(Approximate Message Passing)的迭代去噪过程展开成多层网络.Zheng等[33]提出DCDicL(Deep Convolutional Dictionary Learning), 通过4个子网络分别完成初始化、学习系数先验知识、学习字典先验知识和预测超参的任务, 克服传统算法人为设置先验知识的缺点.

算法展开方法在深度神经网络方法和迭代算法之间建立具体而系统的联系, 可有效克服神经网络缺乏可解释性的缺点.

2 基于截断核范数的图像去噪展开网络

本文采用深度展开网络进行图像去噪, 该任务应满足如下两点.

1)将基于TNN的图像去噪算法作为神经网络的原则性框架.由于每个步骤都具有传统算法的逻辑性, 算法展开继承传统迭代算法的可解释性.

2)神经网络作为一个万能逼近器, 可代替算法中的复杂映射.

本文结合传统迭代算法和神经网络的优势, 提出基于截断核范数的图像去噪展开网络.

2.1 基于模型驱动的TNN图像去噪算法

利用图像数据矩阵的低秩性进行图像去噪, 是将待恢复的图像看作由退化前的数据和误差组成, 其中干净图像可通过低秩矩阵逼近, 噪声具有稀疏性, 相应的模型为式(5).求解这类在约束条件下的极值问题, 通常做法是将其转化为拉格朗日函数的极值问题.因此, 将式(5)改写为增广拉格朗日函数的形式:

L(C, N, Y, μ )= ‖ C‖ * -tr(ACBT)+λ ‖ N‖ 1+ < Y, X-C-N> +‖ μ2-C-N‖ , 12(6)

其中, Y表示拉格朗日乘子,

< Y, X-C-N> =tr(YT(X-C-N)),

表示矩阵的内积, μ > 0, 表示正则化系数.

此时, 有约束条件的优化问题已转化为无约束优化问题.于是, 采用交替方向乘子法(Alternating Direction Method of Multiplier, ADMM)将联合优化改成单独交替迭代的形式:

Cs+1=arg minCL(C, Ns, Ys, μ s), Ns+1=arg minEL(Cs+1, N, Ys, μ s), Ys+1=Ys+μ s(X-Cs+1-Ns+1), μ s+1=min(ρ μ s, μ max),

其中, ρ > 1, 为常数.

在求解式(6)中N时, 为了添加AWGN, 使用N的F范数‖ N‖ F代替式(6)中的l1范数‖ N‖ 1, 于是, 可通过求导得到N的解.根据文献[24], 可得到最后的解为

Ys+1=Ys+μ s(X-Cs+1-Ns+1),

μ s+1=min(ρ μ s, μ max),

其中求解矩阵C时采用奇异值阈值算法(Singular Value Thresholding Algorithm, SVT), 被定义为

SVTμ (Q)=U diag[max(σ -μ , 0)]VT,

U∈ Rm× r, V∈ Rr× n, σ ∈ Rr× 1是由任意给定的矩阵Q∈ Rm× n进行SVD得到的, 即

Q=U diag(σ )VT.

由于SVD和SVT的计算代价过高, 因此本文使用神经网络代替这两个操作, 可减少模型的计算量, 提升效率.

2.2 模型驱动的嵌入网络

确定展开算法之后, 关键的问题就是如何设计网络取代SVD和SVT这两个步骤.基于算法展开的思想, 首先将上述算法的每个迭代步骤展开为相应的网络模块, 使用网络代替SVD和SVT操作, 其它运算使用网络中常用的运算符执行.执行网络的一个阶段相当于传统算法的一次迭代, 连接这些阶段, 形成一个深层神经网络.

本文使用两个结构和参数设置相同的网络A-net和B-net代替SVD操作, 网络输出为代替奇异值矩阵的特征, 分别取其前r个向量, 得到

A=(u1, u2, …, ur)T∈ Rr× m, B=(v1, v2, …, vr)T∈ Rr× n,

再使用一个去噪网络SVT-net代替SVT操作, 更新干净图像.其它操作按照网络中常用的运算符表示.

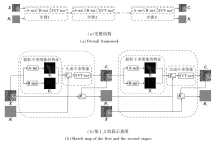
TNNUNet整体设计如图1(a)所示, 共有S个阶段, 将观测图像X和噪声N作为输入, 输出学习得到的干净图像C和噪声N.从第2个阶段开始, 每个阶段都以上一阶段的输出作为输入, 直到遍历所有的阶段.图1(b)为TNNUNet第1、2阶段的网络架构示意图.

图1 TNNUNet框架图Fig.1 Architecture of TNNUNet

本文简单使用五层卷积堆叠的A-net和B-net代替SVD操作, 分别生成代替输入矩阵的左奇异值矩阵和右奇异值矩阵的特征.具体地说, 从第一层到第五层卷积的通道数都设置为64, 采用3× 3的卷积核.在输入层和中间层有整流线性单元(Rectified Linear Units, ReLU)[34]激活函数, 最后一个卷积层后未设置激活函数.并且除了第一层和最后一层, 每层都与BN结合.这两个网络层数的选取将在实验部分进行讨论.

SVT-net的网络结构如图2所示, 它的作用是代替SVT操作, 每一阶段生成干净图像都是在这一步完成的.因为算法展开将所有阶段连接并形成一个深层神经网络, 所以, 采用文献[35]的深度残差网络形式, 避免网络层数较多引起的退化现象.

图2 SVT-net网络结构示意图Fig.2 Sketch map of SVT-net network structure

SVT-net由如下3部分组成.

1)由普通卷积(Conv)和空洞卷积(Dilated Conv)对称排列的稀疏模块, 用于初步提取输入图像的特征;

2)融合初步提取的特征和输入图像特征的特征融合模块, 当网络层数增加时, 强调浅层网络对深层网络的影响;

3)重构模块, 从原始观测图像中去除网络预测的噪声, 重构需要的干净图像.

2.3 网络步骤

本文的损失函数由两部分组成:学习的奇异值矩阵的正交损失和生成的干净图像与真实值的均方误差损失(Mean-Square Error, MSE):

L= ∑s=1Sλ s‖ Cs-C‖ F2+ ∑s=1Ss(‖ ATss-I‖ F2‖ BTss-I‖ F2,

其中, S表示展开网络的阶段数, λ s表示MSE惩罚参数, γ s表示正交损失的惩罚参数.

最终TNNUNet步骤如算法1所示.

算法1 TNNUNet

输入 X, λ , μ 0, μ max, ρ

输出 A, B, C

初始化 C0, N0, Y0;

S表示展开网络的阶段数;

For s=0:S do

给定干净图像Cs, 通过网络计算左奇异值矩阵U和右奇异值矩阵V:

Us+1=A-net(Cs), Vs+1=B-net(Cs).

截断至前r项, 得到As+1, Bs+1.

通过网络计算干净图像Cs+1.

由已知变量计算噪声Ns+1.

更新拉格朗日乘子Ys+1.

更新参数μ s+1.

end for

3 实验及结果分析
3.1 实验数据集

本节中, 本文使用Berkeley Segmentation Dataset(BSD)[36]中的400幅180× 180的图像合成AWGN图像.在这400幅图像上进行如下三步操作以达到数据增强的目的.

1)分别采用尺度因子1、0.9、0.8、0.7对每幅图像进行缩放, 得到4种尺寸的图像.

2)以滑窗的形式, 以步长为10, 将这4种尺寸的图像裁剪成40× 40的小块, 达到扩大数据集的目的.

3)将得到的小块进行镜像和翻转的操作:剪裁后的原图像上下翻转; 剪裁后的原图像逆时针旋转90° , 然后上下翻转; 剪裁后的原图像逆时针旋转90° 两次, 然后上下翻转; 剪裁后的原图像逆时针旋转90° 三次, 然后上下翻转.旋转和翻转操作后每次生成的新图像都放入训练集, 达到增加训练集多样性的目的.最后添加AWGN, 得到合成噪声训练集.

在BSD68[37]、Set12[38]数据集上评估TNNUNet.BSD68数据集包含68幅尺寸为321× 481或481× 321的图像.Set12数据集包含12幅尺寸为256× 256的图像.这两个数据集都广泛用于评估不同场景灰度图像的去噪性能, 不用于训练.

3.2 参数讨论

TNNUNet每个阶段的深度是23层.根据经验设置初始化参数如下:初始学习率为10-3, 学习率下降回合间隔数为20, 学习率调整倍数为0.2, 批量大小为128, 训练模型的迭代次数为180, 正则化参数λ =0.01, 惩罚参数μ =100, 并设置μ 的上限为200, 常数ρ =1.1; 对于X∈ Rm× n, 设置

秩r=0.1min(m, n).

本文将图像裁剪成小块, 不仅可增加训练集数量, 还可减少计算量, 加快运算速度.小块的大小是根据网络的感受野大小设计的, 考虑的主要因素是在卷积过程中接收域的变化.

本文网络涉及如下3种卷积.

1)卷积核为3× 3的普通卷积, 具体地, 对于深度为d的网络, 对应的感受野为(2d+1)× (2d+1).

2)卷积核为1× 1的普通卷积, 不会改变接收域的大小.

3)卷积核为3× 3的空洞卷积, 膨胀因子为2, 可从更广阔的领域接收更多的信息.具体地, 对于深度为d的网络, 接受域大小为(4d+1)× (4d+1).

A-net和B-net的感受野都是11× 11, SVT-net的感受野大小为41× 41, 为了简单起见, 小块的大小选择40× 40.

本节所有的对比实验都在Set12数据集上进行测试, 噪声水平σ =25.使用峰值信噪比(Peak Signal-to-Noise Ratio, PSNR)和结构相似度(Struc-ture Similarity Index Measure, SSIM)作为评价去噪性能的指标.

PSNR定义为

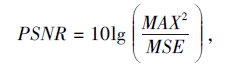
其中, MAX表示图像可能的最大像素值, MSE表示真实干净图像和预测值之间的均方误差.一般来说, PSNR越大, 表示图像质量越好.

SSIM定义为

SSIM= (2μxμy+C1)(2σx, y+C2)μx2+μy2+C1,

其中, μ x、 μ y分别表示x和y的均值, μx2和 μy2分别表示x和y的方差, σ x, y表示x和y的协方差, C1、C2为常数, C1的作用是防止分母等于0.SSIM取值范围是[0, 1], 值越大, 表示图像失真越小.

首先对比A-net和B-net在设置不同层数时的去噪效果, 结果如表1所示, 表中黑体数字表示最优值.由表可见, 仅用5层卷积堆叠就可较好代替SVD操作, 表现出良好的去噪效果.

表1 A-net和B-net在不同层数下的去噪效果 Table1 Denoising results of A-net and B-net with different layers

传统算法的每次迭代相当于运行网络的一个阶段.传统算法需要设计大量迭代, 而算法展开得益于神经网络端到端的学习, 仅需很少量的阶段数即可获得和传统算法相当甚至更优的结果.

下面对比不同阶段数下TNNUNet的去噪效果, 确定最优的阶段数, 结果如表2所示, 表中黑体数字表示最优值.由表可见, 当阶段数为3时达到最优去噪效果.

表2 TNNUNet在不同阶段数下的去噪效果对比 Table 2 Comparison of denoising results of TNNUNet at different stages

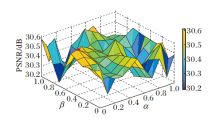
最后对比在不同损失函数系数下TNNUNet的去噪效果, 确定最优损失函数系数, 结果讲图3所示.

图3 损失函数系数不同时TNNUNet的去噪效果Fig.3 Denoising result of TNNUNet with different loss function coefficients

图3中α 表示在第1阶段至第S-1阶段的正交损失函数和生成干净图像的MSE系数, β 表示在最后一个阶段的正交损失函数系数, 在最后一个阶段的生成干净图像的均方误差系数为1.

图3中标注的圆点为对比实验中的最优结果:

α =0.1, β =0.5, PSNR=30.61 dB.

3.3 对比实验结果

本文选择如下对比算法:BM3D(Block Ma-tching and 3D Filtering)[9]、DnCNNs[11]、WNNM[22]、FFDNet[26]、DudeNet[27]、BRDNet[28]、ADNet[29]、EPLL(Expected Patch Log Likelihood)[39]、MLP(Multi-layer Perceptron)[40]、CSF(Inter-leaved Cascade of Shrinkage Fields)[41]、TNRD(Trainable Nonlinear Reaction Diffusion)[42]、文献[43]算法.

一个好的去噪器需要在SSIM和运行时间上都取得良好结果, 同时可视化结果也是判断去噪效果的一个重要因素.因此, 本文使用PSNR和运行时间作为评价去噪性能的指标.

各方法在BSD68数据集上去噪后的平均PSNR对比如表3所示, 表中黑体数字表示最优值, 斜体数字表示次优值.由表可看出, TNNUNet在不同的噪声水平下都取得最优值.

表3 各方法在BSD68数据集上的平均PSNR对比 Table 3 Average PSNR comparison of different methods on BSD68 dataset B

为了方便直观对比各方法的去噪效果, 选取干净图像、噪声图像和通过不同方法恢复的干净图像的同个区域进行放大, 可视化结果如图4所示.

图4 各方法在BSD68数据集上的去噪效果(σ =50)Fig.4 Denoising results of different methods on BSD68 dataset with σ =50

各方法在Set12数据集上的去噪结果如表4~表6所示, 表中黑体数字表示最优值, 斜体数字表示次优值.由表可看出, TNNUNet在不同的噪声水平下的降噪效果最优.

表4 σ =15时各方法在Set12数据集上的平均PSNR对比 Table 4 Average PSNR comparison of different methods with σ =15 on Set12 dataset dB
表5 σ =25时各方法在Set12数据集上的平均PSNR对比 Table 5 Average PSNR comparison of different methods with σ =25 on Set12 dataset dB
表6 σ =50时各方法在Set12数据集上的平均PSNR对比 Table 6 Average PSNR comparison of different methods with σ =50 on Set12 dataset dB

图5为相应的可视化结果.

图5 各方法在Set12数据集上的去噪效果(σ =25)Fig.5 Denoising results of different methods for one image from Set12 dataset with σ =25

BM3D、WNNM、EPLL、MLP、TNRD、CSF、DnCNN、TNNUNet在不同尺寸(256× 256、512× 512和1 024× 1 024)图像上的测试时间对比如表7所示, 表中黑体数字表示最优值, 斜体数字表示次优值.由表可见, 相比传统迭代算法, 深度学习为算法展开提供理想的计算优势.相比神经网络去噪方法, 虽然TNNUNet在运行时间上取得次优的结果, 但也具有竞争力, 精度已超越与之对比的方法.

表7 各方法在不同尺寸噪声图像上的测试时间 Table 7 Running time of different methods for denoising images of different sizes s
3.4 消融实验结果

本文结合深度学习强大的特征提取能力和传统迭代算法的高度可解释性, 构造TNNUNet.为了验证TNNUNet的优势, 在Set12数据集上分别验证如下3种方法的去噪效果.

1)基于模型驱动的SVT-Net;

2)基于数据驱动的LRSD-TNN[24];

3)基于算法展开的TNNUNet.噪声水平σ =25.

3种方法的去噪效果如表8所示, 表中黑体数字表示最优值.由表可看出, 算法展开的去噪效果优于纯模型驱动和纯数据驱动的效果.

表8 各方法的去噪效果对比 Table 8 Denoising result comparison of different methods
4 结束语

针对计算机视觉领域中经典的图像去噪问题, 本文设计基于截断核范数的图像去噪展开网络(TNNUNet).网络结合神经网络与传统迭代算法的优势, 将基于模型驱动的去噪方法作为网络的原则性框架, 提供可解释性.同时, 使用网络代替算法中难以明确设计的映射, 在减少计算量的同时提高去噪效果.遍历网络的所有阶段, 相当于执行有限次迭代算法, 将这些阶段连接后形成一个深层神经网络.实验表明, 相比其它图像去噪方法, TNNUNet具有明显的性能优势.今后可考虑从网络复杂度和运行时间等方面进行改进.

本文责任编委 桑农

Recommended by Associate Editor SANG Nong

参考文献
[1] SAGHEER S V M, GEORGE S N. A Review on Medical Image Denoising Algorithms. Biomedical Signal Processing and Control, 2020. DOI: DOI:10.1016/j.bspc.2020.102036. [本文引用:1]
[2] MINNEN D, JANUSZEWSKI M, SHAPSON-COE A, et al. Denoi-sing-Based Image Compression for Connectomics[C/OL]. [2022-06-25]. https://www.biorxiv.org/content/10.1101/2021.05.29.445828v2.full.pdf. [本文引用:1]
[3] CHEN H A, JIN Y, XU K, et al. Multiframe-to-Multiframe Network for Video Denoising. IEEE Transactions on Multimedia, 2021, 24: 2164-2178. [本文引用:1]
[4] CHEN C, LIU Q D, JIN Y M, et al. Source-Free Domain Adaptive Fundus Image Segmentation with Denoised Pseudo-Labeling // Proc of the International Conference on Medical Image Computing and Computer-Assisted Intervention. Berlin, Germany: Springer, 2021: 225-235. [本文引用:1]
[5] YANG X, YAN J C, LIAO W L, et al. SCRDet++: Detecting Small, Cluttered and Rotated Objects via Instance-Level Feature Denoising and Rotation Loss Smoothing. IEEE Transactions on Pa-ttern Analysis and Machine Intelligence, 2022. DOI: DOI:10.1109/TPAMI.2022.3166956. [本文引用:1]
[6] DE OLIVEIRA V A, CHABERT M, OBERLIN T, et al. Satellite Image Compression and Denoising with Neural Networks. IEEE Geoscience and Remote Sensing Letters, 2022, 19. DOI: DOI:10.1109/LGRS.2022.3145992. [本文引用:1]
[7] FENG X B, ZHANG W X, SU X Q, et al. Optical Remote Sensing Image Denoising and Super-Resolution Reconstructing Using Optimized Generative Network in Wavelet Transform Domain. Remote Sensing, 2021, 13(9). DOI: DOI:10.3390/rs13091858. [本文引用:1]
[8] WEN Y, GUO Z C, YAO W J, et al. Hybrid BM3D and PDE Fil-tering for Non-parametric Single Image Denoising. Signal Processing, 2021, 184. DOI: DOI:10.1016/j.sigpro.2021.108049. [本文引用:1]
[9] DABOV K, FOI A, KATKOVNIK V, et al. Image Denoising by Sparse 3-D Transform-Domain Collaborative Filtering. IEEE Transactions on Image Processing, 2007, 16(8): 2080-2095. [本文引用:2]
[10] ZHANG K, ZUO W M, CHEN Y J, et al. Beyond a Gaussian Denoiser: Residual Learning of Deep CNN for Image Denoising. IEEE Transactions on Image Processing, 2017, 26(7): 3142-3155. [本文引用:2]
[11] KIM M, PARK J, KIM J. Learning Collaborative Policies to Solve NP-Hard Routing Problems // Proc of the 35th International Conference on Neural Information Processing Systems. Cambridge, USA: MIT Press, 2021: 10418-10430. [本文引用:2]
[12] CANDÈS E J, RECHT B. Exact Matrix Completion via Convex Optimization. Foundations of Computational Mathematics, 2009, 9(6): 717-772. [本文引用:1]
[13] HU Y, ZHANG D B, YE J P, et al. Fast and Accurate Matrix Completion via Truncated Nuclear Norm Regularization. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2012, 35(9): 2117-2130. [本文引用:2]
[14] YU T Y, LI S M, LU J T, et al. A Quantum Weak Signal Detection Method for Strengthening Target Signal Features under Strong White Gaussian Noise. Applied Sciences, 2022, 12(4). DOI: DOI:10.3390/app12041878. [本文引用:1]
[15] WANG S Q, CHEN Y Y, JIN Y, et al. Error-Robust Low-Rank Tensor Approximation for Multi-view Clustering. Knowledge-Based Systems, 2021, 215. DOI: DOI:10.1016/j.knosys.2021.106745. [本文引用:1]
[16] ZHANG H N, LIU L J, ZHOU H Y, et al. CMD: Controllable Matrix Decomposition with Global Optimization for Deep Neural Network Compression. Machine Learning, 2022, 111(3): 831-851. [本文引用:1]
[17] FENG S, TANG S L, ZHAO C H, et al. A Hyperspectral Anomaly Detection Method Based on Low-Rank and Sparse Decomposition with Density Peak Guided Collaborative Representation. IEEE Transactions on Geoscience and Remote Sensing, 2021, 60. DOI: DOI:10.1109/TGRS.2021.3054736. [本文引用:1]
[18] LI L, LI W, DU Q, et al. Low-Rank and Sparse Decomposition with Mixture of Gaussian for Hyperspectral Anomaly Detection. IEEE Transactions on Cybernetics, 2020, 51(9): 4363-4372. [本文引用:1]
[19] WRIGHT J, PENG Y G, MA Y, et al. Robust Principal Component Analysis: Exact Recovery of Corrupted Low-Rank Matrices via Convex Optimization // Proc of the 22nd International Conference on Neural Information Processing Systems. Cambridge, USA: MIT Press, 2009: 2080-2088. [本文引用:1]
[20] TIAN R, SUN G L, LIU X C, et al. Sobel Edge Detection Based on Weighted Nuclear Norm Minimization Image Denoising. Electronics, 2021, 10(6). DOI: DOI:10.3390/electronics10060655. [本文引用:1]
[21] WEI Z L, FU N, JIANG S Y, et al. Parameter Measurement of LFM Signal with FRI Sampling and Nuclear Norm Denoising. IEEE Transactions on Instrumentation and Measurement, 2022, 71. DOI: DOI:10.1109/TIM.2022.3158986. [本文引用:1]
[22] GU S H, ZHANG L, ZUO W M, et al. Weighted Nuclear Norm Minimization with Application to Image Denoising // Proc of the IEEE Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2014: 2862-2869. [本文引用:2]
[23] YE H L, LI H, CAO F L, et al. A Hybrid Truncated Norm Regularization Method for Matrix Completion. IEEE Transactions on Image Processing, 2019, 28(10): 5171-5186. [本文引用:1]
[24] CAO F L, CHENG J Y, YE H L, et al. Recovering Low-Rank and Sparse Matrix Based on the Truncated Nuclear Norm. Neural Networks, 2017, 85: 10-20. [本文引用:3]
[25] BENZ P, ZHANG C N, KARJAUV A, et al. Revisiting Batch Normalization for Improving Corruption Robustness // Proc of the IEEE Winter Conference on Applications of Computer Vision. Washington, USA: IEEE, 2021: 494-503. [本文引用:1]
[26] ZHANG K, ZUO W M, ZHANG L. FFDNet: Toward a Fast and Flexible Solution for CNN-Based Image Denoising. IEEE Transactions on Image Processing, 2018, 27(9): 4608-4622. [本文引用:2]
[27] TIAN C W, XU Y, ZUO W M, et al. Designing and Training of a Dual CNN for Image Denoising. Knowledge-Based Systems, 2021, 226. DOI: DOI:10.1016/j.knosys.2021.106949. [本文引用:2]
[28] TIAN C W, XU Y, ZUO W M. Image Denoising Using Deep CNN with Batch Renormalization. Neural Networks, 2020, 121: 461-473. [本文引用:2]
[29] TIAN C W, XU Y, LI Z Y, et al. Attention-Guided CNN for Image Denoising. Neural Networks, 2020, 124: 117-129. [本文引用:2]
[30] ZHANG K, VAN GOOL L, TIMOFTE R. Deep Unfolding Network for Image Super-Resolution // Proc of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2020: 3214-3223. [本文引用:1]
[31] WANG H, XIE Q, ZHAO Q, et al. A Model-Driven Deep Neural Network for Single Image Rain Removal // Proc of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2020: 3100-3109. [本文引用:1]
[32] ZHANG Z H, LIU Y P, LIU J N, et al. AMP-Net: Denoising-Based Deep Unfolding for Compressive Image Sensing. IEEE Transactions on Image Processing, 2020, 30: 1487-1500. [本文引用:1]
[33] ZHENG H Y, YONG H W, ZHANG L. Deep Convolutional Dictionary Learning for Image Denoising // Proc of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2021: 630-641. [本文引用:1]
[34] NOCI L, BACHMANN G, ROTH K, et al. Precise Characterization of the Prior Predictive Distribution of Deep ReLU Networks // Proc of the 35th International Conference on Neural Information Processing Systems. Cambridge, USA: MIT Press, 2021: 20851-20862. [本文引用:1]
[35] ZHANG C N, BENZ P, ARGAW D M, et al. ResNet or Dense-Net? Introducing Dense Shortcuts to ResNet // Proc of the IEEE Winter Conference on Applications of Computer Vision. Washington, USA: IEEE, 2021: 3549-3558. [本文引用:1]
[36] LIN Z, DUAN Z P, ZHANG Z, et al. FocusCut: Diving into a Focus View in Interactive Segmentation // Proc of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2022: 2627-2636. [本文引用:1]
[37] ROTH S, BLACK M J. Fields of Experts // Proc of the IEEE Computer Society Conference on Computer Vision and Pattern Re-cognition. Washington, USA: IEEE, 2005, III: 860-867. [本文引用:1]
[38] MAIRAL J, BACH F, PONCE J, et al. Non-local Sparse Models for Image Restoration // Proc of the 12th IEEE International Conference on Computer Vision. Washington, USA: IEEE, 2009: 2272-2279. [本文引用:1]
[39] ZORAN D, WEISS Y. From Learning Models of Natural Image Patches to Whole Image Restoration // Proc of the International Conference on Computer Vision. Washington, USA: IEEE, 2011: 479-486. [本文引用:1]
[40] BURGER H C, SCHULER C J, HARMELING S. Image Denoising: Can Plain Neural Networks Compete with BM3D? // Proc of the IEEE Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2012: 2392-2399. [本文引用:1]
[41] SCHMIDT U, ROTH S. Shrinkage Fields for Effective Image Restoration // Proc of the IEEE Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2014: 2774-2781. [本文引用:1]
[42] CHEN Y J, POCK T. Trainable Nonlinear Reaction Diffusion: A Flexible Framework for Fast and Effective Image Restoration. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2017, 39(6): 1256-1272. [本文引用:1]
[43] ZHANG K, ZUO W M, GU S H, et al. Learning Deep CNN Denoiser Prior for Image Restoration // Proc of the IEEE Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2017: 2808-2817. [本文引用:1]