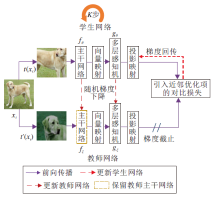
本文提出基于伪孪生网络双层优化的对比学习算法(CLBO), 采用完全对称的伪孪生网络架构, 维护学生网络和教师网络, 具体框架如图1所示.

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 CLBO框架图Fig.1 Framework of CLBO

CLBO主干网络的编码器为ResNet^[31], 投影头由两层MLP构成.这样对称的结构更有利于引入近邻优化算子.在学生网络优化阶段, 使用在线更新方式, 最小化引入InfoNCE, 不仅可拉近相似样本、推远不相似样本, 还可迫使学生网络向教师网络方向优化.因此学生网络可更好地向教师网络学习.在教师网络优化阶段, 使用离线更新方式, 使用先行优化K步的学生网络求得教师网络梯度, 再利用SGD更新教师网络, 得到最优的教师网络.

学生网络和教师网络是通过衡量样本间的相似度协同学习一个用于下游任务的最优编码器.对比学习中学生网络和教师网络采用相同编码器作为主干网络, 因此不同于其它对比学习算法保留学生网络, 本文保留教师网络中的编码器作为下游任务的编码器.求解最优教师网络问题从优化算法角度被建模成双层优化问题:

minξE[ minθ{F(θ )+ λ2‖ θ -ξ ‖22}],

其中, θ 为学生网络迭代过程中所得的近似最优参数, ξ 为所需的教师网络的最优参数,

$\begin{array}{l}F(\theta)= \\ \quad E_{x \sim D}\left[L_{\text {InfoNCE }}\left(g_{\theta}\left(f_{\theta}\left(t\left(x_{i}\right)\right)\right), g_{\xi}\left(f_{\xi}\left(t^{\prime}\left(x_{i}\right)\right)\right)\right)\right]\end{array}$

从数据集D取样本x_i, t(x_i)和t'(x_i)为来自同一样本x_i的两种不同数据增强视图, 损失函数采用InfoNCE.式(1)中包含两个阶段的优化过程.首先, 在学生网络优化阶段, 通过教师网络参数ξ 约束学生网络学习一个近似最优参数θ .然后, 在教师网络优化阶段, 通过近似最优学生网络参数θ , 利用SGD优化教师网络参数ξ , 获得最优教师网络.CLBO主要步骤如算法1所示.

算法1 CLBO

输入 数据集D, 批次大小N,

数据增强策略T和T', 学生网络优化器A,

教师网络学习率τ , 先行优化步数K,

教师网络优化次数S,

随机初始化学生网络参数θ _{0, 0},

包括编码器 fθ0, 0、投影头 gθ0, 0,

随机初始化教师网络参数ξ ₀,

包括编码器 fξ0、投影头 gξ0

输出 教师网络编码器f_ξ

for n=1 to S do//教师网络优化次数

for m=1 to K do//学生网络先行优化次数

{xi}i=1N~D //取样

t~T, t'~T' //抽取数据增强策略

计算学生网络投影

$\begin{array}{l} v_{2 i-1}=g_{\theta_{n-1, m-1}}\left(f_{\theta_{n-1, m-1}}\left(t\left(x_{i}\right)\right)\right) \\ v_{2 i}=g_{\theta_{n-1, m-1}}\left(f_{\theta_{n-1, m-1}}\left(t^{\prime}\left(x_{i}\right)\right)\right)\end{array}$

计算教师网络投影

$\begin{array}{l} v_{2 i-1}^{\prime}=g_{\xi_{n-1}}\left(f_{\xi_{n-1}}\left(t\left(x_{i}\right)\right)\right) \\v_{2 i}^{\prime}=g_{\xi_{n-1}}\left(f_{\xi_{n-1}}\left(t^{\prime}\left(x_{i}\right)\right)\right) \end{array}$

计算包含近邻优化项的总损失

L= 12N∑i=1N[(1(v_2i-1, v'_2i))+(1(v_2i, v'_2i-1))]+

λ2‖ θ _{n-1, m-1}-ξ _n-1 ‖22

更新学生网络

θ _{n-1, m}← θ _{n-1, m-1}+A(L, θ _{n-1, m-1}, d)

end for

随机梯度下降优化教师网络

ξ _n← ξ _n-1+τ λ (θ _{n-1, K}-ξ _n-1)

end for

在学生网络学习优化阶段, 主要在学生网络参数更新时引入近邻优化算子, 学生网络训练学习时的目标函数被重新定义为

minθn, m{F(θ _{n, m})+ λ2‖ θ _{n, m}-ξ _n ‖22}, (1)

其中, λ 为约束学生网络和教师网络参数差异的超参数, θ _{n, m}为在教师网络优化n次后学生网络优化m次后的学生网络参数, ξ _n为教师网络优化n次后的教师网络参数.

近邻优化算子的引入使教师网络从原先作为学生网络优化的初始项变为约束项, 这样不仅有利于学生网络在梯度下降过程中搜索最优解, 加速收敛, 而且通过约束学生网络在优化过程中向教师网络方向优化, 实现学生网络更好地向教师网络学习.

在教师网络优化阶段, 不同于其它算法直接利用学生网络参数动量更新教师网络参数, CLBO利用SGD进一步优化教师网络参数.这样的优化方式使教师网络能实现更快更好的收敛, 获得一个更优的教师网络.

学生网络学习优化阶段目标函数为式(1), 假设F(θ _{n, m})可微, 且λ > 0, θn, m*为目标函数的唯一最优解.由于

θn, m*=arg minθn, mF(θ _{n, m}),

根据一阶最优条件可知:

∇θn, m*F( θn, m*)+λ ( θn, m*-ξ _n)=0.(2)

则由链式法则可求得教师网络参数ξ _n的梯度为

∂F(θn, m* )∂ξn=( ∂θn, m* ∂ξn)^T ∇θn, m*F( θn, m*)+λ ( ∂θn, m* ∂ξn-I)^T( θn, m*-ξ _n)=( ∂θn, m* ∂ξn)^T( ∇θn, m*F( θn, m*)+λ ( θn, m*-ξ _n))-λ ( θn, m*-ξ _n),

由式(2), 教师网络参数ξ _n的梯度可化简为

∂F(θn, m* )∂ξn=-λ ( θn, m*-ξ _n).

上式表明教师网络梯度估计可通过求解学生网络的近似更新得到.

在学生网络优化阶段, 近邻优化项迫使学生网络向教师网络方向优化.在教师网络优化阶段, 近邻优化项可帮助获得教师网络参数梯度的闭式解, 具体为-λ ( θn, m*-ξ _n).因为很难估计精确的学生网络参数最优解 θn, m*, 所以不同于其它对比学习算法仅用优化一步的学生网络参数θ _{n, 1}动量更新教师网络.CLBO在优化时借鉴Lookahead优化器思想, 使用先行优化K步的学生网络参数θ _{n, K}作为次优解代替最优解 θn, m*, 因此教师网络参数ξ _n的梯度为

∂F(θn, K)∂ξn=-λ (θ _{n, K}-ξ _n).

由上式的教师网络梯度, 利用SGD优化教师网络, 进而得到最优教师网络.教师网络优化策略为:

ξ _n+1=ξ _n+τ λ (θ _{n, K}-ξ _n), (3)

其中τ 为教师网络优化时的学习率.

从上述公式推导过程可发现, 本文提出的基于SGD的教师网络优化策略通过近邻优化项可求得教师网络参数梯度.在教师网络优化阶段获得教师网络参数ξ _n梯度的闭式解, 有利于教师网络收敛到一个更精确的最优点, 从而获得最优教师网络.

基于SGD的教师网络优化策略可认为是现有基于伪孪生网络的对比学习算法在教师网络优化时的一般情况.现有算法的教师网络通常采用动量更新策略:

ξ _n+1=η ξ _n+(1-η )θ _{n, 1},

其中η 为动量更新系数.取η =1-τ λ , 经过简单的移项合并, 可得

ξ _n+1=ξ _n+τ λ (θ _{n, 1}-ξ _n).(4)

对比式(3)和式(4)可发现, 式(4)是式(3)中K=1的情况, 因此动量更新策略可认为是基于SGD的教师网络优化策略的特例.正因为这样的内在联系, 可简化算法的调参难度.在现有对比学习算法动量更新系数已知时, 可确定近邻优化系数λ 和教师网络学习率τ 的关系满足

τ = 1-ηλ,

其中, λ ≠ 0, τ ≠ 0.

在实验时, 本文对学生网络和教师网络进行动态优化, 具体为:近邻优化算子系数λ 采用随优化次数增加逐渐以λ · epoch增大的动态调整策略; 教师网络学习率τ 采用随优化次数增加逐渐以τ /epoch衰减的动态调整策略.在训练初始阶段教师网络还未明显优于学生网络时, 较小的约束系数λ 使学生网络学习更多新的知识, 较大学习率τ 有助于加快教师网络收敛.伴随优化次数增加, 教师网络逐渐优于学生网络, 以一个增大的约束系数λ 迫使学生网络注重向教师网络学习, 以较小的学习率τ 保证教师网络收敛的稳定性.所以, 基于SGD的教师网络优化策略结合基于近邻优化的学生网络优化策略, 更有助于获得最优的教师网络.

实验选用当前对比学习任务中常用的5个图像数据集, 分别为CIFAR-10^[32]、CIFAR-100^[32]、STL-10^[33]、ImageNet-100^[34]、Tiny-ImageNet^[34]数据集.数据集具体信息如表1所示.

表1

Table 1

表1(Table 1)

表1 实验数据集 Table 1 Experimental datasets 名称 类别 尺寸 预训练阶段 分类阶段 训练样本 训练样本 测试样本 CIFAR-10 10 32× 32 50000 50000 10000 CIFAR-100 100 32× 32 50000 50000 10000 STL-10 10 96× 96 10000 5000 8000 ImageNet-100 100 224× 224 100000 100000 20000 Tiny-ImageNet 200 64× 64 100000 100000 10000

表1 实验数据集 Table 1 Experimental datasets

在实验中, 遵循现有对比学习算法的预训练及下游任务验证方式.所有算法的主干网络编码器均采用ResNet18, 其中, 在CIFAR数据集上使用Res-Net-18的CIFAR变体, 其它数据集上使用标准Res-Net18.BARLOW TWINS和VICReg使用3层MLP投影头, 其它算法使用2层MLP投影头.

为了确保公平性, 采用相同的数据增强策略, 在CIFAR数据集上不使用高斯模糊, 其它数据集上正常使用.在学生网络优化阶段均使用基础学习率为0.06并伴随迭代轮次余弦衰减、权重衰减为0.000 5、动量为0.9的SGD优化器.使用相同的超参数设定进行实验:批次大小为256、主干网络输出维度为128、投影头的特征维度为512.其它超参数设置如表2所示, -表示未使用到该系数, η 表示动量更新系数, λ 表示近邻优化系数, τ 表示教师网络优化时的学习率, MB表示存储库(Memory Bank)样本数, Var表示方差(Variance)系数, Inv表示不变性(Invariance)系数, RR表示冗余项(Redundancy Reduction)系数.

表2

Table 2

表2(Table 2)

表2 超参数设置 Table 2 Hyperparameters setting 算法 η λ τ MB Var Inv RR SimCLR - - - - - - - MoCo 0.99 - - 4096 - - - BYOL 0.99 - - - - - - SimSiam - - - - - - - MoBY 0.99 - - 4096 - - - BARLOW TWINS - - - - - 1 0.005 VICReg - - - - 25 25 1 CLBO - 0.02 0.5 - - - -

表2 超参数设置 Table 2 Hyperparameters setting

本文遵照2.2节实验设置, 选择SimCLR、MoCo、BYOL、SimSiam、MoBY、BARLOW TWINS、VICReg为对比算法, 在5个图像数据集上进行对比实验, 计算k-NN(k=1)分类精度和线性分类精度.

本节中CLBO学生网络先行优化步数K=2, 并设为消融实验的基线.在预训练阶段, k-NN分类作为监视器, 可实时验证预训练阶段主干网络提取特征的好坏.在下游任务阶段, 冻结主干网络参数直接用于线性分类任务, 通过线性分类精度判别对比学习算法优劣.

各算法在5个数据集上的分类精度对比如表3所示, 所有实验结果为3次实验取平均后的结果.由表可看出, 在各数据集上, CLBO在预训练阶段, 主干网络提取特征在k-NN分类精度上取得最高值, 而在下游线性分类精度上也取得最优值.

表3

Table 3

表3(Table 3)

表3 各算法在5个数据集上的分类精度对比 Table 3 Accuracy comparison of different algorithms on 5 datasets % 数据集 算法 迭代次数 k-NN 分类精度 线性 分类精度 CIFAR-10 SimCLR MoCo BYOL SimSiam MoBY BARLOW TWINS VICReg CLBO 1000 1000 700 800 600 1000 1000 500 89.26 90.61 89.35 89.12 86.41 85.59 87.11 92.63 92.09 92.71 92.12 92.19 90.89 89.47 90.32 94.19 CIFAR-100 SimCLR MoCo BYOL SimSiam MoBY BARLOW TWINS VICReg CLBO 1000 700 700 700 500 1000 1000 400 58.34 59.01 59.82 59.15 57.72 55.38 55.79 63.06 64.32 67.27 67.99 65.68 65.45 60.51 62.75 69.49 STL-10 SimCLR MoCo BYOL SimSiam MoBY BARLOW TWINS VICReg CLBO 1000 1000 1000 1000 1000 1000 1000 700 83.74 87.94 84.25 86.58 83.06 80.66 83.25 90.97 88.92 91.76 89.49 91.03 88.81 86.13 88.02 93.49 ImageNet-100 SimCLR MoCo BYOL SimSiam MoBY BARLOW TWINS VICReg CLBO 1000 1000 1000 1000 1000 1000 1000 1000 75.29 74.27 74.01 76.81 73.02 75.55 76.89 78.87 83.83 82.36 84.41 84.62 82.19 81.76 82.96 85.91 Tiny-ImageNet SimCLR MoCo BYOL SimSiam MoBY BARLOW TWINS VICReg CLBO 1000 1000 1000 1000 1000 1000 1000 1000 35.62 33.85 36.53 34.01 32.72 31.69 32.83 37.13 47.92 47.14 49.29 45.33 45.51 41.32 44.61 51.91

表3 各算法在5个数据集上的分类精度对比 Table 3 Accuracy comparison of different algorithms on 5 datasets %

在本节中, 所有消融实验均采用CIFAR-10数据集, 主干网络编码器均采用ResNet18.

2.4.1 基于近邻优化的学生网络优化策略

为了验证CLBO中基于近邻优化的学生网络优化策略可帮助学生网络更好地学习, 对近邻优化项进行消融实验.学生网络编码器的k-NN分类精度如图2所示, 其中学生网络不采用先行优化策略, 即K=1.由图可知, 引入近邻优化项在预训练阶段的k-NN分类精度优于移除近邻优化项的学生网络编码器, 这表明近邻优化项的引入可帮助学生网络更好地学习.

图2

	Figure Option ViewDownloadNew Window
	图2 引入或移除近邻优化项的k-NN分类精度

Fig.2k-NN classification accuracy with or without nearest neighbor optimization term

下面对比各算法的学生网络下游线性分类精度.为了实验公平, CLBO的学生网络不采用先行优化策略, 即K=1, 这样保证所有对比算法学生网络优化次数相同.实验结果如图3所示.由图可发现, CLBO的学生网络编码器的线性分类精度最高, 由此可证实, 基于伪孪生网络双层优化的对比学习可有效帮助学生网络更好地向教师网络学习, 从而获得更优的学生网络.

图3

Fig.3

	Figure Option ViewDownloadNew Window
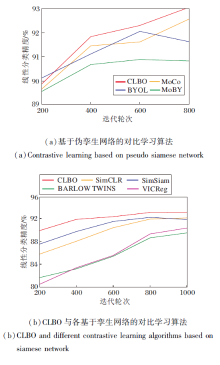	图3 各算法的学生网络编码器的线性分类精度对比Fig.3 Accuracy comparison of linear classification of student encoder of different algorithms

2.4.2 基于随机梯度下降的教师网络优化策略

为了验证基于SGD的教师网络优化策略对教师网络性能的影响, 分别对先行优化步数和随机梯度下降策略进行消融实验.

为了证实学生网络先行优化的设计有助于教师网络的优化, 调整学生网络先行步数K并展示采用不同先行步数获得的教师网络的线性分类精度, 结果如图4所示.

图4

Fig.4

	Figure Option ViewDownloadNew Window
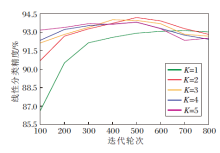	图4 K不同时教师网络编码器的线性分类精度对比Fig.4 Accuracy comparison of linear classification of teacher encoder with different K

由图4可发现, 当先行优化1步时, 教师网络收敛平稳.当先行优化步数增大时, 可加速教师网络的收敛.当迭代轮次为500时, 先行优化2步得到的教师网络的线性分类精度达到最高并饱和衰减.

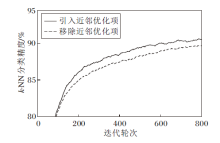
为了验证随机梯度下降策略的有效性, 对比有无近邻优化项对教师网络编码器k-NN分类精度的影响, 结果如图5所示.由图可发现, 近邻优化项的引入可有效改善教师网络性能.

图5

Fig.5

	Figure Option ViewDownloadNew Window
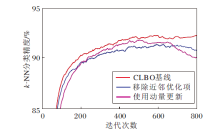	图5 条件改变时教师网络编码器的k-NN分类精度对比Fig.5 Accuracy comparison of k-NN classification of teacher encoder with different conditions

保留近邻优化项, 对比使用动量更新策略与使用SGD更新策略的教师网络编码器k-NN分类精度, 结果如图5所示.由图可发现, 改用动量更新策略的教师网络编码器在收敛性和稳定性上均不如采用基于SGD的教师网络优化策略获得的教师网络编码器, 特别当迭代轮次达到600后, 衰减速度更快.所以, 本文采用的基于SGD的教师网络优化策略不仅可有效提高教师网络的收敛性, 而且在一定程度上可延缓精度衰减.

最后对比各算法教师网络编码器的线性分类精度, 结果如图6所示.由图可见, 在下游分类任务上, CLBO得到的教师网络编码器在各迭代轮数下均最优.实验结果表明本文的基于随机梯度下降的教师网络优化策略可获得更优的教师网络.

图6

Fig.6

	Figure Option ViewDownloadNew Window
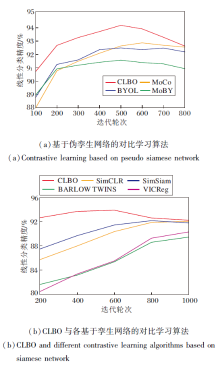	图6 各算法的教师网络编码器的线性分类精度对比Fig.6 Accuracy comparison of linear classification of teacher encoder with different algorithms

2.4.3 网络结构与损失函数

本节分别讨论投影头结构、对称结构、损失函数对CLBO性能的影响, 通过线性分类精度体现设定变化是否有效, 具体实验结果如表4所示.

表4

Table 4

表4(Table 4)

表4 网络结构与损失函数对各算法性能的影响 Table 4 Effect of network structure and loss function on performance of different algorithms projector predictor 损失函数 线性 分类精度/% CLBO 2-layer MLP - InfoNCE 94.19 BYOL 2-layer MLP 􀳫 MSE 92.12 BARLOW TWINS 2-layer MLP - BARLOW TWINS Loss 89.04 VICReg 2-layer MLP - VICReg Loss 89.24 投影头结构 - 1-layer MLP 3-layer MLP - - - InfoNCE InfoNCE InfoNCE 91.19 92.26 94.23 对称结构 2-layer MLP 2-layer MLP 􀳫 􀳫 InfoNCE MSE 93.03 92.71 损失函数 2-layer MLP 2-layer MLP 2-layer MLP - - - MSE BARLOW TWINS Loss VICReg Loss 0.01 90.01 90.88

表4 网络结构与损失函数对各算法性能的影响 Table 4 Effect of network structure and loss function on performance of different algorithms

先讨论投影头结构对性能的影响.对比移除投影头、1层MLP投影头、2层MLP投影头(CLBO)及3层MLP投影头的线性分类精度可发现:投影头的保留对CLBO很必要.投影头结构随着层数的提高确实能带来性能上的提升, 但3层MLP投影头对性能提升作用并不明显, 仅提升0.4%的线性分类精度.因此, 本文使用2层MLP投影头作为基准设定.

表4中BARLOW TWINS与VICReg改用2层MLP投影头后线性分类精度分别为89.04%和89.24%.相比表3中两种算法使用3层MLP投影头的分类精度, BARLOW TWINS的分类精度下降0.43%, VICReg的分类精度下降1.08%.相比BAR-LOW TWINS和VICReg, CLBO对更深的投影头结构的依赖程度更低.

再讨论对称结构对性能的影响.为了强调对称结构对CLBO的重要性, 在学生网络端增加预测头破坏对称结构.在该设定下, 还将损失函数由InfoNCE改为MSE.由表4可知, 无论使用哪种损失函数, 对称结构的破坏都会极大影响CLBO的性能, 这说明对称的结构设计有助于提升CLBO性能.

下面讨论损失函数对性能的影响.选择如下损失函数:MSE、BARLOW TWINS Loss、VICReg Loss、InfoNCE.由表4结果可知, 使用MSE损失, CLBO并不能避免模型塌缩出现平凡解.相比使用BARLOW TWINS Loss或VICReg Loss, InfoNCE可发挥CLBO的最佳性能.

最后讨论CLBO的通用性.观察表4中第9行、第11行、第12行的3种实验设定可发现, 这3种设定可认为是将本文的双层优化拓展到BYOL、BARLOW TWINS与VICReg.使用双层优化策略后, BYOL、BARLOW TWINS、VICReg性能都略有提升, BARLOW TWINS与VICReg提升明显优于BYOL.本文认为这得益于BARLOW TWINS与VICReg的对称网络结构.因此, CLBO具有较强的通用性, 可灵活嵌入现有算法, 改善算法性能, 特别适用于网络结构对称的对比学习算法.

2.4.4 迭代批次

为了探究迭代批次变化对CLBO的影响, 遵循2.2节实验设置, 给出仅改变迭代批次后, 各算法的线性分类精度.对比结果如图7所示.为了消融实验的公平性, 在本节中, BARLOW TWINS、VICReg与其它算法一样, 均使用两层MLP的投影头结构.

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 迭代批次对各算法性能的影响Fig.7 Effect of batch size on performance of different algorithms

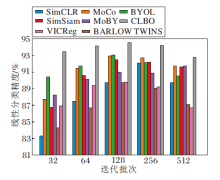
由图7可发现, 当迭代批次改变时, MoCo与MoBY线性分类精度影响较小, 这得益于教师网络端存储库的组件设计拥有额外的对比样本.BYOL、SimSiam、BARLOW TWINS、VICReg的线性分类精度影响适中, 这得益于这些方法无需负样本.SimCLR因为依赖负样本且无存储库的组件设计, 所以线性分类精度影响较大.CLBO对迭代批次大小更鲁棒, 特别在迭代批次较小时优势更明显.

t-SNE(t-Distributed Stochastic Neighbor Embed-ding)^[35]特征可视化可将网络提取的特征从高维空间投射到低维空间.

为了突出CLBO在小迭代批次上的优势, 设定迭代批次为32, 各类算法预训练100轮所得编码器的t-SNE特征可视化结果如图8所示, 10种颜色表示CIFAR-10数据集上的10类样本.由图可发现, 相比其它算法, CLBO提取特征的分散和聚合更合理, 提取的特征能分离出更多的簇, 簇间距离更分散, 簇内实例特征分配更紧密.

图8

Fig.8

	Figure Option ViewDownloadNew Window
	图8 各算法t-SNE特征可视化结果Fig.8 Results of t-SNE visualization of different algorithms

2.4.5 特征维度

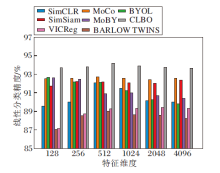
为了探究投影头特征维度对CLBO的影响, 遵循2.2节实验设置, 仅改变投影头特征维度, 各算法线性分类精度如图9所示.由图可知, 随着特征维度增加, SimCLR线性分类精度逐渐增加, 并在特征维度为512时达到饱和, 随后逐渐衰减.当特征维度较小时, BYOL与MoBY表现出较好的分类性能.随着特征维度增加, BYOL与MoBY性能逐渐衰减.BAR-LOW TWINS与VICReg随着特征维度增大而表现出更好的分类性能.MoCo、SimSiam与CLBO的分类精度受特征维度变化的影响较小, 这表明这3种算法对投影头特征维度具有较强的鲁棒性.

图9

Fig.9

	Figure Option ViewDownloadNew Window
	图9 特征维度对各算法线性分类精度的影响Fig.9 Effect of feature dimension on linear classification accuracy of different algorithms