四元组S=< U, C∪ D, V, f > 为一个决策信息系统, 其中:U={x₁, x₂, …, x_N}为对象空间, 是一个有限非空对象集, 称为论域, N表示论域中的样本个数; C={a₁, a₂, …, a_n}表示所有条件属性的非空有限集合, n表示决策信息系统中条件属性的个数; D={d₁, d₂, …, d_m}表示所有决策属性的非空有限集合, m表示决策信息系统中决策属性的个数, C∩ D=Ø ; V= ∪a∈C⋃DV_a, V_a表示属性a的值域.定义映射f:U× C∪ D→ V为一个信息函数, 且∀ a∈ C∪ D, x∈ U, f(x, a)∈ V_a.

定义1^[5] 给定决策表S=< U, C∪ D, V, f > , 对于每个属性子集R⊆A, 定义不可分辨关系:

IND(R)= {(x, y)∈ U× U|a∈ R, f(x, a)=f(y, a)}.

关系IND(R)构成U的一个划分, 表示为U/IND(R), 简记为U/R.U/R中的任何元素

[x]_R={y|∀ a∈ R, f(x, a)=f(y, a)}

称为等价类.不失一般性, 假设决策表S仅有一个决策属性D={d}, 其决策属性值映射为1, 2, …, k, 由D导出的U上的划分为U/D={Z₁, Z₂, …, Z_k}, 其中

Z_i={x∈ U|f(x, D)=i}, i=1, 2, …, k.

不可分辨关系是一种等价关系.

定义2^[35] 给定决策表S=< U, C∪ D, V, f > , 对于每个子集X⊆U和不可分辨关系R, X的下近似集与上近似集分别可由R定义如下:

R¯X=∪ {x∈ U|[x]_R⊆X},

R¯X=∪ {x∈ U|[x]_R∩ X≠ Ø }.

论域U被这2个近似集( R¯X, R¯X)划分为3个不相交的区域:正区域POS_R(X)、负区域NEG_R(X)和边界域BND_R(X), 分别定义如下:

POS_R(X)= ∪X⊂U/DR¯X,

NEG_R(X)=U- ∪X⊂U/DR¯X,

BND_R(X)= ∪X⊂U/D( R¯X- R¯X).

定义3^[28] 给定决策表S=< U, C∪ D, V, f > , 条件属性集C对于U的划分为

U/C={X₁, X₂, …, X_n'},

n'为划分后的子集数量, 则条件属性集C的知识粒度定义为

GP_U(C)= ∑i=1n'( |Xi|2|U|2).

属性集(C∪ D)对于U的划分为

U/(C∪ D)={Y₁, Y₂, …, Y_h},

h为划分后的子集数量, 则条件属性集C相对于决策属性集D的知识粒度定义为

GP_U(D|C)=GP_U(C)-GP_U(C∪ D).

定义4^[28] 给定决策表S=< U, C∪ D, V, f > , 条件属性集C对于U的划分为

U/C={X₁, X₂, …, X_n'},

n'为划分后的子集数量, 属性集B⊆C, ∀ a∈ B, 属性a在B中相对于决策属性集D的内部属性重要度定义为

Si ginnerU(a, B, D)=GP_U(D|(B-a))-GP_U(D|B).

若∀ a∈ (C-B), 则属性a在(C-B)中相对于决策属性集D的外部属性重要度定义为

Si gouterU(a, B, D)=GP_U(D|B)-GP_U(D|(B∪ a)).

定义5^[28] 给定决策表S=< U, C∪ D, V, f > , 属性集B⊆C.当且仅当满足

1)GP_U(D|B)=GP_U(D|C),

2)∀ a∈ B, GP_U(D|(B-a))≠ GP_U(D|B),

则称B为决策表S的相对约简.条件1)表示约简后的属性集B与所有条件属性集C关于D的知识粒度相等, 表现的意义是属性集B与条件属性集C对数据样本U的分类能力相同, 即找到的约简集是合格的.条件2)表示若从B中剔除某个属性之后, 会降低分类能力, 这意味着B中无任何冗余的属性.这两个条件共同作为属性约简的正确性标准.

定理1^[25] 给定决策表S=< U, C∪ D, V, f > , 令A⊆C, U/A表示为{A₁, A₂, …, A_r}, U被划分成多个数据子集{U₁, U₂, …, U_L},

U_i/A={A_i1, A_i2, …, A_ir},

则最终约简集

A_p= ∪1≤i≤LA_ip, p=1, 2, …, r.

证明 如果关于A的任意两个对象相同, 可将它们合并为一个等价类.不同数据拆分之间的相同等价类可组合为更大的等价类.因此, 对于

U/A={A₁, A₂, …, A_r}, U_i/A={A_i1, A_i2, …, A_ir},

可得

A_p= ∪1≤i≤LA_ip, p=1, 2, …, r.

定理2^[25] 并行属性约简算法得到的约简与相应的串行方法得到的约简相同.

证明 传统的属性约简算法主要分为4个基本步骤:子集生成、子集评估、停止标准、结果验证.并行算法和串行算法之间的唯一区别是属性子集评估过程, 主要包括等价类和属性重要度的计算.

1)根据定理1,

U={U₁, U₂, …, U_L}, A_p= ∪1≤i≤LA_ip, p=1, 2, …, r,

这意味着串行算法中的等价类与相应并行算法中的等价类相同.

2)由于串行算法中的等价类与相应并行算法中的等价类相同, 则它们计算所得的属性重要度也相同.

因此, 并行算法得到的约简与相应的串行算法得到的约简相同.

Hadoop MapReduce^[36]是一个分布式计算框架, 允许开发人员使用简单的代码在巨大的集群上实现大规模的数据计算.但由于磁盘I/O和网络传输过多, 不适合迭代计算和在线计算任务.为了克服MapReduce的不足, 学者们提出新一代集群计算引擎Spark.Apache Spark^[37]是在MapReduce基础上改进的分布式计算框架, 具有快速、易用、通用、兼容等优点.

Spark的运行流程主要分为如下步骤.

1)首先启动 SparkContext, 并向Cluster Manager注册, 申请Executor资源, Cluster Manager为 Execu-

tor分配资源并启动进程.

2)SparkContext构建有向无环图(Directed Acyclic Graph, DAG), 将DAG图分解成多个阶段, 并发送给Task Scheduler.

3)Executor向SparkContext申请Task, SparkCon-

text将应用程序代码发放给Executor.

4)Task在Executor上运行完毕后, 把执行结果反馈给Task Scheduler和DAG Scheduler, 并写入数据.最后, SparkContext注销并释放所有资源.

弹性分布式数据集(Resilient Distributed Data-set, RDD)是Spark中基本的数据抽象.在代码中是一个抽象类, 表示一个弹性、不可变、可分区、里面的元素可并行计算的集合.RDD表示只读的分区的数据集, 改动RDD, 只能通过RDD的转换操作, 然后得到新的RDD, 并不会对原RDD有任何的影响.

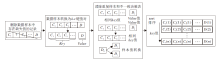
本文改进传统的并行数据预处理算法, 使其更满足后续算法的数据输入要求, 提出原始数据并行预处理算法, 处理原始数据集, 具体流程图如图1所示.具体算法步骤如下所示.

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 原始数据并行预处理算法流程图Fig.1 Flowchart of parallel preprocessing algorithm of raw data

算法1 原始数据并行预处理算法

输入 原始决策表S_raw

输出 处理后的决策表S

step 1 在每个子节点slave_i上读取原始决策表, 删除其中含有缺失属性值的样本数据.

step 2 调用Spark计算引擎中的mapPartitions算子, 将删除后的数据对象转换为键值对RDD数据集合.

step 3 调用Spark计算引擎中的mapValues算子, 对RDD数据集中的value部分进行step 4的操作, 消除决策表中重复样本和不一致部分.

step 4

/* 存在2个数据样本的key值相同时* /

If s₁.key=s₂.key, then

If s₁.value=s₂.value

Remove s₂;

Else

Remove s₂;

s₁.value← value_MAX+1;

End

End

step 5 调用Spark计算引擎中的sortByKey算子, 并对数据按属性值进行由小到大的排序, 方便后续计算.

step 6 返回处理后的决策表S.

算法1的执行过程具体如下.首先, 由于原始数据集中包含许多无法参与计算的含有缺失值的数据, 而包含缺失值的数据会对后续约简计算产生影响, 需要删除此类缺失值数据.然后, 将数据集转化为所有条件属性为key值, 决策属性为value值的k-v键值对.遍历所有样本, 对于key和value相同的重复数据样本, 选择删除其一; 而对于key相同、value不同的一对样本(决策表不一致部分), 删除key值, 并将后者的value值修改为决策表中最大value值加1.最后, 对整个数据子集按属性值进行由小到大的sort排序, 方便后续计算.

如今许多决策系统是随着时间而动态变化的, 为了得到新的约简, 需要重新对决策系统进行约简计算, 耗费大量时间.为了解决该问题, 本文从属性组的概念入手, 引入二叉树的机制, 设计搜索策略寻找约简, 并且借助基于知识粒度的增量约简算法^[31], 将知识粒度加入迭代停止准则中, 提出基于属性树的增量式属性约简算法(IARAT), 具体算法步骤如下所示.

算法2IARAT

输入 原始样本数据U, 增量样本数据U',

原约简集B, 分支阈值α _max

输出 约简子集R

R← B, K← 1;

计算知识粒度GP_U'(D|R)和GP_U'(D|C);

If GP_U'(D|R)=GP_U'(D|C), then

Return R

End

Cluster C into{C₁, C₂, …, C_N};

/* C聚类成N个属性树根结点* /

While GP_U'(D|R)≠ GP_U'(D|C) and K< α _max:

For each tree_i:

tree_i.right.data← tree_i.data∩ R;

/* 存在原约简属性, 置于右节点* /

tree_i.left.data← tree_i.data-tree_i.right.data;

/* 剩下的属性置于左节点* /

For each attribute c being evaluated:

/* 评估无兄弟结点属性树* /

If c是核心属性 then

tree_i.right.data← c;

R← (R∪ c);

tree_i.left.data← tree_i.data-c;

Break

Else

C← (C-c);

End

End

End

For each tree_i:

If tree_i.left≠ Ø then

tree_i=tree_i.left;

Else

remove the tree; /* 移除该树* /

K=K+1;

End

End

End

Return R

IARAT首先需要对决策表进行预先判断:加入增量数据集后是否需要进一步的约简计算.若在增量数据集上, 决策属性D分别关于原约简子集R与条件属性集C的知识粒度相等(GP_U'(D|R)和GP_U'(D|C)), 即在增量数据集上, 约简子集R依然可保持与条件属性集C相同的分类能力, 可知增量数据集的加入未影响原约简结果, 无需进一步计算; 若不相等, 需要进一步计算, 得到新的约简.根据相应聚类算法, 将所有条件属性划分为多个属性树根结点并进行分支操作, 在进行每轮的属性评估过程中, 跳过与约简集相关性较高的属性树, 对剩下的属性树加以评估, 同时根据评估结果的不同, 进行不同子结点的分支.在计算过程中引入分支系数α 并设定阈值, 方便跳出循环, 避免冗余计算和陷入死循环.

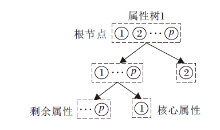
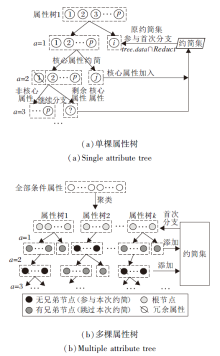
属性树结构如下.根节点包含聚类算法划分的条件属性簇, 在每轮属性树分支中, 将核心属性置于树的右子结点, 其余部分划分为左子结点, 在下次分支中, 根据相应策略对左子结点进行再划分.属性树的结构及分支策略如图2和图3所示.

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 单棵属性树结构Fig.2 Structure of single attribute tree

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 属性树分支策略Fig.3 Branch strategy of attribute tree

在属性树的初始判别阶段, 通过增量机制减少属性评估数量, 提高属性约简的效率和精度, 当多个增量对象加入决策系统时, 可利用增量机制更新约简.在属性评估阶段, 采用Yin等^[38]设计的核心属性约简算法代替传统的属性重要度约简算法, 不仅在计算效率上拥有优势, 而且避免二次循环评估, 提高计算效率.该算法的优化策略每次只判断一个属性是否为核心属性, 避免时间复杂度较高的正区域计算, 减少获取约简子集所需的时间, 时间复杂度仅为|C|.

核心属性约简算法机制如下.在决策表S=< U, C∪ D, V, f > 中, 对于某条件属性c_i, 若删除c_i, 存在2个数据样本x、y的条件属性值(即C-c_i)相等, 而决策属性值不相等, 则认定属性c_i为核心属性, 否则, c_i不是核心属性.

属性树分支策略如下.在预先判断后得知决策属性D分别关于原约简子集R与条件属性集C的知识粒度不相等, 说明增量数据集的加入影响原约简结果, 原数据的约简集已无法对现有增量数据保持有效的分类性能, 所以需要进一步进行如下计算.

1)对加入的增量数据集S'的条件属性C执行相应的聚类算法.根据属性与属性之间相关性及属性与属性簇之间的相关性, 将所有条件属性集C划分成多个属性簇群{C₁, C₂, …, C_N}, 目的是聚集具有较大依赖关系(冗余度高)的属性, 具有高相关性的每个属性子集转换成一棵属性树tree_i的根节点.

2)进行逐棵属性树tree_i的分支.为了避免重复计算, 利用原约简集B, 参与到分支过程中, 把多棵属性树的根节点与原约简集B中相交的部分置于右子结点tree_i.right.这一步是为了找出与原约简集B存在相关性的属性树, 在下轮分支时跳过该树的属性评估, 其余部分划分为左子结点tree_i.left, 后续的分支计算在该结点上进行.同时设置分支系数α 并初始化为1, 在每次分支之后进行递增, 当达到最大阈值时跳出循环, 阈值即属性树的最大分支深度.基于最坏的打算, 为了避免冗余计算和陷入死循环, 一般设置为属性树根结点中最大的属性数量.

3)在每次分支过程中运用核心属性约简算法逐个评估无兄弟结点属性树(即评估本轮与约简集相关性较低的属性树).如果不是核心属性, 直接从节点中删除, 不再参与后续计算, 继续评估下一属性, 直到找出该属性树中第一个核心属性; 如果是核心属性, 加入约简集R并停止本棵树余下属性的评估.

直到所有属性树评估完成, 该轮分支结束.

4)属性树与约简集的相关性度量取决于上一轮中约简集是否加入某棵属性树中的属性.每棵树都是由聚类算法生成的属性簇群, 属性之间存在较高相关性, 若上一轮评估过程中添加某棵树的属性进入约简集, 因为其它属性树中存在核心属性的可能性较高, 所以可跳过对该树的属性评估, 缩小搜索空间, 提升检索效率.

5)在分支过程中, 如果遇到某棵树左节点为空, 说明该属性树分支完成, 所有属性树全部分支完成后, 输出新约简集.

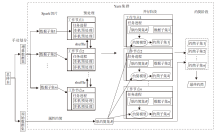
本节首先引入IARAT, 在此基础上, 融入Spark并行机制, 实现分布式的内存计算任务, 在不牺牲性能的情况下找出不同数据子集中的冗余属性并行化数据处理, 降低数据规模和计算时间, 提高效率.由此, 设计基于属性树的并行化增量式动态属性约简算法(PIARAT), 流程图如图4所示.PIARAT具体步骤如下所示.

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 PIARAT流程图Fig.4 Flowchart of PIARAT

算法3PIARAT

输入 原始数据集S_raw

输出 约简子集R

step 1 将原始数据集S_raw存入HDFS文件系统.

step 2 在主节点master中读取文件系统中的数据集.

step 3 将数据集S_raw以1:1的比例划分成原决策表S和增量决策表S'.

step 4 调用算法1对增量决策表S'进行并行预处理操作.

step 5 对原决策表S进行属性约简计算, 得到原约简集B.

step 6 将原决策表S和原约简集B发送到所有子节点slave_i上.

step 7 将增量数据集切分成n份, 分别发送到n个工作节点上.

step 8 在所有子节点slave_i上调用算法2进行基于属性树的增量式属性约简, 返回, 得到各约简子集{R₁, R₂, …, R_n}.

step 9 将各个子节点slave_i上得到的约简子集{R₁, R₂, …, R_n}发送到主节点master上.

step 10 对约简子集B_i进行并集操作, 得到最终约简集R.

step 11 返回 R.

PIARAT首先将搜集的海量大规模数据集存入HDFS(Hadoop Distributed File System)文件系统^[39].再按照比例将数据集划分为原始数据集和增量数据集, PIARAT主要侧重于增量数据集上的并行属性约简, 所以主要对增量数据集进行约简计算.然后, 对增量数据集进行二次划分, 划分成多个数据子集, 并分发到对应的多个工作节点上, 采用基于属性树的增量式属性约简算法, 在各子节点上并行处理数据.最后, 将处理完成的多个结果返回主节点进行最终并集操作, 得到最终约简子集.

为了进一度凸显算法优势, 对IARAT和PIARAT进行时间复杂度分析.给定决策表S=< U, C∪ D, V, f > , 设定U表示原始数据集样本, U'表示增量数据集样本, C表示所有条件属性并聚集成k棵属性树, k≪C, 最终的约简子集为R, 并设置n个并行计算节点.

PIARAT在算法的初始判别阶段, 需要计算知识粒度并判断是否需要进一步约简, 时间复杂度为$O\left(|C|\left|U^{\prime}\right|^{2}\right)$.在step 8的属性遍历过程中, 传统算法是逐个计算属性的重要性, 导致大部分属性的重复计算, 时间复杂度为

$O\left(|C||R|-\frac{|R|^{2}}{2}+\frac{|R|}{2}\right), $

而PIARAT的时间复杂度仅为O(|C|), 有效提升计算效率.

在此基础上, 进一步合理发挥二叉树的优势, 避免某些属性评估, 缩小搜索空间, 进一步减少耗时.为了简化讨论, 假设聚类后每棵树上的属性个数为 |C|k, 则属性树搜索核心属性的时间复杂度为

$O\left(k \log _{2}\left(\frac{|C|}{k}\right)\right).$

最后, IARAT和PIARAT的时间复杂度分别为

$\begin{array}{l} O\left(k \log _{2}\left(\frac{|C|}{k}\right)+|C|\left|U^{\prime}\right|^{2}\right) \\ O\left(\frac{k}{n} \log _{2}\left(\frac{|C|}{k}\right)+\frac{1}{n}|C|\left|U^{\prime}\right|^{2}\right)\end{array}$

由此可得出, PIARAT的时间复杂度远低于传统串行算法, 具有良好的加速性能.

本文从UCI机器学习知识库上选择8个数据集作为实验数据集, 分为5个小型数据集和3个较大数据集.所有数据集的详细信息如表1所示.

表1

Table 1

表1(Table 1)

表1 实验数据集 Table 1 Experimental datasets 名称 样本数 属性数 类别 Qsar 1055 42 2 Mushroom 8124 22 2 Nursery 12960 8 5 Shuttle 14500 9 7 Letter 20000 16 26 PokerHand 1025010 11 10 KDDCUP 4898431 42 3 HIGGS 11000000 28 2

表1 实验数据集 Table 1 Experimental datasets

小型数据集分别为Qsar、Mushroom、Nursery、Shuttle、Letter数据集, 样本量由几千至几万不等.较大数据集为Poker Hand、KDD Cup、HIGGS数据集, 拥有几十个属性, 但包含百万级的样本量.

首先对数据集进行原始数据和增量数据的划分, 从表1中的每个决策系统中选取50%初始的数据样本量作为原始数据集, 然后从剩余的50%数据样本量中分别选取20%, 40%, 60%, 80%, 100%的数据作为增量数据集填充.在原始决策系统中添加增量对象集时, 采用不同的增量约简算法对各决策系统的约简进行更新并进行对比讨论.

在属性聚类阶段, 采用的聚类算法为K-means, 对数据集采用肘部法则^[40]分别确定K值.肘部法则使用的聚类评价指标为:数据集上所有样本点到其簇中心的距离之和的平方.肘部法则会画出不同值的成本函数.随着值的增大, 每类包含的样本数会减少, 于是样本离其重心会更近, 平均畸变程度会更小.而分支系数α 的引入是为了引导算法达到最大阈值时跳出循环, 避免冗余计算和陷入死循环.阈值的确定也就是属性树的最大分支深度, 基于最坏的打算, 一般设置为属性树根结点中最大的属性数量.K值和分支系数α 的选取如表2所示.

表2

Table 2

表2(Table 2)

表2 参数设置 Table 2 Parameter setting 数据集 属性数 K 最大α Qsar 42 5 28 Mushroom 22 9 7 Nursery 8 5 4 Shuttle 9 3 6 Letter 16 3 8

表2 参数设置 Table 2 Parameter setting

本文采用粗糙集中两种常用指标评估寻找的约简子集质量, 分别为近似分类质量(Approximate Classified Quality, AQ)和近似分类精度(Approximate Classified Precision, AP), 并通过运行时间和分类准确率评估算法的加速性能和分类性能.

定义6^[41] 给定决策表S=< U, C∪ D, V, f > , 决策属性D对于U的划分为U/D={Z₁, Z₂, …, Z_m'}, m'为划分后的子集数量, 则条件属性集C关于决策属性集D的近似分类精度为:

AP_C(D)= |POSC(D)|∑i=1m'|C¯Zi|.

定义7^[41] 给定决策表S=< U, C∪ D, V, f > , 条件属性集C关于决策属性集D的近似分类质量为:

AQ_C(D)= |POSC(D)||U|.

如果约简子集的AQ值和AP值与原决策系统相同, 认为该约简子集与原决策系统具有相同的区分能力.

3.3.1 计算时间对比

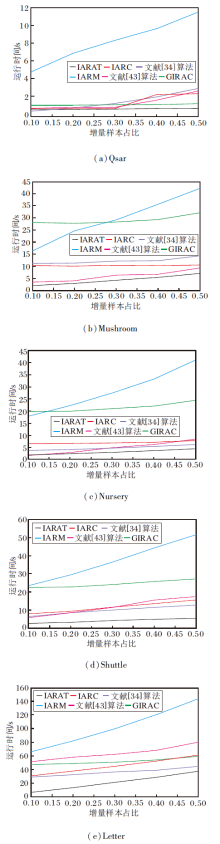
为了验证IARAT在运行时间和分类精度上的高效性和有效性, 在表1所示的前5个不同的小型数据集上对比算法的计算时间.实验中选取的对比算法分别为IARC(An Incremental Algorithm for Redu-ct Computation Based on Knowledge Granularity)^[31]、GIARC(A Group Incremental Algorithm for Reduct Computation)^[33]、文献[34]算法(Bucket and Attri-bute Group for Obtaining Reduct)、IARM(Incremen-tal Attribute Reduction Algorithm)^[42]和文献[43]算法.各算法在5个数据集上的运行时间对比如图5所示.由图可见, 随着动态数据集的增加, 各算法的运行时间都在增加, 而IARAT的运行时间在各数据集上增幅均最小, 在一定范围内随着增量数据占比的增大, IARAT的运行时间也在可控范围内平稳增加.这表明IARAT可有效提高属性约简的计算效率, 减少运行时间.

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 各算法在5个数据集上的运行时间对比Fig.5 Running time comparison of different algorithms on 5 datasets

3.3.2 有效性对比

为了进一步验证IARAT的有效性, 说明其可在不损失分类性能的情况下有效提高搜索速度并找到可行的属性约简, 进行如下对比实验.

本文设置数据集上50%的样本为增量数据, 并且通过CART(Classification and Regression Tree)和10倍交叉验证的方式计算分类准确率.将样本划分为10个不相交的样本组, 在第一轮中设置第一组为测试集, 剩下的样本为训练集, 第二轮中设置第二组为测试集, 以此类推.这里的分类准确率表现为:在多种约简算法分别进行属性约简之后, 每种算法保留下来的核心属性集各不相同, 此时CART利用不同的核心属性集对样本进行分类以计算分类准确率.

分类准确率由CART预测正确的样本数量在全部样本中的占比决定, 计算公式如下:

Accuracy= NCSNAS,

其中, N_CS表示算法预测正确样本的数量, N_AS表示所有预测样本的总数.

为了更直观地展示实验结果, 计算加速比:

Speedup(A)= TmaxTA,

其中, T_max表示运行时间最长的算法耗时, T_A表示算法耗时.加速比越高, 运行时间越少, 效率越高.

各算法在5个数据集上的分类准确率和加速比如表3和表4所示.由表可看出, 在大多数情况下, IARAT分类准确率未下降, 并且略高于其它算法.由于数据集的差异, IARAT的分类准确率在个别情况下略有下降, 但在可接受的范围内, 这表明该算法可在不牺牲分类准确率的情况下有效减少耗时.由此得到如下结论:IARAT是有效且高效的.

表3

Table 3

表3(Table 3)

表3 各算法在5个数据集上的分类准确率对比 Table 3 Classification accuracy comparison of different algorithms on 5 datasets % 算法 Qsar Mushroom Nursery Shuttle Letter IARC 72.30 98.52 91.12 99.91 87.71 GIARC 72.70 98.52 90.16 99.88 85.77 IARM 73.10 98.52 91.20 99.88 85.94 文献[43]算法 72.80 98.52 91.47 99.90 88.02 文献[34]算法 72.60 98.52 91.47 99.88 88.02 IARAT 72.80 98.52 91.91 99.92 88.54

表3 各算法在5个数据集上的分类准确率对比 Table 3 Classification accuracy comparison of different algorithms on 5 datasets %

表4

Table 4

表4(Table 4)

表4 各算法在5个数据集上的加速比对比 Table 4 Speedup ratio comparison of different algorithms on 5 datasets % 算法 Qsar Mushroom Nursery Shuttle Letter IARC 5.0737 4.0000 5.2764 3.3064 2.3422 GIARC 10.1474 1.3106 1.6790 1.8923 2.4156 IARM 1.0000 1.0000 1.0000 1.0000 1.0000 文献[43]算法 4.4776 4.5375 4.8654 2.9496 1.7890 文献[34]算法 4.0157 2.9456 6.6900 4.0387 3.2090 IARAT 18.2064 5.9809 9.2332 9.3182 3.8260

表4 各算法在5个数据集上的加速比对比 Table 4 Speedup ratio comparison of different algorithms on 5 datasets %

3.3.3 加速性能对比

为了更直观地展现PIARAT在并行属性约简方面的加速效果, 选取含有百万数据样本量的Pokerhand、KDD Cup、HIGGS这3个较大型数据集进行对比实验.

IARAT和PIARAT的加速性能对比如表5所示, 表中“ -” 表示IARAT无法运行或运行时间太长.由表可看出, 相比IARAT, PIARAT在处理大规模数据集时总体运行时间大幅缩短, 对于IARAT无法运行的数据集也可在可控的时间内计算出约简结果, 这表明PIARAT具有良好的加速能力.在向决策系统中添加一些对象时, IARAT和PIARAT划分属性子集的AP值和AQ值非常接近或相同, 表现为1或0.99.这说明, 经过Spark并行机制加速后的增量算法生成的约简与原算法生成的约简具有几乎相同的分辨能力, 即算法3找到的约简是可行的.

表5

Table 5

表5(Table 5)

表5 IARAT和PIARAT加速性能对比 Table 5 Comparison of speedup performance between IARAT and PIARAT 数据集 IARAT PIARAT AP AQ 运行时间/s AP AQ 运行时间/s Pokerhand 1 1 1671.156 1 1 188.943 KDDCUP 1 0.99 - 1 0.99 1425.253 HIGGS 1 0.99 - 1 0.99 2572.363

表5 IARAT和PIARAT加速性能对比 Table 5 Comparison of speedup performance between IARAT and PIARAT

本文在8组UCI数据集上进行运行时间、分类性能及加速性能的对比实验.

由图5可看出, IARAT的运行时间在不同数据集上均小于对比算法, 而且在一定范围内随着增量数据规模的增大, 运行时间也在可控范围内平稳增加.例如, 在Qsar数据集上, IARAT和GIRAC在增量数据不断增大的过程中运行时间始终保持平稳, 而IARC和IARM在后半段运行时间涨幅均存在明显变大趋势.而在样本数最大的Letter数据集上, IARAT的计算优势更明显, 这主要是因为在属性树每轮分支过程中只需要评估少量的候选属性(取决于属性树的数量), 由于搜索空间的减小, 可缩短相应的运行时间.同时, 使用核心属性约简算法替代传统约简算法, 避免每轮循环中非常耗时的属性重要性的计算过程, 进一步缩短运行时间.

由表3和表4可得出, IARAT在缩短运行时间的同时, 也保持算法的分类质量及分类精度.这样的结果表明, IARAT通过构建属性树并进行分支的策略可在不牺牲分类准确率的情况下有效减少属性约简的计算时间.然而如下问题值得考虑:1)在属性聚类阶段, 选择K-means, 不同聚类算法的选取是否会影响分类精度; 2)在IARAT中, 对于不同的数据集, 并未相应调整属性树的数量, 如何找到最优的聚类中心数量以达到最低的耗时.这些问题依然值得继续研究.

由表5可看出, 相比IARAT, PIARAT在处理大规模数据集时的总体运行时间大幅缩短, IARAT无法运行或运行时间太长的数据也可进行有效约简计算, 因此, 通过Spark并行计算机制可有效提高算法2的计算效率, 减少运行时间.这主要是因为Spark计算引擎可对属性约简算法进行并行化, 以分布式计算的机制替代传统的串行机制, 由此实现海量数据的并行约简计算.但是, 在并行处理方面, 本文算法的多棵树分支策略和多节点并行机制的深度契合值得进一步优化, 对于不同的数据集(不同样本数量、不同属性数量), 如何进行数据集的最优划分和子集的最优分配将是今后工作的重点.