孙焕良,博士,教授,主要研究方向为空间数据管理、数据挖掘.E-mail:sunhl@sjzu.edu.cn.
作者简介:
刘俊岭,博士,副教授,主要研究方向为时空数据查询、数据挖掘.E-mail:liujl@sjzu.edu.cn.
丁思博,硕士研究生,主要研究方向为时空数据查询.E-mail:dingsibo97@foxmail.com.

于 戈,博士,教授,主要研究方向为数据库理论与系统.E-mail:yuge@mail.neu.edu.cn.

许景科,博士,教授,主要研究方向为时空数据库、数据挖掘.E-mail:xujingke@sjzu.edu.cn.
城市空间功能结构分析是城市地理信息领域的一个重要研究方向,正确分析空间功能可合理规划资源及方便居民利用城市空间.因此,文中提出时间敏感的城市功能区主题模式发现模型,用于分析随时间变化的城市动态功能区结构.模型中将城市空间网格化处理为多个空间单元,结合用户访问数据和兴趣点(Point of Interest, POI)数据对空间单元进行嵌入表示.在时间维度上对主题特征向量进行聚类后得到具有差异性的特征分布矩阵,完成时段划分.在空间维度上对具有类似特征分布的相邻区域进行合并,最终得到具有时间敏感性的城市功能主题模式.基于北京市共享单车轨迹数据和百度地图查询数据划分动态功能区,可视化展示功能区划分的合理性,并利用聚类评价指标验证文中模型的有效性.
SUN Huanliang, Ph.D., professor. His research interests include spatial data management and data mi-ning.
About Author:
LIU Junling, Ph.D., associate professor. Her research interests include spatio-temporal data query and data mining.
DING Sibo, master student. His research interests include spatio-temporal data query.
YU Ge, Ph.D., professor. His research interests include database theory and system.
XU Jingke, Ph.D., professor. His research interests include spatio-temporal database and data mining.
The analysis of urban spatial function structure is a hot research direction in the field of urban geographic information. Correct analysis of spatial function can reasonably plan resources and facilitate residents to utilize urban space. Therefore, a model for discovery of time-sensitive thematic patterns in urban functional areas is proposed to analyze the dynamic urban functional area structure changing with time. In the model, the urban space is gridded into multiple spatial units, and the spatial units are embedded and represented by combining user access data and point of interest data. After clustering the theme feature vectors in the time dimension, the feature distribution matrix with differences is obtained to complete the period division. In the spatial dimension, the adjacent areas with similar feature distribution are merged to obtain a time-sensitive urban function theme model. Based on the shared bicycle trajectory data of Beijing and Baidu map query data, the objective dynamic functional areas are divided, the rationality of functional area division is visualized, and the effectiveness of the proposed model is verified via clustering evaluation measures.
城市功能区为城市中具有某种主题功能分布的空间区域, 如由中央商务区及其周边组成的功能区中包括金融、贸易、服务、购物等功能.城市功能区描述城市空间的使用情况和结构, 合理的功能区划分能用于城市运行规律发现、城市功能规划和推荐、社会空间差异分析等领域, 可有效改进城市资源分配和决策制定[1, 2].
随着基于位置的服务平台广泛普及, 平台获取大量包含居民时空活动的GPS数据, 这些数据可用于发现空间区域功能主题, 进而划分城市功能区.功能区结构可使用功能主题模式表示, 主题模式为给定区域中功能的类别分布.现有基于位置的服务平台数据进行城市功能区划分的方法包括如下3类:1)利用轨迹数据变化差异进行区域划分[3], 仅能完成粗划分; 2)利用兴趣点(Point of Interest, POI)分布特征进行区域划分[4], 可发现空间功能聚集特征, 但对POI数据完整性有较高依赖; 3)利用主题模型, 通过POI类别和轨迹数据, 根据居民活动规律进行区域划分[1, 5, 6], 通过城市主题分布特征得到区域划分.
现有研究中划分的功能区为静态的, 在一定时间段内功能区的表示为单一主题模式, 模式不会随时间而变化.然而, 城市居民活动往往具有时间敏感性, 同一区域在其主题功能上会随时间发生变化.在给定时间跨度上, 功能主题模式为区域内不同时段用户对于各功能活动倾向的分布规律.时间敏感的城市功能区主题模式发现可实现对城市功能区的细粒度功能划分, 应用于构建城市大脑、分时广告投放、智慧交通管理等方面, 如在交通管理中, 对不同时段主题差异大的区域实现人员流动规划与动态交通治理等.
由实例可知, 功能主题模式抽取任务应同时考虑空间与时间两种因素, 因此对城市空间进行动态功能区划分可看作基于功能主题的时空聚类问题.研究目标是在给定时空范围内得到对空间和时间的合理划分.
由于功能主题模式具有时间敏感性, 从单一的静态POI数据中无法获得动态的主题模式, 需要结合用户访问POI的轨迹信息以实现.然而现有行为轨迹数据较稀疏, 存在噪声, 难以直接发现有效的动态功能模式.
为了发现给定时间与空间范围内稳定的模式, 需要将划分的子空间进行聚合, 如何同时考虑时间与空间维度的模式发现是一个挑战.本文提出时间敏感的城市功能区主题模式发现模型.在时间维度上对主题特征向量进行聚类后得到具有差异性的特征分布矩阵, 实现动态的时段划分.采用JS散度(Jensen-Shannon Divergence)度量模式, 将时间段内具有相似分布的功能主题特征进行合并, 得到新的时段划分结果, 对不同周期上的时间段划分进行对齐再合并, 最终得到跨周期的模式时段序列.为了在空间维度上对具有类似特征分布的相邻区域进行合并, 本文提出邻域网格聚类算法, 基于最近邻思想对相似子空间特征矩阵进行聚类, 生成区域边界, 完成空间划分, 最终得到具有动态特征的功能区划分结果.最后, 在真实数据集上分析本文模型, 验证模型的有效性.
模式指对象活动的一般方式, 数据中反映的模式通常用于描述用户的行为规律.Zhang等[7]提取高校学生的行为模式特征, 分析其行为与课程绩效的关联性.在金融领域中, Huang等[8]针对区块链中模式, 提出相似性度量, 用于高精度聚类.在Web应用中, 模式用于发现用户的特征、偏好和习惯, Chovanak等[9]将典型重复的用户行为特征作为行为模式, 实现个性化预测和推荐等任务.同样在Web浏览行为分析上, Hussain等[10]利用用户上网行为模式和网络轨迹, 分析用户兴趣和认知预测.
时空轨迹数据记录用户的位置序列, 近年来学者考虑将出行路径相似的用户进行聚类, 再发现其共同的行为规律.部分研究利用主成分分析提取轨迹数据中稳定的移动模式, 用于用户位置预测或是静态POI对GPS轨迹数据的标注, 再进行语义判断[11, 12].Cao等[13]提出基于表示学习的用户轨迹语义表示系统, 通过向量的形式表示轨迹数据特征.Maiti等[14]针对空间数据中提取的行为模式, 提出相似性度量及对应模式的挖掘方法.
对于多源异构的轨迹数据, 经过融合集成后往往存在高维度和高稀疏性的问题, 无法直接进行模式抽取分析, 通常需要进行降维.Xu等[15]总结大规模异构数据处理时经典的基于机器学习的数据降维方法及其应用.Yan等[16]开发面向轨迹文本数据的特征分析算法, 用于提取数据中的特征, 达到有监督或无监督的数据降维目的.
城市功能区划分是通过POI分布或用户行为发现具有某种主题功能分布的空间区域.随着数据获取途径的增加及GPS的普及, 利用用户轨迹数据进行功能区划分成为主要方法.功能区划分方法主要分为基于统计学划分和基于机器学习划分两种.
基于传统统计学方法, Hu等[4]提出利用城市POI数据的分布和其功能类型比值等统计特征划分城市功能区, 并分析不同功能区的空间分布特征.Qi等[3]根据出租车乘客上下车的时间变化规律进行区域功能判断, 使用聚类的方法划分功能区域.
机器学习技术也被应用于城市分析和功能区划分.Tao等[17]利用GPS数据, 构建四维张量, 发现用户行为在不同时间的规律, 并进行空间聚类以划分城市区域.Papadakis等[18, 19]量化空间信息的语义, 对地理空间赋予功能属性, 整合至地理信息系统中, 进而结合POI属性和数据驱动, 提出基于隐含狄利克雷分布(Latent Dirichlet Allocation, LDA)的功能区划分模型, 并评价划分结果.在此基础上, Wang等[6]为了理解多中心城市区域的空间结构, 提出基于狄利克雷多项式回归的模型, 利用交通模式和POI数据获取城市单元功能, 发现不同区域之间的相互关系及城市的功能分布.Yuan等[1]结合POI数据和出租车轨迹数据, 基于主题的LDA模型提取用户出行规律, 并分析各功能在不同地理位置的强度.
总之, 目前研究大多从空间维度上利用不同方法进行城市功能的划分并得到功能区.
为了从时空数据集中获取有价值的信息, 时空聚类能划分具有相似时间、空间的数据集合, 发现时空要素的发展规律和趋势.
Parente等[20]旨在将具有相似属性的对象分组到各自的类别中, 提出时空排列扫描统计方法, 完成时空聚类任务.Paci等[21]提出以状态空间为中心的贝叶斯半参数混合模型, 完成时间序列的聚类, 引入时空变化的混合权值, 设计基于时空模型的方法, 实现时空数据中的动态聚类, 预测时空依赖性.Meliker等[22]利用依赖于时间最近邻的方法, 对用户居住史进行时空聚类分析, 发现不同类别之间的潜在关系.
许多时空现象具有顺序性和层次性, 研究对象具备固定的空间位置和规则的时间步长.传统的时空周期模式挖掘并未考虑其内在的层次性, Zhang等[23]提出基于Traclus的轨迹聚类算法, 补充时空序列, 在轨迹数据聚类时同时考虑方向、速度等语义时空信息.Pereira等[24]提出时空排列扫描统计量, 识别聚类结果的数量、位置和时空维度, 提高聚类结果的精确度和鲁棒性.
定义1 单元功能主题特征 给定单位时间跨度t为时间维度上的最小划分粒度.空间单元g为空间维度上的最小区域划分, 表示为g=(α , ft), 其中, α 为空间单元g的地理坐标, ft为空间单元g内主题的概率分布向量, 称为单元g的功能主题特征, 其中向量维度表示功能类别, 记为ft(i), 且
ρ 为向量维数.
一个时间段T由多个单位时间跨度t组成, 整体空间G可划分为n个大小相同的空间单元g, 表示为
G={g1, g2, …, gn}.
定义2 功能主题模式 在给定空间区域R上, 一个时间段T内的功能主题分布规律称为该时空域的功能主题模式, 由功能主题分布向量F表示, 记为P(R, T)=F, 其中, 空间区域R由多个主题特征相似的相邻空间单元g组成, 在该时空域中概括各空间单元的功能主题特征, 获得功能主题分布向量F.
功能主题模式旨在发现城市时空演变, 挖掘用户行为习惯规律, 进而划分城市功能区.
定义3 动态城市功能区划分 给定整体空间G与时间段T, 根据功能主题特征对空间区域和时间段划分后有∀ gi⊂G, 对于gi上任意时间跨度ti⊂T, G内两个空间相邻的子区域gi、 gj或时间段相邻的区域gi(ti)、 gi(
sim(P(gi, ti), P(gi,
或
sim(P(gi, t), P(gj, t))≥ θ ,
则两区域可合并, 功能主题模式合并结果为P(R, T'), 其中R={gi, gj}, T'={ti,
基于功能主题模式P(R, T')获得的具有不同时空划分城市动态功能区域是由处于不同时间跨度的时空相邻的空间单元组成.例如, 当时间范围为[9:00, 11:00]时, 主题分布向量为F, 则功能主题模式可表示为P(R, [9:00, 12:00])=F.
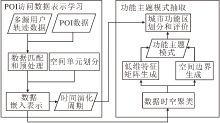
本文提出时间敏感的城市功能区主题模式发现模型, 流程如图1所示.模型包括POI访问数据的表示学习和功能主题模式抽取两个阶段.第一阶段融合多源数据, 利用轨迹数据标记POI访问频率.然后, 对空间进行网格划分, 得到空间单元, 并实现对空间单元的数据嵌入表示学习, 解决数据稀疏和噪声问题.第二阶段对嵌入得到的包含潜在特征的低维主题特征向量进行时空聚类, 对空间和时间段进行切分重组, 对于每个空间单元, 得到由其不同时间跨度的单元功能主题特征构成的主题特征矩阵, 进行区域空间扩展后得到具有时间敏感的功能主题模式.结合功能区评价指标, 获得城市整体空间中随时间变化的动态功能区域划分.
本文以北京市主城区作为分析区域, 网格化处理空间区域, 得到多个相同规格的矩形空间单元.对用户轨迹数据融合并标注北京POI访问次数分布情况, 标注的方法为基于概率传播的匹配模型[25, 26].统计空间单元中各功能类别POI访问次数后获得单元功能主题特征, 其中特征向量的一个维度表示一个主题功能.
由于POI类别的多样性和轨迹数据的稀疏性, 单元功能主题特征分布无法准确表示单元空间内用户的活动规律.为了解决此问题, 本文基于自编码器的表示学习获取数据的潜在低维特征, 用于准确发现单元内部用户活动规律.
自动编码器神经网络是一种应用反向传播的无监督学习算法[27, 28], 对于一组未标记的训练样本集Vn={x1, x2, …, xn}, 自编码器不断学习函数h, 使得hw, b(x)≈ x, 调整权重项W和偏置项b, 使目标输出值等同输入, 即yi= xi.本文使用增加稀疏惩罚项的自编码器, 目的是找到隐藏层中神经元集合s数据内部的规律.方法需要对s中部分神经元进行抑制, aj(xi)表示隐藏层中当输入xi时神经元j的激活度, 可计算该神经元在不同输入下的平均活跃度:
为了保证
Jsparse(W, b)=J(W, b)+β
稀疏自编码器可有效表示高维稀疏的数据, 同时能提升线性可分性.
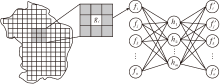
基于自编码器的降维模型输入为空间G内标注后的高维行为数据.为了解决轨迹数据稀疏的问题, 本文选择在模型输入时考虑空间邻域信息, 使单元空间向外扩展, 并将其映射至同一矢量空间进行空间维数压缩并表示.由于城市功能的高度聚集性, 对于扩大范围后的数据, 降维模型能有效降低数据稀疏和噪声数据的影响.整个学习过程如图2所示.
对于空间单元gi, 将其空间邻域网格区域gn(n=1, 2, …, e)数据同gi的主题特征合并为ρ +e× ρ 维向量进行输入.
观察发现, 同空间区域内, 部分相邻时间跨度的主题特征具有相似分布, 需要将向量的细粒度划分合并为粗粒度划分, 用于发现行为规律.本文提出基于嵌入表示的功能主题模式抽取算法(Thematic Patterns Extraction Based on Embedding, TP2E), 将单位时间跨度聚类后对整体区域进行空间划分, 完成时空聚类后, 得到功能主题模式.算法1描述功能主题模式抽取算法的过程, 分为时间维度聚类和空间维度扩展两部分内容.
算法1 TP2E
输入 时段T内的空间G={g1, g2, …, gn}
输出 功能区主题模式集P
1.初始化F={ }, C={ }, P={ };
2.将gi同邻域空间合并后进行表示学习;
3.for (每个空间单元gi)
4. 获取gi在T内功能主题特征向量表示f;
5. Fi=Temporal_Cluster(gi, f ) ;
6. 将主题特征矩阵Fi加入集合F中;
7.end for
8.基于F中时间跨度划分对空间单元gi聚类, 得到
簇C={c1, c2, …, cm};
9.for (每个簇ci)
10. P(R, T')=Spatial_Extension(F, ci) ;
11. P=P∪ P(R, T');
12.end for
13.return P
算法1的执行过程如下.第1~2行将输入的时间段T内最小空间单元gi的主题特征向量进行嵌入表示.第3~7行调用算法2实现时间维度的聚类, 获得重划分时段T内gi特征矩阵Fi并加入集合F中.第8~13行对所有空间单元, 基于时段划分, 利用K-means聚类后得到簇集合C, 调用算法3在每个簇内对gi实现空间扩展, 返回区域划分R和对应时段划分T'的集合, 计算集合内对应的主题分布向量, 并入结果集P中.
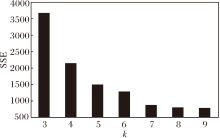
K-means效果较优, 收敛速度较快, 对于时段划分数据较契合, 能通过误差平方和(Sum of Squares due to Error, SSE)肘方法确定K值.
算法2为一个时间维度聚类算法, 对每个空间单元上的主题特征向量进行聚类.
算法2 Temporal_Cluster(gi, f )
1.while(∀ 相邻时间跨度向量JS(ft,
2. 合并向量并更新原本跨度为t'=[t, t+1];
3.得到gi在时间段T上的跨度重划分;
4.计算gi的主题特征向量矩阵Fi;
5.return Fi
算法2执行过程如下.第1~2行判断该单元内在时间跨度t内的主题向量ft和其相邻时间点的向量
在空间单元gi上的部分主题特征向量会发生时间演变.若相邻时间跨度的两个特征向量相似, 呈稳定状态, 需要对向量平均化处理并更新时间跨度.否则表示主题功能结构存在较大差异, 不需要合并.算法2最终会输出各空间单元在新划分时间段T内的低维特征矩阵, 用于后续进行同时考虑时空维度上的区域空间扩展.
本文选择基于KL散度演变的JS散度度量时间演变后的两个功能主题特征之间的相似度, 见算法2第1行.JS散度定义如下:
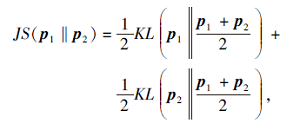
其中pi(i=1, 2)表示d维的概率分布向量.
JS散度结果为[0, 1]的常数, 对于2个向量完全没有重叠时的结果仍有意义, 并解决KL散度非对称的问题, 有效应对稀疏数据中概率为0的情况.
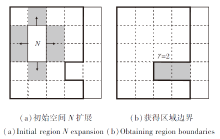
算法3为功能主题模式抽取任务中的空间扩展过程.本文提出空间扩展算法, 进行空间区域划分.该算法在具有相同时段划分的簇内寻找最相似的2个相邻空间单元, 记为初始空间N, 如图3(a)所示.阴影区域作为候选区域, 基于相似度判断是否合并, 不断进行空间边界扩张, 直至簇内剩余空间单元无法合并, 且个数小于给定可忽略值γ (如图3(b)所示), 完成扩展, 得到时空划分集合.可忽略值γ 为簇内数据量过小的单元个数, 取值区间为[0, cnum/2) , 其中cnum表示簇内单元总数.算法3具体步骤如下.
算法3 Spatial_Extension(F, c)
1.初始化R={ }, T'={ };
2.while (c≠ Ø ) do
3. 计算簇c内相邻空间单元相似度;
4. for (c内空间单元数可忽略值大于等于γ ) do
5. 合并簇c内最相似空间单元, 记为N;
6. 空间N的横、纵相邻区域加入候选空间集合Nc中;
7. if (Optimized_Merge(Nc, N)≤ θ ) then
8. N同最相似候选空间合并后更新;
9. 从c内移除候选空间单元信息;
10. else
11. 将空间N存入集合R中;
12. 将所在簇的时段划分存入集合T'中;
13. end if
14. end for
15.return(R, T')
算法3执行过程如下.第4~5行寻找簇内某两个最相似空间, 合并主题特征矩阵后记该空间区域为初始空间N, 利用最小距离法确定相似度阈值θ .最小距离法为分类器内确定分类阈值的基本方法, 求解未知类别向量q到事先已知的各类别中心向量的距离以确定阈值θ .第6行将初始空间N的矩形邻域作为候选空间并存入集合NC中.第7~13行将候选空间集合同空间N进行相似度计算, 选择最相似的两个空间合并, 更新空间N作为合并结果, 移除簇内的空间信息, 完成区域扩展.最后将对应空间划分和时段划分存入集合R和T'中.
对于同簇内不同空间单元来说, 任意2个单元时间段划分仍有不同, 为了更准确地对这种空间单元进行相似性度量, 本文提出优化合并度量的计算方法, 见算法4.
算法4 Optimized_Merge(gx, gy)
1.获取两个子空间的主题特征矩阵Fx、Fy;
2.在各时间跨度内随机取时间点, 加入临时序列L中;
3.按照序列L中的时间点从Fx、Fy抽取向量, 得到临时对比矩阵F'x、F'y;
4.基于F'x、F'y计算相似度ω ;
5.return ω
算法4执行过程如下.第1~2行对于两个相邻空间单元gx、 gy, 根据其不同的时段划分, 在各时间跨度内随机取点, 记为临时序列L.第3~4行对于这两个相邻空间分别按照L中的时间点取出对应向量, 得到两个规格相同的概率分布矩阵后, 计算余弦相似度.算法4能将具有不同时间跨度的空间进行向量抽样, 基于抽样结果进行相似度对比.
相比现有模式发现算法, TP2E考虑模式时间演变问题.获取特征矩阵F后, 将n个空间单元聚类为k个簇, 实现时空聚类的代价为
|F|×
可表示为O(|F|n2), | F|为特征矩阵F的大小.
实验数据包括地理空间数据集和用户访问轨迹数据集.地理空间数据集为北京市187万条POI数据, 包含地理坐标、地址、所在区域等属性.用户访问轨迹数据来自百度地图查询数据和摩拜共享单车轨迹数据这2个真实数据集.
百度地图查询与共享单车数据集上包含用户出发时间、起始位置和终点位置等属性, 数据集样例如表1所示, 起始位置由经纬度表示.百度地图查询数据为2017年5月北京市数据, 本文实验所选区域涉及用户数约72万个, 数据量为1 243万条.摩拜共享单车数据为2017年5月北京市单车骑行轨迹数据, 实验选择区域涉及用户数约61万个, 数据量为321万条.
| 表1 实验数据集样例 Table 1 Examples of experimental datasets |
本文选择如下功能区划分模型进行实验对比.
1)BaseDC.基于密度的功能区划分算法, 确定区域中的子空间后, 计算空间内功能频率密度和功能类别内外排序, 通过POI密度数据发现城市功能分布特征[2, 4].
2)BaseLDA.基于LDA的功能区划分算法, 在利用LDA提取城市功能结构时, 将空间区域视作文档, 将区域内功能视为主题, 而对应POI类别视为元数据, 方法类似于文本上下文中的主题抽取.形成三层贝叶斯模型架构后, 基于LDA模型能使用一个概率分布表示该区域的功能结构, 发现主题关联, 实现功能区划分[1, 6, 19].
3)TPE.本文提出的无降维的功能主题模式抽取算法, 对空间单元数据实现时空聚类后获取主题功能模式, 基于主题模式获取功能区划分.
4)TP2E.本文的功能主题模式抽取算法, 在完成对空间单元数据降维后进行时空聚类, 对各空间单元的时间跨度进行重划分后实现空间扩展, 发现具备时间敏感的功能主题模式, 获取动态城市功能区域的划分.
本文选取北京市朝阳区作为实验区域, 空间面积为470.8 km2, 需要对空间网格化处理.现有相关研究将区域划分为0.5 km× 0.5 km至1 km× 1 km的规则网格[2, 4, 17], 本文选择将实验区域划分为1 km× 1 km的规则网格, 单位时间跨度t为1 h, 选取部分区域展示模型有效性.
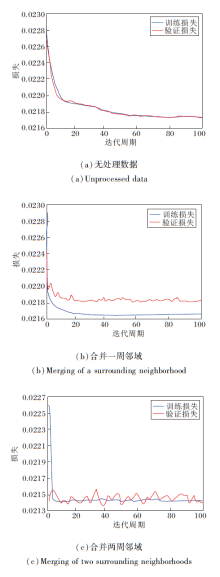
图4为数据嵌入模型的损失曲线变化, 自编码器降维模型可有效降维并解决数据稀疏问题.
图4(a)中无处理数据在自编码器降维模型中的损失呈曲线重叠状态, 对于均匀分布的稀疏数据, 验证损失往往高于训练损失, 而且使用数据量稀疏的空间单元发现功能聚集区域的效果较差, 故需要合并单元的空间邻域.将空间单元与向外一周所有邻域合并, 作为输入进行降维, 损失(如图4(b)所示)趋于收敛, 模型的学习效果较优.选择向外两周的邻域空间单元同目标空间单元合并, 损失(如图4(c)所示)存在波动, 故选择第1种数据嵌入表示方法.
基于主题模式的功能区划分可归属为时空聚类任务, 因此可利用聚类性能评价指标进行评价.本文选择两种典型的聚类评价指标— — 轮廓系数(Silhouette Coefficient, SC)和Calinski-Harabasz系数(CH), 并计算SSE, 利用SSE肘方法发现最优时间跨度聚类个数k, 完成K-means聚类任务.
数据嵌入表示在解决数据稀疏的同时提升聚类性能, 故TP2E聚类效果具有明显优势.不同聚类数量k下的度量值变化如图5所示.
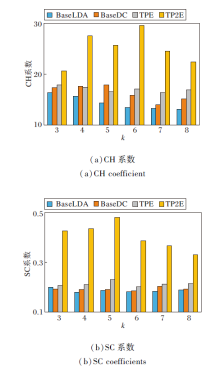 | 图5 簇个数k变化时各模型的聚类性能对比Fig.5 Clustering performance comparison of models with different numbers of cluster k |
各模型的最优聚类数量k及对应指标值如表2所示.由表可见, 基线方法未能解决数据稀疏问题, 导致无法精准选取特征, 不同簇间相似度较高.TP2E增强空间单位对邻域的相关性, 解决数据稀疏问题后, 聚类效果具有明显提升.
| 表2 各模型的最优k值及指标值 Table 2 Optimal k value and index value of different models |
不同周期的相同时段数据合并后的SSE值如图6所示.针对SSE曲线, 通过肘方法取SSE曲线中下降率变缓时的k值, 判断最优时间跨度聚类个数, 并通过CH系数和SC系数验证后, 按照该值对局部区域的时间进行聚类, 获得不同时间跨度.
本文选择功能频率密度和比率指数对划分城市空间区进行可视化, 用于评价划分结果.频率密度
FDi=
其中, i=1, 2, …, ρ , 表示功能类型, ai表示时空单位内i类型的数据量, Ai表示时间单位内i类型的总数.
比率指数
RAi=
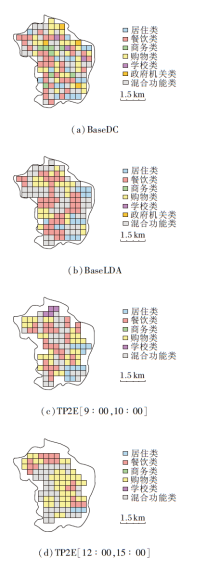
为类别为i的数据在空间单位内的频率密度之比.不同空间内各功能比率指数RA≤ 40%时, 认为是混合功能类区域.本文利用3.2节进行功能主题模式的抽取, 计算各模式的比率指数, 确定各区域的功能, 并以图形化的方式展示.
各模型的功能区划分结果如图7所示, 图中颜色区分不同主题功能.基于主题模式划分的功能区在不同时间跨度具有明显差异.基于密度的功能区域划分结果如图7(a)所示, 在功能空间分布上较分散, 无法获得合适的城市功能区域.基于LDA的功能区域划分结果如图7(b)所示, 能划分合适功能区域, 但对于整个时间周期的区域功能划分粒度过粗.
TP2E获得的9时~10时和12时~15时这2个时间跨度内的功能区划分结果如图7(c)、(d)所示, 在满足一定划分粒度的前提下, 仍能划分较真实的功能区域.对于同一区域, 图7(c)中可看出餐饮类和购物类功能区占比最高, 而在图7(d)中可发现在其它时间跨度变为购物类功能区占主导地位, 即发生城市功能结构时间演变.这种演变是无法通过现有功能区划分方法体现的, 而利用功能主题模式发现的功能区划分方法能更好地诠释这种变化规律.
针对时间敏感的城市功能区主题模式发现问题, 本文提出时间敏感的城市功能区主题模式发现模型, 嵌入用户轨迹数据后, 获取潜在结构, 划分不同的时间跨度, 并扩展功能空间区域, 抽取功能主题模式, 划分动态的城市功能区.本文使用北京市的用户出行轨迹数据进行研究, 证实本文模型的可行性.相比现有方法, 功能主题模式的时空聚类效果更优, 能应对数据稀疏的情况, 并根据主题分布的时空演变发现城市用户活动的时空敏感性, 使功能区划分结果更真实.未来的工作可以研究基于动态功能区的设施选址、兴趣点推荐等问题.
本文责任编委 陈恩红
Recommended by Associate Editor CHEN Enhong
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|
| [19] |
|
| [20] |
|
| [21] |
|
| [22] |
|
| [23] |
|
| [24] |
|
| [25] |
|
| [26] |
|
| [27] |
|
| [28] |
|