引用本文
李凤英, 何晓蝶, 董荣胜. 融合语义信息的知识图谱多跳推理模型. 模式识别与人工智能, 2022,35(11): 1025-1032
LI Fengying, HE Xiaodie, DONG Rongsheng. Multi-hop Inference Model for Knowledge Graphs Incorporating Semantic Information. PATTERN RECOGNITION AND ARTIFICIAL INTELLIGENCE, 2022,35(11): 1025-1032.  
Doi: 10.16451/j.cnki.issn1003-6059.202211007
Permissions
Copyright©2022, 《模式识别与人工智能》编辑部
《模式识别与人工智能》编辑部
融合语义信息的知识图谱多跳推理模型
李凤英1, 何晓蝶1, 董荣胜1
1.桂林电子科技大学 广西可信软件重点实验室 桂林 541004
通信作者：

董荣胜,教授,主要研究方向为知识图谱、机器学习、计算思维.E-mail:ccrsdong@guet.edu.cn.

作者简介：

李凤英,博士,教授,主要研究方向为知识图谱、机器学习、符号计算.E-mail:lfy@guet.edu.cn.

何晓蝶,硕士研究生,主要研究方向为机器学习、知识图谱.E-mail:abu_822@163.com.

收稿日期: 2022-04-28 接受日期: 2022-11-07
资助项目: 国家自然科学基金项目(No.62062029,61762024)资助
摘要

多跳推理模型在知识图谱中充分挖掘和利用实体间的多步关系,组成路径信息,完成知识推理,然而,目前的稀疏知识图谱多跳推理模型大多存在数据稀少及推理路径可靠性较低等问题.为了解决该问题,文中提出融合语义信息的知识图谱多跳推理模型.首先,将知识图谱中的实体和关系嵌入向量空间,作为强化学习训练的外部环境.然后,利用查询关系和推理路径的语义信息,选择相似度最高的(关系,实体)对扩充智能体进行路径搜索的动作空间,以此弥补推理过程中数据稀少的不足.最后,使用推理路径和查询关系的语义相似度评价推理路径的可靠性,并作为奖励函数反馈给智能体.在多个公开稀疏数据集上的实验表明,文中模型明显提升推理性能.

关键词: 知识推理; 强化学习; 知识表示; 语义信息
中图分类号:TP 391
Multi-hop Inference Model for Knowledge Graphs Incorporating Semantic Information
LI Fengying1, HE Xiaodie1, DONG Rongsheng1
1. Guangxi Key Laboratory of Trusted Software, Guilin University of Electronic Technology, Guilin 541004
Corresponding author:
DONG Rongsheng, professor. His research interests include knowledge graph, machine learning and computational thinking.

About Author:
LI Fengying,Ph.D., professor. Her research interests include knowledge graph, machine learning and symbolic computing.
HE Xiaodie, master student. Her research interests include machine learning and know-ledge graph.

Fund:National Natural Science Foundation of China(No.62062029,61762024)
Abstract

In multi-hop inference models, path information is formed by fully mining and utilizing multi-step relationships between entities in the knowledge graph to accomplish knowledge inference. To solve the problems of sparse data and low reliability of inference paths in most of the existing sparse knowledge graph multi-hop inference models, a multi-hop inference model for knowledge graphs incorporating semantic information is proposed. Firstly, entities and relations in the knowledge graph are embedded into the vector space as the external environment for reinforcement learning training. Then, the semantic information of query relations and inference paths is employed to select the (relation, entity) pair with the highest similarity to expand the action space for path search by the agent, and thus the lack of sparse data in the inference process is compensated. Finally, the semantic similarity between the inference path and the query relation is utilized to evaluate the reliability of the inference path and it is fed back to the agent as a reward function. Experiments on several publicly available sparse datasets show that the inference performance of the proposed model is significantly improved.

Key words: Key Words Knowledge Reasoning; Reinforcement Learning; Knowledge Representation; Semantic Information

知识图谱是对真实世界信息的结构化表示.在知识图谱中, 节点表示实体, 标签表示连接它们的关系类型, 边表示连接两个具有关系的实体的特定事实.由于知识图谱能以机器可读的方式建模结构化的复杂数据, 现广泛应用于知识问答、信息检索、基于内容的推荐系统等[1, 2]领域.目前已构建的各种结构化知识图谱有:Freebase[3]、WordNet[4]、DBpe-dia[5].目前由于信息抽取、知识融合等关键技术水平的限制, 这些知识图谱仍处于一个不完备的状态.因此, 知识推理受到广泛关注.

在经典的知识图谱推理模型中, 基于翻译的模型将关系看作头实体到尾实体的翻译向量, Bordes等[6]提出TransE.针对TransE无法有效建模复杂关系的缺点, 学者们相继提出为每个关系构建独立超平面的TransH(Translation on Hyperplanes)[7]、引入关系投影的TransR[8]及使用向量运算替换矩阵运算的TransD[9].基于语义匹配的模型是通过衡量实体和关系的语义信息以衡量三元组的真实性, 例如:Yang等[10]提出DistMult, Nickel等[11]提出HolE(Holographic Embeddings)等.由于翻译模型和语义匹配模型都是在低维向量空间中进行训练, 不能较好地提取深层次特征, 因此为了提高模型提取特征的能力, 深度学习方法被引入知识图谱表示学习领域中, 例如:Dettmers等[12]提出ConvE, 将实体和关系表示成一维嵌入, 然后使用卷积层提取特征.

上述三种知识推理模型虽然在预测目标实体方面表现出强大实力, 但由于是通过向量计算得出推理答案的, 无法对其决策进行解释, 导致可解释性较差.

为了获得更具解释性的知识图谱推理, 近年来, 多跳推理得到广泛研究.多跳推理通过在知识图谱中充分挖掘和利用实体间多步关系组成的路径信息, 从而完成知识推理.最初的多跳推理模型大多通过随机游走算法搜索推理路径, 如Yang等[13]提出的Neural LP(Neural Logic Programming).但是知识图谱中连接大量节点的超级节点会影响推理的准确性, 因此, Xiong等[14]提出DeepPath, 将多跳推理建模成序列决策问题, 利用强化学习算法进行有效的路径搜索.智能体从源实体e_s出发, 每前进一步, 就使用策略网络选择最有前途的关系扩展它的路径, 直到抵达目标实体e_target.然而DeepPath必须先通过预训练得到完整的路径后, 才能进行策略网络的训练.因此, Das等[15]提出MINERVA(Mean-dering in Networks of Entities to Reach Verisimilar Answers), 引入长短期记忆模块(Long Short Term Me-mory, LSTM)记忆智能体走过的路径, 改进Deep-Path的不足.Lin等[16]提出Multi-hop KG, 加入奖励重塑和动作掩膜, 进一步提升多跳路径推理的性能.Zhou等[17]提出PAAR(Path Additional Action-Space Ranking), 认为现有的基于强化学习的多跳推理模型无法利用知识图谱中的层次信息, 因此引入双曲知识图谱嵌入模型, 捕捉层次信息, 并扩展用于推理的动作空间.Zhu等[18]认为在大多数知识图谱中, 由于同对(头实体, 关系)连接的尾实体有多个, 导致强化学习的智能体学习困难.为了解决该问题, Zhu等将经典强化学习框架分层, 分成一个检测关系的高级过程和一个推理实体的低级过程.

然而在稀疏知识图谱上, 现有的多跳推理模型存在两个问题:1)数据稀少.相比大型知识图谱, 稀疏知识图谱包含信息更少, 导致一些推理路径中断, 不能推出正确的答案实体.2)路径不可靠[19].由于智能体是在知识图谱上游走寻找推理路径的, 没有中间监督, 因此可能会出现推理结果正确, 但推理过程不可靠的现象.

近年来的多跳推理模型大多通过扩充智能体用于路径搜索的动作空间以解决数据稀少的问题.Fu等[20]提出CPL(Collaborative Policy Learning), 从背景语料库中抽取新的事实, 添加到动作空间中, 扩充智能体下一步路径的搜索范围.Lü 等[21]提出DacKGR, 根据当前智能体所在位置的状态信息, 通过概率预测与当前状态最接近的事实, 动态扩充智能体, 用于下一步路径搜索的动作空间.

面对路径不可靠的问题, 大多数研究者通过多样化奖励反馈解决此问题.DeepPath鼓励智能体推理的路径长度越短越好, 因为大多数推理结果表明:推理路径越短, 推理的准确性越高; 路径越长, 冗余关系的干扰性越强.Multi-hop KG将嵌入模型得分添入奖励函数中, 通过鼓励“ 预测结果不正确但有推理价值” 的路径, 反向抑制“ 预测结果正确但推理不可靠” 的路径.

为了解决现有多跳推理模型存在的两个问题, 本文提出融合语义信息的知识图谱多跳推理模型(Multi-hop Inference Model for Knowledge Graphs Incorporating Semantic Information, MIMKGISI).在通过表示学习方法构建强化学习的外部环境之后, 利用查询关系和关系路径的语义信息, 扩充智能体的动作空间, 扩大智能体路径搜索的范围, 解决推理过程中数据稀少的问题.路径搜索结束之后, 使用推理路径和查询关系的语义相似度作为奖励反馈给智能体, 通过反馈路径可靠度的形式, 提高智能体选择路径的质量, 提升多跳推理的性能.在4个公开的稀疏数据集上的实验表明, 相比多跳推理的基准模型, MIMKGISI具有更好的推理效果和可解释性.

1 融合语义信息的知识图谱多跳推理模型

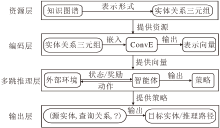
本文提出融合语义信息的知识图谱多跳推理模型(MIMKGISI), 框架如图1所示.在资源层, 使用实体、关系、三元组表示知识图谱; 在编码层, 使用ConvE将实体关系三元组嵌入向量空间, 输出对应的表示向量; 在多跳推理层, 通过强化学习中外部环境和智能体之间的动态交互, 学习得到一个用于搜索推理路径的最佳策略.给定一个查询三元组(源实体, 查询关系, ?), 根据最终训练得到的策略, 直接输出预测的目标实体及推理路径.

图1 MIMKGISI框架图Fig.1 Framework of MIMKGISI

1.1 问题定义

将知识图谱表示为G=(ε , R)的形式, 其中, ε 表示实体集, R表示关系集.知识图谱中的每条有向连接l=(es, r, eo)表示一个三元组.

给定一个查询(es, rq, ?), 其中, es为源实体, rq为查询关系, 对G进行有效搜索, 并收集可能的答案集Eo={eo}, 其中, (es, rq, eo)∉G, 因为知识图谱G是不完整的.

1.2 强化学习框架

近年来, 利用强化学习算法进行多跳推理的问题, 被定义为马尔可夫决策过程(Markov Decision Process, MDP)[15]:给定一个查询三元组(es, rq, ?), 智能体从es出发, 不断通过选择当前实体对应的出边(关系)到达新的实体, 直到抵达目标实体.具体来说, MDP主要由如下4部分构成.

1)状态.在多跳推理过程中, 每跳的状态可定义为st=(et, ht, rq, ep)∈ S, 其中, et为智能体在第t跳到达的实体, ht为前t-1跳的历史路径, rq为查询关系, ep为ε 中每个实体为目标实体的概率.

2)动作.当智能体处于状态st=(et, ht, rq, ep)时, 当前实体et对应的出边(r', e')称为动作, 状态st对应的所有动作组成当前动作空间

At={(r', e')|(et, r', e')∈ G}.

此外, 在每个动作空间中, 都添加一个自循环边.因为多跳推理的跳数是固定不变的, 不能中断, 需设置一个自循环作为推理结束标志.

3)转移.每跳的转移函数定义为S× At=S, 具体地, 如果当前状态选择动作(r', e')∈ At, 那么就会转移到新的状态st+1=(e', ht+1, rq, ep).

4)奖励.若最终第T跳智能体到达的实体eT恰好就是目标实体, 即eT=eo, 反馈的奖励就为1; 否则, 反馈的奖励为实体eT是目标实体的概率, 即嵌入模型分数f(es, rq, eT).具体表达式如下:

$R\left(s_{T}\right)=\left\{\begin{array}{ll} 1, & e_{T}=e_{o} \\ f\left(e_{s}, r_{q}, e_{T}\right), & \text { 其它 } \end{array}\right.$

策略网络指导智能体在不同状态下选择有前途的动作, 进行路径搜索完成多跳推理, 主要通过状态信息和动作信息进行参数化.具体地, G中的实体和关系, 被表示为低维连续向量e和r.由关系向量和实体向量的拼接向量at=[r; e]表示动作(r, e)∈ At, 动作空间At由At中的所有动作表示向量堆叠组成.状态中提到的历史路径ht由LSTM编码, 即

h0=LSTM(0, [r0; es]), ht=LSTM(ht-1, at-1), t> 0,

其中, r0为增加的一个特殊关系(无实义), 便于将源实体es的信息添加到历史路径中.

策略网络π 定义成

π θ (at|st)=σ (At× W2× ReLU(W1× [et; ht; rq; ep])), (1)

其中, W1、W2为2个全连接网络, ReLU(· )为激活函数, σ 为softmax运算符, θ 为参数.

本文采用REINFORCE算法[22]优化策略网络, 并通过随机梯度下降更新参数:

∇θJ(θ )≈ ∇θ∑tln(π θ (at|st))· R(sT|eS, r).

基于强化学习的多跳推理训练细节如下所示.

算法 基于强化学习的多跳推理训练过程

输入 给定的三元组集合

输出 策略网络π θ

1.Initialize θ

2.Pre-train the embedding vector e, r

3.for n← 1 to Epoch num do

4. for t← 1 to Time step do

5. Calculate ht← LSTM(ht-1, at-1)

6. Calculate st

7. Sample action at~π θ (at|st) by Eqs.(1)

8. Update hidden state ht

9. end for

10. Obtain rewards R

11. Optimize θ using

g∝ ∇θ∑tln(π θ (at|st))· R(sT|es, r)

12.end for

算法中, 第2行通过预训练嵌入模型生成实体和关系向量, 第4~9行进行策略网络的多跳推理, 第3~12行迭代训练强化学习的策略网络.

本文模型在嵌入模型预训练三元组向量表示的基础上进行知识推理.在强化学习训练阶段, 通过给定的查询头节点, 对图进行遍历的时间复杂度为O(|V|+|R|)L+1L), 其中, |V|为实体集大小, |R|为关系集大小, L为推理跳数.因此本文模型的时间复杂度为O((|V|+|R)L+1L).

上述就是目前通用的强化学习框架, 然而应用到稀疏知识图谱领域时, 由于数据稀少, 导致智能体的动作空间可能缺乏当前推理所需的关键动作, 本文模型利用查询关系和关系路径的语义信息扩充动作空间, 缓解推理过程中关键关系缺失的现象.另一方面, 对于强化学习搜索的推理路径, 大多模型都仅通过预测目标的正确度反馈指导智能体的搜索方向,

未对推理路径的可靠性进行评判.因此, 本文模型通过推理路径和查询关系的语义相似度评价推理路径的可靠性, 并作为奖励反馈指导智能体的搜索策略.

1.3 动作空间扩展

由于稀疏知识图谱中包含的事实相对较少, 导致智能体在搜索路径时, 经常出现关键路径中断, 不能正确推导目标实体的现象.本文采用扩充动作空间的方法, 缓解多跳推理中数据量不足的问题, 但与DacKGR注重状态层次的关系注意力不同, MIMK-GISI注重语义层次的关系注意力.

当智能体搜索路径时, 由于缺乏中间监督, 会出现一条推理路径上前后关系跳脱、无语义联系性的现象, 称为“ 跳脱型推理” .针对该现象, 本文通过上一跳关系和查询关系的语义信息抑制智能体的跳脱型推理行为, 同时指导智能体的路径搜索方向.换句话说, MIMKGISI在每跳智能体选择有前途的动作之前, 利用与当前查询关系和上一跳推理关系最相似的(关系, 实体)对, 扩充当前实体的动作空间.

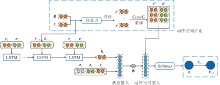
扩充动作空间的过程如图2所示.假设查询三元组(es, rq, ?), 智能体当前位于实体et上, 上一跳经过的出边(关系)为rt-1, 首先计算关系集R中所有关系与rq和rt-1的相似度:

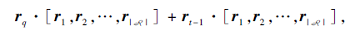
其中, ri为关系集R中第i个关系向量, “ · ” 为点乘运算.

图2 动作空间扩充结构图Fig.2 Structure of action space expansion

然后, 选择前k个与rq和rt-1最相似的关系, 使用底层的ConvE嵌入模型, 预测对应的尾实体组成(关系, 实体)对, 扩充动作空间At.

1.4 奖励函数重构

强化学习过程中没有中间监督, 智能体根据延迟的奖励反馈, 学习得到正确的搜索策略.因此, 智能体会搜索“ 结果正确但推理不可靠” 的路径.从语义层次上看, 对于每个查询三元组(es, rq, ?), 推理路径path应由从源实体es出发到目标实体eo的一组关系组成的, 而查询关系rq理论上是连接源实体es和目标实体eo的直接关系.因此, 可靠的推理路径和查询关系的语义应相近, 不可靠的推理路径与查询关系的语义应相差很大.

本文采用TransE的基本思想表示路径向量:将每个三元组(es, rq, eo)中的关系rq看作从头实体es到尾实体eo的翻译.具体地, 就是头实体向量加上关系向量近似等于尾实体向量:

es+rq≈ eo.

因此, 将推理路径path=(r0, r1, …, rT)表示成关系向量的累加, 即

path=r0+r1+…+rT.

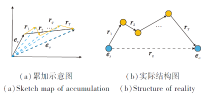
如图3所示, 左边是推理路径在低维向量空间中的累加示意图, 右边是推理路径的实际结构图.

图3 推理路径结构图Fig.3 Structure of reasoning path

本文通过抑制不可靠的推理行为, 达到鼓励智能体进行可靠路径推理的目的.换句话说, 本文使用推理路径和查询关系的相似度, 作为奖励反馈给智能体, 相似度越高, 表示该条推理路径越可靠, 反之不可靠.

奖励函数为:

R_global(sT)=R(sT)+cos< path, rq> ,

其中, cos< · , · > 表示余弦相似度, path表示推理路径, rq表示查询关系.

2 实验及结果分析
2.1 实验数据集

本文针对稀疏知识图谱, 选择在NELL23K、WD-singer、FB15K-237-10%、FB15K-237-20%这4个公开数据集[21]上进行实验, 具体数据集信息见表1.NELL23K数据集为NELL数据集的子集, WD-singer数据集取自Wiki百科数据集(仅选择其中与歌手相关的内容), FB15K-237-10%、FB15K-237-20%数据集分别为FB15K-237数据集随机采样10%、20%数据后生成.

表1 实验数据集 Table 1 Experimental datasets
2.2 基线模型

对于知识图谱多跳推理, 本文选择如下基线模型进行对比分析.

1)NTP(Neural Theorem Provers)[23].结合神经网络模型和基于规则的系统, 使模型能获得可解释性的规则, 学习反向传播过程中的表示, 为预测过程提供逻辑解释.

2)MINERVA[15].利用LSTM模块, 将智能体经历的历史信息编码到状态中.

3)CPL[20].联合策略学习框架, 不仅训练推理智能体, 而且利用事实提取部件, 从背景语料库中抽取新的事实以填充动作空间.

4)Multi-hop KG[16].利用预训练嵌入模型估计未观察到的奖励, 提出随机掩膜边机制, 探索更多样化的路径.

5)DacKGR[21].提出动态预测和补全, 动态扩充动作空间, 探索更多的推理路径.

6)PAAR[17].提出双曲知识图谱嵌入模型, 捕捉知识图谱中的层次信息, 扩展动作空间.

7)文献[18]模型.提出分层强化学习框架, 将推理任务分解为一个检测关系的高级过程和一个推理实体的低级过程.

2.3 度量方法

本文采用链接预测方法评价知识推理任务, 并对比其它模型.链接预测的具体过程是, 将测试数据集上的每个三元组(es, rq, eo), 转换成三元组查询(es, rq, ?), 然后使用嵌入模型或多跳推理模型得出目标实体的排名.本文实验使用“ 过滤后” 的实验结果[6].

本文使用命中率(Hits@3、Hits@10)和平均倒数排名(Mean Reciprocal Rank, MRR)这两个评价指标.Hits@3和Hits@10分别表示测试数据集中真实三元组排名达到前3名或前10名的概率, MRR表示测试数据集中真实三元组的平均倒数排名.在链接预测实验中, 这两个指标越高, 表示该模型推理准确性越高.

2.4 对比实验结果

各模型在4个数据集上的链接预测结果如表2所示, 表中黑体数字表示最优值, MIMKGISI-action表示MIMKGISI删除动作空间扩展后重构的模型, MIMKGISI-reward表示MIMKGISI删除奖励函数后重构的模型.实验中NTP、MINERVA、Multi-hop KG、CPL和DacKGR的实验结果引自DacKGR[21], PAAR和文献[18]模型的实验结果直接引自原文献.

表2 各模型在4个数据集上的链接预测结果 Table 2 Link prediction results of different models on 4 datasets

由表2可见, MIMKGISI在WD-singer、NELL-23K、FB15K-237-10%数据集上的推理性能有明显提升.但是在FB15K-237-20%数据集上, MIMKGISI的推理性能并未提升, MRR、Hits@3和Hits@10指标分别下降0.1%、0.3%和0.3%.根据表1中4个数据集的特征可看出, FB15K-237-20%数据集的稀疏程度最低, 并且一对多关系的占比最大, 可能是由于该数据集的数据量较充足, 语义信息对推理的指导作用不大, 导致模型性能没有提升.而文献[18]也提出, 相比其它数据集, FB15K-237数据集的实体和关系涵盖太多领域, 可能会混淆智能体的推理.

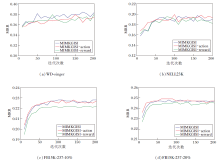
MIMKGISI、MIMKGISI-action、MIMKGISI-reward在4个数据集上的收敛曲线如图4所示.由表2和图4可看出, MIMKGISI-action和MIMKGISI-reward的综合性能都不及MIMKGISI, 表明移除动作空间扩展或奖励函数重构任一部分都会削弱模型的推理性能, 这两个策略都对模型有一定贡献.

图4 各模型在4个数据集上的收敛曲线Fig.4 Convergence curves of different models on 4 datasets

2.5 推理路径分析

为了验证MIMKGISI对知识推理的可解释性, 从智能体在FB15K-237-10%数据集上搜索的推理路径中, 选择如下三元组和3条推理路径:

三元组查询:(Lorenzo Ferrero, category, ?)

目标实体:Pianist

其中箭头表示关系的方向.针对“ Lorenzo Ferrero的类型” 的查询, 第1条推理路径的关系链为instrumentalists_inv→ instrumentalists→ category, 即根据弹奏同一乐器Piano的同行Thelonious Monk的类型为钢琴师, 从而判断Lorenzo Ferrero的类型也为钢琴师.其它推理路径类似, 不再展开分析.由此可看出, MIMKGISI对知识图谱的推理具有较好的可解释性.

3 结束语

本文提出融合语义信息的知识图谱多跳推理模型(MIMKGISI), 充分考虑知识图谱中的推理路径和查询关系的语义信息.首先, 利用知识图谱表示学习方法将实体和关系嵌入低维向量空间中, 并将该空间作为强化学习的外部环境.然后, 选择与查询关系和关系路径最相似的动作, 扩充智能体的搜索空间.最后, 计算推理路径和查询关系的相似度并反馈给智能体.在WD-singer、NELL23K、FB15K-237-10%数据集上的实验表明, MIMKGISI可提升多跳推理的性能, 特别是稀疏知识图谱上的推理任务.然而MIMKGISI在FB15K-237-20%数据集上的推理性能并未提升, 可能是由于该数据集稀疏程度较低、数据量充足, 导致语义信息的指导作用无法体现而造成的.本文还进行消融实验, 分析动作空间和奖励函数的影响.通过对推理路径的分析, 验证MIMKGISI对知识推理可解释性具有增强作用.今后将考虑研究路径的外部语义信息, 如实体的描述信息, 进一步增强多跳推理路径的可靠性.

本文责任编委 张燕平

Recommended by Associate Editor ZHANG Yanping

参考文献
[1] ROSSI A, BARBOSA D, FIRMANI D, et al. Knowledge Graph Embedding for Link Prediction: A Comparative Analysis. ACM Transactions on Knowledge Discovery from Data, 2021, 15(2). DOI: DOI:10.1145/3424672. [本文引用:1]
[2] 丁梦远, 兰旭光, 彭茹, 等. 机器推理的进展与展望. 模式识别与人工智能, 2021, 34(1): 1-13.
(DING M Y, LAN X G, PENG R, et al. Progress and Prospect of Machine Reasoning. Pattern Recognition and Artificial Intelligence, 2021, 34(1): 1-13. ) [本文引用:1]
[3] BOLLACKER K, TUFTS P, PIERCE T, et al. A Platform for Scalable, Collaborative, Structured Information Integration[C/OL]. [2022-04-16]. http://www.aaai.org/Papers/Workshops/2007/WS-07-14/WS07-14-004.pdf. [本文引用:1]
[4] MILLER G A. WordNet: A Lexical Database for English. Communications of the ACM, 1995, 38(11): 39-41. [本文引用:1]
[5] AUER S, BIZER C, KOBILAROV G, et al. DBpedia: A Nucleus for a Web of Open Data // Proc of the International Semantic Web Conference. Berlin, Germany: Springer, 2007: 722-735. [本文引用:1]
[6] BORDES A, USUNIER N, GARCIA-DURÁN A, et al. Translating Embeddings for Modeling Multi-relational Data // Proc of the 26th International Conference on Neural Information Processing Systems. Cambridge, USA: MIT Press, 2013, II: 2787-2795. [本文引用:2]
[7] WANG Z, ZHANG J W, FENG J L, et al. Knowledge Graph Embedding by Translating on Hyperplanes // Proc of the 28th AAAI Conference on Artificial Intelligence. Palo Alto, USA: AAAI, 2014: 1112-1119. [本文引用:1]
[8] LIN Y K, LIU Z Y, SUN M S, et al. Learning Entity and Relation Embeddings for Knowledge Graph Completion // Proc of the 29th AAAI Conference on Artificial Intelligence. Palo Alto, USA: AAAI, 2015: 2181-2187. [本文引用:1]
[9] JI G L, HE S Z, XU L H, et al. Knowledge Graph Embedding via Dynamic Mapping Matrix // Proc of the 53rd Annual Meeting of the Association for Computational Linguistics and the 7th International Joint Conference on Natural Language Processing. Stroudsburg, USA: ACL, 2015: 687-696. [本文引用:1]
[10] YANG B S, YIH W T, HE X D, et al. Embedding Entities and Relations for Learning and Inference in Knowledge Bases[C/OL]. [2022-04-16]. https://arxiv.org/pdf/1412.6575.pdf. [本文引用:1]
[11] NICKEL M, ROSASCO L, POGGIO T. Holographic Embeddings of Knowledge Graphs // Proc of the 30th AAAI Conference on Artificial Intelligence. Palo Alto, USA: AAAI, 2016: 1955-1961. [本文引用:1]
[12] DETTMERS T, MINERVINI P, STENETORP P, et al. Convolutional 2D Knowledge Graph Embeddings // Proc of the 32nd AAAI Conference on Artificial Intelligence and 30th Innovative Applications of Artificial Intelligence Conference and 8th AAAI Symposium on Educational Advances in Artificial Intelligence. Palo Alto, USA: AAAI, 2018: 1811-1818. [本文引用:1]
[13] YANG F, YANG Z L, COHEN W W. Differentiable Learning of Logical Rules for Knowledge Base Reasoning // Proc of the 31st International Conference on Neural Information Processing Systems. Cambridge, USA: MIT Press, 2017: 2316-2325. [本文引用:1]
[14] XIONG W H, HOANG T, WANG W Y. DeepPath: A Reinforcement Learning Method for Knowledge Graph Reasoning // Proc of the Conference on Empirical Methods in Natural Language Processing. Stroudsburg, USA: ACL, 2017: 564-573. [本文引用:1]
[15] DAS R, DHULIAWALA S, ZAHEER M, et al. Go for a Walk and Arrive at the Answer: Reasoning over Paths in Knowledge Bases Using Reinforcement Learning[C/OL]. [2022-04-16]. https://arxiv.org/pdf/1711.05851.pdf. [本文引用:3]
[16] LIN X V, SOCHER R, XIONG C M. Multi-hop Knowledge Graph Reasoning with Reward Shaping // Proc of the Conference on Empirical Methods in Natural Language Processing. Stroudsburg, USA: ACL, 2018: 3243-3253. [本文引用:2]
[17] ZHOU X C, WANG P, LUO Q Q, et al. Multi-hop Knowledge Graph Reasoning Based on Hyperbolic Knowledge Graph Embe-dding and Reinforcement Learning // Proc of the 10th International Joint Conference on Knowledge Graphs. New York, USA: ACM, 2021. DOI: DOI:10.1145/3502223.3502224. [本文引用:2]
[18] ZHU A J, OUYANG D Q, LIANG S, et al. Step by Step: A Hie-rarchical Framework for Multi-hop Knowledge Graph Reasoning with Reinforcement Learning. Knowledge-Based Systems, 2022, 248. DOI: DOI:10.1016/j.knosys.2022.108843. [本文引用:4]
[19] LÜ X, CAO Y X, HOU L, et al. Is Multi-hop Reasoning Really Explainable? Towards Benchmarking Reasoning Interpretability // Proc of the Conference on Empirical Methods in Natural Language Processing. Stroudsburg, USA: ACL, 2021: 8899-8911. [本文引用:1]
[20] FU C, CHEN T, QU M, et al. Collaborative Policy Learning for Open Knowledge Graph Reasoning // Proc of the Conference on Empirical Methods in Natural Language Processing and the 9th International Joint Conference on Natural Language Processing. Stroudsburg, USA: ACL, 2019: 2672-2681. [本文引用:2]
[21] LÜ X, HAN X, HOU L, et al. Dynamic Anticipation and Completion for Multi-hop Reasoning over Sparse Knowledge Graph // Proc of the Conference on Empirical Methods in Natural Language Processing. Stroudsburg, USA: ACL, 2020: 5694-5703. [本文引用:4]
[22] WILLIAMS R J. Simple Statistical Gradient-Following Algorithms for Connectionist Reinforcement Learning. Machine Learning, 1992, 8: 229-256. [本文引用:1]
[23] ROCKTÄSCHEL T, RIEDEL S. End-to-End Differentiable Proving // Proc of the 31st International Conference on Neural Information Processing Systems. Cambridge, USA: MIT Press, 2017: 3791-3803. [本文引用:1]