引用本文
崔彩霞, 王杰, 庞天杰, 梁吉业. 基于自监督学习的不平衡节点分类算法. 模式识别与人工智能, 2022,35(11): 955-964
CUI Caixia, WANG Jie, PANG Tianjie, LIANG Jiye. Imbalanced Node Classification Algorithm Based on Self-Supervised Learning. PATTERN RECOGNITION AND ARTIFICIAL INTELLIGENCE, 2022,35(11): 955-964.  
Doi: 10.16451/j.cnki.issn1003-6059.202211001
Permissions
Copyright©2022, 《模式识别与人工智能》编辑部
《模式识别与人工智能》编辑部
基于自监督学习的不平衡节点分类算法
崔彩霞1,2, 王杰3, 庞天杰2, 梁吉业1
1.山西大学 计算机与信息技术学院 太原 030006
2.太原师范学院 计算机科学与技术学院 晋中 030619
3.太原科技大学 计算机科学与技术学院 太原 030024
通信作者：

梁吉业,博士,教授,主要研究方向为数据挖掘、机器学习、大数据分析、人工智能.E-mail:ljy@sxu.edu.cn.

作者简介:

崔彩霞,博士研究生,主要研究方向为数据挖掘、机器学习.E-mail:cuicaixia@tynu.edu.cn.

王 杰,博士,讲师,主要研究方向为数据挖掘、机器学习.E-mail:wangjie_reg@163.com.

庞天杰,硕士,副教授,主要研究方向为数据挖掘、机器学习.E-mail:pangtj@tynu.edu.cn.

收稿日期: 2022-08-23 接受日期: 2022-11-30
资助项目: 国家自然科学基金项目(No.61976184,62272285)资助
摘要

在现实世界的节点分类场景中,只有少部分节点带标签且类标签是不平衡的.然而,大部分已有的方法未同时考虑监督信息缺乏与节点类不平衡这两个问题,不能保证节点分类性能的提升.为此,文中提出基于自监督学习的不平衡节点分类算法.首先,通过图数据增强生成原图的不同视图.然后,利用自监督学习最大化不同视图间节点表示的一致性以学习节点表示.该算法通过自监督学习扩充监督信息,增强节点的表达能力.此外,在交叉熵损失和自监督对比损失的基础上,设计语义约束损失,保持图数据增强中语义的一致性.在三个真实图数据集上的实验表明,文中算法在解决不平衡节点分类问题上具有较优的性能.

关键词: 自监督学习; 不平衡节点分类; 图神经网络; 数据增强; 语义约束损失
中图分类号:TP 391
Imbalanced Node Classification Algorithm Based on Self-Supervised Learning
CUI Caixia1,2, WANG Jie3, PANG Tianjie2, LIANG Jiye1
1. School of Computer and Information Technology, Shanxi University, Taiyuan 030006
2. College of Computer Science and Technology, Taiyuan Normal University, Jinzhong 030619
3. College of Computer Science and Technology, Taiyuan University of Science and Technology, Taiyuan 030024
Corresponding author:
LIANG Jiye, Ph.D., professor. His research interests include data mining, machine learning, big data analysis and artificial intelligence.

About Author:
CUI Caixia, Ph.D. candidate. Her research interests include data mining and machine learning.
WANG Jie, Ph.D., lecturer. His research interests include data mining and machine learning.
PANG Tianjie, master, associate profe-ssor. His research interests include data mi-ning and machine learning.

Fund:National Natural Science Foundation of China(No.61976184,62272285)
Abstract

In real-world node classification scenarios, only a few nodes are labeled and their class labels are imbalanced. In most of the existing methods, the lack of the supervision information and the imbalance of node classes are not taken into account at the same time, and the improvement of node classification performance cannot be guaranteed. Therefore, an imbalanced node classification algorithm based on self-supervised learning is proposed. Firstly, different views of the original graph are generated through graph data augmentation. Then, node representations are learned by maximizing the consistency of node representations across views using self-supervised learning. The supervised information is expanded and the expressive ability of nodes is enhanced by self-supervised learning. In addition, a semantic constraint loss is designed to ensure semantic consistency in graph data augmentation along with cross-entropy loss and self-supervised contrastive loss. Experimental results on three real graph datasets show that the proposed algorithm achieves better performance on solving the imbalanced node classification problem.

Key words: Self-Supervised Learning; Imbalanced Node Classification; Graph Neural Network; Data Augmentation; Semantic Constraint Loss

图数据分析挖掘在服务经济和社会发展中具有基础性作用, 有效感知、挖掘、利用图数据, 可为相关产业的发展提供巨大的助推力.图数据分析挖掘任务包括节点分类[1]、链路预测[2]、推荐系统[3]等, 节点分类作为其中一项重要的任务受到越来越多的关注.例如:在社交网络中识别用户是人类用户还是机器人用户[4]; 在蛋白质互作用网络中预测蛋白质功能类型[5]; 在引文网络中识别文档主题[6]等.

近年来, 图神经网络(Graph Neural Networks, GNNs)[7, 8, 9, 10]因其对非欧数据强大的表示学习能力, 在节点分类任务上表现出良好的性能.然而, 现有图神经网络的研究大多基于不同类节点平衡的假设, 即不同类标记节点数量大致是相同的.而在一些实际问题中, 收集到的标记节点往往是不平衡的, 某些类的标记节点数量远大于其它类别.同时由于标注代价较高、涉及个人隐私等原因, 节点分类任务也面临只有少部分的节点被标注而大量的节点没有标注的问题.例如, 在社交网络虚假账号识别[11]中, 正常账号远多于虚假账号, 数量严重失衡, 而且由于账号涉及隐私等原因, 只有少部分账号被标注, 而大量的账号是无标记的.因此, 监督信息缺乏和节点不平衡给节点分类任务带来巨大的挑战.

已有一些研究将传统的重采样[12]、重加权[13]、集成学习[14]等不平衡处理技术应用到不平衡节点分类问题上, 使其分类性能得到一定程度的提升.

在重采样方面, Zhao等[15]和Qu等[16]利用上采样技术改善节点的不平衡问题.具体来说, Zhao等[15]提出GraphSMOTE, 将SMOTE(Synthetic Mino-rity Over-sampling Technique)上采样算法[17]推广到图上, 通过插值方式在潜在空间合成少数类节点, 再使用一个预训练的边缘生成器预测合成节点与原节点之间的连通性.通过这种方式, 使不同类节点达到平衡, 提升节点分类的性能.Qu等[16]提出ImGAGN(Imbalanced Network Embedding via Generative Ad-versarial Graph Networks), 利用生成对抗网络(Generative Adversarial Network, GAN)生成少数类节点, 实现对少数类的上采样, 使标记节点达到平衡, 提升不平衡节点二分类的性能.

在重加权方面, Chen等[18]提出ReNode, 根据标记节点对类边界的相对位置自适应地重新加权, 缓解节点不平衡对分类性能的影响, 然而该方法依赖类边界, 在监督信息缺乏时确定的类边界可能不准.

在集成学习方面, Sun等[19]提出AdaGCN(Ada-boosting Graph Convolutional Network), 以图卷积网络(Graph Convolutional Network, GCN)[7]为基分类器, 利用前一个GCN的误差更新下一个GCN的样本权值, 以此纠正错分样本, 提高分类性能.Shi等[20]提出Boosting-GNN, 使用GNN作为基分类器进行Boosting集成, 即在每次提升训练时, 为前一次未正确分类的训练样本设置更高的权重, 从而提高分类精度和可靠性.

综上所述, 现有方法侧重于使用重采样、重加权或集成学习的方式处理节点的不平衡问题, 未同时考虑监督信息缺乏与节点不平衡这两个问题, 从而不能保证节点分类性能的提升.

自监督学习[21]可在不依赖标签的情况下, 从数据本身信息学习到数据的有效表示, 已成功应用到计算机视觉[22, 23]、自然语言处理[24, 25]、图数据分析挖掘[26, 27, 28, 29, 30]等领域.根据模型结构与目标的不同, 自监督学习通常分为两类[31]:基于生成的自监督学习与基于对比的自监督学习.基于生成的自监督学习的目的是恢复输入数据中缺失的部分, 通过重构误差学习表示, 如自编码器[32]、BERT(Bidirectional En-coder Representations from Transformers)[24]等.基于对比的自监督学习(即对比学习)通过对比正负样本的相似度, 拉近正样本, 推开负样本, 构建有效表示, 如MoCo(Momentum Contrast)[22]、SimCLR[23]等.

类似地, 图自监督学习也分为基于生成的图自监督学习与基于对比的图自监督学习.基于生成的图自监督学习关注节点/边特征或邻接矩阵的重构问题, 如经典的图自编码器(Graph Auto-Encoder, GAE)[33]与GraphMAE[34].基于对比的图自监督学习旨在最大化输入图在不同视图上的表示一致性, 如GraphCL(Graph Contrastive Learning)[26]、DGI(Deep Graph Infomax)[29]等.特别地, 自监督学习也应用到不平衡分类研究中.Yang等[35]和Liu等[36]探索自监督学习在不平衡图像分类上的应用, 通过实验分析得出自监督学习可增强图像数据的表达能力, 提升分类性能.

因此, 本文将自监督学习这一有效工具引入不平衡节点分类问题中, 提出基于自监督学习的不平衡节点分类算法(Imbalanced Node Classification Algorithm Based on Self-Supervised Learning, ImSSL).一方面借助自监督学习扩充监督信息, 另一方面增强节点的表达能力.此外, 在交叉熵损失和自监督对比损失的基础上, 设计语义约束损失(Semantic Constraint Loss, SCL), 以此保持图数据增强中语义的一致性.在3个真实的图数据集上执行的大量实验表明, ImSSL性能较优.

1 问题描述

给定一个无向无权图G=(V, ε , X, A), 其中:V={v1, v2, …, vN}表示节点的集合, N表示节点数; ε 表示边的集合, eij=< vi, vj> ∈ ε 表示节点vi、vj之间的边; X={x1, x2, …, xN}∈ RN× F表示特征矩阵, 其中, xi∈ RF表示节点vi的特征, F表示节点特征的维数; 邻接矩阵A=(aij)∈ RN× N表示图G的拓扑结构, aij表示矩阵A在第i行第j列处的元素, 如果eij∈ ε , aij=1, 否则aij=0.对于半监督节点分类, $D=\left\{\left(\boldsymbol{x}_{i}, y_{i}\right)\right\}_{i=1}^{L}$ 表示有标记集合, $V=\left\{\left(\boldsymbol{x}_{i}, y_{i}\right)\right\}_{i=L+1}^{L+M}$ 表示验证集合, $U=\left\{\boldsymbol{x}_{j}\right\}_{j=L+M+1}^{N}$ 表示未标记集合, yi∈ {1, 2, …, m}表示第i个标记节点的标记, m表示类别数目.在图半监督学习中, 仅有一小部分节点有标记, 通常L≪N.半监督节点分类就是利用特征矩阵X、有标记节点集D及图拓扑结构A预测未标记节点集的标记.

本文研究的问题是半监督不平衡节点分类, 即在有标记节点集D中, 一些类的节点数远多于另一些类.

假设图G的节点有m个类C1, C2, …, Cm, $|{{C}_{i}}|$表示属于第i个类的标记节点的数目, 则不平衡比(Imbalance Ratio, IR)定义如下:

IR= max1≤i≤m{|Ci|}min1≤i≤m{|Ci|}.(1)

2 基于自监督学习的不平衡节点分类算法

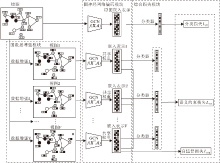
为了弥补监督信息的不足, 同时学习对少数类分类有利的特征表示, 本文提出基于自监督学习的不平衡节点分类算法(ImSSL).算法总体框架如图1所示, 包括数据增强模块、图神经网络编码模块与综合损失模块.

图1 ImSSL总体框架图Fig.1 Framework of ImSSL

2.1 图数据增强模块

图数据增强[26]的目的是在不改变语义的情况下, 通过一定的变换, 创建新的、异于原图的、合理的图数据.目前有如下一些常用方法.

1)基于节点丢弃的方法.对于给定图, 通过随机丢弃一定比例的节点及其相关联的边生成原图的新视图.此方法基于一个假设:丢弃部分节点不会影响图的语义, 每个节点的丢弃概率遵循某一分布, 例如相同的均匀分布或其它分布.

2)基于边扰动的方法.对于给定图, 随机增加或丢弃一定比例的边, 产生原图的新视图.此方法基于这样的假设:图的语义信息对边有一定的鲁棒性.

3)基于节点属性掩码的方法.对于给定图, 随机对节点属性掩码进行一定比例的更改, 更改其属性值.选择掩码比例要考虑这种改动不会对模型的预测造成太大影响.

4)基于子图的方法.对于给定图, 通过随机游走采样图的子图, 前提是假设图的语义在它的局部结构中可得到较大程度的保留.

本文使用基于节点属性掩码的增强方法, 框架具有一般性, 也可使用其它图增强方法.

2.2 图神经网络编码模块

本文采用经典的图卷积网络(GCN)[7]作为图编码器.一个两层的图卷积网络的预测结果为:

$\begin{align} & \mathbf{\hat{Y}}=f(\mathbf{X}, \mathbf{A}) \\ & \text{ }=\text{softmax}(\mathbf{\hat{A}}\text{ReLU(}\mathbf{\hat{A}X}{{\mathbf{W}}^{(0)}}){{\mathbf{W}}^{(1)}}). \\ \end{align}$(2)

其中:W(0)∈ RF× S表示第0层的参数; W(1)∈ RS× m表示第1层的参数;

$\mathbf{\hat{A}}={{\mathbf{D}}^{-\tfrac{1}{2}}}\mathbf{\tilde{A}}{{\mathbf{D}}^{-\tfrac{1}{2}}}$,

$\tilde{A}=A+{{I}_{N}}$,

$D=diag({{d}_{1}}, {{d}_{2}}, \cdots , {{d}_{N}})\in {{\mathbb{R}}^{N\times N}}$

为矩阵A的度矩阵, di= ∑vj∈Vaij表示节点vi的度数;

ReLU(· )=max(0, · ).

嵌入矩阵

$\mathbf{Z}=\mathbf{\hat{A}}\text{ReLU(}\mathbf{\hat{A}X}{{\mathbf{W}}^{(0)}}){{\mathbf{W}}^{(1)}}$

zi表示Z的第i行,

softmax(zi)= exp(zi)∑iexp(zi).

第i个视图的预测结果为:

$\begin{align} & {{{\mathbf{\hat{Y}}}}^{(i)}}=f({{\mathbf{X}}^{(i)}}, \mathbf{A}) \\ & \text{ }=\text{softmax}(\mathbf{\hat{A}}\text{ReLU(}\mathbf{\hat{A}}{{\mathbf{X}}^{(i)}}{{\mathbf{W}}^{(0)}}){{\mathbf{W}}^{(1)}}). \\ \end{align}$ (3)

其中X(i)表示第i个视图的特征矩阵.

第i个视图的嵌入矩阵为:

$\mathbf{Z}_{{}}^{(i)}=\mathbf{\hat{A}}\text{ReLU(}\mathbf{\hat{A}}{{\mathbf{X}}^{(i)}}{{\mathbf{W}}^{(0)}}){{\mathbf{W}}^{(1)}}$.

在ImSSL中, GCN学习不同视图的嵌入表示时权重是共享的, 可减少计算量.值得注意的是, 本文所提框架具有一般性, 也可适应于其它的GNN模型.

2.3 综合损失模块

ImSSL的损失函数包含3部分:分类损失LCE、语义约束损失LSCL和自监督对比损失LSSL, 则

L=λ 1LCE+λ 2LSCL+λ 3LSSL, (4)

其中, λ 1、λ 2和λ 3表示权衡参数.

本文采用交叉熵损失函数计算分类损失, 则

LCE=- ∑i=1L∑j=1myij ln y~ij, (5)

其中, yij与 y~ij分别表示第i个节点属于第j类的真实概率与预测概率.

在进行图数据增强时, 本文希望能保证图语义的一致性, 即不能因为数据增强使其预测标签发生大的变化.为此, 设计语义约束损失, 用于衡量不同视图下类分布与原图语义接近程度, 则

${{\mathcal{L}}_{SCL}}=\frac{1}{V}\sum\limits_{i=1}^{V}{W({{{\mathbf{\hat{Y}}}}^{(i)}}, \mathbf{Y})}, $ (6)

其中, V表示视图数, $W({{\mathbf{\hat{Y}}}^{(i)}}, \mathbf{Y})$表示第i个视图类标签分布 Y︿(i)与原图类标签分布Y之间的Wassers-tein距离.Wasserstein距离是衡量两个分布相似性的度量[37], 优点在于能提供更平滑的结果, 优于优化时参数的更新.

在自监督对比学习中, 要求最大化正例对的相似性、最小化负例对的相似性以学习节点的特征表示.图数据在经过图数据增强模块和图神经网络编码模块后得到多个表示.使用 Zu(i)表示节点u在第i个视图的嵌入表示, 即第i个视图的嵌入矩阵Z(i)中节点u对应的行.本文将同一节点在不同视图下的表示作为正例对, 如节点u, ( Zu(1), Zu(2)), ( Zu(1), Zu(3)), …, ( Zu(1), Zu(V))为正例对, 而将不同节点在所有视图下的表示作为负例对, 如节点u和v, ( Zu(i), Zv(j)), i=1, 2, …, V, j=1, 2, …, V为负例对.形式上, 遵循SimCLR[23], 最大化正例对的相似性, 最小化负例对的相似性, 自监督对比损失为:

LSSL= 1N·V∑u∈V∑i=1Vj=1i≠jL( Zu(i), Zu(j)), (7)

其中,

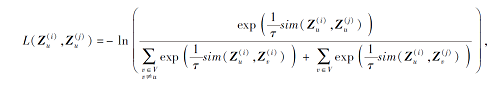
sim(· )表示度量两节点的相似度, τ 表示温度系数,

$\sum_{\substack{v \in V \\ v \neq u}} \exp \left(\frac{1}{\tau} \operatorname{sim}\left(\boldsymbol{Z}_{u}^{(i)}, \boldsymbol{Z}_{v}^{(i)}\right)\right) $

表示节点u与同一视图其它节点的相似度之和,

$ \sum_{v \in V} \exp \left(\frac{1}{\tau} \operatorname{sim}\left(\boldsymbol{Z}_{u}^{(i)}, \boldsymbol{Z}_{v}^{(j)}\right)\right)$

表示节点u与不同视图的节点间的相似度之和.

在每个训练周期, ImSSL首先对图G进行V次数据增强, 生成V个视图 G~1, G~2, …, G~V.然后, 使用GCN编码器得到 G~1, G~2, …, G~V的节点表示Z(1), Z(2), …, Z(V).最后, 优化式(4)中的目标, 更新参数.ImSSL的具体步骤如下.

算法1 基于自监督学习的不平衡节点分类算法

输入 图G的特征矩阵X, 邻接矩阵A, 标记集Y,

训练集D, 验证集V, 测试集U,

最大迭代次数MaxIter, 温度系数τ ,

权衡参数λ 1、λ 2、λ 3

输出 测试集U的预测结果

1.对图G执行数据增强, 生成V个视图 G~1, G~2, …, G~V;

2.FOR i = 1 TO MaxIter DO

3. 分别用GCN编码器对V个视图 G~1, G~2, …, G~V

编码, 得到V个节点嵌入表示Z(1), Z(2), …, Z(V);

4. 利用式(5)计算交叉熵损失LCE;

5. 利用式(6)计算语义约束损失LSCL;

6. 利用式(7)计算自监督对比损失LSSL;

7. 利用式(4)计算综合损失函数L;

8. 应用梯度下降法最小化L, 更新参数.

9.END FOR

10.利用式(2)计算测试集U的预测标签.

11.RETURN U的预测结果.

2.4 时间复杂度分析

算法1的计算复杂性包括3阶段:数据增强阶段(第1行)、学习阶段(第2~9行)和预测阶段(第10行).

在数据增强阶段, 数据增强算法的时间复杂度为O(NF), 生成V个视图执行数据增强的时间复杂度为O(VNF).

在学习阶段, 时间复杂度如下:GCN编码的时间复杂度为

O(|ε |FS+|ε |Sm),

对V个视图进行GCN编码的时间复杂度为

O(V(|ε |FS+|ε |Sm)),

注意到m< F, 时间复杂度为O(V|ε |FS).计算交叉熵损失的时间复杂度为O(Lm), 计算语义约束损失的时间复杂度为O(VL3), 计算自监督对比损失的时间复杂度为O(VN3), 因此, 计算损失函数的时间复杂度为O(Lm+VL3+VN3).注意到U< N, L< N, m≪N, 时间复杂度为O(VN3).由此得出, 学习阶段的时间复杂度为O(V|ε |FS+VN3).

在预测阶段(第10行), 计算U个未标记样本的预测标签的时间复杂度为O(Um)=O(N).

综上所述, 算法1的时间复杂度为

O(V|ε |FS+VN3).

3 实验及结果分析
3.1 实验数据集

本文选用3个广泛使用的引文网络数据集Cora、CiteSeer和PubMed(https://linqs.soe.ucsc.edu/data)作为实验对象.

Cora数据集由2 708篇来源于Cora数据库上的机器学习相关论文组成, 论文之间的文献引用链接有5 229条.这些文献分别属于机器学习理论、概率方法、基于案例的机器学习方法、神经网络、规则学习、遗传算法和增强学习这7种类别.这些论文经过提取词语, 去掉停用词, 再选择文档中出现频次小于10的词语作为文献特征, 最终得到1 433个特征词.数据集上每个节点使用1 433维0-1向量作为该节点的特征.

CiteSeer数据集由3 327部来源于CiteSeer数据库的计算机相关的科学出版物组成, 文献引用链接有4 732条.这些文献分别属于人工智能、数据库、信息检索、机器学习、智能体和人机交互这6个类别.特征提取模式同Cora数据集一样, 最终数据集上每个节点使用3 703维的0-1向量作为节点特征信息.

PubMed数据集由19 717部来源于PubMed数据库的与糖尿病有关的科学出版物组成, 文献引用链接有44 338条.这些文献根据研究的糖尿病种类分为3类:实验性糖尿病、1型糖尿病和2型糖尿病.文献特征由500个单词组成, 每篇文献对应一个词频-逆文档频率向量(Term Frequency-Inverse Document Frequency, TF-IDF), 因此, 数据集上的每个节点均使用500维向量作为节点特征.

本文沿用文献[7]和文献[38]的半监督节点分类设置及文献[18]中的不平衡设置进行分析和实验.具体地, 在3个基准数据集上, 每类 20个标记节点用于训练, 500个节点用于验证, 1 000个节点用于测试.在此基础上, 选训练集上一些类作为少数类, 每个少数类中随机选取20/IR个节点, 不平衡比IR设为10.数据集的详细信息如表1所示.

表1 实验数据集 Table 1 Experimental datasets
3.2 对比算法

为了测试本文算法的性能, 选择如下半监督不平衡节点分类中的算法进行对比.

1)GraphSMOTE[15].SMOTE在不平衡图数据上的扩展.

2)ReNode[18].以拓扑不平衡角度研究不平衡节点分类问题的方法, 根据拓扑位置对标记节点重加权.

3)AdaGCN[19].Adaboost与图神经网络结合的集成学习模型, 在Adaboost训练中以GCN作为基分类器.

4)DR-GCN[39].双正则图卷积网络, 解决图数据中类不平衡学习问题.

3.3 参数设置与评价指标

在ImSSL中, 最大迭代次数设为500, 模型参数τ =0.5.在每个训练阶段使用全批次训练ImSSL.采用Adam(Adaptive Moment Estimation)优化器, 在PyTorch上运行.对于基线算法, 使用原始文献中的代码.所有算法运行实验 5次, 取平均值作为最终结果.

借鉴不平衡多分类的常用评价方法[15, 40, 41], 使用如下3个评价指标:Accuracy, AUC和Macro_F.这些评价指标建立在多分类的混淆矩阵上, 如表2所示, 表中Nij表示分类为Cj类但实际上属于Ci类的样本数量.

表2 多分类的混淆矩阵 Table 2 Confusion matrix for multi-class classification

第i类的查准率

Pi= Nii∑j=1mNji.

第i类的查全率

Ri= Nii∑j=1mNij.

由Pi和Ri计算平均值, 可得到宏查准率

Macro_P= 1m∑i=1mPi,

宏查全率

Macro_R= 1m∑i=1mRi .

宏F(Macro_F)为:

Macro_F= 2·Macro_P·Macro_RMacro_P+Macro_R.

Accuracy表示正确分类的样本数量与测试样本总数的比率, 广泛应用于评估分类器的性能.然而, 在不平衡学习的情况下, Accuracy可能会忽略少数类.因此, 除了Accuracy, 本文还选择AUC和Macro_F, 这两个指标专门用于不平衡分类.对每个类分别计算AUC和Macro_F, 再进行非加权平均, 这样可更好地反映少数类的分类效果.

3.4 实验结果

为了验证ImSSL的有效性, 首先与4种基线算法进行对比, 结果如表3所示.由表可看出, 相比基线方法, ImSSL的所有指标值都最优, 可提高少数类的识别率.由此可得出:在监督节点极度受限且不平衡时, 采用解决不平衡问题的常规办法, 不论是重采样、重加权还是集成学习, 没有同时考虑监督信息缺乏与节点不平衡这两个问题, 不能保证节点分类的性能.而ImSSL有效利用自监督学习能挖掘数据内在的结构获得监督信息的特点, 弥补半监督不平衡节点分类中监督信息的不足, 同时能学习有益于少数类分类的表示, 提高分类性能.

表3 各算法在3个数据集上的性能对比 Table 3 Performance comparison of different algorithms on 3 datasets %

下面研究ImSSL损失函数(式(4))中约束损失与自监督对比损失的贡献, 定义如下对比算法.

1)w/o LSCL.移除约束损失.

2)w/o LSCLLSSL.移除约束损失与自监督对比损失.

在不平衡比为10的Cora数据集上进行对比实验.取各自设置下5次实验的平均结果, 3种算法的消融实验结果如表4所示.由表可见, 相比w/o LSCLLSSL, 增加自监督对比损失后, w/o LSCL的3个指标值皆有大幅提升, 这说明通过自监督方式训练可学习数据内在结构特征, 是解决不平衡节点分类的有效手段.对比w/o LSCL和ImSSL可知, 增加约束损失是有必要的, 约束损失可以从语义上对数据增强进行指导, 弥补图数据上数据增强中语义的一致性.

表4 各算法在Cora数据集上的消融实验结果 Table 4 Ablation experiment results of different algorithms on Cora dataset %

下面对比GCN与ImSSL在不同不平衡比下的性能, 评估不同不平衡比对ImSSL的影响.以Cora数据集作为实验数据集, IR分别设置为1, 2, 5, 10, 20.每次实验进行5次, 平均结果如图2所示.由图可得, ImSSL在各种不平衡比下都能达到最优值.随着不平衡程度的加剧, ImSSL的改善越发显著.下面进一步验证自监督学习对不平衡节点分类任务的有效性.

图2 不平衡比不同时ImSSL与GCN的性能对比Fig.2 Performance comparison of ImSSL and GCN with different imbalance ratios

随着参数λ 1、λ 2、λ 3的取值变化, ImSSL在Cora数据集上不平衡节点的分类结果如图3所示.λ 1、λ 2、λ 3的取值都在[0, 1]内变化, 取值间隔为0.2.

图3 参数取值对性能的影响Fig.3 Effect of parameter setting on algorithm performance

由图3可得到如下结论.

1)当λ 1=0时, 由于没有交叉熵损失监督指导优化方向, 导致随机分类, 表明在节点分类中交叉熵损失是不可或缺的.

2)当λ 1> 0时, 在交叉熵损失指导下分类效果明显提升, 但当λ 2=0, λ 3=0时表现最差, 这是由于

当λ 1> 0, λ 2=0, λ 3=0时等同于GCN, 不适合不平衡节点分类.

3)对于每个图(对应固定的λ 1取值)来说, 当λ 2取值为0.8或1且λ 3取值为0.8时, 性能相对最好, 这表明自监督对比损失和语义约束损失在训练中起到重要作用, 可促使不平衡节点分类获得更优效果.

为了考察参数λ 1对分类结果的影响, 选取结果相对较优的λ 2、λ 3的取值, 即λ 2=0.8、λ 3=0.8, AUC值变化如图4所示.由图可看到, 当λ 1从0开始变大时, 性能提升, 当λ 2达到0.2时, 性能最优, 之后呈现下降趋势.

图4 λ 1对分类性能的影响Fig.4 Effect of λ 1 on classification performance

上述分析表明, 交叉熵损失、自监督对比损失和语义约束损失三者共同作用才能获得较优的不平衡节点分类结果.

4 结束语

监督信息不足与节点不平衡是图数据分析挖掘中面临的一个重要问题.本文提出基于自监督学习的不平衡节点分类算法(ImSSL).一方面通过自监督学习扩充监督信息, 另一方面通过自监督学习增强节点的表达能力.通过对比实验验证本文算法在不平衡节点分类问题上的优势.在下一步的研究工作中, 将针对图数据的动态性, 开展不平衡节点分类问题的研究.

本文责任编委 陈恩红

Recommended by Associate Editor CHEN Enhong

参考文献
[1] RONG Y, HUANG W B, XU T Y, et al. DropEdge: Towards Deep Graph Convolutional Networks on Node Classification[C/OL]. [2022-07-25]. https://arxiv.org/pdf/1907.10903.pdf. [本文引用:1]
[2] ZHANG M H, CHEN Y X. Link Prediction Based on Graph Neural Networks // Proc of the 32nd International Conference on Neural Information Processing Systems. Cambridge, USA: MIT Press, 2018: 5171-5181. [本文引用:1]
[3] FAN W Q, MA Y, LI Q, et al. A Graph Neural Network Framework for Social Recommendations. IEEE Transactions on Knowledge and Data Engineering, 2022, 34(5): 2033-2047. [本文引用:1]
[4] HAMILTON W L. Graph Representation Learning. Synthesis Lec-tures on Artificial Intelligence and Machine Learning, 2020, 14(3): 1-159. [本文引用:1]
[5] NEYSHABUR B, KHADEM A, HASHEMIFAR S, et al. NETAL: A New Graph-Based Method for Global Alignment of Protein-Protein Interaction Networks. Bioinformatics, 2013, 29(13): 1654-1662. [本文引用:1]
[6] SINHA A, SHEN Z H, SONG Y, et al. An Overview of Microsoft Academic Service(mas) and Application // Proc of the 24th International Conference on World Wide Web. New York, USA: ACM, 2015: 243-246. [本文引用:1]
[7] KIPF T N, WELLING M. Semi-Supervised Classification with Graph Convolutional Networks[C/OL]. [2022-07-25]. https://arxiv.org/pdf/1609.02907.pdf. [本文引用:4]
[8] HAMILTON W L, YING R, LESKOVEC J. Inductive Representation Learning on Large Graphs // Proc of the 31st International Conference on Neural Information Processing Systems. Cambridge, USA: MIT Press, 2017: 1025-1035. [本文引用:1]
[9] VELIČKOVIĆ P, CUCURULL G, CASANOVA A, et al. Graph Attention Networks[C/OL]. [2022-07-25]. https://arxiv.org/pdf/1710.10903.pdf. [本文引用:1]
[10] 白铂, 刘玉婷, 马驰骋, 等. 图神经网络. 中国科学(数学), 2020, 50(3): 367-384.
(BAI B, LIU Y T, MA C C, et al. Graph Neural Network. Scientia Sinica Mathematica, 2020, 50(3): 367-384. ) [本文引用:1]
[11] BREUER A, EILAT R, WEINSBERG U. Friend or Faux: Graph-Based Early Detection of Fake Accounts on Social Networks // Proc of the 29th International World Wide Web Conference. New York, USA: ACM, 2020: 1287-1297. [本文引用:1]
[12] 熊冰妍, 王国胤, 邓维斌. 基于样本权重的不平衡数据欠抽样方法. 计算机研究与发展, 2016, 53(11): 2613-2622.
(XIONG B Y, WANG G Y, DENG W B. Under-Sampling Method Based on Sample Weight for Imbalanced Data. Journal of Computer Research and Development, 2016, 53(11): 2613-2622. ) [本文引用:1]
[13] 平瑞, 周水生, 李冬. 高度不平衡数据的代价敏感随机森林分类算法. 模式识别与人工智能, 2020, 33(3): 249-257.
(PING R, ZHOU S S, LI D. Cost Sensitive Rand om Forest Classification Algorithm for Highly Unbalanced Data. Pattern Recognition and Artificial Intelligence, 2020, 33(3): 249-257. ) [本文引用:1]
[14] GALAR M, FERNÁNDEZ A, BARRENECHEA E, et al. A Review on Ensembles for the Class Imbalance Problem: Bagging-, Boosting-, and Hybrid-Based Approaches. IEEE Transactions on Systems, Man, and Cybernetics(Applications and Reviews), 2012, 42(4): 463-484. [本文引用:1]
[15] ZHAO T X, ZHANG X, WANG S H. GraphSMOTE: Imbalanced Node Classification on Graphs with Graph Neural Networks // Proc of the 14th ACM International Conference on Web Search and Data Mining. New York, USA: ACM, 2021: 833-841. [本文引用:4]
[16] QU L, ZHU H S, ZHENG R Q, et al. ImGAGN: Imbalanced Network Embedding via Generative Adversarial Graph Networks // Proc of the 27th ACM SIGKDD Conference on Knowledge Discovery and Data Mining. New York, USA: ACM, 2021: 1390-1398. [本文引用:2]
[17] CHAWLA N V, BOWYER K W, HALL L O, et al. SMOTE: Synthetic Minority Over-Sampling Technique. Journal of Artificial Intelligence Research, 2002, 16: 321-357. [本文引用:1]
[18] CHEN D L, LIN Y K, ZHAO G X, et al. Topology-Imbalance Learning for Semi-Supervised Node Classification // Proc of the 35th International Conference on Neural Information Processing Systems. Cambridge, USA: MIT Press, 2021: 29885-29897. [本文引用:3]
[19] SUN K, ZHU Z X, LIN Z C. AdaGCN: Adaboosting Graph Con-volutional Networks into Deep Models[C/OL]. [2022-07-25]. https://arxiv.org/pdf/1908.05081.pdf. [本文引用:2]
[20] SHI S H, QIAO K, YANG S, et al. Boosting-GNN: Boosting Algorithm for Graph Networks on Imbalanced Node Classification. Frontiers in Neurorobotics, 2021, 15. DOI: DOI:10.3389/fnbot.2021.775688. [本文引用:1]
[21] ERICSSON L, GOUK H, LOY C C, et al. Self-Supervised Representation Learning: Introduction, Advances, and Challenges. IEEE Signal Processing Magazine, 2022, 39(3): 42-62. [本文引用:1]
[22] HE K M, FAN H Q, WU Y X, et al. Momentum Contrast for Unsupervised Visual Representation Learning // Proc of the 30th IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2020: 9726-9735. [本文引用:2]
[23] CHEN T, KORNBLITH S, NOROUZI M, et al. A Simple Framework for Contrastive Learning of Visual Representations // Proc of the 37th International Conference on Machine Learning. San Diego, USA: PMLR, 2020: 1597-1607. [本文引用:3]
[24] DEVLIN J, CHANG M W, LEE K, et al. BERT: Pre-training of Deep Bidirectional Transformers for Language Understand ing // Proc of the Conference of the North American Chapter of the Association for Computational Linguistics(Human Language Technologies). Stroudsburg, USA: ACL, 2019: 4171-4186. [本文引用:2]
[25] GAO T Y, YAO X C, CHEN D Q. SimCSE: Simple Contrastive Learning of Sentence Embeddings // Proc of the 26th Conference on Empirical Methods in Natural Language Processing. Stroudsburg, USA: ACL, 2021: 6894-6910. [本文引用:1]
[26] YOU Y N, CHEN T L, SUI Y D, et al. Graph Contrastive Lear-ning with Augmentations // Proc of the 34th International Confe-rence on Neural Information Processing Systems. Cambridge, USA: MIT Press, 2020: 5812-5823. [本文引用:3]
[27] HASSANI K, KHASAHMADI A H. Contrastive Multi-view Representation Learning on Graphs // Proc of the 37th International Conference on Machine Learning. San Diego, USA: PMLR, 2020: 4116-4126. [本文引用:1]
[28] JIN M, ZHENG Y Z, LI Y F, et al. Multi-scale Contrastive Siamese Networks for Self-Supervised Graph Representation Learning[C/OL]. [2022-07-25]. https://arxiv.org/abs/2105.05682. [本文引用:1]
[29] VELIKOVI P, FEDUS W, HAMILTON W L, et al. Deep Graph Infomax[C/OL]. [2022-07-25]. https://arxiv.org/pdf/1809.10341v1.pdf. [本文引用:2]
[30] JIN W, LIU X R, ZHAO X Y, et al. Automated Self-Supervised Learning for Graphs[C/OL]. [2022-07-25]. https://arxiv.org/pdf/2106.05470v3.pdf. [本文引用:1]
[31] LIU X, ZHANG F J, HOU Z Y, et al. Self-Supervised Learning: Generative or Contrastive. IEEE Transactions on Knowledge and Data Engineering, 2023, 35(1): 857-876. [本文引用:1]
[32] HINTON G E, ZEMEL R S. Autoencoders, Minimum Description Length and Helmholtz Free Energy // Proc of the 6th International Conference on Neural Information Processing Systems. Cambridge, USA: MIT Press, 1993: 3-10. [本文引用:1]
[33] KIPF T N, WELLING M. Variational Graph Auto-Encoders[C/OL]. [2022-07-25]. https://arxiv.org/pdf/1611.07308v1.pdf. [本文引用:1]
[34] HOU Z Y, LIU X, CEN Y K, et al. GraphMAE: Self-Supervised Masked Graph Autoencoders // Proc of the 28th ACM SIGKDD Conference on Knowledge Discovery and Data Mining. New York, USA: ACM, 2022: 594-604. [本文引用:1]
[35] YANG Y Z, XU Z. Rethinking the Value of Labels for Improving Class-Imbalanced Learning // Proc of the 34th International Conference on Neural Information Processing Systems. Cambridge, USA: MIT Press, 2020: 19290-19301. [本文引用:1]
[36] LIU H, HAOCHEN J Z, GAIDON A, et al. Self-Supervised Lear-ning Is More Robust to Dataset Imbalance[C/OL]. [2022-07-25]. https://arxiv.org/pdf/2110.05025.pdf. [本文引用:1]
[37] LICANDRO R, SCHLEGL T, REITER M, et al. WGAN Latent Space Embeddings for Blast Identification in Childhood Acute Myeloid Leukaemia // Proc of the 24th International Conference on Pattern Recognition. Washington, USA: IEEE, 2018: 3868-3873. [本文引用:1]
[38] YANG Z L, COHEN W W, SALAKHUTDINOV R. Revisiting Semi-Supervised Learning with Graph Embeddings // Proc of the 33rd International Conference on Machine Learning. San Diego, USA: PMLR, 2016: 40-48. [本文引用:1]
[39] SHI M, TANG Y F, ZHU X Q, et al. Multi-class Imbalanced Graph Convolutional Network Learning // Proc of the 29th International Joint Conference on Artificial Intelligence. San Francisco, USA: IJCAI, 2021: 2879-2885. [本文引用:1]
[40] JOHNSON J M, KHOSHGOFTAAR T M. Survey on Deep Learning with Class Imbalance. Journal of Big Data, 2019, 6(1): 1-54. [本文引用:1]
[41] SPELMEN V S, PORKODI R. A Review on Hand ling Imbalanced Data // Proc of the International Conference on Current Trends towards Converging Technologies. Washington, USA: IEEE, 2018. DOI: DOI:10.1109/ICCTCT.2018.8551020. [本文引用:1]