假设高维数据分布于多个低维子空间, 子空间聚类目的是寻找这些低维嵌入子空间.该类方法通常利用字典表示思想(X=DZ)学习高维样本数据X的表示矩阵Z, 并以样本集本身作为字典(D=X), 所以也称为自表示模型.其表示矩阵Z可通过求解以下优化模型获得:

minZ, EΩ (Z)+α ||E||_l, s.t. X=XZ+E,

其中, 第1项为自表示矩阵约束, 第2项为重构损失, α 为平衡参数, l-范数针对不同类型的噪声而有所不同.不同子空间聚类方法的差异主要在于模型目标函数第1项函数与第2项范数定义的不同.稀疏子空间聚类(Sparse Subspace Clustering, SSC)利用l₁范数约束自表示矩阵(Ω (Z)=||Z||₁)^[12], 且约束diag(Z)=0, 第2项采用F范数约束噪声.而低秩表示(Low-Rank Representation, LRR)子空间聚类使用秩函数或核范数约束自表示矩阵(Ω (Z)=||Z||_* )^[13], 并利用l_{2, 1}范数约束噪声.

多视角子空间聚类为每个视角数据X^v构造自表示矩阵C^v, 公式如下:

minCv, EvΩ {C^v }v=1m+L{E^v }v=1m, s.t. Xv⁼Xv^Cv⁺Ev, (1)

其中, 第1项Ω {· }为对不同视角自表示矩阵的约束, 第2项L{· }为不同视角的重构损失.多视角样本集的最终邻接矩阵:

$\boldsymbol{W}=\frac{1}{m} \sum_{v=1}^{m}\left(\frac{\left|\boldsymbol{C}^{v}\right|+\left|\boldsymbol{C}^{v \mathrm{~T}}\right|}{2}\right) \text {. } $

多视角数据不但具有一致性信息, 并且每个视角又蕴含差异信息.为了同时表示多视角数据的一致信息和差异信息, 分解式(1)的C^v=Z+D^v.则式(1)的多视角形式为

minZ, Dv, EvΩ {Z}+R{D^v }v=1m+L{E^v }v=1m, s.t. Xv⁼Xv⁽Z+Dv⁾+Ev^.

其中:第1项Ω {· }为自表示矩阵的一致性约束, 可保证多视角数据一致表示矩阵的高类内同质性, 刻画不同视角的共享信息; 第2项R{· }为自表示的差异性约束, 刻画每个视角的差异信息; 第3项L{· }为重构损失.多视角样本集的最终邻接矩阵为:

$\boldsymbol{W}=\frac{|\boldsymbol{Z}|+\left|\boldsymbol{Z}^{\mathrm{T}}\right|}{2}+\frac{1}{m} \sum_{v=1}^{m}\left(\frac{\left|\boldsymbol{D}^{v}\right|+\left|\boldsymbol{D}^{v \mathrm{~T}}\right|}{2}\right) \text {. } $

然后将构造的邻接矩阵W输入传统的谱聚类中, 得到聚类结果.

近年来, 流形学习被应用于多视角子空间聚类.为了保持多视角数据的固有流形结构, 受文献[14]启发, 距离较小的样本更可能来自同一子空间, sijv衡量样本x_i、x_j在第v个视角下的距离, 也称为样本间的相似度, 本文定义样本在第v个视角下的相似度矩阵S^v为

$s_{i j}^{v}= \\ \left\{\begin{array}{ll} \exp \left(-\frac{\left\|\boldsymbol{x}_{i}-\boldsymbol{x}_{j}\right\|_{2}^{2}}{2 \sigma^{2}}\right), & x_{i}^{v} \in N_{k}\left(x_{j}^{v}\right) \text { 或 } x_{j}^{v} \in N_{k}\left(x_{i}^{v}\right) \\ 0, & \text { 其他 } \end{array}\right. $

其中, N_k( xiv)为样本x_i在第v个视角下的k近邻, 即距离最相近的k个数据点.

本文假设在多个视角中距离越近的样本越可能来自同一子空间, 以此描述多视角聚类的一致性原则, 构造多视角流形正则项如下:

$R^{\text {Rultiviven }}=\frac{1}{2} \sum_{i, j}\left\|z_{i}-z_{j}\right\|_{2}^{2}\left(\sum_{v=1}^{m} s_{i j}^{s}\right)= \\ \sum_{v=1}^{m} \operatorname{tr}\left(Z L^{\prime} Z^{\mathrm{T}}\right) \text {, } $

其中拉普拉斯矩阵L^v=D^v-S^v, D^v为对角矩阵,

Diiv= ∑jsijv.

多视角数据是对同一数据的不同特征描述, 理想情况下每个视角学习的自表示矩阵Z应趋于一致, 但是实际上多视角数据含有每个视角固有差异属性, Z不一定满足所有视角的相似性.因此本文提出MR-AWMSC, 同时学习多视角数据的一致性和差异性信息, 具体为

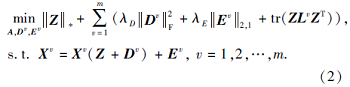
其中:第1项为所有视角的一致性自表示矩阵Z∈ R^{n× n}的核范数, 该项学习全局低秩表示, 充分刻画多视角数据共享信息; 第2项为第v个视角的差异信息表示矩阵D^v∈ R^{n× n}的F范数, 该项利用F范数的组效应性质, 使不同视角的差异表示矩阵具有块对角性, 更利于聚类; 第3项为重构损失项, E^v∈ Rdv×n为第v个视角的误差矩阵, 利用l_{2, 1}范数约束E^v列稀疏, 尽可能有效消除噪声视角, 得到较干净的自表示矩阵Z; 第4项为不同视角流形正则项, 可在新的表示空间Z中保持不同视角数据的局部几何结构, 利用该流形正则项可得到每个视角的贡献; 平衡参数λ _D和λ _E分别用于平衡差异信息表示项和误差项.

已有多数方法计算最终邻接矩阵Z^* 时, 是以平均加权策略集成不同视角差异表示D^v, 再融合一致表示矩阵Z.

MR-AWMSC的视角权重可随流形正则项的大小同步迭代更新, 对于m个视角权重{α ¹, α ², …, α ^m}:

α ^v= 12tr(ZLvZT), v=1, 2, …, m. (3)

在式(3)中, 每个视角的权重能被自适应地设置和更新, 根据流形正则项的大小自动为每个视角分配不一样的权重.由式(2)给出的目标函数可知, 需要最小化各视角的流形正则项tr(ZL^vZ^T), 因此tr(ZL^vZ^T)的值越小表明对应视角v的权重α ^v应越大, 该视角也越重要.

利用m个视角权重可集成多视角差异表示矩阵

D^v, 并融合一致表示矩阵Z, 得到最终的邻接矩阵:

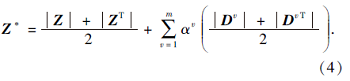
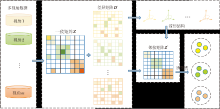
MR-AWMSC示意图如图1所示.在图中, 全局一致性表示矩阵Z体现多视角数据学习的一致性准则, 视角差异矩阵D^v刻画不同视角信息质量的差异性.在保持多视角流形结构的同时, MR-AWMSC在优化过程中通过流形正则项自适应学习每个视角的权重, 避免人工赋权方式导致权重设置困难.最终通过自适应学习得到D^v, 并融合一致表示矩阵Z, 获得邻接矩阵Z^* , 输入谱聚类中, 得到聚类结果.

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 MR-AWMSC示意图Fig.1 Architecture of MR-AWMSC

MR-AWMSC目标函数(式(2))同时从多个视角中学习一致自表示矩阵和多个差异表示矩阵.该问题有多个变量, 本文可利用ADMM求解变量.此外, 本文还引入辅助变量J∈ R^{n× n}, 使目标函数中变量可分离, 并分为多个子问题求解.首先, 引入变量J作为核范数中Z的替代, 则式(2)等价于:

minZ, J, Dv, Ev⁡minZ, J, Dv, EvJ* +∑v=1m(λDDvF2+λEEv2, 1+Tr(ZLvZT)).

s.t.Xv=XvZ+Dv+Ev, Z=J, v=1, 2, …, m.

因此, 上述模型的增广拉格朗日函数形式可写为

LZ, Dv, Ev, J=⁡LZ, Dv, Ev, J=J* +∑v=1mλDDvF2+λEEv2, 1+TrZLvZT

+∑v=1mY1v, Xv-XvZ+Dv-Ev+μ2∑v=1mXv-XvZ+Dv-EvF2

+Y2, Z-J+μ2Z-JF2.

其中, Y1v∈ Rdv×n, Y₂∈ R^{n× n}为拉格朗日乘子, μ 为惩罚系数, < · , · > 为矩阵的内积.ADMM分解该问题为多个凸的子问题, 更新当前变量时固定其余变量, 以t+1次迭代为例, 每个变量更新过程如下.

1)更新一致表示矩阵Z, 固定其余变量,

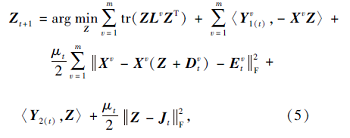
令上式对变量Z的导数为0, 得到方程

AZ+ZB=C.

该方程是Sylvester等式, 可利用MATLAB内置函数(lyap)直接求解, 其中,

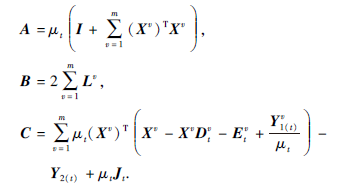
2)更新变量J, 固定其余变量.J的优化问题只与Z_t+1和Y_2(t)有关, 等价于求解如下问题:

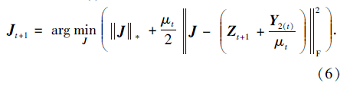
上述问题可使用奇异值阈值^[16]求解.令

K_t+1=Z_t+1+ Y2(t)μt,

先对K_t+1执行矩阵奇异值分解(即K_t+1=UΣ V^T), 得到问题的解:

J_t+1=U S1/μt(Σ )V^T,

其中, S_ε (x)为软阈值算子, Σ 经过软阈值算子S_ε (x)按元素操作, 得到输出矩阵的对应元素为

S_ε (x)= x-ε, x-ε> 00x-ε≤0

3)更新差异信息表示矩阵D^v, 固定其余变量, 则

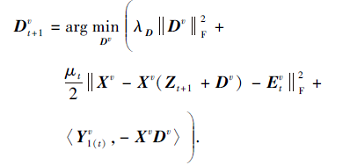
为了得到最优解, 令上式目标函数关于变量D^v的导数为0, 可得到差异信息表示矩阵的最优解:

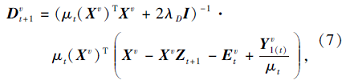
其中I∈ R^{n× n}为单位矩阵.

4)更新误差矩阵E^v, 固定其余变量, 则

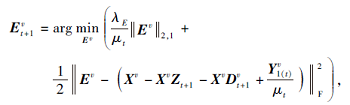
令

Ftv=X^v-X^vZ_t+1-X^v Dt+1v+ Y1(t)vμt,

可得到上式有如下形式的闭解^[17].具体地, Et+1v的第j列解为

Et+1v(:, j)=

(Ftv(∶, j)2-λEμtFtv(∶, j)2)Ftv(∶, j), λEμt< Ftv(∶, j)20, λEμt≥Ftv(∶, j)2(8)

5)更新自适应参数α ^v, 固定其余变量.按照式(3)更新α ^v:

αt+1v= 12tr(Zt+1LvZTt+1).

6)更新拉格朗日乘子 Y1v、Y₂和惩罚参数μ .当更新完其它所有的变量时, 更新拉格朗日乘子和参数如下:

Y1(t+1)v= Y1(t)v+μ _t(X^v-X^vZ_t+1-X^v Dt+1v- Et+1v), Y2_(t+1)=Y2_(t)+μ t₍Zt_+1-Jt₊₁₎, μ t+_1=min (γ μ t, _μ ma_x), (9)

其中, γ > 1, 为控制收敛速度的常数, 惩罚参数μ 通过γ 单调上升, 直到满足最大值μ _max.

当算法收敛后计算得到一致自表示矩阵Z和多个视角的差异信息矩阵{D¹, D², …, D^m}.最后, 根据式(4)计算邻接矩阵Z^* , 并对Z^* 利用谱聚类的Ncut分割方法, 得到最终的聚类结果.

综上分析, MR-AWMSC步骤如下.

算法 MR-AWMSC

输入 多视角数据集 {Xv}v=1m, 参数λ _E、λ _D,

最近邻数k, 图拉普拉斯矩阵 {Lv}v=1m,

Θ ₁为0矩阵

输出 聚类结果

初始化 矩阵Z₁, J₁, Y₂, { E1v, Y1v, D1v}v=1m为0矩阵,

μ =10^-6, μ _max=10⁶, , 迭代次数t=1,

最大迭代次数M=90, ε =10^-6,

权重α ^v= 1m

Repeat:

step 1 根据式(5)更新一致表示矩阵Z_t+1.

step 2 根据式(6)更新变量矩阵J_t+1.

step 3 For v=1 to m:

根据式(7)更新差异表示矩阵 Dt+1v;

根据式(8)更新误差矩阵 Et+1v;

根据式(3)更新自适应权值参数 αt+1v.

step 4 根据式(9)更新拉格朗日乘子和惩罚参数 Y1(t+1)v, Y_2(t+1), μ _t+1.

step 5 计算

Θ _t+1= ∑v=1mXv-XvZt+1-XvDt+1v-Et+1vF2, t=t+1.

Until:

(Θ _t+1-Θ _t)< ε 或t> M.

根据式(4)计算邻接矩阵Z^* , 并对Z^* 执行

Ncut谱聚类, 得到聚类结果.

MR-AWMSC主要的时间复杂度由如下变量控制:Z, J, D^v, E^v和α ^v.更新变量Z为求解Sylvester方程, 时间复杂度为O(n³).更新变量J为进行奇异值阈值分解, 时间复杂度为O(n³).更新D^v的过程主要是对矩阵求逆, 时间复杂度为O(n³+d^vn²).更新α ^v的时间复杂度为O(n³).更新E^v的时间复杂度为O(d^vn).因此, 总的时间复杂度为O(n³+d_maxn²), d_max为多视角数据的最高维度.

本文采用如下6个多视角聚类数据集进行实验:图像数据集MSRC_v1^[18]、树叶数据集100leaves^[8]、电影数据集Movies617^[19]、文本数据集BBCSport^[9]、手写数字数据集UCI-digit^[20]和物体识别数据集Caltech101-20^[9].实验前先对每个视角数据进行归一化处理.6个公开数据集的主要信息如表2所示.

表2

Table 2

表2(Table 2)

表2 多视角数据集主要信息 Table 2 Description of multi-view datasets MSRC_v1 Movies617 100leaves BBCSport UCI-digit Caltech101-20 样本数 210 617 1600 544 2000 2386 类别数 7 17 100 5 10 20 视角1 24 1878 64 3183 216 1984 视角2 576 1398 64 3203 76 512 视角3 512 — 64 — 64 928 视角4 256 — — — — 48 视角5 254 — — — — 40 视角6 — — — — — 254

表2 多视角数据集主要信息 Table 2 Description of multi-view datasets

MSRC_v1数据集包括210幅图像, 9个类别.本文从中选择树、建筑、飞机、奶牛、脸、汽车、自行车这7个类别, 从每幅图像提取5 个视觉特征.

100leaves数据集包含100种不同植物叶片, 每种植物都有16个样本, 共1 600个样本.本文提取形状描述符、细尺度边缘和纹理直方图这3种特征.

Movies617数据集包含从IMDb网站收集的17种类别共617部电影, 包含2个视角.

BBCSport数据集为包含5个主题领域的体育新闻数据集, 包括2004年至2005年从BBC体育网站收集的544份文档, 包含2个视角.

UCI-digit数据集共有2 000幅手写数字图像, 0~9, 共有10类, 每类包含200幅图像, 每幅图像采用3种视觉特征, 构建3个视角.

Caltech101-20数据集包含101个图像类别.本文选择20个物体的2 386幅图像作为最终的数据集, 使用6种特征提取方法提取6个视角特征.

为了验证MR-AWMSC的有效性, 与如下算法进行对比.

1)2种经典单视角子空间聚类算法.

(1)SSC^[12].采用l₁范数约束样本自表示矩阵.

(2)LRR^[13].采用核范数约束样本自表示矩阵.

2)9种经典多视角聚类方法.

(1)ECMSC(Exclusivity Consistency Regularized Multi-view Subspace Clustering)^[21].引入位置注意力排他项, 衡量不同视角之间的差异性, 同时定义指示向量一致性项.

(2)DiMSC(Diversity-Induced Multi-view Sub-space Clustering)^[22].利用希尔伯特-施密特独立性准则生成异构性项, 描述多视角表示的相关性, 多视角融合采用平均加权策略.

(3)LMSC(Latent Multi-view Subspace Cluste-ring)^[23].学习多视角数据潜在的统一子空间表示.

(4)CSMSC(Consistent and Specific Multi-view Subspace Clustering)^[24].利用一致表示刻画不同视角间的共同属性和一组特定表示描述每个视角的内在特性, 多视角融合采用平均加权策略.

(5)FCMSC(Feature Concatenation Multi-view Subspace Clustering)^[19].拼接多视角数据特征, 利用l_{2, 1}范数处理多视角数据中基于样本和簇类的噪声, 多视角融合采用平均加权策略.

(6)ARMSC^[9].采用核范数学习一致性全局低秩表示, 具有组效应的F范数学习残差补偿项, 并构造自动加权多视角正则项, 保持局部几何结构.

(7)GMC(Graph-Based Multi-view Clustering)^[25].将不同视角的图矩阵通过图学习误差自动加权融合为一个一致图矩阵, 并约束图拉普拉斯矩阵的秩.

(8)文献[26]算法.核学习多视角聚类算法, 定义邻居核以保持块对角结构, 增强对基核间噪声和异常值的鲁棒性.线性组合基邻居核, 通过精确秩约束子空间分割构造一致邻接矩阵.

(9)MVC-LFA(Multi-view Clustering via Late Fusion Alignment Maximization)^[27].核学习多视角聚类方法, 最大限度对齐一致核矩阵与加权基核矩阵, 集成多视角数据.

本文实验采用如下4个聚类性能评价指标:聚类准确率(Clustering Accuracy, ACC)、标准互信息(Normalized Mutual Information, NMI)、调整兰德指数(Adjusted Rand Index, ARI)和F-score.指标值越高, 聚类性能越优.

由于本次实验采用多视角数据集, 因此2种单视角子空间聚类算法(SSC和LRR)仅给出最佳视角的聚类结果.为了减少谱聚类结果的随机性, MR-AWMSC执行10次, 取10次结果的平均值作为最终结果.

12种聚类算法在6个多视角实验数据集上的聚类指标分别如表3~表8所示.在表中, 黑体数字表示最优值, 斜体数字表示次优值.由表3~表8可得如下结论.

表3

Table 3

表3(Table 3)

表3 各算法在MSRC_v1数据集上的聚类结果对比 Table 3 Clustering result comparison of different methods on MSRC_v1 dataset 算法 ACC NMI ARI F-score SSC 0.790± 0.005 0.748± 0.004 0.650± 0.006 0.698± 0.004 LRR 0.832± 0.001 0.696± 0.002 0.705± 0.001 0.776± 0.001 ECMSC 0.776± 0.000 0.721± 0.000 0.636± 0.000 0.688± 0.000 DiMSC 0.757± 0.000 0.626± 0.000 0.549± 0.000 0.613± 0.000 LMSC 0.786± 0.000 0.676± 0.000 0.619± 0.000 0.649± 0.000 CSMSC 0.781± 0.000 0.686± 0.000 0.626± 0.000 0.678± 0.000 FCMSC 0.724± 0.000 0.610± 0.000 0.521± 0.000 0.588± 0.000 ARMSC 0.871± 0.000 0.781± 0.000 0.739± 0.000 0.775± 0.000 GMC 0.748± 0.000 0.771± 0.000 0.640± 0.000 0.697± 0.000 文献[26]算法 0.738± 0.000 0.657± 0.000 0.573± 0.000 0.637± 0.000 MVC-LFA 0.733± 0.000 0.635± 0.000 0.559± 0.000 0.612± 0.000 MR-AWMSC 0.902± 0.000 0.807± 0.000 0.778± 0.000 0.813± 0.000

表3 各算法在MSRC_v1数据集上的聚类结果对比 Table 3 Clustering result comparison of different methods on MSRC_v1 dataset

表4

Table 4

表4(Table 4)

表4 各算法在100leaves数据集上的聚类结果对比 Table 4 Clustering result comparison of different methods on 100leaves dataset 算法 ACC NMI ARI F-score SSC 0.621± 0.005 0.813± 0.005 0.504± 0.006 0.512± 0.008 LRR 0.526± 0.011 0.748± 0.001 0.397± 0.006 0.401± 0.008 ECMSC 0.733± 0.005 0.863± 0.004 0.628± 0.009 0.632± 0.009 DiMSC 0.728± 0.000 0.873± 0.000 0.643± 0.000 0.646± 0.000 LMSC 0.741± 0.000 0.871± 0.000 0.645± 0.000 0.648± 0.000 CSMSC 0.769± 0.000 0.888± 0.000 0.690± 0.000 0.693± 0.000 FCMSC 0.750± 0.016 0.884± 0.005 0.666± 0.014 0.669± 0.014 ARMSC 0.655± 0.000 0.821± 0.000 0.536± 0.000 0.540± 0.000 GMC 0.824± 0.000 0.929± 0.000 0.497± 0.000 0.504± 0.000 文献[26]算法 0.817± 0.000 0.932± 0.000 0.778± 0.000 0.780± 0.000 MVC-LFA 0.847± 0.000 0.932± 0.000 0.796± 0.000 0.759± 0.000 MR-AWMSC 0.862± 0.000 0.940± 0.000 0.825± 0.000 0.813± 0.000

表4 各算法在100leaves数据集上的聚类结果对比 Table 4 Clustering result comparison of different methods on 100leaves dataset

表5

Table 5

表5(Table 5)

表5 各算法在Movies617数据集上的聚类结果对比 Table 5 Clustering result comparison of different methods on Movies617 dataset 算法 ACC NMI ARI F-score SSC 0.258± 0.004 0.261± 0.002 0.009± 0.003 0.148± 0.003 LRR 0.274± 0.007 0.267± 0.006 0.103± 0.006 0.155± 0.005 ECMSC 0.143± 0.000 0.140± 0.000 0.004± 0.000 0.111± 0.000 DiMSC 0.302± 0.000 0.306± 0.000 0.144± 0.000 0.197± 0.000 LMSC 0.274± 0.009 0.281± 0.010 0.114± 0.008 0.161± 0.007 CSMSC 0.272± 0.000 0.285± 0.000 0.116± 0.000 0.172± 0.004 FCMSC 0.257± 0.014 0.257± 0.013 0.092± 0.009 0.147± 0.009 ARMSC 0.350± 0.000 0.335± 0.000 0.172± 0.000 0.223± 0.000 GMC 0.235± 0.000 0.263± 0.000 0.024± 0.000 0.131± 0.000 文献[26]算法 0.340± 0.000 0.340± 0.000 0.188± 0.000 0.241± 0.000 MVC-LFA 0.344± 0.000 0.343± 0.000 0.171± 0.000 0.210± 0.000 MR-AWMSC 0.361± 0.000 0.358± 0.000 0.191± 0.000 0.245± 0.000

表5 各算法在Movies617数据集上的聚类结果对比 Table 5 Clustering result comparison of different methods on Movies617 dataset

表6

Table 6

表6(Table 6)

表6 各算法在BBCSport数据集上的聚类结果对比 Table 6 Clustering result comparison of different methods on BBCSport dataset 算法 ACC NMI ARI F-score SSC 0.623± 0.001 0.535± 0.004 0.361± 0.006 0.832± 0.003 LRR 0.834± 0.000 0.698± 0.002 0.703± 0.002 0.773± 0.002 ECMSC 0.959± 0.009 0.885± 0.011 0.894± 0.010 0.919± 0.011 DiMSC 0.922± 0.000 0.785± 0.000 0.813± 0.000 0.858± 0.000 LMSC 0.847± 0.003 0.739± 0.001 0.749± 0.001 0.810± 0.001 CSMSC 0.963± 0.001 0.881± 0.000 0.909± 0.001 0.931± 0.000 FCMSC 0.965± 0.000 0.888± 0.000 0.908± 0.000 0.930± 0.000 ARMSC 0.980± 0.000 0.931± 0.000 0.945± 0.000 0.960± 0.000 GMC 0.739± 0.000 0.796± 0.000 0.601± 0.000 0.721± 0.000 文献[26]算法 0.954± 0.000 0.865± 0.000 0.884± 0.000 0.911± 0.000 MVC-LFA 0.860± 0.000 0.733± 0.000 0.705± 0.000 0.527± 0.000 MR-AWMSC 0.982± 0.000 0.936± 0.000 0.953± 0.000 0.964± 0.000

表6 各算法在BBCSport数据集上的聚类结果对比 Table 6 Clustering result comparison of different methods on BBCSport dataset

表7

Table 7

表7(Table 7)

表7 各算法在UCI-digit数据集上的聚类结果对比 Table 7 Clustering result comparison of different methods on UCI-digit dataset 算法 ACC NMI ARI F-score SSC 0.715± 0.001 0.740± 0.001 0.670± 0.005 0.694± 0.004 LRR 0.771± 0.001 0.668± 0.002 0.636± 0.002 0.663± 0.002 ECMSC 0.696± 0.001 0.794± 0.001 0.676± 0.001 0.711± 0.001 DiMSC 0.854± 0.000 0.826± 0.000 0.809± 0.000 0.806± 0.000 LMSC 0.888± 0.000 0.798± 0.000 0.778± 0.000 0.800± 0.000 CSMSC 0.903± 0.000 0.835± 0.001 0.810± 0.000 0.828± 0.000 FCMSC 0.890± 0.000 0.815± 0.000 0.780± 0.000 0.802± 0.000 ARMSC 0.930± 0.000 0.854± 0.000 0.849± 0.000 0.864± 0.000 GMC 0.850± 0.000 0.821± 0.000 0.824± 0.000 0.843± 0.000 文献[26]算法 0.786± 0.000 0.737± 0.000 0.661± 0.000 0.696± 0.000 MVC-LFA 0.732± 0.000 0.642± 0.000 0.562± 0.000 0.604± 0.000 MR-AWMSC 0.931± 0.000 0.859± 0.000 0.852± 0.000 0.868± 0.000

表7 各算法在UCI-digit数据集上的聚类结果对比 Table 7 Clustering result comparison of different methods on UCI-digit dataset

表8

Table 8

表8(Table 8)

表8 各算法在Caltech101-20数据集上的聚类结果对比 Table 8 Clustering result comparison of different methods on Caltech101-20 dataset 算法 ACC NMI ARI F-score SSC 0.439± 0.000 0.480± 0.000 0.292± 0.000 0.356± 0.000 LRR 0.513± 0.081 0.589± 0.001 0.383± 0.023 0.442± 0.045 ECMSC 0.497± 0.000 0.625± 0.000 0.381± 0.000 0.444± 0.000 DiMSC 0.381± 0.003 0.557± 0.010 0.279± 0.005 0.338± 0.005 LMSC 0.442± 0.005 0.613± 0.001 0.311± 0.001 0.369± 0.001 CSMSC 0.438± 0.025 0.531± 0.035 0.337± 0.016 0.389± 0.021 FCMSC 0.447± 0.000 0.613± 0.000 0.364± 0.000 0.305± 0.000 ARMSC 0.593± 0.000 0.649± 0.000 0.484± 0.000 0.548± 0.000 GMC 0.456± 0.000 0.481± 0.000 0.128± 0.000 0.340± 0.000 文献[26]算法 0.424± 0.000 0.547± 0.000 0.302± 0.000 0.340± 0.000 MVC-LFA 0.451± 0.000 0.590± 0.000 0.390± 0.000 0.448± 0.000 MR-AWMSC 0.598± 0.000 0.601± 0.000 0.490± 0.000 0.549± 0.000

表8 各算法在Caltech101-20数据集上的聚类结果对比 Table 8 Clustering result comparison of different methods on Caltech101-20 dataset

1)MR-AWMSC在6个数据集上的ACC、ARI、F-score值均是最高的.除Caltech101-20数据集之外, MR-AWMSC在其它5个数据集上的NMI值也是最高的.该结果表明流形正则引导的自适应视角权重学习算法是有效的.

2)多视角聚类算法虽然综合多视角的信息, 但单视角子空间聚类算法(SSC、LRR)在MSRC_v1、Caltech101-20数据集上的聚类表现优于ECMSC、DiMSC、FCMSC这3种多视角子空间聚类算法.该结果说明如果未采用合理方式融合多视角数据间的关联信息, 多视角聚类算法性能反而不如单视角聚类算法.

3)相比基于子空间学习的多视角聚类算法FCM-SC、DiMSC和ECMSC, MR-AWMSC引入流形正则项, 保持数据的局部几何结构, 并使用流形正则引导不同视角权重的自适应学习, 因此聚类性能更优.FCMSC直接拼接多视角特征, 忽略不同视角的差异性.DiMSC将所有视角的相似矩阵进行相加, 结果易受噪声视角的影响.ECMSC只考虑不同视角数据的全局结构却忽视不同视角数据局部流形结构的差异.

4)相比基于图学习的多视角聚类方法GMC, MR-AWMSC在6个数据集的各项评价指标上均更优.其原因是GMC未考虑多视角差异信息, 构造的统一相似图易受噪声影响.而MR-AWMSC利用流形正则项自适应学习视角权重, 可更恰当地集成不同视角的差异信息, 获得更优的聚类性能.

5)相比基于核学习的多视角聚类方法(文献[26]算法和MVC-LFA), MR-AWMSC在MSRC_v1、UCI-digit、Caltech101-20数据集上的聚类性能更具竞争力.其原因在于, 核方法中核函数的选择可直接影响最终聚类性能, 同时二者的多视角加权融合策略未考虑不同视角非线性结构的差异.然而相比其它多视角聚类算法, 文献[26]算法和MVC-LFA在一些数据集上的聚类准确率较高, 说明核方法对于改善非线性数据的聚类性能也是有效的.

6)相比同是自适应视角权重学习的ARMSC, MR-AWMSC的聚类准确率更高.其原因在于, 相比ARMSC 的自适应图正则项, 本文的流形正则引导的自适应视角权重更能充分刻画每个视角的一致信息和差异信息, 而 ARMSC在某些视角上的权重分配较低, 往往导致过于关注某个单一视角的困境, 无法充分综合利用多视角信息.

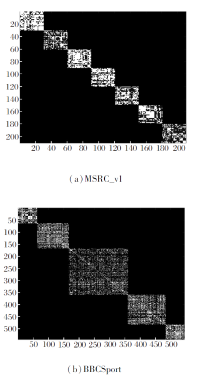
MR-AWMSC在MSRC_v1、BBCSport数据集上学习的邻接矩阵的可视化结果如图2所示.

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 MR-AWMSC在2个数据集上邻接矩阵可视化结果Fig.2 Visualization of adjacency matrix of MR-AWMSC on 2 datasets

由图2可看出, MR-AWMSC在MSRC_v1、BBC-Sport数据上得到的邻接矩阵都具有明显的块对角结构, 由此可说明MR-AWMSC学习得到的邻接矩阵适用于聚类.

为了对比不同加权组合策略对多视角子空间聚类的影响, 本文分别采用平均加权策略和自表示学习误差加权策略作为对比方法.平均加权策略的第v个视角权重α ^v=1/m, m为视角数, 所有视角权重相同.算法其它部分与MR-AWMSC相同, 记为AW-MSC(Average Weighted Multi-view Subspace Clus-tering), 组合得到邻接矩阵:

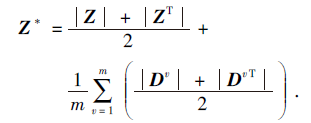
自表示学习误差加权策略的第v个视角权重为:

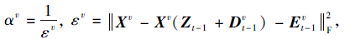
为第t次迭代结果的自表示学习误差, 其中, Z_t-1、 Dt-1v、 Et-1v分别为Z、D^v、E^v第t-1次的迭代结果, 所有视角的权重通过自适应学习得到, ε ^v越小, 该视角自表示学习误差越小, 因此对应的视角权重越大.算法其它部分与MR-AWMSC相同, 记为SL-MSC(Self-Representation Learning Error Based Multi-view Subspace Clustering), 对学习得到的多视角权重α ^v(v=1, 2, …, m)进行归一化处理.组合得到邻接矩阵 Z^* 的计算公式与MR-AWMSC相同.

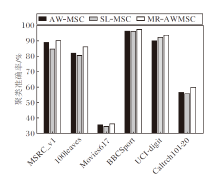
在6个多视角数据集上对AW-MSC、SL-MSC和MR-AWMSC进行聚类实验, 每种方法均取10次聚类平均准确率, 结果如图3所示.

图3

Fig. 3

	Figure Option ViewDownloadNew Window
	图3 3种加权策略的聚类准确率Fig. 3 Clustering accuracy of 3 weighting strategies

由图3可看出, MR-AWMSC在6个数据集上的聚类准确率最高, 而SL-MSC在除了UCI-digit数据集以外的数据集上的聚类准确率均低于AW-MSC.其原因是SL-MSC学习获得的视角权重与数据线性自表示有关, 不能较好地捕获非线性多视角数据的非线性结构特征, 因此学习的视角权重多数情况下还不如AW-MSC有效.相比MR-AWMSC, AW-MSC同等看待每个视角, 忽略不同视角对于聚类效果的贡献具有差异性, 某些数据集上的聚类性能不佳.总之, MR-AWMSC的流形正则引导的视角权重有效提取数据的流形结构信息, 并自动为不同视角差异性分配贡献度, 因此优于SL-MSC和AW-MSC.

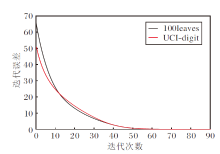
为了观察MR-AWMSC的数值收敛性, 给出100leaves、UCI-digit数据集上算法的迭代误差曲线, 如图4所示.

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 MR-AWMSC在2个数据集上的收敛性分析Fig.4 Convergence analysis of MR-AWMSC on 2 datasets

由图4可看出, 随着迭代次数增加, 迭代误差不断下降, 45次后趋近于收敛, 说明MR-AWMSC是数值收敛的.

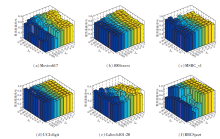
MR-AWMSC包含2个平衡参数λ _E和λ _D, 分别用于平衡误差项和不同视角差异表示矩阵项.为了观察平衡参数对聚类准确率的影响, 采用网格搜索法计算λ _E和λ _D不同取值下的聚类准确率, 如图5所示.λ _E和λ _D的取值范围均为{0.001, 0.005, 0.01, 0.05, 0.1, 0.2, 0.4, 0.5, 1}.

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 不同λ E和λ D取值下的聚类准确率Fig.5 Clustering accuracy with different λ E and λ D

由图5可看出, λ _E和λ _D的取值对聚类准确率的影响是明显的.在Movies617、100leaves数据集上, 平衡参数λ _D值为0.4~1, λ _E值为0.001~0.01时, 可得到较高的聚类准确率.在MSRC_v1、UCI-digit数据集上, λ _D和λ _E的值均为0.001~0.01时, 聚类准确率较高.在Caltech101-20、BBCSport数据集上, λ _D和λ _E值均为0.2~1时, 可得到较高的聚类准确率.因此若在一个合理的范围内选择参数, 可得到较好的聚类结果.