网络决策形式背景下基于因果力的邻域推荐算法

引用本文

范敏, 郭瑞欣, 李金海. 网络决策形式背景下基于因果力的邻域推荐算法. 模式识别与人工智能, 2022,35(11): 977-988
FAN Min, GUO Ruixin, LI Jinhai. Neighborhood Recommendation Algorithm Based on Causality Force under Network Formal Decision Context. PATTERN RECOGNITION AND ARTIFICIAL INTELLIGENCE, 2022,35(11): 977-988. 复制到剪切板

Doi: 10.16451/j.cnki.issn1003-6059.202211003
Permissions

《模式识别与人工智能》编辑部

网络决策形式背景下基于因果力的邻域推荐算法

范敏^1,², 郭瑞欣^1,², 李金海^1,²

1.昆明理工大学数据科学研究中心昆明 650500

2.昆明理工大学理学院昆明 650500

通信作者：

李金海,博士,教授,主要研究方向为认知计算、粒计算、大数据分析、概念格、粗糙集.E-mail: jhlixjtu@163.com.

作者简介：

范敏,博士,副教授,主要研究方向为数据挖掘、粗糙集、粒计算、社会网络分析.E-mail:fmkmust@163.com.

郭瑞欣,硕士研究生, 主要研究方向为数据挖掘、社会网络分析.E-mail:1905248675@qq.com.

收稿日期: 2022-10-18 接受日期: 2022-11-30

资助项目: 国家自然科学基金项目(No.11971211,12171388)资助

摘要

网络数据下的概念认知与知识发现是网络数据分析领域的热门研究方向,已应用于推荐系统领域,但是如何构建合理的弱概念集以提高邻域推荐效果仍是一个难题.为了解决该问题,文中提出变精度弱概念集,诱导出包含较多信息量的邻域,在此基础上提出基于因果力的邻域推荐算法.首先,定义相似性网络聚合中心度,确定专家节点,得到变精度弱概念集,进行邻域划分.然后,在每个邻域中利用变精度共有算子得到对象的条件属性弱概念和对象的决策属性弱概念,通过因果力代换原理和相关推论给出邻域推荐算法.在MovieLens、Filmtrust数据集上的对比实验表明,文中算法在精确度、召回率、 F1值和运行时间上均有明显提升.

关键词: 形式概念分析; 网络决策形式背景; 因果力; 变精度算子; 推荐算法

中图分类号:TP 18

Neighborhood Recommendation Algorithm Based on Causality Force under Network Formal Decision Context

FAN Min^1,², GUO Ruixin^1,², LI Jinhai^1,²

1. Data Science Research Center, Kunming University of Science and Technology, Kunming 650500

2. Faculty of Science, Kunming University of Science and Technology, Kunming 650500

Corresponding author:
LI Jinhai, Ph.D., professor. His research interests include cognitive computing, granular computing, big data analysis, concept lattice and rough set.

About Author:
FAN Min, Ph.D., associate professor. Her research interests include data mining, rough set, granular computing and social network analysis.
GUO Ruixin, master student. Her research interests include data mining and social network analysis.

Fund:National Natural Science Foundation of China(No.11971211,12171388)

Abstract

Concept cognition and knowledge discovery under network data are hot research directions in the field of network data analysis, and they are applied in the field of recommendation system. However, how to construct a reasonable set of weaken-concepts to improve the effectiveness of neighborhood recommendation is still a difficult problem. To solve this problem, a set of variable precision weaken-concepts is proposed to induce neighborhoods with more information, and then a neighborhood recommendation algorithm is developed based on causality force. Firstly, the aggregation centrality degree of similarity network is defined to determine expert nodes, and a set of variable precision weaken-concepts is obtained to divide neighborhoods. Secondly, the variable precision common operators are employed in each neighborhood to obtain the weaken-concepts of conditional attributes and decision attributes of objects. Finally, a neighborhood recommendation algorithm is given based on the principle of causality force and related properties. Experimental results on MovieLens and Filmtrust datasets show that the accuracy, recall, F1 and running time of the proposed algorithm are greatly improved.

Key words: Formal Concept Analysis; Network Formal Decision Context; Causality Force; Variable Precision Operator; Recommendation Algorithm

文章图片

早期形式概念分析(Formal Concept Analysis, FCA)^[1]专注于研究概念及概念层次的数学化和形式化表达.随着FCA的快速发展, 与各领域的交叉研究日渐深入, 现已广泛应用于软件工程^{[2, 3]}、数据挖掘^{[4, 5, 6]}、推荐系统^[7]等具有广阔应用前景的领域.

基于形式背景的概念认知是一个新兴的研究领域, 主要以形式概念分析、粗糙集及粒计算等理论为工具.在大数据环境下, 概念认知学习具有诸多认知优势, 学者们对其进行一系列的研究^{[8, 9, 10]}.在概念认知学习中, 基于各种算子的研究得到不同的概念^[11].Dü ntsch等^[12]给出近似算子— — 必要算子和可能算子, 研究面向属性概念格.Yao^[13]研究面向对象概念格和面向属性概念格, 以及它们之间的关系.闫梦宇等^[14]基于Wille概念格、面向对象概念格和面向属性概念格, 定义共有属性(对象)与独有属性(对象), 并研究它们的算子性质.将上述算子结合变精度思想可得到各种变精度算子, 进一步与实际应用结合, 有利于丰富概念认知理论与应用的研究.如何将概念认知学习方法与网络中的因果推断、规则提取结合, 是一个有意义的课题.

目前, 常见的推荐系统包括以下几种:Zaier等^[15]提出的基于邻域的推荐系统, 主要是通过计算相似度找到相关邻域, 根据邻域信息进行推荐; Garcia等^[16]提出的组推荐系统(Group Recommender System), 推荐对象为整个群组.基于邻域的推荐方法常见于协同过滤推荐系统中, 主要分为基于用户的协同过滤推荐^[17]和基于项目的协同过滤推荐^[18].前者是根据用户之间的相似度进行推荐, 后者是根据项目之间的相似度进行推荐.组推荐系统通过研究所有邻域成员偏好之间的关联性得到邻域偏好, 最后利用邻域偏好进行推荐^[19].

由上述研究可知, 基于邻域的推荐算法需要解决两个问题:1)如何得到相关邻域, 并使这些邻域中能涌现足够多的规律; 2)如何根据每个邻域信息得到邻域偏好之间的关联性, 构建推荐算法.

Pearl^[20]在《Causality》中指出:因果关系不应被视为单一关系, 而应被视为具有两个维度— — 充分性和必要性.该书结合概率论的相关知识, 给出充分性与必要性的定义, 为研究因果力奠定基础.之后Pearl又深入研究当代的因果分析方法, 将因果科学从一个模糊的概念变成一个可以量化的理论, 并广泛应用于数理统计^[21]、人工智能^{[22, 23]}、认知科学^{[24, 25]}等领域.

之后, 学者们重新定义因果力的衡量标准^[26], 并将PNS=suff(e|c)+nec(e|c)-1作为度量因果关系的新标准.Hoel等^[27]提出使用一般的因果关系度量有效信息以衡量因果有效性, 并在文献[28]中列举十几种较通用的因果力测量方法.学者们结合各种因果力的研究与规则挖掘, 得到更有效的规则挖掘算法, 进一步应用于推荐系统^{[29, 30, 31]}.

当前, 基于概念格的推荐方法已取得如下研究成果:基于概念邻域的Top-N推荐^[7]、启发式构造概念格进行推荐^[32]、基于RSS(Really Simple Syndi-cation)的电子学习推荐^[33]、模拟退火法构造概念集进行推荐^[34]、PRS(Personalized Recommendation System)^[35]、形式概念分析和协同过滤推荐结合^[36].然而概念格构造效率太低, 几乎与形式背景的规模增长呈指数关系^{[37, 38, 39]}, 使基于经典概念集的社区划分在实际数据中难以实现.

为了解决在进行组推荐时应用概念格划分社区出现的高复杂度问题, 范敏等^[40]提出基于弱概念相似度的组推荐算法(Group Recommendation Algori-thm Based on Weaken-Concept Similarity, GRAWS), 通过* 算子诱导的弱概念集划分论域形成社区, 并在划分社区时计算属性弱概念下限相似度, 以此进行组推荐, 降低划分社区的计算复杂度, 同时提高推荐效果.但是, * 算子的约束条件过于严格, 诱导的弱概念集频繁出现空集, 因此无法保证获得足够多的弱概念, 导致诱导的规则集应用于组推荐效果不佳.

针对上述问题, 本文将对象之间的完全包含关系弱化成部分包含关系, 在网络决策形式背景下定义 $_{α}^{*}$ 算子和 $_{β}^{*}$ 算子, 得到变精度弱概念, 并将基于相似度的邻域推荐与复杂网络中心度结合, 把对象相似矩阵看作网络拓扑结构, 求得相似矩阵中每个对象的中心度.中心度越大的对象意味着与它相似的对象越多, 于是可将这些对象与它的一阶邻居聚合形成一个网络, 即相似性聚合网络, 进而利用变精度弱概念对论域进行有效划分.另一方面, 由于邻域成员之间的偏好关联性可通过因果关系描述, 所以通过揭示因果力和规则置信度之间的关系, 进一步提出基于因果力的邻域推荐算法.总之, 本文结合网络决策形式背景、 $_{α}^{*}$ 算子、 $_{β}^{*}$ 算子、因果力和邻域推荐思想, 提出基于因果力的邻域推荐算法(Neighbor-hood Recommendation Algorithm Based on Causality Force, NRACF).首先, 根据相似性聚合网络中心度找到专家节点, 得到相似性聚合网络变精度弱概念, 并在相应的约束条件和目标函数下划分论域, 形成社区.然后, 在划分的社区中计算条件属性与决策属性之间的因果力, 得到推荐规则, 对社区成员进行邻域推荐.在MovieLens、Filmtrust数据集上的对比实验表明, NRACF在精确度、召回率、F1值和运行时间上均有明显提升.

1 相关定义

定义1^[1] 三元组(U, A, I)称为形式背景, 其中, U={x₁, x₁, …, x_n}为非空有限对象集, A={a₁, a₂, …, a_m}为非空有限属性集, I为笛卡尔积U× A上的二元关系.约定(x, a)∈ I表示对象x拥有属性a; (x, a)∉I表示对象x不拥有属性a.

为了从形式背景中诱导出概念, 给出如下算子的定义.对于∀ X∈ 2^U, B∈ 2^A, 有

1)xI={a∈ A|(x, a)∈ I},

2)Ia={x∈ U|(x, a)∈ I},

3)X^*={a∈ A|∀ x∈ X, (x, a)∈ I},

4)B^*={x∈ U|∀ a∈ B, (x, a)∈ I},

其中, xI表示对象x拥有的所有属性组成的集合, Ia表示拥有属性a的所有对象组成的集合, X^*表示X中所有对象共同拥有的属性, B^*表示拥有B中所有属性的对象.

定义2 五元组(U, M, C, D, I)称为网络决策形式背景, 其中:U={x₁, x₁, …, x_n}为非空有限节点集; M={M₁, M₂, …, M_n}为网络邻接矩阵集, M_l= $(m_{ij}^{l})_{n \times n}$ 为l阶邻接矩阵; C={c₁, c₂, …, c_r}为非空有限条件属性集; D={d₁, d₂, …, d_t}为非空有限决策属性集, I={I₁, I₂, …, I_k, I_C, I_D}为二元关系集合, I_l, l=1, 2, …, k为笛卡尔积U× U上的二元关系, I_C为笛卡尔积U× C上的二元关系, I_D为笛卡尔积U× D上的二元关系.约定(x_i, x_j)∈ I_l表示节点x_i和节点x_j是l阶邻接的; (x_i, c_s)∈ I_C表示节点x_i拥有条件属性c_s, 又记为I_C(x_i, c_s)=1; (x_i, d_p)∈ I_D表示节点x_i拥有决策属性d_p, 又记为I_D(x_i, d_p)=1.

例1 已知评分矩阵Q(见表1), 由定义2结合用户矩阵, 可得到网络决策形式背景(见表2).

表1 评分矩阵Q Table 1 Scoring matrix Q

表2 网络决策形式背景(U, M, C, D, I) Table 2 Network formal decision context(U, M, C, D, I)

表1给出的评分矩阵Q描述用户x_i对项目a_j的评分情况.v(x₁, a₁)=4表示用户x₁对项目a₁的评分为4, v(x₁, a₂)=0表示用户x₁没有对项目a₂做出评分.表2描述用户之间的连接关系和用户对项目的拥有情况.

在表1中, 首先, 采用

WR(a_k)=（ $\frac{v_{a_{k}}}{v_{a_{k}} + m}$ ）R(a_k)+（ $\frac{m}{v_{a_{k}} + m}$ ） $\bar{v}$

对项目评分进行修正(https://blog.csdn.net/Joenyye/article/details/80902717), 其中, $v_{a_{k}}$ 为项目a_k的评论人数, m为项目评论标准人数, R(a_k)为项目a_k评分的均值, $\bar{v}$ 为所有项目评分的均值.

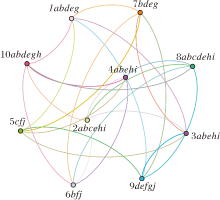
其次, 根据修正后的评分进行条件属性集C={c₁, c₂, …, c_r}与决策属性集D={d₁, d₂, …, d_t}的划分, 选取修正评分的中位数Md作为划分属性集的阈值, 评分大于等于Md的属性作为条件属性集C, 评分小于Md的属性作为决策属性集D.若v(x_i, c_i)> 0, 则在表2中I_C(x_i, c_i)=1表示用户x_i拥有项目c_i.同理, 若v(x_i, c_t)=0, 则在表2中I_C(x_i, c_t)=0表示用户x_i不拥有项目c_t.若v(x_i, d_j)> 0, 则在表2中I_D(x_i, d_j)=1表示用户x_i拥有项目d_j.同理, 若v(x_i, d_s)=0, 则在表2中I_D(x_i, d_s)=0表示用户x_i不拥有项目d_s. $m_{12}^{1}$ =1表示用户x₁和用户x₂之间有一条边相连, $m_{12}^{1}$ =0表示用户x₁和用户x₂之间没有边相连, $m_{21}^{k}$ =1表示用户x₂和用户x₁之间通过k条边相连, $m_{21}^{k}$ =0表示用户x₂和用户x₁之间不能通过k条边相连.

例2 已知一个电影推荐网络图(见图1), 根据该网络图可得到它对应的网络决策形式背景(见表3), 其中, U={x₁, x₁, …, x₁₀}表示观看电影的10位对象, C={a, b, c, d, e, f}表示6部顶级热门电影, D={g, h, i, j}表示4部较热门电影.M₁= $(m_{ij}^{1})_{n \times n}$ 表示一阶邻接矩阵, $m_{13}^{1}$ =1表示对象x₁和对象x₃之间有一条边相连, $m_{12}^{1}$ =0表示对象x₁和对象x₂之间没有边相连, I_C(x₁, a)=1表示对象x_i观看热门电影a, I_D(x₁, g)=1表示对象x_i观看较热门电影g.

	Figure Option View Download New Window
	图1 电影推荐网络图Fig.1 Movie recommendation network

表3 图1对应的网络决策形式背景(U, M, C, D, I) Table 3 Network formal decision context(U, M, C, D, I) of Fig.1

2 问题描述与解决

本文将主要解决如下两个问题:1)通过变精度弱概念划分论域, 构建社区; 2)利用因果力代换实现邻域推荐.

2.1 变精度弱概念

文献[40]通过构建弱概念集进行组推荐时, 需满足约束条件:1)得到的弱概念集要覆盖形式背景的所有对象, 即保证每个对象都至少属于一个弱概念; 2)挖掘的弱概念内涵的规模必须大于预设阈值.由于* 算子约束条件较严格, 诱导出的对象弱概念或属性弱概念组成的集合频繁出现空集, 因此, 按上述方式构建弱概念集可能出现无法找到足够多的弱概念满足上述约束条件的现象.

为了避免出现上述情况, 本文将对象之间的完全包含关系弱化成部分包含关系, 在网络决策形式背景下定义 $_{α}^{*}$ 算子和 $_{β}^{*}$ 算子, 得到变精度弱概念.进一步, 构建变精度弱概念集实现邻域推荐.在描述问题之前先给出相似性聚合中心度 $、_{α}^{*}$ 算子 $、_{β}^{*}$ 算子和变精度弱概念的定义.

定义3 对于评分矩阵Q,

V_i={v(x_i, a_p), ∀ a_p∈ A}

为用户x_i对项目集的评分,

V_j={v(x_j, a_p), ∀ a_p∈ A}

为用户x_j对项目集的评分, 则用户间的相似矩阵

S=(s(i, j))_n_×_n,

其中

s(i, j)= $\{\begin{array}{l} 1, \frac{d (i, j)}{\max {d (i, j)}} > \frac{\max {d (i, j)}}{2} \\ 0, \frac{d (i, j)}{\max {d (i, j)}} \leq \frac{\max {d (i, j)}}{2} \end{array}$ d(i, j)=‖ Vi_-Vj_‖2_.

由定义2和定义3可将相似矩阵S转换为网络邻接矩阵M.

定义 4 给定网络决策形式背景(U, M, C, D, I), 则节点x_i的相似性聚合中心度定义为

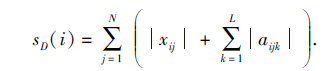
其中:当节点x_j和节点x_i一阶邻接时有|x_ij|=1, 此时, $\overset{L}{\sum_{k = 1}}$ |a_ijk|表示节点x_i与其邻接节点x_j的共有属性的个数, 当节点x_i与其邻接节点x_j共同拥有第k个属性时, 有|a_ijk|=1, 否则, |a_ijk|=0.当节点x_i与节点x_j不是一阶邻接时, 有|x_ij|=0, 此时, $\overset{L}{\sum_{k = 1}}$ |a_ijk|=0, N为网络决策形式背景中节点的总个数, L为网络决策形式背景中属性集的属性总数.

定义5 给定一个网络决策形式背景(U, M, C, D, I), 对∀ X∈ 2^U, C∈ 2^C, D∈ 2^D, 变精度共有算子定义如下:

1) $X_{α_{1}}^{* C}$ = $\{c_{i} \in C | \frac{|I_{C} c_{i} ⋂ X|}{|X|} > α_{1}\}$ , 0≤ α ₁< 1;

2) $X_{α_{2}}^{* D}$ = $\{d_{i} \in D | \frac{|I_{D} d_{i} ⋂ X|}{|X|} > α_{2}\}$ , 0≤ α ₂< 1;

3) $C_{β_{1}}^{* U}$ = $\{x_{i} \in U | \frac{|x_{i} I_{C} ⋂^{} C|}{|C|} > β_{1}\}$ , 0≤ β ₁< 1;

4) $D_{β_{2}}^{* U}$ = $\{x_{i} \in U | \frac{|x_{i} I_{D} ⋂^{} D|}{|D|} > β_{2}\}$ , 0≤ β ₂< 1.

例3 在例2的电影推荐网络中, C为顶级热门电影集, D为较热门电影集, $X_{α_{1}}^{* C}$ 表示对象集X中有大于比例α 1的对象看过的顶级热门电影, $X_{α_{2}}^{* D}$ 表示对象集X中有大于比例α 2的对象看过的较热门电影, $C_{β_{1}}^{* U}$ 表示看过观看率大于比例β 1的顶级热门电影的对象集, $D_{β_{2}}^{* U}$ 表示看过观看率大于比例β 2的较热门电影的对象集.

性质1 设(U, M, C, D, I)为一个网络决策形式背景, 对∀ X∈ 2^U, C∈ 2^C, D∈ 2^D, 下述结论成立:

1)α ₁> α ₂⇒ $X_{α_{2}}^{* C}$ ⊇ $X_{α_{1}}^{* C}$ , $X_{α_{2}}^{* D}$ ⊇ $X_{α_{1}}^{* D}$ ,

2)β ₁> β ₂⇒ $C_{β_{2}}^{* U}$ ⊇ $C_{β_{1}}^{* U}$ , $D_{β_{2}}^{* U}$ ⊇ $D_{β_{1}}^{* U}$ .

证明先证1).对∀ X∈ 2^U, 由定义5可得

$X_{α_{1}}^{* C}$ = $\{c_{i} \in C | \frac{|I_{C} c_{i} ⋂ X|}{|X|} > α_{1}\}$ , 0≤ α ₁< 1,

$X_{α_{2}}^{* C}$ = $\{c_{i} \in C | \frac{|I_{C} c_{i} ⋂ X|}{|X|} > α_{2}\}$ , 0≤ α ₂< 1,

对于∀ c_i∈ $X_{α_{1}}^{* C}$ , 有

$\frac{|I_{C} c_{i} ⋂ X|}{|X|}$ > α ₁> α ₂,

故c_i∈ $X_{α_{2}}^{* C}$ , 从而 $X_{α_{2}}^{* C}$ ⊇ $X_{α_{1}}^{* C}$ .同理可证 $X_{α_{2}}^{* D}$ ⊇ $X_{α_{1}}^{* D}$ .

再证2).对∀ C∈ 2^C, 由定义5可得

$C_{β_{1}}^{* U}$ = $\{x_{i} \in U | \frac{|x_{i} I_{C} ⋂^{} C|}{|C|} > β_{1}\}$ , 0≤ β ₁< 1,

$C_{β_{2}}^{* U}$ = $\{x_{i} \in U | \frac{|x_{i} I_{C} ⋂^{} C|}{|C|} > β_{2}\}$ , 0≤ β ₂< 1,

对于∀ x_i∈ $C_{β_{1}}^{* U}$ , 有

$\frac{|x_{i} I_{C} ⋂^{} C|}{|C|}$ > β ₁> β ₂,

故x_i∈ $C_{β_{2}}^{* U}$ , 从而 $C_{β_{2}}^{* U}$ ⊇ $C_{β_{1}}^{* U}$ .同理可证 $D_{β_{2}}^{* U}$ ⊇ $D_{β_{1}}^{* U}$ .

定义6 给定网络决策形式背景(U, M, C, D, I), 称(X, $X_{α}^{* C}$ , $X_{β}^{* D}$ )为由X诱导的变精度弱概念.

在上述定义1~定义6的基础上提出问题1, 描述如下.

问题1 通过变精度弱概念划分论域U

输入网络决策形式背景(U, M, C, D, I)

输出划分集C_S

优化目标 min(|C_S|)

约束条件1 $\cup_{(}^{X_{i}}$ X_i=U

约束条件2 ∀ (X_i, $X_{iα}^{* C}$ , $X_{iβ}^{* D}$ )∈ C_S,

| $X_{iα}^{* C}$ |≥ ω ₁, | $X_{iβ}^{* D}$ |≥ ω ₂

其中

C_S={(X_i, $X_{iα}^{* C}$ , $X_{iβ}^{* D}$ ), X_i⊆U}.

优化目标表示最小化社区数量, 用于提高模型的拟合能力.约束条件1表示变精度弱概念集覆盖论域U中所有对象, 即每个对象至少划分在一个邻域(社区)中.约束条件2表示挖掘的变精度条件弱概念内涵规模不小于ω ₁, 变精度决策弱概念内涵规模不小于ω ₂, 即只有当用户拥有的项目足够多时, 形成的邻域(社区)才有意义.下面进一步研究邻域推荐算法.

2.2 基于因果力的邻域推荐

本节首先给出推荐规则、规则置信度与规则因果力的概念.

定义7 推荐规则r(c_i, d_j)表示向拥有条件属性c_i的对象推荐决策属性d_j, 即r(c_i, d_j):c_i→ d_j.

定义8 对于规则r(c_i, d_j):c_i→ d_j, 称

μ _ij= $\frac{|c_{i}^{*} ⋂ d_{j}^{*}|}{|c_{i}^{*}|}$

为规则r(c_i, d_j)的置信度.

定义9 设规则r(d_j, c_i):d_j→ c_i为规则r(c_i, d_j):c_i→ d_j的反规则, 称

μ _ji= $\frac{|c_{i}^{*} ⋂ d_{j}^{*}|}{|d_{j}^{*}|}$

为反规则r(d_j, c_i)的置信度.

Pearl^[20]在《Causality》中定义必要性概率:

nec(e|c)=P(~e|~c),

即反事实概率.也就是如果原因c没有发生, 结果e就不会发生的概率.定义充分性概率

suff(e|c)=P(e|c),

即原因c导致结果e发生的概率.并且, 给出衡量因果力的标准:

PNS=nec(e|c)+suff(e|c)-1.

Eells^[29]从另外一个角度提出, c是e的原因需满足

p(e|c)> p(e|C-c),

其中C为原因集.并且可用这两个量之间的差衡量因果强度:

SC_Eells=p(e|c)-p(e|C-c)=suff(e|c)+nec(e|c)-1.

下面基于文献[20]、文献[29]和定义7~定义9, 研究因果关系充分性和必要性与定义8、定义9中规则置信度的关系, 并给出c_i和d_j之间因果力的定义.

定义10 对于规则r(c_i, d_j):c_i→ d_j, 充分性

suff(d_j, c_i)= $\frac{|c_{i}^{*} ⋂ d_{j}^{*}|}{|c_{i}^{*}|}$ =μ _ij.

特别地, 若

P(d_j|c_i)=1,

表示c_i的发生必然导致d_j发生, 也可理解为规则r(c_i, d_j):d_j→ c_i的置信度为1.

定义11 对于规则r(c_i, d_j):c_i→ d_j, 必要性

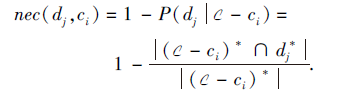
特别地, 若

1-P(d_j|C-c_i)=1,

则

P(d_j|C-c_i)=0,

即在C中删除c_i之后, d_j不发生, 表示c_i的发生对d_j的发生是必要的.

定理1 对于反向规则

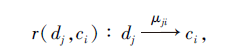
有如下结论成立:

μ _ji=1⇔ P(d_j|C-c_i)=0.

证明先证充分性.若

μ _ji=P(c_i|d_j)= $\frac{|c_{i}^{*} ⋂ d_{j}^{*}|}{|d_{j}^{*}|}$ =1,

即

$|c_{i}^{*} ⋂ d_{j}^{*}|$ = $|d_{j}^{*}|$ ,

从而有 $c_{i}^{*}$ ∩ $d_{j}^{*}$ = $d_{j}^{*}$ , 则 $d_{j}^{*}$ ⊆ $c_{i}^{*}$ , 故

$d_{j}^{*}$ ∩ $(~ c_{i})^{*}$ =Ø ,

即

$d_{j}^{*}$ ∩ $(C - c_{i})^{*}$ =Ø ,

故

P(d_j|C-c_i)=0.

必要性显然成立.

推论1 对于反向规则

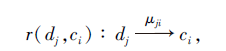
有如下结论成立:

μ _ji=P(c_i|d_j)=1⇔ nec(d_j, c_i)=1.

由定理1和推论1可知, 若P(c_i|d_j)=1, 表示c_i的发生对d_j的发生是必要的.也可理解为规则r(d_j, c_i)的置信度μ _ji=1, 反之亦然.

定理2 对于反向规则

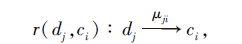
置信度μ _ji与nec(d_j, c_i)呈正相关关系.

证明假设

μ _ji=P(c_i|d_j)= $\frac{|c_{i}^{*} ⋂ d_{j}^{*}|}{|d_{j}^{*}|}$ =β ,

从而

P(~c_i|d_j)=1-P(c_i|d_j)=1-β ,

进一步得

$|(C - c_{i})^{*} ⋂ d_{j}^{*}|$ = $|d_{j}^{*}|$ (1-β ),

又因为

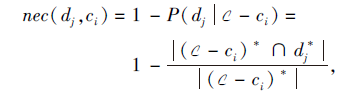
所以

nec(d_j, c_i)=1- $\frac{|d_{j}^{*}|}{|(C - c_{i})^{*}|}$ + $\frac{μ_{ji} |d_{j}^{*}|}{|(C - c_{i})^{*}|}$ .

故置信度μ _ji与nec(d_j, c_i)呈正相关关系.

根据上述研究并结合文献[20]中因果力的定义, 可得到如下因果力的定义.

定义12 对于规则

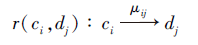
及其反规则

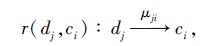
c_i和d_j之间的因果力定义为

CP=μ _ij+μ _ji-1.

显然CP∈ [-1, 1].

文献[39]指出, 当SC_Eells< 0时, 不能说明c是e的原因, 即:当CP< 0时, 不能说明c_i是d_j的原因; 反之, 当CP≥ 0时, 要么c_i是d_j的原因, 要么d_j是c_i的原因, 要么c_i和d_j互为因果.

下面讨论c_i和d_j互为因果的情形.假设当μ _ij≥ ξ 时, c_i是d_j的原因, 即c_i→ d_j成立.同理, 当μ _ji≥ ξ 时, d_j是c_i的原因, 即d_j→ c_i成立.同时满足μ _ij+μ _ji≥ 1, 于是有

$\begin{matrix} μ_{ij} \geq ξ, μ_{ji} \geq ξ, μ_{ij} + μ_{ji} \geq 1, \end{matrix}$

从而2ξ ≥ 1, 进一步得到ξ ≥ 0.5.

因此, 根据上述研究可得到如下推论2.

推论2 若μ _ij≥ 0.5, 有c_i→ d_j成立, 否则有c_i→ ¬ d_j成立.同理, 若μ _ji≥ 0.5, 有d_j→ c_i成立, 否则有d_j→ ¬ c_i成立.

在问题1输出划分集C_S的基础上结合上述定理和推论, 进一步可研究如下问题2.

问题2 基于因果力代换的邻域推荐

输入C_S, 置信度阈值η 、δ

输出推荐规则r(c_i, d_j)

优化目标 max(F1)

约束条件 对∀ c_i∈ $X_{iα}^{* C}$ , ∀ d_j∈ $X_{iβ}^{* D}$ ,

1)若μ _ij≥ η , 则向拥有属性c_i的对象推荐属性d_j,

2)若μ _ji≥ δ , 则向拥有属性d_j的对象推荐属性c_i.

其中, 优化目标是最大化综合评价指标F1, 用于提高模型的质量.约束条件表示在社区X_i中, 若μ _ij≥ η , 则将属性d_j推荐给社区X_i中拥有属性c_i的节点; 若μ _ji≥ δ , 则将属性c_i推荐给社区X_i中拥有属性d_j的节点.

特别地, 由推论2可知, 在提取推荐规则时, 置信度阈值η ≥ 0.5, δ ≥ 0.5.因此, 在后面实验部分设置置信度阈值分别为η =δ =0.5.

3 基于因果力的邻域推荐算法

3.1 算法步骤

基于因果力的邻域推荐算法(NRACF)框图如图2所示.

	Figure Option View Download New Window
	图2 NRACF框架图Fig.2 Flowchart of NRACF

下面给出NRACF的具体步骤.

算法1 基于因果力的邻域推荐算法(NRACF)

输入网络决策形式背景(U, M, C, D, I),

专家比例λ , 置信度阈值η 、δ

输出推荐规则r(c_i, d_j), r(d_j, c_i)

step 1 计算网络中所有节点的聚合中心度:

将所有的聚合度中心度s_D(i)按从大到小的顺序排列, 并依据λ 选取专家集, 记为E={e₁, e₂, …, e_h}, 其中h=λ |U|.

step 2 依次选取E中的节点e_i, 及其一阶邻接节点集构成社区N={X₁, X₂, …, X_h}.

step 3 依次选取N中的社区X_s, 计算每个条件属性c_i在社区X_s中的密度

ρ _c= $\{\frac{|I_{C} c_{i} ⋂ X_{s}|}{|X_{s}|}, c_{i} \in C\}$ ,

以及每个决策属性d_j在社区X_s中的密度

ρ _d= $\{\frac{|I_{D} d_{j} ⋂ X_{s}|}{|X_{s}|}, d_{j} \in D\}$ .

在此基础上, 计算每个社区ρ _c的均值μ 及标准差σ , 并对所有社区的μ -σ 求平均值, 记为条件属性密度α 的阈值, 同理得到决策属性密度β 的阈值.

step 4 依次选取N中的社区X_s, 计算

$X_{sα}^{* C}$ = $\{c_{i} \in C | \frac{|I_{C} c_{i} ⋂ X_{s}|}{X_{s}} > α\}$ ,

$X_{sβ}^{* D}$ = $\{d_{j} \in D | \frac{|I_{D} d_{j} ⋂ X_{s}|}{|X_{s}|} > β\}$ .

step 5 对于∀ c_i∈ $X_{sα}^{* C}$ , d_j∈ $X_{sβ}^{* D}$ , 计算

μ _ij= $\frac{|c_{i}^{*} ⋂ d_{j}^{*}|}{|c_{i}^{*}|}$ , μ _ji= $\frac{|c_{i}^{*} ⋂ d_{j}^{*}|}{|d_{j}^{*}|}$ .

若μ _ij≥ η , 输出推荐规则r(c_i, d_j); 若μ _ji≥ δ , 输出推荐规则r(d_j, c_i); 若μ _ij≥ η 且μ _ji≥ δ , 输出推荐规则r(c_i, d_j)和r(d_j, c_i); 否则, 返回step 4.

step 6 利用获取的推荐规则对网络中的节点进行推荐预测, 算法结束.

3.2 时间复杂度分析

假设网络决策形式背景中有n位用户和m个属性, 属性包括p个条件属性, q个决策属性, m=p+q, 则选取的专家个数为λ n, 通过专家节点划分社区的时间复杂度为O(λ n²).在划分的社区中, 计算条件弱概念内涵的时间复杂度为O(λ n²p), 计算决策弱概念内涵的时间复杂度为O(λ n²q), 对于w个条件弱概念内涵和v个决策弱概念内涵, 计算条件弱概念内涵与决策弱概念内涵间因果力的时间复杂度为O(wv).由于要遍历所有社区进行推荐, 所以算法1的时间复杂度为O(λ ²n³m+λ nwv).

注意到, 对象拥有的属性个数小于m, 因此, 构造弱概念集进行邻域划分的时间复杂度小于O(λ n²m).对比构造概念格进行邻域划分的时间复杂度O(n2^m)^[37]和文献[40]的时间复杂度O(λ n³m²), NRACF具有明显的计算优势.

4 实验及结果分析

4.1 实验环境

本文实验选取电影评分MovieLens数据集(https://grouplens.org/datasets/movielens)上的ML-1m数据集与ML-100k数据集的5个抽样数据集和电影评分Filmtrust数据集(https://guoguibing.github.io/librec/datasets.html), 数据集信息如表4所示.

表4 实验数据集信息 Table 4 Information of experimental datasets

在实验中, 首先将所用数据集进行预处理, 再随机选取80%的数据作为训练集, 剩余20%的数据作为测试集.然后在训练集上利用算法1得到推荐规则.进一步, 在测试集上进行推荐列表预测, 并计算该算法在数据集上的精确度、召回率和F1值.最后, 将算法1的结果与常见的6种推荐算法进行对比.

下面说明数据集的预处理步骤.

1)构造决策形式背景.首先, 由于部分电影评论人数较少, 可用性不强, 故选择评论人数前30%的电影作为属性集.然后, 将筛选的属性集按照例1中方法分为条件属性集C与决策属性集D.最后, 在电影评分矩阵Q中:若v(x_i, c_i)> 0, 则I_C(x_i, c_i)=1, 否则, I_C(x_i, c_i)=0; 若v(x_i, d_j)> 0, 则I_D(x_i, d_j)=1, 否则, I_D(x_i, d_j)=0, 得到决策形式背景.

2)构造网络邻接矩阵.对于电影评分矩阵Q, 根据定义3将对象间的相似性矩阵S转化为网络邻接矩阵M, 得到对象间的网络邻接矩阵.

本文采用如下推荐系统常用的评价指标.

1)精确度(Precision):

precision= $\frac{| R (x) ⋂ T (x) |}{| R (x) |}$ .

2)召回率(Recall):

recall= $\frac{| R (x) ⋂ T (x) |}{| T (x) |}$ .

3)F1-measure:

F1= $\frac{2 \times precision \times recall}{precision + recall}$ .

其中, R(x)为根据训练集得到的推荐预测列表, T(x)为用于验证结果的测试列表.

4.2 参数讨论

本节分析参数λ 对F1值的影响, 并讨论算法1中计算参数α 、 β 方法的合理性.

在算法1中, 选取λ =0.1、0.3、0.5、0.7、0.9, 依次计算F1值, 结果如表5所示, 表中黑体数字表示最大值.由表可知, 随着λ 的增大, 各数据集上F1值逐渐减小, 变化幅度较小, 但均在λ =0.1时取得最大值.这说明当专家比例达到0.1时, 算法1在各数据集上的指标值最优.

表5 参数λ 对F1值的影响 Table 5 Effect of λ on F1

在算法1中, 根据统计原理求得条件属性密度阈值α =0.2, 决策属性密度阈值β =0.1.

下面分别定义α =0.1, 0.2, …, 0.9, β =0.1, 0.2, …, 0.9, 根据算法1获取推荐规则集, 并在测试集上计算F1值, 结果如表6和表7所示, 表中黑体数字表示最大值.另外, 当α =0.5, 0.6, …, 0.9时, F1值都为0, 所以未显示在表6中.而当β =0.4, 0.5, …, 0.9时, F1值都为0, 所以也未显示在表7中.

表6 参数α 对F1值的影响 Table 6 Effect of α on F1

表7 参数β 对F1值的影响 Table 7 Effect of β on F1

由表6可知, 当α 从0.1增大到0.2时, 各数据集上的F1值逐渐增大, 并在α =0.2时取得最大值.而当α 继续增大时, 各数据集上的F1值逐渐减小直至为0.这是因为当α 达到一定值时, 若继续增大, 社区中满足条件的条件属性会减少, 获取的推荐规则也会减少, 最终导致F1值越来越小.所以, 在算法1中, 根据统计原理求得α 的方法是可行的.

由表7可知, 随着β 的增大, 各数据集上的F1值逐渐减小, 直至为0, 但均在β =0.1时取得最大值.这是因为当β 达到一定值时, 若继续增大, 社区中满足条件的决策属性就会减少, 获取的推荐规则也会减少, 最终导致F1值越来越小.所以, 在算法1中, 根据统计原理求得β 的方法也是可行的.

综上所述, 本文将算法1的参数设置为λ =0.1, η =δ =0.5, 并进行如下对比实验.

4.3 对比实验结果

GRAWS^[40]是基于弱概念相似度的组推荐算法, 主要通过* 算子诱导的网络弱概念进行社区划分, 并在划分的社区中根据属性弱概念下限相似度进行组推荐.对于n位用户和m个属性的网络决策形式背景, GRAWS的时间复杂度为O(λ n³m²).为了验证NRACF的有效性与运行效率, 将其与GRA-WS在不同的数据集上进行对比实验, 结果如表8所示, 表中黑体数字部分表示最优值.

表8 NRACF与GRAWS的推荐效果及运行时间对比 Table 8 Comparison of recommendation results and running time between NRACF and GRAWS

由表8可知, 在7个数据集上, 相比GRAWS, NRACF的推荐效果有小幅提升, 但在运行效率上有明显提高.具体地, 在精确度上, NRACF均优于GRAWS.在召回率上, NRACF在ML-1m、ML-100k-u2、ML-100k-u5、Filmtrust数据集上优于GRAWS.在F1值方面, 除了ML-100k-u1、ML-100k-u4数据集, NRACF在其它数据集上都取得最优值.在运行时间上, NRACF的运行时间明显短于GRAWS, GRAWS的平均运行时间为6 407.21 s, 而NRACF的平均运行时间为1 708.43 s, 计算效率提升超过2倍.

为了进一步验证NRACF的有效性, 将其与如下5种常见的推荐算法进行对比.

1)User-Based CF(User-Based Collaborative Filtering)^[17].基于用户的协同过滤推荐算法, 通过用户之间的相似性对目标用户进行预测评分.

2)Item-Based CF(Item-Based Collaborative Filtering)^[18].基于项目的协同过滤推荐算法, 通过计算项目之间的相似度, 并根据评分信息预测目标项目.

3)GraphRec^[41].基于图神经网络的社交推荐算法, 利用图神经网络对社交网络中的用户和项目的特征进行学习, 预测评分.

4)ETBRec(A Novel Recommendation Algorithm Combining the Double Influence of Trust Relationship and Expert Users)^[42].结合用户信任关系和专家用户影响的协同过滤推荐算法, 通过用户之间的相似性构造信任关系矩阵, 并根据用户的信任度和积极态度计算各用户成为专家的可能, 结合信任关系矩阵和专家进行预测评分.

5)TF* Clarity(Term Frequency* Clarity)^[43].结合标签相关性和用户社会关系的推荐算法, 构建标签相关矩阵和社交关系相似矩阵, 获取用户标签矩阵, 并进行预测评分.

各对比算法在各数据集上的精确度、召回率和F1值的对比结果如表9~表11所示, 表中黑体数字表示最优值.

表9 各算法在7个数据集上的精确度对比 Table 9 Accuracy comparison of different algorithms on 7 datasets

表10 各算法在7个数据集上的召回率对比 Table 10 Recall comparison of different algorithms on 7 datasets

表11 各算法在7个数据集上的F1值对比 Table 11 F1 value comparison of different algorithms on 7 datasets

由表9~表11可知:在精确度上, NRACF在所有数据集上都优于其它算法; 在召回率上, NRACF在ML-1m、ML-100k-u2、Filmtrust数据集上优于其它算法; 在F1值上, 除了ML-100k-u4数据集, NRACF在其它数据集上都得到最优值.

综上所述, 在选取的大部分数据集上, NRACF在精确度、召回率和F1值上均表现出明显优势.因此, 对于网络邻域推荐任务, 当数据集上的条件属性与决策属性之间存在较强的因果力时, 建议采用NRACF.

5 结束语

本文结合网络决策形式背景、变精度算子、Pearl因果力理论, 提出基于因果力的邻域推荐算法(NRACF), 并运用在MovieLens、Filmtrust数据集上.通过对比实验发现, NRACF整体上性能较优, 这有助于形式概念分析与因果推断的交叉融合研究.今后, 还可进一步结合因果涌现、因果推断与网络形式背景, 开展其它研究.

本文责任编委梁吉业

Recommended by Associate Editor LIANG Jiye

参考文献

文献选项

[1]	WILLE R. Restructuring Lattice Theory: An Approach Based on Hierarchies of Concepts // RIVAL I, ed. Ordered Sets. Berlin, Germany: Springer, 1981: 445-470. [本文引用:2]
[2]	许佳卿, 彭鑫, 赵文耘. 一种基于模糊概念格和代码分析的软件演化分析方法. 计算机学报, 2009, 32(9): 1832-1844. (XU J Q, PENG X, ZHAO W Y. An Evolution Analysis Method Based on Fuzzy Concept Lattice and Source Code Analysis. Chinese Journal of Computers, 2009, 32(9): 1832-1844. ) [本文引用:1]
[3]	ROCCO C M, HERNANDEZ-PERDOMO E, MUN J. Introduction to Formal Concept Analysis and Its Applications in Reliability Engineering. Reliability Engineering and System Safety, 2020, 202. DOI: DOI:10.1016/j.ress.2020.107002. [本文引用:1]
[4]	POELMANS J, IGNATOV D I, KUZNETSOV S O, et al. Formal Concept Analysis in Knowledge Processing: A Survey on Applications. Expert Systems with Applications, 2013, 40(16): 6538-6560. [本文引用:1]
[5]	ZOU L, LIN H M, SONG X Y, et al. Rule Extraction Based on Linguistic-Valued Intuitionistic Fuzzy Layered Concept Lattice. International Journal of Approximate Reasoning, 2021, 133: 1-16. [本文引用:1]
[6]	KAYTOUE M, KUZNETSOV S O, NAPOLI A, et al. Mining Gene Expression Data with Pattern Structures in Formal Concept Analysis. Information Sciences, 2011, 181(10): 1989-2001. [本文引用:1]
[7]	陈昊文, 王黎明, 张卓. 基于概念邻域的Top- N推荐算法. 小型微型计算机系统, 2017, 38(11): 2553-2559. (CHEN H W, WANG L M, ZHANG Z. Top- N Recommendation Algorithm Based on Conceptual Neighborhood. Journal of Chinese Computer Systems, 2017, 38(11): 2553-2559. ) [本文引用:2]
[8]	米允龙, 李金海, 刘文奇, 等. MapReduce框架下的粒概念认知学习系统研究. 电子学报, 2018, 46(2): 289-297. (MI Y L, LI J H, LIU W Q, et al. Research on Granular Concept Cognitive Learning System under MapReduce Framework. Acta Electronica Sinica, 2018, 46(2): 289-297. ) [本文引用:1]
[9]	马娜, 范敏, 李金海. 复杂网络下的概念认知学习. 南京大学学报(自然科学版), 2019, 55(4): 609-623. (MA N, FAN M, LI J H. Concept-Cognitive Learning under Complex Network. Journal of Nanjing University(Natural Science), 2019, 55(4): 609-623. ) [本文引用:1]
[10]	KUMAR C A, ISHWARYA M S, LOO C K. Formal Concept Analysis Approach to Cognitive Functionalities of Bidirectional Associative Memory. Biologically Inspired Cognitive Architectures, 2015, 12: 20-33. [本文引用:1]
[11]	YAO Y Y. Concept Lattices in Rough Set Theory // Proc of the IEEE Annual Meeting of the Fuzzy Information. Washington, USA: IEEE, 2004: 796-801. [本文引用:1]
[12]	DÜNTSCH I, GEDIGA G. Modal-Style Operators in Qualitative Data Analysis // Proc of the IEEE International Conference on Data Mining. Washington, USA: IEEE, 2002: 155-162. [本文引用:1]
[13]	YAO Y Y. A Comparative Study of Formal Concept Analysis and Rough Set Theory in Data Analysis // Proc of the 4th International Conference on Rough Sets and Current Trends in Computing. Berlin, Germany: Springer, 2004: 59-68. [本文引用:1]
[14]	闫梦宇, 李金海. 概念格共有与独有属性(对象)的关系研究. 计算机科学与探索, 2019, 13(4): 702-710. (YAN M Y, LI J H. Research on Relationship Between Common and Unique Attributes(Objects) of Concept Lattice. Journal of Frontiers of Computer Science and Technology, 2019, 13(4): 702-710. ) [本文引用:1]
[15]	ZAIER Z, GODIN R, FAUCHER L. Recommendation Quality Evolution Based on Neighborhood Size // Proc of the 3rd International Conference on Automated Production of Cross Media Content for Multi-channel Distribution. Washington, USA: IEEE, 2007: 33-36. [本文引用:1]
[16]	GARCIA I, PAJARES S, SEBASTIA L, et al. Preference Elicitation Techniques for Group Recommender Systems. Information Sciences, 2012, 189: 155-175. [本文引用:1]
[17]	YI J, ZHANG L, PHELAN C A. A Novel Recommendation Stra-tegy for User-Based Collaborative Filtering in Intelligent Marketing. Journal of Digital Information Management, 2016, 14(2): 81-91. [本文引用:2]
[18]	SARWAR B, KARYPIS G, KONSTAN J, et al. Item-Based Co-llaborative Filtering Recommendation Algorithms // Proc of the 10th International Conference on World Wide Web. New York, USA: ACM, 2001: 285-295. [本文引用:2]
[19]	张玉洁, 杜雨露, 孟祥武. 组推荐系统及其应用研究. 计算机学报, 2016, 39(4): 745-764. (ZHANG Y J, DU Y L, MENG X W. Research on Group Recommender Systems and Their Applications. Chinese Journal of Computers, 2016, 39(4): 745-764. ) [本文引用:1]
[20]	PEARL J. Causality. 2nd Edition. Cambridge, UK: Cambridge University Press, 2009. [本文引用:4]
[21]	FAN Y, CHEN J Q, SHIRKEY G, et al. Applications of Structu-ral Equation Modeling(SEM) in Ecological Studies: An Updated Review. Ecological Processes, 2016, 5. DOI: DOI:10.1186/s13717-016-0063-3. [本文引用:1]
[22]	MARIA-YANELI A A, NICANDRO C R, EFRÉN M M, et al. Assessment of Bayesian Network Classifiers as Tools for Discriminating Breast Cancer Pre-diagnosis Based on Three Diagnostic Methods // Proc of the 11th Mexican International Conference on Artificial Intelligence. Berlin, Germany: Springer, 2012: 419-431. [本文引用:1]
[23]	WOLFF P. Direct Causation in the Linguistic Coding and Individuation of Causal Events. Cognition, 2003, 88(1): 1-48. [本文引用:1]
[24]	NADATHUR P, LAUER S. Causal Necessity, Causal Sufficiency, and the Implications of Causative Verbs. Glossa: A Journal of General Linguistics, 2020, 5(1). DOI: DOI:10.5334/GJGL.497. [本文引用:1]
[25]	SLOMAN S, BARBEY A K, HOTALING J M. A Causal Model Theory of the Meaning of Cause, Enable, and Prevent. Cognitive Science, 2009, 33(1): 21-50. [本文引用:1]
[26]	GEFFNER H, DECHTER R, HALPERN J Y. Probabilistic and Causal Inference: The Works of Judea Pearl. New York, USA: ACM, 2022. [本文引用:1]
[27]	HOEL E P, ALBANTAKIS L, TONONI G. Quantifying Causal Emergence Shows that Macro Can Beat Micro. Proceedings of the National Academy of Sciences of the United States of America, 2013, 110(49): 19790-19795. [本文引用:1]
[28]	COMOLATTI R, HOEL E. Causal Emergence Is Widespread Across Measures of Causation[C/OL]. [2022-09-03]. https://arxiv.org/pdf/2202.01854.pdf. [本文引用:1]
[29]	EELLS E. Probabilistic Causality. Cambridge, UK: Cambridge Uni-versity Press, 2008. [本文引用:3]
[30]	CHENG P W, NOVICK L R. Causes Versus Enabling Conditions. Cognition, 1991, 40(1/2): 83-120. [本文引用:1]
[31]	LEWIS D. Causation. Journal of Philosophy, 1973, 70: 556-567. [本文引用:1]
[32]	刘忠慧, 邹璐, 杨梅, 等. 启发式概念构造的组推荐方法. 计算机科学与探索, 2020, 14(4): 703-711. (LIU Z H, ZOU L, YANG M, et al. Group Recommendation with Concept of Heuristic Construction. Journal of Frontiers of Computer Science and Technology, 2020, 14(4): 703-711. ) [本文引用:1]
[33]	MAIO C D, FENZA G, GAETA M, et al. RSS-Based E-Learning Recommendations Exploiting Fuzzy FCA for Knowledge Modeling. Applied Soft Computing, 2012, 12(1): 113-124. [本文引用:1]
[34]	刘忠慧, 陈建宇, 宋国杰, 等. 基于模拟退火法的概念集构造算法. 模式识别与人工智能, 2021, 34(8): 723-732. (LIU Z H, CHEN J Y, SONG G J, et al. Construction Algorithm of Concept Set Based on Simulated Annealing Algorithm. Pattern Recognition and Artificial Intelligence, 2021, 34(8): 723-732. ) [本文引用:1]
[35]	ZOU C F, ZHANG D Q, WAN J F, et al. Using Concept Lattice for Personalized Recommendation System Design. IEEE Systems Journal, 2017, 11(1): 305-314. [本文引用:1]
[36]	DU BOUCHER-RYAN P, BRIDGE D. Collaborative Recommending Using Formal Concept Analysis. Knowledge-Based Systems, 2006, 19(5): 309-315. [本文引用:1]
[37]	GODIN R, MISSAOUI R, ALAOUI H. Incremental Concept Formation Algorithms Based on Galois(Concept) Lattices. Computa-tional Intelligence, 1995, 11(2): 246-267. [本文引用:2]
[38]	DJOUADI Y, PRADE H. Interval-Valued Fuzzy Galois Connections: Algebraic Requirements and Concept Lattice Construction. Fundamenta Informaticae, 2010, 99(2): 169-186. [本文引用:1]
[39]	ALBANTAKIS L, MARSHALL W, HOEL E, et al. What Caused What? A Quantitative Account of Actual Causation Using Dynamical Causal Networks. Entropy(Basel), 2019, 21(5). DOI: DOI:10.3390/e21050459. [本文引用:2]
[40]	范敏, 张洁, 李金海. 基于弱概念相似度的组推荐方法[J/OL]. [2022-09-03]. https: //www. researchgate. net/publication/366874633_Group_Recommendation_Method_Based_on_Weaken-concept_Similarity. (FAN M, ZHANG J, LI J H. Group Recommendation Method Based on Weaken-Concept Similarity[J/OL]. [2022-09-03]. https://www.researchgate.net/publication/366874633_Group_Recommendation_Method_Based_on_Weaken-concept_Similarity. ) [本文引用:4]
[41]	FAN W Q, MA Y, LI Q, et al. Graph Neural Networks for Social Recommendation // Proc of the World Wide Web Conference. New York, USA: ACM, 2019: 417-426. [本文引用:1]
[42]	DUAN Z C, XU W H, CHEN Y T, et al. ETBRec: A Novel Re-commendation Algorithm Combining the Double Influence of Trust Relationship and Expert Users. Applied Intelligence, 2022, 52(1): 282-294. [本文引用:1]
[43]	MA H F, JIA M H Z, ZHANG D, et al. Combining Tag Correlation. Combining Tag Correlation and User Social Relation for Microblog Recommendation. Information Sciences, 2017, 385/386: 325-337. [本文引用:1]

1981

0.0

... 早期形式概念分析(Formal Concept Analysis, FCA)^[1]专注于研究概念及概念层次的数学化和形式化表达 ...

... 1 相关定义定义1^[1] 三元组(U,A,I)称为形式背景,其中,U={x₁,x₁,…,x_n}为非空有限对象集,A={a₁,a₂,…,a_m}为非空有限属性集,I为笛卡尔积U#cod#x000D7 ...

2009

0.0