张清华,博士,教授,主要研究方向为粗糙集、模糊集、粒计算、三支决策等.E-mail:zhangqh@cqupt.edu.cn.
作者简介:

肖嘉瑜,硕士研究生,主要研究方向为智能信息处理、数据挖掘.E-mail:xiaojiayuhhh@163.com.

艾志华,硕士研究生,主要研究方向为智能信息处理、数据挖掘.E-mail:azh15213138308@163.com.

王国胤,博士,教授,主要研究方向为粗糙集、粒计算、认知计算、数据挖掘、智能信息处理等.E-mail:wanggy@cqupt.edu.cn.
在邻域粗糙集中,邻域分类器简单高效.然而,邻域半径作为决定邻域分类器分类性能的关键因素,构建方式存在不足.一方面,邻域半径的构建由于未经过训练过程而缺乏通用性;另一方面,当数据样本分布不均出现空邻域时可导致分类器失效.针对上述问题,文中提出自适应半径选择的近邻邻域分类器(Near Neighborhood Classifier with Adaptive Radius Selection, NNC-AR).首先,基于 K近邻算法为训练样本构建训练邻域半径.然后,为了克服传统方法选取邻域半径参数的主观性,对待测试样本定义自适应的近邻邻域半径.最后,为分类器失效的部分测试样本定义新的近似邻域半径,有效提升分类器的泛化能力.实验表明,NNC-AR的 F1值和分类精度均较高.
ZHANG Qinghua, Ph.D., professor. His research interests include rough sets, fuzzy sets, granular computing and three-way decision-making.
About Author:
XIAO Jiayu, master student. Her research interests include intelligent information processing and data mining.
AI Zhihua, master student. His research interests include intelligent information processing and data mining.
WANG Guoyin, Ph.D., professor. His research interests include rough sets, granular computing, cognitive computing, data mining and intelligent information processing.
In neighborhood rough sets, the neighborhood classifier is an intuitive and effective classification method in data mining. However, the neighborhood radius, as a key factor to determine the classification performance of the neighborhood classifier, has some defects in construction. The construction of the neighborhood radius is not universal due to the lack of the training stage. When the data samples are not uniformly distributed and then empty neighborhoods appear, the classifier fails. Aiming at these problems, a near neighborhood classifier with adaptive radius selection(NNC-AR) is proposed. Firstly, for training samples, a training neighborhood radius based on K-nearest neighbor is defined. For test samples, an adaptive neighborhood radius is defined to overcome the subjectivity of the artificial parameter in the traditional neighborhood radius. Finally, for the test samples with classifier failure, an approximate neighborhood radius is defined to improve the generalization ability of the classifier. The experimental results show that the F1 score and classification accuracy of NNC-AR model are significantly improved.
粗糙集模型[1, 2]作为一种处理不完备、不确定性信息的数据分析工具, 广泛应用在机器学习[3, 4]、模式识别[5, 6]、特征选择[7, 8, 9]、数据挖掘[10, 11, 12]、不确定性信息处理[13, 14, 15]等众多领域中.然而经典粗糙集模型建立在等价关系的基础上, 将样本数据划分成等价类, 只能处理名义型数据.对于现实生活中广泛存在的数值型数据, 经典粗糙集模型处理原始数据时必须先离散化, 导致部分信息丢失.为了克服经典粗糙集这个缺陷, 大量研究工作在非等价关系上推广经典粗糙集模型, 如邻域粗糙集(Neighborhood Rough Set, NRS)[16, 17, 18]、模糊粗糙集[19, 20, 21]、覆盖粗糙集[22, 23]等.
胡清华等[24, 25]基于拓扑空间球形邻域引入邻域粗糙集, 使用邻域近似(邻域)代替经典粗糙集中的等价关系, 使其既可以支持离散型数据又可以支持数值型数据.之后, 该理论成功扩展到特征选择[26, 27]、分类[28, 29, 30]、机器学习[31, 32]等众多应用领域.在分类应用中, Hu等[33]基于NRS实现基于多数原则的邻域分类器(Neighborhood Classifiers, NNC).之后, 学者们以NNC为基本框架展开相关研究.徐苏平等[34]在协同表达分类(Collaborative Representation Based Classification, CRC)思想的基础上, 提出邻域协同分类器(Neighborhood Collaborative Classifiers, NCC).亓慧等[35]提出扩充粒化的序列邻域分类方法(Expanded Granulation Based Sequen-tial Neighborhood Classification, ESNC), 设计得分评估机制, 排序测试样本, 并标注最靠前的待测样本, 将其加入训练集, 以此扩充待测样本潜在的邻域粒化空间.Rao等[36]提出FNEC-NNC, 将邻域策略引入标签噪声数据的分析中, 不仅去除带噪声标签的样本, 而且与基于最近邻域的滤波器进行对比, 可有效克服噪声样本的影响.Kumar等[37]提出NRSC(Neighborhood Rough Set Based Classification), 在疾病预测和决策过程中, 分类性能较优.
在上述邻域分类器中:对于训练样本, 标签已知, 不需要计算邻域半径, 只考虑其与待测试样本的距离; 对于测试样本, 标签未知, 需要计算其邻域半径, 获取邻域, 进而预测标签.并且邻域分类器在预测标签过程中, 仅涉及测试阶段.因此, 基于已有的邻域分类器, 邻域半径作为决定邻域分类器分类性能的关键因素, 构建方式主要存在如下不足.1)缺乏训练过程.传统分类器中缺乏训练阶段, 没有计算训练样本的邻域半径, 未充分挖掘训练样本的条件属性与其标签之间的有效关联信息.2)邻域半径不通用.传统邻域半径仅通过人工参数调节大小, 不能较好地适用于所有测试样本邻域的构建.3)分类器失效.面对数据中样本分布不均匀等特殊情况, 邻域半径划分得到的部分样本邻域可能出现无样本的情况, 导致分类器失效而无法预测测试样本标签.
为了解决上述问题, 本文引入K近邻算法(K Nearest Neighbor, KNN)[38, 39], 并为邻域半径增添训练阶段, 构建新的训练邻域半径、近邻邻域半径和近似邻域半径, 由此提出自适应半径选择的近邻邻域分类器(Near Neighborhood Classifier with Adaptive Radius Selection, NNC-AR).对于训练集上的样本, 基于K近邻算法得到每个训练样本能被正确分类的邻域半径, 定义新的训练邻域半径, 为邻域半径增添训练阶段.同时充分挖掘训练样本的条件属性与其已知标签之间的有效关联信息.对于测试集上的样本, 定义自适应的近邻邻域半径, 克服选取传统邻域半径参数时的主观性.结合近邻思想, 以训练邻域半径为有效依据, 最大化利用训练样本与测试样本间的相似性等关联信息, 有效提升样本邻域的分类精度和自适应性.对于分类器失效的测试样本, 定义新的近似邻域半径.结合近邻思想, 有效解决数据分布不均匀时邻域中无样本导致分类器失效的问题, 进一步提升邻域分类器的精度和泛化能力.在多个UCI数据集上的实验表明, NNC-AR的F1值和分类精度均较高.
本节简要介绍邻域分类器的相关定义, 详细介绍可见文献[33]和文献[40].
在分类学习中, 常把决策信息系统表示为四元组
S=< U, C∪ D, V, f > .
其中,
U={x1, x2, …, xn},
表示为由n个训练样本构成的非空有限集合, 称为论域或样本空间.在分类任务中:通常将U划分为训练样本空间UTr和测试样本空间UTe;
C={a1, a2, …, am}
表示U中所有样本的条件属性集合;
D={d1, d2, …, dp}
表示决策属性值集合, 对于∀ x∈ U, d(x)表示决策属性值, 即标签; Va表示特征a的值域; f:U× C→ V表示信息函数.
由决策属性D可诱导样本空间U生成若干个决策类
U/IND(D)={D1, D2, …, Dp},
其中, IND(D)表示U上的一个等价关系, 且对任一决策类, 包含所有标签为dk的样本集合
Dk={x∈ U|d(x)=dk},
其中dk表示第k个标签.
定义1[41] 给定一个决策信息系统
S=< U, C∪ D, V, f > ,
属性集合
C={a1, a2, …, am},
对于∀ x∈ U, y∈ U, 在条件属性集合C下, 不同样本间的闵可夫斯基距离定义如下:
Δ (x, y)=[
其中, ∀ ai∈ C, f(x, ai)表示样本x在条件属性ai上的取值.距离的度量常采用欧氏距离函数, 即P=2.
定义2[33] 给定一个决策信息系统
S=< U, C∪ D, V, f > ,
对于∀ x∈ U, 样本x对应的邻域
δ (x)={y∈ U|Δ (x, y)≤ δ },
其中δ 表示邻域半径.
在构建邻域分类器模型过程中, 为了将NRS进一步适用于分类任务, Hu等[33]定义δ 作为邻域半径, 通过邻域决策完成样本分类.
定义3[33] 给定一个决策信息系统
S=< U, C∪ D, V, f > ,
对于测试样本x∈ U, 样本x的邻域半径为
δ =min(Δ (x, yi))+ω (max(Δ (x, yi))-min(Δ (x, yi))).
其中:ω ∈ (0, 1], 表示一个随机参数; min(Δ (x, yi))表示距离x最短的训练样本yi与x之间的距离; max(Δ (x, yi))表示距离x最长的训练样本yi与x之间的距离.
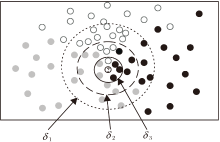
邻域半径δ 决定邻域分类器分类性能优劣.然而, 传统邻域分类器在构建δ 时采用带有人工参数ω 的动态调节方式, 具有一定程度上的不确定性和主观性.随着δ 逐渐增大, 邻域δ (x)也越大, 即落到x的邻域空间中的样本越多.如图1所示, 在邻域分类器中存在3个不同的邻域半径, 相应存在3个不同大小的邻域, 分别使用实线、虚线和点线表示.因此在邻域分类器中, 邻域半径设定偏大或偏小时都会直接影响测试样本标签的预测.
定义4[31] 给定一个决策信息系统
S=< U, C∪ D, V, f > ,
对于测试样本x∈ U, 利用邻域δ (x)得出x属于每种决策类Dj的邻域粗糙隶属度, 邻域粗糙隶属函数为
P(dj|δ (x))=
其中, Dj∈ U/IND(D), 表示论域U根据决策属性D划分并诱导生成的决策类.
以定义4中的邻域粗糙隶属度为依据, 邻域分类器进一步通过多数投票原则, 为测试集中的样本完成最终的邻域决策:当决策类Dj对应的决策标签dj满足
dj=arg
时, 测试样本x的标签被预测为dj.
如图1所示, 邻域分类器中δ 1> δ 2> δ 3.当邻域半径为δ 3时, 根据多数投票规则测试样本将被预测为黑色标签; 当邻域半径增加到δ 2时, 测试样本将被预测为邻域粗糙隶属度最大的灰色标签; 当邻域半径继续增加到δ 1时, 测试样本会被标注为白色标签.由此可见, 邻域半径的构建会直接干扰邻域分类器对测试样本的邻域决策.因此, 邻域半径作为决定预测样本标签过程的关键因素还需要进一步优化.
KNN分类算法是模式识别中简单有效的经典算法之一, 基本原理如下:给定一组已知类别的训练样本和待分类样本, 找到训练样本中距离待分类样本最近的K个最近邻居, 进而将K个近邻中最多个数的标签分配给待分类样本.
对于待分类样本xte∈ UTe, KNN的分类过程如下.首先, 为待分类样本xte定义一组超过K个相似的目标邻居, 即按照xte与训练样本之间的欧氏距离递增排序, 取排名前K个训练样本.再利用多数投票原则, 根据K个最近邻居的标签, 预测得出待分类样本xte的标签.重复上述步骤, 直到所有待分类样本预测结束.
已有的邻域分类器模型仅涉及测试阶段, 对于已知标签的训练样本, 不需要计算邻域半径, 也未构建邻域进行邻域决策, 只考虑其与待测样本之间的距离作为待测试样本邻域决策的依据.为了进一步利用训练样本的有效信息, NNC-AR结合KNN, 为训练样本定义训练邻域半径, 增添邻域半径的训练阶段, 为提升待测试样本的预测精度提供有效根据.
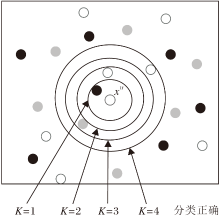
训练邻域半径的构建过程如下:结合KNN, 对每个已知标签的训练样本xtr, 选取距离xtr最近的K个样本, 进而根据这K个样本的标签值, 基于多数表决原则预测得到xtr的标签, 依次取K=1, 2, …, 10直至xtr被预测正确.最后得到xtr被预测成功时的值, 选取距离xtr排名的第K个近邻点与xtr之间的距离, 作为训练样本xtr的邻域半径, 即训练邻域半径.
如图2所示, 当K=4时, 训练样本xtr的标签能被正确预测为白色, 继而将距离xtr排名的第4个近邻点与xtr之间的距离作为xtr的训练邻域半径.
定义5 给定一个决策信息系统
S=< U, C∪ D, V, f > ,
其中
U=UTr∪ UTe.
对于训练样本xtr∈ UTr, 训练邻域半径为:
δ tr=Δ (xtr, NNk(xtr)),
其中, NNk(xtr)表示与当前训练样本xtr距离排名第K个的近邻点, 也是使xtr能被正确分类的最近邻, K=1, 2, …, 10.另外若依次取K=1, 2, …, 10, 训练样本xtr都无法被分类, 即只有K> 10时, 训练样本xtr才能被正确预测为已知标签, 这表明训练样本xtr显然偏离其它同类训练样本的正常分布范围, 因此将样本xtr归为噪声点并删除, 不参与NNC-AR本轮训练阶段和测试阶段的构建.
NNC-AR通过KNN计算已知标签的训练样本能被正确预测时的训练邻域半径, 为邻域半径的构建增添训练阶段, 充分挖掘训练样本条件属性与决策属性之间的有效关联性信息, 有利于构建预测精度较高、分类性能较强的NNC-AR.
在已有分类器模型的预测阶段中, 动态调节人工参数以构建待测样本的邻域半径, 具有一定程度上的主观性和不确定性.因此, 在NNC-AR的测试阶段, 考虑待测试样本与训练样本之间的相似性以解决待测试样本标签的预测问题.基于近邻思想, 选取距离待测试样本最近的训练样本, 并以训练邻域半径为根据, 为待测试样本构建新的近邻邻域半径, 有效克服传统邻域半径中的动态调节方式带来的不确定性问题.
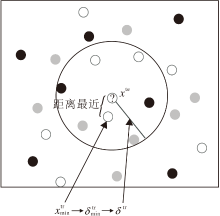
近邻邻域半径的构建过程如下:结合训练邻域半径和近邻思想, 根据定义5得到每个训练样本被预测成功的邻域半径δ tr.进而求取距离待测试样本xte最近的训练样本, 将其对应的训练邻域半径作为该待测样本xte的邻域半径, 即近邻邻域半径.
如图3所示, 先计算距离待测试样本xte最近的训练样本
定义6 给定一个决策信息系统
S=< U, C∪ D, V, f > ,
其中
U=UTr∪ UTe.
对于测试样本xte∈ UTe, 近邻邻域半径δ te=
表示
表示与当前测试样本xte距离最近的训练样本.
由于训练邻域半径的构建是基于已知标签的训练样本能被正确预测, NNC-AR将其进一步融入测试阶段.结合近邻思想选取距离待测试样本最近的训练样本构建近邻邻域半径, 不仅考虑测试样本与训练样本之间的关联性, 还能极大程度以训练阶段的有效信息为根据准确预测待测试样本的标签, 克服以往邻域分类器模型选取邻域半径参数时的不确定性问题, 一定程度上提升邻域半径的合理性和自适应性, 有效提升NNC-AR的分类性能.
在待测试样本的标签预测阶段中, 通过近邻邻域半径构建邻域能完成大多数测试样本标签的正确预测.然而, 对于少数分布不均匀的待测试样本, 采用近邻邻域半径构造的邻域可能会出现无样本的情况, 导致分类器失效而无法预测样本标签.为了进一步提升分类器模型的泛化能力, NNC-AR结合近邻思想, 为少数分类器失效的待测试样本构建新的近似邻域半径, 解决部分样本邻域中无样本的情况.
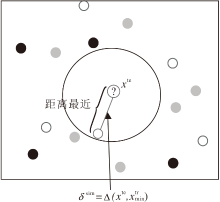
近似邻域半径的构建过程如下:根据定义6先求取待测试样本xte的近邻邻域半径, 用于划分xte的邻域.若发现邻域内没有样本, 表示分类器失效, 进而将距离xte最近的训练样本与xte之间的距离作为xte的邻域半径, 即近似邻域半径.
如图4所示,
定义7 给定一个决策信息系统
S=< U, C∪ D, V, f > ,
其中
U=UTr∪ UTe.
对于测试样本xte∈ UTe, 近似邻域半径为:
δ sim=Δ (xte,
其中
表示与当前测试样本距离最近的训练样本.
综上所述, NNC-AR结合近邻思想, 对于少数分布不均匀、出现空邻域的待测试样本, 利用其与距离最近的训练样本构建近似邻域半径, 完成对标签信息的有效预测, 有效解决测试阶段中的分类器失效问题, 提升NNC-AR的泛化性能.
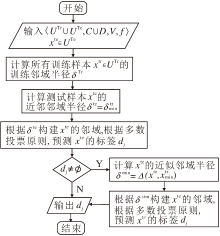
最终, 得到NNC-AR步骤如算法1所示.
算法1 NNC-AR
输入 决策信息系统< UTr∪ UTe, C∪ D, V, f > ,
待测试样本xte∈ UTe
输出 输出测试样本xte的标签dj
#计算所有训练样本的半径及删除噪点样本
for xtr∈ UTr:
计算δ tr=Δ (xtr, NNk(xtr));
if i> 10 then:
从UTr剔除样本xtr;
end if
end for
#计算测试样本的半径并对测试样本预测
计算δ te=
计算dj=arg
δ (xte)={xtr∈ UTr|Δ (xte, xtr)≤ δ te};
if dj=Ø then:
计算δ sim=Δ (xte,
计算dj=arg
δ (xte)={xtr∈ UTr|Δ (xte, xtr)≤ δ sim};
end if
return dj
为了清晰分析NNC-AR的时间复杂度, 假设训练集中样本个数为n1, 删除噪声点样本后的样本总数为n2.因此, 算法第1阶段主要计算所有训练样本的半径并删除噪声点样本点, 时间复杂度为O(
NNC-AR的流程图如图6所示.
在本节中, 将NNC-AR与其它目前较先进的模型进行实验对比.对比的模型有NNC[33]、NCC[34]、ESNC[35]; 对比算法有KNN, ID3(Iterative Dicho-tomiser 3), CART(Classification and Regression Tree)、NB(Naive Bayes).在实验中, ESNC分为ESNC1(Score1 Based ESNC)和ESNC2(Score2 Based ESNC).NCC、NNC和ESNC的邻域半径均采用动态调节的方式, 设定随机参数ω =0.1.
实验共选取10个UCI标准数据集, 数据集信息如表1所示.
| 表1 实验数据集 Table 1 Experimental datasets |
实验采用5折交叉验证, 实验环境为Windows操作系统, 16 GB内存, 3.60 Hz主频, 编程语言采用Python.
为了直观展示算法之间的对比效果, 采用的分类指标为准确率(Accuracy)和F1值.因此, 给定一个数据集合, 假设TP表示正确预测为正例的样本数, FP表示错误预测为正例的样本数, TN表示正确预测为负例的样本数, FN表示错误预测为负例的样本数, 准确率和F1值的定义为
accuracy=
其中,
precision=
表示精确率,
recall=
表示召回率.
为了对比NNC-AR的有效性, 在10个UCI数据集上同时对比分类模型和经典算法, 将5折交叉验证实验的平均分类准确率作为最终结果, 具体如表2所示, F1值对比结果如表3所示, 表中黑体数字表示最优值.
| 表2 各模型在10个数据集上的分类准确率对比 Table 2 Classification accuracy comparison of different models on 10 datasets % |
| 表3 各模型在10个数据集上的F1值对比 Table 3 F1 score of different models on 10 datasets % |
实验参数设置如下:NCC、NNC和ESNC的邻域半径均采用动态调整方法, 人工参数ω =0.1, NCC的正则化参数λ =0.01, KNN中K=10.
由表2和表3可见, 相比NCC、NNC、ESNC1和ESNC2, NNC-AR通过训练集找到最优的半径阈值, 能有效适应不同的数据分布, 提升分类准确率, 在大部分数据集上均能达到最优值, 同样F1值也均能达到最优效果.
相比KNN、ID3、CART和NB, NNC-AR和KNN能达到较优的分类结果.但是KNN容易受到数据分布的影响, 进而影响分类效果.相比而言, NNC-AR可动态调整邻域半径, 在训练集上找到最优半径, 适应不同分布下的数据场景.
NNC-AR中引入KNN构造训练阶段, 同时将K> 10时仍无法被分类的训练样本视为噪声点.由于在对比算法中, 没有为邻域分类器构建训练阶段, 未使用KNN为训练样本构建邻域半径, 因此在噪声点检测方面, 无法与其余算法完成对比.因此, 在10个数据集上, 分别统计NNC-AR删除的噪声点个数, 取5折交叉验证实验的平均值作为结果.统计结果如下:Satimage数据集上NNC-AR删除的噪声点有264.8个, Banknote数据集上有1.6个, Wbc数据集上有9.6个, Mushroom数据集上有0.2个, Breast数据集上有10.0个, Heart数据集上有24.6个, Parkinson数据集上有2.2个, Pima数据集上有90.4个, Credit数据集上有48.6个, Ionosphere数据集上有25.4个.噪声点删除个数与数据集分布状况总体呈正相关.在分布较好的数据集(如Mushroom数据集)上, 删除的噪声点较少, 在分布较差的数据集(如Satimage数据集)上, 删除的噪声点较多.通过删除噪声点, 不仅能提升后续模型的分类精度, 还能降低模型在分类时的时间损耗.
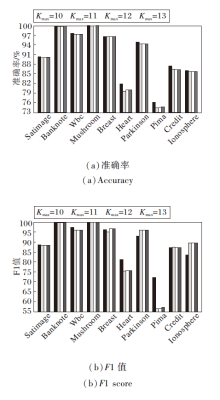
为了进一步凸显噪声点定义中K的最大阈值设定为10 的有效性, 计算K取不同最大值, 即Kmax=11, 12, 13时, NNC-AR的准确率和F1值, 并与NNC-AR的原始实验结果进行对比.具体对比结果如图7所示.由图可见, 相比Kmax=11、12、13, Kmax=10时NNC-AR在大部分数据集上达到最优的分类效果.
总之, NNC-AR通过增添邻域半径的训练阶段、克服邻域半径人为参数的不确定性缺陷、解决数据分布不均出现空邻域的问题等措施, 有效提升邻域分类器的F1值和分类准确率.
本文针对邻域半径缺乏训练过程、邻域半径不通用、分类器失效等问题, 提出自适应半径选择的近邻邻域分类器(NNC-AR).构建训练邻域半径, 充分挖掘训练样本中条件属性与其已知标签间的有效关联信息, 为待测样本标签的预测阶段提供有力依据.构建近邻邻域半径, 调整以往分类器模型预测阶段选取邻域半径参数时的主观性.在一定程度上提升邻域半径的合理性和自适应性, 有效提升NNC-AR的分类性能.构建近似邻域半径, 解决测试阶段分类器失效的问题, 提升NNC-AR的泛化性能.在10组UCI数据集上的对比实验表明, NNC-AR的F1值和分类准确率都取得显著提升.下一步的研究工作是从时间性能方面实现邻域分类器性能的进一步提升.
本文责任编委 苗夺谦
Recommended by Associate Editor MIAO Duoqian
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|
| [19] |
|
| [20] |
|
| [21] |
|
| [22] |
|
| [23] |
|
| [24] |
|
| [25] |
|
| [26] |
|
| [27] |
|
| [28] |
|
| [29] |
|
| [30] |
|
| [31] |
|
| [32] |
|
| [33] |
|
| [34] |
|
| [35] |
|
| [36] |
|
| [37] |
|
| [38] |
|
| [39] |
|
| [40] |
|
| [41] |
|