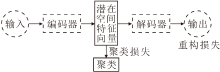引用本文
侯海薇, 丁世飞, 徐晓. 基于无监督表征学习的深度聚类研究进展. 模式识别与人工智能, 2022,35(11): 999-1014
HOU Haiwei, DING Shifei, XU Xiao. Research Progress of Deep Clustering Based on Unsupervised Representation Learning. PATTERN RECOGNITION AND ARTIFICIAL INTELLIGENCE, 2022,35(11): 999-1014.  
Doi: 10.16451/j.cnki.issn1003-6059.202211005
Permissions
Copyright©2022, 《模式识别与人工智能》编辑部
《模式识别与人工智能》编辑部
基于无监督表征学习的深度聚类研究进展
侯海薇1, 丁世飞1,2, 徐晓1,2
1.中国矿业大学 计算机科学与技术学院 徐州 221116
2.中国矿业大学 矿山数字化教育部工程研究中心 徐州 221116
通信作者：

丁世飞,博士,教授,主要研究方向为模式识别、机器学习、数据挖掘.E-mail:dingsf@cumt.edu.cn.

作者简介：

侯海薇,博士研究生,主要研究方向为机器学习、深度学习、深度聚类.E-mail:hou_haiwei@cumt.edu.cn.

徐 晓,博士,讲师,主要研究方向为机器学习、聚类分析.E-mail:xu_xiao@cumt.edu.cn.

收稿日期: 2022-08-30 接受日期: 2022-11-28
资助项目: 国家自然科学基金项目(No.61976216,62276265,61672522)资助
摘要

在大数据时代,数据通常具有规模大、维度高、结构复杂的特点,深度聚类利用深度学习结合表征学习与聚类任务,大幅提高聚类在大规模高维数据中的性能.现有文献少有着重从表征学习的角度归纳和分析目前深度聚类的发展概况,也未通过实验分析传统聚类算法、深度聚类算法及不同深度聚类算法之间的差异.因此,文中首先基于无监督表征学习,简要整理深度聚类中常用的聚类算法,重点将深度聚类算法分成基于生成模型的深度聚类与基于判别模型的深度聚类,分析聚类任务中各深度模型的表征学习过程.然后,通过实验对比分析多类算法,归纳总结优缺点,便于开展针对具体任务中的算法选择.最后,为了深度聚类的进一步发展,描述其应用场景,并讨论未来的发展趋势.

关键词: 神经网络; 表征学习; 深度聚类; 无监督学习; 损失函数
中图分类号:TP 311
Research Progress of Deep Clustering Based on Unsupervised Representation Learning
HOU Haiwei1, DING Shifei1,2, XU Xiao1,2
1. School of Computer Science and Technology, China University of Mining and Technology, Xuzhou 221116
2. Engineering Research Center of Mine Digitization of Ministry of Education, China University of Mining and Technology, Xuzhou 221116
Corresponding author:
DING Shifei, Ph.D., professor. His research interests include pattern recognition, machine learning and data mining.

About Author:
HOU Haiwei, Ph.D. candidate. Her research interests include machine learning, deep learning and deep clustering.
XU Xiao, Ph.D., lecturer. Her research interests include machine learning and clustering analysis.

Fund:National Natural Science Foundation of China(No.61976216,62276265,61672522)
Abstract

In the era of big data, data usually has the characteristics of large scale, high dimension and complex structure. Deep learning is utilized to combine representation learning and clustering tasks in deep clustering. Therefore, the performance of deep clustering for large-scale and high-dimensional data is greatly improved. The development of deep clustering is rarely summarized from the perspective of representation learning. The difference between traditional and deep clustering algorithms and the heterogeneity of deep clustering algorithms are seldom analyzed. Firstly, common clustering algorithms in deep clustering are summarized. Deep clustering algorithms are divided into generative and discriminative models based deep clustering algorithms, and representation learning process of deep models in clustering tasks is analyzed. Secondly, the comparative analysis of multiple types of algorithms is carried out through experiments. And the advantages and disadvantages of different algorithms are summarized to select models for specific tasks. Finally, application scenarios are described and the future development trend of deep clustering is discussed.

Key words: Neural Network; Representation Learning; Deep Clustering; Unsupervised Learning; Loss Function

一般而言, 聚类是指将没有标签的数据集, 通过某种相似性度量方法分为若干个簇的过程, 这是一种典型的无监督学习方法[1].聚类在机器学习[2]、图像识别[3]、计算机视觉[4]等领域都具有广泛应用.随着互联网和移动设备的发展, 数据维度越来越高, 规模越来越大, 所以学者们广泛开展数据降维和特征提取方法的研究[5].目前存在的数据降维方法包括主成分分析的线性方法[6]和基于核函数的非线性方法[7]等.

传统聚类算法聚焦于给定数据表征并在表征空间进行聚类, 而真实场景中很多数据难以使用简单的表征进行描述.深度聚类结合深度学习和神经网络的优势, 可有效提取复杂类型数据的非线性表征, 并应用于较大规模数据集上.深度学习[8]概念来源于人工神经网络的研究, 结合底层特征, 形成更抽象、更高层次的属性表征, 深层次地发现数据的分布特征表示[9].

随着神经网络的发展[10], 深度学习广泛应用于各领域, 如自然语言处理[11]、语音识别[12]、目标检测[13]等.由于深度学习在特征降维与表征学习方面的优异表现, 越来越多的研究者将重点转移到如何获取数据的有效表征以提高聚类性能, 因此将基于深度学习的聚类称为深度聚类[14].在深度聚类中, 整个模型可分为表征学习模块和聚类模块, 表征学习模块将复杂的数据类型转化为传统聚类容易处理的特征向量形式.

神经网络具有强大的非线性特征提取能力, 使深度聚类在大规模高维数据集上具有较好的聚类效果.深度聚类不仅能发挥原有聚类算法的作用, 而且能更好地适应当今大数据时代的需求, 更有效地处理大规模高维数据[15].神经网络需要进行监督训练才能服务具体的任务.某些特定任务无法获得足够的标签, 如罕有疾病图像数据的研究、军事信息等机密数据的分析等, 而深度聚类可为这些任务提供辅助作用, 分配标签, 为网络训练提供监督信号.

由于深度聚类应用的广泛性, 近些年吸引大量学者对其探索, 涌现很多深度聚类算法, 却缺少深度聚类的综述对其总结分析, 无法为初步研究者提供理论基础, 也不能为学者们提供新的思路.

本文是对深度聚类的系统阐述和总结.首先, 总结深度聚类算法中常用的传统聚类算法并归纳总结其优缺点.再基于深度聚类中表征学习方法的不同, 对算法进行综述, 包括基于生成式模型的深度聚类、基于判别式模型的深度聚类.然后, 通过实验对比分析各类算法, 总结算法特点.最后, 总结深度聚类的常用损失函数和评估标准, 讨论深度聚类的应用场景.

1 传统聚类算法

传统聚类算法主要包含如下5类:基于划分的聚类算法、基于层次的聚类算法、基于密度的聚类算法、基于图的聚类算法、基于模型的聚类算法.各类算法的优缺点总结如表1所示.

表1 传统聚类算法优缺点总结 Table 1 Summary of advantages and disadvantages of traditional clustering algorithms

基于划分的聚类算法主要思想是预先指定聚类中心, 通过迭代运算不断降低与目标函数的误差值, 当目标函数收敛时, 获得最终的聚类结果.K-means是基于划分的聚类算法的经典算法, 也是在深度聚类算法中常用的方法之一.该算法需要事先指定簇的个数K, 然后随机选取数据中的K个点作为聚类中心, 在每次迭代中, 每个样本被分配到距离最近的聚类中心, 更新簇, 使每个样本与其聚类中心的平方距离和最小.

基于层次的聚类算法的主要思想是通过构造数据之间的树状型层次关系实现聚类.根据构建层次关系的方式不同, 可将层次聚类分为自底向上的凝聚聚类(Agglomerative Clustering, AC)[16]和自顶向下的分裂聚类[17].用于深度聚类的一般是凝聚聚类.凝聚聚类的特点是刚开始将每个点作为一个簇, 在每次迭代中, 合并原始特征域中最接近的两个点, 并依此更新聚类中心, 直至达到结束条件.

基于密度的聚类算法的主要思想是根据数据的密度发现任意形状的簇, 将簇看作是数据空间中相对于其它部分密度更大的区域.密度峰值聚类算法(Density Peaks Clustering, DPC)[18]是近年来的通用算法.DPC的聚类过程基于两个假设:簇中心为密度峰值; 非中心点与其最近的高密度点的簇相同.

基于图的聚类算法利用图划分理论, 首先将数据表示为图数据, 再将聚类问题转化为图划分问题[19].随着互联网的发展及人们日益增长的需求, 图数据大量涌现, 图聚类可充分利用图数据中的属性和结构信息, 对图数据进行分析及理解, 成为近年来的研究热点.谱聚类(Spectral Clustering, SC)[20]是图聚类的典型代表, 也与深度聚类联系紧密.谱聚类是将给定数据集的样本看作空间中的点, 计算样本的相似度矩阵、度矩阵及拉普拉斯矩阵, 再进行特征分解, 得到特征向量, 进而聚类特征向量, 得到最终划分.

基于模型的聚类算法主要思想是假设每个簇是一个模型, 然后寻找与该模型拟合的最好数据[21].高斯混合模型(Gaussian Mixture Models, GMM)是经典的基于概率生成模型的聚类算法, 是多个高斯分布函数的线性组合.GMM假设所有样本数据均服从混合高斯分布, 并对其概率密度函数进行估计, 采用期望最大算法(Expectation Maximization, EM)进行求解, 得到的模型就是高斯模型的线性组合, 其中每个高斯分布表示一个簇.

2 深度聚类算法

为了解决大规模、高维数据的降维和特征表示问题, 在聚类任务中引入深度学习, 以无监督表征学习为研究中心, 提高聚类性能.所以本文基于无监督表征学习分类深度聚类算法, 归纳典型的相关算法, 并简要介绍各类算法的优缺点.

2.1 基于生成模型的深度聚类

基于生成模型的深度聚类通过尽可能生成与输入相同的样本或相同的分布以确保获得有效的表征, 再推断聚类分配.因此往往需在中间层加入聚类层联合表征学习与聚类或在表征学习完成之后进行聚类.在深度聚类中, 常用的是基于自动编码器的表征学习方法和基于生成对抗网络的表征学习方法.而自动编码器(Autoencoder, AE)又包含堆叠自动编码器、卷积自动编码器和变分自动编码器.本节将以上述表征学习方式为分类依据, 对经典深度聚类算法进行总结分析.

2.1.1 基于自动编码器的深度聚类

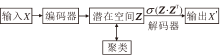
自动编码器是一种应用于无监督学习的神经网络, 由编码器和解码器两部分组成.输入数据通过编码器得到潜在空间, 解码器重构潜在空间特征向量, 得到输出.自动编码器最小化原始输入数据与重构数据的误差, 尽可能地保留数据有效的表征信息, 不需要额外的标签信息进行监督学习, 这一属性使其广泛应用于无监督的聚类任务中.深层次的网络结构能提取抽象的数据特征, 所以深度聚类多采用堆叠自动编码器(Stacked AE, SAE)[22]对数据进行降维和特征提取.基于AE的深度聚类结构如图1所示.

图1 基于AE的深度聚类结构图Fig.1 Structure of autoencoder for deep clustering

基于AE, Xie等[23]提出DEC(Deep Embedded Clustering).DEC是具有代表性的深度聚类算法之一, 核心思想是辅助目标分布P的构造, 实现无监督表征学习和聚类任务的同时进行.目标分布P的定义遵循如下原则:1)增强预测; 2)更重视分配的高置信度数据点; 3)归一化每个聚类中心的损失贡献.DEC首先利用重构损失函数对堆叠自动编码器进行预训练, 初始化网络参数, 使潜在空间变为输入的有效表示.然后丢弃解码器部分, 加入聚类层, 将编码器编码后的表征作为聚类输入, 使用K-means初始化聚类中心, 采用学生t分布(Student's t-distribu-tion)作为内核, 衡量聚类中心和嵌入点的相似度, 得到软标签分布Q, 随后利用KL散度对网络进行微调, 即最小化目标辅助函数P和软标签分布Q的KL散度.

DEC突出的贡献是对辅助目标分布P的定义与引入, 使无监督的聚类任务能在有监督的深度学习中得到发展, 通过神经网络获得数据的非线性表征并降维, 大幅提高聚类在大规模高维数据上的准确度.后续的很多深度聚类算法都是以此为基础进行改进或叠加其它思想.Guo等[24]提出IDEC(Impro-ved DEC), 在DEC的基础上, 在微调阶段保留解码器, 加入重构损失, 保护数据的局部结构.为了更好地利用卷积神经网络(Convolutional Neural Network, CNN)对图像进行特征提取, Guo等[25]又提出DCEC(Deep Convolutional Embedded Clustering), 利用卷积自动编码器对图像数据集进行特征提取, 提高自动编码器对图像数据的聚类结果.

K-means常应用在嵌入空间, 得到相应的聚类中心, 而这类方法容易形成数据崩塌, Opochinsky等[26]提出K-DAE(K-Deep-Autoencoder), 每个簇由每个自动编码器表示, 将数据点分配给重构误差最小的编码器, 全局重构损失最小的一组即为最优聚类.通过此方法, 可使每个簇获得更丰富的表示, 避免造成数据崩塌, 并且无需加入正则化, 网络训练相对简单.

虽然重构损失实现无监督的表征学习, 但是很难学习到具有判别性的表征, 因此一些样本在聚类层一直被错误分类.为了增强表征的判别性, Cai等[27]提出DCCF(Deep Clustering with Contractive Representation Learning and Focal Loss), 在嵌入层中加入雅克比矩阵F-范数约束项, 增强表征的收缩性, 在损失函数中加入焦点损失, 增强表征的判别性, 提高聚类分配准确度.

为了满足更多的要求及提高聚类性能, 研究者们在学习表征的过程中加入交替更新优化的思想.Dijazi等[28]提出DEPICT(Deep Embedded Regula-rized Clustering), 作为一个端到端的联合学习框架, 避免堆叠自动编码器的逐层预训练.首先使用深度卷积自动编码器将数据映射到一个可判别的子空间.再在KL散度的基础上加入正则化项, 平衡样本分配, 避免出现平凡解.最后采用交替学习步骤优化目标函数.在期望步骤中, 固定参数, 估计目标函数Q.在最大化步骤中, 假设目标函数Q已知, 更新参数.交替更新目标函数的思想同样用在Yang等[29]提出的DCN(Deep Clustering Network)中.

上述算法利用KL散度聚类损失函数, 结合聚类与神经网络, 发掘神经网络在聚类任务的应用前景, 所以学者们开始探索如何使神经网络提取的表征更适合于某个具体的聚类算法, 更好地按需应用.DCN以K-means为例, 探索如何使表征更有利于K-means, 即将样本均匀分布在聚类中心, 采用重构损失函数进行约束, 增加K-means损失函数, 获得聚类“ 友好” 空间.DCN使用随机梯度下降的方法交替更新神经网络参数、分配函数及聚类中心, 固定聚类中心和分配函数, 更新神经网络参数.然后固定神经网络参数, 更新聚类中心和分配函数.DCN为聚类和神经网络结合时设计优化规则提供了方向.

上述深度聚类算法均采用K-means初始化聚类中心, 但存在如下局限:1)在现实条件下, 时常难以预知聚类数目; 2)基于划分的K-means不能发现球形簇, 在不平衡数据上性能较差; 3)K-means具有随机性, 会造成聚类结果不稳定.因此Yang等[30]提出Deep Spectral Clustering Using Dual Autoencoder Net-work, 利用双自编码器获得鲁棒性特征, 即在获得的表征中加入噪声后再进行重构, 加入互信息获得更具判别性表征, 即最大化输入与表征分布的互信息, 最后同时进行谱聚类与表征学习.Ren等[31]提出DDC(Two-Stage Deep Density-Based Image Cluste-ring), 不同于联合进行的聚类与表征学习, DDC采用二阶段方法, 分开进行表征学习与聚类.首先采用卷积自动编码器获取表征, 再采用t-SNE(t-Distribu-ted Stochastic Neighbor Embedding)流形方法获得二维表征以有利于基于密度的聚类方法, 最后设计基于密度的聚类算法, 获得最终结果.McConville等[32]提出N2D, 也采用二阶段方法, 先用自动编码器获取数据表征, 再用流形学习技术代替聚类网络, 寻找表征中更适合聚类的流形.然后采用传统聚类算法, 获得聚类结果.二阶段的方法及流形学习技术再次应用于DERC(Deep Embedded Dimensionality Reduction Clustering)[33]中, DERC替换自动编码器为卷积神经网络, 采用高斯混合模型进行聚类.

为了增强表征的鲁棒性, Yang等[34]提出Adver-sarial Learning for Robust Deep Clustering, 在表征中加入搅动特征作为对抗样本, 提出对抗攻击策略, 使搅动特征生成的样本与干净样本尽可能一致, 进而提高表征的鲁棒性.

2.1.2 基于变分自动编码器和生成对抗网络的深度聚类

变分自动编码器(Variational AE, VAE)和生成对抗网络(Generative Adversarial Network, GAN)都是深度生成学习模型[35].VAE最大化数据对数似然的下界, GAN在生成器和判别器对抗训练中找到平衡.之所以将二者放在一起, 是因为VAE和GAN不仅可联合表征学习和聚类, 同时还能生成样本数据.

VAE是自动编码器的变体, 使AE的潜在特征服从一个预先定义的分布.用于聚类的VAE通常采用高斯混合分布模型作为先验, 因为该模型较利于描述聚类结构.判断数据点属于哪一个簇等同于判断数据点是由哪类潜在模型产生, 所以在最大化证据下界之后, 可通过学习到的高斯混合模型得到数据点的聚类.

GAN的目标是学习一个与数据真实分布相似的生成分布.生成网络G从噪声中产生一个样本, 判别网络D会判断样本数据是真实的还是生成的, 若判别器判断正确, 对判别器进行奖励, 否则对生成器进行惩罚, 继续进行下一个周期, 直到判别器无法判断真伪.GAN的结构如图2所示.

图2 GAN结构图Fig.2 Structure of GAN

基于上述神经网络, Jiang等[36]提出VaDE(Varia-tional Deep Embedding), 基于VAE和高斯混合模型, 使用混合高斯分布先验代替单个高斯分布先验, 更有利于聚类任务.VaDE与其它聚类任务的根本区别是能生成指定簇中的样本.VaDE流程如下:1)初始化参数.通过SAE预训练, 得到初始的潜在向量z.再采用GMM拟合z, 初始化高斯分布的均值u、方差σ 及GMM中簇的先验概率π .2)编码.原始数据X经过映射函数g得到均值、方差, 即后验分布, 再在后验分布中采样得到z.3)解码.经过映射函数f对z进行解码, 重构X.4)利用反向传播更新参数u、σ 、π .

上述生成过程可将联合概率p(x, z, c)表示为

p(x, z, c)=p(x|z)p(z|c)p(c),

其中, c为簇, z为潜在向量, x为真实数据.由于VaDE中的推断是采用变分的方法, 所以可采用SGVB(Stochastic Gradient Variational Bayes)估计器和参数化技巧优化ELBO(Evidence Lower Bound).

Xu等[37]将最大化互信息引入变分自动编码器网络模型中, 提出DC-VAE(Deep Clustering via V-AE), 首先将深度聚类问题在VAE框架中定义为软聚类分配, 然后对可观测数据和信息表示实施互信息最大化, 防止进行软聚类分配时扭曲学习到的表征, 最后推导新的泛化证据下界对象.

GAN通过生成对抗学习思想生成样本或用于分类, 但聚类将样本划分成簇, 却缺少标签对网络进行监督训练, 所以信息理论在基于GAN的聚类任务中得到广泛应用.互信息I(X; Y)表示在已知Y的情况下可得到多少X的信息.如X与Y无关, 则I(X; Y)=0, 取得最小值; 如已知Y能确定X, 则I(X; Y)取得最大值.Springenberg[38]提出CatGAN(Catego-rical GAN), 从未标记数据中学习一个判别分类器D, 可看作是GAN的泛化和正则化信息最大化的扩展.CatGAN与GAN的不同之处是:1)GAN中的判别器D的判断结果只有两类, 即数据是真实样本还是来自于生成器G的样本, 而CatGAN中的判别器D是将输入划分成预先已知的k个类, 从而变为一个分类器; 2)GAN中的生成器G是生成数据集中的样本, 而CatGAN的生成器G是生成属于k类中的样本.将分类转化为聚类问题, 通常使用距离作为度量原则, 而本文采用熵H作为度量, 对确定度进行衡量, 即CatGAN的判别器D使真实数据不仅有较高的确信度划分为真实样本, 而且具有较大的确信度划分到现有的类别中去, 但对于生成器产生的样本则不确定划分到现有的哪个类别, 即不确定度较大.数学化表示为, 最大化H[p(y|x, D)]和H[p(y|D)], 而最小化H[p(y|G(z), D)], 其中, y为类别标签, x为真实样本, z为随机噪声, G(z)为生成器产生的样本, E为期望.所以判别器和生成器的目标函数分别为:

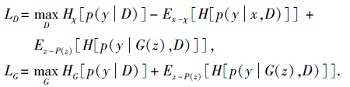
同样将信息理论扩展到GAN的还有Chen等[39]提出的InfoGAN(Information Maximizing GAN), 在无监督的方式下学习数据的分解表示(Disentangled Representation), 将表征学习变得更具体, 有利于聚类任务.原来的GAN是对一段连续单一的噪声z进行生成, 无法通过控制z的某些维度以生成特定的语义特征.而InfoGAN是把原始的输入噪声分成两部分:一部分为不可再分解的噪声z, 另一部分叫作潜在编码c, 是由若干个潜在变量组成, 这些变量具有先验概率分布, 代表不同维度的特征.例如:MNIST数据集的手写数字特征可分成多个维度(数字粗细, 倾斜角度等).所以生成器分布变成G(z, c).为了避免出现平凡解, 加入信息论的互信息[40]进行约束.隐编码c输入生成器, 使生成器G产生的数据具有可解释性, 所以c和G(z, c)的互信息越大, 说明保留的c信息越多, 所以InfoGAN的目标函数为:

minGmaxDVI(D, G)=V(D, G)-λ I(c; G(z, c)),

其中, V(D, G)为标准GAN的目标函数, I(c; G(z, c))为信息理论的正则化项, λ 为超参数.在计算互信息I(c; G(z, c))的过程中, 后验分布P(c|x)不易获得, 所以采用变分推断的思想, 定义辅助分布Q(c|x)逼近P(c|x), 所以InfoGAN的目标函数为:

minG, QmaxDVInfoGAN(D, G, Q)=V(D, G)-λ LI(G, Q).

生成模型虽然能估计聚类的潜在分布及生成数据, 但学习到的数据表征缺乏判别性, 不同簇的分布往往具有重叠性.为了解决该问题, Yang等[41]提出IMDGC(Mutual Information Maximization Deep Gene-rative Clustering), 与InfoGAN直接生成数据不同的是, IMDGC中生成数据的过程具有层次性, 即先从潜在编码中学习先验, 后从先验中生成数据.这种具有层次性的结构和互信息最大化可通过低密度区域分离不同簇, 提高表征的判别性.

为了解决聚类算法中使用浅层模型无法获得数据有效的非线性表征及深度模型参数量过多造成过拟合的问题, Dizaji等[42]提出ClusterGAN, 与上述引入互信息进行无监督学习的方法不同, ClusterGAN包括3部分:生成器、聚类器、判别器.生成器从具有类别信息的变量z中生成样本x', 聚类器对真实样本x提取表征并生成具有类别信息的变量z', 判别器判断(z, x)是来自生成器还是聚类器.通过三者之间的对抗关系实现无监督学习, 为了提高聚类器的泛化能力, 增加相对熵损失和平衡自步学习损失.平衡自步学习算法是在训练过程中逐渐降低选择的样本难度, 同时逐步增加选择样本的数量.

Larsen等[43]提出VAE-GAN, 提高生成样本的质量, 却无法直接应用到聚类.VaDE将聚类应用于变分自动编码器.因此Yang等[44]提出WGAN-GP(Clustering Approach Based on Wasserstein GAN with Gradient Penalty), 结合VAE-GAN与VaDE的优势.采用具有梯度惩罚的Wasserstein GAN与具有高斯混合模型的VAE, 两个模型的结合提高模型训练的稳定性及聚类结果.具体来说, Wasserstein GAN的引入缓解GAN训练不稳定的问题, GAN通过VaDE中的高斯混合模型先验生成潜在表征, 后续为了增加模型对离群值的鲁棒性, 将高斯混合模型替换为SMM(Student's t-mixture Model).

2.2 基于判别模型的深度聚类

判别式模型直接学习到具有判别性的表征用于聚类, 模型输出对聚类结果的预测, 其中常用的就是卷积神经网络(CNN)[45].CNN往往与其它网络结合, 或特定于某个聚类算法进行设计改造, 达到较优的聚类结果.CNN能获得图像的多维复杂特征, 有利于图像的特征提取.近些年来, 随着深度学习的不断发展, CNN得到广泛应用.但是, 由于需要标注大量的样本对其训练以获得有效表征, 造成昂贵的时间与人力成本, 因此如何将无标签的聚类任务与表征学习统一, 成为研究者们关注的热点话题.目前, CNN在聚类任务中的表征学习主要分为基于伪标签信息的深度聚类与基于对比学习的深度聚类两类.

2.2.1 基于伪标签信息的深度聚类

聚类任务中伪标签信息的获取主要可分为:1)通过聚类算法获得伪标签, 引导CNN进行训练.2)自定义一种方法, 估计伪标签, 监督CNN训练.Yang等[46]提出Recurrent Framework for Joint Unsuper-vised Learning of Deep Representations and Image Clusters, 利用一个循环框架, 通过迭代的方式更新优化参数.神经网络提取的表征使聚类算法获得更优的聚类结果, 而聚类算法产生的聚类结果又能作为监督信号对神经网络进行监督训练, 所以二者相辅相成.该算法首先通过ImageNet预训练CNN, 并选取k个样本作为初始的聚类中心, 然后采用小批量K-means, 为每个样本分配聚类标签.优化过程采用迭代方式:在前向过程中, 固定神经网络的参数, 利用层次聚类中的凝聚聚类聚类表征, 并更新聚类标签; 在后向过程中, 固定聚类标签, 更新神经网络参数, 获得更优的表征.该算法为了解决小批量K-means连续迭代之间的特征不匹配而引起的漂移误差问题, 约束聚类中心的更新.通过实验发现, 该算法在图像数据集上具有较好的聚类效果, 学习到的表征表示能迁移到其它图像数据集上, 但凝聚聚类采用的相似方法为有向图, 需要构建相似矩阵, 因此计算复杂度较高.

为了模拟CNN在图像分类上的巨大成功, 研究者们尝试在聚类任务中加入约束以产生标签信息.Chang等[47]提出DAC(Deep Adaptive Clustering), 并提出标签特征理论以获得伪标签.DAC假设成对图像的关系是在二进制基础上, 即两幅图像在一个簇中或不在一个簇中, 将图像聚类问题转变成一个二进制成对分类问题.首先输入无标记的图像, 通过CNN得到图像的标签特征, 并利用余弦距离得到标签特征的相似度.为了获得标签特征的one-hot向量, 对标签特征加入约束.为了解决图像聚类任务中真实相似度(Ground-Truth Similarities)未知的问题, DAC提出交替迭代自适应算法.在固定神经网络的基础上选择成对的图像估计相似度, 又通过选定的标记样本训练CNN, 最终图像自动通过标签特征进行聚类, 当所有样本都训练后算法收敛.DAC是将聚类问题巧妙转换为分类问题, Niu等[48]将标签特征理论继续深化, 提出GATCluster(Self-Super-vised Gaussian Attention Network for Image Cluste-ring), 基于标签特征理论, 设计4个自监督学习任务对平移不变性、分离最大化、熵分析和注意力映射这4个方面进行约束.平移不变性是最大化样本和任意平移样本的相似度, 即原图像与平移旋转后图像特征尽可能相似.分离最大化任务对每对样本探索相似性和分离性, 引导模型学习, 即相似样本尽可能聚集, 不相似样本尽可能远离.熵分析任务是为了避免平凡解.基于判别性信息通常在局部区域假设, 提出注意力机制, 捕捉物体的语义信息.

在没有标签的情况下, 只能在现有数据中挖掘它们之间更多的相互关系, 并以此提供监督信息.Wu等[49]提出DCCM(Deep Comprehensive Correlation Mining), 将图像之间的相互关系分为4种关系:样本之间的关系、特征之间的联系、内在关系及局部鲁棒性.样本之间的关系通过加入约束, 使网络预测的特征接近one-hot, 然后计算余弦距离构造相似图, 在相似图和预测特征的基础上, 设置一个阈值, 获得高置信的伪图和伪标签, 用此监督网络训练.特征之间的联系是指最大化深层特征和浅特征的互信息.局部鲁棒性是指原输入图像的特征和几何变换后图像输入的特征距离应尽量相近.内在关系是指组合上述三个关系.

在非参数实例判别方法[50]中, 作者在有监督学习结果中观察发现, 判别式学习可自动发现语义类别之间的相似性, 而不需要人为标注.由此想到, 如果把每个实例当作一个类别, 可将有监督的分类学习转换为无监督的实例学习, 而通过判别式学习就能获得实例之间语义的相似性.但这样需要面临一个问题, 即类别数等于实例数, 将softmax的输出扩展到与实例数相同是不可行的, 所以作者采用NCE(Noise-Contrastive Estimation)逼近softmax的分布.由此Tao等[51]提出Clustering-Friendly Represen-tation Learning Method Using Instance Discrimina-tion and Feature Decorrelation, 在实例判别中加入对控制分布参数的讨论, 提升表征学习的效果.特征去关联是指将获得的特征正交以获得独立的特征, 确保冗余信息的减少, 最后通过谱聚类获得聚类结果.

2.2.2 基于对比学习的深度聚类

基于伪标签信息的深度聚类目标是将无监督的深度聚类转化为有监督的方式对神经网络进行训练, 进而获得适合聚类的表征.随着自监督表征学习的发展, 对比学习应用于聚类任务中.对比学习的基本思想是将原始数据映射到表征空间, 其中正样本对相似性最大化, 负样本对相似性最小化, 以此获得判别性的表征.在早期工作中, 正负样本是作为已知的先验, 近期研究表明样本对的质量对对比学习结果至关重要, 而先验存在一定的局限性, 因此学者们开始采用无监督的方式构建样本对.具体地, 原样本的增强样本作为正样本, 其它样本作为负样本.

Tsai等[52]提出MiCE(Mixture of Contrastive Ex-perts), 同时利用对比学习获得判别式的表征以及利用潜在混合模型获得语义结构, 受MoE(Mixture of Experts)的启发, 引入潜变量, 表示图像的聚类标签, 形成混合条件模型.每个条件模型学会区分实例的子集, 将数据集根据语义信息划分为子集.

MiCE通过对比学习获得聚类所需的判别性表征, 但只将对比学习应用于实例级别.因此Li等[53]提出CC(Contrastive Clustering), 将对比学习同时应用于实例级别和簇级别.数据经过神经网络获得特征矩阵, 将矩阵的行看作实例表征, 矩阵的列看作簇表征.图像经过随机旋转平移之后经过另一个共享权重的神经网络, 得到增强特征矩阵, 将两个矩阵的行和列分别最大化相似度.经过上述两个目标函数优化神经网络后, 取每列特征最大值作为簇标签.

上述基于对比学习的深度聚类均取得优异的聚类性能, 但都仅应用对比学习的基本框架, 即假设样本和它的增强样本的特征与分配应尽可能相似, 却忽略潜在的类别信息. Zhong等[54]提出GCC(Graph CC), 同时考虑实例级别与簇级别的一致性.但与对比聚类不同的是, GCC采用图的方式表示样本之间及簇间的关系, 而非直接最大化原特征与增强特征的一致性.具体来说, 首先根据神经网络获得的表征构造相似图, 对于实例级别, 采用基于图拉普拉斯的对比损失, 对于簇级别, 又构造样本的K近邻(K-Nearest Neighbor, KNN)图, 且假设样本和它们的邻居应有相同的聚类分配, 因此最大化样本及其邻居样本簇分配的相似性.

Zhong等[55]提出DRC(Deep Robust Clustering), 提高深度聚类的鲁棒性.DRC为了解决目前深度聚类交替更新造成的误差传播问题, 将深度聚类研究从分配特征与分配概率两个角度进行, 并且挖掘互信息与对比学习的联系, 将常用的最大化互信息转化为最小化对比损失, 并成功应用于分配特征与分配概率.DRC定义分配特征为CNN中全连接网络层的输出, 为K(类别数)维向量, 分配概率为softmax层的输出.具体来说:一是从全局角度最大化原始图像与增强图像的分配概率的互信息, 增加簇间方差, 并获得高置信度的划分; 二是从局部角度最大化原始图像与增强图像的分配特征的互信息, 减少类内方差, 并获得更具有鲁棒性的簇. 最近研究表明, 相比互信息, 在无监督学习训练中对比学习更有效, 因此DRC将最大化互信息转换为最小化对比损失.

2.3 基于图表征学习的深度聚类

严格来说, 基于图表征学习的深度聚类可按照表征学习思想的不同划分到上述的生成式和判别式两类模型中.但由于图神经网络的特殊性, 将基于图表征学习的深度聚类单独作为一个章节, 方便读者更好地理解与分析应用于深度聚类中的图神经网络和图表征学习.

由于现实生活中存在很多图数据, 如社交网络、电子购物、交通网络等.为了更好地挖掘图数据存在的结构和属性信息, Gori等[56]提出图神经网络的概念.CNN在图像数据中取得不错成绩后, 学者们开始思考如何将卷积操作加入图神经网络中, 所以Bruna等[57]结合基于频域的卷积操作与图神经网络, 将可学习的卷积操作用于图数据之上.但基于频域的卷积操作要求处理整个图, 并需要进行矩阵分解, 时间复杂度较高, 难以应用于大规模的图数据. Kipf等[58]简化频域图卷积, 使图卷积能在空域中进行, 大幅提升图卷积模型的计算效率.常用于深度聚类的图神经网络结构如图3所示, 图中σ (· )表示激活函数.

图3 基于图表征学习的深度聚类结构图Fig.3 Deep clustering structure based on graph representation learning

基于图神经网络的图表征学习目的在于获得节点在低维空间中向量表示的同时保存图结构中节点之间的结构关系, 正是由于这个属性, 图神经网络可挖掘数据之间的结构信息, 增加表征中包含的信息.Kipf等[59]提出VGAE(Variational Graph Autoenco-der), 对节点进行低维向量表示, 使用图卷积网络作为编码器, 得到所有节点的潜在表示Z, 然后采用隐向量的内积作为解码器输出重构图.Wang等[60]提出DAEGC(Deep Attentional Embedded Graph Cluste-ring), 利用图神经网络获得图数据的结构信息, 在输入中同时加入节点的属性信息, 融合节点信息和结构信息进行表征学习, 并引用注意力机制, 更有效地对节点的邻居节点进行聚合, 在得到的潜在表示中使用K-means初始化聚类中心.借鉴DEC自监督的训练方式, 得到重构损失和KL散度统一的目标函数, 对聚类中心和神经网络参数进行联合优化. Bo等[61]提出SDCN(Structural Deep Clustering Network), 不仅利用图神经网络挖掘数据结构信息, 并且将输入数据从图数据拓展到规则化数据, 面对非图结构数据集时, 利用KNN得到无向K近邻图, 作为图卷积网络的输入.SDCN另一方面将原始数据作为自动编码器的输入, 并将自动编码器每层学习到的表示逐层输入图卷积网络中, 与对应层数据的结构信息结合, 经过堆叠图卷积网络的编码, 在其最后一层使用softmax激活函数, 得到数据的分配概率Z, 并将Z看作概率分布.在自动编码器得到的潜在表示中, 使用K-means初始化聚类中心, 使用学生t分布作为内核, 衡量聚类中心和嵌入点的相似度, 得到Q.利用Q得到目标辅助分布P, 将P与Q进行KL散度处理, 得到自动编码的聚类损失函数Lclus, P与Z进行KL散度处理, 得到图卷积网络的损失函数Lgcn, 二者加上自编码器的重构损失Lres, 得到整个模型的目标函数.

与传统的自动编码器不同, 图自动编码器是采用内积距离重构图, 因此学习到的表征是在内积空间中而不是在欧几里得空间中, 而继续采用基于欧几里得的K-means会影响聚类结果, 所以, Zhang等[62]提出EGAE(Embedding Graph Autoencoder), 采用松弛K-means进行聚类.

图聚类是采用无监督的方法将节点划分为若干个簇.正因如此, 图聚类常常与图神经网络结合, 将样本看作节点, 节点之间的连接权重看作相似性.图神经网络具有推断样本和邻居连接性的强大能力.样本经过图神经网络之后, 会获得节点之间边的权重, 再采用图聚类的方法切割子图.Qi等[63]提出RGCN(Deep Face Clustering Method Using Residual Graph Convolutional Network), 将每张人脸看作节点, 采用KNN获得图数据, 输入图神经网络后, 获得节点之间的边权重, 再采用图聚类进行切图.为了避免图神经网络的过平滑问题, 将残差学习思想引入图神经网络中, 提高聚类结果.

谱聚类是图聚类中的经典方法, 但谱聚类中的拉普拉斯矩阵分解复杂度较高, 且谱聚类未用到节点特征, 因此Bianchi等[64]提出Spectral Clustering with Graph Neural Networks for Graph Pooling, 在图神经网络中加入池化层, 提出mincut, 可求导而不需要求解, 并学习一个分配矩阵, 同时加入约束, 在正交空间中寻找可行解, 避免出现平凡解.

图神经网络不但在图聚类中, 也在集成聚类中得到发展.Tao等[65]提出AGAE(Adversarial Graph Auto-Encoders), 结合对抗性图自动编码器与集成聚类, 具体表现在将一致图和原始数据的特征矩阵作为输入, 解决传统集成聚类忽略原始数据特征重利用的问题.引入对抗性正则化引导网络进行训练, 图卷积网络作为概率编码器, 对潜在表示的后验分布建模, 矩阵内积作为解码器, 多层神经网络当作判别器, 通过这种方法将自适应划分先验引入聚类任务中.杜航原等[66]提出深度自监督聚类集成算法, 将集成聚类结果采用加权连同三元组计算相似度矩阵, 将集成聚类从特征空间的数据表示转换为图数据表示, 进而将集成聚类的一致性问题转换为图聚类.该算法将相似度矩阵作为输入, 图卷积网络作为编码器, 得到图的低维嵌入, 矩阵内积作为解码器.并依据低维嵌入似然分布估计聚类集成的目标分布, 将二者的KL散度与重构损失函数的和作为目标函数, 对图自编码器进行训练, 得到最优的集成结果.

3 实验及结果分析

为了进一步分析各类算法, 本文选择传统聚类算法与深度聚类算法中具有代表性的算法进行对比实验.

实验软硬件环境如下:AMD Ryzen 4800H 2.90 GHz, 内存16 GB, 操作系统为Windows 10, 编程语言为python.DEC采用tensorflow 1.15框架, VaDE、DAC采用theano 1.0框架, InfoGAN、DAEGC采用torch 1.0框架.

3.1 实验数据集

本文采用UCI机器学习数据库中常用的WDBC数据集与深度学习中常用的MNIST数据集, 针对传统聚类算法与深度聚类算法进行对比实验; 采用Core、Citeseer图数据集, 针对谱聚类与基于图神经网络的深度聚类算法进行对比实验.数据集具体信息如表2所示.

表2 实验数据集 Table 2 Experimental datasets
3.2 深度聚类算法性能对比

为了对比传统聚类算法与深度聚类算法在不同规模与维度数据集上的性能差异, 本文选取如下传统聚类算法:基于划分的K-means、基于密度的DPC、基于层次的AC、基于图的SC、基于模型的GMM.深度聚类算法选择基于生成模型的DEC、VaDE、InfoGAN与基于判别模型的DAC.各算法的聚类准确率(Accuracy, ACC)对比如表3所示.

表3 各聚类算法在2个数据集上的聚类准确率对比 Table 3 Clustering accuracy comparison of different clustering algorithms on 2 datasets %

WDBC数据集与MNIST 数据集在规模与维度方面存在显著差异, 由表3可看出, 由于DPC与AC空间复杂度较高, 在本实验环境下会超出内存, 无法得到实验结果.InfoGAN与DAC无法直接处理WDBC数据, 体现传统聚类算法在大规模高维数据的局限性及CNN对非图像数据处理的局限性.传统聚类算法在WDBC数据集上表现较优, GMM得到最高准确率, DEC次之, 深度聚类算法VaDE准确率最低.而在MNIST数据集上, 传统聚类算法与深度聚类算法具有明显差距, 传统聚类算法准确率均低于70%, 需要较高的空间内存运行算法, 而深度聚类算法聚类准确率均高于80%, VaDE和DAC的准确率甚至超过90%.因此在大数据的时代背景下, 深度聚类算法会发挥更重要的作用.

由于实验环境中内存的限制, 本文采用MNIST_test数据集进行实验, MNIST_test数据集除了数据样本数为10 000之外, 其余均与MNIST数据集相同.

传统聚类算法在MNIST_test数据集上的聚类性能如表4所示.由表可看出, 各算法的准确率都较低, 再次验证传统聚类算法在大规模数据上的局限性.从聚类时间可看出:DPC最长, 准确率最低; K-mean效率最快, 准确率差于AC和SC; AC虽然空间复杂度较高, 但性能方面较优; SC在聚类准确率与效率之间达到均衡.

表4 传统聚类算法在MNIST_test数据集上的聚类性能对比 Table 4 Clustering performance comparison of traditional clustering algorithms on MNIST_test dataset

为了验证基于图神经网络的深度聚类算法与传统图聚类算法的差异, 在Core、Citeseer数据集上对比SC和DAEGC, 结果如表5所示.由表可发现, DA-EGC在ACC与标准化互信息(Normalized Mutual Information, NMI)上明显优于SC, 尤其在Citeseer数据集上, SC的2项指标未达到DAEGC的50%, 原因在于Citeseer数据集图像维度达3 703维.对于高维数据, 基于图神经网络的表征学习优于传统聚类算法, 因此基于图神经网络的深度聚类可更有效处理目前的高维图数据.

表5 SC和DAEGC的聚类性能对比 Table 5 Clustering performance comparison of SC and DAEGC

为了对比深度聚类算法中不同算法的复杂度, 得到各算法的参数量如下:DEC为12.7 M, VaDE为10.03 M, InfoGAN为50.52 M, DAC为1.71 M, DAEGC为0.95 M.DEC、VaDE中分别包含自动编码器与变分自动编码器, InfoGAN含有 GAN, DAC中含有CNN, DAEGC含有图神经网络.由参数量可看出, InfoGAN参数量最多, DAEGC参数量最少, DAC参数量次少, DEC与VaDE参数量相当.InfoGAN较复杂, 在MNIST数据集上准确率较低, 但能生成指定样本, 适用于数据缺失的样本.DAEGC参数量较少, 这是由于图神经网络过深容易产生过平滑问题, 因此图神经网络一般是2~3层, 但是图神经网络要求输入为矩阵, 因此构建非图数据集时仍需要较高的空间复杂度, 更适合于图数据集.DAC不但参数较少, 在MNIST数据集上性能也较优, 但局限于图像数据集.DEC泛化性最好, 在小规模数据集与大规模数据集上的表现都较好, 模型参数量适中.

3.3 总结与分析

生成式模型中的基于自动编码器的深度聚类最早将无监督表征学习与聚类任务结合.重构损失的存在使模型学习的表征鲁棒性较好.主要原因是聚类任务中缺少标签, 缺乏确定的先验性信息, 重构损失能在聚类损失得到充分优化的同时将表征约束在合理范围之内, 以防只有聚类损失将潜在空间扭曲而失去实际意义.首先是采用最常用的K-means聚类算法, 联合表征学习与聚类, 后来为了减少预训练阶段及更好地结合其它聚类算法, 在优化过程中加入交替更新的思想, 并从此出现其它聚类算法损失与表征学习结合的深度聚类.

随着研究的不断深入, 研究者们发现将表征学习与聚类任务分开进行, 也能获得较好的聚类结果, 并在表征学习中加入流形学习、数据增强、正则化、对抗学习等技术, 不断提高聚类性能.但由于自动编码器具有对称的结构特性, 会限制神经网络的深度, 进而影响表征学习能力.

基于VAE的表征学习模型, 为了使无监督的训练网络模型获得较好的表征用于聚类, 将VAE中的先验由单一分布换成混合高斯分布, 并采用SGVB优化证据下界, 损失函数拥有完备的理论保证, 提高模型的鲁棒性, 而GAN的先验分布更灵活, 因此在生成数据方面, GAN性能较优.在GAN中加入信息论, 最大化互信息, 避免平凡解及提高表征的判别性, 提高聚类结果.即便如此, GAN的聚类性能仍较差, 原因在于对抗训练的方式收敛速度较慢.

判别式模型由于没有生成式模型框架的束缚, 如固有的解码器、判别器等, 所以可扩展性较强.损失函数一般只包括聚类损失函数.该类算法的目标函数简单、易于优化, 网络结构灵活, 可使算法应用到大型复杂数据集, 但由于没有非聚类损失函数的限制, 可能会出现特征空间扭曲、坍塌等问题.

在无监督表征学习和聚类任务中, 一般有如下思路.

1)聚类标签和网络参数交替更新, 将聚类结果作为监督信号促使学习有效的表征, 而学习的表征又提高聚类结果.

2)对输出预测施加一定约束, 获得one-hot标签特征, 将聚类任务转换为分类任务.

3)利用自监督学习的思想, 根据聚类任务的属性挖掘样本之间的关系, 由此作为目标函数优化神经网络, 获得适合于聚类的表征, 再进行聚类或加入聚类损失函数联合聚类.

4)根据判别式学习能自动获得样本之间语义相似性, 即根据语义相似性利用聚类算法进行划分.

基于图神经网络的图表征学习首先在面向图数据的深度聚类算法中得到应用, 图神经网络对图数据具有强大的编码能力, 能有效利用数据的属性和结构信息, 使学习到的特征信息更丰富, 进而提高聚类效果.但由于图神经网络的输入为图数据, 对于其它类型数据集首先需要构造图数据, 空间复杂度会随着图复杂度急剧增长.利用图自动编码器无监督训练的属性, 在K-means、图聚类、集成聚类等方面用于数据的表征学习、图划分, 但图神经网络大多是半监督的训练方式及存在训练不稳定、过平滑等问题, 所以图表征学习需要更深入研究如何结合自监督训练任务与聚类、集成聚类.

4 损失函数与评估标准
4.1 损失函数

4.1.1 聚类损失函数

聚类损失函数是针对特定聚类算法及约束神经网络学习适合该聚类算法的特征.聚类损失函数大致可分为K-means损失函数、簇分配强化损失函数(Cluster Assignment Hardening Loss)和平衡分配损失函数(Balanced Assignment Loss)[67].

为了保证学习到的表示有利于K-means聚类算法进行聚类, 使数据均匀分布在聚类中心, K-means损失函数表示如下:

L(θ )= ∑i=1N∑k=1Ksik‖ zi-uk‖ 2,

其中, zi为嵌入到子空间的点, uk为聚类中心, sik为布尔变量表示zi是否分配到uk中的点.

簇分配强化损失函数使用软分配将数据分配到簇中.例如, 使用t分布作为内核衡量聚类中心和数据点的相似度, 即

qij= (1+1v‖zi-uj‖2)-α+12∑j'(1+1v‖zi-uj'‖2)-α+12,

其中, uj为聚类中心, zi为嵌入点, α 为自由度, 通常定义为α =1.

数据点和聚类中心的归一化可看成是软分配, 又通过KL散度接近辅助目标分布P, 使软分配概率更严格.辅助目标分布P的目的是为了提高聚类纯度, 重点放在高置信度的点上, 并且防止大的簇扭曲潜在空间.辅助目标分布P和KL散度定义如下:

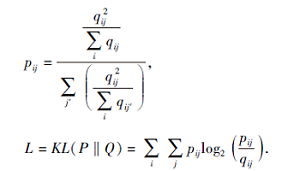
平衡分配损失函数的目的是为了使簇分配平衡, 定义如下:

Lba=KL(G‖ U),

其中, U为均匀分布, G为一个点分配到每个簇的概率分布,

gk=P(y=k)= 1N∑iqik,

通过最小化KL散度使每个点分配到某些簇的概率相同.

4.1.2 网络辅助损失函数

网络辅助损失函数独立于聚类算法, 通常是为了对学习模型施加需要的约束, 辅助模型训练.通过对模型的参数施加约束, 可提升表征学习的有效性, 避免平凡解.典型的非聚类损失函数有重构损失函数(Reconstruction Loss)[68]和自我加强损失函数(Self-Augmentation Loss).

重构损失函数最小化输入xi和解码器重构的f(xi)的距离, 保证数据有用的特征信息在经过编码器的编码之后不会丢失, 函数表示如下:

L=dAE(xi, f(xi))= ∑i‖ xi-f(xi)‖ 2.

自我加强损失组合原始样本和它们的增强样本, 函数表示如下:

L=- 1N∑Ns(f(x), f(T(x))),

其中, x为原始样本, T为加强函数, f(x)为通过模型产生的表示, s为相似度度量方法, N为样本总数.

4.2 性能评估标准

两个无监督的评估标准已广泛用于深度聚类, 分别为聚类准确率(ACC)和标准化互信息(NMI)[69].

聚类准确率(ACC)度量聚类算法分配的正确率:

ACC= maxm[ 1N∑i=1n1{yi=m(ci)}],

其中, yi为真实标签, ci为通过算法产生的聚类分配, m(· )为映射函数, N为样本总数, 将聚类分配与标签一一对应.

互信息是指两个随机变量之间的关联程度, 标准化互信息(NMI)是将互信息归一化为[0, 1].数学表示如下:

NMI(Y, C)= 2I(Y, C)[H(Y)+H(C)],

其中, Y为真实标签, C为聚类标签, I为互信息, H为熵.

调整兰德系数(Adjusted Rand Index, ARI)为衡量聚类标签和真实标签相似性的度量标准, 需要数据集本身有标签.ARI的取值范围为[-1, 1], 值越大表示聚类效果越优.ARI数学表示如下:

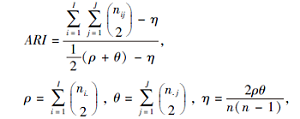
其中, I为聚类得到的簇的个数, J 为数据集真实的类别数, ni.为第i个簇中的样本数, n.j为标签j中的样本数, nij 为在第i个簇中包含标签j的样本总数, n 为总的样本数.

5 算法应用

随着互联网的发展及移动通讯工具的普及, 面对海量数据, 如何快速给用户推荐需要、值得关注的信息是亟待解决的问题, 因此个性化信息推荐成为计算机领域的一个研究热点.

在新闻推荐领域, 首先聚类新闻内容, 再结合用户行为对用户进行个性化的信息推荐.新闻推荐大多是对本文信息进行聚类.李悦[70]提出基于CNN的文本聚类方法, 能较好地处理目前高维和大规模的数据, 克服传统聚类算法需要人为设定特征提取器等问题.在视频推荐中, 大多是对图像进行聚类, 李文杰等[71]提出融合时间因素的用户偏好和聚类加权的聚类方法, 使推荐视频更符合用户的需求, 提高用户的满意度.

随着深度聚类的发展, 将深度聚类算法应用于多维的医疗数据, 对疾病进行预测及防控, 已成为研究热点.王振飞等[72]使用自适应模块化神经网络预测心血管疾病, 首先使用密度峰值聚类确定数据集的聚类中心, 确定每个模块的训练样本集, 再采用反向传播(Backpropagation)训练网络.

周峰[73]提出基于神经网络的慢性乙肝相关疾病患者聚类及医疗费用预测研究, 由于影响医疗费用的因素分布呈现类型复杂、高维度等特点, 所以采用基于SOM(Self-Organizing Feature Map)神经网络对患者入院时的检测结果及住院时的治疗方案进行聚类分析, 可帮助建立有效的住院费用预测模型, 对今后患者的治疗方法和住院费用提供有力依据.

随着计算机技术和互联网的不断发展, 网络和信息安全问题逐渐得到社会重视.深度聚类能较好地挖掘大数据中的有效、异常信息, 因此得到广泛应用.在网络安全领域, 僵尸网络变得日益复杂和危险, 为此Chowdhury等[74]提出Botnet Detection Using Graph-Based Feature Clustering, 基于图节点特征, 采用自组织映射聚类对网络中的节点进行聚类, 能将僵尸节点隔离在小的簇中, 同时同一大型簇中包含大多数正常节点, 因此可通过搜索很小数量的节点检测到僵尸网络.

在信息领域, 人脸识别系统已应用于生活的各方面, 如支付宝付款、手机开锁等.人脸欺骗检测对于人脸识别系统的安全性起到关键作用.EL-DIN等[75]提出DCDA(Deep Clustering Guided Unsuper-vised Domain Adaptation).传统的人脸欺骗检测方法假设攻击来自与训练相同的域, 而不能较好地应用于隐形攻击场景, 为此DCDA提出域自适应的端到端训练框架, 提高模型的泛化能力.而单独在人脸欺骗检测中使用域自适应方法不能较好地适应在不同设备和攻击类型下的目标域, 因此为了保持目标域的内在属性, 在目标样本中需要进行深度聚类.

6 结束语

由于深度聚类在大规模高维数据表现的优越性, 深度聚类现已成为研究热点.神经网络强大的表征学习能力大幅提高传统聚类算法性能.面对目前的海量数据与高维数据, 神经网络与传统聚类算法结合会有更广泛的应用前景.

本文系统阐述深度聚类算法, 将深度聚类按照表征学习方法的不同进行分类, 综述各类具有代表性的算法, 描述深度聚类的应用前景.

基于上述总结与分析, 深度聚类还可在如下方向进行深入研究.

1)多样化的网络结构.(1)目前深度聚类多集中于对图像的聚类研究, 对时序数据的研究较少, 如语音、文件等, 今后可探索聚类算法与其它类型网络结构的结合.(2)目前表征学习的网络结构大多集中于主流架构, 通过施加约束达到适合聚类表征的目的, 如何利用机器学习思想设计针对聚类的网络结构也是值得探索的方向之一.

2)深度聚类模型推理性的研究.目前深度聚类用到的深度模型都是连续的几何变换, 将一个向量空间映射到另一个, 使深度学习缺少推理能力, 阻碍其向更深层次应用方面的发展.例如:对于即使有足够的产品使用说明书的数据进行训练以聚类, 深度生成学习模型也无法生成指定产品的使用说明程序.

3)在线深度聚类算法的研究.目前深度聚类都是以离线形式完成的, 导致训练神经网络学习到有效的表征需要整个数据集, 而无法处理数据流形式的样本, 进而限制深度聚类算法在更大规模在线学习场景的应用.因此在线计算的深度聚类算法研究将是一个重要的研究方向.

4)可解释深度聚类算法的研究.即使深度聚类能解决高维数据线性不可分问题, 应用广泛, 但面对目前更复杂的数据和场景, 理解模型的决策和机理显得更重要.由于神经网络“ 黑盒子” 的特性, 其工作机制难以理解, 需要费时费力且无依据的调整超参数以达到满意结果.相比有监督的分类任务, 无监督的聚类任务可解释性的难度更高, 因为分类解释为什么样本被分到某类, 而聚类需要解释模型发现簇的语义信息, 即前者是模型的可解释性, 后者是样本的可解释性.所以如何设计可解释的深度聚类模型或加强对深度聚类模型的可解释性都是值得关注的研究方向.

本文责任编委 陈松灿

Recommended by Associate Editor CHEN Songcan

参考文献
[1] 朱杰, 陈黎飞. 核密度估计的聚类算法. 模式识别与人工智能, 2017, 30(5): 439-447.
(ZHU J, CHEN L F. Clustering Algorithm with Kernel Density Estimation. Pattern Recognition and Artificial Intelligence, 2017, 30(5): 439-447. ) [本文引用:1]
[2] 古天龙, 李龙, 常亮, 等. 公平机器学习: 概念、分析与设计. 计算机学报, 2022, 45(5): 1018-1051.
(GU T L, LI L, CHANG L, et al. Fair Machine Learning: Concepts, Analysis, and Design. Chinese Journal of Computers, 2022, 45(5): 1018-1051. ) [本文引用:1]
[3] 化春键, 张爱榕, 蒋毅, 等. 基于改进模糊 C均值聚类算法的草坪杂草识别. 华南农业大学学报, 2022, 43(3): 107-115.
(HUA C J, ZHANG A R, JIANG Y, et al. Lawn Weed Recognition Based on Improved Fuzzy C-means Clustering Algorithm. Journal of South China Agricultural University, 2022, 43(3): 107-115. ) [本文引用:1]
[4] 卢宏涛, 罗沐昆. 基于深度学习的计算机视觉研究新进展. 数据采集与处理, 2022, 37(2): 247-278.
(LU H T, LUO M K. Survey on New Progresses of Deep Learning Based Computer Vision. Journal of Data Acquisition and Processing, 2022, 37(2): 247-278. ) [本文引用:1]
[5] 王鑫, 张鑫, 宁晨. 基于多特征降维和迁移学习的红外人体目标识别方法. 计算机应用, 2019, 39(12): 3490-3495.
(WANG X, ZHANG X, NING C. Infrared Human Target Recognition Method Based on Multi-feature Dimensionality Reduction and Transfer Learning. Journal of Computer Applications, 2019, 39(12): 3490-3495. ) [本文引用:1]
[6] 韩敏, 李宇, 韩冰. 基于改进结构保持数据降维方法的故障诊断研究. 自动化学报, 2021, 47(2): 338-348.
(HAN M, LI Y, HAN B. Research on Fault Diagnosis of Data Dimension Reduction Based on Improved Structure Preserving Algorithm. Acta Automatica Sinica, 2021, 47(2): 338-348. ) [本文引用:1]
[7] 季伟东, 孙小晴, 林平, 等. 基于非线性降维的自然计算方法. 电子与信息学报, 2020, 42(8): 1982-1989.
(JI W D, SUN X Q, LIN P, et al. Natural Computing Method Based on Nonlinear Dimension Reduction. Journal of Electronics and Information Technology, 2020, 42(8): 1982-1989. ) [本文引用:1]
[8] LECUN Y, BENGIO Y, HINTON G. Deep Learning. Nature, 2015, 521: 436-444. [本文引用:1]
[9] 刘睿馨, 刘新媛, 李晨. 基于低秩表示的标记分布学习算法. 模式识别与人工智能, 2021, 34(2): 146-156.
(LIU R X, LIU X Y, LI C. Label Distribution Learning Method Based on Low-Rank Representation. Pattern Recognition and Artificial Intelligence, 2021, 34(2): 146-156. ) [本文引用:1]
[10] BASHAR A. Survey on Evolving Deep Learning Neural Network Architectures. Journal of Artificial Intelligence and Capsule Networks, 2019, 1(2): 73-82. [本文引用:1]
[11] 杜鹏, 丁世飞. 基于混合词向量深度学习模型的DGA域名检测方法. 计算机研究与发展, 2020, 57(2): 433-446.
(DU P, DING S F. A DGA Domain Name Detection Method Based on Deep Learning Models with Mixed Word Embedding. Journal of Computer Research and Development, 2020, 57(2): 433-446. ) [本文引用:1]
[12] 吕坤儒, 吴春国, 梁艳春, 等. 融合语言模型的端到端中文语音识别算法. 电子学报, 2021, 49(11): 2177-2185.
(LÜ K R, WU C G, LIANG Y C, et al. An End-to-End Chinese Speech Recognition Algorithm Integrating Language Model. Acta Electronica Sinica, 2021, 49(11): 2177-2185. ) [本文引用:1]
[13] 寇大磊, 权冀川, 张仲伟. 基于深度学习的目标检测框架进展研究. 计算机工程与应用, 2019, 55(11): 25-34.
(KOU D L, QUAN J C, ZHANG Z W. Research on Progress of Object Detection Framework Based on Deep Learning. Computer Engineering and Applications, 2019, 55(11): 25-34. ) [本文引用:1]
[14] 谢娟英, 侯琦, 曹嘉文. 深度卷积自编码图像聚类算法. 计算机科学与探索, 2019, 13(4): 586-595.
(XIE J Y, HOU Q, CAO J W. Image Clustering Algorithms by Deep Convolutional Autoencoders. Journal of Frontiers of Computer Science and Technology, 2019, 13(4): 586-595. ) [本文引用:1]
[15] ZHOU S, XU H J, ZHENG Z N, et al. A Comprehensive Survey on Deep Clustering: Taxonomy, Challenges, and Future Directions[C/OL]. [2022-07-15]. https://arxiv.org/pdf/2206.07579v1.pdf. [本文引用:1]
[16] 贾宗维, 崔军. 一种发现社团结构的快速凝聚聚类算法. 湘潭大学自然科学学报, 2012, 34(4): 103-107.
(JIA Z W, CUI J. A Fast Agglomerate Clustering Algorithm for Detecting Community Structure. Natural Science Journal of Xiangtan University, 2012, 34(4): 103-107. ) [本文引用:1]
[17] 谢宜婷, 王爱平, 邹海. 基于自顶向下分裂聚类的图像匹配算法研究. 计算机应用研究, 2017, 34(5): 1590-1593.
(XIE Y T, WANG A P, ZHOU H. Research of Image Matching Algorithm Based on Top-Down Split Clustering. Application Research of Computers, 2017, 34(5): 1590-1593. ) [本文引用:1]
[18] 徐晓, 丁世飞, 丁玲. 密度峰值聚类算法研究进展. 软件学报, 2022, 33(5): 1800-1816.
(XU X, DING S F, DING L. Survey on Density Peaks Clustering Algorithm. Journal of Software, 2022, 33(5): 1800-1816. ) [本文引用:1]
[19] 柳菁, 李琪. DisHAP: 基于层次亲和聚类的分布式大图划分算法. 电子学报, 2021, 49(10): 2002-2011.
(LIU J, LI Q. DisHAP: A Distributed Partition Algorithm for Large Scale Graphs Based on Hierarchical Affinity Clustering. Acta Electronica Sinica, 2021, 49(10): 2002-2011. ) [本文引用:1]
[20] 袁泉, 晏飞扬, 文志云, 等. 基于谱聚类的社交网络差分隐私保护算法研究. 计算机工程与科学, 2022, 44(2): 251-256.
(YUAN Q, YAN F Y, WEN Z Y, et al. A Differential Privacy Protection Algorithm in Social Network Based on Spectral Clustering. Computer Engineering and Science, 2022, 44(2): 251-256. ) [本文引用:1]
[21] 万仁霞, 王大庆, 苗夺谦. 基于三支决策的高斯混合聚类研究. 重庆邮电大学学报(自然科学版), 2021, 33(5): 806-815.
(WANG R X, WANG D Q, MIAO D Q. Gaussian Mixture Clustering Based on Three-Way Decision. Journal of Chongqing University of Posts and Telecommunications(Natural Science Edition), 2021, 33(5): 806-815. ) [本文引用:1]
[22] XU R B, CHE Y, WANG X M, et al. Stacked Autoencoder-Based Community Detection Method via an Ensemble Clustering Framework. Information Sciences, 2020, 526: 151-165. [本文引用:1]
[23] XIE J Y, GIRSHICK R, FARHADI A. Unsupervised Deep Embedding for Clustering Analysis // Proc of the 33rd International Conference on Machine Learning. San Diego, USA: JMLR, 2016: 478-487. [本文引用:1]
[24] GUO X F, CAO L, LIU X W, et al. Improved Deep Embedded Clustering with Local Structure Preservation // Proc of the 26th International Joint Conference on Artificial Intelligence. San Francisco, USA: IJCAI, 2017: 1753-1759. [本文引用:1]
[25] GUO X F, LIU X W, ZHU E, et al. Deep Clustering with Convolutional Autoencoders // Proc of the International Conference on Neural Information Processing. Berlin, Germany: Springer, 2017: 373-382. [本文引用:1]
[26] OPOCHINSKY Y, CHAZAN S E, GANNOT S, et al. K-Autoencoders Deep Clustering // Proc of the IEEE International Confe-rence on Acoustics, Speech and Signal Processing. Washington, USA: IEEE, 2020: 4037-4041. [本文引用:1]
[27] CAI J Y, WANG S P, XU C Y, et al. Unsupervised Deep Clustering via Contractive Feature Representation and Focal Loss. Pattern Recognition, 2022, 123. DOI: DOI:10.1016/j.patcog.2021.108386. [本文引用:1]
[28] DIZAJI K G, HERANDI A, DENG C, et al. Deep Clustering via Joint Convolutional Autoencoder Embedding and Relative Entropy Minimization // Proc of the IEEE International Conference on Computer Vision. Washington, USA: IEEE, 2017: 5747-5756. [本文引用:1]
[29] YANG B, FU X, SIDIROPOULOS N D, et al. Towards K-means-Friendly Spaces: Simultaneous Deep Learning and Clustering // Proc of the 34th International Conference on Machine Learning. San Diego, USA: JMLR, 2017: 5888-5901. [本文引用:1]
[30] YANG X, DENG C, ZHENG F, et al. Deep Spectral Clustering Using Dual Autoencoder Network // Proc of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2019: 4061-4070. [本文引用:1]
[31] REN Y Z, WANG N, LI M X, et al. Deep Density-Based Image Clustering. Knowledge-Based Systems, 2020, 197. DOI: DOI:10.1016/j.knosys.2020.105841 [本文引用:1]
[32] MCCONVILLE R, SANTOS-RODRÍGUEZ R, PIECHOCKI R J, et al. N2D: (Not Too) Deep Clustering via Clustering the Local Manifold of an Autoencoded Embedding // Proc of the 25th International Conference on Pattern Recognition. Washington, USA: IEEE, 2021: 5145-5152. [本文引用:1]
[33] YAN Y J, HAO H Y, XU B L, et al. Image Clustering via Deep Embedded Dimensionality Reduction and Probability-Based Triplet Loss. IEEE Transactions on Image Processing, 2020, 29: 5652-5661. [本文引用:1]
[34] YANG X, DENG C, WEI K, et al. Adversarial Learning for Robust Deep Clustering // Proc of the 34th International Conference on Neural Information Processing Systems. Cambridge, USA: MIT Press, 2020: 9098-9108. [本文引用:1]
[35] AGGARWAL A, MITTAL M, BATTINENI G. Generative Adversarial Network: An Overview of Theory and Applications. International Journal of Information Management Data Insights, 2021, 1(1). DOI: DOI:10.1016/j.jjimei.2020.100004. [本文引用:1]
[36] JIANG Z X, ZHENG Y, TAN H C, et al. Variational Deep Embedding: An Unsupervised and Generative Approach to Clustering[C/OL]. [2022-07-15]. https://arxiv.org/abs/1611.05148. [本文引用:1]
[37] XU C Y, DAI Y F, LIN R J, et al. Deep Clustering by Maximizing Mutual Information in Variational Auto-Encoder. Knowledge-Based Systems, 2020, 205. DOI: DOI:10.1016/j.knosys.2020.106260. [本文引用:1]
[38] SPRINGENBERG J T. Unsupervised and Semi-Supervised Lear-ning with Categorical Generative Adversarial Networks[C/OL]. [2020-06-30]. https://arxiv.org/pdf/1511.06390.pdf. [本文引用:1]
[39] CHEN X, DUAN Y, HOUTHOOFT R, et al. InfoGAN: Interpretable Representation Learning by Information Maximizing Generative Adversarial Nets // Proc of the 30th International Conference on Neural Information Processing Systems. Cambridge, USA: MIT Press, 2016: 2180-2188. [本文引用:1]
[40] GU X Y, GUO J C, XIAO L J, et al. Conditional Mutual Information-Based Feature Selection Algorithm for Maximal Relevance Mi-nimal Redundancy. Applied Intelligence, 2022, 52(2): 1436-1447. [本文引用:1]
[41] YANG X J, YAN J C, CHENG Y, et al. Learning Deep Generative Clustering via Mutual Information Maximization. IEEE Tran-sactions on Neural Networks and Learning Systems, 2022. DOI: DOI:10.1109/TNNLS.2021.3135375. [本文引用:1]
[42] DIZAJI K G, WANG X Q, DENG C, et al. Balanced Self-Paced Learning for Generative Adversarial Clustering Network // Proc of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2019: 4386-4395. [本文引用:1]
[43] LARSEN A B L, SϕNDERBY S K, LAROCHELLE H, et al. Autoencoding Beyond Pixels Using a Learned Similarity Metric // Proc of the 33rd International Conference on Machine learning. San Diego, USA: JMLR, 2016: 1558-1566. [本文引用:1]
[44] YANG L, FAN W T, BOUGUILA N. Clustering Analysis via Deep Generative Models with Mixture Models. IEEE Transactions on Neural Networks and Learning Systems, 2022, 33(1): 340-350. [本文引用:1]
[45] ZHANG Y, LIU Y, SUN P, et al. IFCNN: A General Image Fusion Framework Based on Convolutional Neural Network. Information Fusion, 2020, 54: 99-118. [本文引用:1]
[46] YANG J W, PARIKH D, BATRA D. Joint Unsupervised Learning of Deep Representations and Image Clusters // Proc of the IEEE Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2016: 5147-5156. [本文引用:1]
[47] CHANG J L, WANG L F, MENG G F, et al. Deep Adaptive Image Clustering // Proc of the IEEE International Conference on Computer Vision. Washington, USA: IEEE, 2017: 5880-5888. [本文引用:1]
[48] NIU C, ZHANG J, WANG G, et al. GATCluster: Self-Supervised Gaussian-Attention Network for Image Clustering // Proc of the European Conference on Computer Vision. Berlin, Germany: Springer, 2020: 735-751. [本文引用:1]
[49] WU J L, LONG K Y, WANG F, et al. Deep Comprehensive Correlation Mining for Image Clustering // Proc of the IEEE/CVF International Conference on Computer Vision. Washington, USA: IEEE, 2019: 8149-8158. [本文引用:1]
[50] WU Z R, XIONG Y J, YU S X, et al. Unsupervised Feature Learning via Non-parametric Instance Discrimination // Proc of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2018: 3733-3742. [本文引用:1]
[51] TAO Y L, TAKAGI K, NAKATA K. Clustering-Friendly Representation Learning via Instance Discrimination and Feature Decorrelation[C/OL]. [2022-07-15]. https://arxiv.org/pdf/2106.00131.pdf. [本文引用:1]
[52] TSAI T W, LI C X, ZHU J. Mice: Mixture of Contrastive Experts for Unsupervised Image Clustering[C/OL]. [2022-07-15]. https://arxiv.org/pdf/2105.01899.pdf. [本文引用:1]
[53] LI Y F, HU P, LIU Z T, et al. Contrastive Clustering. Procee-dings of the AAAI Conference on Artificial Intelligence, 2021, 35(10): 8547-8555. [本文引用:1]
[54] ZHONG H S, WU J L, CHEN C, et al. Graph Contrastive Clustering // Proc of the IEEE/CVF International Conference on Computer Vision. Washington, USA: IEEE, 2021: 9204-9213. [本文引用:1]
[55] ZHONG H S, CHEN C, JIN Z M, et al. Deep Robust Clustering by Contrastive Learning[C/OL]. [2022-07-15]. https://arxiv.org/pdf/2008.03030.pdf. [本文引用:1]
[56] GORI M, MONFARDINI G, SCARSELLI F. A New Model for Learning in Graph Domains // Proc of the IEEE International Joint Conference on Neural Networks. Washington, USA: IEEE, 2005: 729-734. [本文引用:1]
[57] BRUNA J, ZAREMBA W, SZLAM A, , et al. Spectral Networks. Spectral Networks and Deep Locally Connected Networks on Graphs[C/OL]. [2022-07-15]. https://arxiv.org/pdf/1312.6203.pdf. [本文引用:1]
[58] KIPF T N, WELLING M. Semi-Supervised Classification with Gra-ph Convolutional Networks[C/OL]. [2022-07-15]. https://arxiv.org/pdf/1609.02907.pdf. [本文引用:1]
[59] KIPF T N, WELLING M. Variational Graph Auto-Encoders[C/OL]. [2022-07-15]. https://arxiv.org/pdf/1611.07308.pdf. [本文引用:1]
[60] WANG C, PAN S R, HU R Q, et al. Attributed Graph Clustering: A Deep Attentional Embedding Approach // Proc of the 28th International Joint Conference on Artificial Intelligence. San Francisco, USA: IJCAI, 2019: 3670-3676. [本文引用:1]
[61] BO D Y, WANG X, SHI C, et al. Structural Deep Clustering Network // Proc of the World Wide Web Conference. New York, USA: ACM, 2020: 1400-1410. [本文引用:1]
[62] ZHANG H Y, LI P, ZHANG R, et al. Embedding Graph Auto-Encoder for Graph Clustering. IEEE Transactions on Neural Networks and Learning Systems, 2022. DOI: DOI:10.1109/TNNLS.2022.3158654. [本文引用:1]
[63] QI C, ZHANG J M, JIA H J, et al. Deep Face Clustering Using Residual Graph Convolutional Network. Knowledge-Based Systems, 2021. DOI: DOI:10.1016/j.knosys.2020.106561. [本文引用:1]
[64] BIANCHI F M, GRATTAROLA D, ALIPPI C. Spectral Clustering with Graph Neural Networks for Graph Pooling // Proc of the 37th International Conference on Machine Learning. San Diego, USA: JMLR, 2020: 874-883. [本文引用:1]
[65] TAO Z Q, LIU H F, LI J, et al. Adversarial Graph Embedding for Ensemble Clustering // Proc of the 28th International Joint Confe-rence on Artificial Intelligence. San Francisco, USA: IJCAI, 2019: 3562-3568. [本文引用:1]
[66] 杜航原, 张晶, 王文剑. 一种深度自监督聚类集成算法. 智能系统学报, 2020, 15(6): 1113-1120.
(DU H Y, ZHANG J, WANG W J. A Deep Self-Supervised Clustering Ensemble Algorithm. CAAI Transactions on Intelligent Systems, 2020, 15(6): 1113-1120. ) [本文引用:1]
[67] ALJALBOUT E, GOLKOV V, SIDDIQUI Y, et al. Clustering with Deep Learning: Taxonomy and New Methods[C/OL]. [2022-07-15]. https://arxiv.org/pdf/1801.07648.pdf. [本文引用:1]
[68] MIN E X, GUO X F, LIU Q, et al. A Survey of Clustering with Deep Learning: From the Perspective of Network Architecture. IEEE Access, 2018, 6: 39501-39514. [本文引用:1]
[69] ESTÉVEZ P A, TESMER M, PEREZ C A, et al. Normalized Mutual Information Feature Selection. IEEE Transactions on Neural Networks, 2009, 20(2): 189-201. [本文引用:1]
[70] 李悦. 基于聚类算法的吉林大学校园新闻推荐系统的设计与实现. 硕士学位论文. 长春: 吉林大学, 2017.
(LI Y. Design and Implementation of Campus News Recommendation System Based on Clustering Algorithm in Jilin University. Master Dissertation. Changchun, China: Jilin University, 2017. ) [本文引用:1]
[71] 李文杰, 薛花, 张德干. 一种融合时间因素的用户偏好和距离加权的聚类方法: CN109241203B. 2021-08-31.
(LI W J, XUE H, ZHANG D G. A User Preference and Distance Weighted Clustering Method Incorporating Time Factors: CN109241203B. 2021-08-31. [本文引用:1]
[72] 王振飞, 陈金磊, 郑志蕴, 等. 面向心血管疾病的自适应模块化神经网络预测模型. 小型微型计算机系统, 2019, 40(1): 232-235.
(WANG Z F, CHEN J L, ZHENG Z Y, et al. Adaptive Modula-rized Neural Network Prediction Model for Cardiovascular Disease. Journal of Chinese Computer Systems, 2019, 40(1): 232-235. ) [本文引用:1]
[73] 周峰. 基于神经网络模型的慢乙肝相关疾病患者聚类及医疗费用预测研究. 硕士学位论文. 广州: 广东药科大学, 2018.
(ZHOU F. Clustering of Hepatitis B Related Diseases and Prediction of Medical Expenditures Based on Neural Network Model. Master Dissertation. Guangzhou, China: Guangdong Pharmaceutical University, 2018. ) [本文引用:1]
[74] CHOWDHURY S, KHANZADEH M, AKULA R, et al. Botnet Detection Using Graph-Based Feature Clustering. Journal of Big Data, 2017, 4(1). DOI: DOI:10.1186/s40537-017-0074-7. [本文引用:1]
[75] EI-DIN Y S, MOUSTAFA M N, MAHDI H. Adversarial Unsupervised Domain Adaptation Guided with Deep Clustering for Face Presentation Attack Detection[C/OL]. [2022-07-15]. https://arxiv.org/pdf/2102.06864.pdf. [本文引用:1]