基于重构对比的广义零样本图像分类

引用本文

许睿, 邵帅, 曹维佳, 刘宝弟, 陶大鹏, 刘伟锋. 基于重构对比的广义零样本图像分类. 模式识别与人工智能, 2022,35(12): 1078-1088
XU Rui, SHAO Shuai, CAO Weijia, LIU Baodi, TAO Dapeng, LIU Weifeng. Generalized Zero-Shot Image Classification Based on Reconstruction Contrast. PATTERN RECOGNITION AND ARTIFICIAL INTELLIGENCE, 2022,35(12): 1078-1088. 复制到剪切板

Doi: 10.16451/j.cnki.issn1003-6059.202212003
Permissions

《模式识别与人工智能》编辑部

基于重构对比的广义零样本图像分类

许睿¹, 邵帅², 曹维佳³, 刘宝弟¹, 陶大鹏⁴, 刘伟锋¹

1.中国石油大学(华东) 控制科学与工程学院青岛 266580

2.之江实验室基础理论研究院杭州 311121

3.中国科学院空天信息创新研究院遥感卫星应用国家工程研究中心北京 100094

4.云南大学信息学院昆明 650500

通讯作者:

刘伟锋,博士,教授,主要研究方向为模式识别、机器学习.E-mail:liuwf@upc.edu.cn.

作者简介:

许睿,博士研究生,主要研究方向为小样本学习、零样本学习.E-mail:ruixu@s.upc.edu.cn.

邵帅,博士,主要研究方向为字典学习、小样本学习.E-mail:shaoshuai0914@gmail.com.

曹维佳,博士,助理研究员,主要研究方向为图像加密、图像压缩、图像分类.E-mail:caowj@aircas.ac.cn.

刘宝弟,博士,副教授,主要研究方向为计算机视觉、机器学习.E-mail:thu.liubaodi@gmail.com.

陶大鹏,博士,教授,主要研究方向为机器学习、计算机视觉、云计算.E-mail:dapeng.tao@gmail.com.

收稿日期: 2022-05-20 接受日期: 2022-11-21

资助项目: 国家自然科学基金项目(No.61671480)、中国石油天然气集团公司重大科技项目(No.ZD2019-183-008)、模式识别国家实验室开放项目(No.202000009)、中国石油大学项目(华东)研究生创新基金项目(No.YCX2021123)资助

摘要

广义零样本图像分类中常使用生成模型重构视觉信息或语义信息用于再进一步学习.然而,基于变分自编码器的方法对重构样本利用不够充分,表示性能欠缺.因此,文中提出基于重构对比的广义零样本图像分类模型.首先,使用两个变分自编码器将视觉信息和语义信息编码为同维度的低维隐向量,再将隐向量分别解码到两种模态.然后,使用投影模块投影视觉信息与语义模态的隐向量重构的视觉模态信息.最后,对投影后的特征进行重构对比学习.在保持变分自编码器重构性能的基础上增强编码器重构的判别性能,提高预训练特征在广义零样本图像分类任务上的应用能力.在4个标准数据集上的实验证实文中模型的有效性.

关键词: 广义零样本图像分类; 变分自编码器; 对比学习; 语义信息; 视觉信息

中图分类号:TP391;TP18

Generalized Zero-Shot Image Classification Based on Reconstruction Contrast

XU Rui¹, SHAO Shuai², CAO Weijia³, LIU Baodi¹, TAO Dapeng⁴, LIU Weifeng¹

1. College of Control Science and Engineering, China University of Petroleum(East China), Qingdao 266580

2. Research Institute of Basic Theories, Zhejiang Laboratory, Hangzhou 311121

3. National Engineering Research Center of Remote Sensing Satellite Applications, Aerospace Information Research Institute, Chinese Academy of Sciences, Beijing 100094

4. School of Information Science and Engineering, Yunnan University, Yunnan 650500

Corresponding author:
LIU Weifeng, Ph.D., professor. His research interests include pa-ttern recognition and machine learning.

About Author:
XU Rui, Ph.D. candidate. Her research interests include few-shot learning and zero-shot learning.
SHAO Shuai, Ph.D. His research inte-rests include dictionary learning and few-shot learning.
CAO Weijia, Ph.D. assistant professor. Her research interests include image encryption, image compression and image classification.
LIU Baodi, Ph.D., associate professor. His research interests include computer vision and machine learning.
TAO Dapeng, Ph.D., professor. His research interests include machine learning, computer vision and cloud computing.

Fund:National Natural Science Foundation of China(No.61671480), Major Scientific and Technological Projects of CNPC(No.ZD2019-183-008), Open Project of the National Laboratory of Pattern Recognition (NLPR)(No.202000009), Graduate Innovation Project of China University of Petroleum(East China)(No.YCX2021123)

Abstract

In generalized zero-shot image classification, generative models are often exploited to reconstruct visual or semantic information for further learning. However, the representation performance of the methods based on variational autoencoders is poor due to the underutilization of the reconstructed samples. Therefore, a generalized zero-shot image classification model based on reconstruction and contrastive learning is proposed. Firstly, two variational self-encoders are utilized to encode visual information and semantic information into low dimensional latent vectors of the same dimension, and then the latent vectors are decoded into two modes respectively. Next, the project modules are utilized to project both the original visual information and the visual information reconstructed from semantic modal latent vectors. Then, reconstruction contrastive learning is performed to learn the features after projection. The reconstruction performance of the encoder is maintained, the discriminative performance of the encoder is enhanced, and the application ability of pre-training features on the generalized zero-shot task is improved by the proposed method. The effectiveness of the proposed model is verified on four benchmark datasets.

Key words: Generalized Zero-Shot Image Classification; Variational Autoencoders; Contrastive Lear-ning; Semantic Information; Visual Information

文章图片

近些年, 随着深度学习的兴起, 基于深度学习的分类方法取得巨大突破.此类方法往往需要依赖大量的有标签数据.然而, 在很多真实场景中, 收集标签昂贵甚至不切实际.因此, 如何让深度模型可在没有标签或标签不足的条件下依然达到令人满意的精度, 受到学者们的广泛关注, 进而延伸出对应的零样本学习(Zero-Shot Learning, ZSL)和小样本学习(Few-Shot Learning, FSL).零样本图像分类亟待解决的问题为:如何通过可见类样本中的信息对不可见类样本进行分类, 其中可见类样本和不可见类样本没有交叉.为了让该任务更贴合实际应用, 研究者又提出广义零样本学习(Generalized ZSL, GZSL), 旨在同时对可见类样本和不可见类样本进行分类.

广义零样本图像分类任务中的样本主要包含两种模态信息:视觉模态信息和语义模态信息.视觉模态信息指图像特征表示; 语义模态信息指类别属性或类标签表示^[1], 可见类和不可见类具有共享的属性空间.在此任务中, 为了获得较好的视觉模态信息, 往往借助预训练模型(如ImageNet^[2])提取特征.当前大多数广义零样本图像分类方法首先学习视觉模态信息和语义模态信息之间的映射, 即从可见类中学习属性在图像特征中的通用表示, 然后以属性为纽带, 将共享知识迁移到对无标签样本的分类中.

根据模态映射形式的不同, 广义零样本图像分类方法主要包括4类.1)将视觉模态信息映射到语义模态^{[3, 4]}, 学习两个模态信息在语义空间上的关系; 2)将语义模态信息映射到视觉模态^{[5, 6, 7]}, 再在视觉模态空间学习; 3)将视觉模态信息和语义模态信息映射到共享子空间^{[8, 9]}, 再在子空间进行学习; 4)两个模态信息互相映射^[10], 即把两种模态信息都映射到另一个模态空间, 学习两个模态信息的对齐关系.

在这4类模型中, 1)、2)、4)类都包含将一种模态特征映射为另一模态信息的过程, 即重构图像或语义, 这些过程的本质是生成任务, 需要使用生成模型.在第3)类模态映射形式中虽然没有直接生成某种模态信息, 但是将某种模态信息映射到子空间, 同样可用生成模型实现.

综上所述, 基于生成模型的方法是零样本学习领域的一个重要研究方向.生成模型的主流方法有两种:变分自编码器(Variational Auto-encoder, VAE)^[11]和生成对抗网络(Generative Adversarial Network, GAN)^[12] .Xian等^[13]提出f-CLSWGAN, 使用不可见类的语义信息生成不可见类的图像, 用于扩充训练样本, 在扩充后的样本集上训练分类器, 提高模型对不可见类样本的分类性能.由于GAN容易产生模式崩溃问题^[14], VAE较稳定, 学者们提出一些基于条件变分自编码器的零样本学习算法, 如CVAE(Con-ditional Variational Autoencoders)^[15]、SE-GZSL(Syn-thesized Examples for GZSL)^[16]和Re-ViSE(Robust Semi-Supervised Visual-Semantic Embeddings)^[17].但是这些方法未关注模态对齐, 忽略不同模态信息尺度不同的问题.

为了更好地进行模态对齐, Schö nfeld等^[18]提出CADA-VAE(Cross and Distribution Aligned VAE), 通过分布对齐损失和交叉对齐损失, 学习跨模态共享的隐向量, 提升模型效果.然而在基于VAE的模型^{[14, 15, 16, 17, 18]}中, 通常仅使用约束距离实现各种对齐, 编码器重构的样本判别力仍存在不足.对比学习可缓解这一问题.对比学习通过构造相似实例和不相似实例, 即正例和负例, 习得一个表示学习模型^{[19, 20, 21]}.通过这个模型, 使相似的实例在投影空间中较接近, 而不相似的实例在投影空间中距离更远, 使模型学习到更有判别性的表示方法, 现已成为近年来的研究热点.Chen等^[19]提出SimCLR(A Simple Framework for Contrastive Learning of Visual Representations), 结合对比学习与数据增强, 提高模型的表示能力, 在无监督学习的实验中取得媲美有监督学习的结果.Han等^[20]提出CE-GZSL(Hybrid GZSL Framework with Contrastive Embedding), 结合GAN的生成模型, 提出带有对比嵌入的混合GZSL框架, 提升模型的分类准确率.上述模型都已证实对比学习的有效性.

在VAE的模型中, 重构样本可为对比学习提供大量的正例和负例.因此本文将对比学习引入VAE的广义零样本图像分类方法中, 并提出基于重构对比的广义零样本图像分类模型.此外, 在对比损失之间引入可学习的非线性映射, 大幅提高学习表示的质量, 学习更有用的表征.本文借鉴SimCLR在对比损失之间引入可学习的非线性投影模块的思想, 在预训练特征和语义信息生成特征的投影子空间特征之间构建正例和负例, 使模型学习更具有判别性的表示, 增强编码器的性能.在传统的标准数据集上, 在广义零样本和广义小样本图像分类设置下对本文模型进行广泛的实验评估, 验证模型的优越性.

1 基于重构对比的广义零样本图像分类模型

本文提出基于重构对比的广义零样本图像分类模型, 在预训练特征的投影和变分自编码器使用语义信息重构的视觉特征的投影之间引入对比学习, 其中投影模块提取两部分特征中更本质的表示.对比学习使投影特征之间判别性更强, 从而增强VAE

的编码性能, 充分挖掘预训练的视觉特征.

在零样本学习中, 定义训练集

D_tr= ${x_{i}^{(1)}, x_{i}^{(2)}, y_{i}}_{i = 1}^{N_{tr}}$ ∈C_s,

其中, $x_{i}^{(1)}$ 表示第i个样本的特征, y_i表示该样本对应的标签, $x_{i}^{(2)}$ 表示该样本对应的属性信息, C_s表示可见类, N_tr表示训练样本的个数.测试集

D_ts= ${x_{i}^{(1)}, x_{i}^{(2)}}_{i = 1}^{N_{ts}}$ ∈C_u,

其中:C_u表示不可见类, 它与可见类类别不同, 即

C_s∩ C_u=Ø ;

N_ts表示测试样本的个数.训练集和测试集样本不同, 即

D_tr∩ D_ts=Ø .

而在广义零样本图像分类中, 识别集中不仅包括不可见类, 同时也包括可见类, 即

D_ts= ${x_{i}^{(1)}, x_{i}^{(2)}}_{i = 1}^{N_{ts}}$ ∈[C_s∪ C_u].

本文的目标是根据训练集提供的信息, 预测测试集样本的标签.模型整体框架如图1所示.

	Figure Option View Download New Window
	图1 本文模型框架图Fig.1 Framework of the proposed model

模型的输入包含两种模态信息:视觉模态信息 $x_{i}^{(1)}$ 和语义模态信息 $x_{i}^{(2)}$ .视觉模态信息使用ImageNet^[2]预训练的ResNet-101^[22]提取原始图像特征, 语义模态信息是专家标注、原始图像相同类的属性.每个模态由一个独立的变分自编码器模块进行编码解码, 基于视觉模态的编码器模块E₁(·)和基于语义模态的编码器E₂(·)将不同维度的视觉特征和语义特征嵌入相同维度的低维空间.除了变分自编码器损失的约束, 模型还添加重构对比模块, 对齐两个模态信息, 并在低维空间训练一个分类器.

1.1 变分自编码器模块

变分自编码器能利用神经网络同时拟合生成模型和推断模型.推断模型是自编码器中的编码层, 生成模型是自编码器中的解码层.使用x表示原始数据特征, z表示编码器得到的隐向量.

变分推断的目的是找出隐向量上的真实条件概率分布p_θ(z|x).由于分布的相互作用性, 可使用变分下限最小化其距离, 找到最近的代理后验分布q_ϕ(z|x)以近似.变分自编码器的目标函数为:

L= $E_{q_{ϕ} (z | x)}$ [ln p_θ(x|z)]-D_KL(q_ϕ(z|x)‖p_θ(z)).(1)

其中:公式第1项表示经生成模型解码后数据与原始数据的差异, 为重构误差; 第2项表示推理模型q(z|x)和p(z)之间的KL散度, 度量两个分布之间的距离损失.先验的一个常见选择是多元标准高斯分布.设定编码器预测均值μ和方差σ ², 后验分布服从

q_ϕ(z|x)=N(μ, σ ²),

通过重参数化技巧^[23]生成一个隐向量z.

本文模型使用2个独立的变分自编码器, 视觉模态的变分自编码器对应图1中的编码器E₁和解码器D₁.编码器E₁把视觉模态信息映射到一个低维空间, 获得该模态的隐向量 $z_{i}^{(1)}$ .为了减少信息损失, 变分自编码器通过解码器D₁(·)将隐向量 $z_{i}^{(1)}$ 重构为原始数据.语义模态的变分自编码器对应图1中的编码器E₂和解码器D₂.

在图1中使用 $L_{VAE}^{1}$ 标注视觉模态变分自编码器的损失, $L_{VAE}^{2}$ 标注语义模态变分自编码器的损失, 根据式(1)得到视觉模态和语义模态的2个变分自编码器损失和:

$\begin{align} & {{\mathcal{L}}_{VAE}}=\sum\limits_{j}^{2}{{{\mathbb{E}}_{{{q}_{{{\phi }^{(j)}}}}(z_{i}^{(j)}\mid x_{i}^{(j)})}}}\left[ \log {{p}_{{{\theta }^{(j)}}}}\left( x_{i}^{^{(j)}}\mid z_{i}^{^{(j)}} \right) \right] \\ & \text{ }-\beta {{D}_{KL}}\left( {{q}_{{{\phi }^{^{(j)}}}}}\left( z_{i}^{^{(j)}}\mid x_{i}^{^{(j)}} \right)\|{{p}_{{{\theta }^{(j)}}}}(z_{i}^{^{(j)}}) \right) \\ \end{align}$ (2)

为了使变分自编码器学习跨模态的相似表示, 本文使用3部分损失对两种模态的对齐进行约束, 分别是分布对齐(Distribution-Alignment, DA)损失、交叉对齐(Cross-Alignment, CA)损失和重构特征对比损失.

分布对齐损失目的是对齐视觉和语义两个模态在公共的低维隐向量 $z_{i}^{(1)}$ 、 $z_{i}^{(2)}$ 的多元高斯分布, 本文模型用2-Wasserstein距离^[24]表示2个分布距离.由于编码器预测的对角线协方差矩阵为交换矩阵, 这个距离可简化为

L_DA=(‖μ⁽¹⁾-μ⁽²⁾‖ $_{2}^{2}$ +‖σ ⁽¹⁾-σ ⁽²⁾‖ $_{Frobenius}^{2})^{\frac{1}{2}}$ .(3)

交叉对齐损失目的是对齐跨模态重构的特征.在两个模态对齐的情况下, 使用另一模态的隐向量重构的特征应和当前模态的原始特征相似.使用变分自编码器模块使两个模态信息在编码后得到相同维度的隐向量 $z_{i}^{(1)}$ 、 $z_{i}^{(2)}$ .视觉模态的解码器D₁(·)对语义模态编码后的隐向量 $z_{i}^{(2)}$ 解码重构出和视觉模态预训练特征相同维度的特征D₁( $z_{i}^{(2)}$ ).语义模态的解码器D₂(·)对视觉模态编码后的隐向量 $z_{i}^{(1)}$ 解码重构出和语义模态特征相同维度的特征D₂( $z_{i}^{(1)}$ ).因此, 度量跨模态重构的特征和原始特征可得到交叉对齐损失:

$\begin{align} & {{\mathcal{L}}_{CA}}=\sum\limits_{m}^{2}{\sum\limits_{n\ne m}^{2}{{{\left\| x_{i}^{(m)}-{{D}_{m}}\left( {{E}_{n}}\left( x_{i}^{(n)} \right) \right) \right\|}_{1}}}} \\ & \text{ }=\sum\limits_{m}^{2}{\sum\limits_{n\ne m}^{2}{{{\left\| x_{i}^{(m)}-{{D}_{m}}\left( z_{i}^{(n)} \right) \right\|}_{1}}}} \\ & \text{ }=\mathcal{L}_{CA}^{1}\text{+}\mathcal{L}_{CA}^{2} \\ \end{align}$ (4)

其中, E₁(·)表示视觉模态的编码器, E₂(·)表示语义模态的编码器, D₁(·)表示视觉模态的解码器, D₂(·)表示语义模态的解码器, L_CA表示2个交叉对齐损失之和, $L_{CA}^{1}$ 表示视觉模态的预训练特征和语义信息重构的视觉特征之间的交叉对齐损失, $L_{CA}^{2}$ 表示语义模态的原始特征和视觉信息重构的语义特征之间的交叉对齐损失.因为视觉模态和语义模态被认为是同等重要的, 因此 $L_{CA}^{1}$ 和 $L_{CA}^{2}$ 的权重系数相同.

重构特征对比损失计算视觉模态预训练特征和属性信息重构的视觉特征同类样本投影后的对比学习损失.跨模态重构的特征是真实视觉特征增强后的特征, 对于真实视觉特征和增强特征, 可建立一个分类子问题区分唯一的一个正例 $x_{i}^{(1)}$ 和全部的负例, 正例 $x_{i}^{(1)}$ 与D₁(E₂( $x_{i}^{(2)}$ ))具有相同的类标签, 而负例的类标签与 $x_{i}^{(1)}$ 的类标签不同.

遵循SimCLR^[19]的策略, 在投影空间中添加一个非线性投影模块H(·), 对视觉样本 $x_{i}^{(1)}$ 的嵌入记为

h_i=H( $x_{i}^{(1)}$ ),

对于对应的增强样本的嵌入记为

$h_{i}^{+}$ =H(D₁(E₂( $x_{i}^{(2)}$ ))).

具体来说, 对于1个正例和K个负例, K+1分类问题的交叉熵损失计算如下:

${{\ell }_{c}}\left( {{h}_{i}}, {{h}^{+}} \right)=-\log \frac{\exp \left( h_{i}^{\top }{{h}^{+}}/\tau \right)}{\exp \left( h_{i}^{\top }{{h}^{+}}/\tau \right)+\sum\limits_{k=1}^{K}{\exp }\left( h_{i}^{\top }h_{k}^{-}/\tau \right)} $ (5)

其中, τ > 0表示对比嵌入的温度参数, $h_{k}^{-}$ 表示负例, K表示负例数.通常大量的负例能使模型捕获同类样本中真实样本和重构样本共享的强判别信息和结构.

在这一过程中编码器D₁(·)、解码器E₂(·)直接参与生成语义模态重构的视觉特征D₁(E₂( $x_{i}^{(2)}$ )).非线性投影模块H(·)将视觉模态预训练特征和属性信息重构的视觉特征投影到一个低维共享空间.因此重构特征对比损失只与D₁(·)、E₂(·)和H(·)相关.计算的损失函数为

L_C(D₁, E₂, H)= $E_{h_{i}, h +}$ [L_c(h_i, h⁺)].(6)

结合变分自编码器模块和重构对比模块, 结合式(2)~式(4)和式(6), 整个模型的损失函数如下:

L=L_VAE+γ L_CA+δL_DA+λL_C, (7)

其中, γ 表示分布对齐损失L_CA的权重因子, δ表示交叉对齐损失L_DA的权重因子, λ表示重构特征对比损失L_C的权重因子.

2 实验及结果分析

2.1 实验环境

本节在Caltech-USCD Birds-200-2011(CUB)^[25]、SUN Attribute(SUN)^[26]、Animals with Attributes 2(AWA2)^[27] 、Attribute Pascal and Yahoo (APY)^[28]这4个广泛应用的标准数据集上进行实验.所有数据集都为每个样本提供对应的属性信息(即a_i).本文按照标准划分^[27]将数据集划分成可见类样本和不可见类样本.具体来说:CUB数据集包含150个可见类样本与50个不可见类样本; SUN数据集包含645个可见类样本与72个不可见类样本; AWA2数据集包含40个可见类样本与10个不可见类样本; APY数据集包含12个可见类样本与20个不可见类样本.在广义零样本图像分类和广义小样本图像分类中, 训练集只包含可见类样本, 测试集包含可见类样本与不可见类样本.实验数据集详细信息如表1所示.

表1 实验数据集 Table 1 Experimental datasets

通常使用ImageNet预训练的ResNet-101^[22]提取视觉模态特征x_i, 输出的特征维度为2 048.输出后的特征会被送入变分自编码器中进行编码.模型中所有的编码器和解码器都是具有一个隐藏层的多层感知器.语义模态特征编码器使用1 560个隐藏单元, 解码器使用1 660个隐藏单元.语义模态特征编码器使用1 450个隐藏单元, 解码器使用660个隐藏单元.隐向量 $z_{i}^{1}$ 、 $z_{i}^{2}$ 的维度为64.重构特征对比损失的投影模块H(·)的输入维数设置为2 048, 输出为512维.根据隐藏单元数和投影模块输出维数可得, 基线方法CVDA-VAE^[18]的计算复杂度为8.3 MB, 加上重构对比模块, 计算复杂度为13.3 MB.

本文模型批量大小设置为50, 使用Adam(Ada-ptive Moment Estimation)优化器.其它参数参考CADA-VAE的实验设置.所有的实验在32 GB内存的Tesla-V100GPU上执行.

遵循文献[27]中提出的评估策略, 在广义零样本图像分类情景下, 分别评估可见类样本和未可见类样本的top1精度, 分别表示为S和U.广义零样本图像分类的性能通过调和平均值

H= $\frac{2 SU}{S + U}$

衡量, 相比U和S, H为更重要的度量标准, 在U和S精度最平衡时H达到最大.

2.2 对比模型

本文选择如下15种相关模型进行对比实验:DeViSE(Deep Visual-Semantic Embedding Model)^[5]、文献[7]模型、PREN(Progressive Ensemble Net-works)^[8]、f-CLSWGAN^[13] 、CVAE^[15]、SE-GZSL^[16]、Re-ViSE^[17]、CADA-VAE^[18]、SJE(Structured Joint Embe-dding)^[29]、SP-AEN(Semantics-Preserving Adversarial Embedding Networks)^[30]、Cycle-CLSWGAN^[31]、ALE(Attribute Label Embedding)^[32] 、ESZSL(Embarra-ssingly Simple ZSL)^[33]、文献[34]模型、文献[35]模型.

上述模型在不同的角度上增强广义零样本和广义小样本的分类性能, 其中:CVAE、SE-GZSL、f-CL-SWGAN利用数据增强的方式; DeViSE、SJE、ALE、ESZSL引入线性函数或其它相似度量的方法, 增强视觉与语义特征之间的交互; PREN使用一个集成网络; 文献[7]模型利用多模态的思想, 引入多个神经网络学习非线性嵌入; SP-AEN引入独立的视觉-语义空间嵌入, 防止语义损失; Cycle-CLSWGAN将循环一致性引入基于GAN的零样本模型; 文献[34]模型对齐类嵌入空间和加权二分图; ReViSE使用自动编码器学习图像特征和类属性之间共享的潜在流形; 文献[35]模型提出三元组损失, 并应用在零样本学习模型中; CADA-VAE使用编码器将两个模态特征映射到同一个低维空间, 学习共享跨模态的隐向量.

2.3 实验结果对比

各模型在广义零样本图像分类和广义小样本图像分类上的性能对比如表2所示, 表中黑体数字表示最优值.

表2 各模型在4个数据集上的分类性能对比 Table 2 Classification performance comparison of different models on 4 datasets %

由表2可见, 本文模型首先与基线方法CADA-VAE对比, 在SUN、CUB数据集上, 本文模型在不可见类上的精度与CADA-VAE持平, 在S和H指标上都高于CADA-VAE.在AWA2数据集上, 本文模型在所有指标上都远高于CADA-VAE.在APY数据集上, 本文模型在U和H指标上高于CADA-VAE, 但在S指标上低于CADA-VAE.

值得注意的是, 在S指标上本文模型的表现无法达到最高值, 这是因为可见类和不可见类的类别不重叠, 存在域差异, 模型在适应不可见类的分类时往往会降低对可见类的性能.

再对比其它模型, 尽管在可见类和不可见类单项的分类精度上, 本文模型有时不如其它模型, 但在最重要的H指标上, 却高于其它模型.

H指标的提升从一定程度上反映本文模型的有效性, 这些结果也表明基于重构对比的广义零样本模型具有竞争力.

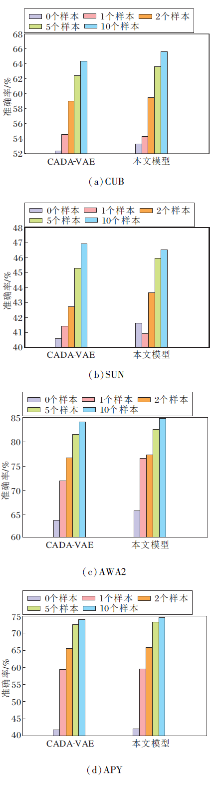
为了进一步验证本文模型的有效性, 在广义小样本图像分类的0个、1个、2个、5个和10个样本分类任务中与CVDA-VAE进行对比, 结果如图2所示.由图可知, 除了在少数的情况下, 相比CADA-VAE, 本文模型会产生一些波动, 在其它的所有设置中, 本文模型都优于CVDA-VAE.该现象表明本文模型在同等监督样本条件下, 精度高于CADA-VAE.需要注意的是, 本文的广义小样本图像分类和传统小样本学习以任务为单位的学习设置不同.传统小样本学习的任务通常对5个类进行分类, 本文是在广义零样本图像分类的框架下对数据集所有测试类别进行分类, 这个类别数通常远大于5.

	Figure Option View Download New Window
	图2 本文模型和CADA-VAE在广义小样本图像分类中的性能对比Fig.2 Performance comparison of generalized FSL between the proposed model and CVDA-VAE models

2.4 实验结果可视化

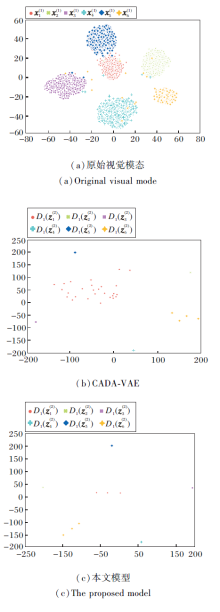
本文模型与CVDA-VAE在AWA2数据集上6个类别样本的t-SNE(t-Distributed Stochastic Neighbor Embedding)投影的可视化结果如图3所示.

	Figure Option View Download New Window
	图3 本文模型和CADA-VAE的t-SNE可视化结果Fig.3 t-SNE visualization result of the proposed model and CADA-VAE

图3(a)表示图1中预训练的特征提取器提取的原始视觉模态的特征 $x_{i}^{(1)}$ 的可视化结果, (b)、(c)分别表示CVDA-VAE和本文模型下属性重构的视觉模态特征D₁(E₂( $x_{i}^{(2)}$ )), 即D₁( $z_{i}^{(2)}$ )的可视化结果.

由图3(a)可看出, 经过预训练模型提取的特征分为6簇, 大部分样本可聚类到正确类别, 少部分样本会聚类到错误的其它类别.通过对比(b)和(c)可看出, 本文模型在 $x_{1}^{(1)}$ 和 $x_{6}^{(1)}$ 对应的类上表现明显变好, 让样本聚类到更集中的区域, D₁( $z_{1}^{(2)}$ )对应第1类从27个点变成3个点, D₁( $z_{6}^{(2)}$ )对应第1类从4个点变成3个点.在其余4个类上无明显区别.

总之, 相比CADA-VAE, 本文模型的样本聚类效果更优, 类内距离更小, 类间距离更大, 说明本文模型可提高编解码器的性能, 增强属性重构的视觉模态特征D₁( $z_{i}^{(2)}$ )的判别性, 提高学习表示的质量.

2.5 消融实验结果

本节进行消融实验, 对比CADA-VAE、删除投影模块的本文模型、包含投影模块的本文模型.各模型在4个数据集上的准确率对比如表3所示.

表3 投影模块的消融实验结果 Table 3 Ablation experiment results of projection module %

由表3可看出, 在4个数据集上, 包含投影模块的效果都优于不使用投影模块.不使用投影模块, 在CUB、SUN、AWA2数据集上本文模型的性能都优于CADA-VAE, 在APY数据集上有所下降.但是投影模块可修正在APY数据集上产生的下降, 甚至比CADA-VAE提升0.2%.因此投影模块对提高模型性能至关重要.

2.6 参数敏感性分析

通过1.2节的描述可知, 式(7)中3个权重因子γ 、δ和λ可影响模型性能, 因此设置

γ =2.5e^-1, 5e^-1, 1, 2, 4;

δ=2.5e-^1,5e-¹^,1, 2, 4;

λ=1, 5, 10, 15, 20.

对比实验结果如图4所示.

	Figure Option View Download New Window
	图4 参数敏感性分析Fig.4 Parameter sensitivity analysis

由图4(a)可看出, 随着γ 的增大, 模型性能先提升后缓慢下降, 在γ =1时可得到最优值.这说明交叉对齐损失对模型整体效果有所提升, 但对参数值相对不敏感.

由图4(b)可看出, 随着δ的增大, 模型性能先提升后迅速下降, 在δ=1时得到最优值.这说明分布对齐损失对参数非常敏感, 尤其在参数增大时会导致模型性能急剧下降.

由图4(c)可知, 并不是所有的权重都能提升模型性能, 权重的选择非常重要.在CUB数据集上, 性能上下波动, λ=1时获得最优值.在SUN数据集上, 性能有一个峰值, λ=15时获得最优值.在AWA2数据集上, λ=10时获得最优值.

在最优值附近本文都使用更小的间隔1测试模型性能, 在CUB数据集上, 在λ=1附近进行细调, 在λ=2时得到表2中53.3%的最优值, 在SUN、AWA2数据集上, 最优值附近无法得到更优结果.在APY数据集上, λ=5时可得到最优值.虽然在图4(c)中可能会得到差于CADA-VAE的结果, 但是在较大的参数范围内都可实现性能提升, 由此表明本文模型的鲁棒性.

由图4可看出, 本文模型对权重因子λ最不敏感, 对权重因子γ 略微敏感, 对权重因子δ相对敏感.产生这种现象的原因是, 视觉信息包含类别信息和一些和类别无关的信息, 语义信息只包含类别信息.当权重因子δ变大时, 模型会更多地约束两种模态信息的低维隐向量 $z_{i}^{(1)}$ 、 $z_{i}^{(2)}$ 之间的对齐, 导致视觉信息中一些和类别无关的信息和语义信息进行对齐, 而这些类别无关的信息对于下游的分类任务会产生负面影响.此外, 交叉对齐损失和重构特征对比损失都需要使用隐向量 $z_{i}^{(1)}$ 、 $z_{i}^{(2)}$ 解码的特征进行计算, 隐向量表示性能不佳也会导致解码的特征变差, 影响交叉对齐损失和重构特征对比损失的作用.而交叉对齐损失和重构特征对比损失对分布对齐影响有限, 因此导致模型变差的影响也有限, 权重因子λ和权重因子γ 大小相对不敏感.

3 结束语

广义零样本大多考虑使用度量表示视觉信息和语义信息映射的效果, 很少使用对比学习约束双模态信息的映射, 本文提出基于重构对比的广义零样本图像分类模型, 将对比学习应用在预训练特征的投影和语义信息重构的视觉特征的低维投影特征之间.投影模块过滤语义模态和视觉模态中互不相关的噪声信息, 提取更本质的信息作为对比学习的输入.对比学习在保证变分自编码器本身重构性能的基础上提升编码器提取特征的判别性能.因此本文模型可较好地适用于广义零样本任务, 并在4个中等规模标准数据集上得到比CADA-VAE更高的准确率, 以及在广义小样本图像分类任务大部分设置中获得性能的改善.尽管本文模型获得比基线方法更具竞争力的效果, 但未同适用于视觉和语义特征提取的模型Transformer结合, 今后将进一步研究和Transformer结合的方法, 获得更好的信息表示, 提高模型性能.

本文责任编委陶卿

Recommended by Associate Editor TAO Qing

参考文献

文献选项

[1]	冯耀功, 于剑, 桑基韬, 等. 基于知识的零样本视觉识别综述. 软件学报, 2021, 32(2): 370-405. (FENG Y G, YU J, SANG J T, et al. Survey on Knowledge-Based Zero-Shot Visual Recognition. Journal of Software, 2021, 32(2): 370-405. ) [本文引用:1]
[2]	DENG J, DONG W, SOCHER R, et al. ImageNet: A Large-Scale Hierarchical Image Database // Proc of the IEEE Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2009: 248-255. [本文引用:2]
[3]	LI Y, ZHANG J G, ZHANG J G, et al. Discriminative Learning of Latent Features for Zero-Shot Recognition // Proc of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2018: 7463-7471. [本文引用:1]
[4]	YU F X, CAO L L, FERIS R S, et al. Designing Category-Level Attributes for Discriminative Visual Recognition // Proc of the IEEE Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2013: 771-778. [本文引用:1]
[5]	FROME A, CORRADO G S, SHLENS J, et al. DeViSE: A Deep Visual-Semantic Embedding Model // Proc of the 26th International Conference on Neural Information Processing Systems. Cambridge, USA: MIT Press, 2013: 2121-2129. [本文引用:2]
[6]	KODIROV E, XIANG T, FU Z Y, et al. Unsupervised Domain Adap-tation for Zero-Shot Learning // Proc of the IEEE International Conference on Computer Vision. Washington, USA: IEEE, 2015: 2452-2460. [本文引用:1]
[7]	ZHANG L, XIANG T, GONG S G. Learning a Deep Embedding Model for Zero-Shot Learning // Proc of the IEEE Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2017: 3010-3019. [本文引用:3]
[8]	YE M, GUO Y H. Progressive Ensemble Networks for Zero-Shot Recognition // Proc of the IEEE Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2019: 11728-11736. [本文引用:2]
[9]	钟小容, 胡晓, 丁嘉昱. 基于潜层向量对齐的持续零样本学习算法. 模式识别与人工智能, 2021, 34(12): 1152-1159. (ZHONG X R, HU X, DING J Y. Continual Zero-Shot Learning Algorithm Based on Latent Vectors Alignment. Pattern Recognition and Artificial Intelligence, 2021, 34(12): 1152-1159. ) [本文引用:1]
[10]	WANG W L, PU Y C, VERMA V K, et al. Zero-Shot Learning via Class-Conditioned Deep Generative Models // Proc of the 32nd AAAI Conference on Artificial Intelligence and 30th Innovative Applications of Artificial Intelligence Conference and 8th AAAI Symposium on Educational Advances in Artificial Intelligence. Palo Alto, USA: AAAI, 2018: 4211-4218. [本文引用:1]
[11]	KINGMA D P, WELLING M. Auto-Encoding Variational Bayes[C/OL]. [2022-04-20]. https://arxiv.org/pdf/1312.6114.pdf. [本文引用:1]
[12]	GOODFELLOW I J, POUGET-ABADIE J, MIRZA M, et al. Gene-rative Adversarial Nets // Proc of the 27th International Conference on Neural Information Processing Systems. Cambridge, USA: MIT Press, 2014: 2672-2680. [本文引用:1]
[13]	XIAN Y Q, LORENZ T, SCHIELE B, et al. Feature Generating Networks for Zero-Shot Learning // Proc of the IEEE/CVF Confe-rence on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2018: 5542-5551. [本文引用:2]
[14]	ARJOVSKY M, BOTTOU L. Towards Principled Methods for Trai-ning Generative Adversarial Networks[C/OL]. [2022-04-20]. https://arxiv.org/pdf/1701.04862.pdf. [本文引用:2]
[15]	MISHRA A, REDDY S K, MITTAL A, et al. A Generative Model for Zero Shot Learning Using Conditional Variational Autoencoders // Proc of the IEEE/CVF Conference on Computer Vision and Pa-ttern Recognition Workshops. Washington, USA: IEEE, 2018: 2269-2277. [本文引用:3]
[16]	VERMA V K, ARORA G, MISHRA A, et al. Generalized Zero-Shot Learning via Synthesized Examples // Proc of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2018: 4281-4289. [本文引用:3]
[17]	TSAI Y H H, HUANG L K, SALAKHUTDINOV R. Learning Robust Visual-Semantic Embeddings // Proc of the IEEE Internatio-nal Conference on Computer Vision. Washington, USA: IEEE, 2017: 3591-3600. [本文引用:3]
[18]	SCHÖNFELD E, EBRAHIMI S, SINHA S, et al. Generalized Zero-and Few-Shot Learning via Aligned Variational Autoencoders // Proc of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2019: 8239-8247. [本文引用:4]
[19]	CHEN T, KORNBLITH S, NOROUZI M, et al. A Simple Framework for Contrastive Learning of Visual Representations // Proc of the 37th International Conference on Machine Learning. San Diego, USA: JMLR, 2020: 1597-1607. [本文引用:3]
[20]	HAN Z Y, FU Z Y, CHEN S, et al. Contrastive Embedding for Generalized Zero-Shot Learning // Proc of the IEEE/CVF Confe-rence on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2021: 2371-2381. [本文引用:2]
[21]	HE K M, FAN H Q, WU Y X, et al. Momentum Contrast for Unsupervised Visual Representation Learning // Proc of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2020: 9726-9735. [本文引用:1]
[22]	HE K M, ZHANG X Y, REN S Q, et al. Deep Residual Learning for Image Recognition // Proc of the IEEE Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2016: 770-778. [本文引用:2]
[23]	HIGGINS I, MATTHEY L, PAL A, et al. β -VAE: Learning Ba-sic Visual Concepts with a Constrained Variational Framework[C/OL]. [2022-04-20]. https://openreview.net/pdf?id=Sy2fzU9gl. [本文引用:1]
[24]	GIVERS C R, SHORTT R M. A Class of Wasserstein Metrics for Probability Distributions. Michigan Mathematical Journal, 1984, 31(2): 231-240. [本文引用:1]
[25]	WAH C, BRANSON S, WELINDER P, et al. The Caltech-UCSD Birds-200-2011 Dataset[DB/OL]. [2022-04-20]. https://authors.library.caltech.edu/27452/1/CUB_200_2011.pdf. [本文引用:1]
[26]	PATTERSON G, HAYS J. Sun Attribute Database: Discovering, Annotating, and Recognizing Scene Attributes // Proc of the IEEE Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2012: 2751-2758. [本文引用:1]
[27]	XIAN Y Q, LAMPERT C H, SCHIELE B, et al. Zero-Shot Lear-ning-A Comprehensive Evaluation of the Good, the Bad and the Ugly. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2019, 41(9): 2251-2265. [本文引用:3]
[28]	FARHADI A, ENDRES I, HOIEM D, et al. Describing Objects by Their Attributes // Proc of the IEEE Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2009: 1778-1785. [本文引用:1]
[29]	AKATA Z, REED S, WALTER D, et al. Evaluation of Output Embeddings for Fine-Grained Image Classification // Proc of the IEEE Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2015: 2927-2936. [本文引用:1]
[30]	CHEN L, ZHANG H W, XIAO J, et al. Zero-Shot Visual Recognition Using Semantics-Preserving Adversarial Embedding Networks // Proc of the IEEE/CVF Conference on Computer Vision and Pa-ttern Recognition. Washington, USA: IEEE, 2018: 1043-1052. [本文引用:1]
[31]	FELIX R, KUMAR V B G, REID I, et al. Multi-modal Cycle-Consistent Generalized Zero-Shot Learning // Proc of the 15th European Conference on Computer Vision. Berlin, Germany: Sprin-ger, 2018: 21-37. [本文引用:1]
[32]	AKATA Z, PERRONNIN F, HARCHAOUI Z, et al. Label-Embedding for Image Classification. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2016, 38(7): 1425-1438. [本文引用:1]
[33]	ROMERA-PAREDES B, TORR P H S. An Embarrassingly Simple Approach to Zero-Shot Learning // Proc of the 32nd International Conference on Machine Learning. San Diego, USA: JMLR, 2015: 2152-2161. [本文引用:1]
[34]	CHANGPINYO S, CHAO W L, GONG B Q, et al. Synthesized Classifiers for Zero-Shot Learning // Proc of the IEEE Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2016: 5327-5336. [本文引用:2]
[35]	LE CACHEUX Y, LE BORGNE H, CRUCIANU M. Modeling Inter and Intra-Class Relations in the Triplet Loss for Zero-Shot Learning // Proc of the IEEE/CVF International Conference on Computer Vision. Washington, USA: IEEE, 2019: 10332-10341. [本文引用:2]

2021

0.0

... 语义模态信息指类别属性或类标签表示^[1],可见类和不可见类具有共享的属性空间 ...

2009

0.0

... 在此任务中,为了获得较好的视觉模态信息,往往借助预训练模型(如ImageNet^[2])提取特征 ...

... 视觉模态信息使用ImageNet^[2]预训练的ResNet-101^[22]提取原始图像特征,语义模态信息是专家标注、原始图像相同类的属性 ...

2018

0.0

... 1)将视觉模态信息映射到语义模态^[3,4],学习两个模态信息在语义空间上的关系 ...

2013

0.0

... 1)将视觉模态信息映射到语义模态^[3,4],学习两个模态信息在语义空间上的关系 ...

2013

0.0

... 2)将语义模态信息映射到视觉模态^[5,6,7],再在视觉模态空间学习 ...

... 2 对比模型本文选择如下15种相关模型进行对比实验:DeViSE(Deep Visual-Semantic Embedding Model)^[5]、文献[7]模型、PREN(Progressive Ensemble Net-works)^[8]、f-CLSWGAN^[13] 、CVAE^[15]、SE-GZSL^[16]、Re-ViSE^[17]、CADA-VAE^[18]、SJE(Structured Joint Embe-dding)^[29]、SP-AEN(Semantics-Preserving Adversarial Embedding Networks)^[30]、Cycle-CLSWGAN^[31]、ALE(Attribute Label Embedding)^[32] 、ESZSL(Embarra-ssingly Simple ZSL)^[33]、文献[34]模型、文献[35]模型 ...

2015

0.0

... 2)将语义模态信息映射到视觉模态^[5,6,7],再在视觉模态空间学习 ...

2017

0.0

... 2)将语义模态信息映射到视觉模态^[5,6,7],再在视觉模态空间学习 ...

... 文献[7]模型利用多模态的思想,引入多个神经网络学习非线性嵌入 ...

2019

0.0

... 3)将视觉模态信息和语义模态信息映射到共享子空间^[8,9],再在子空间进行学习 ...

2021

0.0

... 3)将视觉模态信息和语义模态信息映射到共享子空间^[8,9],再在子空间进行学习 ...

2018

0.0

... 4)两个模态信息互相映射^[10],即把两种模态信息都映射到另一个模态空间,学习两个模态信息的对齐关系 ...

0.0

... 生成模型的主流方法有两种:变分自编码器(Variational Auto-encoder, VAE)^[11]和生成对抗网络(Generative Adversarial Network, GAN)^[12] ...

2014

0.0

... 生成模型的主流方法有两种:变分自编码器(Variational Auto-encoder, VAE)^[11]和生成对抗网络(Generative Adversarial Network, GAN)^[12] ...

2018

0.0

... Xian等^[13]提出f-CLSWGAN,使用不可见类的语义信息生成不可见类的图像,用于扩充训练样本,在扩充后的样本集上训练分类器,提高模型对不可见类样本的分类性能 ...

0.0

... 由于GAN容易产生模式崩溃问题^[14],VAE较稳定,学者们提出一些基于条件变分自编码器的零样本学习算法,如CVAE(Con-ditional Variational Autoencoders)^[15]、SE-GZSL(Syn-thesized Examples for GZSL)^[16]和Re-ViSE(Robust Semi-Supervised Visual-Semantic Embeddings)^[17] ...