引用本文
张大宝, 赵建伟, 周正华. 基于 l1诱导轻量级深度网络的图像超分辨率重建 . 模式识别与人工智能, 2022,35(12): 1101-1121
ZHANG Dabao, ZHAO Jianwei, ZHOU Zhenghua. Image Super-Resolution Reconstruction Based on l1 Induced Lightweight Deep Networks . PATTERN RECOGNITION AND ARTIFICIAL INTELLIGENCE, 2022,35(12): 1101-1121.  
Doi: 10.16451/j.cnki.issn1003-6059.202212005
Permissions
Copyright©2022, 《模式识别与人工智能》编辑部
《模式识别与人工智能》编辑部
基于 l1诱导轻量级深度网络的图像超分辨率重建
张大宝1, 赵建伟1,2, 周正华1
1.中国计量大学 理学院 杭州 310018
2.中国计量大学 信息工程学院 浙江省电磁波信息技术与计量检测重点实验室 杭州 310018
通讯作者:

赵建伟,博士,教授,主要研究方向为深度学习、图像处理等.E-mail:zhaojw@amss.ac.cn.

作者简介:

张大宝,硕士研究生,主要研究方向为深度学习、图像处理等.E-mail:2569049998@qq.com.

周正华,博士,副教授,主要研究方向为深度学习、图像处理等.E-mail:zzhzjw2003@163.com.

收稿日期: 2022-10-08 接受日期: 2022-12-30
资助项目: 浙江省自然科学基金项目(No.LY22F020002,LSY19F020001)资助
摘要

现有的基于深度学习的超分辨率重建方法主要通过加深网络以提高网络的重建性能,但是加深网络会导致网络权值数量急剧增加,给网络训练和存储带来巨大负担.考虑到噪声的稀疏性、网络训练的成本及重建图像边缘的清晰度,文中融合模型驱动与数据驱动的思想,提出基于 l1诱导轻量级深度网络的图像超分辨率重建方法.先利用分裂Bregman算法和软阈值算子,构建边缘正则的 l1重建模型,并推演有效的迭代算法.再在迭代算法的指导下,设计相应的递归深度网络进行图像重建.因此,文中网络是在优化模型指导下设计的,推导出的递归结构由于其权值共享的特性,可减少网络权值的数量.实验表明,文中方法在网络权值数量较少时,仍能取得较优的图像重建性能.

关键词: 超分辨率重建; 深度学习; 轻量级网络; 模型驱动; 数据驱动
中图分类号:TP391
Image Super-Resolution Reconstruction Based on l1 Induced Lightweight Deep Networks
ZHANG Dabao1, ZHAO Jianwei1,2, ZHOU Zhenghua1
1. College of Sciences, China Jiliang University, Hangzhou 310018
2. Key Laboratory of Electromagnetic Wave Information Technology and Metrology of Zhejiang Province, College of Information Engineering, China Jiliang University, Hangzhou 310018
Corresponding author:
ZHAO Jianwei, Ph.D., professor. Her research interests include deep learning and image processing.

About Author:
ZHANG Dabao, master student. His research interests include deep learning and image processing.
ZHOU Zhenghua, Ph.D., associate professor. His research interests include deep learning and image processing.

Fund:Natural Science Foundation of Zhejiang Province(No.LY22F020002,LSY19F020001)
Abstract

Existing deep-learning based super-resolution reconstruction methods improve the reconstruction performance of networks by deepening networks. However, sharp increase of the number of network weights is caused by deepening networks, resulting in a huge burden for the storage and training network. With the consideration of the sparsity of noise, the cost of training network and the sharpness of reconstructed edges, an image super-resolution reconstruction is proposed based on l1 induced lightweight deep networks integrating with the idea of model-driven and data-driven. Firstly, the split Bregman algorithm and soft threshold operator are utilized to deduce an effective iterative algorithm from the l1 reconstruction optimization model with an edge regularization term. Secondly, a corresponding recursive deep network is designed for image reconstruction under the guidance of the iterative algorithm. Therefore, the proposed deep network is designed under the guidance of the reconstruction optimization model, and its derived recursive structure reduces the number of network weights due to its property of weight sharing. Experimental results show that the proposed method achieves good reconstruction performance with less number of network weights.

Key words: Super-Resolution Reconstruction; Deep Learning; Lightweight Network; Model Driven; Data Driven

图像超分辨率(Super-Resolution, SR)在航空影像[1]和医疗成像[2]等领域被广泛应用, 主要原理是从观测到的一幅或多幅低分辨率(Low Resolution, LR)图像重建高分辨率(High Resolution, HR)图像.一般地, 图像的退化模型可表示为

y=Ax+n, (1)

其中, y表示观测到的低分辨率图像, A表示退化操作, x表示未知的高分辨率图像, n表示加性噪声.显然, 从退化后的低分辨率图像y中恢复高分辨率图像x是个不适定问题.

关于上述不适定问题, 学者们提出许多高效的超分辨率重建方法, 主要分为基于插值的方法[3]、基于重建的方法[4]和基于学习的方法[5].特别地, 随着深度学习的快速发展和应用, 基于深度学习的超分辨率重建方法得到学者的关注.该类方法主要利用深度网络拟合低分辨率图像到高分辨率图像之间的映射关系.Dong等[6, 7]将深度卷积网络引入图像超分辨率重建中, 先后提出SRCNN(Super-Reso-lution Convolutional Neural Network)和FSRCNN(Fast Super-Resolution Convolutional Neural Net-work).

在此基础上, 学者们提出许多基于深度网络的图像超分辨率重建方法.Shi等[8]引入有效的亚像素卷积, 提出ESPCN(Efficient Sub-Pixel Convo-lutional Neural Network).为了提高深度网络的重建性能, Kim等[9]利用残差连接将网络深度加深到20层, 提出VDSR.Lai等[10]利用逐级放大的思想, 提出LapSRN(Laplacian Pyramid Super-Resolution Network).Zhang等[11]利用残差连接和关注机制, 提出RCAN(Very Deep Residual Channel Attention Networks).Zhang等[12]提出RDN(Residual Dense Network), 利用残差连接和密集连接的思想, 提取丰富的局部特征和全局特征.Li等[13]结合多尺度特征融合和局部残差学习, 提出MSRN(Multi-scale Residual Network).Zhang等[14, 15, 16]将物理学中的流体力学、热传导理论和曲率一致应用到芯片和自然图像的超分辨率重建中.

上述超分辨率重建方法主要通过不断构造更深、更复杂的深度网络以提高网络重建性能, 但是网络的加深会导致网络权值数量的急剧增加, 给网络训练和存储带来巨大负担.因此, 学者们开始探讨轻量级深度网络模型的设计.为了减少网络的权值数量并尽量保持网络的重建性能, Kim等[17]基于递归权值共享的思想, 提出DRCN(Deeply Recursive Convolutional Network), 大幅减少网络的权值数量.在此基础上, Tai等[18]结合残差连接, 提出DRRN(Deep Recursive Residual Network).

尽管基于递归的权值共享可减少深度网络的权值数量, 但该类网络的递归模块是人为设计的, 没有在专家先验知识的指导下进行网络设计.Reichstein等[19]指出融合模型驱动与数据驱动是未来研究系统科学问题的主流方向之一.因此, 学者们开始探讨将模型驱动和数据驱动相结合进行基于轻量级深度网络的超分辨率图像重建的研究.Ren等[20]提出PEP-DSP, 从l2图像退化模型出发推导优化迭代算法, 并根据迭代算法设计轮廓增强先验网络及去噪统计先验网络, 实现图像重建.同时, Dong等[21]提出DPDNN(Denoising Prior Driven Deep Neural Net-work), 也从l2图像退化模型出发推导其优化迭代算法, 并根据迭代算法设计多尺度残差卷积网络去噪器.

上述PEP-DSP和DPDNN是从l2图像退化优化模型出发推导迭代算法, 在算法的指导下设计深度网络进行图像重建.由于l2数据保真项对高斯类噪声具有较好的平滑作用, 但对于具有稀疏性的椒盐噪声处理效果并不明显, 因此PEP-DSP和DPDNN对带有稀疏噪声图像的重建效果不明显.考虑到实际应用中图像噪声具有一定的稀疏性, 而l1保真项能较好地刻画噪声的稀疏性.同时, 评价图像的重建效果除峰值信噪比(Peak Signal to Noise Ratio, PSNR)和结构相似性(Structural Similarity, SSIM)以外, 图像的视觉效果即图像具有清晰的轮廓也很重要.

因此, 本文基于模型驱动与数据驱动结合的思想, 提出基于l1诱导轻量级深度网络(l1 Induced Lightweight Deep Networks, l1ILDN)的图像超分辨率重建方法.先利用分裂Bregman算法[22]和软阈值算子, 从带有边缘正则项的l1重建优化模型推演有效的迭代算法.再在上述迭代算法的指导下设计相应的递归深度网络用于图像重建.不同于现有的深度网络依赖人为模块设计, 本文的深度网络是在重建优化模型的指导下设计的, 推导的递归结构由于其权值共享的特性, 可减少网络权值的数量.同时, 由带有边缘正则项的l1保真项诱导的轻量级深度网络能更好地增强重建图像的锐度.

1 基于l1诱导轻量级深度网络的图像超分辨率重建

本文利用l1保真项比l2保真项能更好地刻画图像噪声的稀疏性的特点, 在深度学习的基础上融合专家先验知识, 提出基于l1诱导轻量级深度网络(l1ILDN)的图像超分辨率重建方法.

1.1 网络设计原理

由于l1ILDN是在重建优化模型的指导下设计的, 避免传统深度网络盲目加深网络带来的网络权值急剧增加的问题, 因此, 本节先推导l1诱导轻量级深度网络的设计原理.

对于图像退化问题(1), 超分辨率重建的主要目的是从低分辨率图像y中重建高分辨图像x.根据贝叶斯条件[23], 图像退化问题(1)的解可由最大后验概率p(y|x)表示, 即

$\begin{align} & \mathbf{x}\text{=arg}\underset{\text{x}}{\mathop{\text{max}}}\, \text{ log}\mathbf{ }p\mathbf{(x|y)} \\ & \text{=arg}\underset{\text{x}}{\mathop{\text{max}}}\, \text{log}\mathbf{ }p\mathbf{(y|x)+}\text{log }p\mathbf{(x), } \\ \end{align}$

其中, lg p(y|x)表示似然项, lg p(x)表示先验项.

在PEP-DSP和DPDNN中, 似然项选取l2保真项‖ y-Ax‖ 2, 先验项选取关于x的正则项J(x),

即

x=argminx‖ y-Ax‖ 2+λ J(x), (2)

其中λ 表示正则化系数.

不同于PEP-DSP和DPDNN, 本文方法考虑到实际应用中图像噪声具有一定的稀疏性, 而相比l2保真项, l1保真项能更好地刻画图像噪声的稀疏性, 因此本文选取‖ y-Ax‖ 1作为数据保真项.另外, 不同于PEP-DSP和DPDNN中采取抽象的正则项, 为了提高重建图像的视觉效果, 增强重建图像的锐度, 本文选取图像边缘的方差作为先验正则项, 即

x=argminx‖ y-Ax‖ 1-λ Var(Bx), (3)

其中, ‖ · ‖ 1表示l1范数, B表示图像边缘提取算子, Var(· )表示方差.显然, 上述带有边缘正则项的l1重建优化模型能较好地体现图像噪声的稀疏性和重建图像的局部结构.

由于上述l1重建优化模型(3)中的l1范数是不可微的, 因此求解该优化问题比求解l2重建优化模型(2)更复杂.

首先, 利用变量分离策略将l1重建优化模型(3)转化为如下形式:

(x, d)=argminx, d‖ d‖ 1-λ Var(Bx),

s.t. d=Ax-y.(4)

接着, 利用分裂Bregman算法将约束问题(4)转化为如下无约束问题:

$(\mathbf{x, d})=\text{arg}\underset{\text{x, d}}{\mathop{\text{min}}}\, \left\| \mathbf{d} \right\|_{1}^{{}}-\lambda \text{Var}(\mathbf{Bx})+\frac{\eta }{2}\left\| \mathbf{d -( Ax-y)} \right\|_{2}^{2}$ (5)

其中η 表示惩罚系数.利用文献[21]中的Bregman分离策略, 式(5)可转化为

$\left\{ _{{{\mathbf{b}}^{k+1}}\mathbf{=}{{\mathbf{b}}^{k}}\mathbf{+}\left( \mathbf{(A}{{\mathbf{x}}^{k+1}}\mathbf{-y)-}{{\mathbf{d}}^{k+1}} \right), }^{\mathbf{(}{{\mathbf{x}}^{k+1}}\mathbf{, }{{\mathbf{d}}^{k+1}}\mathbf{)=}\text{arg}\underset{\mathbf{x, d}}{\mathop{\text{min}}}\, \left\| \mathbf{d} \right\|_{\mathbf{1}}^{{}}\mathbf{-}\lambda \text{Var}\mathbf{(Bx)+}\frac{\eta }{2}\left\| \mathbf{ d -( Ax-y+}{{\mathbf{b}}^{k}}\mathbf{)} \right\|_{\mathbf{2}}^{\mathbf{2}}} \right.$

其中b表示辅助变量.此时, 上述迭代方法可分解为如下迭代公式:

$\left\{ \begin{align} & {{\mathbf{x}}^{k+1}}\mathbf{=}\text{arg}\underset{\mathbf{x}}{\mathop{\text{min}}}\, \frac{\eta }{2}\left\| \mathbf{ }{{\mathbf{d}}^{k}}\mathbf{ -( Ax-y+}{{\mathbf{b}}^{k}}\mathbf{)} \right\|_{\mathbf{2}}^{\mathbf{2}}\mathbf{-}\lambda \text{Var}\left( \mathbf{Bx} \right) \\ & {{\mathbf{d}}^{k+1}}\mathbf{=}\arg \underset{\mathbf{d}}{\mathop{\min }}\, \left\| \mathbf{d} \right\|_{\mathbf{1}}^{{}}\mathbf{+}\frac{\eta }{2}\left\| \mathbf{ d -}\left( \mathbf{A}{{\mathbf{x}}^{k+1}}\mathbf{-y+}{{\mathbf{b}}^{k}} \right) \right\|_{\mathbf{2}}^{\mathbf{2}} \\ & {{\mathbf{b}}^{k+1}}\mathbf{=}{{\mathbf{b}}^{k}}\mathbf{+}\left( \left( \mathbf{A}{{\mathbf{x}}^{k+1}}\mathbf{-y} \right)\mathbf{-}{{\mathbf{d}}^{k+1}} \right). \\ \end{align} \right.$ (6)

对于式(6)中的x子问题, 由于l2范数和Var是可微的, 因此采用经典的梯度下降法求解, 得

${{\mathbf{x}}^{\text{k}+1, l+1}}={{\mathbf{x}}^{k+1, l}}+\beta \eta {{A}^{T}}\left( {{d}^{k}}-A{{\mathbf{x}}^{k+1, l}}+y-{{b}^{k}} \right)+\lambda \beta {{B}^{T}}\left( B{{\mathbf{x}}^{k+1, l}}-\overline{U} \right), $

其中, xk+1, l表示式(6)中xk+1子问题的第l步迭代解, β 表示迭代步长,U¯中每个元素的值为Bxk+1, l的均值.

对于式(6)中的d子问题, 由于l1是不可微的, 因此求解变得困难.本文采用软阈值算子求解d子问题, 得

dk+1=Soft1η(Axk+1-y+bk),

其中Soft(· )表示软阈值算子.

综上所述, 式(6)的解可表述为如下迭代形式:

$\left\{ \begin{align} & {{\mathbf{x}}^{\text{k}+1}}:={{\mathbf{x}}^{\text{k}+1, l+1}}={{\mathbf{x}}^{k+1, l}}+\beta \eta {{A}^{T}}\left( {{d}^{k}}-A{{\mathbf{x}}^{k+1, l}}+y-{{b}^{k}} \right) \\ & +\lambda \beta {{B}^{T}}\left( B{{\mathbf{x}}^{k+1, l}}-\overline{U} \right), \\ & {{\mathbf{d}}^{k+1}}\mathbf{=}\text{Sof}{{\text{t}}_{\frac{1}{\eta }}}\left( \mathbf{A}{{\mathbf{x}}^{k+1}}\mathbf{-y+}{{\mathbf{b}}^{k}} \right), \\ & {{\mathbf{b}}^{k+1}}\mathbf{=}{{\mathbf{b}}^{k}}\mathbf{+}\left( \left( \mathbf{A}{{\mathbf{x}}^{k+1}}\mathbf{-y} \right)\mathbf{-}{{\mathbf{d}}^{k+1}} \right), \\ \end{align} \right.$ (7)

其中, xk+1表示内部进行L步迭代后得到的解, 再参与dk+1和bk+1的外部迭代运算.

1.2 网络结构

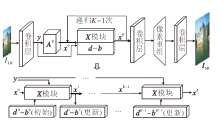
经典的基于深度学习的超分辨率重建方法在设计网络时主要通过人为设计网络模块, 提高重建性能, 而本文方法在1.1节中推导的算法指导下, 设计相应的深度网络, 避免盲目增加网络权值参数量, 网络结构如图1所示.

图1 l1诱导轻量级深度网络结构Fig.1 Structure of l1 induced lightweight deep network

具体网络的设计过程如下.对于给定的低分辨率图像ILR∈Rm1×n1×3, 为了便于后续模块中的卷积操作获得充足的通道数, 本文方法首先使用64组3× 3的卷积核对ILR进行卷积操作, 得到的特征图作为观测的低分辨率图像y.由于本文的深度网络是在1.1节中的算法指导下设计的, 而从式(7)可知, 重建的高分辨率图像x具有双重递归结构.因此, 本文令

x0=ATy

作为递归的初始值.为了提高重建性能, 本文选取多尺度残差块[13]作为退化矩阵AT.

对于式(7)中的y、bk和dk, 令X模块表示高分辨率图像x的L次内部递归过程, 结构如图2所示.对于第l次内部迭代输入xk+1, l, 利用多尺度残差块作用于xk+1, l, 得到Axk+1, l, 再与y、bk和dk进行相应的运算, 得到

dk-Axk+1, l+y-bk,

再经过AT和参数β η 的作用后得到

β η AT(dk-Axk+1, l+y-bk).

同理, xk+1, l在特征提取矩阵B的作用下得到Bxk+1, l, 再根据方差的定义进行取平均和相减操作, 得到

Bxk+1, l-U¯,

然后经过β λ BT的作用后, 得到

$\lambda \beta {{B}^{T}}\left( B{{\mathbf{x}}^{k+1, l}}-\overline{U} \right)$

最后与xk+1, l相减, 完成xk+1, l的更新.

图2 X模块结构Fig.2 Structure of X module

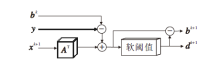
进行完X模块的L次内部递归后, 需要更新辅助变量bk+1、dk+1, 保证式(7)中高分辨率图像x的外部递归过程.d-b模块更新过程如图3所示.

图3 d-b更新过程Fig.3 Updating process of d-b

给定输入变量xk+1、bk和y, 首先对xk+1实行对应于退化A的卷积运算, 然后将其与bk和y进行相应的和差运算, 得

rk+1=Axk+1+bk+1-y.

最后, 将rk+1输入软阈值函数Soft(· )中, 得

dk+1=Soft(rk+1).

同理, rk+1与dk+1相互作用, 可得

bk+1=rk+1-dk+1.

通过上述X模块和d-b模块双重递归过程, x0经过K次迭代后, 得到特征图xK∈Rm1×n1×64.最后, 使用像素重组将xK放大r倍, 得到重建的高分辨率图像ISR∈Rm1×n1×3.

1.3 损失函数

对于设计好的网络, 损失函数的设计很影响网络的性能.对于训练样本集{(Yi, Xi)}i=1N, 经典的损失函数有两种, 即L1损失和均方误差损失(Mean Square Error, MSE), 相应公式如下:

${{L}_{1}}\left( \theta \right)=\frac{1}{N}\sum\limits_{i=1}^{N}{\mathop{\left\| {{X}_{i}}-I(\theta ; {{Y}_{i}}) \right\|}_{1}^{{}}}$,

$MSE\left( \theta \right)=\frac{1}{N}\sum\limits_{i=1}^{N}{\mathop{\left\| {{X}_{i}}-I(\theta ; {{Y}_{i}}) \right\|}_{2}^{2}}$,

其中, θ 表示网络中需要训练的权值和参数, Yi表示输入的低分辨率图像块, Xi表示原始的高分辨率图像块, I(θ ; Yi)表示经网络重建后的高分辨率图像块.由于本文网络是根据l1数据保真项推导的算法而设计的, 因此在损失函数的选择上采用收敛更快且鲁棒性更强的L1损失函数.另外, 本文采取经典的Adam(Adaptive Moment Estimation)优化器[24]优化损失函数.

2 实验及结果分析
2.1 实验环境

本文选择DIV2K数据集[25]中前800幅图像构造网络训练集, 通过对图像进行旋转操作以增强数据集.同时, 本文选择Set5[26]、Set14[27]、BSD100[28]和Urban100[29]数据集进行重建测试.选择PSNR和SSIM作为重建性能的评价指标.一般地, PSNR和SSIM值越高, 方法的重建性能越优.

在训练阶段, 各方法将DIV2K数据集上的高分辨率图像进行双三次下采样后得到的图像作为低分辨率图像, 然后将图像减去数据集的平均值进行预处理.低分辨率图像大小为48× 48, 网络训练的批次大小为16.在训练网络时, Adam优化器的相关参数设置为β 1=0.9, β 2=0.999, ε =10-8, 初始学习率为10-4, 每200代后学习率减半.

本文实验均是在Pytorch 1.1.0框架下实施的, 在Intel(R) Xeon(R) E5-1620@3.50 GHz、8核处理器、32 GB内存、RTX 2060显卡和Windows 10操作系统下实现.

2.2 参数分析

本文的深度网络包含3个网络结构重要参数:X模块内部结构中递归次数L、网络中X模块递归次数K和软阈值算子中的超参数η .本节通过实验讨论这3个参数对网络重建性能的影响.

考虑到网络训练的时间, 在较合适的网络规模, 即LK=12的情况下讨论不同的递归次数L和K对重建性能的影响, 在Set5数据集上, L、K取值不同时的PSNR值和SSIM值如表1所示.由表可知, 在L=3, K=4时, 网络取得最优的重建性能.随着L的增加和K的减少, 网络性能有所下降.这主要是网络的外递归的影响比X模块的内递归的影响要大.

表1 L、K取不同值时对网络性能的影响 Table 1 Influence of different L and K on network performance

下面讨论软阈值算子中的参数η 对网络重建性能的影响.在Set5数据集上η 不同时的PSNR值和SSIM值如表2所示.由表可知, 在η -1=0.01时, 网络取得最优的重建性能.主要原因是η -1太小时, 软阈值算子在网络上的作用较小; 而当η -1较大时, 不能使d-(Ax-y)近似于0.

表2 η 取不同值时对网络性能的影响 Table 2 Influence of different η on network performance
2.3 消融实验结果

本节通过消融实验说明l1ILDN的创新性.首先, 为了说明多尺度残差块(Multi-Scale Residual Block, MSRB)和先验项约束的意义, 将退化模型中A选取普通卷积、l1优化模型中无先验正则项导出的网络作为基本网络, 记为Based-net.其次, 为了凸显在先验指导下设计网络的意义, 将LK个MSRB递归网络记为Deep-net.最后, 为了说明损失函数L1的优点, 将使用本文网络结构而损失函数为MSE损失的网络记为l1ILDN-l2.

Based-net、Deep-net、l1ILDN-l2和l1ILDN的消融实验结果如表3所示.由表可看出, l1ILDN的重建结果在4个数据集上都最优.相比Based-net, l1ILDN具有明显优势主要是因为退化模型中A选取MSRB, 比普通卷积具有更好的特征提取能力.同时, 在推演模型算法时, 使用先验正则项, 使根据算法设计的网络具有更好的拟合能力.l1ILDN的重建结果优于Deep-net, 说明在模型推导下设计网络具有重要意义.l1ILDN的重建结果优于l1ILDN-l2, 说明即使网络结构一样, 但网络训练选取损失函数的不同, 将产生不同的重建结果.

表3 本文方法的消融实验结果 Table 3 Results of ablation experiments of the proposed method
2.4 复杂度分析

本节讨论l1ILDN的复杂性.选择如下4种对比方法:DRCN[17]、DPDNN[21]、MemNet(Very Deep Per-sistent Memory Network)[30]、MADNet[31].选择Set5数据集, 各方法的实验结果(放大因子为2)如表4所示, 表中FLOPS(Floating-Point Operations per Second)表示每秒浮点运算次数.

表4 各方法在Set5数据集上的复杂度对比 Table 4 Complexity comparison of different methods on the Set5 dataset

由表4可看出, l1ILDN使用最少的参数量和最小的FLOPS实现最高的PSNR和SSIM.究其原因, 本文方法是在先验知识诱导的算法指导下进行网络设计的, 避免盲目加深网络带来的参数冗余, 使网络能在参数较少时得到较好的网络重建效果.

2.5 对比实验结果

本节选择如下对比方法进行对比实验:Bicubic、SRCNN[6]、FSRCNN[7]、ESPCN[8]、VDSR[9]、LapSRN[10]、DRCN[17]、DRRN[18]、PEP-DSP[20]、DP-DNN[21]、文献[29]方法、MemNet[30]、MADNet[31]、A+(Adjusted Anchored Neighborhood Regression)[32]、IDN(Information Distillation Network)[33]、RiRSR(Resnet in Resnet Architecture)[34].

选择放大因子r=2、3、4, 各方法在Set5、Set14、B100、Urban100数据集上的PSNR和SSIM对比结果如表5~表7所示, 表中黑体数字表示最优值.

表5 r=2时各方法的指标值对比 Table 5 Comparison of index values of different methods with r=2
表6 r=3时各方法的指标值对比 Table 6 Comparison of index values of different methods with r=3
表7 r=4时各方法的指标值对比 Table 7 Comparison of index values of different methods with r=4

由表5~表7可知, 本文方法取得最高的PSNR和SSIM.究其原因, 本文方法考虑噪声的稀疏性和先验知识, 在算法的指导下设计深度网络, 避免盲目构造网络造成的冗余.

2.6 重建图像对比

l1ILDN、ESPCN、VDSR、DRCN、DPDNN、RiRSR的重建高分辨率图像对比如图4所示.从图中右下角的放大图像可看出, l1ILDN能重建具有更清晰纹理、更少伪影的图像, 而ESPCN重建的3幅图像非常模糊.究其原因, 主要是l1ILDN是在带有边缘正则项的重建模型推导的算法指导下进行设计的, 边缘正则项的约束使重建图像具有更好的边缘清晰度.

图4 各方法重建图像对比Fig.4 Reconstructed image comparison of different methods

3 结束语

现有的基于深度学习的方法主要通过加深网络以提高网络的重建性能, 但是直接加深网络会造成网络参数带来的冗余, 给网络训练和内存存储带来负担.考虑到噪声的稀疏性和减小网络参数带来的冗余, 并增强重建图像的清晰度, 本文结合数据驱动和模型驱动, 提出基于l1诱导轻量级深度网络的图像超分辨率重建方法.从带有正则项的l1优化模型出发, 推导轻量级深度网络的设计原理.然后根据该原理设计相应的轻量级深度网络, 进行图像重建.因此, 本文方法是在模型的指导下设计轻量级深度网络, 避免盲目加深网络造成的参数冗余, 可体现数据驱动和模型驱动的优势.实验表明, 本文方法重建性能较优.重建优化模型和迭代算法决定深度网络的结构和性能.因此, 深入挖掘重建先验知识, 构造更能反映图像退化过程的轻型深度网络将是进一步的研究重点.

本文责任编委 兰旭光

Recommended by Associate Editor LAN Xuguang

参考文献
[1] YILDIRIM D, GÜNGÖR O. A Novel Image Fusion Method Using IKONOS Satellite Images. Journal of Geodesy and Geoinformation, 2012, 1(1): 27-34. [本文引用:1]
[2] 李仲年, 张涛, 张道强. 基于自监督边缘融合网络的MRI影像重建. 模式识别与人工智能, 2021, 34(4): 361-366.
(LI Z N, ZHANG T, ZHANG D Q. Self-Supervised Edge-Fusion Network for MRI Reconstruction. Pattern Recognition and Artificial Intelligence, 2021, 34(4): 361-366. ) [本文引用:1]
[3] ZHANG L, WU X L. An Edge-Guided Image Interpolation Algorithm via Directional Filtering and Data Fusion. IEEE Transactions on Image Processing, 2006, 15(8): 2226-2238. [本文引用:1]
[4] ZHANG K B, GAO X B, TAO D C, et al. Single Image Super-Re-solution with Non-local Means and Steering Kernel Regression. IEEE Transactions on Image Processing, 2012, 21(11): 4544-4556. [本文引用:1]
[5] FREEMAN W T, JONES T R, PASZTOR E C. Example-Based Super-Resolution. IEEE Computer Graphics and Applications, 2002, 22(2): 56-65. [本文引用:1]
[6] DONG C, LOY C C, HE K M, et al. Learning a Deep Convolutional Network for Image Super-Resolution // Proc of the European Conference on Computer Vision. Berlin, Germany: Springer, 2014: 184-199. [本文引用:2]
[7] DONG C, LOY C C, TANG X O. Accelerating the Super-Resolution Convolutional Neural Network // Proc of the European Confe-rence on Computer Vision. Berlin, Germany: Springer, 2016: 391-407. [本文引用:2]
[8] SHI W B, CABALLERO J, HUSZÁR F, et al. Real-Time Single Image and Video Super-Resolution Using an Efficient Sub-Pixel Convolutional Neural Network // Proc of the IEEE Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2016: 1874-1883. [本文引用:2]
[9] KIM J, LEE J K, LEE K M. Accurate Image Super-Resolution Using Very Deep Convolutional Networks // Proc of the IEEE Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2016: 1646-1654. [本文引用:2]
[10] LAI W S, HUANG J B, AHUJA N, et al. Deep Laplacian Pyramid Networks for Fast and Accurate Super-Resolution // Proc of the IEEE Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2017: 5835-5843. [本文引用:2]
[11] ZHANG Y L, LI K P, LI K, et al. Image Super-Resolution Using Very Deep Residual Channel Attention Networks // Proc of the European Conference on Computer Vision. Berlin, Germany: Sprin-ger, 2018: 294-310. [本文引用:1]
[12] ZHANG Y L, TIAN Y P, KONG Y, et al. Residual Dense Network for Image Super-Resolution // Proc of the IEEE/CVF Confe-rence on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2018: 2472-2481. [本文引用:1]
[13] LI J C, FANG F M, MEI K F, et al. Multi-scale Residual Network for Image Super-Resolution // Proc of the European Conference on Computer Vision. Berlin, Germany: Springer, 2018: 527-542. [本文引用:2]
[14] ZHANG M J, WU Q Q, ZHANG J, et al. Fluid Micelle Network for Image Super-Resolution Reconstruction. IEEE Transactions on Cybernetics, 2023, 53(1): 578-591. [本文引用:1]
[15] ZHANG M J, WU Q Q, GUO J, et al. Heat Transfer-Inspired Network for Image Super-Resolution Reconstruction. IEEE Transactions on Neural Networks and Learning Systems, 2022. DOI: 10.1109/TNNLS.2022.3185529. [本文引用:1]
[16] ZHANG M J, XIN J W, ZHANG J, et al. Curvature Consistent Network for Microscope Chip Image Super-Resolution. IEEE Tran-sactions on Neural Networks and Learning Systems, 2022. DOI: 10.1109/TNNLS.2022.3168540. [本文引用:1]
[17] KIM J, LEE J K, LEE K M. Deeply-Recursive Convolutional Network for Image Super-Resolution // Proc of the IEEE Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2016: 1637-1645. [本文引用:3]
[18] TAI Y, YANG J, LIU X M. Image Super-Resolution via Deep Recursive Residual Network // Proc of the IEEE Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2017: 2790-2798. [本文引用:2]
[19] REICHSTEIN M, CAMPS-VALLS G, STEVENS B, et al. Deep Learning and Process Understand ing for Data-Driven Earth System Science. Nature, 2019, 566: 195-204. [本文引用:1]
[20] REN C, HE X H, PU Y F, et al. Learning Image Profile Enhancement and Denoising Statistics Priors for Single-Image Super-Resolution. IEEE Transaction on Cybernetics, 2021, 51(7): 3535-3548. [本文引用:2]
[21] DONG W S, WANG P Y, YIN W T, et al. Denoising Prior Driven Deep Neural Network for Image Restoration. IEEE Transaction on Pattern Analysis and Machine Intelligence, 2019, 41(10): 2305-2318. [本文引用:4]
[22] GOLDSTEIN T, OSHER S. The Split Bregman Method for L1-Re-gularized Problems. SIAM Journal on Imaging Sciences, 2009, 2(2): 323-343. [本文引用:1]
[23] CHAN S H, WANG X R, ELGENDY O A. Plug-and -Play ADMM for Image Restoration: Fixed-Point Convergence and Applications. IEEE Transaction on Computational Imaging, 2017, 3(1): 84-98. [本文引用:1]
[24] KINGMA D P, BA J L. Adam: A Method for Stochastic Optimization[C/OL]. [2022-11-07]. https://arxiv.org/pdf/1412.6980.pdf. [本文引用:1]
[25] TIMOFTE R, AGUSTSSON E, VAN GOOL L, et al. NTIRE 2017 Challenge on Single Image Super-Resolution: Methods and Results // Proc of the IEEE Conference on Computer Vision and Pattern Recognition Workshops. Washington, USA: IEEE, 2017: 1110-1121. [本文引用:1]
[26] BEVILACQUA M, ROUMY A, GUILLEMOT C, et al. Low-Complexity Single-Image Super-Resolution Based on Nonnegative Neighbor Embedding // Proc of the British Machine Vision Confe-rence. Guildford, UK: BMVA Press, 2012. DOI: 10.5244/C.26.135 [本文引用:1]
[27] ZEYDE R, ELAD M, PROTTER M. On Single Image Scale-Up Using Sparse-Representations // Proc of the 7th International Conference on Curves and Surfaces. Berlin, Germany: Springer, 2010: 711-730. [本文引用:1]
[28] ARBELÁEZ P, MAIRE M, FOWLKES C, et al. Contour Detection and Hierarchical Image Segmentation. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2011, 33(5): 898-916. [本文引用:1]
[29] HUANG J B, SINGH A, AHUJA N. Single Image Super-Resolution from Transformed Self-Exemplars // Proc of the IEEE Confe-rence on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2015: 5197-5206. [本文引用:2]
[30] TAI Y, YANG J, LIU X M, et al. MemNet: A Persistent Memory Network for Image Restoration // Proc of the IEEE International Conference on Computer Vision. Washington, USA: IEEE, 2017: 4549-4557. [本文引用:2]
[31] LAN R S, SUN L, LIU Z B, et al. MADNet: A Fast and Lightweight Network for Single-Image Super Resolution. IEEE Transactions on Cybernetics, 2021, 51(3): 1443-1453. [本文引用:2]
[32] TIMOFTE R, DE SMET V, VAN GOOL L. A+: Adjusted Anchored Neighborhood Regression for Fast Super-Resolution // Proc of the Asian Conference on Computer Vision. Berlin, Germany: Springer, 2014: 111-126. [本文引用:1]
[33] HUI Z, WANG X M, GAO X B. Fast and Accurate Single Image Super-Resolution via Information Distillation Network // Proc of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2018: 723-731. [本文引用:1]
[34] PANG S R, CHEN Z, YIN F L. Image Super-Resolution Based on Generalized Residual Network. Arabian Journal for Science and Engineering, 2022, 47(2): 1903-1920. [本文引用:1]