引用本文
张泽东, 陇盛, 鲍蕾, 陶卿. 基于AdaBelief的Heavy-Ball动量方法. 模式识别与人工智能, 2022,35(2): 106-115
ZHANG Zedong, LONG Sheng, BAO Lei, TAO Qing. AdaBelief Based Heavy-Ball Momentum Method. PATTERN RECOGNITION AND ARTIFICIAL INTELLIGENCE, 2022,35(2): 106-115.  
Doi: 10.16451/j.cnki.issn1003-6059.202202002 中图法分类号 TP 181
Permissions
Copyright©2022, 《模式识别与人工智能》编辑部
《模式识别与人工智能》编辑部 所有
基于AdaBelief的Heavy-Ball动量方法
张泽东1, 陇盛1, 鲍蕾1, 陶卿1
1.中国人民解放军陆军炮兵防空兵学院 信息工程系 合肥 230031;

陶卿,博士,教授,主要研究方向为模式识别、机器学习、应用数学.E-mail:qing.tao@ia.ac.cn.

张泽东,硕士研究生,主要研究方向为模式识别、机器学习.E-mail:1632783823@qq.com.

陇盛,硕士研究生,主要研究方向为模式识别、机器学习.E-mail:ls15186322349@163.com.

鲍蕾,博士,讲师,主要研究方向为模式识别、计算机视觉.E-mail:baolei1219@sina.cn.

收稿日期: 2021-05-24 接受日期: 2021-11-25
资助项目: 国家自然科学基金项目(No.62076252)资助
摘要

同时使用动量和自适应步长技巧的自适应矩估计(Adaptive Moment Estimation, Adam)型算法广泛应用于深度学习中.针对此方法不能同时在理论和实验上达到最优这一问题,文中结合AdaBelief灵活调整步长提高实验性能的技巧,以及仅采用指数移动平均(Exponential Moving Average, EMA)策略调整步长的Heavy-Ball动量方法加速收敛的优点,提出基于AdaBelief的Heavy-Ball动量方法.借鉴AdaBelief和Heavy-Ball动量方法收敛性分析的技巧,巧妙选取时变步长、动量系数,并利用添加动量项和自适应矩阵的方法,证明文中方法对于非光滑一般凸优化问题具有最优的个体收敛速率.最后,在凸优化问题和深度神经网络上的实验验证理论分析的正确性,并且证实文中方法可在理论上达到最优收敛性的同时提高性能.

关键词: AdaBelief; Heavy-Ball动量方法; 个体收敛速率; 深度神经网络
AdaBelief Based Heavy-Ball Momentum Method
ZHANG Zedong1, LONG Sheng1, BAO Lei1, TAO Qing1
1.Department of Information Engineering, Army Academy of Artillery and Air Defense of PLA, Hefei 230031
TAO Qing, Ph.D., professor. His research interests include pa-ttern recognition, machine learning and applied mathematics.

ZHANG Zedong, master student. His research interests include pattern recognition and machine learning.

LONG Sheng, master student. His research interests include pattern recognition and machine learning.

BAO Lei, Ph.D., lecturer. Her research interests include pattern recognition and computer vision.

Fund:Supported by National Natural Science Foundation of China(No.62076252)
Abstract

Adaptive moment estimation algorithms with momentum and adaptive step techniques are widely applied in deep learning. However, these algorithms cannot achieve the optimal performance in both theory and experiment. To solve the problem, an AdaBelief based heavy-ball momentum method, AdaBHB, is proposed. The AdaBelief technique of adjusting step size flexibly is introduced to improve the algorithm performance in experiments. The heavy ball momentum method with step size adjusted by exponential moving average strategy is employed to accelerate convergence. According to the convergence analysis techniques of AdaBelief and Heavy-ball momentum methods, time-varying step size and momentum coefficient are selected skillfully and the momentum term and adaptive matrix are added. It is proved that AdaBHB gains the optimal individual convergence rate for non-smooth general convex optimization problems. Finally, the correctness of the theoretical analysis of the proposed algorithm is verified by experiments on convex optimization problems and deep neural networks, and AdaBHB is validated to obtain the optimal convergence in theory with performance improved.

Key words: Key Words AdaBelief; Heavy-Ball Momentum Method; Individual Convergence Rate; Deep Neural Network

随机梯度下降法[1]是解决优化问题的经典算法之一, 在其基础上添加动量和自适应步长技巧是机器学习领域用于提升优化算法性能常用的两种方式.动量方法利用梯度的历史累积信息调整解向量的更新方向, 而自适应步长技巧利用梯度的历史信息调整梯度在不同维度上的步长.从理论分析的角度上说:动量方法能加速梯度下降方法的收敛速率, 避开非凸优化中的局部极小点和鞍点[2, 3]; 自适应步长方法能降低对人为指定步长的依赖, 在处理稀疏学习问题时具有更紧的收敛界[4, 5].

Kingma等[6]同时采用动量的指数移动平均(Exponential Moving Average, EMA)形式和自适应步长调整技巧, 提出自适应矩估计(Adaptive Moment Estimation, Adam), 其中EMA是指当前位置梯度与历史累积梯度的一个凸组合, 可通过调整凸组合中权系数的大小, 强调当前位置的梯度信息, 并逐渐遗忘历史梯度信息.动量的EMA形式使Adam在深度学习的实际应用中取得一定成功[7], 同时具有较好的直观解释, Adam也因此成为目前深度学习中使用最普遍的一种优化算法.但是, Reddi等[8]重新审视Adam的收敛性分析, 发现即使对于简单的凸优化问题, Adam都无法收敛到全局极小值, 这一问题也称为Reddi问题.虽然Reddi等[8]提出AMSGrad和AdamNC修正算法, 但在线AMSGrad在一般凸情况下只获得O( tlnt)的遗憾(Regret)界, 与投影次梯度的O( t)的regret界[9]仍有差距, 其中t为算法的迭代步数.

为了进一步提升Adam性能, 学者们开始试图对自适应步长方法进行更精细的改进[10].特别是Zhuang等[11]提出AdaBelief, 在Adam的基础上将动量的EMA形式看成是下一次迭代的预估方向, 根据当前位置梯度方向是否与动量的EMA形式方向一致而灵活地调整步长.当梯度方向与动量的EMA形式方向一致时, 选择相信, 采用较大的步长; 当两者方向相反时, 选择怀疑, 采用较小的步长.AdaBelief的这种步长策略更好地适应问题自身的特征, 同时具有Adam快速收敛特性和随机梯度下降法的泛化性能.实验表明, AdaBelief在训练和测试精度方面均取得较优的实际效果, 但由于其使用与Adam一样的EMA策略, 仍无法避免收敛性方面存在的Reddi问题, 导致未能较好体现动量的加速性能.

实际上, 使用动量的EMA形式不仅在收敛性分析上导致目前仍无法解决的困难, 在实际应用中还存在其它问题.Zou等[12]指出, EMA形式的动量仅利用当前步的学习率信息, 当动量系数趋近于1时, 动量的EMA 策略会导致算法迭代陷入停滞, 但Heavy-Ball动量由于利用历史的学习率信息, 不会出现此问题.为此, Tao等[13]在Heavy-Ball型动量方法中放弃对动量使用EMA策略, 提出仅采用EMA策略调整步长的动量方法, 即自适应重球(Adaptive Heavy-Ball, AdaHB), 克服理论分析中采用平均输出方式与实际应用中却采用最后一次迭代作为输出的不一致问题.与文献[13]一样, 本文称以所有迭代平均为最终输出时的收敛速率为平均收敛速率, 称最后一步迭代作为输出时的收敛速率为个体收敛速率.相比平均, 个体输出在处理稀疏优化问题时往往具有更好的稀疏性, 但是却更难获得个体收敛速率[14, 15].对于非光滑凸问题, 相比使用动量EMA策略的Adam, AdaHB获得O(1/ t)的最优个体收敛速率, 克服Adam甚至平均收敛速率也无法达到最优的缺陷.

在不影响Adam收敛性证明的基础上, AdaBelief的步长调整技巧提高实际性能.另一方面, 仅采用EMA策略调整步长的Heavy-Ball动量方法可获得最优的个体收敛速率.因此, 本文结合AdaBelief步长调整的思想与Heavy-Ball动量方法, 提出基于AdaBelief的Heavy-Ball动量方法(AdaBe-lief Based Heavy-Ball Moment Method, AdaBHB).结合采用EMA策略调整步长的Heavy-Ball型动量方法的个体收敛性, 与AdaBelief的平均收敛性分析的一般思路, 并借鉴AdaBelief中处理步长项的方法, 证明本文方法在非光滑凸情形下具有O(1/ t)的最优个体收敛速率, 克服Adam型算法只能得到平均收敛速率的缺陷, 并去除收敛速率中的 lnt因子, 体现动量的加速效果.在非光滑凸问题上的实验验证理论分析的正确性.在深度神经网络上的实验证实AdaBHB在提高收敛性及泛化性能方面的良好效果.

1 相关知识

本节介绍动量方法和自适应算法, 以及它们的收敛性.

考虑约束优化问题:

minw∈Qf(w),

其中, f(w)为目标函数, 一般为凸函数, Q⊆Rn为有界闭凸集.投影次梯度方法的迭代步骤[1]为

wt+1=wt-α tgt.

其中:wt为w在第t次迭代的输出; α t为设置的衰减学习率, 一般凸情形下取α t=α / t, α > 0; gt为f(w)在wt处的次梯度.

对于投影次梯度等算法, 平均收敛速率是指f( w˙t)-f(w* )的收敛速率, 其中

w˙t= 1t∑k=1twk,

w* 为问题的最优解.个体收敛速率是指f(wt)-f(w* )的收敛速率.非光滑凸条件下投影次梯度算法的平均收敛速率为O(1/ t)[16], 个体最优收敛速率为O(ln t/ t)[17].这与非光滑凸问题本身的最优个体收敛速率之间还存在ln t因子的差距.

为了简单起见, 与文献[8]和文献[13]一样, 在算法的更新公式中省略偏差修正步骤.Adam更新公式如下[6]:

mt=β 1, tmt-1+(1-β 1, t)gt, Vt=β 2, tVt-1+(1-β 2, t) gt2wt+1=wt-α tm Vt-1/2.

其中:为了收敛性分析的需要, 均采取时变的学习率α t代替常数α ; β 1, t为时变动量的加权系数, β 2, t为自适应矩阵的加权系数; mt为EMA形式的动量; Vt为自适应矩阵; gt2=diag(gt gTt), 为梯度的外积矩阵的对角阵.

可以看出, Adam与投影次梯度算法的不同主要体现在使用动量的EMA形式mt调整参数更新方向, 并采用自适应矩阵Vt调整参数更新的每维步长.

AMSGrad具体形式如下:

V︿t=max V︿t-1, Vt, wt+1=wt-α t􁀄 V︿t-1/2t.

它只是在Adam自适应矩阵上添加一个使步长衰减的操作, 获得O( tlnt)的regret界[8].

AdaBelief更新公式如下:

mt=β 1, tmt-1+(1-β 1, t)gt, St=β 2, tSt-1+(1-β 2, t)(gt-mt)2, wt+1=wt-α tm St-1/2,

可以看出, AdaBelief仅是在Adam的基础上更改计算自适应矩阵的方式, 自适应矩阵由原来的 gt2的指数移动平均Vt, 改为(gt-mt)2的指数移动平均St, 当梯度方向与动量的EMA形式方向一致时, (gt-mt)2每维分量变小, 从而使St每维分量减小, 步长α t St-1/2的每维会相应地增大, 当梯度方向与动量的EMA形式方向相反时则相反, 从而使步长选取更好地适应问题本身的特征, 但是由于AdaBelief采用动量的EMA形式, 在非光滑凸情形下也只能获得O( tlnt)的regret界[11].

Heavy-Ball动量方法的迭代公式为

wt+1=wt-α tgt+β t(wt-wt-1),

其中, α t为设置的衰减学习率, β t∈ [0, 1)为动量系数[2], wt-wt-1为动量项.当动量系数为常数时, 分别将Heavy-Ball动量和EMA动量展开为梯度累加和的形式, 可得

HB: wt+1=wt- ∑i=1tα igiβ t-i, EMA: wt+1=wt-(1-β )α t ∑i=1tiβ t-i.

可以看出, Heavy-Ball动量在参数更新时利用α i(i=1, 2, …, t)的信息, 而动量的EMA形式仅利用α t的信息, 另外当动量系数β 趋近于1时, (1-β )→ 0, 使用动量的EMA形式时, wt+1≈ wt, 而使用Heavy-Ball动量却不会出现这样的问题[12].

AdaHB迭代公式为

Vt=β 2, tVt-1+(1-β 2, t) gt2, V︿tVt1/2δtId, wt+1=wt-α tg V︿t-1+β 1t(wt-wt-1).

AdaHB只是在Heavy-Ball动量的基础上引入Adam的自适应矩阵Vt, δ 为常数因子, 确保分子不为0.通过 V︿t自动调节每维参数的更新步长α t V︿t-1.通过选择合适的时变学习率α t及动量参数β 1t, 能够证明AdaHB在非光滑凸情形下可获得O(1/ t)的最优个体收敛速率[13].

2 基于AdaBelief的Heavy-Ball动量方法

本节提出基于AdaBelief的Heavy-Ball动量方法(AdaBHB), 给出在目标函数为非光滑一般凸情况下算法的最优个体收敛性证明.

将AdaBelief策略下的自适应步长技巧与AdaHB结合, 提出AdaBHB, 迭代形式为

St=β 2tSt-1+(1-β 2t)[gt-(wt-wt-1)]2, S︿tSt1/2δtId, wt+1=wt-α tg S︿t-1+β 1t(wt-wt-1). (1)

不同于AdaHB, AdaBHB中自适应矩阵St的更新借鉴AdaBelief的思想, 即对当前梯度与动量项差值的外积矩阵对角阵进行EMA平均, 与之不同的是动量项不再采用EMA形式的动量mt, 而是借鉴AdaHB的思想, 采用Heavy-Ball动量wt-wt-1.

在进行最优个体收敛性的证明时, 参考Tao等[13]提出的仅采用EMA策略调整步长的Heavy-Ball动量方法的收敛性分析思路, 引入加权动量项

pt=t(wt-wt-1),

巧妙选取时变步长α t和动量因子β 1t, 从而将AdaBHB的迭代方式转化为类似于投影次梯度法的形式[13]:

wt+1+pt+1=wt+pt- αtV︿t-1gt.

借鉴此方法处理迭代, 得到如下引理1.为了证明的简洁性, 这里的证明采用无约束情况下的证明方式, 有约束情况下的证明只需在此基础上利用投影的非扩张性即可.

引理1 令

pt=t(wt-wt-1),

假设wt由式(1)产生, 取

β 1t= tt+2, α t= α(t+2)t,

则有

wt+1+pt+1=wt+pt- αtS︿t-1gt.(2)

证明 根据迭代式(1), 并令

pt=t(wt-wt-1),

有

wt+1+pt+1=wt+1+(t+1)(wt+1-wt)=(t+2)wt+1-(t+1)wt=wt-(t+2)α t S︿t-1gt+(t+2)β 1t(wt-wt-1),

代入

α t= α(t+2)t, β 1t= tt+2,

可得

wt+1+pt+1=wt+pt- αtS︿t-1gt.

证毕可以看出, 不同于AdaHB, AdaBHB的自适应矩阵由原来的 V︿t变成 S︿t.又借鉴Zhuang等[11]证明在线AdaBelief的regret界时处理自适应矩阵 S︿t使用的技巧, 即假设 S︿t, i存在下界, 其中 S︿t, i为对角矩阵 S︿t的第i维元素, 由 S︿t的计算方式可知假设正确, 由此可证明AdaBHB具有最优的个体收敛速率.

基于式(2)可证明定理1, 但为了解决变步长和动量系数导致的递归问题, 先提出引理2.

引理2 令

D= maxw∈Q, u∈Q‖ w-u‖ ,

假设‖ gt‖ ≤ G, 存在常数c, 使得 S︿t, i≥ c> 0, 则有

∑t=1Tt‖wt-w* ‖S˙t2-‖wt+1-w* ‖S˙t2+ ∑t=1T1tgt ‖S˙t-12DT2∑i=1dS︿T, iG2c2 T1).

证明 使用Zhuang等[11]证明在线AdaBelief的regret界时采用的迭代技巧, 进行如下整理:

$\sum^{T}_{t=1} \sqrt{t}\{|| wt-w*||^{2}_{\dot{s}t}-||wt+1-w*||^{2}_{\dot{s}t}\}+\sum^{T}_{t=1} \frac{1}{\sqrt{t}}||gt||^{2}_{\dot{s}_{t}-1}≤ \\ ||w1.w*||^{2}_{\dot{s}1}\sum^{T}_{t=2} \{\sqrt{t}wt-w*||^{2}_{\dot{s}t}\sqrt{t-1}wt-w*||^{2}_{\dot{s}t-1} \}\frac{1}{\sqrt{c}}\sum^{T}_{t=1}\frac{G^{2}}{\sqrt{t}} \\ ||w1-w*+||^{2}_{\dot{s}_{1}}\sum^{T}_{t=2} \{||\sqrt{t}t-w*-||^{2}_{\dot{s}t}||\sqrt{t-1}t-w*||^{2}_{\dot{s}_{t-1}}\} \frac{G^{2}}{\sqrt{c}}\sum^{T}_{t=1}\frac{1}{\sqrt{t}} \\ ||w1-w*+||^{2}_{\dot{s}_{1}}\sum^{T}_{t=2}\sum^{d}_{i=2} \{,i-)2w,*i(\sqrt{t}\widehat{S}t,i\sqrt{t-1}\widehat{S}_{t-1,i})\}2\frac{G^{2}}{\sqrt{c}}-1\sqrt{T}≤ \\ \sum^{d}_{i=1}\{D^{2}_{\widehat{S}1,i}\}\sum^{T}_{t=2}\sum^{d}_{i=1}\{D^{2}_{(} (\sqrt{t}\widehat{S}_{t,i}\sqrt{t-1}\widehat{S}_{t-1,i})\}\frac{G^{2}}{\sqrt{c}}1)\sqrt{T}+D^{2}_{\sqrt{T}}\sum^{d}_{i=1}\widehat{S}_{T,i}-\frac{G^{2}}{\sqrt{c}}).\sqrt{T}$

证毕

定理1 设f(w)为一般凸函数, 取

β 1t= tt+2, α t= α(t+2)t,

假设存在常数c, 使得 S︿t, i≥ c> 0, wt由式(1)产生, 则

f(wT)-f(w* )≤ f(w0)-f(w* )1+T+ DT22α(1+T)∑i=1dS︿T, i+ α(2T-1)2(1+T)cG2.

证明 由引理1及投影的非扩张性可得

‖ wt+1+pt+1-w* ‖S˙t2≤ wt+pt-w* - αtS︿t-1gt ‖S˙t2=‖ wt+pt-w* ‖S˙t2 ‖αtt ‖S˙t-122< wt+pt-w* , αtt> ≤ ‖ wt+pt-w* + ‖S˙t2 ‖αt ‖S˙t-12( αt(wt)-f(w* ))-2 ( αtt(wt)-f(wt-1)), ‖ wt+1+pt+1-w* + ‖S˙t2f 2α(1+t)twt)-f(w* ))≤ ‖ wt+pt-w* + ‖S˙t2t ‖αt+ ‖S˙t-12( 2αttt-1)-f(w* )).

等式两边同时乘以 t, 得

t‖ wt+1+pt+1-w* ‖S˙t2+2α (1+t)(f(wt)-f(w* ))≤ twt+pt-w* ‖S˙t2α2tgt ‖2S˙t-12α t(f(wt-1)-f(w* )).

将上式从t=1, 2, …, T累加, 得

2α (1+T)(f(wT)-f(w* ))≤ 2α (f(w0)-f(w* ))+ ∑t=1Ttwt+pt-w* ‖S˙t2‖wt+1+pt+1-w* ‖S˙t2 ∑t=1Tα2tgt ‖S˙t-12

根据引理2, 可得

f(wT)-f(w* )≤ f(w0)-f(w* )1+T+ DT22α(1+T)∑i=1dS︿T, i+ α(2T-1)2(1+T)cG2.

证毕

推论1 设f(w)为一般凸函数, 取

β 1t= tt+2, α t= α(t+2)t, S︿t, i≥ c> 0,

wt由式(1)产生, 则

f 1T∑t=1Twt-f(w* )≤ O 1T.

推论1也表明个体收敛速率比平均收敛速率更难以获得.综上所述, 获得AdaBHB在非光滑一般凸条件下的个体收敛速率.然而上述证明都是在批处理条件下完成的, 所以这种操作并不适用于大规模数据集.为了使AdaBHB适合处理大规模机器学习问题, 接下来将算法推广至随机形式.

考虑较简单的二分类问题, 训练样本集:

S={(xi, yi)|i=1, 2, …, m}⊆Rn× {1, -1},

其中, xi为样本特征, yi为样本的标签值, 假设(xi, yi)是独立同分布的.

假设非光滑学习问题的损失函数为hinge损失, 即

fi(w)=max{0, 1-yi< w, xi> },

则优化目标函数为:

minw∈Qf(w)= 1m∑i=1mfi(w).

由于hinge损失函数的次梯度有多种计算方式, 这里采用文献[18]的方式进行计算, 即

fi(wt)= 1m∑(xi, yi)∈Ay+yixi, (3)

其中,

At⊆S, At+={(xi, yi)∈ At∶ yi< w, xi> < 1},

实验中设定|At|=1, i是算法迭代到第t步时为计算当前梯度而随机抽取的样本序号.当样本满足独立同分布条件时, 经过随机抽取方式计算得到的随机次梯度fi(wt)就是梯度在wt处的无偏估计.

约束条件下随机形式的AdaBHB的迭代公式如下:

wt+1=PQ wt-αtS︿t-1fi(wt)+β1t(wt-wt-1), S︿tSt1/2δtId, St=β 2tSt-1+(1-β 2t)[gt-(wt-wt-1)]2. (4)

相比批处理形式下次梯度gt的每次计算都需遍历样本集, 随机次梯度fi(wt)只需选取一个样本即可.

AdaBHB的执行步骤如下所示.

算法 AdaBHB

输入 循环次数T

输出 wT

初始化 向量w1∈ Q

For t=1 to T

等可能地选取i=1, 2, …, m

根据式(3)计算次梯度fi(wt)

取β 1t= tt+2, α t= α(t+2)t

通过式(4)计算wt+1

End for

从算法中可看出, 随机形式的算法只是将批处理形式下目标函数的梯度替换为无偏估计.Rakhlin等[19]给出将批处理算法的regret界转换为随机算法regret界的技巧, 该技巧对于定理1同样成立.与文献[14]和文献[15]类似, 本文可将定理1推广至随机形式, 得到定理2.

定理2 设f(w)为一般凸函数, 取

β 1t= tt+2, α t= α(t+2)t, S︿t, i≥ c> 0,

wt由式(4)产生, 则

E(f(wT)-f(w* ))≤ f(w0)-f(w* )1+T+ DT22α(1+T)∑i=1dS︿T, i+ α(2T-1)2(1+T)cG2.

由定理2可知, AdaBHB具有O(1/ t)的最优个体收敛速率.在算法复杂度方面, 假设样本数量为n, AdaBHB的空间复杂度为O(n).由于AdaBHB在不增加每步迭代计算代价的基础上, 更合理地利用历史梯度的信息, 时间复杂度仅取决于达到特定精度所需的迭代步数, 即收敛速率, 因此, 对于非光滑一般凸问题, AdaBHB达到收敛精度ε , 时间复杂度为Ω (1/ε 2).

3 实验及结果分析

凸优化实验中的问题模型为支持向量机中常见的hinge损失.本文采用Astro、A9a、Covtype、Ijcnn1、Rcv1、W8a标准数据集, 均来源于LIBSVM网站.

在深度学习实验中, 按照Wang等[20]和Tao等[13]的思路, 模型为典型的ResNet-18网络及构造的一般4层卷积神经网络(Convolutional Neural Net-work, CNN), 采用CIFAR10、CIFAR100和MNIST常用标准数据集.CIFAR10数据集包含50 000个训练样本, 10 000个测试样本.CIFAR100数据集包含50 000个训练样本, 10 000个测试样本.MNIST数据集包含60 000个训练样本, 10 000个测试样本.

为了验证AdaBHB既在理论上具有最优收敛性, 又在实验上具有良好效果, 对比算法选取理论上收敛性最优的Heavy-Ball(HB)算法、AdaHB, 以及在实验上表现良好的随机梯度下降(Stochastic Gradient Descent, SGD)、Adam、Ada-Belief.

两组实验使用相同的参数设置.对于所有算法共同具有的超参数α , 采取从{1, 0.1, 0.01, 0.001, 0.0001}中线性搜索的方式, 并取其中最优的一次实验结果, 作为算法的最终输出.对比算法的其它参数设置均采用文献中该算法在实验表现最佳的参数.SGD的学习率α t=α / t.HB的计算方式及学习率取自文献[15].根据文献[6]和文献[11], 在Adam和AdaBelief中, α t=α / t, ε =1e-8, β 1=0.9, β 2=0.99.AdaHB和AdaBHB按照本文的设置选取

α t= α(t+2)t, β 1t= tt+2, β 2t=0.99.

为了降低随机因素产生的影响, 各算法在每个数据集上均运行5次, 取平均值作为最后输出.

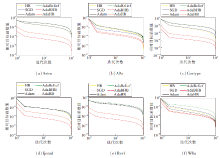
在凸优化实验中, 调用有效投影稀疏学习(Spares Learning with Efficient Projections, SLEP)工具箱的函数, 实现投影的计算, PQ为l1范数球

{w∶ ‖ w≤ z‖ 1}

上的投影算子.根据数据集的不同, z对应选取不同的值, 并且各算法均取相同的约束参数.从理论分析的角度出发, AdaBHB应具有最优的收敛速率.

各算法在6个数据集上的收敛速率对比如图1所示, 图中纵坐标表示当前目标函数值与最优目标函数值之差.由图可见, 在100步迭代之后, 各算法在6个标准数据集上都达到10-4的精度, 收敛趋势基本相同, AdaBHB收敛最快, 这与理论分析是吻合的.

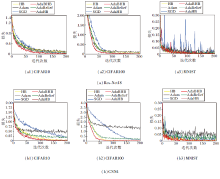
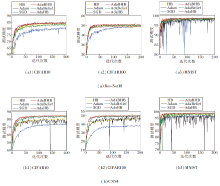
图1 各算法在6个数据集上的收敛速率对比Fig.1 Comparison of convergence rate of different algorithms on 6 datasets

在深度学习实验中, 采用参数权重衰减和批量归一化策略以减少过拟合, 所用的损失为交叉熵.图2为各算法在2个网络上的损失对比, 图3为各算法在2个网络上的测试精度对比.

图2 各算法在2个网络上的损失对比Fig.2 Loss value comparison of different algorithms on 2 networks

图3 各算法在2个网络上的测试精度对比Fig.3 Comparison of test accuracy of different algorithms on 2 networks

由图2和图3可见, AdaBHB在损失降低速率上明显占优, 这也促进其在测试精度上效果良好.在其它深度学习网络上的实验也验证AdaBHB取得较优的实验效果, 因此具有普遍性.由于论文篇幅限制, 本文仅展示较典型的残差网络Res-Net18和CNN4上的结果.

实验表明, AdaBHB不仅在非光滑凸条件下理论上可获得最优的个体收敛速率, 并且在深度学习实验中也取得性能的提升.这也说明AdaBelief 的步长调整技巧可作为一般性的减少震荡、提升算法泛化性能的方法.AdaBHB结合传统动量方法的优点, 可发展出更多性能良好的优化算法.

4 结束语

本文结合AdaBelief的步长调整技巧和Heavy-Ball型动量项, 提出基于AdaBelief的Heavy-Ball动量方法(AdaBHB), 证明算法具有最优的个体收敛速率, 并在深度学习实验中得到验证.今后将研究强凸情况下AdaBHB的个体收敛速率, 以及将Nesterov加速梯度(Nesterov Accelerated Gradient, NAG)型动量与AdaBelief的步长调整技巧结合的优化算法的收敛速率等问题.

参考文献
[1] ROBBINS H, MONRO S. A Stochastic Approximation Method. The Annals of Mathematical Statistics, 1951, 22(3): 400-407. [本文引用:2]
[2] POLYAK B T. Some Methods of Speeding up the Convergence of Iteration Methods. USSR Computational Mathematics and Mathematical Physics, 1964, 4(5): 1-17. [本文引用:2]
[3] NESTEROV Y. A Method of Solving a Convex Programming Problem with Convergence Rate. Soviet Mathematics Doklady, 1983, 27(2): 372-376. [本文引用:1]
[4] DUCHI J, HAZAN E, SINGER Y. Adaptive Subgradient Methods for Online Learning and Stochastic Optimization. Journal of Machine Learning Research, 2011, 12: 2121-2159. [本文引用:1]
[5] MUKKAMATA M C, HEIN M. Variants of RMSProp and ADAGrad with Logarithmic Regret Bounds // Proc of the 34th International Conference on Machine Learning. New York, USA: ACM, 2017: 2545-2553. [本文引用:1]
[6] KINGMA D P, BA J. Adam: A Method for Stochastic Optimization[C/OL]. [2021-04-20]. https: //arxiv. org/pdf/1412. 6980. pdf. [本文引用:3]
[7] KRIZHEVSKY A, SUTSKEVER I, HINTON G E. ImageNet Classification with Deep Convolutional Neural Networks. Communications of the ACM, 2017, 60(6): 84-90. [本文引用:1]
[8] REDDI S J, KALE S, KUMAR S. On the Convergence of Adam and Beyond[C/OL]. [2021-04-20]. https: //openreview. net/pdf?id=ryQu7f-RZ. [本文引用:4]
[9] ZINKEVICH M. Online Convex Programming and Generalized Infi-nitesimal Gradient Ascent // Proc of the 20th International Confe-rence on Machine Learning. New York, USA: ACM, 2003: 928-936. [本文引用:1]
[10] AZAMI H, SANEI S, MOHAMMADI K. Improving the Neural Network Training for Face Recognition Using Adaptive Learning Rate, Resilient Back Propagation and Conjugate Gradient Algorithm. International Journal of Computer Applications, 2011, 34(2): 22-26. [本文引用:1]
[11] ZHUANG J T, TANG T, DING Y F, et al. AdaBelief Optimizer: Adapting Stepsizes by the Belief in Observed Gradients[C/OL]. [2021-04-20]. https: //arxiv. org/pdf/201007468v2. pdf. [本文引用:5]
[12] ZOU F Y, SHEN L, JIE Z Q, et al. A Sufficient Condition for Convergences of Adam and RMSProp // Proc of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2019: 11119-11127. [本文引用:2]
[13] TAO W, LONG S, WU G W, et al. The Role of Momentum Parameters in the Optimal Convergence of Adaptive Polyak's Heavy-Ball Methods[C/OL]. [2021-04-20]. https: //openreview. net/pdf?id=L7WD8ZdscQ5. [本文引用:7]
[14] 陶蔚, 潘志松, 储德军, 等. 使用 Nesterov 步长策略投影次梯度方法的个体收敛性. 计算机学报, 2018, 41(1): 164-176.
(TAO W, PAN Z S, CHU D J, et al. The Individual Convergence of Projected Subgradient Methods Using the Nesterov's Step-Size Strategy. Chinese Journal of Computers, 2018, 41(1): 164-176. ) [本文引用:2]
[15] 程禹嘉, 陶蔚, 刘宇翔, 等. Heavy-Ball 型动量方法的最优个体收敛速率. 计算机研究与发展, 2019, 56(8): 1686-1694.
(CHENG Y J, TAO W, LIU Y X, et al. Optimal Individual Convergence Rate of the Heavy-Ball-Based Momentum Methods. Chinese Journal of Computer Research and Development, 2019, 56(8): 1686-1694. ) [本文引用:3]
[16] AGARWAL A, BARTLETT P L, RAVIKUMAR P, et al. Information-Theoretic Lower Bounds on the Oracle Complexity of Stochastic Convex Optimization. IEEE Transactions on Information Theory, 2012, 58(5): 3235-3249. [本文引用:1]
[17] SHAMIR O, ZHANG T. Stochastic Gradient Descent for Non-smooth Optimization: Convergence Results and Optimal Averaging Schemes // Proc of the 30th International Conference on Machine Learning. New York, USA: ACM, 2013: 71-79. [本文引用:1]
[18] SHALEV-SHWARTZ S, SINGER Y, SREBRO N, et al. Pegasos: Primal Estimated Sub-Gradient Solver for SVM. Mathematical Programming, 2011, 127: 3-30. [本文引用:1]
[19] RAKHLIN A, SHAMIR O, SRIDHARAN K. Making Gradient Descent Optimal for Strongly Convex Stochastic Optimization // Proc of the 29th International Conference on Machine Learning. New York, USA: ACM, 2012: 449-456. [本文引用:1]
[20] WANG G H, LU S Y, CHENG Q, et al. SAdam: A Variant of Adam for Strongly Convex Functions[C/OL]. [2021-04-20]. https: //arxiv. org/pdf/1905. 02957v1. pdf. [本文引用:1]