基于Triplet注意力的循环卷积神经网络模型

引用本文

汪璟玢, 雷晶, 张璟璇, 孙首男. 基于Triplet注意力的循环卷积神经网络模型. 模式识别与人工智能, 2022,35(2): 116-129
WANG Jingbin, LEI Jing, ZHANG Jingxuan, SUN Shounan. Circular Convolutional Neural Networks Based on Triplet Attention. PATTERN RECOGNITION AND ARTIFICIAL INTELLIGENCE, 2022,35(2): 116-129. 复制到剪切板

Doi: 10.16451/j.cnki.issn1003-6059.202202003 中图法分类号 TP 391
Permissions

《模式识别与人工智能》编辑部所有

基于Triplet注意力的循环卷积神经网络模型

汪璟玢¹, 雷晶¹, 张璟璇¹, 孙首男¹

1.福州大学计算机与大数据学院福州 350108

通信作者：

汪璟玢,硕士,副教授,主要研究方向为知识图谱、关系推理、分布式数据管理、知识表示.E-mail:wjb@fzu.edu.cn.

作者简介：

雷晶,硕士研究生,主要研究方向为知识图谱、关系推理、知识表示.E-mail: 1084961608@qq.com.

张璟璇,硕士研究生,主要研究方向为知识图谱、关系推理、知识表示.E-mail: 980807745@qq.com.

孙首男,硕士研究生,主要研究方向为知识图谱、关系推理、知识表示.E-mail: 954752598@qq.com.

收稿日期: 2021-08-23 接受日期: 2022-01-17

资助项目: 国家自然科学基金项目(No.61672159)、福建省自然科学基金项目(No.2021J01619)资助

摘要

现有的融合文本或邻居信息的知识补全模型忽略文本和邻居之间的相互作用,难以捕获与实体具有较强语义相关性的信息,加上基于卷积神经网络的模型未考虑实体中的关系相关信息,导致预测性能不佳.因此,文中结合文本信息和拓扑邻居信息,提出基于Triplet注意力的循环卷积神经网络模型.首先,通过语义匹配的方式,选取文本描述中与实体具有较强语义相关性的单词.再与拓扑邻居复合作为实体邻居,增强实体表示.然后,重塑实体的融合表示和关系表示.最后,利用Triplet注意力优化卷积输入,使卷积操作能提取实体中与关系相关的特征,提升模型性能.在多个公开数据集上的链路预测实验表明,文中模型性能较优.

关键词: 知识图谱补全; 文本信息; 拓扑邻居; 循环卷积; Triplet注意力

Circular Convolutional Neural Networks Based on Triplet Attention

WANG Jingbin¹, LEI Jing¹, ZHANG Jingxuan¹, SUN Shounan¹

1.College of Computer and Data Science, Fuzhou University, Fuzhou 350108

Corresponding author:

WANG Jingbin, master, associate professor. Her research interests include knowledge graph, relation reasoning, distributed data management and knowledge representation.

About Author:

LEI Jing, master student. Her research interests include knowledge graph, relation reasoning and knowledge representation.

ZHANG Jingxuan, master student. Her research interests include knowledge graph, relation reasoning and knowledge representation.

SUN Shounan, master student. His research interests include knowledge graph, relation reasoning and knowledge representation.

Fund:Supported by National Natural Science Foundation of China(No.61672159), Natural Science Foundation of Fujian Province(No. 2021J01619)

Abstract

In the existing knowledge completion models with textual or neighbor information, the interaction between texts and neighbors is ignored. Therefore, it is difficult to capture the information with strong semantic relevance to entities. In addition, the relationship-specific information in the entities is not taken into account in the models based on convolutional neural networks, which results in poor prediction performance. In this paper, a circular convolutional neural network model based on triplet attention is proposed combining textual and neighbor information. Firstly, the words with strong semantic relevance to entities in textual descriptions are selected by semantic matching, and then they are combined with topological neighbors as entity neighbors to enhance entity representations. Next, the fusion representations of the entity and the relation representations are reshaped. Finally, the triplet attention is utilized to optimize the input of the convolution and the convolution operation can extract the features related to the relations in the entities, which improves the model performance. Experiments on several public datasets show that the performance of the proposed model is superior.

Key words: Key Words Knowledge Graph Completion; Textual Information; Topological Neighbors; Circular Convolution; Triplet Attention

文章图片

知识图谱为实体和关系提供大量的结构化信息, 现已成功应用于人工智能任务, 如推荐系统^[1]、语义解析^[2]、信息抽取^[2]、问答^[3]等.典型的知识库有YAGO^[4]、 Freebase^[5]、 DBpedia^[6]等.

然而, 大型的知识图谱, 即使包含数十亿个三元组, 仍是不完整的, 会缺失很多有效的三元组^[7].为了补全知识图谱, 预测不完整三元组中缺失值, Bengio等^[8]提出基于知识图谱的表示学习方法— — 知识表示学习(Knowledge Representation Learning, KRL).Bordes等^[9]提出TransE(Translating Embe-dding), 将关系视为头实体到尾实体的一种平移变换.在欧拉恒等式的启发下, Sun等^[10]提出RotatE(Knowledge Graph Embedding by Relational Rotation in Complex Space), 并取得较优效果.Yang等^[11]提出DistMult, 将多关系矩阵限制为对角矩阵, 进行多关系表示学习.Trouillon等^[12]提出ComplEx(Com-plex Embeddings), 将DistMult拓展到复数空间, 对不对称关系进行建模.Dettmers等^[13]提出ConvE(Convolutional 2D Knowledge Graph Embeddings), 将卷积神经网络(Convolutional Neural Network, CNN)用于表示学习的模型.Vashishth等^[14]提出Inter-actE, 在ConvE的基础上增加实体和关系之间的交互, 大幅增强ConvE的表现力.

虽然上述模型取得良好效果, 但都只利用三元组本身的结构信息, 不可避免地会受到知识库的稀疏性和不完整性的影响, 导致模型区分能力较弱.

为了解决稀疏性问题, 学者们开始引入文本信息, 增强知识表示, 并取得不错效果.Yao等^[15]提出KG-BERT(Bidirectional Encoder Representations from Transformers(BERT) for Knowledge Graph Comple-tion), 利用预训练模型BERT, 结合丰富的文本信息, 将实体和关系的描述或名称全部放入BERT中, 实现知识补全.然而, 实体的文本描述通常包含数百个单词, 含有很多不必要的单词, 会造成冗余, 这些冗余的单词会稀释实体特征, 阻碍潜在关系的表达^[16].KG-BERT无法处理冗长文本, 导致计算成本较高且预测结果容易受到文本中冗余信息的影响, 存在一定的局限性.

为了解决长文本的冗余问题, 并提取文本中的关键信息, Veira等^[17]提出WWV(Weighted Word Vectors).作者认为文本中相同的单词在不同的关系下贡献度是不同的, 因此, 引入注意力机制, 关注文本中的关键单词.然而, 注意力机制的使用还是会忽略一些与实体语义相关性较强的单词.

近年来, 模型中引入拓扑邻居的方法也得到学者的广泛关注.Vashishth等^[18]提出CompGCN(Com-position-Based Multi-relational Graph Convolution Networks), 考虑多种关系, 将邻居信息通过图神经网络融入实体嵌入中, 增强知识表示.然而CompGCN忽略不同邻居贡献度不同的性质, 容易受到邻居中噪声的影响.Kong等^[19]提出LENA(Loca-lity-Expanded Neural Embedding for Knowledge Base Completion), Bansal等^[20]提出A2N(Attending to Neighbors for Knowledge Graph Inference), 都利用注意力机制聚合邻居, 可减轻邻居中噪声的影响.

然而, 通过注意力机制给邻居分配权重的方式会忽略实体和邻居之间的语义相关性, 阻碍模型性能的进一步提升.实际上, 在知识图谱中, 如果邻居出现在实体的文本描述中, 说明该邻居与实体具有较强的语义相关性.LENA和A2N虽然会为实体的邻居分配不同的注意力权重, 但权值的分配未考虑文本描述对邻居的影响, 容易丢失拓扑邻居中隐含的语义信息, 影响模型性能.

在知识图谱中, 不同的关系会关注实体的不同属性和特征.现有的基于CNN的知识补全模型在提取关系和实体的交互特征时, 容易受到实体中与关系无关的属性和特征的影响.

为了更好地捕获文本描述中与实体具有较强语义相关性的单词, 本文提出基于Triplet注意力的循环卷积神经网络模型(Circular Convolution Neural Networks Based on Triplet Attention, CCTA).首先, 通过语义匹配的方式选取文本中的关键单词作为实体的语义邻居.然后从拓扑邻居中选取与实体相关性较强的邻居与语义邻居结合, 作为实体的实体邻居, 进一步增强实体表示.为了区分实体在不同关系下呈现的不同含义, 提高CNN提取关键特征的能力, 本文利用Triplet注意力^[21]优化CNN的输入, 给特定关系下的实体特征赋予更高的权重, 避免受到预测无关信息的干扰, 提高模型的区分能力和补全性能.在两个公开数据集上的实验表明, CCTA在多个评估指标上性能较优, 由此证实其有效性.

1 基于Triplet注意力的循环卷积神经网络模型

1.1 符号表示

本文将知识库定义为G={E, R, T}, 其中, E为实体的集合, R为关系的集合, T为知识的集合.一个知识也称为一个三元组(h, r, t)∈ T, 其中h∈ E表示头实体, r∈ R表示关系, t∈ E表示尾实体.使用e∈ R^d和r∈ R^d表示实体e和关系r的嵌入表示, 其中, |R|表示关系数量, |E|表示实体数量, d表示嵌入维度.实体e的语义邻居集合

N^text(e)={ $n_{1}^{text}$ , $n_{2}^{text}$ , …, $n_{m}^{text}$ }, $n_{i}^{text}$ ∈ E;

拓扑邻居集合

N^stru(e)={ $n_{1}^{stru}$ , $n_{2}^{stru}$ , …, $n_{n}^{stru}$ }, $n_{i}^{stru}$ ∈ E;

实体邻居集合

N'(e)={n₁, n₂, …, n_k}, n_i∈ E;

名称单词集合

Word(e)={word₁, word₂, …, word_u}, word_i∈ E.

本文定义:e_neigh为实体的邻居表示, e_name为实体的名称表示, e_{name_stru}为实体的名称结构表示, e_stru为实体的结构表示, e_add为实体的融合表示.

1.2 模型组成部分

基于Triplet注意力的循环卷积神经网络模型(CCTA)总体框架如图1所示.CCTA主要由4部分组成.

1)融合表示生成模块.从文本描述和拓扑邻居中收集得到实体邻居, 并对其进行编码, 再结合实体名称信息进一步增强语义, 最后生成实体的融合表示.

2)实体关系交互模块.将得到的融合表示和关系表示进行特征重排和特征重塑, 以捕获特征之间丰富的交互作用.

3)基于Triplet注意力的循环卷积神经网络模块.使用Triplet注意力跨维度交互计算注意力, 弱化输入特征中的冗余特征, 再通过循环卷积操作提取实体和关系的交互特征, 得到特征图.

4)三元组评分.将特征图拉平, 再通过一个全连接层映射到实体嵌入维度, 最后与尾实体矩阵进行点积和归一化, 得到三元组的评分和概率.

	Figure Option View Download New Window
	图1 CCTA总体框图Fig.1 Overall framework of CCTA

1.2.1 融合表示生成模块

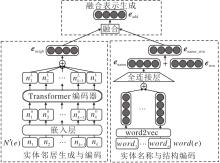
融合表示生成模块是为了生成实体e的融合表示, 主要由实体邻居生成与编码、实体名称与结构编码、融合表示生成组成, 具体结构如图2所示.

1)实体邻居生成与编码.在生成实体邻居之前, 本文首先借助实体的文本描述, 构造其对应的语义邻居.通过名称匹配的方式, 从文本描述中提取相关性较强的单词构成语义邻居.本文定义实体e的语义邻居为实体e的文本描述中提到的其它实体, 或文本描述中实体e的语义邻居集合:

N^text(e)= {ei|i_∈De_,ei_≠e}∪ {ej|∈ $D_{e_{j}}$ ej_≠e},

其中, D_e表示实体e的文本描述中的单词集合, e∈ E, e_i∈ E, e_j∈ E.

	Figure Option View Download New Window
	图2 融合表示生成模块结构图Fig.2 Structure of fusion representation generation module

本文合并实体e的拓扑邻居集合

N^stru(e)={ $n_{1}^{stru}$ , $n_{2}^{stru}$ , …, $n_{n}^{stru}$ }

和语义邻居集合

N^text(e)={ $n_{1}^{text}$ , $n_{2}^{text}$ , …, $n_{m}^{text}$ },

作为实体e的实体邻居.考虑到简单合并上述两个邻居集合的元素, 在某些情况下, 数量会多达数百个, 大幅降低计算效率, 因此, 需要筛选具有代表性的邻居, 才能在准确表示实体语义的情况下减少计算量.

对于每个实体, 最多从两个邻居集合中选择k个邻居作为最终的实体邻居, 具体的选择机制如下.给定一个实体e, 首先选择同时出现在两个邻居集合的邻居, 即两个集合的交集:

N_∩=N^text(e)∩ N^stru(e).

如果取交集后的邻居个数超过k个, 选择邻居中的前k个作为最终的实体邻居集合N'(e), 如果取交集后的邻居个数不足k个, 通过随机采样剩余的邻居填充实体邻居, 直到个数达到k个, 即

N'(e)= $\{\begin{array}{l} Selec t_{k} (N_{⋂}), & | N_{⋂} | > k \\ N_{⋂} ⋃ N_{sample}, & | N_{⋂} | < k \end{array}$

其中,

N_sample=Sampl $e_{k - | N_{⋂} |}$ (N^text(e)∪ N^stru(e)-N_∩),

Select_k(· )表示选取前k个邻居, Sampl $e_{k - | N_{⋂} |}$ (· )表示随机采样k-|N_∩|个邻居.

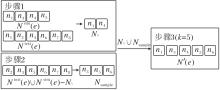
实体邻居选择示意图如图3所示, 以选取实体邻居个数k=5且|N_∩|< k为例.

	Figure Option View Download New Window
	图3 实体邻居选择示意图Fig.3 Illustration of entity neighbors selection

通过上述策略, 得到实体e的实体邻居

N'(e)={n₁, n₂, …, n_k}.

为了编码实体邻居, 先将实体邻居进行初始化, 使用一个维数为d的嵌入层emb, 得到实体邻居的初始表示:

$n_{i}^{0}$ =emb(n_i), i=1, 2, …, k.

接下来, 将得到的实体邻居的初始表示序列{ $n_{1}^{0}$ , $n_{2}^{0}$ , …, $n_{k}^{0}$ }输入L层的Transformer中, 对初始表示序列进行编码:

$n_{i}^{l}$ =Transformer( $n_{i}^{l - 1}$ ), l=1, 2, …, L,

其中 $n_{i}^{l}$ 表示第l层的隐层状态.将第L层的隐层状态求平均, 得到实体的邻居表示:

e_neigh=σ $[\frac{1}{N' (e)} \overset{k}{\sum_{i=1}} n_{i}^{L}]$ ,

其中, σ 表示激活函数, $n_{i}^{L}$ 表示Transformer编码器第L层的隐层状态.当本文设置σ =tanh时, 实验取得最优效果.

2)实体名称与结构的编码.本文利用实体的名称单词进一步增强实体表示.对于实体e的名称单词序列

Word(e)={word₁, word₂, …, word_u}

中的每个单词, 使用word2vec进行初始化, 对词向量求平均, 经过一个全连接层降维到实体嵌入空间, 得到实体的名称表示:

e_name=W1 $[\frac{1}{| Word (e) |} \overset{u}{\sum_{i=1}} w ord 2 v ec (w ordi))]$ b1_,

其中W₁、b₁表示全连接层的权重矩阵和偏置.

然后, 将实体的名称表示e_name和实体的结构表示e_stru相加, 得到实体的名称结构表示:

e_{name_stru}=e_name+e_stru.

3)融合表示生成.将上述得到的邻居表示e_neigh和名称结构表示e_{name_stru}进行融合, 得到实体的融合表示e_add.

本文设计如下3种融合方式.

(1)门控融合(Gate).考虑到邻居表示e_neigh和名称结构表示e_{name_stru}对实体e的贡献度可能不同, 引入门控机制, 如图4(a)所示.实体的融合表示e_add定义为

e_add=α e_neigh+(1-α )e_{name_srtu},

其中, α ∈ [0, 1]表示学习的参数, 用于调整两部分的比例.

(2)相加融合(Add).将邻居表示e_neigh和名称结构表示e_{name_stru}直接相加, 如图4(b)所示.实体的融合表示e_add定义为

e_add=e_neigh+e_{name_srtu}.

(3)连接映射融合(Conmap).将邻居表示e_neigh和名称结构表示e_{name_stru}进行拼接操作, 将拼接后的表示经过全连接层, 映射到与实体表示相同的维度空间, 得到e_add.如图4(c)所示.实体的融合表示e_add定义为

e_add=W₂[e_neigh; e_{name_srtu}]+b₂,

	Figure Option View Download New Window
	图4 融合方式Fig.4 Different ways of fusion

其中, [; ]为拼接操作, W₂表示映射矩阵, b₂表示偏置.

1.2.2 实体关系交互模块

假设实体融合表示e_add=(a₁, a₂, …, a_d), 关系表示r=(b₁, b₂, …, b_d), 其中, a_i∈ R, b_i∈ R, 表示特征.本文通过如下2步实现实体和关系的充分交互.

1)特征重排.对于融合表示e_add和关系表示r, 分别生成对应的随机排列.然而若不加以限制, 随机排列的个数会非常大, 因此本文限制生成的随机排列个数为C, 可用集合

P={( $e_{add}^{1}$ , r¹), ( $e_{add}^{2}$ , r²), …, ( $e_{add}^{C}$ , r^C)}

表示, P_i表示集合P中第i个元素.特征重排过程如图5(a)所示.

2)特征重塑.定义重塑函数ϕ , 将P_i转化为矩阵ϕ (P_i)∈ R^p^×^q, p× q=2d, 使两个相邻的特征经过重塑后不再相邻.将重塑函数ϕ 作用于每个P_i(i=1, 2, …, C), 再将ϕ (P_i)进行拼接, 得到张量

X=[ϕ (P₁); ϕ (P₂); …; ϕ (P_C)],

其中[; ]为拼接操作.具体重塑方式如图5(b)所示.

	Figure Option View Download New Window
	图5 实体关系交互步骤Fig.5 Interaction steps of entities and relations

1.2.3 基于Triplet注意力的循环卷积神经网络

模块

对于重塑后的张量X∈ R^C^×^H^×^W, 显然, X中并不是所有特征都对补全有用, 无用的信息会影响卷积的性能, 因此在卷积之前, 使用Triplet注意力关注实体表示中与关系更相关的特征, 给更有用的信息赋予更高的权重, 过滤不必要的噪声.Triplet注意力是一种通过使用三分支结构捕获跨维度交互以计算注意力权重的方法.

在计算Triplet注意力的过程中, 会涉及到Z-pool的操作, 对于输入张量M, Z-pool操作的具体运算过程如下:

Z-pool(M)=[MaxPool₀_d(M); AvgPool₀_d(M)],

其中, MaxPool表示最大池化, AvgPool表示平均池化, [; ]为拼接操作, 0d表示进行最大池化和平均池化操作的第0维.例如, 一个形状为C× H× W的张量进行Z-pool操作后会产生一个形状为2× H× W的张量.

对于输入张量X∈ R^C^×^H^×^W, 首先将它传递给Triplet注意力模块中的3个分支, 3个分支的具体运算如下.

在第1个分支中, 捕获空间H维度和通道C维度之间的跨通道交互.首先X沿着H轴逆时针旋转90° , 得到 $X_{H^{-}}$ ∈ R^W^×^H^×^C, 然后 $X_{H^{-}}$ 在W维度上进行Z-pool操作, 再进行卷积操作, 经过Sigmoid激活函数生成注意力权重.将得到的注意力权重与 $X_{H^{-}}$ 进行点乘, 再沿着H轴顺时针旋转90° , 得到 $X_{H}^{*}$ , 保持X的原始输入状态.第1个分支的计算过程表示为

$X_{H}^{*}$ =( $X_{H^{-}}$ σ (ω ₁* (Z-pool( $X_{H^{-}}$ )) $)_{H^{+}}$ ,

其中, H^-表示沿H轴逆时针旋转90° , H⁺表示沿H轴顺时针旋转90° , ω ₁表示卷积核, * 表示卷积操作, σ 表示激活函数.

类似地, 在第2个分支中, 捕获通道C维度和空间W维度的相互作用.首先X沿着W轴逆时针旋转90° , 得到 $X_{W^{-}}$ ∈ R^H^×^C^×^W.然后, $X_{W^{-}}$ 在H维度上进行Z-pool操作, 再进行卷积操作, 经过Sigmoid激活函数生成注意力权重.将得到的注意力权重与 $X_{W^{-}}$ 进行点乘, 然后沿着W轴顺时针旋转90° 得到 $X_{W^{-}}^{*}$ , 保持X的原始输入状态.第2个分支的计算过程表示为

$X_{W^{-}}^{*}$ =( $X_{W^{-}}$ σ (ω ₂* (Z-pool( $X_{W^{-}}$ ))) $)_{W^{+}}$ ,

其中, W^-表示沿W轴逆时针旋转90° , W⁺表示沿W轴顺时针旋转90° , ω ₂表示卷积核, * 表示卷积操作, σ 表示激活函数.

对于最后一个分支, 输入张量X, 通过Z-pool操作, 通道数减少为2, 再进行卷积操作, 经过Sigmoid激活函数产生注意力权重, 将注意力权重与X进行点乘, 得到最终的张量:

X^*=Xσ (ω ₃* (Z-pool(X))),

其中, ω ₃表示卷积核, * 表示卷积操作, σ 表示激活函数.

简单地平均3个分支的张量, 得

X'= $\frac{1}{3}$ ( $X_{H}^{*}$ + $X_{W}^{*}$ +X^*).

最后将X'输入循环卷积神经网络中, 卷积完后得到特征映射

V=σ （X $'^{\overset{⌒}{*}}$ ω ）,

其中, $\overset{⌒}{*}$ 表示循环卷积操作, ω 表示卷积核, σ 表示ReLU激活函数.

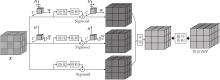
基于Triplet注意力的循环卷积神经网络模块结构如图6所示.

	Figure Option View Download New Window
	图6 基于Triplet注意力的循环卷积神经网络模块结构图Fig.6 Circular convolution neural networks based on Triplet attention

1.2.4 三元组评分

将得到的特征图V经过拉平操作变成向量I=vec(V), 经过一个全连接层, 将向量I映射到实体嵌入维度, 得到输出向量P, 再与尾实体矩阵进行点积, 得到三元组的得分.CCTA的得分函数定义为

f(h, r, t)=σ (I· W₃+b₃)· e_t,

其中, σ 表示ReLU激活函数, W₃表示全连接层的变换矩阵, b₃表示偏置.

然后使用Sigmoid处理得分函数, 将其映射到0-1区间, 得到候选实体的概率分布:

p=Sigmoid(f(h, r, t)).

本文使用交叉熵损失函数训练模型, 具体定义如下:

L=- $\frac{1}{| E |} \overset{|E|}{\sum_{i=1}}$ [y_iln(p_i)+(1-y_i)ln(1-p_i)], yi₌ $\{\begin{array}{l} 1, & (h, r, t) \in G \\ 0, & (h, r, t) \in G' \end{array}$

其中, G表示正确的三元组集合, G'表示不正确的三元组集合(通过随机替换头尾实体得到).

2 实验及结果分析

2.1 实验环境

本文在FB15k-237、WN18RR数据集上评估CCTA.FB15k-237数据集是Freebase数据集的子集, 包含237种关系、14 541个实体.WN18RR数据集包含11种关系、40 943个实体.本文使用ConvE^[20]提供的数据集, 各数据集统计信息如表1所示.

表1 实验数据集 Table 1 Experimental datasets

在训练期间, 本文使用自适应低阶矩估计优化器(Adaptive Estimates of Lower-Order Moments)进行优化.在训练时, 使用网格搜索法寻找最优参数.

为了防止过拟合, 本文引入如下失活参数:循环卷积之前的inp_drop, 循环卷积之后的feat_drop, 全连接层之后的hidden_drop.

本文模型需要调整的超参数及其范围如下:嵌入维度d=100, 200, 300, 批处理大小batch=128, 256, 学习率lr=0.000 1, 0.000 5, 0.001, 0.005, 卷积核数量num_filt=36, 64, 96, 128, 卷积核大小ker_sz=7× 7, 9× 9, 11× 11, 实体邻居个数k=10, 20, 30, 40, Transformer头数att_head=1, 2, 3, 4, Transformer层数att_layer=1, 2, 3, 4, 重塑特征个数perm=1, 2, …, 7, hid_drop=0.1, 0.2, …, 0.5, feat_drop=0.1, 0.2, …, 0.5, inp_drop=0.1, 0.2, …, 0.5.

CCTA的最优参数设置如表2所示.

为了评估本文方法的有效性, 选择如下3类对比模型.1)基于三元组结构的模型:TransE^[9]、RotatE^[10]、DistMult^[11]、ComplEx^[12]、InteractE^[14].这类方法建模知识图谱中的三元组结构, 学习实体和关系的嵌入.2)融合拓扑邻居信息的模型:CompGCN^[18]、 LENA^[19]、 A2N^[20].这类方法通过邻居信息增强实体表示.3)融合外部信息的模型:KG-BERT^[15]、WWV^[17]、 PE-WWV(Parameter-Efficient WWV)^[17], FeatureSum^[17].对于WWV、PE-WWV和FeatureSum, 本文只展示基于TransE的结果.这类方法融合知识图谱结构外的信息, 学习实体和关系的嵌入.

表2 本文模型在2个数据集上的最优参数 Table 2 Optimal parameters of the proposed model on 2 datasets

本文使用链路预测^[22]评估模型性能, 链路预测的目标是预测头尾实体, 即对于缺失头或尾实体的三元组(?, r, t)和(h, r, ?), 预测缺失的头实体或尾实体.对于每个三元组, 通常使用数据集上的全部实体分别替换头实体或尾实体, 并过滤新生成的三元组集合中已存在于训练集、验证集和测试集的三元组.然后, 分别计算替换后每个三元组的得分, 计算真实三元组的评分在所有三元组的评分中的排名以评判模型优劣, 期望真实三元组的排名越高越好.

本文将使用链路预测中常用的两种评估指标以评估模型的有效性, 分别为平均倒数排名(Mean Reciprocal Rank, MRR), 排名前N个的命中概率(Hits@N), N=1, 3, 10.MRR和Hits@N值越大越好.

2.2 链路预测结果

各模型在WN18RR、FB15k-237数据集上的链路预测结果如表3所示.在表中, TransE、DisMult、ComplEx、RotatE结果来自文献[10], InteractE结果来自文献[14], WWV、PE-WWV、FeatureSum是将源码应用于新的数据集得到的结果, CompGCN、KG-BERT、LENA、A2N结果来自原论文, 黑体数字表示最优结果, 斜体数字表示次优结果.WWV、PE-WWV、FeatureSum采用如下参数设置进行源码的复现:epochs=200, batch=1 024, lr=0.1, d=100, 超参数γ =1.0.CCTA-Gate、CCTA-Add、CCTA-Conmap分别表示CCTA应用1.2.1节提到的3种不同融合方式得到的结果.

表3 各模型在2个数据集上的链路预测结果 Table 3 Link prediction results of different models on 2 datasets

由表3可得如下结论.

1)Gate、Add、Conmap这3种融合方式都取得较优效果, 相对而言, 采取Add融合方式的模型效果最优.

2)相比只利用三元组结构信息的模型, 在WN-18RR数据集上, 不管采用哪种融合方式, CCTA总体上链路预测结果最优.相比同样利用CNN的InteractE, CCTA-Add在MRR、Hits@10、Hits@1上分别提升4.54%, 6.06%、3.95%.相比复数模型RotatE, CCTA-Add在MRR、Hits@3、Hits@1上分别提升1.68%、1.02%、4.44%.在FB15k-237数据集上, CCTA在大部分情况下链路预测结果最优.相比InteractE, CCTA-Add在Hits@10上提升0.50%, 其它指标跟InteractE相当.相比RotatE, CCTA-Add在MRR、Hits@3、Hits@1上分别提升4.73%、1.00%、8.71%.CCTA利用附加信息增强实体的表示, 提高知识表示的区分能力, 并利用Triplet注意力关注实体中关系相关的部分, 进一步提升补全的性能.而InteractE只利用三元组结构信息, 忽略丰富的外部信息, 而且对于输入特征未进一步过滤噪声, 导致模型性能不佳.

3)相比利用邻居信息的模型, CCTA具有一定的竞争力.相比A2N, CCTA的指标值在两个数据集上都有大幅提升, 在WN18RR数据集上, 相比A2N, CCTA-Add在MRR、Hits@10、Hits@3、Hits@1上分别提升7.56%、9.80%、8.04%、6.43%.在FB15k-237数据集上, 相比A2N, CCTA-Add在MRR、Hits@10、Hits@3、Hits@1上分别提升11.67%、10.70%、11.78%、13.36%.相比CompGCN, 在WN18RR数据集上, CCTA-Add在MRR、Hits@10、Hits@3、Hits@1上分别提升1.04%、2.56%、0.61%、0.90%, 在FB15k-237数据集上, CCTA-Add的所有指标与CompGCN基本持平.

为了进一步分析邻居个数对实验结果的影响, 本文统计两个数据集的邻居个数, 结果如表4所示.由表可看出, WN18RR数据集的平均拓扑邻居个数很少, 导致A2N和CompGCN利用邻居信息给模型带来的性能增益有限, 而CCTA能利用语义信息从另一个角度反映实体的属性和特征, 进一步增强实体表示, 提升模型性能.在FB15k-237数据集上, 相比CompGCN, CCTA性能提升不明显, 主要是因为FB15k-237数据集的平均语义邻居个数和平均拓扑邻居个数都很多, 此时拓扑邻居占据实体邻居的主要部分, 稀释语义特征, 加上拓扑邻居中含有较多的噪声, 容易影响模型性能.相比A2N, CCTA性能有大幅提升, 主要是由于A2N在利用注意力机制分配权重时忽略语义信息的影响, 且相比使用神经网络的CompGCN和CCTA, A2N表达性较弱.

表4 2个数据集上邻居个数统计 Table 4 Neighbor numbers of 2 datasets

4)相比利用文本信息的模型, CCTA在两个数据集上指标值都取得显著提升.相比KG-BERT:在WN18RR数据集上, CCTA-Add在Hits@10、Hits@3上分别提升6.87%、77.50%; 在FB15k-237数据集上, CCTA-Add在Hits@10、Hits@3上分别提升28.10%、50.78%.这说明相对传统的融合文本信息的模型, 利用文本描述生成的实体邻居对链路预测性能有更进一步的提升, 以这种方式提取的文本信息会减少不相关信息带来的影响, 在此基础上进一步融合拓扑邻居信息和实体名称信息, 使模型性能更具鲁棒性.

2.3 不同关系类型链路预测实验

为了进一步分析模型特性, 本文参考TransE^[9], 对WN18RR测试集上关系类型进行统计, 划分4种不同类型的子集:一对一(1-to-1)、一对多(1-to-N)、多对一(N-to-1)、多对多(N-to-N).具体的划分方式为:计算每个关系的头实体个数和尾实体个数, 如果平均个数小于1.5, 标记为1, 否则标记为N.

WNT8RR、FB15k-237数据集上不同关系类型链路预测结果如表5所示, 表中黑体数字表示最优结果, 斜体数字表示次优结果.由表可看出, 在不同关系类型上, CCTA在WN18RR数据集上的链路预测结果均有所提升.相比InteractE, CCTA-Add在1-to-N复杂关系类型上, MRR、Hits@10、Hits@3、Hits@1分别提升25.5%、28.8%、22.2%、22.7%, 在N-to-1复杂关系类型上, MRR、Hits@10、Hits@3、Hits@1分别提升23.5%、15.5%、23.6%、30.4%.在FB15k-237数据集上的N-to-1、1-to-N和N-to-N复杂关系类型上, CCTA在4个指标上都至少有3个可取得最优.上述分析说明CCTA在处理复杂关系上更有优势, 这得益于外部信息提高知识表示的区分能力.

表5 各模型在不同关系类型上的链路预测结果 Table 5 Link prediction results of different models for different relationship types

为了进一步验证CCTA在处理复杂关系上的优势, 对于两个具有相同头实体和关系的三元组(h₁, r₁, t₁)和(h₁, r₁, t₂), 本文分析在1-to-N关系中不同尾实体的相似度.理论上说, 为了区分两个不同的尾实体, 模型学习到的表示应越不相似越好.本文参照文献[23], 定义两个实体之间的相似性:

similarity= $\frac{| t_{2} - t_{1} |}{|t_{2}|}$ .

similarity越小表示两个实体越相似, 模型的区分能力越差, 否则越强.

Czech Republic和Ottoman Empire这两个实体在InteractE和CCTA中相似性的可视化结果如图7所示.将长度d=200的向量重塑为一个10× 20的矩阵, 矩阵中的每个格子表示两个实体在相同维度下的相似度值, 值越接近于1, 对应的格子颜色越浅.由图7可看出, CCTA比InteractE包含更多接近于1的区域(即颜色较浅的区域), 说明CCTA能更好地区分Czech Republic和Ottoman Empire, 而InteractE区分得不够明显, 容易学到相似的向量表示, 混淆两个实体.

	Figure Option View Download New Window
	图7 Czech Republic和Ottoman Empire相似性的可视化结果Fig.7 Visualization of similarity between "Czech Republic" and "Ottoman Empire"

2.4 模型结构消融实验

为了进一步评估CCTA中每个模块的效果, 在WN18RR数据集上进行消融实验.将应用不同融合方式的模型记为CCTA-X; 移除Triplet注意力模块的模型记为CCTA-X(-TA); 移除Transformer编码器模块的模型记为CCTA-X(-Transformer), 此处, 将实体邻居的表示进行求平均, 消除Transformer编码器带来的影响; 同时移除Triplet模块和Trans-former编码器模块的模型记为CCTA-X(-TA-Trans-former).为了确保评估的合理性, CCTA-X(-TA)、CCTA-X(-Transformer)和CCTA-X(-TA-Transformer)均采用与CCTA-X相同的参数.

CCTA结构消融实验结果如表6所示, 表中黑体数字表示最优结果, 斜体数字表示次优结果.

表6 CCTA在WN18RR数据集上的结构消融实验结果 Table 6 Results of structure ablation experiment of CCTA on WN18RR dataset

由表6可看出, 不管是采取哪种融合方式的模型, 任何一个模块的缺失, 都会降低模型性能, 说明Triplet注意力模块、Transformer编码器模块都是CCTA中至关重要的一部分, 尤其是Transformer编码器模块, 这说明Transformer编码器可捕获实体邻居中重要的特征信息, 比简单地对向量求平均性能更强.移除Triplet注意力模块后模型性能下降, 说明在计算注意力权重时捕获跨维度交互的重要性, Triplet注意力模块可在卷积之前通过捕获跨维度交互关注对预测更有用的信息, 给这些信息赋予更高的权重, 进一步提升模型性能.

2.5 附加信息的消融实验

为了验证附加信息的有效性, 在WN18RR数据集上对不同的附加信息进行消融实验.将移除拓扑邻居的模型记为CCTA-X(-top); 移除语义邻居的模型记为CCTA-X(-sem); 移除实体名称的模型记为CCTA-X(-name); 移出所有附加信息的模型记为CCTA-X(-all).

CCTA附加信息消融实验结果如表7所示, 表中黑体数字表示最优结果, 斜体数字表示次优结果.由表可得到如下结论.

表7 CCTA在WN18RR数据集上的附加信息消融实验结果 Table 7 Results of additional information ablation experiment of CCTA on WN18RR dataset

1)不消融的模型效果最优, 说明只利用三元组结构信息的模型存在一定的局限性, 可通过引入附加信息提升模型性能.

2)相比CCTA-X, CCTA-X(-name)和CCTA-X(-top)性能略微下降, 说明引入实体名称和拓扑邻居对模型性能具有一定提升作用, 但提升效果有限.一方面是因为实体名称的单词序列较短, 蕴含的语义信息较少; 另一方面是因为拓扑邻居中包含较多的不相关信息, 影响模型性能.

3)相比CCTA-X, CCTA-X(-sem)性能明显下降, 说明语义邻居的引入对模型性能的提升具有显著影响, 这得益于本文通过名称匹配进行语义邻居的筛选, 能过滤很大一部分不相关的信息.

4)CCTA-X(-all)效果优于CCTA-X(-sem), 原因是拓扑邻居中包含的不相关信息会给模型带来负面影响.从CCTA-X(-name)和CCTA-X(-sem)的效果可看出, 在包含拓扑邻居的基础上, 引入语义邻居的模型性能得到显著提升, 这说明语义邻居能抵消一部分不相关信息带来的性能衰减, 提升补全效果.

2.6 不同类型邻居个数的影响

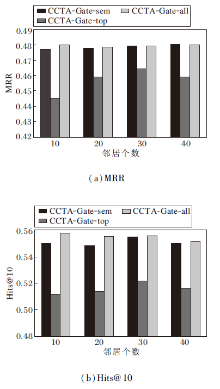
为了验证不同类型邻居个数对模型性能的影响, 进一步分析邻居个数.在以融合方式为Gate的CCTA-Gate上进行实验.记CCTA-Gate-top为只利用拓扑邻居的模型, CCTA-Gate-sem为只利用语义邻居的模型, CCTA-Gate-all为利用实体邻居的模型.

3个模型的MRR、Hit@10值对比结果如图8所示.由图可得出如下结论.

	Figure Option View Download New Window
	图8 邻居个数对指标值的影响Fig.8 Influence of neighbor numbers on index value

1)CCTA-Gate-top性能最差, 说明拓扑邻居的引入对模型性能带来的提升效果较有限.随着拓扑邻居个数的增加, CCTA-Gate-top的性能呈现先提升后下降的趋势, 说明随着拓扑邻居个数的增加, 可提升模型性能, 但是当达到峰值后, 继续增加拓扑邻居的个数会引入大量的不相关信息, 降低模型效果.

2)在总体情况下, CCTA-Gate-all性能最优, 很稳定, 不易受到实体邻居个数的影响, 说明同时结合两种类型的邻居可进一步提升模型性能.另一方面, CCTA-Gate-all性能不易受到拓扑邻居中不相关信息的影响, 说明语义邻居可抵消一部分拓扑邻居带来的负面影响, 使模型更具有鲁棒性.

3)CCTA-Gate-sem效果也很稳定, 但是会略差于CCTA-Gate-all, 说明只引入语义邻居, 模型性能就已得到很大提升, 但在此基础上引入拓扑邻居, 还可进一步提升模型性能.

2.7 特征重排效果

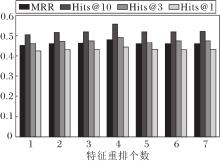
为了验证CCTA中特征重排的效果, 在WN18RR数据集上进行模型在不同特征重排个数下的实验.CCTA-Gate的性能随特征重排个数影响的结果如图9所示.由图可看出, 随着特征重排个数的增加, CCTA的MRR、Hits@10、Hits@3、Hits@1值都有所提升, 当特征重排个数为4时, 模型达到最优效果, 当特征重排个数继续增加时, 模型性能不升反降.这说明实体和关系之间的交互是有用的, 同时也是有限的, 当特征重排个数较少时, 模型得到的交互信息很少, 对性能起不到促进作用.随着特征重排个数的增加, 模型能学习到的交互信息会越来越丰富, 性能也随之提升, 之后由于交互过多又会引入额外的噪声, 限制模型性能.

	Figure Option View Download New Window
	图9 特征重排个数对指标值的影响Fig.9 Influence of permutation numbers on index value

2.8 实体邻居编码器对比

为了进一步证实Transformer编码器的有效性, 在WN18RR数据集上使用如下编码器对实体邻居进行编码:Linear表示线性变换, MLP表示多层感知机, GCN^[24]表示图卷积神经网络编码器, GAT^[25]表示带注意力的图卷积神经网络编码器.各编码器的指标值结果如表8所示, 表中黑体数字表示最优结果.由表可看出, Linear和MLP的时间复杂度虽然小于Transformer, 但效果却不如Transformer.适用于捕获图结构信息的GCN和GAT编码器效果也差于Transformer编码器, 而且GCN和GAT需要为每个实体建立一个邻接矩阵, 复杂度较高.总之, Trans-fomer在编码实体邻居上具有一定优势, 但是复杂性相对会高一些.

表8 编码器对指标值的影响 Table 8 Influence of encoder on index value

2.9 卷积层数敏感性实验

为了进一步分析模型中卷积层数对实验结果的影响, 在WN18RR数据集上进行卷积层数的敏感性实验, 结果如表9所示, 表中黑体数字表示最优结果.由表可看出, 使用一层卷积操作的效果仍最优, 多层卷积的使用并未提升性能, 而且复杂性也会随着层数的增加而增加, 因此本文仍保留一层卷积的实验结果.

表9 卷积层数的敏感性实验结果 Table 9 Experimental results on the sensitivity of the number of convolutional layers

3 结束语

本文提出基于Triplet注意力的循环卷积神经网络模型(CCTA).模型利用文本描述、实体名称和拓扑邻居共同增强实体表示, 并通过特征重排、特征重塑增加实体和关系之间的交互, 最后利用带有Triplet注意力模块的循环卷积神经网络提取交互特征.实验表明, 本文模型能达到较优性能.特别地, 语义邻居的引入可提升文本质量和补全性能.在卷积操作之前, Triplet注意力的使用能使模型关注到实体中关系相关的属性与特征, 增强卷积操作提取特征的能力, 进一步提升模型的补全性能.今后将进一步融合图像信息, 改进知识表示, 并将模型应用到开放世界中, 预测知识库中不存在的实体或关系.此外, 本文模型虽然取得具有竞争力的效果, 但使用Transformer编码器对实体邻居进行编码, 复杂性较高, 今后将进一步研究更有效的编码方式, 降低模型的复杂度.

参考文献

文献选项

[1]	ZHANG F Z, YUAN N J, LIAN D F, et al. Collaborative Know-ledge Base Embedding for Recommender Systems//Proc of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York, USA: ACM, 2016: 353-362. [本文引用:1]
[2]	BERANT J, CHOU A, FROSTIG R, et al. Semantic Parsing on Freebase from Question-Answer Pairs//Proc of the Conference on Empirical Methods in Natural Language Processing. Stroudsburg, USA: ACL, 2013: 1533-1544. [本文引用:2]
[3]	BORDES A, CHOPRA S, WESTON J. Question Answering with Subgraph Embeddings//Proc of the Conference on Empirical Me-thods in Natural Language Processing. Stroudsburg, USA: ACL, 2014: 615-620. [本文引用:1]
[4]	SUCHANEK F M, KASNECI G, WEIKUM G. YAGO: A Core of Semantic Knowledge//Proc of the 16th International Conference on World Wide Web. New York, USA: ACM, 2007: 697-706. [本文引用:1]
[5]	BOLLACKER K, EVANS C, PARITOSH P, et al. Freebase: A Collaboratively Created Graph Database for Structuring Human Knowledge//Proc of the ACM SIGMOD International Conference on Management of Data. New York, USA: ACM, 2008: 1247-1249. [本文引用:1]
[6]	AUER S, BIZER C, KOBILAROV G, et al. DBpedia: A Nucleus for a Web of Open Data//Proc of the International Semantic Web Conference. Berlin, Germany: Springer, 2007: 722-735. [本文引用:1]
[7]	WEST R, GABRILOVICH E, MURPHY K, et al. Knowledge Base Completion via Search-Based Question Answering//Proc of the 23rd International Conference on World Wide Web. New York, USA: ACM, 2014: 515-526. [本文引用:1]
[8]	BENGIO Y, COURVILLE A, VINCENT P. Representation Lear-ning: A Review and New Perspectives. IEEE Transactions on Pa-ttern Analysis and Machine Intelligence, 2013, 35(8): 1798-1828. [本文引用:1]
[9]	BORDES A, USUNIER N, GARCIA-DURÁN A, et al. Translating Embeddings for Modeling Multi-relational Data//Proc of the 26th International Conference on Neural Information Processing Systems. Cambridge, USA: The MIT Press, 2013, II: 2787-2795. [本文引用:3]
[10]	SUN Z Q, DENG Z H, NIE J Y, et al. RotatE: Knowledge Graph Embedding by Relational Rotation in Complex Space[C/OL]. [2021-08-20]. https://openreview.net/references/pdf?id=BJqafQvBE. [本文引用:3]
[11]	YANG B S, YIH W T, HE X D, et al. Embedding Entities. Embedding Entities and Relations for Learning and Inference in Knowledge Bases[C/OL]. [2021-08-20]. https: //arxiv. org/pdf/1412. 6575. pdf. [本文引用:2]
[12]	TROUILLON T, WELBL J, RIEDEL S, et al. Complex Embe-ddings for Simple Link Prediction//Proc of the 33rd International Conference on Machine Learning. New York, USA: ACM, 2016: 2071-2080. [本文引用:2]
[13]	DETTMERS T, MINERVINI P, STENETORP P, et al. Convolutional 2D Knowledge Graph Embeddings//Proc of the 32nd AAAI Conference on Artificial Intelligence. Palo Alto, USA: AAAI, 2018: 1811-1818. [本文引用:1]
[14]	VASHISHTH S, SANYAL S, NITIN V, et al. InteractE: Improving Convolution-Based Knowledge Graph Embeddings by Increa-sing Feature Interactions. Proceedings of the AAAI Conference on Artificial Intelligence, 2020, 34(3): 3009-3016. [本文引用:3]
[15]	YAO L, MAO C S, LUO Y. KG-BERT: BERT for Knowledge Graph Completion[C/OL]. [2021-08-20]. https: //arxiv. org/pdf/1909. 03193. pdf. [本文引用:2]
[16]	FAN M, ZHOU Q, ZHENG T F, et al. Distributed Representation Learning for Knowledge Graphs with Entity Descriptions. Pattern Recognition Letters, 2017, 93: 31-37. [本文引用:1]
[17]	VEIRA N, KENG B, PADMANABHAN K, et al. Unsupervised Embedding Enhancements of Knowledge Graphs Using Textual Associations//Proc of the 28th International Joint Conference on Artificial Intelligence. San Francisco, USA: IJCAI, 2019: 5218-5225. [本文引用:4]
[18]	VASHISHTH S, SANYAL S, NITIN V, et al. Composition-Based Multi-relational Graph Convolutional Networks[C/OL]. [2021-08-20]. https: //openreview. net/attachment?id=BylA_C4tPr&name=original_pdf. [本文引用:2]
[19]	KONG F S, ZHANG R C, MAO Y Y, et al. LENA: Locality-Expand ed Neural Embedding for Knowledge Base Completion. Proceedings of the AAAI Conference on Artificial Intelligence, 2019, 33(1): 2895-2902. [本文引用:2]
[20]	BANSAL T, JUAN D C, RAVI S, et al. A2N: Attending to Neigh-bors for Knowledge Graph Inference//Proc of the 57th Annual Meeting of the Association for Computational Linguistics. Stroudsburg, USA: ACL, 2019: 4387-4392. [本文引用:3]
[21]	MISRA D, NALAMADA T, ARASANIPALAI A U, et al. Rotate to Attend: Convolutional Triplet Attention Module//Proc of the IEEE/CVF Winter Conference on Applications of Computer Vision. Washington, USA: IEEE, 2021: 3139-3148. [本文引用:1]
[22]	BORDES A, WESTON J, COLLOBERT R, et al. Learning Structured Embeddings of Knowledge Bases//Proc of the 25th AAAI Conference on Artificial Intelligence. Palo Alto, USA: AAAI, 2011: 301-306. [本文引用:1]
[23]	XU C J, NAYYERI M, ALKHOURY F, et al. TeRo: A Time-Aware Knowledge Graph Embedding via Temporal Rotation//Proc of the 28th International Conference on Computational Linguistics. Stroudsburg, USA: ACL, 2020: 1583-1593. [本文引用:1]
[24]	KIPF T N, WELLING M. Semi-Supervised Classification with Graph Convolutional Networks[C/OL]. [2021-12-03]. https: //arxiv. org/pdf/1609. 02907. pdf. [本文引用:1]
[25]	VELI$\check{C}$KOVI$\acute{C}$ P, CUCURULL G, CASANOVA A, et al. Graph Attention Networks[C/OL]. [2021-08-20]. https: //arxiv. org/pdf/171010903. pdf. [本文引用:1]

2016

0.0

... 知识图谱为实体和关系提供大量的结构化信息,现已成功应用于人工智能任务,如推荐系统^[1]、语义解析^[2]、信息抽取^[2]、问答^[3]等 ...

2013

0.0

... 知识图谱为实体和关系提供大量的结构化信息,现已成功应用于人工智能任务,如推荐系统^[1]、语义解析^[2]、信息抽取^[2]、问答^[3]等 ...

2014

0.0

... 知识图谱为实体和关系提供大量的结构化信息,现已成功应用于人工智能任务,如推荐系统^[1]、语义解析^[2]、信息抽取^[2]、问答^[3]等 ...

2007

0.0

... 典型的知识库有YAGO^[4]、 Freebase^[5]、 DBpedia^[6]等 ...

2008

0.0

... 典型的知识库有YAGO^[4]、 Freebase^[5]、 DBpedia^[6]等 ...

2007

0.0

... 典型的知识库有YAGO^[4]、 Freebase^[5]、 DBpedia^[6]等 ...

2014

0.0

... 然而,大型的知识图谱,即使包含数十亿个三元组,仍是不完整的,会缺失很多有效的三元组^[7] ...

2013

0.0

... 为了补全知识图谱,预测不完整三元组中缺失值,Bengio等^[8]提出基于知识图谱的表示学习方法#cod#x02014 ...

0.0

... Bordes等^[9]提出TransE(Translating Embe-dding),将关系视为头实体到尾实体的一种平移变换 ...

... 1)基于三元组结构的模型:TransE^[9]、RotatE^[10]、DistMult^[11]、ComplEx^[12]、InteractE^[14] ...

... 3 不同关系类型链路预测实验为了进一步分析模型特性,本文参考TransE^[9],对WN18RR测试集上关系类型进行统计,划分4种不同类型的子集:一对一(1-to-1)、一对多(1-to-N)、多对一(N-to-1)、多对多(N-to-N) ...

0.0

... 在欧拉恒等式的启发下,Sun等^[10]提出RotatE(Knowledge Graph Embedding by Relational Rotation in Complex Space),并取得较优效果 ...

... 1)基于三元组结构的模型:TransE^[9]、RotatE^[10]、DistMult^[11]、ComplEx^[12]、InteractE^[14] ...

... 在表中,TransE、DisMult、ComplEx、RotatE结果来自文献[10],InteractE结果来自文献[14],WWV、PE-WWV、FeatureSum是将源码应用于新的数据集得到的结果,CompGCN、KG-BERT、LENA、A2N结果来自原论文,黑体数字表示最优结果,斜体数字表示次优结果 ...

0.0

... Yang等^[11]提出DistMult,将多关系矩阵限制为对角矩阵,进行多关系表示学习 ...

... 1)基于三元组结构的模型:TransE^[9]、RotatE^[10]、DistMult^[11]、ComplEx^[12]、InteractE^[14] ...

2016

0.0

... Trouillon等^[12]提出ComplEx(Com-plex Embeddings),将DistMult拓展到复数空间,对不对称关系进行建模 ...

... 1)基于三元组结构的模型:TransE^[9]、RotatE^[10]、DistMult^[11]、ComplEx^[12]、InteractE^[14] ...

2018

0.0

... Dettmers等^[13]提出ConvE(Convolutional 2D Knowledge Graph Embeddings),将卷积神经网络(Convolutional Neural Network, CNN)用于表示学习的模型 ...

2020

0.0

... Vashishth等^[14]提出Inter-actE,在ConvE的基础上增加实体和关系之间的交互,大幅增强ConvE的表现力 ...

... 1)基于三元组结构的模型:TransE^[9]、RotatE^[10]、DistMult^[11]、ComplEx^[12]、InteractE^[14] ...

0.0

... Yao等^[15]提出KG-BERT(Bidirectional Encoder Representations from Transformers(BERT) for Knowledge Graph Comple-tion),利用预训练模型BERT,结合丰富的文本信息,将实体和关系的描述或名称全部放入BERT中,实现知识补全 ...

... 3)融合外部信息的模型:KG-BERT^[15]、WWV^[17]、 PE-WWV(Parameter-Efficient WWV)^[17],FeatureSum^[17] ...

2017

0.0

... 然而,实体的文本描述通常包含数百个单词,含有很多不必要的单词,会造成冗余,这些冗余的单词会稀释实体特征,阻碍潜在关系的表达^[16] ...

2019

0.0

... 为了解决长文本的冗余问题,并提取文本中的关键信息,Veira等^[17]提出WWV(Weighted Word Vectors) ...

... 3)融合外部信息的模型:KG-BERT^[15]、WWV^[17]、 PE-WWV(Parameter-Efficient WWV)^[17],FeatureSum^[17] ...

0.0

... Vashishth等^[18]提出CompGCN(Com-position-Based Multi-relational Graph Convolution Networks),考虑多种关系,将邻居信息通过图神经网络融入实体嵌入中,增强知识表示 ...

... 2)融合拓扑邻居信息的模型:CompGCN^[18]、 LENA^[19]、 A2N^[20] ...

2019

0.0

... Kong等^[19]提出LENA(Loca-lity-Expanded Neural Embedding for Knowledge Base Completion),Bansal等^[20]提出A2N(Attending to Neighbors for Knowledge Graph Inference),都利用注意力机制聚合邻居,可减轻邻居中噪声的影响 ...

... 2)融合拓扑邻居信息的模型:CompGCN^[18]、 LENA^[19]、 A2N^[20] ...

2019

0.0

... 本文使用ConvE^[20]提供的数据集,各数据集统计信息如表1所示 ...

... 2)融合拓扑邻居信息的模型:CompGCN^[18]、 LENA^[19]、 A2N^[20] ...

2021

0.0

... 为了区分实体在不同关系下呈现的不同含义,提高CNN提取关键特征的能力,本文利用Triplet注意力^[21]优化CNN的输入,给特定关系下的实体特征赋予更高的权重,避免受到预测无关信息的干扰,提高模型的区分能力和补全性能 ...

2011

0.0

... 本文使用链路预测^[22]评估模型性能,链路预测的目标是预测头尾实体,即对于缺失头或尾实体的三元组(?,r,t)和(h,r,?),预测缺失的头实体或尾实体 ...

2020

0.0

... 本文参照文献[23],定义两个实体之间的相似性: ...

0.0

... 8 实体邻居编码器对比为了进一步证实Transformer编码器的有效性,在WN18RR数据集上使用如下编码器对实体邻居进行编码:Linear表示线性变换,MLP表示多层感知机,GCN^[24]表示图卷积神经网络编码器,GAT^[25]表示带注意力的图卷积神经网络编码器 ...

0.0