引用本文
孙林, 黄金旭, 徐久成, 马媛媛. 基于自适应鲸鱼优化算法和容错邻域粗糙集的特征选择算法. 模式识别与人工智能, 2022,35(2): 150-165
SUN Lin, HUANG Jinxu, XU Jiucheng, MA Yuanyuan. Feature Selection Based on Adaptive Whale Optimization Algorithm and Fault-Tolerance Neighborhood Rough Sets. PATTERN RECOGNITION AND ARTIFICIAL INTELLIGENCE, 2022,35(2): 150-165.  
Doi: 10.16451/j.cnki.issn1003-6059.202202006 中图法分类号 TP 311
Permissions
Copyright©2022, 《模式识别与人工智能》编辑部
《模式识别与人工智能》编辑部 所有
基于自适应鲸鱼优化算法和容错邻域粗糙集的特征选择算法
孙林1,2, 黄金旭1, 徐久成1, 马媛媛1
1.河南师范大学 计算机与信息工程学院 新乡 453007
2.河南师范大学 智慧商务与物联网技术河南省工程实验室 新乡 453007

通信作者：

孙林,博士,副教授,主要研究方向为粒计算、大数据挖掘、生物信息学.E-mail:sunlin@htu.edu.cn.

作者简介:

黄金旭,硕士研究生,主要研究方向为数据挖掘.E-mail:983993140@qq.com.

徐久成,博士,教授,主要研究方向为粒计算、大数据挖掘、智能信息处理.E-mail:xjc@htu.edu.cn.

马媛媛,博士,副教授,主要研究方向为粒计算、智能信息处理.E-mail:mayuanyuan@htu.edu.cn.

收稿日期: 2021-09-22 接受日期: 2021-11-19
资助项目: 国家自然科学基金项目(No.62076089,61976082,62002103)、河南省科技攻关项目(No.212102210136)资助
摘要

针对传统鲸鱼优化算法(WOA)不能有效处理连续型数据、邻域粗糙集对噪声数据的容错性较差等问题,文中提出基于自适应WOA和容错邻域粗糙集的特征选择算法.首先,为了避免WOA过早陷入局部最优,基于迭代周期构建分段式动态惯性权重,改进WOA的收缩包围和螺旋捕食行为,设计自适应WOA.然后,为了解决邻域粗糙集对噪声数据缺乏容错性的问题,引入邻域内相同决策特征所占的比例,定义容错邻域上下近似集、容错近似精度和近似粗糙度、容错依赖度及容错近似条件熵.最后,基于容错邻域粗糙集构造适应度函数,使用自适应WOA,不断迭代以获取最优子群.高维数据集上采用费雪评分算法进行初步降维,降低算法的时间复杂度.在8个低维UCI数据集和6个高维基因数据集上的实验表明,文中算法可有效选择特征个数较少且分类精度较高的特征子集.

关键词: 鲸鱼优化算法(WOA); 特征选择; 邻域粗糙集; 邻域熵; 适应度函数
Feature Selection Based on Adaptive Whale Optimization Algorithm and Fault-Tolerance Neighborhood Rough Sets
SUN Lin1,2, HUANG Jinxu1, XU Jiucheng1, MA Yuanyuan1
1.College of Computer and Information Engineering, Henan Normal University, Xinxiang 453007
2.Henan Engineering Laboratory of Smart Business and Internet of Things Technology, Henan Normal University, Xinxiang 453007

Corresponding author:

SUN Lin, Ph.D., associate professor. His research interests include granular computing, big data mining and bioinformatics.

About Author:

HUANG Jinxu, master student. His research interests include data mining.

XU Jiucheng, Ph.D., professor. His research interests include granular computing, big data mining and intelligent information processing.

MA Yuanyuan, Ph.D., associate profe-ssor. Her research interests include granular computing and intelligent information proce-ssing.

Fund:Supported by National Natural Science Foundation of China(No.62076089,61976082,62002103), Key Scientific and Technology Program of Henan Province(No.212102210136)
Abstract

Traditional whale optimization algorithm(WOA) cannot handle continuous data effectively, and the tolerance of neighborhood rough sets(NRS) for noise data is poor. To address the issues, an algorithm of feature selection based on adaptive WOA and fault-tolerance NRS is presented. Firstly, a piecewise dynamic inertia weight based on iteration cycle is proposed to prevent the WOA from falling into local optimum prematurely. The shrinkage enveloping and spiral predation behaviors of WOA are improved, and an adaptive WOA is designed. Secondly, the ratio of the same decision features in the neighborhood is introduced to make up for the fault tolerance lack of NRS model for noise data, and the upper and lower approximations, approximation precision and approximation roughness, fault-tolerance dependence and approximation conditional entropy of fault-tolerance neighborhood are defined. Finally, a fitness function is constructed based on the fault-tolerance NRS, and then the adaptive WOA searches for the optimal feature subset through continuous iterations. The Fisher score is employed to reduce the dimensions of high-dimensional datasets preliminarily and the time complexity of the proposed algorithm effectively. The proposed algorithm is tested on 8 low-dimensional UCI datasets and 6 high-dimensional gene datasets. Experimental results demonstrate that the proposed algorithm selects fewer features effectively with high classification accuracy.

Key words: Key Words Whale Optimization Algorithm(WOA); Feature Selection; Neighborhood Rough Sets; Neighborhood Entropy; Fitness Function

特征选择作为数据预处理的关键步骤, 目前已广泛应用于机器学习、模式识别、数据挖掘等领域[1, 2].根据评价准则的不同, 特征选择一般分为3类:包装法、过滤法和嵌入法[3].包装法使用已确定的学习算法, 直接使用分类性能作为特征重要性程度的评价标准.过滤法是先对特征集进行筛选, 再使用学习算法进行训练, 特征选择的过程与学习算法无关.嵌入法是在使用学习算法进行训练的过程中, 自动进行特征选择.过滤法的评价准则依赖学习算法, 所选特征的准确率低于包装法, 但是包装法的计算开销较大.

粗糙集模型在处理数值型数据时需要对数据进行离散化处理, 然而离散化处理可能会导致数据出现信息损失[4, 5, 6].为此, 刘艳等[7]运用K-S检验, 提出基于邻域粗糙集的混合数据特征选择算法, 直接处理含有数值型和符号型数据的邻域信息系统.Chen等[8]分析邻域粗糙集中上下边界域的模糊性和类的不均匀分布, 提出基于差别矩阵的特征选择算法.Sun等[9]提出基于费雪评分算法(Fisher Score)和多标记邻域粗糙集的多标签分类特征选择方法.

但是, 上述邻域粗糙集模型通常沿用经典粗糙集求解上下近似时的包含关系, 导致邻域粗糙集理论缺乏一定的容错性[10].为了解决此问题, 彭潇然等[10]利用决策粗糙集模型中的最小风险决策规则, 在邻域空间中进行决策风险分析, 提出基于容错改进的邻域粗糙集属性约简算法.但是, 此研究是基于容错正域的约简算法, 并未讨论邻域粗糙集中依赖度、精度、粗糙度和特征重要度.

当前, 大部分邻域粗糙集模型通常仅是从代数观点或信息论观点研究特征选择方法.Hu等[11]基于矩阵的正域、负域和边界域, 设计动态更新近似方法, 提出基于矩阵的特征选择算法.Wang等[12]基于距离测度, 研究模糊粗糙集理论, 提出基于依赖度和特征重要度的特征约简算法.上述文献都是仅从代数角度进行特征选择, 只能反映特征对确定分类子集的影响[13].

目前, 基于信息论的特征选择已得到广泛研究.Sun等[14]研究联合信息熵, 结合Fisher score设计特征选择算法.然而, 如果仅从信息论单方面构造特征重要度, 那么只能反映特征对不确定分类子集的影响, 因此, 结合代数和信息论观点成为新的研究课题.Wang[15]给出代数和信息论观点下的特征重要度概念, 设计启发式约简算法.Sun等[16]结合ReliefF和邻域互信息, 提出特征选择算法.Sun等[17]基于Lebesgue测度和熵, 设计FSNTDJE(Fea-ture Selection Algorithm Based on the Neighborhood Tolerance De-pendency Joint Entropy).

群智能优化算法具有操作简单、全局寻优能力强等优点[18, 19, 20].学者们结合群智能优化算法与粗糙集理论, 研究特征选择算法, 已提出大量的群智能优化算法.例如:粒子群优化算法、蚁群优化算法、果蝇优化算法、蚱蜢算法、鲸鱼优化算法(Whale Opti-mization Algorithm, WOA)[20]等.相比传统的特征选择方法, 结合群智能优化算法的特征选择方法性能更优.Wang等[21]提出PSORSFS(Particle Swarm Optimization for Rough Set-Based Feature Selection Algorithm).孙林等[22]提出基于邻域粗糙集和帝王蝶优化的特征选择算法.

鲸鱼优化算法(WOA)通过模拟鲸鱼的收缩包围、螺旋式更新位置和随机捕猎的觅食机制进行寻优, 具有参数设置简单、收敛速度较快、寻优精度较高等特点, 同时具有良好的寻优能力[20].但是, 传统的WOA存在过早收敛和容易陷入局部最优的问题[23].因此, 本文使用自适应惯性权重改进WOA, 并与容错邻域粗糙集结合, 提出基于自适应WOA和容错邻域粗糙集的特征选择算法(Feature Selection Based on Adaptive WOA and Fault-Tolerance Neighborhood Rough Sets, FSAWFN).首先, 提出分段式的动态惯性权重, 改进WOA的收缩包围和螺旋捕食阶段, 设计自适应WOA(Adaptive WOA, A-WOA).再针对邻域粗糙集的零容错问题, 引入邻域内相同决策特征比例, 给出具有容错性的上下近似、精度、粗糙度的概念.然后, 将容错粗糙度引入熵中, 提出容错邻域近似条件熵的概念, 实现代数观点和信息论观点的结合.最后, 基于容错邻域粗糙集构造适应度函数, 使用A-WOA, 不断迭代以获取最优子群.针对高维数据集, 采用Fisher Score进行初步降维, 降低算法的时间复杂度.在8个低维UCI数据集和6个高维基因数据集上的实验表明, 本文算法可有效选择特征个数较少且分类精度较高的特征子集.

1 基础知识
1.1 鲸鱼优化算法

鲸鱼优化算法(WOA)是模拟座头鲸捕食行为而提出的一种寻优算法, 主要包括包围猎物、气泡网攻击和随机搜索3种行为[20].下面简要介绍3种行为的位置更新模型.

1)包围猎物.由于目标位置或最优个体位置未知, WOA需要假设目标位置.一般选择初始适应度值最大的个体位置为目标位置, 鲸鱼群体就会游向目标位置, 位置更新公式如下:

S(j+1)=S* (j)-AM.

其中:M=|ES* (j)-S(j)|, 为鲸鱼个体位置到目标位置的距离,

E=2r2 (1)

为系数变量, r2为0~1之间的随机数, S* (j)为假设的目标位置, S(j)为当前鲸鱼个体的位置, j为迭代次数;

A=2kr1-k, (2)

为系数变量,

k=2- 2jMaxiter,

为收敛因子, 在2~0之间递减, r1为0~1之间的随机数.

2)气泡网攻击.WOA模拟鲸鱼的气泡网攻击行为模型主要有如下2种.

(1)收缩包围圈.通过减少A中k值实现, A的取值范围为(-k, k), 随着k在2~0之间递减, A也在递减, 鲸鱼个体越来越接近目标位置.

(2)螺旋更新位置.计算鲸鱼个体到目标位置的距离, 利用螺旋线公式进行位置更新:

S(j+1)=M'ehlcos(2π l)+S* (j),

其中,

M'=|S* (j)-S(j)|,

为鲸鱼个体到目标位置的距离, h为螺旋线常数, l为(-1, 1)内的随机数.

一般情况下, 鲸鱼在捕猎时是边螺旋游向猎物, 边收缩包围圈, 以0.5为阈值描述气泡网攻击, 则

S(j+1)= S* (j)-AM, p< 0.5M'ehlcos(2πl)+S* (j), p≥0.5

其中, M为鲸鱼个体位置到目标位置的距离, p为0~1之间的随机数.

3)随机搜索.鲸鱼还可利用|A|的变化进行随机搜索.为了增强WOA的全局寻优能力, 当|A| > 1时, 强制鲸鱼群体根据随机选择的个体进行位置更新:

S(j+1)=Srand(j)-AM, (3)

其中,

M=|ESrand(j)-S(j)|,

Srand(j)为当前群体中随机一个鲸鱼的位置.

1.2 邻域粗糙集

给定邻域决策系统NDS=< U, C, D, δ > , U为论域, C为条件特征集, D为决策特征集, δ ∈ [0, 1]为邻域半径参数.对于∀ xi∈ U, 条件特征子集B⊆C, Δ B为距离函数, 则xi关于B的邻域类[7]表示为:

nBδ(xi)={xi∈ U, yi∈ U|Δ B(xi, yi)≤ δ }.

给定邻域决策系统NDS=< U, C, D, δ > , 对于任意特征子集B⊆C, 论域U上任意2个样本点xi和yi, i=1, 2, …, |U|之间的欧氏距离[8, 9]为:

Δ B(xi, yi)= ∑i=1U||xi-yi|2.

给定邻域决策系统NDS=< U, C, D, δ > , 对于任意条件特征子集B⊆C, 样本子集X⊆U, ∀ xi∈ U, i=1, 2, …, |U|, 则X关于B的邻域上/下近似集[8]表示为:

B¯(X)δ ={xi∈ U| nBδ(xi)∩ X≠ Ø }, B¯X)δ ={xi∈ U| nBδxi)⊆X}.

给定邻域决策系统NDS=< U, C, D, δ > , 对于任意条件特征子集B⊆C, 样本子集X⊆U, 则X关于B的邻域近似精度和邻域近似粗糙度[22]为:

αBδ(X)= B¯(X)δB¯(X)δ, ρBδ(X)=1- αBδ(X).

给定邻域决策系统NDS=< U, C, D, δ > , 对于任意条件特征子集B⊆C, 决策特征D导出的划分U/D={D1, D2, …, Dl}, 则D关于B的正域和依赖度[22]为:

POSB(D)= ∑t=1lB¯(Dt)δ , γ B(D)= |POSB(D)||U|,

其中, Dt∈ U/D, t=1, 2, …, l.

给定邻域决策系统NDS=< U, C, D, δ > , 对于任意条件特征子集B⊆C, ∀ xi∈ U, i=1, 2, …, |U|, nBδ(xi)表示xi关于B的邻域类, 则B的邻域熵[17]为:

H(B)=- ∑i=1U||nBδ(xi)||U|log2 |nBδ(xi)||U|.

2 基于自适应鲸鱼优化算法和容错邻域粗糙集的特征选择算法
2.1 自适应鲸鱼优化算法

褚鼎立等[23]强调:惯性权重的取值对算法的寻优能力和收敛能力具有至关重要的影响.在传统的WOA中, 惯性权重取较大的固定值, 虽然保证WOA的全局寻优能力, 但不利于WOA后期的局部寻优.因此, 本文将WOA的收缩包围和螺旋捕食行为都分为前期、中期和后期3个阶段, 根据迭代周期对惯性权重的取值进行动态调整.

定义1 基于迭代周期的分段式动态惯性权重为:

ω = 1-exp(rand(jMaxiter-1)), j≥13Maxiter1, j< 13Maxiter (4)

其中, rand表示0~1之间的随机数, j为迭代次数, Maxiter表示最大迭代次数.

在WOA前期, ω 仍保持较大的固定值, 使鲸鱼具有较大的搜索步长; 在WOA中后期, 随着迭代的进行, ω 的取值非线性递减, 使鲸鱼向全局最优解靠近, 加快WOA收敛.

根据式(4)计算惯性权重ω 的值.式(4)保证ω 的取值在[0, 1]内, 同时, 随着WOA的执行, ω 的取值呈现非线性递减, 有利于避免WOA后期陷入局部最优、无法跳出的现象.

定义2 依据动态惯性权重ω , 自适应WOA的收缩包围和螺旋捕食行为表示为:

S(j+1)=ω S* (j)-AM, (5)

S(j+1)=M'ehlcos(2π l)+ω S* (j), (6)

其中, ω 为动态惯性权重, A为系数变量, S* (j)为假设的目标位置, M'表示鲸鱼个体到目标位置的距离, h为螺旋线常数, l为(-1, 1)内的随机数.

A-WOA的具体步骤如下.首先, 设置最优位置或目标位置; 再根据迭代次数计算动态惯性权重ω ; 然后, 根据A和E的值, 进行包围猎物、气泡网攻击和随机搜索3种位置更新; 最后, 确定最优解和最优位置.

2.2 容错邻域粗糙集

邻域粗糙集继承传统粗糙集在构造上下近似时的包含关系, 导致邻域粗糙集缺乏一定的容错性[10].为了解决这一问题, 本文将容错性分析推广到邻域粗糙集模型中, 构建容错邻域粗糙集模型, 并定义基于容错的邻域近似精度、粗糙度和依赖度.

定义3 给定邻域决策系统NDS=< U, C, D, δ > , 对于任意条件特征子集B⊆C, nBδ(xi)表示xi关于B的邻域类, U/D={D1, D2, …, Dl}, 则邻域内相同决策特征所占的比例为:

μnBδ(xi)= |{x∈nBδ(xi)|D=Di}||nBδ(xi)|,

其中Di表示xi对应的等价类.同时, 需要说明的是:

1)若 μnBδ(xi)≥ α , 则xi∈ POS'(X), 其中, α ∈ [0, 1], 为概率阈值[10];

2)若 μnBδ(xi)< α 且 μnBδ(xi)> β , 则xi∈ BND'(X), 其中, α 、 β 为概率阈值, 0≤ β < α ≤ 1;

3)若 μnBδ(xi)≤ β , 则xi∈ NEG'(X), 其中, β ∈ [0, 1], 为概率阈值.

在传统的邻域粗糙集中, 有正域

POS(X) = B¯(X)

和边界域

BND(X) = B¯(X)- B¯(X).

定义4 给定邻域决策系统NDS=< U, C, D, δ > , 对于任意条件特征子集B⊆C, 样本子集X⊆U, 则X关于B的容错邻域上/下近似集为:

TB¯(X)δ =POS'(X)∪ BND'(X), TB¯X)δ =POS'(X).

定义5 给定邻域决策系统NDS=< U, C, D, δ > , 对于任意条件特征子集B⊆C, 样本子集X⊆U, 则X关于B的容错邻域近似精度和近似粗糙度为:

α B(X)= |TB¯(X)δ||TB¯(X)δ|, ρ B(X)=1-α B(X).

定义6 给定邻域决策系统NDS=< U, C, D, δ > , 对于任意条件特征子集B⊆C, 则决策特征D关于B的容错依赖度为:

γ 'B(D)= |POS'B(D)||U|.

粗糙度反映知识的不确定性程度, 邻域条件熵反映信息粒度引起的知识不确定性[14, 17].于是, 将基于容错的粗糙度引入邻域条件熵中, 得到基于容错的邻域近似条件熵.

定义7 给定邻域决策系统NDS=< U, C, D, δ > , 对于任意条件特征子集B⊆C, ∀ xi∈ U, i=1, 2, …, |U|, U/D={D1, D2, …, Dl}, α B(Dt)为容错邻域近似精度, ρ B(Dt)为近似粗糙度, 那么决策特征D相对于B的容错近似条件熵为:

H(D|B)=- ∑t=1llog2(1+ρB(Dt))· ∑t=1l∑i=1U||nBδ(xi)⋂Dt||U|og2|nBδ(xi)⋂Dt||nBδ(xi)| (7)

定理1 给定邻域决策系统NDS=< U, C, D, δ > , 对于任意条件特征子集B⊆C, xi关于B的邻域为 nBδ(xi), U/D={D1, D2, …, Dl}, 则有:

1)当且仅当∀ xi∈ U, nBδ(xi)=U, ∀ Dt∈ U/D, |Dt|=1时, H(D|B)取最大值|U|log2(|U|);

2)当且仅当所有对象都是正域中的元素时, H(D|B)取最小值0.

证明 先证明1).当|Dt|=1, nBδ(xi)=U时, 由定义4可知,

ρ B(Dt)=1, log2(1+ρ B(Dt))=1,

又因为

|nBδ(xi)⋂Dt||U|log2 |nBδ(xi)⋂Dt||nBδ(xi)|= 1|U|log2 1|U|,

因此, H(D|B)取最大值|U|log2(|U|).

再证明2).∀ xi∈ U, xi都是正域中的元素时, 有

α B(Dt)=1, ρ B(Dt)=1-α B(Dt)=0,

所以

log2(1+ρ B(Dt))=0,

H(D|B)取最小值0.

定理2 给定邻域决策系统NDS=< U, C, D, δ > , 对于任意2个条件特征子集P⊆C, Q⊆C, 如果Q⊆P, 那么

H(D|P) ≤ H(D|Q).

证明 对于任意条件特征子集Q⊆P⊆C, 样本xi∈ U,

U/D={D1, D2, …, Dl},

于是可得,

BQ¯(X)⊆ BP¯(X), BQ¯(X)⊇ BP¯(X), α P(X)≥ α Q(X), ρ P(X)≤ ρ Q(X).

另外

0≤ - |nPδ(xi)⋂Dt||U|log2 |nPδ(xi)⋂Dt||nPδ(xi)|≤ - |nQδ(xi)⋂Dt||U|og2 |nQδ(xi)⋂Dt||nQδ(xi)|

所以

H(D|P)≤ H(D|Q).

因此, 随着条件特征的增加, H(D|B)是单调递减的.

定义8 给定邻域决策系统NDS=< U, C, D, δ > , 对于∀ B⊆C, 当且仅当

1)H(D|B) = H(D|C),

2)对于∀ a∈ B, 有

H(D|B-{a})> H(D|C),

则称B是C相对于D的约简.

定义9 给定邻域决策系统NDS=< U, C, D, δ > , 对于任意条件特征子集B⊆C, ∀ a∈ B相对于D的内部特征重要度为:

Siginner(a, B, D)=H(D|B-{a})-H(D|B).(8)

定义10 给定邻域决策系统NDS=< U, C, D, δ > , 对于∀ a∈ C, 如果

H(D|C-{a})> H(D|C),

即

Siginner(a, C, D)> 0,

称特征a为C相对于D的核特征.

定义11 给定邻域决策系统NDS=< U, C, D, δ > , 对于任意条件特征子集B⊆C, 则对于任意条件特征a∈ C-B, 关于决策特征D的外部特征重要度为:

Sigouter(a, B, D)=H(D|B)-H(D|B∪ {a}).

Sigouter(a, B, D)的值越大, 说明在已知B的条件下, 特征a对于决策特征D越重要.

2.3 适应度函数

目前, 适应度函数中的特征依赖度只针对已选取的特征进行计算, 而缺少对特征空间中其它特征的分析和评价[18, 24].如果加入一个特征后不改变论域中确定分类的实例, 但是不确定性却有所变化, 则该特征的重要度在代数观点下为0, 在信息论观点下重要度却不为0.因此, 本文引入基于容错邻域近似条件熵的特征重要度, 结合特征依赖度构造适应度函数.

定义12 给定邻域决策系统NDS=< U, C, D, δ > , 对于任意条件特征子集B⊆C, 任意条件特征a∈ C-B, 基于容错邻域粗糙集的新的适应度函数为:

fitness=λ 1γ 'B(D)+λ 2 11+exp(Sigouter(a, B, D))λ 3 |C|-|B||C|

其中, λ 1为特征依赖度参数, λ 2为特征重要度参数, λ 3为特征子集长度参数, λ 1+λ 2+λ 3=1, γ 'B(D)为决策特征D关于B的依赖度, Sigouter(a, B, D)为决策特征D的外部特征重要度, |B|为选择特征子集的个数, |C|为所有条件特征的个数.该适应度函数能对所有特征进行评价, 并选择依赖度较大、剩余特征重要度较小、长度较短的特征子集.

2.4 算法步骤

FSAWFN首先初始化鲸鱼群体.然后根据更新策略更新位置, 选择适应度最佳的个体.最后利用信息熵进行特征选择.具体伪代码如算法1所示.

算法1 FSAWFN

输入 邻域决策系统NDS=< U, C, D, δ > ,

鲸鱼群体N, 最大迭代次数Maxiter,

依赖度限制因子α 、 β , 权重系数λ

输出 特征子集R

1.随机产生大小为N、维度为|C|的鲸鱼群体

POP={S1, S2, …, SN}, Si={s1, s2, …, s|C|}, si∈ [0, 1], R=Ø ;

2.For iter=1, 2, …, Maxiter

3. 将鲸鱼群体POP转化为二进制POP';

4. 根据式(4)计算惯性权重ω ;

5. 根据式(1)和式(2)计算A、E;

6. If |A|< 1

7. If p> 0.5.

8. 根据式(5)更新鲸鱼个体的位置si;

9. Else

根据式(6)更新鲸鱼个体的位置si;

10. End if

11. Else

根据式(3)更新鲸鱼个体的位置si;

12. End if

13.End for

14.计算适应度值, 选择适应度值最佳的个体ai;

15.根据式(7)和式(8)计算容错邻域近似条件熵H(D|ai)和特征重要度Siginner(ai, C, D);

16.If Siginner(ai, C, D)> 0,

则R=R∪ {ai};

17. If H(D|ai)=H(D|C)

18. 令S=C-R, 对于∀ a∈ S, 计算

Sigouter(a, C, D);

19. 选出ai, 满足

Sigouter(ai, C, D)=

max{a|Sigouter(a, C, D), a∈ S};

20. 令S=S-ai, R=R∪ {ai}, 计算H(D|R);

21. If H(D|R)=H(D|C),

转入26;

22. Else

返回1;

23. End if

24. End if

25.End if

26.输出特征子集R.

设群体大小为n, 维度为m, 初始化种群的时间复杂度为O(nm), 计算惯性权重的时间复杂度为O(n).步骤6~步骤12更新位置的时间复杂度为O(nm).在最坏情况下, 步骤17计算H(D|B)的时间复杂度为O(n2m), 需要计算m次, 为O(n2m2).步骤16~步骤25计算每个特征重要度的时间复杂度为O(n2m), 在最坏的情况下需要计算m次, 时间复杂度为O(n2m2).因此, FSAWFN总的时间复杂度为

O(2n2m2+ n2m + 2nm + n), 约为O(n2m2).

3 实验及结果分析
3.1 自适应鲸鱼优化算法性能分析

为了验证动态惯性权重在WOA搜索后期局部寻优的能力, 对本文提出的自适应WOA(A-WOA)进行寻优能力测试, 选择文献[25]中6个基准函数, 如表1所示.表中单峰函数f1~f3主要测试算法的寻优精度和收敛能力, 多峰函数f4~f6检测算法的全局寻优能力和避免局部收敛的能力.

对比算法选择如下:海洋捕食者算法(Marine Predators Algorithm, MPA)[26]、水循环算法(Water Cycle Algorithm, WCA)[27]、WOA[20].

表1 基准函数信息 Table 1 Information of benchmark functions

为了保证实验的公平性, 4种算法参数保持一致, 即种群规模N=30, 空间维度dim=30, 50, 最大迭代次数Maxiter=300, 每种算法分别独立运行30次.实验环境设置为Windows 10 、Intel(R) CPU 3.40 GHz、8.00 GB内存, MATLAB R2016a.

4种优化算法在6个基准函数上的最优值、最差值和平均值对比如表2所示, 表中黑体数字表示最优值.

表2 各算法在6个基准函数上的性能对比 Table 2 Performance comparison of different algorithms on 6 benchmark functions

由表2可看出, A-WOA在6个基准函数上性能最优, 尤其是在函数f1~f4、 f6上, A-WOA的性能具有较大幅度提升.当维度为30时, 在函数f5上, MPA、WOA和A-WOA最优值均为0, 另外, A-WOA的最差值和平均值也达到0.当维度为50时, 在函数f3上, 4种算法在最优值上相差不大, 但是, A-WOA在最差值和平均值上大幅优于其它3种算法.在函数f4上, WOA和A-WOA结果相差无几且明显优于MPA和WCA, 但是, A-WOA取得的最优值和平均值都优于WOA.

综上所述, 无论是单峰函数还是多峰函数, A-WOA表现出优越的局部寻优性能, 充分说明基于动态惯性权重改进的A-WOA较好地解决WOA容易陷入局部最优和局部寻优性能不稳定的问题.

3.2 算法性能分析

为了说明FSAWFN的分类性能, 在14个数据集上进行仿真实验, 具体信息如表3所示, 其中:前8个数据集为低维UCI数据集, 选自UCI Machine Lear-ning Repository(http://archive.ics.uci.edu/ml/index.php); 后面6个为高维基因数据集, 选自Cancer Program Datasets(http://portals.broadinstitute.Org/cgi-bin/cancer/datasets.cgi).

表3 实验数据集 Table 3 Experimental datasets

在WEKA软件中选择J48、Naive Bayes(NB)、K近邻(K Next Neighbor, KNN)(k=10)、CART这4种分类器, 验证算法的分类性能.

所有实验都通过10折交叉验证实现[28, 29].依据文献[10]、文献[20]、文献[30]的参数设置方法, 分别设置容错分析阈值α = 0.8, 适应度函数参数λ 1=0.6, λ 2=0.3, λ 3=0.1.

3.2.1 种群个数和迭代次数的影响

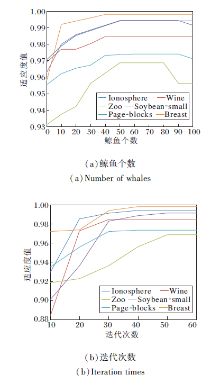
为了验证鲸鱼个数和迭代次数对实验的影响, 选取Ionosphere、Wine、Zoo、Soybean-small、Page-blocks、Breast数据集进行实验, 鲸鱼个数和迭代次数对适应度值的影响如图1所示.

图1 鲸鱼个数和迭代次数对适应度值的影响Fig.1 Influence of number of whales and iteration times on fitness value

由图1(a)可看出:当鲸鱼个数由0增至50时, 适应度值也增加; 当鲸鱼个数由50增至100时, 适应度值趋于稳定.这说明当鲸鱼个数达到一定程度时, FSAWFN趋于稳定, 对鲸鱼数量不敏感.由(b)可看出, 适应度值随着迭代次数的增加而增加, 当迭代次数增加到一定程度时, 适应度值趋于稳定, 说明FSAWFN经过迭代可收敛.因此, 本文选取种群个数为50, 迭代次数为50, 进行后续的特征选择实验.

3.2.2 邻域半径的选择

由于邻域半径的不同, 特征选择得到的约简子集和分类精度也不同, 直接影响实验结果, 于是通过研究不同邻域参数对特征子集的约简率[1]和分类精度的影响, 为每个数据集选择最优的邻域半径.对于6个高维基因数据集, 为了有效降低算法的时空复杂度, 采用Fisher score[9, 14]初步降维, 在WEKA上获取7种不同维度下的分类精度如表4所示, 表中黑体数字表示最优结果.由表可见, 当分类精度最优时, Colon数据集上选择合适的维度是500维, DLBCL、Leukemia数据集上选择合适的维度是300维, Breast数据集上选择合适的维度是50维, Prostate数据集上选择合适的维度是100维, MLL数据集上选择合适的维度是200维.

表4 6个高维基因数据集在7种不同维度下的分类精度 Table 4 Classification accuracy of 6 high-dimensional gene datasets in 7 different dimensions

在14个数据集上, 使用WEKA中的J48和NB分类器计算分类精度, 参照文献[1]、文献[17]最大限度地平衡分类精度和约简率的方法, 通过实验选择最优邻域半径, 设置邻域半径δ ∈ [0.05, 0.95], 以0.1为步长.于是, FSAWFN在不同的邻域半径下进行特征选择, 平衡分类精度和约简率, 为每个数据集选择最优的邻域半径, 具体如表5所示.

表5 2个不同分类器在14个数据集上的最优邻域半径 Table 5 Optimal neighborhood radia with 2 different classifiers on 14 datasets

3.2.3 优化特征选择算法性能对比

为了有效体现WOA[20]在特征选择上的运用及其实验效果, 本文构建基于WOA的特征选择算法(Feature Selection Based on WOA, WOAFS)和基于A-WOA的特征选择算法(Feature Selection Based on A-WOA, A-WOAFS), 进一步分析WOAFS、A-WOAFS和FSAWFN的分类性能.从表3中选择10个数据集进行特征选择实验, 分类精度如表6所示, 表中黑体数字表示最优结果.

表6 3种基于WOA的优化特征选择算法的分类精度 Table 6 Classification accuracies of 3 optimization feature selection algorithms based on WOA

由表6可知, A-WOAFS选择的特征个数均少于WOAFS, 在分类精度方面, 除了Wine、Tic-tac-toe数据集以外, A-WOAFS在J48和NB分类器上所得的分类精度高于WOAFS.在Wine数据集上, 虽然A-WOAFS在J48和NB分类器上所得的分类精度略低于WOAFS, 但特征个数少于WOAFS, 获得的分类精度仅略低于WOAFS.在Tic-tac-toe数据集上, 虽然A-WOAFS在NB分类器上的分类精度比WOAFS降低0.032, 但A-WOAFS选择特征个数少于WOAFS, 并且在J48分类器上的分类精度高于WOAFS, 因此, A-WOAFS性能优于WOAFS. FSAWFN在10个数据集上选择特征个数少于A-WOAFS, 并且分类精度高于A-WOAFS, 由此可看出, 将本文改进的A-WOA与容错邻域粗糙集结合能选择特征个数较少且分类精度较高的特征子集.

3.2.4 在低维UCI数据集上的实验结果

根据由表5得到的邻域半径, 从选择的特征数量和分类精度两方面对比分析FSAWFN在低维UCI数据集上的分类性能.对比算法如下:PSORSFS[21]、DQBGOA_MR(Dynamic Population Quantum Binary Grasshopper Optimization Algorithm Based on Mutual Information and Rough Set Theory)[30]、ARRSFA(Attribute Reduction Based on Rough Sets and Discrete Firefly Algorithm)[31]、FSARSR(Fin-ding Rough Set Reducts with Fish Swarm Algori-thm)[32]、QCSIA_FS(Cooperative Swarm Intelligence Algorithm for Feature Selection Based on Quan-tum-Inspired and Rough Sets)[33].对比算法实验结果均来自于文献[30].

各算法在8个低维UCI数据集上选择的特征个数如表7所示, 表中黑体数字表示最优结果.由表可看出, FSAWFN在8个低维UCI数据集上选择的特征个数较少, 优势较明显, 选择的平均特征个数最少.在Soybean-small、Zoo数据集上, FSAWFN和DQ-BGOA_MR得到的平均特征个数相近, 但都达到最小值, 并且少于其它4种算法得到的平均特征个数.在Ionosphere、Mushroom、Tic-tac-toe、Vote数据集上, FSAWFN选择的平均特征个数均达到最小值, 优势显著.在Wine数据集上, FSAWFN选择的平均特征个数较多.在Page-blocks数据集上, FSAWFN的平均特征个数与QCSIA_FS和DQBGOA_MR相同, 但都是最小值.

表7 各算法在8个低维UCI数据集上选择的特征个数对比 Table 7 Number of features selected by different algorithms on 8 low-dimensional UCI datasets

综上所述, FSAWFN在8个低维UCI数据集上能选择较小的特征子集.最终FSAWFN选择的最优特征子集如表8所示.

表8 FSAWFN在8个低维UCI数据集上选择的最优特征子集 Table 8 Optimal feature subset selected by FSAWFN on 8 low-dimensional UCI datasets

各算法在J48和NB分类器上得到的分类精度和标准差如表9所示, 表中黑体数字表示最优结果.由表可知, FSAWFN在J48和NB分类器上的分类精度多数能达到最大值, 大于其它5种算法.在J48分类器上, 除了Mushroom、Vote数据集以外, FSAWFN在其它6个数据集上均得到最大分类精度, 并且在Mushroom、Vote数据集上仅比最大值分别降低0.21%和0.54%, 同时FSAWFN在这2个数据集上也选择最小的特征子集.在NB分类器上, 除了Ionosphere、Page-blocks数据集以外, FSAWFN在其它6个数据集上均得到最大分类精度, 尤其在Tic-tac-toe、Vote、Wine、Zoo数据集上优势更显著.在Iono-sphere、Page-blocks数据集上, FSAWFN在NB分类器上的分类精度虽然略低于最大分类精度, 但是, 结合表7可知, FSAWFN选择的特征子集最小.结合表9给出的J48和NB分类器上的分类精度对应的标准差可看出, J48和NB分类器对应的标准差能达到较小值.

综上所述, FSAWFN在J48和NB分类器上能得到较小的特征子集、较大的分类精度和较小的标准差, 因此具有较好的分类性能.

表9 J48和NB分类器上6种算法的分类精度 Table 9 Classification accuracy of 6 algorithms with J48 and NB classifiers

3.2.5 在高维基因数据集上的实验结果

为了验证FSAWFN在高维基因数据集上的分类性能, 选择如下对比算法:FSNTDJE[17]、CFS(Co-rrelation Feature Selection)[29]、FCBF(Fast Correla-tion-Based Filter Algorithm)[34]、INT(Interacting Fea-tures Selection Algorithm)[34]、IG(Information Gain Based Feature Selection Algorithm)[35].

为了方便验证和实验对比, 根据文献[17]和文献[32]的实验设计, 选择Colon、DLBCL、Breast、Prostate高维基因数据集, 在J48和NB分类器上进行对比实验.

通过10折交叉验证, 各算法选择的基因个数如表10所示, 表中黑体数字表示最优结果.FSAWFN选择的最优基因子集如表11所示.

由表10可看出, 除了DLBCL数据集以外, FSAWFN优势明显, 均选择最小的基因子集.在DLBCL数据集上, 尽管FSAWFN选择的特征个数多于IG, 但优于CFS、FCBF、INT和FSNTDJE.在NB分类器上, FSAWFN在Colon数据集上优势显著, 选择最小的基因子集; 在J48分类器上, FSAWFN在Prostate数据集上优势显著.总之, FSAWFN能选择较小基因子集, 并获得较少平均基因个数.

表10 各算法在4个高维基因数据集上选择的基因个数 Table 10 The number of genes selected by different algorithms on 4 high-dimensional gene datasets
表11 FSAWFN在2个分类器上选择的最优基因子集 Table 11 Optimal gene subsets selected by FSAWFN with 2 classifiers

下面依据文献[17]和文献[25]中3个评价指标, 即精度(Accuracy, Acc)、真正例率(True Posi-tive Rate, TPR)、假正例率(False Positive Rate, FPR), 评价FSAWFN在Colon、DLBCL、Breast、Pros-tate数据集上的分类结果.通常TPR越大, FPR越小, 算法性能越优.NB和J48分类器上各算法在4个数据集上的指标值如表12和表13所示, 表中ODP表示原始数据处理算法, 黑体数字表示最优值.

由表12和表13可看出, 除了J48分类器上的DLBCL数据集和NB分类器上的Prostate数据集以外, FSAWFN都能得到较好的分类精度.从整体上看, 相比其它算法, FSAWFN能得到较高的Acc值和较低的FPR值.在NB分类器上, 在DLBCL数据集上, 虽然FSAWFN选择的基因个数多于IG, 但3个指标值均优于IG, 并且TPR达到最大值, FPR达到最小值.对于Acc指标, FSAWFN在Colon、Breast、Prostate数据集上表现较优.对于TPR指标, FSAWFN在DLBCL数据集上达到最大值1.对于FPR指标, FSAWFN在DLBCL、Prostate数据集上达到最小.

表12 各算法在NB分类器下的指标值 Table 12 Indexes of different algorithms with NB classifier
表13 各算法在J48分类器下的指标值 Table 13 Indexes of different algorithms with J48 classifier

同样地, 在J48分类器上, FSAWFN在Prostate数据集上获得的Acc、TPR值都略小于最优值, 但是选择的基因个数最少, 并且FPR也达到最小值.对于Acc指标, FSAWFN在Colon、DLBCL、Breast数据集上表现较优.对于TPR指标, FSAWFN在DLBCL数据集上达到最大值1.对于FPR指标, FSAWFN在Prostate数据集上达到最小.

为了进一步验证FSAWFN在高维数据集上的分类性能, 选取Colon、Leukemia、Breast、MLL数据集.对比算法选择ODP、FSNTDJE[17]、DMRA(Dis-cernibility Matrix-Based Reduction Algorithm)[36]、FPR(Fuzzy Positive Region Reduction)[37]、FRFS(Fuzzy-Rough Feature Selection Algorithm)[38]、IFPR(Intuitionistic Fuzzy Positive Region Based Gene Selection Algorithm)[39].通过10折交叉验证, 获得KNN(k=10)和CART分类器上的分类精度如表14所示.

表14 KNN和CART分类器上7种算法的分类精度 Table 14 Classification accuracy of 7 algorithms under KNN and CART classifier

由表14可见, FSAWFN在4个高维数据集上均取得最大的分类精度.在KNN分类器上, FSAWFN在Leukemia、Breast数据集上优势明显.在Colon、MLL数据集上, FSAWFN分类精度略高于FSNTDJE, 但优于ODP、DMRA、FPR、FRFS、IFPR.在CART分类器上, FSAWFN在Leukemia、Breast、MLL数据集上优势明显.在Colon数据集上, FSAWFN分类精度率略高于FSNTDJE, 但优于ODP、DMRA、FPR、FRFS、IFPR.因此FSAWFN具有较好的分类效果.

3.3 统计分析

为了对FSAWFN的分类结果进行统计验证, 选择Friedman检验和Bonferroni-Dunn检验, 分别定义如下:

χF2= 12Ts(s+1)∑a=1sRa2-s(s+1)24, FF= (T-1)χF2T(s-1)-χF2

其中, s为算法数量, T为数据集数量, Ra(a=1, 2, …, s)为第a种算法的平均排序.FF服从F分布, 如果通过Friedman检验得到的所有算法性能明显不一样, 需要post-hoc检验以对比各算法, 常用的后续检验为Nemenyi检验, 临界差值[40]为:

CDα =qα s(s+1)6T,

其中, α 为显著性水平, 这里选择α =0.1, qα 为临界值.

根据表9中各算法在8个UCI数据集上的分类精度, 进行Friedman检验, 结果如表15所示.当α =0.1时,

q0.1=2.326, CD=2.176, F(5, 35)=2.02, χF25)=9.24.

由表15可知, 在J48和NB分类器上各对比算法性能显著不同, 于是进行post-hoc检验.

表15 J48和NB分类器上6种算法的统计结果 Table 15 Statistical results of 6 algorithms with J48 and NB classifiers

为了直观说明算法的差异, 6种算法在J48和NB分类器上的Bonferroni-Dunn检验结果如图2所示.

由图2(a)可知, FSAWFN平均排序最小, 与DQBG-OA_MR、FSARSR、PSORSFS无显著性差距, 但明显优于ARRSFA和QCSIA_FS.由(b)可知, FSAWFN平均排序最小, 明显优于FSARSR.总之, FSAWFN性能最优.

图2 J48和NB分类器上6种算法的Bonferroni-Dunn检验结果Fig.2 Bonferroni-Dunn test results of different algorithms with J48 and NB classifiers

对表14中4个高维基因数据集的分类精度进行Friedman检验, 结果如表16所示.当α =0.1时,

q0.1=2.326, CD=3.077, F(5, 15)=2.27, χF2(5)=9.24.

根据表16可知, 在KNN和CART分类器上各算法的性能显著不同, 因此进行post-hoc检验.

表16 KNN和CART分类器上6种算法的统计结果 Table 16 Statistical results of 6 algorithms with KNN and CART classifiers

各算法在KNN和CART分类器上的Bon-ferroni-Dunn检验结果如图3所示.由(a)可看出, FSAWFN平均排序最小, 与FSNTDJE、DMRA、IFPR无显著性差距, 优于FRFS和FPR.由(b)可知, FSAWFN平均排序最小, 优于FRFS、FPR、DMRA.总之, FSAWFN明显优于其它算法.

图3 KNN和CART分类器上各算法的Bonferroni-Dunn检验结果Fig.3 Bonferroni-Dunn test results of different algorithms with KNN and CART classifiers

4 结束语

利用WOA操作简单、计算参数较少、全局寻优能力较强等优点, 本文提出基于自适应WOA和容错邻域粗糙集的特征选择算法(FSAWFN).首先, 提出动态惯性权重, 设计自适应WOA.然后, 解决邻域粗糙集缺乏容错性问题, 提出容错上下近似集、容错近似精度、容错近似粗糙度、容错依赖度及容错近似条件熵.最后, 使用自适应WOA进行预处理, 获取最优子群, 进而结合容错邻域粗糙集设计特征选择算法.在8个UCI数据集和6个高维基因数据集上的实验表明:本文算法是有效的, 通过对WOA进行的自适应改进, 能更容易收敛到最优或接近最优解; 将自适应WOA与容错邻域粗糙集结合能使算法更快找到最小特征子集.但是, 在运行时效上, 本文算法的改善效果并不明显, 这是下一步需要研究的内容.

参考文献
[1] SUN L, WANG L Y, DING W P, et al. Feature Selection Using Fuzzy Neighborhood Entropy-Based Uncertainty Measures for Fuzzy Neighborhood Multigranulation Rough Sets. IEEE Transactions on Fuzzy Systems, 2021, 29(1): 19-33. [本文引用:3]
[2] DING W P, LIN C T, CAO Z H. Deep Neuro-Cognitive Co-evolution for Fuzzy Attribute Reduction by Quantum Leaping PSO with Nearest-Neighbor Memeplexes. IEEE Transactions on Cybernetics, 2019, 49(7): 2744-2757. [本文引用:1]
[3] 邓威, 郭钇秀, 李勇, 等. 基于特征选择和Stacking集成学习的配电网网损预测. 电力系统保护与控制, 2020, 48(15): 108-115.
(DENG W, GUO Y X, LI Y, et al. Power Losses Prediction Based on Feature Selection and Stacking Integrated Learning. Power System Protection and Control, 2020, 48(15): 108-115. ) [本文引用:1]
[4] YUE X D, ZHOU J, YAO Y Y, et al. Shadowed Neighborhoods Based on Fuzzy Rough Transformation for Three-Way Classification. IEEE Transactions on Fuzzy Systems, 2020, 28(5): 978-991. [本文引用:1]
[5] 薛占熬, 庞文莉, 姚守倩, 等. 基于前景理论的直觉模糊三支决策模型. 河南师范大学学报(自然科学版), 2020, 48(5): 31-36, 79.
(XUE Z A, PANG W L, YAO S Q, et al. The Prospect Theory Based Intuitionistic Fuzzy Three-Way Decisions Model. Journal of Henan Normal University (Natural Science Edition), 2020, 48(5): 31-36, 79. ) [本文引用:1]
[6] 韩素敏, 郑书晴, 何永盛. 基于粗糙集贪心算法的逆变器开路故障诊断. 电力系统保护与控制, 2020, 48(17): 122-130.
(HAN S M, ZHENG S Q, HE Y S. Open Circuit Fault Diagnosis for Inverters Based on a Greedy Algorithm of a Rough Set. Power System Protection and Control, 2020, 48(17): 122-130. ) [本文引用:1]
[7] 刘艳, 程璐, 孙林. 基于K-S检验和邻域粗糙集的特征选择方法. 河南师范大学学报(自然科学版), 2019, 47(2): 21-28.
(LIU Y, CHENG L, SUN L. Feature Selection Method Based on K-S Test and Neighborhood Rough Sets. Journal of Henan Normal University(Natural Science Edition), 2019, 47(2): 21-28. ) [本文引用:2]
[8] CHEN H M, LI T R, FAN X, et al. Feature Selection for Imba-lanced Data Based on Neighborhood Rough Sets. Information Sciences, 2019, 483: 1-20. [本文引用:3]
[9] SUN L, WANG T X, DING W P, et al. Feature Selection Using Fisher Score and Multilabel Neighborhood Rough Sets for Multilabel Classification. Information Sciences, 2021, 578: 887-912. [本文引用:3]
[10] 彭潇然, 刘遵仁, 纪俊. 基于容错改进的邻域粗糙集属性约简算法. 计算机应用研究, 2018, 35(8): 2256-2259, 2314.
(PENG X R, LIU Z R, JI J. Attribute Reduction Algorithm Based on Fault-Tolerance Improvement of Neighborhood Rough Set. Application Research of Computers, 2018, 35(8): 2256-2259, 2314. ) [本文引用:5]
[11] HU C X, ZHANG L, WANG B J, et al. Incremental Updating Knowledge in Neighborhood Multigranulation Rough Sets under Dynamic Granular Structures. Knowledge-Based Systems, 2018, 163: 811-829. [本文引用:1]
[12] WANG C Z, HUANG Y, SHAO M W, et al. Fuzzy Rough Set-Based Attribute Reduction Using Distance Measures. Knowledge-Based Systems, 2019, 164: 205-212. [本文引用:1]
[13] SUN L, WANG L Y, DING W P, et al. Neighborhood Multi-gra-nulation Rough Sets-Based Attribute Reduction Using Lebesgue and Entropy Measures in Incomplete Neighborhood Decision Systems. Knowledge-Based Systems, 2020. DOI: DOI:10.1016/j.knosys.2019.105373. [本文引用:1]
[14] SUN L, ZHANG X Y, QIAN Y H, et al. Joint Neighborhood Entropy-Based Gene Selection Method with Fisher Score for Tumor Classification. Applied Intelligence, 2019, 49(4): 1245-1259. [本文引用:3]
[15] WANG G Y. Rough Reduction in Algebra View and Information View. International Journal of Intelligent Systems, 2003, 18(6): 679-688. [本文引用:1]
[16] SUN L, YIN T Y, DING W P, et al. Multilabel Feature Selection Using ML-Relieff and Neighborhood Mutual Information for Multilabel Neighborhood Decision Systems. Information Sciences, 2020, 537: 401-424. [本文引用:1]
[17] SUN L, WANG L Y, QIAN Y H, et al. Feature Selection Using Lebesgue and Entropy Measures for Incomplete Neighborhood Decision Systems. Knowledge-Based Systems, 2019, 186. DOI: DOI:10.1016/j.knosys.2019.104942. [本文引用:8]
[18] 刘琨, 封硕. 加强局部搜索能力的人工蜂群算法. 河南师范大学学报(自然科学版), 2021, 49(2): 15-24.
(LIU K, FENG S. An Improve Artificial Bee Colony Algorithm for Enhancing Local Search Ability. Journal of Henan Normal University(Natural Science Edition), 2021, 49(2): 15-24. ) [本文引用:2]
[19] 刘振, 郭恒光, 任建存. 一种局部搜索能力增强的狮群算法. 河南师范大学学报(自然科学版), 2019, 47(3): 35-41.
(LIU Z, GUO H G, REN J C. An Enhanced Local Search Lion Optimization Algorithm. Journal of Henan Normal University(Natural Science Edition), 2019, 47(3): 35-41. ) [本文引用:1]
[20] MIRJALILI S, LEWIS A. The Whale Optimization Algorithm. Advances in Engineering Software, 2016, 95: 51-67. [本文引用:7]
[21] WANG X Y, YANG J, TENG X L, et al. Feature Selection Based on Rough Sets and Particle Swarm Optimization. Pattern Recognition Letters, 2007, 28(4): 459-471. [本文引用:2]
[22] 孙林, 赵婧, 徐久成, 等. 基于邻域粗糙集和帝王蝶优化的特征选择算法[J/OL]. [2021-08-21]. https: //kns. cnki. net/kcms/detail/51. 1307. TP. 20210928. 1342. 002. html.
(SUN L, ZHAO J, XU J C, et al. Feature Selection Algorithm Based on Neighborhood Rough Sets and Monarch Butterfly Optimization[J/OL]. [2021-08-21]. https: //kns. cnki. net/kcms/detail/51. 1307. TP. 20210928. 1342. 002. html. ) [本文引用:3]
[23] 褚鼎立, 陈红, 王旭光. 基于自适应权重和模拟退火的鲸鱼优化算法. 电子学报, 2019, 47(5): 992-999.
(CHU D L, CHEN H, WANG X G. Whale Optimization Algorithm Based on Adaptive Weight and Simulated Annealing. Acta Electronica Sinica, 2019, 47(5): 992-999. ) [本文引用:2]
[24] ABHISHEK B, RADHA T G, KUNTAL M. A Feature Selection Technique Based on Rough Set and Improvised PSO Algorithm(PSORS-FS) for Permission Based Detection of Android Malwares. International Journal of Machine Learning and Cybernetics, 2019, 10(7): 1893-1907. [本文引用:1]
[25] 汤安迪, 韩统, 徐登武, 等. 混沌精英哈里斯鹰优化算法. 计算机应用, 2021, 41(8): 2265-2272.
(TANG A D, HAN T, XU D W, et al. Chaotic Elite Harris Hawks Optimization Algorithm. Journal of Computer Applications, 2021, 41(8): 2265-2272. ) [本文引用:2]
[26] FARAMAIZI A, HEIDARINEJAD M, MIRJALILI S, et al. Marine Predators Algorithm: A Nature-Inspired Metaheuristic. Expert Systems with Applications, 2020, 152. DOI: DOI:10.1106/j.eswa.2020.113377. [本文引用:1]
[27] ESKANDAR H, SADOLLAH A, BAHREININEJAD A, et al. Wa-ter Cycle Algorithm-A Novel Metahertistic Optimization Method for Solving Constrained Engineering Optimization Problems. Computer and Structures, 2021, 110/111: 151-166. [本文引用:1]
[28] SUN L, WANG L Y, XU J C, et al. A Neighborhood Rough Sets-Based Attribute Reduction Method Using Lebesgue and Entropy Measures. Entropy, 2019, 21(2). DOI: DOI:10.3390/e21020138. [本文引用:1]
[29] PAUL A, SIL J, MUKHOPADHYAY C D. Gene Selection for Designing Optimal Fuzzy Rule Base Classifier by Estimating Missing Value. Applied Soft Computing, 2017, 55: 276-288. [本文引用:2]
[30] WANG D, CHEN H M, LI T R, et al. A Novel Quantum Grasshopper Optimization Algorithm for Feature Selection. International Journal of Approximate Reasoning, 2020, 127: 33-53. [本文引用:3]
[31] LONG N C, MEESAD P, UNGER H. Attribute Reduction Based on Rough Sets and the Discrete Firefly Algorithm // Proc of the 10th International Conference on Computing and Information Technology. Berlin, Germany: Springer, 2014: 13-22. [本文引用:1]
[32] CHEN Y M, ZHU Q X, XU H R. Finding Rough Set Reducts with Fish Swarm Algorithm. Knowledge-Based Systems, 2015, 81: 22-29. [本文引用:2]
[33] ZOUACHE D, ABDELAZIZ F B. A Cooperative Swarm Intelligence Algorithm Based on Quantum-Inspired and Rough Sets for Feature Selection. Computers and Industrial Engineering, 2018, 115: 26-36. [本文引用:1]
[34] ZHAO Z, LIU H. Searching for Interacting Features in Subset Selection. Intelligent Data Analysis, 2009, 13(2): 207-228. [本文引用:2]
[35] LEE C, LEE G G. Information Gain and Divergence Based Feature Selection for Machine Learning Based Text Categorization. Information Processing and Management, 2006, 42(1): 155-165. [本文引用:1]
[36] CHEN D G, ZHANG L, ZHAO S Y, et al. A Novel Algorithm for Finding Reducts with Fuzzy Rough Sets. IEEE Transactions on Fuzzy Systems, 2012, 20(2): 385-389. [本文引用:1]
[37] QIAN Y H, WANG Q, CHENG H H, et al. Fuzzy-Rough Feature Selection Accelerator. Fuzzy Sets and Systems, 2015, 258: 61-78. [本文引用:1]
[38] JENSEN R, SHEN Q. New Approaches to Fuzzy-Rough Feature Selection. IEEE Transactions on Fuzzy Systems, 2009, 17(4):
824-838. [本文引用:1]
[39] TAN A H, WU W Z, QIAN Y H, et al. Intuitionistic Fuzzy Rough Set-Based Granular Structures and Attribute Subset Selection. IEEE Transactions on Fuzzy Systems, 2019, 27(3): 527-539. [本文引用:1]
[40] SUN L, YIN T Y, DING W P, et al. Feature Selection with Mi-ssing Labels Using Multilabel Fuzzy Neighborhood Rough Sets and Maximum Relevance Minimum Redundancy. IEEE Transactions on Fuzzy Systems, 2021. DOI: DOI:10.1109/TFUZZ.2021.3053844. [本文引用:1]