引用本文
张所娟, 黄松, 余晓晗, 陈恩红. 基于模糊测度的知识关联性建模方法. 模式识别与人工智能, 2022,35(2): 95-105
ZHANG Suojuan, HUANG Song, YU Xiaohan, CHEN Enhong. Modeling Method of Knowledge Relevance Based on Fuzzy Measures. PATTERN RECOGNITION AND ARTIFICIAL INTELLIGENCE, 2022,35(2): 95-105.  
Doi: 10.16451/j.cnki.issn1003-6059.202202001 中图法分类号 G 434
Permissions
Copyright©2022, 《模式识别与人工智能》编辑部
《模式识别与人工智能》编辑部 所有
基于模糊测度的知识关联性建模方法
张所娟1,2, 黄松1, 余晓晗1, 陈恩红2
1.中国人民解放军陆军工程大学 指挥控制工程学院 南京 210007
2.中国科学技术大学 计算机科学与技术学院 大数据分析与应用安徽省重点实验室 合肥 230027

通信作者：

黄松,博士,教授,主要研究方向为软件测试、数据挖掘.E-mail:huangsong@aeu.edu.cn.

作者简介：

张所娟,博士研究生,副教授,主要研究方向为教育数据挖掘、认知诊断.E-mail:suojuanzhang@aeu.edu.cn.

余晓晗,博士,副教授,主要研究方向为人工智能.E-mail:yuxh@aeu.edu.cn.

陈恩红,博士,教授,主要研究方向是机器学习、数据挖掘、教育大数据分析、个性化推荐等.E-mail:cheneh@ustc.edu.cn.

收稿日期: 2021-09-22 接受日期: 2022-01-10
资助项目: 重点研发计划项目(No.2018YFB1403400)、国家自然科学基金项目(No.U20A20229)资助
摘要

在教学应用场景中,知识之间的关联性广受关注,但现有研究通常偏重两两知识点之间关系的建模,忽视知识集合中复杂的关联关系,导致研究结果出现偏差.因此,文中引入模糊测度对知识集合进行量化度量,并在此基础上提出基于模糊测度的知识关联性建模方法.首先,基于认知心理学理论,分析知识间存在的三种不同关系,并利用模糊测度建模知识间的关联性,通过实际教学场景论证方法的实用性.然后,在模糊测度建模的基础上,从知识关联性的视角讨论知识的重要度和交互指标.最后,研究知识关联性在认知诊断中的应用.真实数据集上的实验证实知识关联性对认知诊断的影响,不仅有效提升预测精度,也提供更好的可解释性.

关键词: 知识关联性; 模糊测度; 认知诊断; 知识集合; 知识交互
Modeling Method of Knowledge Relevance Based on Fuzzy Measures
ZHANG Suojuan1,2, HUANG Song1, YU Xiaohan1, CHEN Enhong2
1.College of Command and Control Engineering, Army Engineering University of PLA, Nanjing 210007
2.Anhui Province Key Laboratory of Big Data Analysis and Application, School of Computer Science and Technology, University of Science and Technology of China, Hefei 230027
Corresponding author：HUANG Song, Ph.D., professor. His research interests include software testing and data mining.

About Author:ZHANG Suojuan, Ph.D. candidate, asso-ciate professor. Her research interests include educational data mining and cognitive diagnosis.

YU Xiaohan, Ph.D., associate professor. His research interests include artificial intelligence.

CHEN Enhong, Ph.D., professor. His research interests include machine learning, data mining, education big data analysis and personalized recommendation system.

Fund:Supported by National Key Research and Development Program of China(No.2018YFB1403400), National Natural Science Foundation of China(No.U20A20229)
Abstract

The relevance between knowledge in the instructional scenarios draws much attention. The existing research usually focuses on modeling the relationship between two knowledge points. However, the complex relevance in knowledge sets is ignored, which results in the deviation of the research results. Aiming at this problem, the fuzzy measure is introduced to quantify the knowledge set, and then a modeling method of knowledge relevance based on fuzzy measures is proposed. Firstly, three different knowledge relationships are analyzed grounded on the cognitive theory, and the knowledge relevance is modeled with fuzzy measures. Then, the practicability of the modeling method is demonstrated by the practical scenario. Secondly, based on fuzzy measure modeling, the importance and interaction of knowledge are discussed from the perspective of knowledge relevance. Finally, the application of knowledge relevance in cognitive diagnosis is studied. The influence of knowledge relevance on cognitive diagnosis is demonstrated through the experiments on real-world datasets. The results show that the proposed method predicts precisely with better interpretability.

Key words: Key Words Knowledge Relevance; Fuzzy Measure; Cognitive Diagnosis; Knowledge Set; Knowledge Interaction

在学习场景中, 知识的关联性普遍存在[1], 这种关联性强调各个知识并不是孤立存在[2, 3], 学习不是多个知识的简单累加, 而是“ 整体大于部分之和” [4]的过程.在不同的学习场景下, 知识的关联性发挥不同的作用.对于教师而言, 在有限的教学时间内, 需要根据知识的关联性[5, 6]合理设计编排教学内容, 有效组织教学活动.对于学生来说, 需要找出知识系统的薄弱环节, 分析影响学习的关键点.另外, 科学合理的试题建立需要覆盖课程知识体系中的重难点.无论在何种场景下, 解决教师教学、学生学习、题库建设的有效性和知识间的关联性都不可忽视.

在认知诊断和知识追踪模型中, 大多数研究者将知识看作是独立的[7, 8].然而, 学习中的知识之间通常具有密切关系[9].其中, 忽略知识关系的一个主要原因是一旦知识属性与模型及其聚合关系一起引入时, 知识之间的关系就变得不清楚[10].针对此问题, Leighton等[11]提出AHM(Attribute Hierarchy Method), 认为学习过程中知识之间构成一个相互关联的网络.AHM将知识构成一个层次结构以建立知识间的关联[12].

现有知识关联的研究更多集中在对知识先决关系的讨论[13, 14, 15, 16], 在认知诊断[17]和知识追踪[18, 19]中均有考虑知识结构信息, 将知识概念之间的先决关系纳入模型中.先决关系是指学生要达到教学目标必须掌握的各级知识间的从属关系, 如特征分析是主成分分析的先决条件[15].同时, 要考虑在学习达成目标时可能存在多种解决问题的路径[20, 21], 不同解题路径对应不同的知识点[22].从单个知识之间的联系上看, 无法明确知识之间的关系, 而是要置于集合中考虑知识间的关联.因此, 有必要对知识集合之间的关系建模.

但是, 在现有研究中, 对知识之间关联性的研究较单一, 仅考虑单个知识间的关系, 未考虑知识集合之间的关联, 更无法处理集合间的复杂关系.因此, 本文引入模糊测度对知识集合进行量化度量, 并在此基础上提出基于模糊测度的知识关联性建模方法.首先, 基于认知心理学理论, 分析知识间存在的三种不同关系, 并利用模糊测度建模知识间的关联性, 通过实际教学场景论证方法的实用性.然后, 在模糊测度建模的基础上, 从知识关联性的视角讨论知识的重要度和交互指标.最后, 研究知识关联性在认知诊断中的应用, 真实数据集上的实验证实知识关联性对认知诊断的影响, 不仅有效提升预测精度, 也提供更好的可解释性.

1 知识关联性建模方法
1.1 知识集合间的关系

由于知识集合之间的关联性, 学习的发生可看作是知识集合之间相互作用的结果.依据认知心理学理论[1], 划分如下3种集合关系, 描述知识集合间的关联性.

1)负协同关系或冗余关系.当学生掌握多个知识点后, 由于知识之间的相似性, 在一定程度上对学习造成干扰, 形成负协同增强的关系.举例来说, 学习字母d之前, 学生很容易辨认字母b, 但由于字母b、d很相似, 会产生混淆, 字母d的学习干扰对字母b的识别.还有一种情况, 知识x1(分数)是知识x2(分数减法)的先决条件.相比只掌握x2, 同时掌握知识集合{x1, x2}并不能明显提高学生在解答分数计算上的学习表现, 那么知识x1、x2存在冗余关系.

2)增强促进关系.知识集合之间存在促进作用, 多个知识集合共同作用有助于提高整体的学习表现.例如, 针对分数减法问题4 824-2 712, 使用知识集合{x1, x2, x3}(x1对应减法操作, x2对应约分, x3对应通分)的解答正确概率高于分别使用知识集合{x1, x2}、{x1, x3}, 说明知识集合{x1, x2}、{x1, x3}之间互补促进, 存在协同增强的关系.同样, 在阅读理解时, 相比分别使用掌握单词含义和句子语法的知识组合或使用单词含义和理解作者意图的组合, 掌握单词含义和句子语法、理解作者意图的知识技能组合更有可能正确理解文章.

3)相互独立关系.当不符合上述两种关系时, 认为知识集合之间存在独立关系.

上述3种关系表达知识集合间复杂的非线性关系, 这对知识关联性的量化建模提出挑战.本文引入模糊测度, 对知识集合进行量化度量, 并在此基础上提出基于模糊测度的知识关联性建模方法.

1.2 基于模糊测度的知识关联性建模方法

为了更好地表达知识集合间复杂的非线性关系, 本文引入模糊测度的概念, 建模知识的关联性.经典测度具有可加性.例如, 使用测度表示区域的面积, 那么两个不相交的区域之和的面积等于这两个区域面积之和.概率测度就是一个可加性测度的例子.但是, 经典测度在很多情况下无法满足可加性, 如两人合作的工作效率不一定等于两个人工作效率之和, 效率可能提高也可能降低.Sugeno[23]提出使用较弱的单调性代替可加性的一类集函数, 即以集合为定义域的函数[24], 称为模糊测度.模糊测度的主要特征是非可加性.相比可加性测度, 模糊测度更符合客观实际的情况.

定义1 对于一个有限集合X, 模糊测度可看作是一个实值集函数v∶ 2X→ [0, 1]:

1)v(Ø )=0, v(X)=1,

2)如果A⊆X, B⊆X, A⊆B, 则v(A)≤ v(B)

定义2X表示X的幂集, 即X的所有子集构成的集合.模糊测度目前已广泛应用于不同场景中, 可被描述为重要性、可靠性、满意度等相似的概念[25].例如, 采纳专家意见评价某设备的性能, 可以使用模糊测度表示专家意见的可靠性.在教育领域, 可将定义1中的X看作是达成学习目标所需的n个知识的集合X={x1, x2, …, xn}.令X1⊆X, X2⊆X, 模糊测度v(X1)为一个集函数, 表示知识集合X1促进目标达成的重要程度.显然, 知识集合覆盖所有n个知识时, v(X)=1且v(X1)∈ (0, 1], v(X2)∈ (0, 1].v(X1∪ X2)表示考虑知识集X1∪ X2对于目标达成的重要程度, 不仅要考虑知识集X1、X2本身的重要性, 还要考虑知识集X1、X2之间的关联性.而知识关联性可能是显性确定的, 也可能是隐性模糊的.例如, 进位加法是以十进制加法运算为基础, 它们之间存在显著的关联关系.而加法运算和乘法运算的交互关系是隐性的, 较模糊.知识集合之间是否存在关联性及关联程度, 可通过模糊测度建模, 量化表达知识集合间的关系.

1)负协同关系或冗余关系建模.表示知识组合后对目标达成的贡献度低于单独使用各个知识的贡献度之和.也就是说, 掌握该知识集合的重要度弱于单独使用其子集重要度的总和, 则知识集合间的关系是负协同关系.设知识集合为X1, X2, 同时X1⊆X, X2⊆X.知识集合间的模糊测度关系为:

v(X1∪ X2)< v(X1)+v(X2).

满足上式时, 知识集合之间的关联为负协同关系.

冗余关系可看作负协同关系的一种特例, 用于表达知识集合间的先决条件, 若知识x1为x2的先决条件.令X1={x1}, X2={x2}, 根据定义1中2), 即模糊测度的弱单调性, 知识集合间的模糊测度关系为:

v(X1∪ X2)=v(X2).

满足上式时, 知识集合之间的关联为冗余关系.也就是知识组合后对目标达成的贡献与单独使用知识集合X2相比没有变化, 对于目标达成的重要程度不产生增强的作用.

2)增强促进关系建模.多个知识组合后有助于学习目标的达成, 也就是说掌握该知识集合比单独使用其子集之和更重要, 说明知识集合间互补促进, 存在协同增强的关系.当知识集合的模糊测度符合

v(X1∪ X2)> v(X1)+v(X2)

时, 认为知识集合存在协同增强的关系.上式表示知识集X1、X2共同构成的集合X1∪ X2对于目标达成的重要程度高于各个知识属性集重要度之和.当知识集X1、X2组合后激发出一种新的潜在关联, 对促进目标的达成更重要.

3)相互独立关系建模.两个知识集组合后的对于学习目标达成的重要度等于这两个知识集单独使用时的重要度之和, 当模糊测度满足

v(X1∪ X2)=v(X1)+v(X2)

时, 说明知识集之间是相互独立, 不存在关联性.

通过知识集合模糊测度的对比, 可获得知识集合间3种非线性的关系, 由此完成对知识关联性的建模.在不同的教育应用场景下, 模糊测度可赋予不同的含义以帮助理解教与学的过程.在教学场景中, 模糊测度可帮助教师更好地理解知识间的联系, 以此作为编排教学内容的依据.而学习场景中加入模糊测度, 在诊断学生认知水平时, 基于关联性考虑知识集的重要程度, 可更准确地找出知识学习中的薄弱点.在评价场景中, 以模糊测度为基础检查知识体系中重点知识的覆盖范围.因此, 通过模糊测度建模知识关联性, 有助于不同教育场景下的目标达成.本文在下述讨论中统一将模糊测度作为知识集合促进目标达成的重要程度.通过模糊测度建模可更好地表达知识集合的关联性, 同时反映知识集合的特征, 为学习活动的有效开展提供数据支持和指导.

案例分析1 以教学内容的编排呈现顺序为例, 若达成学习目标需要3个知识共同作用完成, 令X={x1, x2, x3},

v({x1})=0.45, v({x2})=0.45, v({x3})=0.3, v({x1, x2})=0.5, v({x1, x3})=0.9, v({x2, x3})=0.9, v({x1, x2, x3})=1.

这里模糊测度v表示知识集合促进达成目标的重要程度.例如, 知识集合{x1, x2}对于目标达成的重要程度为0.5.

根据已知的模糊测度值, 考虑知识的学习序列, 通过不同的编排顺序对学生产生不同的学习刺激.存在如下知识关联性:

v({x1, x2})< v({x1})+v({x2}), v({x1, x3})> v({x1})+v({x3}), v({x2, x3})> v({x2})+v({x3}).

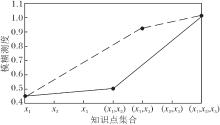
由此可知知识集{x3}与知识集{x1}、{x2}之间均存在协同增强关系, 而知识集{x1}、{x2}之间是负协同增强关系, 显然知识集{x3}在目标达成中发挥积极作用.在不考虑先决关系的条件下, 假定以知识点x1作为学习起点, 设计不同的学习次序.如图1中实线所示, 可知序列1对应的学习顺序为

x1→ {x1, x2}→ {x1, x2, x3},

而序列2对应图中的虚线部分, 知识的学习顺序可表达为

x1→ {x1, x3}→ {x1, x2, x3}.

图1 不同序列下的教学设计Fig.1 Instructional design with different sequences

在序列1指导下的学习活动中, 学生学习知识点x1、x2后并未有明显提升, 直到完成知识点x3的学习后才有较明显的飞跃.序列1的设计更适合一般学习者, 持续平缓地获得学习成就.对于序列2的学习, 在前期(学习知识点x1、x3后)学生可获得显著的进步, 而后期进步并不明显.序列2设计更适合于学习动机不强的学生, 通过较快获得学习成就激励学生.

2 模糊测度计算
2.1 依赖于专家知识的模糊测度计算

相比其它领域, 专家知识在教育系统中发挥更重要的作用.对于专家而言, 相对较容易给出两个知识集合之间的关联指标Δ j(X1, X2).首先以单知识集的情况为例, 选择3~5位专家, 给出单个知识的模糊测度v({xi})、v({xj})及知识集间的关联指标Δ j({xi, xj}).根据各位专家的意见取平均值, 获得更客观的结果.由已知的单个知识模糊测度及关联指标, 可计算2个知识点构成集合的模糊测度:

v({xi, xj})=v({xi})+v({xj})+Δ j({xi, xj}).

由此, 可进一步扩展为多个知识点构成的集合

L={xi, xi+1, …, xi+n, …}

的关联指标[26, 27]:

Δ j(L)=vj(L)- ∑B∈L(k-1)vj(B)+ ∑B∈L(k-2)vj(B)-…+ (-1)k-l􁀄 ∑B∈L(l)j(B),

其中, k表示集合L中的维数, 即元素个数, L(l)表示l维子集构成的集合.由此可完成所有知识集合模糊测度的计算.

2.2 数据驱动的模糊测度计算

在涉及单个知识点集时, 可由领域专家根据经验给定模糊测度, 但是随着知识数量的增加, 给出各个集合的关联指标具有一定的主观性且工作量较大.若能通过学生的学习数据获得模糊测度, 结果更客观有效.通过数据驱动的方法表示和学习模糊测度, 使输入更大的知识数目时模糊测度这一参数的学习是可计算的[28].举例来说, 若完成学习任务涉及知识x1、x2、x3, 则需要计算的模糊测度个数为

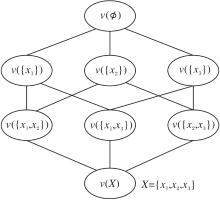
23-2=6, v(Ø )=0, v({x1, x2, x3})=1,

如图2所示.

为了实现计算目的, 可将模糊测度v值存储在大小为2n的数组中, 建立子集X'⊆X和二进制表示方法之间一对一的映射关系.若X'={x1, x2, x3}, 则v({x1})表示为v(001), v({x1, x2})表示为v(011), v({x1, x2, x3})表示为v(111).基于模糊测度的弱单调性, 构成不同子集间模糊测度的约束关系, 如v({x1})≤ v({x1, x2}), 且v({x1, x2, x3})=1.若已知函数的有限离散值α =(α 1, α 2, …α K)和模糊测度v, 模糊积分计算得到实际值s.由此, 已知输入值α 和实际值s, 可通过遗传算法或神经网络找到最优的模糊测度v, 使损失函数值最小.

图2 模糊测度的计算规模Fig.2 Computing scale of fuzzy measures

具体算法如下所示.

算法1 模糊测度学习算法

输入 输入值α , 实际值s //α 为某函数f的离散值

输出 模糊测度的值

设置迭代次数t=0

初始化模糊测度v(0)=( v1(0), …, vK(0), …, v1, 2, …k(0)) //对应2K-2个模糊测度值

While t< tmaxdo //tmax为最大迭代次数

v1, v2, …, vL=search(μ (t)) //搜索可行解

for l← 1 to L do

s˙=fuzzy integral(α , vl)

//通过模糊积分计算获得预测值

end for

l* =arg minl∈{1, 2, …, L}‖ s˙-s‖ 2//根据目标函数计算损失l

vt+1= vl* //更新参数

end while

Return v(tmax)

然而在实际应用中, 知识点的数量可能远超过3个, 那么模糊测度的计算会面临复杂性急剧增长的问题.当|X|=n时, 需确定模糊测度的数量为2n个参数值.例如, 涉及知识点数量为10时, 所需确定的模糊测度值为210=1 024个.当n值变大时, 模糊测度的数量呈指数级增长, 确定模糊测度变得非常困难.为了应对上述问题, 可进一步引入k可加模糊测度[29], 在模糊测度的复杂性和表达能力方面进行折衷.

3 知识的全局重要度和交互指标
3.1 知识的全局重要度

在实现模糊测度的计算后, 可得出知识的全局重要度及知识之间的交互指数.基于知识的关联性, 综合单个知识点的模糊测度值及同时考虑包含该知识点所有集合对应的测度值.可采用合作博弈中Shapley指标度量知识的全局重要度[30].

定义2 令v为一个模糊测度, 对于∀ xi∈ X, 全局重要度指数为:

ϕ (xi)= ∑A⊆X\{xi}(n-|A|-1)!|A|!n!·vA∪xi-vA盒 (1)

其中, n为知识集X中的知识点个数, n=|X|, A为知识点集合, A⊆X.

具体算法如下所示.

算法2 计算知识全局重要度

输入 二进制序列编码的模糊测度幂集

输出 知识点xi的全局重要度

for xi← x1 to xn do

获得局部知识集合Ai=X\{xi}, 求得局部全集A中所有含k个元素的子集K

for k← 0 to n-1 do

计算系数γ k= (n-k-1)!k!n!, k=|K|

end for

vK∪ i=vK∪ vi //Ai各子集对应编码的模糊测度为vK

ϕ (xi)= ∑i=1nγ k ∑K⊆AiK|=k(vK∪ i-vK)

end for

根据案例1中模糊测度值及式(1), 计算知识点x1的全局重要度:

ϕ (x1)= (3-0-1)!0!3![v(x1)-v(Ø )]+ 􁀄 (3-1-1)!1!3!v(x1, x2)-v(x2)]+􁀄[ (3-1-1)!1!3!(x1, x3)-v(x3)]+􁀄[v (3-2-1)!2!3!x1, x2, x3)-v(x2, x3)]=0.292.

同理可得, 知识点x2、x3的全局重要度分别为

ϕ (x2)=0.292, ϕ (x3)=0.416.

除了知识自身的重要性以外, 还考虑其超集的模糊测度.尽管知识x3的模糊测度值不高, 但它和其它知识关联后产生的模糊测度值较高, 因此知识x3的全局重要性最高.在此情况下, 可将知识x3看作是后续学习中的重点内容, 在教学和学习过程中加以关注, 并在知识x3上分配相应的教学时间, 设置练习的推荐.

3.2 知识的交互指标

通过模糊测度还可反映知识间的交互指标.例如, 某些知识与其它知识总是存在积极的交互作用, 可看作是学习中的关键点, 说明这个知识点需要被重点关注或优先推荐学习巩固.

定义3 知识点xi、xj关于模糊测度v的交互作用指标[31]定义为

I(xi, xj)= ∑A⊆X\{xi, xj}(n-|A|-2)!|A|!(n-1)!·[v(A∪{xi, xj})-v(A∪{xi})-v(A∪{xj})+v(A)], (2)

其中

n=|X|, I(xi, xj)∈ [-1, 1],

A⊆X为知识点集合, 交互指标反映两两知识点在整个知识集合中的交互作用.

具体算法如下所示.

算法3 计算知识交互指标

输入 按二进制序列编码的模糊测度幂集

输出 知识对{xi, xj}的交互指标

for xi← x1 to xn do

for xj← xi+1 to xn do

获得局部知识集合Aij=X\{xi, xj}中所有含k个元素的子集K

for k← 0 to n-2 do

计算系数ξ k= (n-k-2)!k!(n-1)!, k=|K|

end for

vK∪ i=vK∪ vi //Aij各子集对应编码的模糊测度为vK

I(xi, xj)= ∑k=0n-2ξ k ∑K⊆AijK|=k(vi∪ j∪ K-vi∪ K-vj∪ K+vK) // {xi, xj}交互指标

end for

end for

同样根据案例1的模糊测度值及式(2), 可得知识对{x1, x2}的交互指标值:

I(x1, x2)= (3-0-2)!0!(3-1)![v(Ø ∪ {x1, x2})-

v(Ø ∪ {x1})-v(Ø ∪ {x2})+v(Ø )]+

(3-1-2)!1!(3-1)![v({x1, x2, x3})-

v({x1, x3})-v({x2, x3})+v(x3)]=

1×1×(0.5-0.45-0.45)2!+

1×1×(1-0.9-0.9+0.3)2!=

-0.45.

同理可得,

I(x1, x3)=0.1, I(x2, x3)=0.1.

通过交互指标可看出, 知识点x3与知识点x1、x2交互值均大于0, 说明知识点x3对于学习目标的达成较重要.

4 在认知诊断中的应用
4.1 融合知识关联性的认知诊断

知识关联性建模可应用到认知诊断等实际学习场景中, 为教师教学、学生学习及试题建设提供有效的辅助决策支持.认知诊断旨在识别认知过程, 并评估学生是否已掌握或拥有特定的认知技能或知识[32, 33], 进而实现对学习者表现的预测.

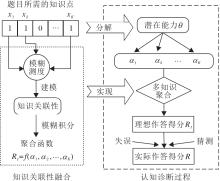
本文建立融合知识关联性的认知诊断框架, 如图3所示.

图3 知识关联性融合的认知诊断框架Fig.3 Cognitive diagnosis framework based on knowledge relevance

在认知诊断过程中, 若某道题目涉及K个知识点(x1, x2, …, xK), 题目所需的知识点标记为1, 否则为0, 那么学生的潜在能力θ 被分解为在这几个知识点上的掌握水平

α ={α 1, α 2, …, α K},

聚合多个知识点后获得理想的作答情况RI.同时, 还需要考虑学生做题时猜测和失误的影响, 得到实际的作答情况R.将认知诊断中多知识聚合表达为

RI=f(α 1, α 2, …, α K),

其中, f∶ [0, 1]k→ [0, 1]表示聚合函数, 即聚合每个知识点上的掌握水平以获得理想作答情况.

在现有研究中, 多个知识间的聚合方式通常为联结型和补偿型[34], 由不同的聚合函数表示.但无论何种聚合函数, 都未从知识集合间关联性角度进行考虑.由于模糊积分[35]是以模糊测度为核心建立的聚合方法, 可通过模糊积分中的模糊测度表达知识集合间的关联性, 本文引入模糊积分作为聚合函数.融合知识关联性的认知诊断具体实现如下.首先获得各个知识点及知识集合间的模糊测度, 利用模糊测度建模知识的关联性, 通过模糊积分聚合多个知识的掌握水平α , 这里选择模糊积分中的一类典型代表Choquet积分[35]实现聚合计算:

RI= ∑k=1K[α k-α k-1](v({xl|α l≥ α k})),

其中, α k表示学习者在第k个知识点上的掌握水平, 模糊测度v表示各知识集合对于正确作答的重要程度.那么Choquet积分聚合的结果就表示学生的理想作答情况, 由此实现认知诊断过程中的知识关联性融合.

4.2 实验设置与结果分析

由于FuzzyCDF(Fuzzy Cognitive Diagnosis Frame-work)[36]完整体现认知诊断过程, 本次实验以FuzzyCDF作为实验框架, 通过预测学习者的学习表现验证本文方法的可行性.实验中使用模糊积分替换FuzzyCDF中原有的聚合函数.

从公平性角度出发, 本文实验采用与FuzzyCDF相同的参数, 具体实现细节见文献[37].学生潜在能力θ 及知识掌握水平α 通过M-H(Metro-polis-Hastings)的马尔科夫蒙特卡洛算法学习获得.对于聚合函数Choquet 积分中模糊测度的参数学习, 由模糊积分神经网络[38]实现.

首先将由FuzzyCDF得到学生在各知识点上的掌握水平作为输入, 输出是学生在每道题目上的作答得分.根据定义1, 模糊测度

v(A)= ∨B⊂Av(B)+Δ v(A),

其中, Δ v(A)∈ R+, 由此可确保模糊测度的单调性.模糊积分神经网络根据模糊测度的单调性约束设计基于随机梯度下降的优化方法, 实现模糊测度的训练(算法描述见2.2节).在获得各知识点的模糊测度后, 使用Choquet积分计算多知识聚合后学生的理想作答情况.

实验选择公开数据集Math1和Math2(http://staff.ustc.edu.cn/~qiliuql/data/math2015.rar), Math1数据集包含15道客观题和5道主观题, Math2数据集包含16道客观题和4道主观题, 客观题的得分为{0, 1}, 主观题得分为[0, 1].

使用AUC(Area Under the Curve)和MAE(Mean Absolute Error)作为评估指标, 对比认知诊断模型预测效果.

实验将Choquet积分作为聚合函数的模型(简称为CHI(Choquet Integral)方法)(https://github.com/kathy-sj/Choquet-integrals), 并将CHI和其它基准方法对比.选择FuzzyCDF、 IRT(Item Response Theory)[39]、DINA(Deterministic Inputs, Noisy "And" Gate Model)[40]作为对比方法.

同时构造2种不同比例的训练数据集, 首先随机抽取80%的数据用于训练, 20%的数据用于测试模型效果.为了进一步观察各预测方法在不同数据稀疏度情况下的预测效果, 再随机抽取20%的数据用于训练, 80%的数据用于测试模型.

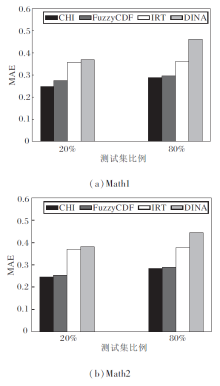
各方法在Math1、Math2数据集上的得分预测结果如图4所示.由图可知, 在认知诊断模型中融合知识关联性后, 即使使用CHI进行预测, 相比FuzzyCDF, 在训练数据占 80% 的情况下, MAE值分别下降2.8%(Math1数据集)和0.8%(Math2数据集), 比IRT和DINA更有优势.在训练数据占20%的情况下, MAE值平均降低 0.7%.由此证实CHI在数据稀疏时仍有效.

图4 各方法在2个数据集上的得分预测结果对比Fig.4 Predicting result comparison of different methods on 2 datasets

另一方面, 针对数据集中的客观题计算AUC值, 如图5所示.由图可看出, 在考虑知识关联性后, 预测精度更高.此外, 随着训练数据稀疏度的增加, 优势依然存在.

由图4和图5可看出, 融合知识关联性的认知诊断模型在预测学习者表现时, 相比未考虑知识的关联性, 可得到更优的预测效果.对比Math1、Math2数据集上的实验结果发现, 在Math1数据集上的优势更显著.而在Math2数据集上, 在80%数据用于训练, 20%数据用于测试的情况下, CHI仅有微弱的优势.这和Math2数据集上知识点本身的特征有关, 知识点之间存在的关联性较弱(如掌握不等式的性质和计算能力之间相对独立), 因此是否融合知识关联性进行预测对结果影响并不大.但同时也可说明模糊积分作为聚合函数对于认知诊断工作的通用性, 对关联性较弱的数据集同样适用, 并具有相对较优的性能.

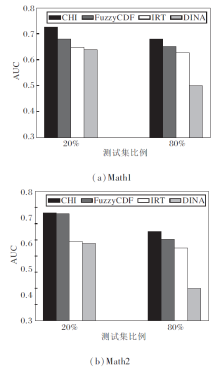图5 各方法在2个数据集上的客观题预测结果对比Fig.5 Predicting result comparison of different methods for objective questions on 2 datasets

此外, 为了验证聚合函数本身对预测效果的影响, 进行扩展实验.在不计算失误和猜测这两个因素的情况下, 直接将聚合函数的输出作为最终分数与实际得分进行对比, 观察预测表现的影响, 结果如表1所示.由表可看出, 在Math1、Math2数据集上, 考虑知识关联性的模糊积分方法, MAE值分别降低6.2%和1.6%, 比考虑失误和猜测参数时优势更明显.而在客观题上的AUC值分别提高5.2%和1.4%.从结果上看, 预测误差被部分转移到失误和猜测参数中.

表1 不同聚合函数对指标值的影响 Table 1 Influence of different aggregation functions on indexes%

此外, 从模型的解释性上看, 融合知识关联性的认知诊断模型可通过模糊测度更好地反映知识之间的关联性.根据3.1节和3.2节的讨论, 以模糊测度为基础, 计算各个知识点的全局重要度和两两知识点间的交互指标, 可更好地理解和解释知识的关联性.下面举例说明.

案例分析2 以Math1数据集上的第15题为例, 题目涉及如下6个知识点:函数的性质(x1)、函数的象限(x2)、空间想象(x3)、抽象归纳(x4)、推理论证(x5)、计算(x6).根据各知识点及知识集合的模糊测度, 可计算得出每个知识的全局重要度及两两知识之间的交互指标(见式(1)、式(2)).其中知识点函数的性质(x1)、函数的象限(x2)的全局重要程度较高,

ϕ (x1)=0.241, ϕ (x2)=0.212,

而重要性程度最低(ϕ (x6)=0.091)的是知识点计算(x6)这一通用技能.对于考察函数相关的问题, 这一结果是可接受和合理的.

另外, 通过交互指标可体现知识之间的关联性, 通过模糊测度计算可得知识点x1、x2交互指标 I(x1, x2)=-0.206, 知识点x1、x6交互指标 I(x1, x6)=-0.068.一般而言:交互指标越高, 互补性越强[41]; 交互指标越低, 知识点之间的关联性越高.根据计算结果可看出, 知识点x1、x2之间的关联性更强.从知识点本身上看, 函数的性质(x1)和函数的象限(x2)之间的关联性必然强于函数的性质(x1)和计算(x6)之间的联系.这与交互指标显示的结果一致, 也说明模糊测度表征知识关联性的有效性.

案例分析3 以Math1数据集上的主观题为例, 知识全局重要度与影响得分程度之间的关系如图6所示.图中横轴表示每道题涉及知识点对应的全局重要度, 基于模糊测度计算得出全局重要度(见式(1)).纵轴表示是否掌握知识点对得分的影响程度, 由计算知识点掌握水平与实际得分的皮尔逊相关系数表示.

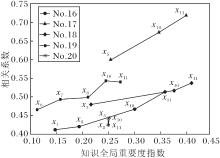图6 知识全局重要度与影响得分程度的关系Fig.6 Relationship between global importance of knowledge and the degree of influence on score

由图6可见, 题17需要3个知识点{x5, x10, x11}, 对应的全局重要度分别为

ϕ (x5)=0.25, ϕ (x10)=0.35, ϕ (x11)=0.4,

这3个知识点的知识掌握水平与实际得分的相关系数分别为0.6, 0.67, 0.72.知识的重要性越高意味着该知识对于学生实际得分的影响越大.题16、18、19也有同样趋势.而对于第20题, 由于各个知识点的全局重要度相近, 对应的知识点掌握水平与得分的相关系数也接近.由图6可看出, 越重要的知识, 其掌握水平与实际得分的相关系数就越大, 这一趋势符合一般认知规律, 进一步说明模糊测度建模的合理性.

5 结 束 语

关联性存在于知识及知识集合之间, 这种关联性可能是显性确定的, 也可能是隐性模糊的.本文通过模糊测度建模知识的关联性, 量化表达知识及知识集合复杂的关系, 这对于理解学生的认知过程具有积极意义.本文同时以模糊测度为基础, 拓展延伸至知识全局重要度和交互指标及知识关联性在认知诊断这一场景中的应用, 充分体现知识关联性对实际学习场景的现实意义.基于现有的认知诊断框架, 引入模糊测度对知识关联性进行表征.本文对于框架中参数的学习问题开展研究, 然而如何学习获得更优化的参数仍是一个挑战.为此, 下一步将考虑借助其它研究工作实现参数优化, 并基于此着力解决认知水平和知识关联性统一表征的认知诊断框架实现问题.

参考文献
[1] SLAVIN R E. Educational Psychology: Theory and Practice. 7th Edition. London, UK: Pearson, 2002. [本文引用:2]
[2] 钟卓, 唐烨伟, 钟绍春, 等. 人工智能支持下教育知识图谱模型构建研究. 电化教育研究, 2020, 41(4): 62-70.
(ZHONG Z, TANG Y W, ZHONG S C, et al. Research on Constructing Model of Educational Knowledge Map Supported by Artificial Intelligence. E-Education Research, 2020, 41(4): 62-70. ) [本文引用:1]
[3] PIAGET J, BROWN T, THAMPY K J. The Equilibration of Cognitive Structures: The Central Problem of Intellectual Development. Chicago, USA: University of Chicago Press, 1985. [本文引用:1]
[4] 徐显龙, 周知恂, 嵇云, 等. 基于4C/ID模型的复杂技能综合学习设计及成效. 中国电化教育, 2019(10): 124-131.
(XU X L, ZHOU Z X, JI Y, et al. Design and Effectiveness of Comprehensive Learning for Complex Skills Based on 4C/ID Model. China Educational Technology, 2019(10): 124-131. ) [本文引用:1]
[5] THORNDIKE E L, WOODWORTH R S. The Influence of Improvement in One Mental Function upon the Efficiency of Other Functions(I). Psychological Review, 1901, 8(3): 247-261. [本文引用:1]
[6] MAYER R. Applying the Science of Learning. London, UK: Pearson, 2010. [本文引用:1]
[7] GUO L, BAO Y, WANG Z R, et al. Cognitive Diagnostic Assessment with Different Weight for Attribute: Based on the Dina Model. Psychological Reports, 2014, 114(3): 802-822. [本文引用:1]
[8] 罗照盛. 认知诊断评价理论基础. 北京: 北京师范大学出版社, 2019.
(LUO Z S. Fundamentals of Cognitive Diagnostic Assessment. Beijing, China: Beijing Normal University Press, 2019. ) [本文引用:1]
[9] MENG L L, ZHANG M X, ZHANG W X, et al. CS-BKT: Introducing Item Relationship to the Bayesian Knowledge Tracing Model. Interactive Learning Environments, 2019, 29(8): 1393-1403. [本文引用:1]
[10] CARMONA C, MILLÁN E, PÉREZ-DE-LA-CRUZ J L, et al. Introducing Prerequisite Relations in a Multi-layered Bayesian Stu-dent Model // Proc of the International Conference on User Mode-ling. Berlin, Germany: Springer, 2005: 347-356. [本文引用:1]
[11] LEIGHTON J P, GIERL M J, HUNKA S M. The Attribute Hierarchy Method for Cognitive Assessment: A Variation on Tatsuoka's Rule-Space Approach. Journal of Educational Measurement, 2004, 41(3): 205-237. [本文引用:1]
[12] WANG C J, GIERL M J. Using the Attribute Hierarchy Method to Make Diagnostic Inferences about Examinees' Cognitive Skills in Critical Reading. Journal of Educational Measurement, 2011, 48(2): 165-187. [本文引用:1]
[13] CHEN P H, LU Y, ZHENG V W, et al. Prerequisite-Driven Deep Knowledge Tracing // Proc of the IEEE International Conference on Data Mining. Washington, USA: IEEE, 2018: 39-48. [本文引用:1]
[14] LIANG C, YE J B, WU Z H, et al. Recovering Concept Prerequisite Relations from University Course Dependencies // Proc of the 31st AAAI Conference on Artificial Intelligence. Palo Alto, USA: AAAI, 2017: 4786-4791. [本文引用:1]
[15] ROY S, MADHYASTHA M, LAWRENCE S, et al. Inferring Concept Prerequisite Relations from Online Educational Resources // Proc of the 31st AAAI Conference on Innovative Applications of Artificial Intelligence. Palo Alto, USA: AAAI, 2019: 9589-9594. [本文引用:2]
[16] YANG Y M, LIU H X, CARBONELL J, et al. Concept Graph Learning from Educational Data // Proc of the 8th ACM International Conference on Web Search and Data Mining. New York, USA: ACM, 2015: 159-168. [本文引用:1]
[17] GAO W B, LIU Q, HUANG Z Y, et al. RCD: Relation Map Driven Cognitive Diagnosis for Intelligent Education Systems // Proc of the 44th International ACM SIGIR Conference on Research and Development in Information Retrieval. New York, USA: ACM, 2021: 501-510. [本文引用:1]
[18] 张暖, 江波. 学习者知识追踪研究进展综述. 计算机科学, 2021, 48(4): 213-222.
(ZHANG N, JIANG B. Review Progress of Learner Knowledge Tracing. Computer Science, 2021, 48(4): 213-222. ) [本文引用:1]
[19] TONG S W, LIU Q, HUANG W, et al. Structure-Based Know-ledge Tracing: An Influence Propagation View // Proc of the IEEE International Conference on Data Mining. Washington, USA: IEEE, 2020: 541-550. [本文引用:1]
[20] MA W C. A Diagnostic Tree Model for Polytomous Responses with Multiple Strategies. British Journal of Mathematical and Statistical Psychology, 2019, 72(1): 61-82. [本文引用:1]
[21] DE LA TORRE J, DOUGLAS J A. Model Evaluation and Multiple Strategies in Cognitive Diagnosis: An Analysis of Fraction Subtraction Data. Psychometrika, 2008, 73(4): 595-624. [本文引用:1]
[22] MA W C, GUO W J. Cognitive Diagnosis Models for Multiple Strategies. British Journal of Mathematical and Statistical Psycho-logy, 2019, 72(2): 370-392. [本文引用:1]
[23] SUGENO M. Theory of Fuzzy Integrals and Its Applications. Ph. D. Dissertation. Tokyo, Japan: Tokyo Institute of Technology, 1974. [本文引用:1]
[24] BELIAKOV G, DIVAKOV D. On Representation of Fuzzy Mea-sures for Learning Choquet and Sugeno Integrals. Knowledge-Based Systems, 2020, 189. DOI: DOI:10.1016/j.knosys.2019.105134. [本文引用:1]
[25] TORRA V, NARUKAWA Y. The Interpretation of Fuzzy Integrals and Their Application to Fuzzy Systems. International Journal of Approximate Reasoning, 2006, 41(1): 43-58. [本文引用:1]
[26] 余晓晗, 徐泽水, 刘守生, 等. 复合打击下的火力分配方案评估. 系统工程与电子技术, 2014, 36(1): 84-89.
(YU X H, XU Z S, LIU S S, et al. Evaluations of Fire Assignment Alternatives in the Situation of Composite Strikes. System Engineering and Electronics, 2014, 36(1): 84-89. ) [本文引用:1]
[27] BELIAKOV G, PRADERA A, CALVO T. Aggregation Functions: A Guide for Practitioners. Berlin, Germany: Springer, 2007. [本文引用:1]
[28] ISLAM M A, ANDERSON D T, PINAR A J, et al. Data-Driven Compression and Efficient Learning of the Choquet Integral. IEEE Transactions on Fuzzy Systems, 2017, 26(4): 1908-1922. [本文引用:1]
[29] JAVIER M, SERGE G, PILAR B. k-Maxitive Fuzzy Measures: A Scalable Approach to Model Interactions. Fuzzy Sets and Systems, 2017, 324: 33-48. [本文引用:1]
[30] MURRAY B, ISLAM M A, PINAR A J, et al. Explainable AI for Understand ing Decisions and Data-Driven Optimization of the Choquet Integral // Proc of the IEEE International Conference on Fuzzy Systems. Washington, USA: IEEE, 2018. DOI: DOI:10.1109/FUZZ-IEEE.2018.8491501. [本文引用:1]
[31] MUROFUSHI T, SONEDA S. Techniques for Reading Fuzzy Mea-sures(III): Interaction Index // Proc of the 9th Fuzzy System Symposium. Tokyo, Japan: JST, 1993: 693-696. [本文引用:1]
[32] GIERL M J. Making Diagnostic Inferences About Cognitive Attri-butes Using the Rule-Space Model and Attribute Hierarchy Method. Journal of Educational Measurement, 2007, 44(4): 325-340. [本文引用:1]
[33] 刘淇, 陈恩红, 朱天宇, 等. 面向在线智慧学习的教育数据挖掘技术研究. 模式识别与人工智能, 2018, 33(1): 77-90.
(LIU Q, CHEN E H, ZHU T Y, et al. Research on Educational Data Mining for Online Intelligent Learning. Pattern Recognition and Artificial Intelligence, 2018, 33(1): 77-90. ) [本文引用:1]
[34] PARDOS Z A, HEFFERNAN N T, RUIZ C, et al. The Composition Effect: Conjunctive or Compensatory? An Analysis of Multi-skill Math Questions in ITS // Proc of the 1st International Conference on Educational Data Mining. Berlin, Germany: Springer, 2008: 147-156. [本文引用:1]
[35] GRABISCH M, MUROFUSHI T, SUGENO M. Fuzzy Measures and Integrals: Theory and Applications. Berlin, Germany: Sprin-ger, 2000. [本文引用:2]
[36] WU R Z, LIU Q, LIU Y P, et al. Cognitive Modelling for Predicting Examinee Performance[C/OL]. [2021-09-14]. http://staff.ustc.edu.cn/~cheneh/paper_pdf/2015/Runze-Wu-IJCAI.pdf. [本文引用:1]
[37] LIU Q, WU R Z, CHEN E H, et al. Fuzzy Cognitive Diagnosis for Modelling Examinee Performance. ACM Transactions on Intelligent Systems and Technology, 2018, 9(4): 1-26. [本文引用:1]
[38] ISLAM M A, ANDERSON D T, PINAR A J, et al. Enabling Explainable Fusion in Deep Learning with Fuzzy Integral Neural Networks. IEEE Transactions on Fuzzy Systems, 2020, 28(7): 1291-1300. [本文引用:1]
[39] DRASGOW F, HULIN C L. Item Response Theory // DUNNETTE M D, HOUGH L M, eds. Hand book of Industrial and Organizational Psychology. Palo Alto, USA: Consulting Psychologists Press, 1990: 577-636. [本文引用:1]
[40] DECARLO L T. On the Analysis of Fraction Subtraction Data: The DINA Model, Classification, Latent Class Sizes, and the Q-Matrix. Applied Psychological Measurement, 2011, 35(1): 8-26. [本文引用:1]
[41] GRABISCH M. The Representation of Importance and Interaction of Features by Fuzzy Measures. Pattern Recognition Letters, 1996, 17(6): 567-575. [本文引用:1]