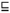李进金,博士,教授,主要研究方向为一般拓扑学、粗糙集、概念格.E⁃mail:jinjinlimnu@126.com.
作者简介:

孙晓燕,硕士,讲师,主要研究方向为一般拓扑学、粗糙集、概念格.E⁃mail:sxy96001@aliyun.com.
在程序性知识的评估中,技能是指与项目的解决相关的操作路径.基于程序性知识的学习评价,文中提出由项目自身的状态结构诱导多分知识结构的方法,目的是建立适用于问题解答的多分评估体系.首先,根据各项目的解答或操作过程设定响应值,得到项目特定的响应值集.通过项目状态转移函数定义项目状态空间,将问题空间推广到多分情形.然后,由操作路径导出合取的技能映射,讨论由合取的技能映射诱导的多分知识结构.结果表明由技能映射通过合取模型诱导的多分知识结构满足逐项交封闭.最后,给出诱导多分知识结构的算法步骤,并举例说明算法的有效性.
LI Jinjin, Ph.D., professor. His research interests include topology, rough set and concept lattice.
About Author:
SUN Xiaoyan, master, lecturer. Her research interests include topology, rough set and concept lattice.
In the assessment of procedural knowledge, skills refer to the operation paths relevant to the solution of an item. Based on the learning assessment of procedural knowledge, a method of delineating polytomous knowledge structure from the state structure of the item itself is proposed to establish a polytomous assessment system for problem solving. Firstly, the response values are set according to the solution or operation process of each item to obtain the item-specific response value set. The item state space is defined by item state transition function, and the problem space is extended to polytomous case. Then,the conjunctive skill maps are derived from the operation paths, and the polytomous knowledge structures delineated by the conjunctive skill maps are discussed. The results show that the polytomous knowledge structure delineated by a skill map based on the conjunctive model satisfies the item-wise intersection closure. Finally, the algorithm steps of delineating polytomous knowledge structure are given, and the effectiveness of the proposed algorithm is illustrated by an example.
本文责任编委 张燕平
Recommended by Associate Editor ZHANG Yanping
传统的二分KST假设个体对项目的回答为正确(用1表示)或错误(用0表示), 在对知识和学习进行评价时具有局限性.针对这一局限性, Schrepp[8]将KST推广到有两个以上答案的问题, 使用线性有序集评估解决方案的质量.Bartl等[9]讨论具有分级知识状态的知识空间.Stefanutti等[10]提出KST的多分推广, 假设项目集上的水平集为完备格.在Stefanutti等[10]的基础上, Heller[11]将拟序知识空间推广到多分情形, 提出多分知识结构的两个条件, 并考虑项目特定的响应尺度.
在程序性知识的评估中, 技能是指与项目的解决相关的解路径或操作路径[18].李金海等[23]提出概念的渐进式认知, 体现人们认识事物是一个从不完全到完全的逐步完善过程, 能根据阶段性认知及时指导下一步的行动, 并逐渐实现完全认知.同样地, 对程序性知识的学习及其技能的掌握也是渐进式认知过程.概念格是形式概念分析理论中用于数据分析与处理的核心工具, 也是一种挖掘数据关联的有效方法[24].这为进一步研究程序性知识的学习与评价提供方法和工具.
本文基于Stefanutti[18]提出的程序性知识的评估框架, 结合Stefanutti等[10]与Heller[11]的知识空间理论的多分推广, 以对初中数学知识中的解答题、应用题等主观题的学习与技能评价为例, 将问题空间推广到多分情形.首先, 根据各项目的操作元集设定响应值, 得到项目特定的响应值集, 通过项目状态转移函数定义项目状态空间.然后, 由操作路径导出合取的技能映射, 证明由合取的技能映射通过合取模型诱导的多分知识结构满足逐项交 
在KST中, 知识域Q是一组关于特定主题的项目集合, 其中项目的答案可被二分为正确(用1表示)或不正确(用0表示).知识状态K为Q的子集, 表示个人有能力在理想条件(即假设粗心的错误和幸运的猜对不会发生)下正确回答的项目集合.知识结构是二元组(Q, K), 其中K为一个由Q的子集构成的知识状态集族, 至少包含空集Ø 和全集Q.知识域Q上的知识结构K的对偶是由K中所有知识状态的余集构成的知识结构
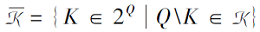
设Q为有限集, 有限知识结构(Q, K)是并封闭的当且仅当对于∀ K1∈ K, K2∈ K, 有K1∪ K2∈ K.有限知识结构(Q, K)是交封闭的当且仅当对于∀ K1∈ K, K2∈ K, 有K1∩ K2∈ K.满足并封闭的知识结构(Q, K)称为知识空间.满足交封闭的知识结构(Q, K)称为简单闭包空间.Q的子集的集合K形成Q上的知识空间当且仅当K的对偶结构
在KST中, 通过技能映射将知识域Q中的每个项目与有助于解决这个项目的技能联系起来, 并从这个关联中推断知识状态.设非空的知识域Q, 非空的技能集S, 技能映射是三元组(Q, S, τ ), 其中, τ :Q→ 2S\{Ø }, 为从Q到S的非空幂集的映射.给定T⊆S, 由T通过析取模型诱导的知识状态为

由T通过合取模型诱导的知识状态为

取遍T⊆S, 所有通过析取模型诱导的知识状态的集合是由τ 通过析取模型诱导的知识结构; 所有通过合取模型诱导的知识状态的集合是由τ 通过合取模型诱导的知识结构.由τ 通过析取模型诱导的知识结构是知识空间; 由τ 通过合取模型诱导的知识结构是简单闭包空间.由同一技能映射通过析取模型和合取模型诱导的知识结构是对偶的.有关技能映射及其诱导的知识结构的详细背景参见文献[6]和文献[7].
在KST的多分推广中, 知识域Q中的项目的解决质量由水平集L中的级别l∈ L表示.在Schrepp[8]提出的KST多分推广中, L为线性有序集.Stefanutti等[10]设定L为完备格.
设X为非空集, ≤ 为X上的偏序关系(即满足自反性、传递性、反对称性的二元关系), 则称(X, ≤ )为偏序集.设(X, ≤ )为偏序集, 对于∀ A⊆X, A的最小上界称为A的上确界, 记为sup A或∨ A; A的最大下界称为A的下确界, 记为inf A或∧ A.若∀ A⊆X, 恒有sup A与inf A存在, 则称(X, ≤ )为完备格.若∀ a∈ X, b∈ X, 恒有
sup{a, b}=a∨ b, inf{a, b}=a∧ b
存在, 则称(X, ≤ )为格.有限格是完备格.有关格理论的详细背景知识参见文献[2]、文献[25]和文献[26].
在Heller[11]提出的KST多分推广中, 个体对知识域Q中各项目的掌握程度用有限的响应值集V表示, 且设非空有限响应值集V是格, 由于V是有限的, 所以V是完备格.
多分知识状态是Q到V的映射K:Q→ V, 表示将Q中每个项目对应V中的一个响应值.一切这样的映射的集合记为
VQ=
1.2.1 多分知识状态的表示法
多分知识状态有两种表示形式, 分别由Heller[11]和Stefanutti等[10]提出.
集合表示法[11].多分知识状态K为Q× V的特定子集, 即对于∀ K∈ VQ, K⊆Q× V, 记
pv=(p, v)∈ Q× V,
对于∀ K∈ VQ, 规定
pv∈ K⇔ K(p)=v,
则
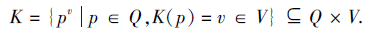
向量表示法[10].在给定的有限知识域Q中, 设
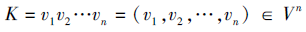
其中vi=K(qi), i=1, 2, …, n.
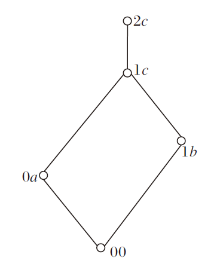
例如, 设Q={a, b, c}, V={0, 1, 2}, 多分知识状态K:Q→ V定义为K(a)=1, K(b)=2, K(c)=0, 则多分知识状态K的集合形式为

固定各项目顺序为q1=a, q2=b, q3=c, 则多分知识状态K的向量形式为

为了避免记号的混乱, 在下述论述与推导中, 本文均采用多分知识状态的集合表示法, 向量表示法仅出现在图形中.
1.2.2 多分知识状态的集合表示法的扩展
设(V, ≤ )为偏序集, v∈ V, v的下集记为
↓ v={u∈ V:u≤ v},
V的所有下集的集合记为
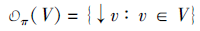
则(V, ≤ )与( 

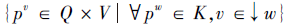
例如, 设Q={a, b, c}, V={0, 1, 2, 3}, 多分知识状态K:Q→ V定义为

则多分知识状态K的集合形式为

由于
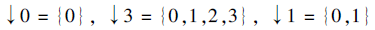
故K的扩展多分知识状态为

程序性知识是一种经过学习自动化的关于行为步骤的知识, 如运算法则、解题步骤、操作程序等.在Stefanutti[18]提出的程序性知识的评估中, 问题的解决过程被描述为从操作集合中获取操作序列, 操作序列应用于问题的某初始状态, 产生一个最终状态, 由此定义问题空间, 并诱导知识空间.本节基于程序性知识的评估框架, 通过项目状态转移函数将项目的状态与相关的操作程序对应, 将问题空间推广到多分情形.
设非空有限的程序性知识域Q={q1, q2, …, qn}, 根据各项目的解答或操作过程设定响应值集.不同项目的解答或操作过程具有不同的结构特点, 因此需要考虑项目特定的响应值集.在这里, 本文采用Heller[11]提出的KST多分推广中的假设, 即使用非空有限响应值集Vi表示个体对项目qi∈ Q的掌握程度.设
inf(Vi)=∧ i(Vi)
称为Vi的底元, 记为丄i;
sup(Vi)=∨ i(Vi)
称为Vi的顶元, 记为丅i.特别地, 对于Ø ⊆Vi, 规定
∨ i(Ø )=丄i, ∧ i(Ø )=丅i, i=1, 2, …, n.
例1 设Q={q1, q2},
项目q1:已知等腰三角形的腰长为5 cm, 底边长比腰长多1 cm, 周长为多少?
项目q2:已知等腰三角形的一条边长为5 cm, 另一条边长为6 cm, 周长为多少?
根据项目解答过程的类型设定响应值集, 两个项目的响应值集的格结构是不同的.

由于q1的解答过程是层层递推的, 所以设定V1为有限线性序集, 即V1={0, 1, 2}.V1的底元为丄1=0, V1的顶元为丅1=2.

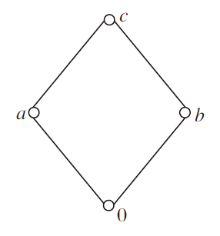
由于q2的解答中有分类讨论, 所以V2不是线性序集.设V2={0, a, b, c}, 其中
0≤ 2a, 0≤ 2b, a≤ 2c, b≤ 2c,
a与b不可比较, 且a∨ 2b=c, 如图1所示.V2的底元为丄2=0, V2的顶元为丅2=c.
例2 设Q={q1, q2},
项目q1:计算7+4× 2;
项目q2:计算7+(4-2)× 6.
对于层层递推的项目解答或操作过程, 根据步骤数设定响应值集, 响应尺度可能不同.

q1的解答是层层递推的, 步骤数为2, 所以设定V1为三分的线性序集, 即V1={0, 1, 2}.

q2的解答是层层递推的, 步骤数为3, 所以设定V2为四分的线性序集, 即V2={0, 1, 2, 3}.
定义1[11, 25] 设知识域Q={q1, q2, …, qn}, Q上的非空有限响应值集族
其中
∀ K1∈ VQi, K2∈ VQi, K1 

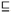
注1 对于∀ K1∈
K1=K2⇔ K1(qi)=i K2(qi), i=1, 2, …, n;
K1 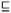
K1 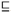
定义2 设知识域Q={q1, q2, …, qn}及其响应值集族{Vi
Ω =
Ω 称为知识域Q的状态集.
注2 多分知识状态K∈
{
其中vi∈ Vi, i=1, 2, …, n.特别地,
inf(
称为
sup(
称为
例如, 在例2中,
Q={q1, q2}, V1={0, 1, 2}, V2={0, 1, 2, 3}.
q1的初始状态为
Ω 1={q1}× V1={
项目q2的初始状态为
Ω 2={q2}× V2={
于是
Ω =Ω 1∪ Ω 2={
设多分知识状态K∈
定义3[11] 设知识域Q={q1, q2, …, qn}及其响应值集族
1)K至少包含
2)
K(pv)={K∈ K:pv∈ K}≠ Ø .
例3 续例1.
Q={q1, q2}, V1={0, 1, 2}, V2={0, a, b, c},
其中, 0≤ 2a, 0≤ 2b, a≤ 2c, b≤ 2c, 则
Ω ={
K1={{
由于{
K2={{
由于
所以K2不满足定义3中条件2), K2不是多分知识结构.
K3={{
由
{
知, K3满足定义3中条件1); 由
知, K3满足定义3中条件2).
如图2所示, K3是多分知识结构.
注3[10, 11] 任意给定多分知识结构(Q,

其中
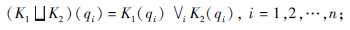
K1与K2的逐项交是

其中

特别地, 对于Ø ⊆K, 规定
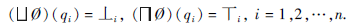
任意给定有限多分知识结构(Q,{Vi}ni=1, K), K满足逐项并 



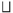
例如, 在例3中, K1和K2都不是多分知识结构, 所以K1和K2都不是多分知识空间.K3是多分知识结构, 由

得, K3满足逐项并 
设程序性知识域Q={q1, q2, …, qn}, 根据各项目的解答或操作过程设定响应值集.为了保证操作步骤的有限性, 下述论述中均假定各项目的解答或操作是非循环的.∀ qi∈ Q, 项目qi的操作集是由其解答或操作过程的每个步骤构成的集合, 记为Π i.在这里, 本文仅考虑每个项目的某个特定的解法, 对于一题多解的情形将在能力模型中考虑.
命题1 对于∀ q∈ Q, 设q的解答或操作非循环且步骤数有限, 则项目q的操作集Π 是有限集.设Π ={π 1, π 2, …, π r}, 根据每步操作逐一设定响应值, 得到项目q的响应值集V是有限格.
1)如果项目q的解答或操作是层层递推的, 且步骤数为r, 记第k步操作为π k, k=1, 2, …, r, 则q的操作集Π ={π 1, π 2, …, π r}.设项目q的初始状态为q0, 即q的响应值集V的底元为0, 根据每步操作逐一设定响应值, 即每步操作产生新的项目状态, 对应的响应值加1, 则项目q的响应值集V是有限线性序集, 且V={0, 1, …, r}.
2)如果q的解答或操作中有n个分支, 则V不是线性序集.先按各分支的层层递推的步骤数设定各分支上线性有序的响应值集, 再将任意k(2≤ k≤ n)个不可比较的响应值的上确界(称为分支定向并[11])设为新的响应值, 规定:当n=2时, 设a1与b1不可比较, a2与b2不可比较, 且
a1∨ b1=c, a2∨ b2=d,
如果a1≤ a2且b1≤ b2, 则c≤ d.当n> 2时, 若∀ l∈ A, 恒有m∈ B, 使得l≤ m, 则∨ A≤ ∨ B.这样得到的项目q的响应值集V是有限格.
例如, 例1中的项目q1的解答步骤是层层递推的, 步骤数为2, 所以V1={0, 1, 2}.项目q2的解答中有分支, 2个分支的步骤数均为1, 所以2个分支上的响应值集分别{0, a}和{0, b}, 其中
0≤ 2a, 0≤ 2b.
由于a和b不可比较, 于是设响应值c=a∨ 2b, 得到项目q2的响应值集V2={0, a, b, c}.V2是有限格.
如果项目的解答或操作中有分支, 且至少一个分支的步骤数大于1, 则按照命题1中2)的规定给出各分支定向并的序关系, 如例4所示.
例4 设项目q:解方程|x-3|=3x-5.q的解答中有2个分支, 各分支的步骤数均为2, 即
则
0≤ 1a≤ 2a, 0≤ 1b≤ 2b.
将{1a, 2a, 1b, 2b}中任意2个不可比较的响应值的上确界设为新的响应值, 即
1a∨ 1b=2c, 2a∨ 1b=3d,
1a∨ 2b=3e, 2a∨ 2b=4.
由1a≤ 2a, 1b≤ 1b得
(1a∨ 1b)≤ (2a∨ 1b),
即2c≤ 3d.同理可得
2c≤ 3e, 3d≤ 4, 3e≤ 4.
由于1a≤ 2a, 1b≤ 2b, 所以2a∨ 1b与1a∨ 2b不可比较, 即3d与3e不可比较.如图3所示, 项目q的响应值集
V={0, 1a, 2a, 1b, 2b, 2c, 3d, 3e, 4}
是有限格.
设程序性知识域Q={q1, q2, …, qn}.对于∀ qi∈ Q, 设qi的操作集Π i为有限集, 根据qi的每步操作逐一设定响应值.对于∀
这里只考虑由错误操作导致的错误状态.例如, 将“ 7+4× 2” 错误操作为“ 11× 2” .不考虑由操作不熟练或粗心导致的错误状态.例如, 将“ 7+4” 错误计算为“ 12” .由
表示项目qi的错误状态集.
项目qi的单个操作对项目状态转移的作用可用定义4中的项目状态转移函数φ i表示.
定义4 设程序性知识域Q={q1, q2, …, qn}, 项目qi的非空有限操作集为Π i, 根据每步操作逐一设定响应值, 得到qi的响应值集Vi, i=1, 2, …, n.记

其中, Ω i为qi的状态集,Ωi-为qi的错误状态集.∀ qi∈ Q, 项目状态转移函数φ i是从 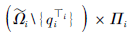
1)对于∀
φ i(
响应值由k变为l, 称(
φ i(
响应值k保持不变, 称(
2)对于∀
φ i(
且响应值k保持不变.
因为不考虑操作不熟练或粗心导致的错误状态, 所以当项目的初始状态及操作步骤给定时, 操作路径的终止状态是唯一确定的.因此, 设(
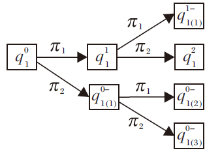
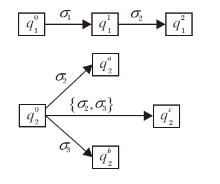
例5 续例2, 考察q1、q2的项目状态转移函数.假设学生已掌握加、减、乘的单独运算, 项目q1、q2是为了考察学生掌握四则运算顺序的情况.项目q1的操作集Π 1={π 1, π 2}, 项目q2的操作集Π 2={π 1, π 2, π 3}, 其中, π 1表示“ 先乘、除” , π 2表示“ 从左往右依次计算” , π 3表示“ 计算括号内的运算” .项目q1、q2的解答是层层递推的, 由命题1中1)知,
V1={0, 1, 2}, V2={0, 1, 2, 3}.
项目q1的初始状态为
q1的项目状态转移如图4所示.由图4得以下状态转移函数:
φ 1(
φ 1(
φ 1(
φ 1(
φ 1(
φ 1(
q1的终止状态.
因此, q1的正确单一操作路径为
q2的项目状态转移如图5所示.q2的初始状态为
终止状态为
定义5[18] 设非空有限操作集Π , 由Π 中s个操作元组成的操作序列π 1π 2…π s∈ Π s, 称为Π 的一个长度为s的操作序列.具有任意长度的所有操作序列(包括空操作序列ε , 即s=0)的集合记为Π ∧ , 即
Π ∧ =
其中, 空操作序列ε 表示不施以任何操作, ε 为Π ∧ 的单位元, 即
∀ π ∈ Π ∧ , ε π =π ε =π .
对于∀ qi∈ Q, 补充定义
φ i(
则项目状态转移函数φ i扩充为从
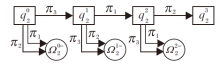
注4[18] 设程序性知识域Q={q1, q2, …, qn}, 任意项目qi的状态转移满足如下性质:
1)自反性.对于∀
2)传递性.对于∀
φ i(
记
Φ i(
则
Φ i(
传递性具体说明如图6所示.
定义6 设程序性知识域Q={q1, q2, …, qn}及其响应值集族
定义7 设非空有限操作集Π , 操作序列集Π ∧ , 对于∀ s∈ Z+, 任意给定长度为s的操作序列π 1π 2…π s∈ Π s, π 1π 2…π s的子序列是操作序列π iπ i+1…π i+t, 其中, 1≤ i≤ s, 0≤ t≤ s-i.
定义8 设非空有限操作集Π , 操作序列集Π ∧ , 对于任意2个非空操作序列σ 1∈ Π ∧ \{ε }, σ 2∈ Π ∧ \{ε }, 规定σ 1≤ σ 2当且仅当σ 1是σ 2的子序列.任意给定非空操作序列σ ∈ Π ∧ \{ε }, σ 的所有子序列中关于“ ≤ ” 的极小者称为σ 的极小子序列.
命题2 设操作序列
σ =π 1π 2…π s∈ Π ∧ \{ε },
其中s∈ Z+, 则σ 的极小子序列为π j, j=1, 2, …, s.
例如, 设非空操作序列σ =π 1π 2π 3, σ 的所有子序列为π 1, π 1π 2, π 1π 2π 3, π 2,
π 1≤
取关于“ ≤ ” 的极小者得π 1; 由于
π 2≤
取关于“ ≤ ” 的极小者得π 2; 由于
π 3≤
取关于“ ≤ ” 的极小者得π 3.所以σ 的极小子序列为π 1、π 2和π 3.
由定义4可知, 项目状态转移函数φ i表示项目qi的单个操作对项目状态的作用, 而由注4可知, 项目qi的一个操作序列对给定项目状态的作用由定义9中的过程函数Φ i表示.
定义9 设程序性知识域Q={q1, q2, …, qn}, 项目qi的非空有限操作集为Π i,
1)任意给定
2)任意给定操作序列π 1π 2…π s∈
φ i(
则
Φ i(
称π 1π 2…π s为qi的正确操作序列, (
对于∀ qi∈ Q,
Φ i(
所以空操作序列ε 为任意项目的正确操作序列.但是ε 未实现状态的转移, 因此下述分析中均不考虑空操作路径.
例6 续例5, 考察项目q1的正确非空操作路径.由图4看出, 对于操作序列π 1、π 2和π 1π 2, 有过程函数:
Φ 1(
其余均为错误操作序列.所以, q1的正确操作路径为
推论1 对于解答或操作步骤数较多的复杂项目q, 将q的操作过程划分为t个正确非空操作序列, 以此构成q的操作元集
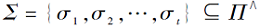
根据每个操作元σ k(k=1, 2, …, t)逐一设定响应值, 得到项目q的响应值集V是有限格.
1)如果q的解答或操作是层层递推的, 则q的响应值集V为有限线性序集.操作元σ k(k=1, 2, …, t)作用于qk-1产生新的项目状态qk, 响应值由k-1变为k, 即φ (qk-1, σ k)=qk, 称(qk-1, σ k, qk)是以qk-1为初始状态, σ k为操作元, qk为终止状态的正确单一操作路径, 简记为qk-1σ k, k=1, 2, …, t.于是, 得到项目q的响应值集V={0, 1, …, t}.
2)如果q的解答或操作中有分支, 对q的操作过程进行不同划分, 可能使V具有不同的格结构.
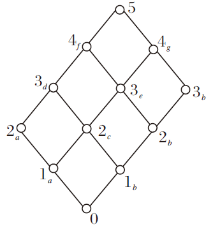
例7 设项目q:解方程
项目q的操作集
Π ={π 1, π 2, π 3, π 4, π 5, π 6},
其中, π 1表示“ 当x≥ 0时, |x|去绝对值” , π 2表示“ 方程移项与合并同类项” , π 3表示“ 解一元一次方程” , π 4表示“ 当x≤ 0时, |x|去绝对值” , π 5表示“ 一元二次多项式的因式分解” , π 6表示“ 解一元二次方程” .
1)将q的操作过程划分成5个正确非空操作序列, 构成操作元集
Σ ={π 1, π 2π 3, π 4, π 2π 5, π 6}.
根据各分支上的每个操作元逐一设定响应值, 得到2个分支上的响应值集{0, 1a, 2a}和{0, 1b, 2b, 3b}, 其中
0≤ 1a≤ 2a, 0≤ 1b≤ 2b≤ 3b.
取分支定向并, 即
1a∨ 1b=2c, 2a∨ 1b=3d, 1a∨ 2b=3e, 2a∨ 2b=4f, 1a∨ 3b=4g, 2a∨ 3b=5.
依照命题1中2)的规定得到{2c, 3d, 3e, 4f, 4g, 5}的序, 于是有限格
V1={0, 1a, 2a, 1b, 2b, 3b, 2c, 3d, 3e, 4f, 4g, 5}
为q的响应值集, 如图7所示.
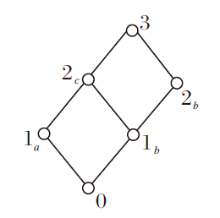
2)将q的操作过程划分成4个正确非空操作序列, 构成操作元集
Σ ={π 1π 2, π 3, π 4π 2, π 5π 6},
则q的响应值集
V2={0, 1a, 2a, 1b, 2b, 2c, 3d, 3e, 4}
为有限格, 如图3所示.
3)将q的操作过程划分成3个正确非空操作序列, 构成操作元集
Σ ={π 1π 2π 3, π 4π 2, π 5π 6},
则
V3={0, 1a, 1b, 2b, 2c, 3}
为有限格, 如图8所示.
命题1是推论1的特殊情形, 即将每个操作步骤划分为一个操作元σ k=π k, k=1, 2, …, r, 得到操作元集
Σ ={σ 1, σ 2, …, σ r}=Π ⊆Π ∧ .
因此, 过程函数Φ i的定义9可做如下推广.
定义10 设程序性知识域Q={q1, q2, …, qn}, qi的操作元集Σ i={σ 1, σ 2, …,
qi的响应值集Vi为有限格, i=1, 2, …, n.∀ qi∈ Q, 过程函数Φ i为从
1)任意给定
2)任意操作序列
ω =σ 1σ 2…σ s∈
如果存在项目状态序列
φ i(
则
Φ i(
称ω =σ 1σ 2…σ s为qi的正确非空操作序列, (
如果项目q的解答或操作中有分支, Vq不是线性序集, 需要考虑操作组合对项目状态的作用.
定义11 设程序性知识域Q={q1, q2, …, qn}, 项目qi的操作元集Σ i={σ 1, σ 2, …,
Φ i(
其中, a与b不可比较, a∨ i b=c, 则将{ω 1, ω 2}作用于
Φ i(
称{ω 1, ω 2}为qi的正确非空操作组合, (
例8 续例7.记
σ 1=π 1π 2π 3, σ 2=π 4π 2, σ 3=π 5π 6,
取q的操作元集Σ ={σ 1, σ 2, σ 3}, 由例7中3)可知, q的响应值集
V={0, 1a, 1b, 2b, 2c, 3}.
q的项目状态转移图如图9所示.由图可知, q的正确非空操作序列为σ 1、σ 2、σ 3和σ 2σ 3.由
Φ (q0, σ 1)=
1a与1b不可比较, 1a∨ 1b=2c, 可知,
Φ (q0, {σ 1, σ 2})=
即{σ 1, σ 2}为q的正确操作组合, 其中q0σ 1和q0σ 2是q0{σ 1, σ 2}的极小子路径.同理,
Φ (q0, {σ 1, σ 2σ 3})=q3,
即{σ 1, σ 2σ 3}为q的正确操作组合, 其中q0σ 1、q0σ 2和
定义12 设程序性知识域Q={q1, q2, …, qn}, 项目qi的操作元集Σ i={σ 1, σ 2, …,
ω j∈ (
如果存在操作程序δ =ω 1ω 2…ω l, 及项目状态序列
Φ i(
则
Φ i(
称δ =ω 1ω 2…ω l为qi的正确操作程序, (
例9 设项目q:已知直角三角形的两条边长分别为4 cm和6 cm, 第三条边长为多少?项目q的解答过程如下:

项目q的操作集Π ={π 1, π 2, π 3, π 4}, 其中, π 1表示“ 勾股定理” , π 2表示“ 将x=4, y=6代入方程x2+y2=z2” , π 3表示“ 解一元二次方程” , π 4表示“ 将x=4, z=6代入方程x2+y2=z2” .记
σ 1=π 1, σ 2=π 2π 3, σ 3=π 4π 3, Σ ={σ 1, σ 2, σ 3},
则q的响应值集V={0, 1, 2a, 2b, 3}, q的项目状态转移图如图10所示.
由图10可知, q的正确非空操作序列为σ 1、σ 2、σ 3、
Φ (q0, σ 1)=q1, Φ (q1, {σ 2, σ 3})=q3,
所以
Φ (q0, σ 1{σ 2, σ 3})=q3,
σ 1{σ 2, σ 3}为项目q的正确操作程序, 操作路径q0σ 1{σ 2, σ 3}的极小子路径为q0σ 1、q1σ 2和q1σ 3.因此, 项目q的所有正确操作路径为q0σ 1、q1σ 2、q1σ 3、q0σ 1σ 2、q0σ 1σ 3、q1{σ 2, σ 3}和q0σ 1{σ 2, σ 3}.
个体掌握操作路径
定义 13 设程序性知识域Q={q1, q2, …, qn}, 项目qi的操作元集Σ i={σ 1, σ 2, …,
由于项目qi的任意一个正确操作路径的极小子路径为Σ i中的构成该路径的操作元对应的正确单一操作路径, 所以, qi的技能集为Σ i中的各操作元对应的正确单一操作路径的集合.
例10 续例8, 考察项目q的技能集.记
σ 1=π 1π 2π 3, σ 2=π 4π 2, σ 3=π 5π 6,
q的操作元集Σ ={σ 1, σ 2, σ 3}, 响应值集
V={0, 1a, 1b, 2b, 2c, 3}.
由图9可知, q的所有正确操作路径为q0σ 1、q0σ 2、
定义14 设程序性知识域Q={q1, q2, …, qn}, 项目qi的操作元集Σ i={σ 1, σ 2, …,
Σ =
对于∀ σ ∈ Σ ,
[σ ]=
表示以σ 为操作元的正确单一操作路径的等价类, 知识域Q的技能集为
S={[σ ]|∀ σ ∈ Σ }.
例11 续例5, 考察例2的项目q1、q2的技能集, 以及知识域Q的技能集.记
σ 1=π 1, σ 2=π 2, σ 3=π 3, Σ 1={σ 1, σ 2}, Σ 2={σ 3, σ 1, σ 2},
则
Σ =Σ 1∪ Σ 2={σ 1, σ 2, σ 3}.
由图4可知, 项目q1的所有正确单一操作路径为
S1={
由图5可知, 项目q2的所有正确单一操作路径为
S2={
因此, 记
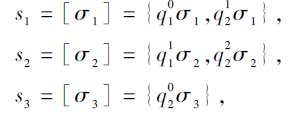
则Q的技能集
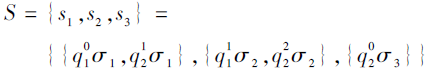
已知程序性知识域Q={q1, q2, …, qn}及其响应值集族
设Q的技能集S={s1, s2, …, sm}.技能状态T是技能集S的子集, T⊆S, T表示个体掌握(或没掌握)技能的集合.在合取模型中, 个体必须掌握所有的相关技能, 才能达到相应的项目状态.因此, 对于∀
定义15 设程序性知识域Q={q1, q2, …, qn}及其响应值集族
对于∀
例12 续例11, 考察例2中q1的项目状态
所以
故
定义16 设程序性知识域Q={q1, q2, …, qn}
及其响应值集族
记
Ω +=
设从Ω +到S的非空幂集的映射τ , 其中, 对于∀
定理1 设Ω +上的映射τ :Ω +→ 2S\{Ø }, ∀
K={
记
H={i|
则
τ (K)=
证明 ∀ i∈ H, 设
δ =
则δ 能实现从{
另一方面, ∀ i∈ H, 记
Ki={
则
τ (Ki)=τ (
由
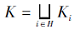
知, ∀ s∈ τ (K), 必定存在i∈ H, 使得
s∈ τ (Ki)=τ (
即
s∈
从而
τ (K)⊆
因此
τ (K)=
例13 续例12.
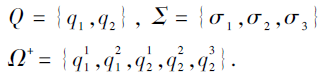
由例12可知,
τ (
同理可得q2的项目状态
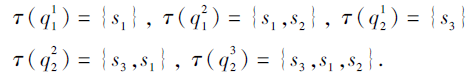
由Ω +上的技能映射τ 可张成
τ ({
同理可得
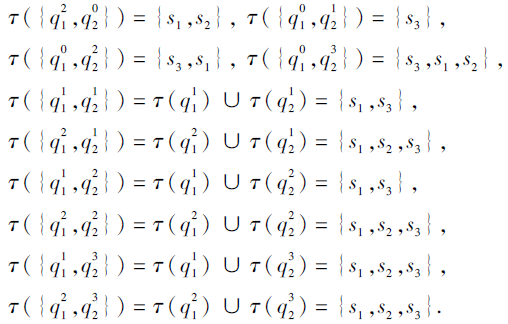
定义17 设程序性知识域Q={q1, q2, …, qn}及其响应值集族
由于仅考虑每个项目的某个特定解法, 所以对于∀ qi∈ Q,
另一方面, 根据Σ i的每个操作元逐一设定响应值, 则对于∀ v∈ Vi\{0}, w∈ Vi\{0}, v≠ i w, 从
命题3 设合取的技能映射(Ω +, S, τ ), 其中τ :Ω +→ 2S\{Ø }, 则对于∀ qi∈ Q, τ 满足如下2个条件:
1)兼容性.∀ v∈ Vi\{0}, w∈ Vi\{0}, v< i w, 则τ (
2)差异性.∀ v∈ Vi\{0}, w∈ Vi\{0}, v与w不可比较, 则
τ (
在合取模型中, 个体必须掌握所有的相关技能, 才能达到相应的项目状态.因此, 设个体掌握的技能状态为T, T⊆S, 如果τ (
定义18 设合取的技能映射(Ω +, S, τ ), 其中τ :Ω +→ 2S\{Ø }.给定技能状态T⊆S, T表示个体掌握的技能的集合, 由T通过合取模型诱导的多分知识状态为

命题4 由合取的技能映射τ 通过合取模型诱导的所有多分知识状态的集合K至少包含{
证明 设个体掌握的技能状态T=Ø , ∀
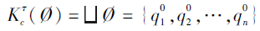
设个体掌握的技能状态T=S, ∀

定理2 设合取的技能映射(Ω +, S, τ ), 其中τ :Ω +→ 2S\{Ø }.取遍所有的技能状态T⊆S, 所有通过合取模型诱导的多分知识状态的集合
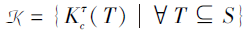
是多分知识结构.
证明 首先, 由命题4可知, K满足定义3中1).然后, 在合取模型中, 对于∀ qi∈ Q,
τ (
于是τ (

由于
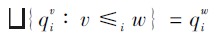
故

于是, ∀ qi∈ Q,

因此, ∀
所以, K满足多分知识结构的定义3中2).综上所述, 取遍所有的T⊆S, 所有通过合取模型诱导的多分知识状态的集合K为多分知识结构.
定义19 设合取的技能映射(Ω +, S, τ ), 其中τ :Ω +→ 2S\{Ø }.取遍所有的技能状态T⊆S, 所有通过合取模型诱导的多分知识状态的集合K称为由技能映射τ 通过合取模型诱导的多分知识结构.
例14 续例13.
Q={q1, q2}, Ω +={
合取的技能映射τ 定义为

取遍所有的技能状态T⊆S, 得到如下通过合取模型诱导的多分知识状态:
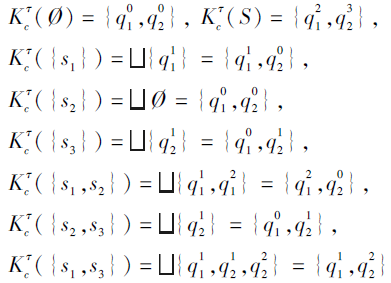
所以, 由τ 通过合取模型诱导的多分知识结构为
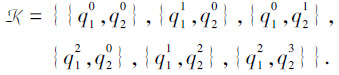
如图11所示, K满足逐项交 
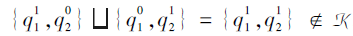
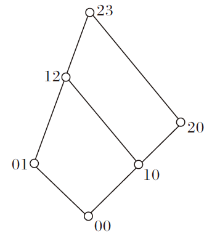 | 图11 例14中多分知识结构(K,   |
所以K不满足逐项并 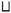
注5 命题3中1)对于通过合取模型诱导多分知识结构是必要的.如果技能映射τ 不满足该条件, 则由τ 通过合取模型诱导的多分知识状态的集合可能不满足定义3中2).
例如, 在例14中, 若定义技能映射τ '为

其中τ '(
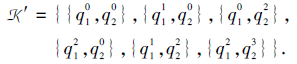
由于
所以K'不满足定义3中2), K'不是多分知识结构.
根据项目qi的操作元集Σ i逐一设定响应值, 得到qi的响应值集Vi不一定是线性有序集.
例15 续例1.
Q={q1, q2}, Π 1={π 1, π 2}, Π 2={π 2, π 3}.
记
σ 1=π 1, σ 2=π 2, σ 3=π 3, Σ 1={σ 1, σ 2}, Σ 2={σ 2, σ 3},
则

由项目状态转移(图12)可得
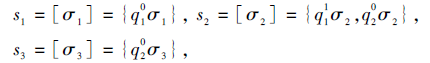
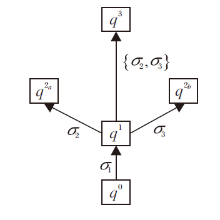
则S={s1, s2, s3}.由操作路径导出的合取的技能映射τ 为

取遍所有的技能状态T⊆S, 得到由τ 通过合取模型诱导的多分知识结构为
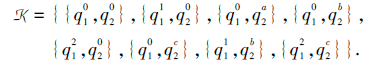
如图13所示, K满足逐项交 
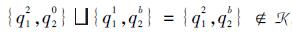
 | 图13 例15中多分知识结构(K,   |
所以K不满足逐项并 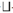
注6 命题3中2)对于通过合取模型诱导多分知识结构是必要的.如果技能映射τ 不满足该条件, 则由τ 通过合取模型诱导的多分知识状态的集合可能不满足定义3中2).
例如, 在例15中, 若定义技能映射τ '为
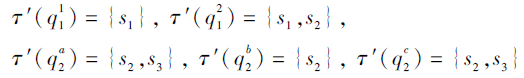
其中, a与b不可比较,
τ '(
但是
τ '(
不满足命题3中2).由τ '通过合取模型诱导的所有多分知识状态的集合为
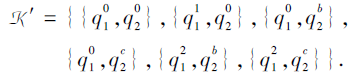
由于
所以K'不满足定义3中2), K'不是多分知识结构.
命题5 设合取的技能映射(Ω +, S, τ ), 其中τ :Ω +→ 2S\{Ø }.给定技能状态T⊆S, T表示个体掌握的技能的集合, 由T诱导的个体能达到的项目状态的集合记为

由T通过合取模型诱导的多分知识状态
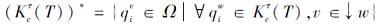
则G(T)为
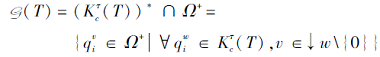
记

称
证明 设
∀ v∈ ↓ w\{0}, τ (
于是 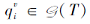
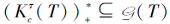
另一方面, 对于 

知, 必存在
由命题5和定义18可得推论2.
推论2 设合取的技能映射(Ω +, S, τ ), 其中τ :Ω +→ 2S\{Ø }.给定技能状态T⊆S, T表示个体掌握技能的集合, 由T通过合取模型诱导的多分知识状态为
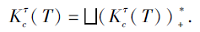
定理3 设合取的技能映射(Ω +, S, τ ), 其中τ :Ω +→ 2S\{Ø }.由技能映射τ 通过合取模型诱导的多分知识结构K满足逐项交 
证明 对于∀ K1∈ K, K2∈ K, 其中Ki是由技能状态Ti通过合取模型诱导的多分知识状态, 即
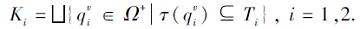
记

记

由T1∩ T2⊆Ti得G⊆Gi, i=1, 2.因此, G⊆G1∩ G2.另一方面, 设q 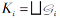
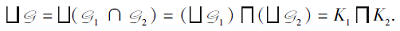
因为
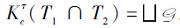
所以 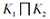
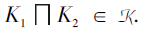

在合取模型中, 个体必须掌握所有的相关技能, 才能达到相应的项目状态.因此, 只要存在至少一个相关技能是个体没有掌握的, 则该个体不能达到相应的项目状态.于是, 设合取的技能映射(Ω +, S, τ ), 其中τ :Ω +→ 2S\{Ø }, 设个体没有掌握技能的集合为T⊆S, 只要存在至少一个t∈ τ (
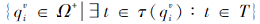
设技能状态T表示个体没有掌握技能的集合, 则 $\bar{T}$=S\T表示个体掌握的技能集.显然, 由T诱导的个体没达到的项目状态的集合与由 $\bar{T}$诱导的个体能达到的项目状态的集合互为余集.由命题5知, 由$\bar{T}$诱导的个体能达到的项目状态的集合为 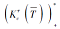
推论3 设合取的技能映射(Ω +, S, τ ), 其中τ :Ω +→ 2S\{Ø }.给定技能状态T⊆S, T表示个体没有掌握技能的集合, 由T诱导的个体没达到的项目状态的集合记为
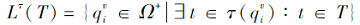
则Lτ (T)为 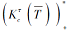
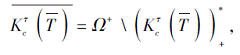
则
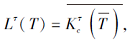
称
例如, 在例14中, 取个体没有掌握技能的集合T={s2}, 则
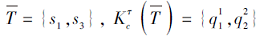
由
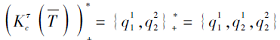
所以, 由{s2}诱导的个体没达到的项目状态的集合是由{s1, s3}通过合取模型诱导的扩展多分知识状态
Lτ ({s2})=Ω +\
记

则

推论4 设合取的技能映射(Ω +, S, τ ), 其中τ :Ω +→ 2S\{Ø }.T⊆S表示个体没有掌握技能的集合.取遍T⊆S, 由τ 诱导的个体没达到的项目状态的集合为

设K是由τ 通过合取模型诱导的多分知识结构,
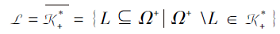
L满足集合并∪ -封闭.
例如, 在例14中, 由τ 通过合取模型诱导的多分知识结构为
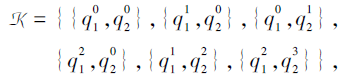
则K的扩展多分知识结构为
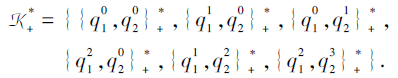
于是,
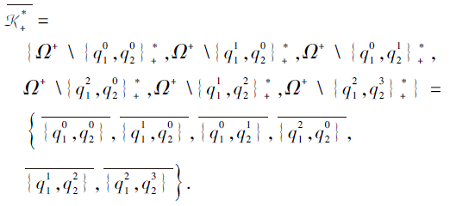
所以, 由推论3可知, 取遍个体没有掌握的技能状态, 所有由τ 诱导的个体没达到的项目状态的集合为
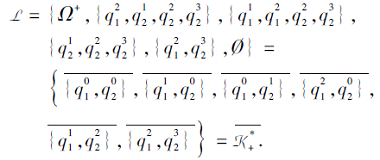
如图14所示, 由于
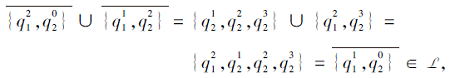
 | 图14 例14中多分知识结构的对偶(L,   |
同理可得,
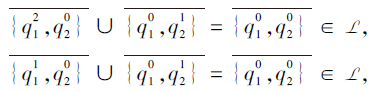
所以L满足集合并∪ -封闭.但是, 因为
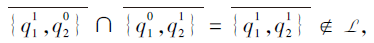
所以L不满足集合交∩ -封闭.
定义20[27] 称三元组(U, A, I)为一个形式背景, 其中U={x1, x2, …, xn}为对象集, 每个xi(1≤ i≤ n)称为一个对象; A={a1, a2, …, am}为属性集, 每个aj(1≤ j≤ m)称为一个属性; I⊆U× A为U和A之间的二元关系, 若(x, a)∈ I, 则称对象x具有属性a, 若(x, a)∉I, 则称对象x不具有属性a.
用1表示(x, a)∈ I, 用0表示(x, a)∉I, 则形式背景可表示为只有0和1的表格, 如表1所示.
| 表1 形式背景表 Table 1 Formal background |
设合取的技能映射(Ω +, S, τ ), 其中τ :Ω +→ 2S\{Ø }.将Ω +视为对象集, S视为属性集, I⊆Ω +× S是Ω +和S之间的二元关系, 规定
(
(
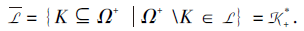
又由推论2可知, 由τ 通过合取模型诱导的多分知识结构为
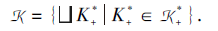
作为本节的小结, 给出从程序性知识域Q的项目状态空间通过合取模型导出多分知识结构的算法.设Q={q1, q2, …, qn}及其响应值集族
算法1 在Q的项目状态空间中以
n)为起点的所有操作路径导出合取的技
能映射(Ω +, S, τ ).
step 1 构造Q的项目状态空间中以
初始设置.由qi的所有正确单一操作路径构成队列
Wi={
并将Wi中任意有限条起点相同的路径的组合添加到Wi中, 得
迭代步k=0时,
迭代步k=1时, 从
迭代步k> 1时, 对所有的i=1, 2, …, n, 从
Φ i(
则将
设Φ i(
Φ i(
其中w≤ i v, 且u、v不可比较, 则将
继续迭代, 直到
step 2 由操作路径集Pi(
对于∀ qi∈ Q,
Φ i(
则τ (
τ (
其中,
算法2 由形式背景(Ω +, S, I)导出L, 利用L与
的对偶性得到由τ 通过合取模型诱导的多
分知识结构K.
step 1 在形式背景(Ω +, S, I)中, 规定
(
(
step 2 取个体没有掌握的技能状态Ti={si}, 由(Ω +, S, I)导出Ti诱导的没达到的项目状态Lτ (Ti), i=1, 2, …, m.由{Lτ (T1), Lτ (T2), …, Lτ (Tm)}取集合并∪ -封闭, 张成所有由τ 诱导的个体没达到的项目状态的集合L.
step 3 取L的对偶得到由τ 通过合取模型诱导的扩展多分知识结构
算法1采用起点固定的广度优先路径搜索算法(Breadth First Search, BFS).这是基于队列这种数据结构的搜索方式, 特点是由每个状态扩展出许多状态, 然后再以此扩展, 直到处理完毕队列中所有状态.算法1中step 1的时间复杂度为O(|S|+|Ω +|).算法2中step 2的时间复杂度为O(|Ω +|· |S|).在算法2中, 可考虑结合形式背景或概念格中的已有结果, 如对象约简或属性约简, 从而去除计算中的冗余部分, 达到算法的简化.
例16 设Q={q1, q2}, 项目q1是例7中的q:解方程|x2-6|=x2-2x+2; 项目q2:已知x> 1, 且|x-1|=x2-4x+5, 求x.q2的解答:
x> 1: |x-1|=x2-4x+5
⇒ x-1=x2-4x+5 操作步骤π 1
⇒ x2-5x+6=0 操作步骤π 2
⇒ (x-2)(x-3)=0 操作步骤π 5
⇒ x=2或x=3 操作步骤π 6
记
σ 1=π 1π 2, σ 2=π 3, σ 3=π 4π 2, σ 4=π 5π 6,
由例7中2)可知,
V1={0, 1a, 2a, 1b, 2b, 2c, 3d, 3e, 4}, V2={0, 1, 2}.
Σ ={σ 1, σ 2, σ 3, σ 4},
记

项目状态转移如图15所示.
由算法1中step 1可得
P1(
{
P2(
再由算法1中step 2可得, 导出的合取的技能映射τ 为

由于1a∨ 11b=2c, 且
τ (
所以
Ω ++=Ω +\{
由算法2得到由形式背景(Ω ++, S, I)导出的个体没达到的项目状态的集合L, 从而得到由τ 通过合取模型诱导的多分知识结构K.
1)在形式背景(Ω ++, S, I)中, 规定
(
(
| 表2 例16中技能映射(Ω ++, S, τ )的形式背景表 Table 2 Formal background of skill map(Ω ++, S, τ ) in example 16 |
2)由表2导出个体没达到的项目状态.取
Ti={si}, i=1, 2, 3, 4,
则

由{Lτ (T1), Lτ (T2), Lτ (T3), Lτ (T4)}取∪ -封闭张成τ 诱导的个体没达到的项目状态的集合:
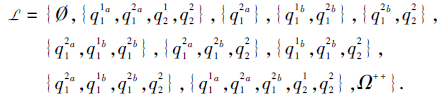
3)取L的对偶, 即
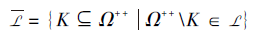
得到τ 通过合取模型诱导的Ω ++上的扩展多分知识结构:
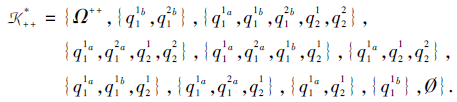
对
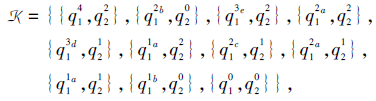
K的Hasse图如图16所示.由定理3可知, K满足逐项交 
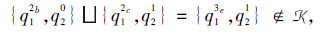
所以K不满足逐项并 
本文根据程序性知识域中各项目的操作元逐一设定响应值, 得到项目特定的响应值集.基于程序性知识的学习评价[18], 通过项目状态转移函数定义项目状态空间, 并导出合取的技能映射, 证明由技能映射通过合取模型诱导的多分知识结构满足逐项交封闭.最后讨论由合取的技能映射通过合取模型诱导的多分知识结构与所有没达到的项目状态的集合之间的对偶性, 并给出诱导多分知识结构的算法步骤.值得注意的是, 在本文框架中, 仅考虑每个项目的某个特定解法, 对于一题多解的情形将在后续的能力模型中考虑.为了保证操作集的有限性, 假定各项目的解答或操作是非循环的, 所以可在后续研究中考虑对循环解路径的约简.
知识空间的形式背景与形式概念分析[27, 28]密切相关, 因此可考虑将KST的多分推广与面向属性或面向对象概念格的相关结果[29, 30, 31, 32]结合.程序性知识学习与形式概念分析中的概念认知学习有诸多关联, 因此, 基于程序性知识的学习评价与概念认知学习的交叉融合也是今后研究的方向.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|
| [19] |
|
| [20] |
|
| [21] |
|
| [22] |
|
| [23] |
|
| [24] |
|
| [25] |
|
| [26] |
|
| [27] |
|
| [28] |
|
| [29] |
|
| [30] |
|
| [31] |
|
| [32] |
|