引用本文
郑文萍, 王英楠, 杨贵. 基于双监督网络嵌入的社区发现算法. 模式识别与人工智能, 2022,35(3): 283-290
ZHENG Wenping, WANG Yingnan, YANG Gui. Dual Supervised Network Embedding Based Community Detection Algorithm. PATTERN RECOGNITION AND ARTIFICIAL INTELLIGENCE, 2022,35(3): 283-290.  
Doi: 10.16451/j.cnki.issn1003-6059.202203008
Permissions
Copyright©2022, 《模式识别与人工智能》编辑部
《模式识别与人工智能》编辑部
基于双监督网络嵌入的社区发现算法
郑文萍1,2,3, 王英楠1, 杨贵1
1.山西大学 计算机与信息技术学院 太原 030006
2.山西大学 计算智能与中文信息处理教育部重点实验室 太原 030006
3.山西大学 智能信息处理研究所 太原 030006
通讯作者:

郑文萍,博士,教授,主要研究方向为复杂网络分析、生物信息学.E-mail:wpzheng@sxu.edu.cn.

作者简介:

王英楠,硕士研究生,主要研究方向为图神经网络、社区发现.E⁃mail:1291533544@qq.com.

杨 贵,博士,高级实验师,主要研究方向为数据挖掘、生物信息学.E⁃mail:gyang@sxu.edu.cn.

收稿日期: 2021-04-28 接受日期: 2021-07-22
资助项目: 国家自然科学基金项目(No.62072292)、山西省1331工程项目资助
摘要

针对基于网络嵌入的社区检测算法中节点嵌入和聚类过程独立进行时容易陷入局部极值的问题,文中提出基于双监督网络嵌入的社区发现算法.首先利用图自编码器,得到可保持网络的一阶相似性的节点嵌入.优化模块度,发现拓扑连接紧密的社区.采用自监督聚类优化,发现嵌入空间上相似的社区.引入互监督机制,使发现的社区在模块度优化和自监督聚类这两个角度上具有一致性,同时避免算法陷入局部极值.4个真实网络上的对比实验表明,DSNE性能较优.

关键词: 社区发现; 网络嵌入; 图自编码器; 模块度
中图分类号:TP 391
Dual Supervised Network Embedding Based Community Detection Algorithm
ZHENG Wenping1,2,3, WANG Yingnan1, YANG Gui1
1. School of Computer and Information Technology, Shanxi University, Taiyuan 030006
2. Key Laboratory of Computational Intelligence and Chinese Information Processing of Ministry of Education, Shanxi University, Taiyuan 030006
3. Institute of Intelligent Information Processing, Shanxi University, Taiyuan 030006
Corresponding author:
ZHENG Wenping, Ph.D., professor. Her research inte-rests include complex network analysis and bioinformatics.

About Author:
WANG Yingnan, master student. His research interests include graph neural network and community detection.
YANG Gui, Ph.D., senior experimentalist. His research interests include data mining and bioinformatics.

Fund:National Natural Science Foundation of China(No.62072292), 1331 Engineering Project of Shanxi Province
Abstract

A network embedding based community detection algorithm is easy to fall into local extremes during the independent node embedding or clustering process. Aiming at this problem, a dual supervised network embedding based community detection algorithm(DSNE) is proposed. Firstly, a graph auto-encoder is utilized to gain the embedding of nodes to maintain the first-order similarity of the network. Then, the modularity is optimized to find the communities with nodes tightly connected. The communities with similar nodes in the embedding space are discovered by self-supervised clustering optimization. A mutual supervision mechanism is introduced into DSNE to keep the consistency between the discovered communities in modularity optimization and self-supervised clustering and prevent the algorithm from falling into local extremes. Results of comparative experiments show DSNE exhibits better performance on 4 real complex networks.

Key words: Key Words Community Detection; Network Embedding; Graph Auto-Encoder; Modularity

本文责任编委 陈松灿

Recommended by Associate Editor CHEN Songcan

许多复杂系统都可表示为复杂网络, 一组节点通过相对紧密的连接形成网络模块(也称为社区结构), 行使系统功能, 如蛋白质互作用网络中的蛋白质复合体、科学协作网络中的科研群体、在线购物网络中的社区对应同类商品的集合.同一社区内的节点拓扑连接相对紧密, 属性信息更相似, 而不同社区的节点之间连接相对稀疏, 属性信息差异较大.有效发现复杂网络中的社区结构, 有助于深入理解复杂系统的结构和功能.

许多社区发现算法都是基于模块度优化的层次型社区发现算法[1, 2, 3].郭昆等[4]提出基于密度聚类的增量动态社区发现算法(Incremental Dynamic Co-mmunity Detection Algorithm Based on Density Clus-tering, IDCDDC), 在社区合并中引入模块度增益, 发现动态网络的社区结构.以模块度为优化目标, 可得到模块度较高的社区结构, 社区内节点连边较紧密, 社区之间节点连边较稀疏.然而, 此类算法在每次迭代中都需要知道网络的全局信息, 计算代价较大.

Raghavan等[5]提出LPA(Label Propagation Algorithm), 根据节点的直接邻域信息更新社区标签, 具有接近线性的时间复杂度, 但由于在标签更新过程中具有较大的随机性, 难以得到稳定的社区发现结果.近年来, 研究者们提出一些改进的LPA, 如LPAm(Modularity-Specialized LPA)[6], LPAm+(Advan-ced LPAm)[7], Stepping LPA-S(Stepping Community Detection Algorithm Based on Label Propagation and Similarity)[8]等.然而当节点的一步邻域内的标签信息不确定性较高时, 仍无法得到稳定的社区发现结果.

基于“ 种子扩展” 策略的算法以社区代表性强的节点作为种子节点, 选择与种子节点最相似的节点对种子节点进行扩展, 得到社区[9].郭昆等[10]提出基于边密度聚类的重叠社区发现算法(Over-lapping Community Detection Based on Edge Density Clustering, OCDEDC), 基于边相似度选择核心边, 通过密度聚类方式扩展边社区, 得到重叠社区结构.如何有效度量网络中节点或边之间的相似性是基于“ 种子扩展” 策略算法的关键问题.由于不同网络拓扑结构的差异较大, 无法定义一种大多数网络中通用的节点间相似性度量指标, 因此这类算法泛化性较低.

复杂网络通常具有节点较多、节点属性数据维度较高、节点间连接稀疏的特点, 在节点低维嵌入的基础上可较好地进行社区发现.目前, 学者们已提出许多有效的节点嵌入方法, 如深度游走(Deep-Walk)[11]、node2vec[12]、SDNE(Structural Deep Net-work Embedding, )[13]、DNGR(Deep Neural Networks for Learning Graph Representation)[14]、M-NMF(Modularized Nonnegative Matrix Factorization)[15]等, 从节点的拓扑结构信息学习保持节点相似性的低维向量表示.网络中的节点通常包含丰富的属性信息, 将节点属性与网络拓扑结合网络嵌入有助于学习到更好的节点表示.Yang等[16]提出TADW(Text-Asso-ciated Deep-Walk), 在概率转移矩阵中添加节点的文本属性信息, 得到网络嵌入.Huang等[17]提出AANE(Accelerated Attributed Network Embedding), 通过节点属性关联矩阵得到节点嵌入, 同时利用邻接矩阵对嵌入进行近邻约束.Kifp等[18]提出VGAE(Variational Graph Auto-Encoder), 以图神经网络(Graph Convolutional Network, GCN)[19]为编码器, 得到尽可能保持网络原始拓扑结构的节点嵌入.Salehi等[20]提出GATE(Graph Attention Auto-En-coders), 重构网络的邻居矩阵和属性特征, 得到节点嵌入, 再利用传统聚类算法对节点进行聚类, 发现社区.由于网络嵌入方法没有直接面向社区发现任务, 节点嵌入和社区发现过程相互独立, 因此优化过程容易过早陷入局部极值, 影响社区发现质量.

在深度聚类耦合获取数据表示和聚类过程中, 可得到面向聚类任务的数据低维嵌入.Xie等[21]提出DEC(Deep Embedding Clustering), 使用深度神经网络同时学习特征表示和聚类分配.近年来, 有学者利用深度聚类进行复杂网络社区发现.Wang等[22]提出DAEGC(Deep Attentional Embedded Graph Clus-tering), 结合注意力机制学习邻居节点的权重和节点表示, 并利用聚类损失监督聚类过程, 优化重构损失与聚类损失构成的损失函数, 实现同时在图上的嵌入与聚类.Bo等[23]提出SDCN(Structural Deep Clus-tering Network), 将结构信息集成到深度聚类中, 设计传递算子, 将自编码器学习的表示传递到相应的GCN层, 并设计双重自监督机制, 统一这两种不同的深层神经结构, 指导整个模型的更新.现有基于网络嵌入的社区发现算法通常仅保持原始网络的低阶相似性, 使属性相似的节点在嵌入空间中距离更近, 忽略子图、社区结构等更高阶的拓扑关系, 容易发现内部连接紧密的社区, 却难于发现内部连接较稀疏的社区, 导致无法发现拓扑结构和嵌入空间上一致的社区结构.

因此, 本文同时利用节点的拓扑结构和属性信息进行社区发现, 提出基于双监督网络嵌入的社区发现算法(Dual Supervised Network Embedding Based Community Detection Algorithm, DSNE), 引入双监督机制, 使从拓扑结构得到的社区发现结果与从嵌入空间上得到的节点聚类结果尽可能一致.DSNE包括节点嵌入模块、模块度优化模块、聚类优化模块3个主要部分.算法采用重构损失和模块度损失进行模型预训练, 获得一个综合考虑拓扑信息和属性信息的初始节点嵌入, 为聚类优化模块提供合理的类中心.采用重构损失、模块度损失和聚类损失对模型进行联合训练, 引入模块度优化和聚类优化的互监督机制, 使发现的社区在模块度优化和自监督聚类这两个角度上具有一致性.最终的社区不仅在拓扑结构上连接紧密, 而且在嵌入空间上距离也更近.在Cora、Citeseer、ACM、DBLP数据集上的对比实验证实DSNE性能较优.

1 基于双监督网络嵌入的社区发现算法

给定一个图G=(V, E, X), V为节点集合, E为节点之间边的集合, X∈ Rn× m为节点属性矩阵, n为节点数, m为属性个数.A∈ Rn× n为图G的邻接矩阵.本文提出基于双监督网络嵌入的社区发现算法(DSNE), 包括节点嵌入模块、模块度优化模块、聚类优化模块.

节点嵌入模块采用基于图卷积的自编码器对节点拓扑结构与属性信息进行编码, 得到节点低维嵌入, 尽量保持网络的一阶相似性.模块度优化模块根据节点嵌入得到节点的社区归属, 从拓扑结构上得到具有最优模块度的社区发现.聚类优化模块采用自监督聚类方法, 获取节点在嵌入空间的聚类结果, 使在嵌入空间上类内节点尽可能相近, 类间节点尽可能远离.模块度优化模块与聚类优化模块构成互监督机制, 引入双监督机制, 使从拓扑结构得到的社区发现结果与从嵌入空间上得到的节点聚类结果尽可能一致.

1.1 节点嵌入模块

节点嵌入模块采用图自动编码器对节点拓扑结构与属性信息进行编码, 得到节点低维嵌入.图自动编码器由2个图卷积层构成, 每个节点嵌入聚合其2步邻域内节点的属性特征, 采用ReLU函数作为激活函数, 使习得的嵌入同时包含图的拓扑结构和节点的属性信息.节点嵌入矩阵为:

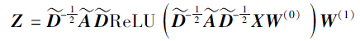
其中, X∈ Rn× m为节点属性矩阵, D~ij= ∑j=1nA~ij为对角矩阵, A~=A+In, W(0)、W(1)为图卷积层权重矩阵.

为了使学习到的嵌入尽可能地保持网络的一阶相似性, 采用嵌入Z重构网络的邻接矩阵:

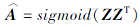
因此, 节点嵌入部分的损失函数表示为原始邻接矩阵A和重构矩阵 A^之间的重构误差:

1.2 模块度优化模块

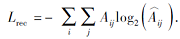
模块度优化模块以得到的节点嵌入为输入, 通过一个全连接层得到节点对不同社区的归属程度.节点社区归属矩阵为:

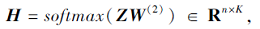
其中W(2)为全连接层权重矩阵.

采用松弛的模块化定义[25], 计算H对应的社区发现结果的模块度:

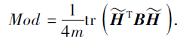
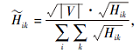
其中:B为模块度矩阵, Bij=Aij- didj2m, di为节点vi的度, m=|E|为网络边数; tr为矩阵的迹; H~为松弛后的社区归属矩阵,

V为网络中节点个数.

为了得到具有最优模块度的社区发现结果, 定义模块度损失:

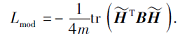
最大化模块度损失可进行梯度优化:

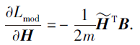
模块度可度量发现的社区结构是否明显, 模块度越高, 发现的社区结构内部连接比外部连接更紧密.利用模块度指标进行优化可确保得到的节点嵌入保留原始网络的高阶社区结构.

为了防止解退化, 缓解将大部分样本分配给少数几个聚类或将一个聚类分配给离群样本的情况, 对通过优化模块化得到的聚类分配添加正则化项:

Lreg=KL(f‖ u).(1)

其中:u为均匀分布, uk= 1K, 1≤ k≤ K; f为每个聚类的目标分布, fk表示模块化得到的第k类平均归属度

fk=P(y=k)= 1N∑ihik, 1≤ k≤ K,

K为网络中真实社区的个数.

通过平衡社区分配的目标分布, 可使模型间接具有更平衡的社区发现结果, 如果具有关于社区分布概率的先验, 可将先验从均匀分布改为目标函数中先验分布.

1.3 聚类优化模块

为了使得到的嵌入保持节点在嵌入空间拥有较优的聚类特性, 在聚类优化模块首先采用K-means聚类算法对预训练后得到的嵌入进行初始聚类, 得到K个初始类.再采用自监督方法构造聚类损失函数, 使节点嵌入面向低维嵌入空间的聚类任务, 联合优化网络嵌入和聚类.

在网络嵌入矩阵上执行K-means聚类算法, 获得初始社区中心μ =(μ 1, μ 2, …, μ k), 使用t分布测量节点vi的嵌入zi与第k个社区中心μ k间的相似性, 样本i被分配到社区k的概率为:

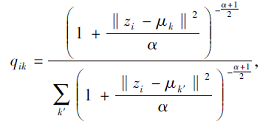
其中, α 为t分布的自由度, 设α = 1.引入辅助目标分布P:

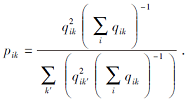
聚类优化损失定义为类分布Q和辅助分布P之间的KL散度:

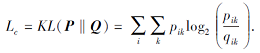
自监督聚类损失使用梯度下降算法进行优化, 同步更新社区中心μ 和低维嵌入Z:

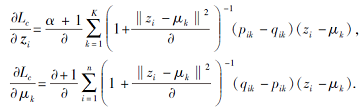
利用聚类优化模块, 可使节点在嵌入空间上具有良好的聚类特性, 即在嵌入空间上相近的节点更有可能为同类.

1.4 模块度优化和聚类优化的互监督机制

利用模块度指标进行优化可确保得到的节点嵌入保留原始网络的高阶社区结构, 有利于得到拓扑结构紧密的社区结果H.而利用聚类优化模块, 可使节点在嵌入空间上具有良好的聚类特性, 在嵌入空间相近的节点更有可能在同一类, 有利于得到嵌入空间上分布紧密的节点聚类结果P.两个角度聚类结果的不一致, 可能导致梯度下降过早收敛至局部最优.

针对上述问题, 本文引入互监督机制, 使两种聚类结果达到一致.根据两个聚类分布的相对熵定义聚类一致性损失:

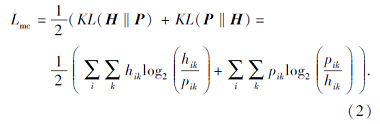
Lmc不仅可得到一致的聚类结果, 也使节点嵌入和节点聚类形成联合优化的闭环, 消除实验结果的不稳定, 提高社区发现质量.

1.5 训练过程

DSNE首先通过预训练阶段得到节点低维嵌入, 通过优化重构损失与模块度损失, 使嵌入不仅保留网络低阶的拓扑结构, 还使嵌入保留原始网络的高阶社区结构, 即

Lpretrain=Lrec+α Lmod .(3)

完成预训练后, 运用K-means聚类算法, 得到聚类优化模块需要的初始社区中心.随后采用模块度优化和聚类优化构成的双监督组件进行社区发现.总体损失为:

L=Lrec+α Lmod+β Lc+γ Lmc+λ Lreg, (4)

其中, α 、 β 、γ 、λ 为权衡不同损失权重的超参数, Lrec为重构损失, Lmod为模块化损失, Lc为聚类优化模块的自监督聚类损失, Lmc为双监督组件的聚类一致性损失, Lreg为用于平衡聚类的正则化项.

本文使用随机梯度下降联合优化节点嵌入与社区发现结果, 最后将模块度优化节点的社区分配作为节点vi的社区标签:

si=arg maxkhik.

DSNE具体步骤如算法1所示.

算法 1 DSNE

输入 图G=(V, E, X), 社区个数K, α , β , γ , λ ,

最大预训练迭代数T1, 最大训练迭代数T2

输出 节点的社区标签分配S

for epoch in 0, 1, …, T1 do

根据式(3)进行预训练, 更新W(0), W(1), W(2);

end

在嵌入Z上利用K-means得到K个社区中心μ ;

for epoch in 0, 1, …, T2 do

计算模块度损失Lmod;

根据式(1)计算聚类正则化项Lreg;

计算自监督聚类损失Lc;

计算双监督聚类一致性损失Lmc;

根据式(4)更新W(0), W(1), W(2), μ ;

end

for vi in V do

计算vi的社区标签si;

end

return S={si|1≤ i≤ n}.

2 实验及结果分析

本文选用Cora、ACM、Citeseer、DBLP这4个带标签的真实网络数据集进行实验, 基本信息如表1所示.

表1 实验数据集基本信息 Table 1 Description of experimental datasets

评价指标采用准确率(Accuracy, ACC)、标准互信息(Normalized Mutual Information, NMI)、调整兰德系数(Adjusted Rand Index, ARI)和F1分数.

本文采用如下对比算法.1)传统社区发现算法:K-means、BGLL[1]、LPA[5]、Infomap(Maps of Random Walks Based Information Flows)[24].2)基于网络嵌入的社区发现算法:DeepWalk[11]、M-NMF[15]、GAE(Graph Auto-Encoder)[18]、VGAE[18]、GATE[20]、DE-C[21]、DAEGC[22]、SDCN[23].在对比算法中, BGLL[1]、LPA、Infomap利用拓扑信息进行社区发现, DeepWalk、M-NMF利用网络的拓扑信息得到节点嵌入, K-means、DEC利用网络中节点的属性信息进行社区发现, GAE、VGAE、GATE同时利用网络属性与拓扑信息得到节点嵌入, DAEGC、SDCN同时利用网络属性与拓扑信息进行社区发现.

在实验中, 在DeepWalk、GAE、VGAE、M-NMF、GATE得到嵌入后, 利用K-means对节点嵌入进行聚类, 得到社区发现结果.

对比算法采用文献提供的默认参数.DSNE中的社区数K设为网络中的真实社区数, α =0.1, β =0.1, γ =0.05, λ =0.01, T1=100, T2=300, 采用自适应矩估计(Adaptive Moment Estimation, Adam)优化器优化网络权重, 学习率为0.001.DSNE采用2层图卷积网络, 维度分别为256和16.

DSNE与3种基于网络拓扑信息的传统社区发现算法对比结果如表2所示, 表中黑体数字表示最优值.由表可看出, DSNE明显优于对比算法, 这说明在真实网络中, 社区结构不仅与网络的拓扑结构信息相关, 也与节点的属性信息关系密切.

表2 DSNE和传统社区算法的指标值对比 Table 2 Index value comparison of DSNE and traditional community algorithms

DSNE和9种利用节点嵌入进行社区发现的算法的指标值对比如表3所示, 表中黑体数字表示最优结果.由表可见, 在真实网络上利用节点属性进行社区发现的算法的性能优于仅利用拓扑信息的社区发现算法:一方面是因为网络数据中存在较多的假阳性或假阴性的连接; 另一方面是随着网络规模的增大, 连接也更稀疏, 基于拓扑信息的算法发现内部连接相对稀疏的社区的能力有限.基于网络嵌入的算法性能整体优于非嵌入的社区发现算法, 说明拓扑结构或属性信息的低维嵌入可得到原始数据的有效特征, 提升社区发现的质量.基于网络嵌入和社区发现过程耦合训练的算法性能整体优于非耦合训练的算法, 说明利用聚类损失约束网络嵌入的学习过程可提升社区发现的质量.

表3 各算法在4个数据集上的指标值对比 Table 3 Index value comparison of different algorithms on 4 datasets

在Cora数据集上, DSNE的ACC、NMI值比排名第二的DAEGC提升1.0%和3.1%, 在ARI指标上略低于DAEGC, 在F1分数上与DAEGC持平.在ACM数据集上, DSNE的ACC、ARI、F1值分别比排名第二的算法提升1.7%、2.5%、1.1%.在Citeseer数据集上, DSNE的ACC、ARI、F1值均优于对比算法, 在NMI指标上略低于排在第二的DAEGC和SDCN.在DBLP数据集上, DSNE的ACC、NMI、ARI、F1值分别比排名第二的算法提升2.5%、3.9%、5.3%、1.8%.由此可看出, DSNE的性能优于大多数算法.

Citeseer数据集上使用不同损失预训练后的聚类散点图如图1所示, 图中6种颜色的点的集合表示在得到的嵌入基础上使用K-means将数据集分为6类.由图可看出, 重构损失+模块度损失的联合预训练得到的节点嵌入类内聚集性和类间分离性更优.

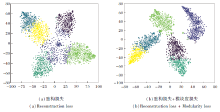图1 Citeseer网络上使用不同损失预训练的聚类散点图Fig.1 Clustering scatter plots pre-trained with different losses on Citeseer network

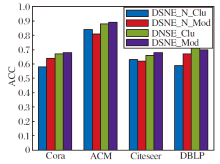
在4个数据集上互监督机制对ACC值的影响如图2所示:DSNE_Clu表示DSNE采用聚类优化社区分配矩阵P所得的社区结果; DSNE_Mod表示DSNE采用模块度优化社区分配矩阵H所得的社区结果; DSNE_N_Clu表示去掉DSNE中互监督机制, 采用聚类优化社区分配矩阵P所得的社区结果; DSNE_N_Mod表示去掉DSNE中的互监督机制, 采用模块度优化社区分配矩阵H所得的社区结果.

图2 互监督机制对ACC值的影响Fig.2 Influence of mutual supervision mechanism on ACC values

由图2可看出, 由于引入互监督机制, DSNE_Clu和DSNE_Mod的社区发现性能优于DSNE_N_Clu和DSNE_N_Mod.由于未引入互监督机制, DSNE_N_ Mod与DSNE_N_Clu的ACC值会存在较大差异, 引入互监督机制之后, DSNE_Mod与DSNE_Clu结果较相近.由此表明, 引入互监督机制后社区发现结果更优, 且模块度优化和聚类优化过程得到的社区发现结果也更接近, 这也避免优化过程过早收敛于局部最优.

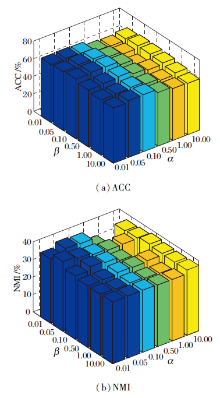
DSNE中α 、 β 表示权衡模块化损失与自监督聚类损失的超参数.在DBLP数据集上不同的α 、 β 对ACC、NMI值的影响如图3所示, 图中α 、 β 的取值范围为{0.01, 0.05, 0.1, 0.5, 1, 10}.由图可看出, α 、 β 不同时, ACC、NMI值有所不同, 但整体起伏不大, 说明DSNE对α , β 具有较好的鲁棒性.

图3 在DBLP数据集上α , β 对ACC和NMI值的影响Fig.3 Influence of α , β on ACC and NMI values on DBLP dataset

DSNE采用模块度优化模块, 保留网络的高阶结构信息, 并与自监督聚类模块构成互监督机制.算法首先需要得到网络的模块度矩阵, 在读入网络时, 利用邻接矩阵可直接得到网络的模块度矩阵, 不需要额外代价计算模块度矩阵.由于采用式(2)作为互监督损失, 可同时进行模块度优化和聚类优化, 因此DSNE在未增加计算代价的情况下得到性能提升.

3 结束语

本文提出基于双监督网络嵌入的社区发现算法(DSNE), 包括节点嵌入模块、模块度优化模块、自监督聚类模块.节点嵌入模块采用基于图卷积的自编码器, 对节点拓扑结构与属性信息进行编码, 得到节点低维嵌入, 尽量保持网络的一阶相似性.模块度优化模块根据节点嵌入得到节点的社区归属, 从拓扑结构上得到具有最优模块度的社区发现.聚类优化模块采用自监督聚类方法获取节点在嵌入空间的聚类结果, 使在嵌入空间上类内节点尽可能近, 类间节点尽可能远.DSNE引入互监督机制, 保证模块度优化和自监督聚类结果的一致, 避免优化过程过早陷入局部极值.实验表明, DSNE性能较优.

在图深度聚类过程中引入模块度优化机制, 可发现网络中具有较高模块度的社区结构, 但模块度优化算法通常存在精度限制问题[26], 倾向于发现网络中规模分布较均匀的社区结构.实际上, 现实网络中存在大量规模分布不均匀的社区结构, 如何利用图深度聚类以更好识别这些社区是下一步的研究方向.

参考文献
[1] BLONDEL V D, GUILLAUME J, LAMBIOTTE R. Fast Unfolding of Communities in Large Networks [J/OL]. [2021-03-21]. http://antipaedo.lip6.fr/T12/communities.pdf. [本文引用:3]
[2] NEWMAN M E J. Fast Algorithm for Detecting Community Structure in Networks. Physical Review E, 2004, 69(6). DOI: DOI:10.1103/PhysRevE.69.066133. [本文引用:1]
[3] CLAUSET A, NEWMAN M E J, MOORE C. Finding Community Structure in Very Large Networks. Physical Review E, 2004, 70(6). DOI: DOI:10.1103/PhysRevE.70.066111. [本文引用:1]
[4] 郭昆, 彭胜波, 陈羽中, 等. 基于密度聚类的增量动态社区发现算法. 模式识别与人工智能, 2018, 31(11): 965-978.
(GUO K, PENG S B, CHEN Y Z, et al. Incremental Dynamic Community Detection Algorithm Based on Density Clustering. Pa-ttern recognition and Artificial Intelligence, 2018, 31(11): 965-978. ) [本文引用:1]
[5] RAGHAVAN U N, ALBERT R, KUMARA S. Near Linear Time Algorithm to Detect Community Structures in Large-Scale Networks. Physical Review E, 2007, 76(3). DOI: DOI:10.1103/PhysRevE.76.036106. [本文引用:2]
[6] BARBER M J, CLARK J W. Detecting Network Communities by Propagating Labels under Constraints. Physical Review E, 2009, 80(2). DOI: DOI:10.1103/PhysRevE.80.026129. [本文引用:1]
[7] LIU X, MURATA T. Advanced Modularity-Specialized Label Propagation Algorithm for Detecting Communities in Networks. Physica A: Statistical Mechanics and Its Applications, 2010, 389(7): 1493-1500. [本文引用:1]
[8] LI W, HUANG C, WANG M, et al. Stepping Community Detection Algorithm Based on Label Propagation and Similarity. Physica A: Statistical Mechanics and Its Applications, 2017, 472: 145-155. [本文引用:1]
[9] 王杰. 数据驱动的蛋白质互作用网络中复合体检测算法研究. 博士学位论文. 太原: 山西大学, 2019.
(WANG J. Data-Driven Research on Algorithms of Protein Complex Detection in Protein Interaction Networks. Ph. D. Dissertation, Taiyuan, China: Shanxi University, 2019. ) [本文引用:1]
[10] 郭昆, 陈而宝, 郭文忠. 基于边密度聚类的重叠社区发现算法. 模式识别与人工智能, 2018, 31(8): 693-703.
(GUO K, CHEN E B, GUO W Z. Overlapping Community Detection Based on Edge Density Clustering. Pattern Recognition and Artificial Intelligence, 2018, 31(8): 693-703. ) [本文引用:1]
[11] PEROZZI B, AL-RFOU R, SKIENA S. DeepWalk: Online Lear-ning of Social Representations // Proc of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York, USA: ACM, 2014: 701-710. [本文引用:2]
[12] GROVER A, LESKOVEC J. node2Vec: Scalable Feature Learning for Networks // Proc of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York, USA: ACM, 2016: 855-864. [本文引用:1]
[13] WANG D X, CUI P, ZHU W W. Structural Deep Network Embe-dding // Proc of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York, USA: ACM, 2016: 1225-1234. [本文引用:1]
[14] CAO S S, LU W, XU Q K. Deep Neural Networks for Learning Graph Representations // Proc of the 30th AAAI Conference on Artificial Intelligence. Palo Alto, USA: AAAI, 2016: 1145-1152. [本文引用:1]
[15] WANG X, CUI P, WANG J, et al. Community Preserving Network Embedding // Proc of the 31st AAAI Conference on Artificial Intelligence. Palo Alto, USA: AAAI, 2017: 203-209. [本文引用:2]
[16] YANG C, LIU Z Y, ZHAO D L. Network Representation Learning with Rich Text Information // Proc of the 24th International Joint Conference on Artificial Intelligence. New York, USA: ACM, 2015: 2111-2117. [本文引用:1]
[17] HUANG X, LI J D, HU X. Accelerated Attributed Network Embedding // Proc of the SIAM International Conference on Data Mining. Philadelphia, USA: SIAM, 2017: 633-641. [本文引用:1]
[18] KIPF T N, WELLING M. Variational Graph Auto-Encoders[C/OL]. [2021-03-21]. http://arxiv.org/pdf/1611.07308.pdf. [本文引用:3]
[19] KIPF T N, WELLING M. Semi-supervised Classification with Gra-ph Convolutional Networks[C/OL]. [2021-03-21]. https://arxiv.org/pdf/1609.02907v3.pdf. [本文引用:1]
[20] SALEHI A, DAVULCU H. Graph Attention Auto-Encoders // Proc of the 32nd IEEE International Conference on Tools with Artificial Intelligence. Washington, USA: IEEE, 2020: 989-996. [本文引用:2]
[21] XIE J Y, GIRSHICK R, FARHADI A. Unsupervised Deep Embedding for Clustering Analysis // Proc of the 33rd International Conference on Machine Learning. New York, USA: ACM, 2016: 478-487. [本文引用:2]
[22] WANG C, PAN S R, HU R Q, et al. Attributed Graph Clus-tering: A Deep Attentional Embedding Approach // Proc of the 28th International Joint Conference on Artificial Intelligence. San Francisco, USA: Morgan Kaufmann, 2019: 3670-3676. [本文引用:2]
[23] BO D Y, WANG X, SHI C, et al. Structural Deep Clustering Network // Proc of the 29th International World Wide Web Confe-rence. New York, USA: ACM, 2020: 1400-1410. [本文引用:2]
[24] ROSVALL M, BERGSTROM C T. Maps of Rand om Walks on Com-plex Networks Reveal Community Structure. Proceedings of the National Academy of Sciences of the United States of America, 2008, 105(4): 1118-1123. [本文引用:1]
[25] YANG L, CAO X C, HE D X, et al. Modularity Based Community Detection with Deep Learning // Proc of the 25th International Joint Conference Artificial Intelligence. New York, USA: ACM, 2016: 2252-2258. [本文引用:1]
[26] FORTUNATO S, BARTHELEMY M. Resolution Limit in Community Detection. Proceedings of the National Academy of Sciences of the United States of America, 2007, 104(1): 36-41. [本文引用:1]