
吴伟志,博士,教授,主要研究方向为粗糙集、粒计算、数据挖掘、人工智能.E-mail:wuwz@zjou.edu.cn.
作者简介:

王金波,硕士研究生,主要研究方向为粗糙集、粒计算.E-mail:1638346787@qq.com.
多尺度数据分析是当前粒计算研究领域的热门研究方向,它模拟人类思考模式,以建立多层次的复杂数据和信息处理的有效计算模型为目标.在多尺度数据分析中,一个关键的问题是从系统中选择一个合适的子系统用于最终的分类或决策,这个子系统对应的每个属性的尺度水平的组合称为系统的一个最优尺度组合.针对广义多尺度覆盖决策系统中的知识获取问题,首先,在协调广义多尺度覆盖决策系统中,使用信任函数和似然函数刻画最优尺度组合.然后,在不协调广义多尺度覆盖决策系统中定义7种最优尺度组合的概念,并给出它们之间的关系,结果表明实际有4种不同的最优尺度组合,阐明使用似然函数和信任函数可以定量刻画不协调广义多尺度覆盖决策系统的上、下近似最优尺度组合的特征.最后,举例说明文中方法可用在不完备广义多尺度决策系统和广义多尺度集值决策系统中的最优尺度组合的选择.
WU Weizhi, Ph.D., professor. His research interests include rough set, granular computing, data mining and artificial intelligence.
About Author:
WANG Jinbo, master student. His research interests include rough set and granular computing.
Multi-scale data analysis is a hot research direction in the field of granular computing. It simulates the mode of human thinking to establish effective computation models for dealing with multi-level complex data and information. A critical problem in multi-scale data analysis is to select a suitable sub-system from a given system for final classification or decision, and the combination of scale level of each attribute corresponding to the sub-system is called an optimal scale combination of the system. To solve the problem of knowledge acquisition in generalized multi-scale covering decision systems, scale combinations are firstly characterized by belief and plausibility functions in consistent generalized multi-scale covering decision systems. Then, the concepts of seven types of optimal scale combinations in inconsistent generalized multi-scale covering decision systems are defined and their relationships are clarified. It is showed that there are actually four different types of optimal scale combinations. Moreover, it is illuminated that belief and plausibility functions can be applied to characterize lower-approximation optimal scale combinations and upper-approximation optimal scale combinations in inconsistent generalized multi-scale covering decision systems, respectively. Finally, it is illustrated that the proposed methods can be applied to the optimal scale combination selection in incomplete generalized multi-scale decision systems and generalized multi-scale set-valued decision systems, respectively.
本文责任编委 苗夺谦
Recommended by Associate Editor MIAO Duoqian
粒计算[1, 2, 3, 4]是当前人工智能领域中活跃的研究方向之一.它以粒为基本计算单位, 强调对数据进行多角度、多层次的分析与处理.目前, 学者们已提出较多涉及具体应用背景的粒计算模型与方法.在这些研究中, 粗糙集理论[5]对粒计算研究的发展起到重要作用.
粗糙集理论中的典型数据结构称为信息系统和决策系统, 又称信息表和决策表.经典粗糙集理论通过信息系统和决策系统中的数据定义等价关系, 用等价类描述粒度, 进而对信息系统或决策系统进行知识约简和规则提取.
由于等价关系这个条件过于严格, 限制粗糙集理论的应用, 因此, 一些学者对粗糙集模型进行推广.一方面, 将等价关系推广为一般的二元关系, 得到各种关系下的推广粗糙集模型[6, 7, 8], 并用于各种信息系统和决策系统的知识获取; 另一方面, 将等价关系生成的划分推广为一般的覆盖, 得到各种覆盖粗糙集模型, 并应用于覆盖信息(决策)系统的知识获取[9, 10, 11, 12, 13, 14].Zhu等[12]给出论域的单个覆盖保持集合下近似和上近似不变的约简方法与近似算子的公理化刻画.Couso等[13]建立不完备信息系统和覆盖粗糙集理论之间的联系.Yao等[14]在统一框架下研究基于覆盖的粗糙近似算子.
然而, 在传统的粗糙集数据分析中, 不论是Pawlak粗糙集及其应用的信息(决策)系统, 还是覆盖粗糙集及其应用的信息(决策)系统, 每个对象在每个属性下只能取单个尺度的属性值.但现实生活中人们可能需要在不同的尺度下关于同一对象在同一属性下对系统进行观察、分析, 因此如何在这样的数据集上发现知识成为重要问题.
针对这一问题, Wu等[15]提出多尺度决策系统的粗糙集数据分析模型, 给出这类系统的信息粒表示和多尺度规则提取方法.Wu等[16]又进一步给出不完备多尺度决策系统的知识获取方法, 这个数据处理模型又称为Wu-Leung模型[17].多尺度粗糙集数据分析的主要思想是:根据决策目标, 对每个属性选择一个合适的尺度或粒度, 构成一个新的单尺度信息系统, 然后在保持相同目标约束的前提下进行属性约简(特征选择)、决策规则提取及不确定性分析.因此, 保持某种性质(可以是定性的也可以是定量的)不变意义下选择最粗的尺度标记(称为最优尺度选择或最优粒度选择)成为多尺度决策数据中知识获取的一个关键问题, 是多尺度粗糙集数据分析研究的一个重要方向.Li等[17]针对Wu-Leung模型中要求所有不同属性都有相同的尺度个数这一限制, 提出广义多尺度决策系统的概念, 并给出补模型和格模型两种方法用于分析此类数据的知识获取问题.Li等[18]利用格模型中定义的最优尺度组合概念进一步研究不协调广义多尺度决策系统中的6种最优尺度组合.Wu等[19]在不协调广义多尺度决策系统中定义7种最优尺度组合, 并研究各种最优尺度组合之间的关系.Li等[20]将多尺度粗糙集数据分析的方法引入覆盖粗糙集理论中, 提出多尺度覆盖的概念, 并研究协调与不协调广义多尺度覆盖决策系统的最优尺度组合.陈应生等[21]使用矩阵方法研究广义多尺度覆盖决策系统的最优尺度组合.Chen等[22]研究基于信息熵的广义多尺度覆盖决策系统的最优尺度组合.也有一些学者提出广义多尺度集值决策系统的概念, 陈应生等[23]定义广义多尺度集值决策系统的最优尺度组合.胡军等[24]研究基于最小化不确定性和代价的广义多尺度集值决策系统的最优尺度组合选择方法.
证据理论[25]是另一种有效处理不确定性的数学工具, 该理论的基本概念是由mass函数生成的信任结构, 根据信任结构可导出一对对偶的测度, 即信任函数和似然函数, 以此度量知识的不确定性.学者们研究证据理论与粗糙集理论之间的关系.在理论方面, Yao等[26]给出有限论域中一般二元关系产生的粗糙集中的下近似与证据理论中的信任函数之间的关系, 一方面, 证明集合的下近似的概率是该集合的信任度, 另一方面, 给定一个信任结构和信任函数, 则一定存在一个对应的近似空间, 使该近似空间导出的信任函数就是给定的信任函数.Wu等[27, 28, 29]研究模糊环境下粗糙集理论与证据理论之间的关系, 给出无限论域中基于模糊蕴含算子的粗糙近似空间导出的下近似算子与上近似算子和信任结构及其生成的信任函数与似然函数的相互表示.在应用发展方面, Chen等[9]对若干覆盖粗糙集进行分类, 建立覆盖粗糙集与证据理论的关系, 并设计基于信任函数的属性约简算法[10].Tan等[30]在不完备信息系统中使用证据理论定量刻画多粒度粗糙集的上近似与下近似, 设计基于证据理论的属性约简算法.吴伟志等[31, 32]使用证据理论给出不协调广义多尺度决策系统的最优尺度组合和不完备广义多尺度决策系统的最优尺度组合的特征.车晓雅等[33]研究4种多粒度覆盖粗糙集与证据理论之间的关系.这些研究表明, 证据理论可定量刻画各种系统中知识的不确定性, 因此可使用证据理论分析信息(决策)系统中的知识获取问题.
迄今尚未有用证据理论刻画广义多尺度覆盖决策系统中的最优尺度组合的相关研究, 本文在文献[19]和文献[20]的基础上, 使用证据理论分别刻画协调与不协调广义多尺度覆盖决策系统的最优尺度组合, 给出各种最优尺度组合概念之间的关系.
本节回顾一些覆盖粗糙集的基本概念.
本文使用U表示一个非空有限集合, 称为论域.U的全体子集记为P(U).若C⊆P(U), Ø ∉C, 且C中所有集合的并集为U(即∪ C=U), 则称C为U上的一个覆盖.U上的所有覆盖全体表示为
C(U)={C⊆P(U)|(Ø ∉C)∧ (∪ C=U)}.
一个二元组(U, C)称为一个覆盖信息系统, 其中, C={C1, C2, ···, Cm}为U上的一族覆盖, 若D={D1, D2, ···, Dr}为U上的一个划分, 则称三元组(U, C, D)为一个覆盖决策系统.
定义1[14] 设C是论域U上的一个覆盖, ∀ x∈ U, 集族
mdC(x)={K∈ C|x∈ K∧ (∀ S∈ C(x∈ S∧ S⊆K⇒ K=S))},
MDC(x)={K∈ C|x∈ K∧ (∀ S∈ C(x∈ S∧ S⊇K⇒ K=S))},
分别称为x关于C的极小描述和极大描述.
论域U上的一个映射N:U→ P(U)称为U上的一个邻域算子.基于邻域算子N, 集合X⊆U的下近似和上近似分别定义如下:
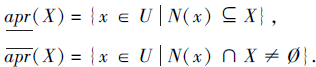
可以证明$\underline{\operatorname{apr}}(X)$和$\overline{\operatorname{apr}}(X)$是对偶的, 即
$\underline{\operatorname{apr}}(X)$= $\overline{\operatorname{apr}}(~X)$,
这里~X表示X关于U的补集, 即
~X={x∈ U|x∉X}.
接下来给出覆盖信息系统中4种邻域算子的定义.
定义2[14] 设C为论域U上的一个覆盖, ∀ x∈ U, x关于C的4种邻域N
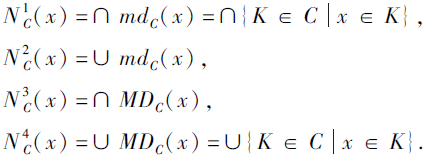
特别地, 当C为U上的一个划分时, 则
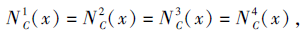
且它们均为划分C中元素x的等价类.
定义3[33] 设(U, C)为一个覆盖信息系统, 其中C={C1, C2, ···, Cm}为U上的一族覆盖.∀ x∈ U, x关于C的4种邻域NiC(x)(i∈ {1, 2, 3, 4})定义如下:
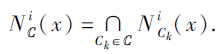
根据上述4种邻域, 分别定义X⊆U关于覆盖信息系统(U, C)的4对上、下近似如下:
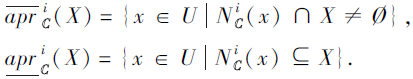
此外, 还可定义U上4种诱导的覆盖
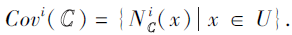
性质1[7, 14] 设(U, C)为一个覆盖信息系统, X⊆U, Y⊆U, i∈ {1, 2, 3, 4}, 则

定义4[20] 设U为论域, C1∈ C(U), C2∈ C(U), 若对∀ K1∈ C1, ∃K2∈ C2, 使得K1⊆K2, 则称C1比C2细, 或C2比C1粗, 记为C1$\sqsubseteq$C2.
定义5[20, 33] 设(U, C, D)为一个覆盖决策系统, i∈ {1, 2, 3, 4}, 若
$\operatorname{Cov}^{i}(\mathbb{C}) \sqsubseteq D$,
则称(U, C, D)为第i型协调的.
定义6[25] 设U为非空有限论域, 集函数
m:P(U)→ [0, 1]
称为U上的一个mass函数, 若满足
1)m(Ø )=0,
2)
称A∈ P(U)为m的焦元, 若m(A)> 0.记
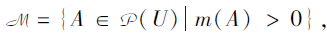
则序对(M, m)称为U上的一个信任结构.
定义7[25] 设(M, m)为U上的一个信任结构, 集函数
Bel:P(U)→ [0, 1]
称为U上的信任函数, 若
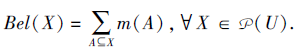
集函数
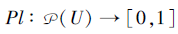
称为U上的似然函数, 若
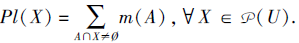
由同一信任结构导出的信任函数和似然函数是对偶的, 即
Pl(X)=1-Bel(~X).
反之, 信任结构中的mass函数可通过Mö bius变换用信任函数表示, 即∀ X∈ P(U),
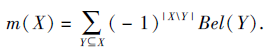
信任函数和似然函数还可等价地用公理定义.集函数
Bel:P(U)→ [0, 1]
为U上的一个信任函数, 当且仅当满足如下公理:
1)Bel(Ø )=0,
2)Bel(U)=1,
3)对∀ X1⊆U, X2⊆U, ···, Xl⊆U, 有
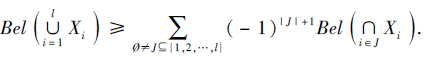
同样地, 集函数
Pl:P(U)→ [0, 1]
为U上的一个似然函数, 当且仅当满足如下公理:
1)Pl(Ø )=0,
2)Pl(U)=1,
3)对∀ X1⊆U, X2⊆U, ···, Xl⊆U, 有
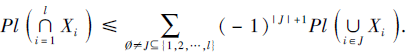
一些学者研究覆盖粗糙集与证据理论之间的关系[9, 33], 为了在统一框架下研究本文的广义多尺度覆盖粗糙集模型在各种多尺度系统中的应用, 给出如下定理1与定理2.
定理1[9, 33] 设(U, C)为一个覆盖信息系统, 其中C为U上的一族覆盖, i∈ {1, 2, 3, 4}, 定义关系划分函数ji:Covi(C)→ P(U),
ji(X)={x∈ U|X=NiC(x)},
则{ji(X)|X∈ Covi(C)}构成U上的一个划分.
设U为一个非空有限论域, 本文使用P表示均匀概率分布, 即∀ X⊆U,
$P(X)=|X| /|U|$,
|X|表示集合X的基数.
定理2[9, 33] 设(U, C)为一个覆盖信息系统, i∈ {1, 2, 3, 4}, ∀ X⊆U, 记
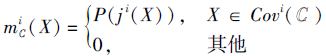
则
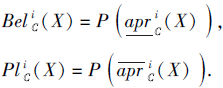
在覆盖决策系统(U, C, D)中, C={C1, C2, ···, Cm}为U上的一族覆盖, 若C中每个覆盖都有多个尺度, 则称(U, C, D)为一个广义多尺度覆盖决策系统.下面结合文献[20]和文献[22]给出具体的定义.首先, 定义8给出两个覆盖之间的尺度关系.
定义8[22] 设U为论域, C'∈ C(U), C″∈ C(U), 若存在一个满射f:C'→ C″满足对∀ K″∈ C″,
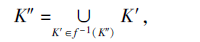
则称C″为基于C'的粒度变换覆盖, f为粒度变换函数.
本文使用C'▷C″表示C″为基于C'的粒度变换覆盖.
性质2[20] 设U为论域, 则▷满足如下性质:
1)自反性.C1▷C1, ∀ C1∈ C(U);
2)传递性.对于∀ C1∈ C(U), C2∈ C(U), C3∈ C(U), 若C1▷C2, C2▷C3, 则 C1▷C3.
性质3[20] ∀ C'∈ C(U), C″∈ C(U), 若C'▷C″, 则对∀ x∈ U, X⊆U, i∈ {1, 2, 3, 4}, 有
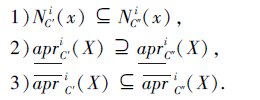
定义9[20] 称
S=(U, C={C1, C2, ···, Cm}, D)
为一个广义多尺度覆盖决策系统, 其中
1)C={C1, C2, ···, Cm}为U上的一个覆盖族,
2)Cj={
3)D={D1, D2, ···, Dr}为U上的划分.
在一个广义多尺度覆盖决策系统
S=(U, C={C1, C2, ···, Cm}, D)
中, 若覆盖Cj∈ C取第lj个尺度,
1≤ lj≤ Ij, j∈ {1, 2, ···, m},
记L=(l1, l2, ···, lm), 则称L为S的一个尺度组合.显然, 每个尺度组合对应一个单尺度的覆盖决策系统
SL=(U, CL={
记S的尺度组合全体为L.设
L'=(l'1, l'2, ···, l'm)∈ L, L″=(l″1, l″2, ···, l″m)∈ L.
若对∀ j∈ {1, 2, ···, m}, 有l'j≤ l″j, 则称L'比L″细, 或L″比L'粗, 记为L'⪯L″.若L'⪯L″, 且存在j∈ {1, 2, ···, m}, 使得l'j< l″j, 则称尺度组合L'严格细于L″, 或L″严格粗于L', 记为L'≺L″.可验证(L, ⪯)为一个偏序集, 进一步定义
L'∧ L″=(l'1∧ l″1, l'2∧ l″2, ···, l'm∧ l″m), L'∨ L″=(l'1∨ l″1, l'2∨ l″2, ···, l'm∨ l″m),
则(L, ⪯, ∧ , ∨ )为一个有界格, 也是一个完备格, 最小元L1=(1, 1, ···, 1), 最大元为(I1, I2, ···, Im).
性质4[20] 设
S=(U, C={C1, C2, ···, Cm}, D)
为一个广义多尺度覆盖决策系统, L'∈ L, L″∈ L, X⊆U, i∈ {1, 2, 3, 4}, 若L'⪯L″, 则
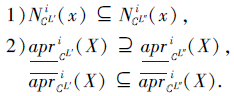
定义10[20] 设
S=(U, C={C1, C2, ···, Cm}, D)
为一个广义多尺度覆盖决策系统, i∈ {1, 2, 3, 4}.若
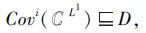
则称S为第i型协调的, 否则称S为第i型不协调的.设S为第i型协调的, L'∈ L, 若SL'为第i型协调的, 但对∀ L″∈ L满足L'≺L″(若{L″∈ L|L'≺L″}≠ Ø ), SL″不是第i型协调的, 则称L'为S的一个第i型最优尺度组合.
本节使用证据理论刻画协调广义多尺度覆盖决策系统的最优尺度组合.
定理3 在广义多尺度覆盖决策系统
S=(U, C={C1, C2, ···, Cm}, D)
中, L'∈ L, L″∈ L, X⊆U, i∈ {1, 2, 3, 4}, 若L'⪯L″, 则
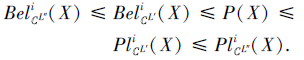
证明 由定理2、性质1和性质4可得.
证毕.
定理4 设
S=(U, C={C1, C2, ···, Cm}, D={D1, D2, ···, Dr})
为一个第i型协调的广义多尺度覆盖决策系统, L∈ L, i∈ {1, 2, 3, 4}, 若SL为第i型协调的, 则
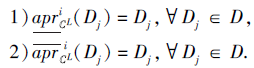
证明 1)一方面, 对∀ Dj∈ D, 根据性质1, 有
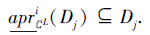
另一方面, 对∀ x∈ Dj, 有x∈ Ni
Ni
从而 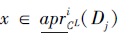
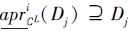
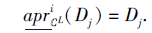
2)一方面, 对∀ Dj∈ D, 根据性质1, 有
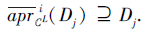
另一方面, 对 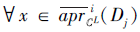
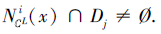
设
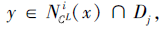
从而
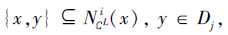
又根据协调性及D={D1, D2, ···, Dr}为U上的划分, 有Ni
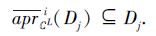
因此

证毕.
定理5 设
S=(U, C={C1, C2, ···, Cm}, D)
为一个第i型协调的广义多尺度覆盖决策系统, L=(l1, l2, ···, lm)∈ L, i∈ {1, 2, 3, 4}, 则如下条件等价:
1)SL=(U, CL={
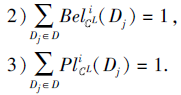
证明 1)⇒ 2).若SL为第i型协调的, 则对∀ Dj∈ D, 根据定理4, 有
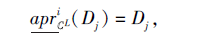
而D为U上的一个划分, 从而
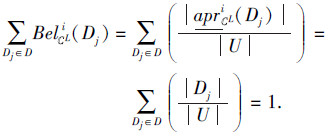
2)⇒ 1).由于S为第i型协调的, 故
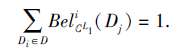
若
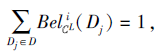
则
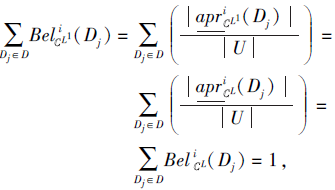
即
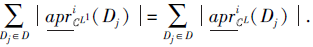 |
由于L1⪯L, 根据性质4, 对∀ Dj∈ D, 有
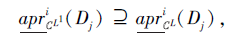
再根据式(1), 可得
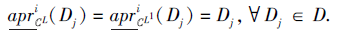
下证对∀ x∈ U, 有
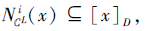
[x]D表示划分D中包含元素x的等价类.由于
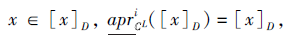
故
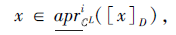
再根据下近似的定义, 有
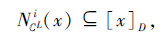
从而SL为第i型协调的.
1)⇒ 3).若SL为第i型协调的, 对∀ Dj∈ D, 根据定理4, 有
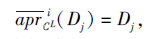
而D为U上的一个划分, 从而
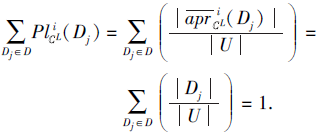
3)⇒ 1).反证法, 若SL不是第i型协调的, 则∃x∈ U, 使得
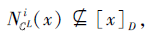
即∃y∈ Ni
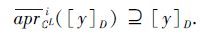
由于
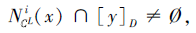
故 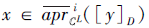
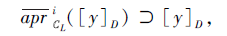
再结合定理3可得
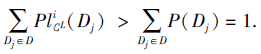
这与
矛盾, 于是SL为第i型协调的.
证毕.
由定理5可知, 可通过决策类的信任度和似然度定量刻画第i型协调的广义多尺度覆盖决策系统的最优尺度组合, 根据证据理论刻画的最优尺度组合和通过覆盖粗糙集理论定义的最优尺度组合可看作对系统保持协调性不变的最粗的尺度组合特征的定量刻画与定性刻画.在定理5的基础上可进一步得到定理6.
定理6 设
S=(U, C={C1, C2, ···, Cm}, D)
为第i型协调的广义多尺度覆盖决策系统, L∈ L, i∈ {1, 2, 3, 4}, 则如下条件等价:
1)L为S的一个第i型最优尺度组合.
2) $\sum_{D_{j} \in D} \operatorname{Bel}_{C^{L}}^{i}\left(D_{j}\right)=1$, 且对∀ L'∈ L, 满足L'≻L, 有
3)
证明 由定义10、定理3和定理5可证.
证毕.
本节在文献[19]的基础上, 讨论不协调的广义多尺度覆盖决策系统的各种最优尺度组合和它们之间的关系.
设
S=(U, C={C1, C2, ···, Cm}, D)
为第i型不协调的广义多尺度覆盖决策系统, L∈ L, X⊆U, Y⊆U, Y≠ Ø , 定义
P(X|Y)=
可证明
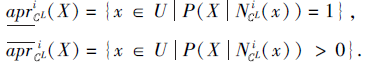
记
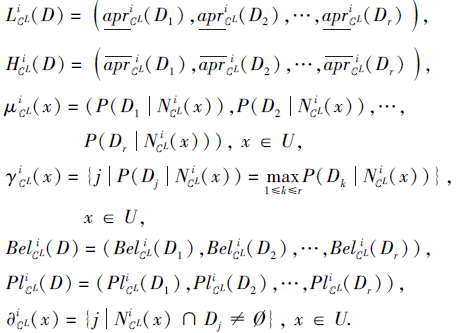
定义11 设
S=(U, C={C1, C2, ···, Cm}, D)
为第i型不协调的广义多尺度覆盖决策系统, L'∈ L, i∈ {1, 2, 3, 4}, 则
1)若
则称SL'为第i型下近似协调的.若SL'是第i型下近似协调的, 而对∀ L″∈ L, 满足L'≺L″(若{L″∈ L|L'≺L″}≠ Ø ), SL″不是第i型下近似协调的, 则称L'为S的一个第i型下近似最优尺度组合.
2)若
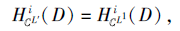
则称SL'为第i型上近似协调的.若SL'为第i型上近似协调的, 而对∀ L″∈ L, 满足L'≺L″(若{L″∈ L|L'≺L″}≠ Ø ), SL″不是第i型上近似协调的, 则称L'为S的一个第i型上近似最优尺度组合.
3)若∀ x∈ U,
则称SL'为第i型分布协调的.若SL'为第i型分布协调的, 而对∀ L″∈ L, 满足L'≺L″(若{L″∈ L|L'≺L″}≠ Ø ), SL″不是第i型分布协调的, 则称L'为S的一个第i型分布最优尺度组合.
4)若∀ x∈ U,
则称SL'为第i型最大分布协调的.若SL'为第i型最大分布协调的, 而对∀ L″∈ L满足L'≺L″(若{L″∈ L|L'≺L″}≠ Ø ), SL″不是第i型最大分布协调的, 则称L'为S的一个第i型最大分布最优尺度组合.
5)若
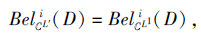
则称SL'为第i型信任分布协调的.若SL'为第i型信任分布协调的, 而对∀ L″∈ L满足L'≺L″(若{L″∈ L|L'≺L″}≠ Ø ), SL″不是第i型信任分布协调的, 则称L'为S的一个第i型信任分布最优尺度组合.
6)若
P
则称SL'为第i型似然分布协调的.若SL'为第i型似然分布协调的, 而对∀ L″∈ L满足L'≺L″(若{L″∈ L|L'≺L″}≠ Ø ), SL″不是第i型似然分布协调的, 则称L'为S的一个第i型似然分布最优尺度组合.
7)若∀ x∈ U,
则称SL'为第i型广义决策协调的.若SL'为第i型广义决策协调的, 而对∀ L″∈ L满足L'≺L″(若{L″∈ L|L'≺L″}≠ Ø ), SL″不是第i型广义决策协调的, 则称L'为S的一个第i型广义决策最优尺度组合.
下面讨论这7种最优尺度组合之间的关系.
定理7 设
S=(U, C={C1, C2, ···, Cm}, D)
为第i型不协调的广义多尺度覆盖决策系统, i∈ {1, 2, 3, 4}, L∈ L, 若对∀ x∈ U,
则
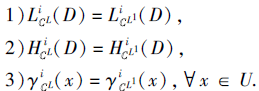
证明 1)一方面, 由于L1⪯L, 根据性质4, 对∀ Dj∈ D, 有
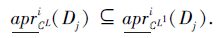
另一方面, 对∀ Dj∈ D, ∀ xk∈ U, 若
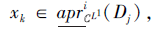
即$N_{C^{L}}^{i}\left(x_{k}\right) \subseteq D_{j}$, 有
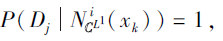
根据
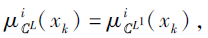
得
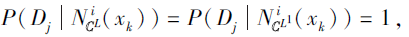
即$N_{C^{L}}^{i}\left(x_{k}\right) \subseteq D_{j}$, 从而$x_{k} \in \underline{a p r}_{C^{L}}^{i}\left(D_{j}\right)$, 所以
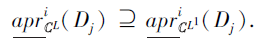
因此, 对∀ Dj∈ D,
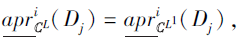
即
2)一方面, 由于L1⪯L, 根据性质4, 对∀ Dj∈ D, 有
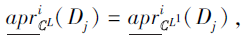
另一方面, 对∀ Dj∈ D, ∀ xk∈ U, 若xk∈
即
Ni
有
P(Dj|Ni
根据
得
P(Dj|Ni
即
Ni
从而xk∈
因此, 对∀ Dj∈ D,
即
Hi
3)显然可证.
证毕.
但定理7的逆命题不成立, 下面用例1和例2说明.
例1 设
S=(U, C={C1, C2}, D)
为广义多尺度覆盖决策系统, 其中U={x1, x2, ···, x6}, C1有2个尺度, C2有1个尺度, 分别表示如下:

于是S共有2个尺度组合(1, 1)与(2, 1).容易验证, S为第1、2、3、4型不协调的, 计算可得, (1, 1)是唯一的第1、2、3、4型分布最优尺度组合和最大分布最优尺度组合, (2, 1)是唯一的第1、2、3、4型上近似最优尺度组合和下近似最优尺度组合.
结合定理7和例1可得, 由SL为第i型分布协调的可推出SL为第i型上近似协调、第i型下近似协调的.
例2 设
S=(U, C={C1, C2}, D)
为广义多尺度覆盖决策系统, 其中U={x1, x2, ···, x6}, C1有2个尺度, C2有1个尺度, 分别表示如下:
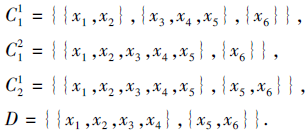
于是S共有2个尺度组合(1, 1)与(2, 1).容易验证, S为第1、2、3、4型不协调的, 计算可得, (1, 1)是唯一的第1、2、3、4型分布最优尺度组合、上近似最优尺度组合和下近似最优尺度组合, (2, 1)是唯一的第1、2、3、4型最大分布最优尺度组合.
结合定理7和例2可得, 由SL为第i型分布协调的可推出SL为第i型最大分布协调的.结合例1和例2可知, 在第i型不协调的广义多尺度覆盖决策系统中, 第i型最大分布最优尺度组合与第i型上近似最优尺度组合、第i型下近似最优尺度组合之间无必然关系.
文献[21]证明第1型上近似最优尺度组合和第1型广义决策最优尺度组合是等价的, 下面定理8统一证明第i型上近似最优尺度组合和第i型广义决策最优尺度组合也是等价的.
定理8 设
S=(U, C={C1, C2, ···, Cm}, D)
为第i型不协调的广义多尺度覆盖决策系统, i∈ {1, 2, 3, 4}, L∈ L, 则下述等价:

证明 1)⇒ 2).若
Hi
则对∀ Dj∈ D, 有
从而∀ x∈ U,
Ni
所以
j∈ ∂ i
故对∀ x∈ U,
2)⇒ 1).若∀ x∈ U,
则对∀ Dj∈ D,
j∈
即
Ni
因此对∀ Dj∈ D,
所以
Hi
证毕.
由定理8可知, SL为第i型上近似协调的当且仅当SL为第i型广义决策协调的.
定理9 设
S=(U, C={C1, C2, ···, Cm}, D)
为第i型不协调的广义多尺度覆盖决策系统, i∈ {1, 2, 3, 4}, L∈ L, 则下述等价:
1)
2)Beli
3)
证明 1)⇒ 2).若
则对∀ Dj∈ D, 有
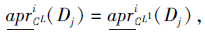
从而
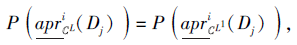
故
Beli
2)⇒ 3).显然可证.
3)⇒ 1).若
则
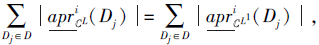 |
又根据性质4,
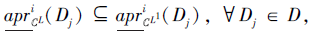
即
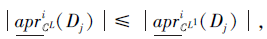
再结合式(2)可得, ∀ Dj∈ D,
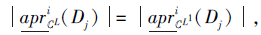
根据式(3)可得, 对∀ Dj∈ D, 有
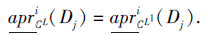
所以
证毕.
由定理9可知, L为S的一个第i型下近似最优尺度组合当且仅当L为S的一个第i型信任分布最优尺度组合.S的一个尺度组合对应一个单尺度的覆盖决策系统, 也对应一个信任结构, 根据覆盖粗糙集理论定义的下近似最优尺度组合与根据证据理论定义的信任分布最优尺度组合可视为系统对保持确定性知识不变的最粗的尺度组合特征的定性与定量刻画.
定理10 设
S=(U, C={C1, C2, ···, Cm}, D)
为第i型不协调的广义多尺度覆盖决策系统, i∈ {1, 2, 3, 4}, L∈ L, 则下述等价:
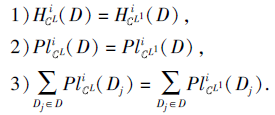
证明 与定理9证明类似.
证毕.
由定理10可知, L为S的一个第i型上近似最优尺度组合当且仅当L为S的一个第i型似然分布最优尺度组合.类似地, 根据覆盖粗糙集理论定义的上近似最优尺度组合与根据证据理论定义的似然分布最优尺度组合可视为系统保持可能性知识不变的最粗的尺度组合特征的定性与定量刻画.
定理11 设
S=(U, C={C1, C2, ···, Cm}, D)
为第i型不协调的广义多尺度覆盖决策系统, i∈ {1, 2, 3, 4}, L∈ L, 则
Hi
证明 一方面, 由于L1⪯L, 根据性质4, 对∀ Dj∈ D, 有
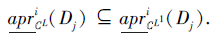
另一方面, 若
则对∀ Dj∈ D, 有
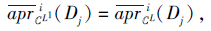
即对∀ x∈ U,

对 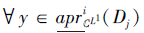
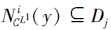
Ni
且
Ni
再根据式(4)可得, ∀ k≠ j,
Ni
且
Ni
因此 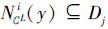
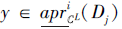
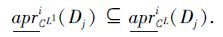
综上所述, 对∀ Dj∈ D, 有
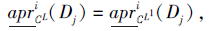
因此
证毕.
例3说明定理11的逆命题不成立.
例3 设
S=(U, C={C1, C2}, D)
为第i型不协调的广义多尺度覆盖决策系统, 其中U={x1, x2, ···, x6}, C1有2个尺度, C2有1个尺度, 分别表示如下:
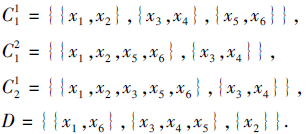
于是S共有2个尺度组合(1, 1)与(2, 1).计算可得, (2, 1)是唯一的第1、2、3、4型下近似最优尺度组合, 而(1, 1)是唯一的第1、2、3、4型上近似最优尺度组合.
结合定理11和例3可知, 由SL为第i型上近似协调的可推出SL为第i型下近似协调的.
通过本节的讨论, 可得到在第i型不协调的广义多尺度覆盖决策系统中7种协调性之间的关系, 直观表示如图1所示.由图可知, 在第i型不协调的广义多尺度覆盖决策系统中实际有4种不同的最优尺度组合, 这一结果与文献[19]中讨论的不协调完备广义多尺度决策系统中7种最优尺度组合之间的关系类似.
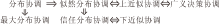 | 图1 不协调广义多尺度覆盖决策系统中7种协调性之间的关系Fig.1 Relationships among 7 types of consistencies in inconsistent generalized multi-scale covering decision systems |
需要指出的是, 在第i型协调的广义多尺度覆盖决策系统S中, 第i型下近似最优尺度组合、第i型上近似最优尺度组合、第i型分布最优尺度组合、第i型信任分布最优尺度组合、第i型似然分布最优尺度组合和第i广义决策最优尺度组合都是等价的且它们都与定义10定义的第i型最优尺度组合等价(结合图1、定理4和定理5易证).此外, 由SL为第i型分布协调的可推出SL为第i型最大分布协调(根据定理7易证), 但反之不成立, 下面用例4说明.
例4 设S=(U, C={C1, C2}, D)为广义多尺度覆盖决策系统, 其中U={x1, x2, ···, x7}, C1有2个尺度, C2有1个尺度, 分别表示如下:
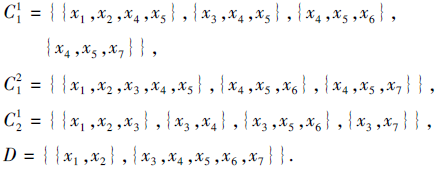
于是S共有2个尺度组合(1, 1)与(2, 1).容易验证, S为第1、2、3、4型协调的.计算可得, (1, 1)是唯一的第1、2、3、4型最优尺度组合和分布最优尺度组合, 而(2, 1)是唯一的第1、2、3、4型最大分布最优尺度组合.
综上可知, 在第i型协调的广义多尺度覆盖决策系统中, 本节定义的7种最优尺度组合之间的关系可用图2表示, 这一结果与文献[19]讨论的协调广义多尺度决策系统中的结论不同.
本节给出广义多尺度覆盖决策系统的最优尺度选择模型在不完备广义多尺度决策系统和广义多尺度集值决策系统中的应用.
定义12[32] 一个广义多尺度决策系统为一个二元组(U, AT∪ {d}), 其中, U={x1, x2, ···, xn}为非空有限论域, d为决策属性, d:U→ Vd, Vd为决策属性的值域, 由d导出的决策划分为
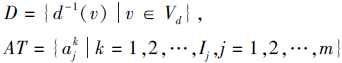
为非空有限属性集, 其中,
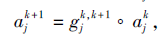
即
称
在广义多尺度决策系统中, 若某个对象在某个属性上的取值未知, 则称该系统为不完备广义多尺度决策系统, 用* 表示缺省值, 即若ak(x)=* , 则认为x在属性ak上的取值未知.此时不同尺度之间的属性值变换为
其中, k∈ {1, 2, ···, Ij-1}, j∈ {1, 2, ···, m}, x∈ U.
在对不完备广义多尺度决策系统进行知识获取时, 通常的方法是定义一个相似关系[32], 得到每个对象的相似类, 进而定义相关的协调性和最优尺度组合等概念.根据文献[20], 一个不完备广义多尺度决策系统可转化为一个广义多尺度覆盖决策系统.
对∀ v∈ V
(
显然, 对∀ j∈ {1, 2, ···, m}, k∈ {1, 2, ···, Ij},
a-1(V
为U上的一个覆盖.易证[20], 对
k∈ {1, 2, ···, Ij-1}, a-1(V
从而由一个不完备广义多尺度决策系统
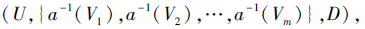
导出一个广义多尺度覆盖决策系统
(U, {a-1(V1), a-1(V2), ···, a-1(Vm)}, D),
其中
a-1(Vj)={a-1(V
将一个不完备广义多尺度决策系统转化为一个广义多尺度覆盖决策系统后, 可根据第3节和第4节的讨论, 计算该系统的最优尺度组合.文献[20]已证明按照本文讨论的第4型邻域计算得到的最优尺度组合与按照定义一个相似关系得到的最优尺度组合是等价的, 具体见文献[20], 这里不再详细讨论, 下面使用例5进行说明.
例5[16]表1给出一个不协调的不完备广义多尺度决策系统(U, AT∪ {d}), 其中
U={x1, x2, x3, x4, x5, x6, x7, x8, x9, x10},
AT={a1, a2, a3},
a1、a2、a3都有3个尺度, S、M、L、E、G、Y和N分别表示小、中、大、优、良、是和否, d为单尺度决策属性.
| 表1 不协调的不完备广义多尺度决策系统 Table 1 An inconsistent incomplete generalized multi-scale decision system |
计算可得
a-1(V
a-1(V
a-1(V
a-1(V
a-1(V
a-1(V
a-1(V
a-1(V
a-1(V
D={D1, D2},
其中
D1={x1, x2, x3, x4, x5, x6}, D2={x7, x8, x9, x10}.
令
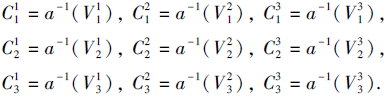
从而
S=(U, C={
为广义多尺度覆盖决策系统.所有的尺度组合为
L={(l1, l2, l3)|l1, l2, l3∈ {1, 2, 3}},
因此S共有27个尺度组合.
经计算可得
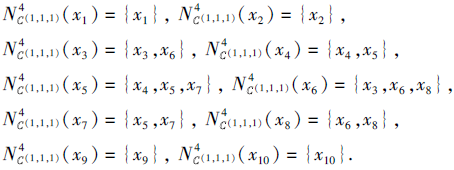
由于
N4
且
N4
所以S为第4型不协调的, 根据第4节中的讨论, 计算可得
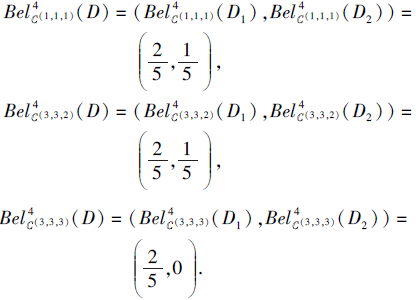
所以(3, 3, 2)为S的一个第4型信任分布最优尺度组合, 也是原不完备广义多尺度决策系统的一个信任分布最优尺度组合.同时, 计算可得
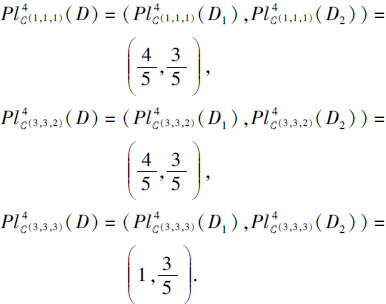
所以(3, 3, 2)为S的一个第4型似然分布最优尺度组合, 也是原不完备广义多尺度决策系统的一个似然分布最优尺度组合.并且, 可得到论域中的对象在不同尺度组合下的分布, 如表2所示.
| 表2 例5中的对象在不同尺度组合下的分布 Table 2 Distribution of objects under different scale combinations in Example 5 |
易见, (1, 1, 2)为S的一个第4型分布最优尺度组合, 也是原不完备广义多尺度决策系统的一个分布最优尺度组合, (1, 1, 2)为S的一个第4型最大分布最优尺度组合, 也是原不完备广义多尺度决策系统的一个最大分布最优尺度组合.
结合例5和本节的讨论, 将一个不协调的不完备广义多尺度决策系统转化为一个广义多尺度覆盖决策系统后, 可用本文第4节的方法计算该系统的4种最优尺度组合, 因此本文第4节中的结论可视为文献[19]中讨论的不协调广义多尺度决策系统的最优尺度组合之间的关系在不完备情形下的推广.
在一个决策系统中, 若某个对象的某个属性有多个取值, 称这样的系统为集值决策系统.以往关于集值决策系统的研究中, 每个属性只有一个尺度, 文献[22]~文献[24]定义广义多尺度集值决策系统, 并讨论广义多尺度集值决策系统中的最优尺度选择问题, 但这些研究均未使用证据理论刻画最优尺度组合.下面讨论将一个广义多尺度集值决策系统转化为广义多尺度覆盖决策系统后, 结合第3节和第4节中的结论, 使用证据理论刻画相关的最优尺度组合.
定义13[22] 称(U, AT∪ {d})为广义多尺度集值决策系统, 其中, U={x1, x2, ···, xn}为非空有限论域, d为决策属性, d:U→ Vd, Vd为决策属性的值域, 由d导出的决策划分为
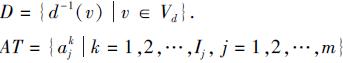
为非空有限属性集,
V
使
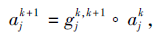
即
称
下面讨论广义多尺度集值决策系统与广义多尺度覆盖决策系统之间的关系.
定义集合类
其中
Kv={x∈ U|v∈
可验证
S=(U, {
将一个广义多尺度集值决策系统转化为一个广义多尺度覆盖决策系统后, 可根据第3节和第4节中的讨论, 计算协调、不协调广义多尺度集值决策系统的最优尺度组合, 下面用例6简单描述协调广义多尺度集值决策系统的最优尺度组合的计算方法.
注 将一个广义多尺度集值决策系统转化为一个多尺度覆盖决策系统后, 可采用本文定义的4种邻域中的一种用于计算系统的最优尺度组合, 有些研究[22, 23]采用第1型邻域, 也有一些研究[24]采用第4型邻域, 例6采用第1型邻域.
(U, AT={
不同尺度间的信息粒度变换为
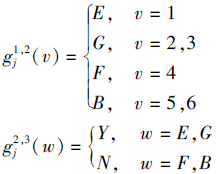
| 表3 一个广义多尺度集值决策系统 Table 3 A generalized multi-scale set-valued decision system |
根据本节的讨论, 由它导出的广义多尺度覆盖决策系统为
S=(U, C={
其中
{x2, x5, x6}, {x3, x4, x6}, {x2, x3, x4}},
{x2, x5, x6}, {x2, x3, x4, x6}},
{x1, x2, x3, x6}, {x5, x6, x7, x8}, {x5, x6, x8}},
{x5, x6, x7, x8}},
D={D1, D2, D3, D4},
其中
D1={x1, x2}, D2={x3, x4},
D3={x5, x6}, D4={x7, x8}.
S共有9个尺度组合.由于
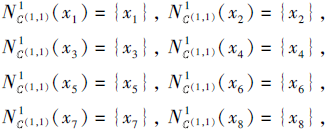
从而S是第1型协调的, 计算可得
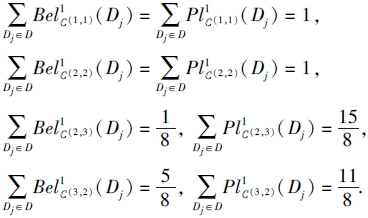
根据第3节中的讨论可知, (2, 2)为S的一个第1型最优尺度组合, 也是原广义多尺度集值决策系统的一个最优尺度组合.
证据理论和粗糙集理论都是处理数据的不确定性问题的有效方法, 本文结合证据理论和粗糙集理论, 定量、定性地研究广义多尺度覆盖决策系统中的最优尺度组合的选择问题.在协调广义多尺度覆盖系统中, 使用证据理论中的信任函数和似然函数刻画最优尺度组合的数值特征.在不协调广义多尺度覆盖决策系统中, 定义7种最优尺度组合概念, 并给出它们之间的关系.将本文方法应用于不完备广义多尺度决策系统和广义多尺度集值决策系统的最优尺度组合的选择问题, 阐明可在统一框架下研究这些多尺度系统的最优尺度组合选择问题.在后续的研究中, 一方面可用证据理论研究广义多尺度覆盖系统的局部最优尺度组合的选择问题, 另一方面可进一步研究相应的知识约简与规则提取问题.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|
| [19] |
|
| [20] |
|
| [21] |
|
| [22] |
|
| [23] |
|
| [24] |
|
| [25] |
|
| [26] |
|
| [27] |
|
| [28] |
|
| [29] |
|
| [30] |
|
| [31] |
|
| [32] |
|
| [33] |
|



