倪志伟,博士,教授,主要研究方向为机器学习、智能管理、大数据.E-mail:zhwnelson@163.com.
作者简介:

宋 娟,博士研究生,主要研究方向为智能管理、决策分析.E-mail:songjuan134@163.com.

武文颖,博士研究生,主要研究方向为模糊决策.E-mail:wuwenying0318@163.com.

金飞飞,博士,副教授,主要研究方向为智能管理、决策分析.E-mail:shexian19880129@163.com.

李 萍,博士,讲师,主要研究方向为模式识别、机器学习.E-mail:apple151691@126.com.
概率对偶犹豫模糊集包含隶属度、非隶属度及相应的概率信息,是刻画不确定决策信息的重要工具.针对属性权重信息未知的概率对偶犹豫模糊多属性决策问题,文中提出基于概率对偶犹豫模糊信息相关性系数的多属性决策方法.首先,运用概率对偶犹豫模糊信息熵计算属性客观权重,并与决策者给定的主观权重结合,得到属性综合权重.然后,提出概率对偶犹豫模糊信息相关性系数和加权相关性系数,用于衡量决策信息之间的相关性水平,并分析提出的相关性系数的优良性质.最后,设计基于概率对偶犹豫模糊信息相关性系数的多属性决策方法,并应用于雾霾治理措施的选择实验.实验表明,文中方法具有较好的鲁棒性和有效性.
NI Zhiwei, Ph.D., professor. His research interests include machine learning, intelligent management and big data.
About Author:
SONG Juan, Ph.D. candidate. Her research interests include intelligent management and decision analysis.
WU Wenying, Ph.D. candidate. Her research interests include fuzzy decision ma-king.
JIN Feifei, Ph.D., associate professor. His research interests include intelligent ma-nagement and decision analysis.
LI Ping, Ph.D., lecturer. Her research interests include pattern recognition and machine learning.
The probabilistic dual hesitant fuzzy set contains membership degree, non-membership degree and their corresponding probability information. It is an important tool to describe uncertain decision-making information. To solve the probabilistic dual hesitant fuzzy multiple-attribute decision-making problem with unknown attribute weight information, a multiple-attribute decision-making method is proposed based on the correlation coefficient of probabilistic dual hesitant fuzzy information. Firstly, the objective attribute weight is calculated by probabilistic dual hesitant fuzzy information entropy and combined with the subjective attribute weight given by decision-maker to obtain the comprehensive weight of attribute. Secondly, a correlation coefficient and a weighted correlation coefficient are proposed to measure the correlation level between decision-making information, and the excellent properties of the proposed correlation coefficients are analyzed. Finally, a multi-attribute decision-making method based on the correlation coefficient of probabilistic dual hesitant fuzzy information is designed and applied to the selection experiment of haze control strategies. Experimental results show that the proposed method produces good robustness and effectiveness.
本文责任编委 梁吉业
Recommended by Associate Editor LIANG Jiye
作为决策理论的重要组成部分, 多属性决策在工程、管理和经济等领域被广泛应用[1, 2, 3, 4].然而, 决策环境的复杂性和人类认知的局限性使决策专家难以利用精确值描述决策信息.自模糊集(Fuzzy Set, FS)的概念提出后, FS成为处理复杂多属性决策问题的有力工具[5, 6, 7, 8, 9, 10].随着FS理论研究的发展, 学者们提出FS的多种扩展形式, 例如:直觉模糊集[11, 12, 13, 14]、单值中智集[15, 16, 17, 18]和毕达哥拉斯模糊集[19, 20, 21, 22].针对决策者表达决策信息时对几个评价值犹豫不定的情形, Torra[23]提出FS的重要扩展形式— — 犹豫模糊集.在犹豫模糊集的基础上, Zhu等[24]考虑非隶属度是犹豫的情形, 提出对偶犹豫模糊集, 但未考虑隶属度和非隶属度出现的不同可能性.朱斌[25]结合概率信息与犹豫模糊集, 提出概率犹豫模糊集, 但未考虑非隶属度及其相应的重要性.因此, 如何结合隶属度、非隶属度与概率信息, 进而更好地解决多属性决策问题有待于进一步研究.
属性权重确定和属性信息融合是模糊决策领域的两个重要研究课题.一方面, 针对属性权重确定问题的研究已取得许多成果.在双层次犹豫模糊语言环境下, Krishankumar等[26]利用数学规划模型计算属性权重, 提出VIKOR的多属性决策方法.Zheng等[27]利用熵权法计算属性权重, 并提出基于直觉梯形模糊逼近理想解排序法(Technique for Order Preference by Similarity to Ideal Solution, TOPSIS)的多属性决策方法.Wan等[18]最大化每个备选方案的总体知识测度, 建立多目标规划模型以确定属性权重, 并提出毕达哥拉斯模糊数序关系, 用于备选方案的排序.Wang等[28]利用最大离差法确定属性权重, 提出基于距离测度的概率语言多属性决策方法.在属性权重是决策专家主观赋值的情形下, 向南等[29]设计基于专家信任网络的不完全犹豫模糊多属性群决策方法.另一方面, 针对属性信息融合问题, 学者们把相关性系数引入模糊多属性决策中.Song等[30]给出概率犹豫模糊集之间的相关性系数和加权相关性系数, 并在此基础上解决概率犹豫模糊环境下的多属性决策问题.Meng等[31]定义对偶犹豫模糊加权相关性系数和Shapley相关性系数, 并给出其在工程管理中的应用.曾守桢等[32]给出基于改进的概率语言类综合Pearson相关性系数的多属性决策方法.Li等[33]构建属于[-1, 1]内的犹豫模糊语言相关性系数, 并通过算例验证其在多属性决策中的有效性.Sun等[34]提出改进的犹豫模糊相关性系数, 并用于医学诊断和聚类分析.
考虑到结合隶属度、非隶属度与概率信息后, 能更好地解决多属性决策问题, Hao等[35]提出概率对偶犹豫模糊集(Probabilistic Dual Hesitant FS, PDHFS)和基于概率对偶犹豫模糊熵的可视化多属性决策方法.基于PDHFS, 文献[36]~文献[38]分别提出基于二部图论、相关性系数和Maclaurin集成的概率对偶犹豫模糊多属性决策方法.但是, 文献[35]~文献[38]中的属性权重是决策者主观给出, 容易造成决策结果带有主观随意性.此外, Garg等[37]提出概率对偶犹豫模糊相关性系数, 只能显示PDHFS间的相关强度, 不能反映相关的正负极性.Ren等[39]应用层次分析法(Analytic Hierarchy Process, AHP)确定属性权重, 提出概率对偶犹豫模糊环境下的集成VIKOR-AHP多属性决策方法.Garg等[40]利用最大离差法计算属性权重, 提出基于概率对偶犹豫模糊信息距离测度的多属性决策方法.但是, 文献[39]和文献[40]中的属性权重是利用决策信息计算得到的客观权重, 决策结果容易忽视决策者的主观经验.
针对上述不足, 本文结合属性主观权重和利用熵权法确定的属性客观权重, 提出基于概率对偶犹豫模糊信息相关性系数的多属性决策方法, 并给出符合传统相关性系数定义的改进的概率对偶犹豫模糊相关性系数和加权相关性系数.最后, 利用本文方法实现雾霾治理措施的择优排序.
定义1[35] 设X为一个非空集合, 定义在X上的PDHFS为
T={(xi, a(xi)|p(xi), b(xi)|q(xi))|xi∈ X},
其中, a(xi)、b(xi)为[0, 1]区间内几个不同数的集合, 分别表示xi属于集合T的可能隶属度和可能非隶属度, p(xi)、q(xi)分别为相应的概率.对于
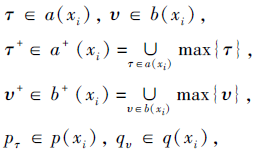
满足
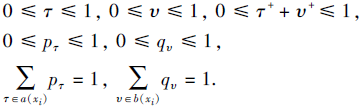
注1 t(xi)=(a(xi)|p(xi), b(xi)|q(xi))称为概率对偶犹豫模糊元(Probabilistic Dual Hesitant Fuzzy Element, PDHFE), 为了方便起见, 将PDHFE
t(xi)=(a(xi)|p(xi), b(xi)|q(xi))
记为
t=(a|p, b|q),
则
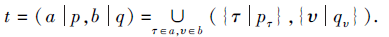
定义2[35] 设t=(a |p, b |q)为一个PDHFE, 定义
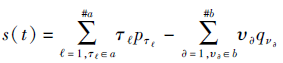
为t的得分函数,
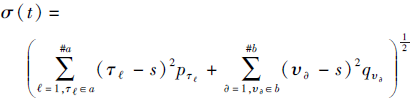
为t的偏差函数, 其中, #a、#b分别表示集合a|p和b|q中所含元素的个数.
记tk(k=1, 2)为任意2个PDHFE, s(tk)和σ (tk)为相应的得分函数和偏差函数, Hao等[35]给出如下PDHFE之间的比较法则:
1)若s(t1)> s(t2), 则t1优于t2, 记为t1≻t2; 类似地, 若s(t1)< s(t2), 则t1劣于t2, 记为t1≺t2.
2)若s(t1)=s(t2), 则
(1)若σ (t1)> σ (t2), 则t1劣于t2, 记为t1≺t2;
(2)若σ (t1)=σ (t2), 则t1等价于t2, 记为t1~t2;
(3)若σ (t1)< σ (t2), 则t1优于t2, 记为t1≻t2.
文献[35]定义如下PDHFE之间的运算法则:
令
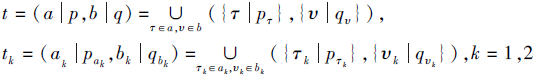
为3个PDHFE, λ ≥ 0, 有
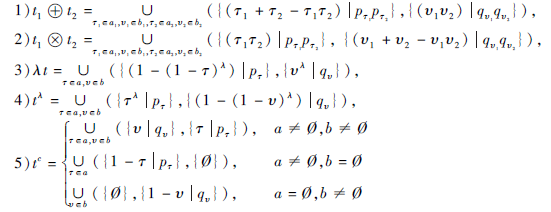
定义3[35] 令
tk=(ak|
为一列PDHFE, φ =(φ 1, φ 2, ···, φ n)T为相应的权重向量, 满足
φ k≥ 0, φ 1+φ 2+···+φ n=1,
则概率对偶犹豫模糊加权平均算子为
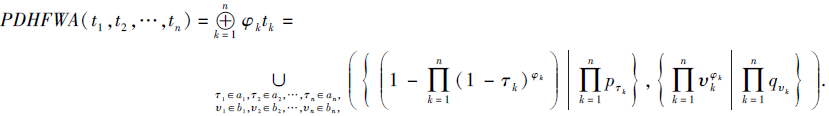
当
φ 1=φ 2=···=φ n=
时, 概率对偶犹豫模糊加权平均算子为概率对偶犹豫模糊平均(Probabilistic Dual Hesitant Fuzzy Ave-raging, PDHFA)算子.
定义4[35] 对于任意的PDHFE
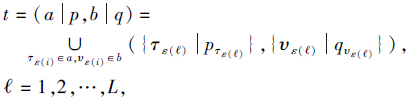
将每个隶属度值与非隶属度值之间的差异度和犹豫度分别定义为
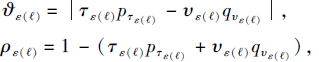
其中, τ ε (ℓ)、υ ε (ℓ)分别为隶属度和非隶属度中第ℓ小的元素,
L=max(#a, #b).
PDHFE t=(a|p, b|q)的熵I为关于ϑ ε (ℓ)和ρε (ℓ)的函数, 满足如下条件:
1)0≤ I(t)≤ 1;
2)I(t)=0当且仅当ϑ ε (ℓ)=1, ρε (ℓ)=0;
3)I(t)=1当且仅当ϑ ε (ℓ)=0, ρε (ℓ)=1;
4)I(tc)=I(t);
5)I为关于ϑ ε (ℓ)的单调递减函数, 同时, I为关于ρε (ℓ)的单调递增函数.
本节提出综合属性主观权重和属性客观权重的属性权重确定方法, 得到合理、全面的属性权重信息.决策专家根据经验和自身的知识水平给出属性主观权重, 记为
ω1=(
下面利用熵权法计算属性客观权重.
PDHFS的信息熵是度量PDHFS的不确定程度的有效工具, 但是文献[35]提出的概率对偶犹豫模糊信息熵要求隶属度和非隶属度中的元素个数相同, 在实际的决策问题中, 隶属度和非隶属度中的元素个数通常是不同的, 而给隶属度或非隶属度添加元素会破坏原始的评价信息.
为此, 本文给出改进的概率对偶犹豫模糊信息熵.对于任意的PDHFE t=(a|p, b|q), 将t的隶属度与非隶属度的平均差异度ϑ 和平均犹豫度ρ定义为
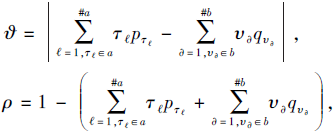
则t=(a|p, b|q)的熵I是关于ϑ 和ρ的函数.本文将t=(a|p, b|q)的信息熵定义为
I(t)=1-
不难看出, 本文定义的信息熵不需要隶属度和非隶属度中的元素个数相同.
熵权法是根据属性指标包含信息量的多少以确定属性权重的客观赋值法.属性的概率对偶犹豫模糊熵值越大, 说明该属性提供的信息量越小, 在方案评价中的作用越小, 应赋予该属性较小的权重; 否则, 应赋予该属性较大的权重.
设PDHFE tij=(aij|pij, bij|qij)表示决策专家对第i个备选方案在第j个属性上的评价值, 利用熵权法确定属性客观权重的计算过程如下.
1)计算第j个属性的熵值.由式(1)得到
tij=(aij|pij, bij|qij)
的熵为
I(tij)=1-
其中
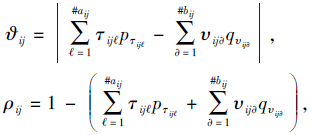
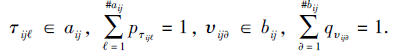
在本文中, 令
ϕ =ψ =
根据决策专家的评价值计算第j个属性的熵值为
Ij=
2)计算第j个属性的客观权重.基于第j个属性的熵值(式(2)), 第j个属性的客观权重为
然后, 决策专家根据决策问题的具体情况设定参数δ(0≤ δ≤ 1)对属性的主客观权重进行集结, 得到属性权重为
ωj=δ
其中δ(0≤ δ≤ 1)反映决策者的主观偏好.当δ< 0.5时, 表明决策者更关注评价信息中属性指标包含信息量; 当δ> 0.5时, 表明决策者更重视决策专家的经验.
针对概率对偶犹豫模糊环境下的相关性分析, Garg等[37]提出如下概率对偶犹豫模糊相关性系数公式.
设
X={x1, x2, ···, xn}
为一个非空集合,
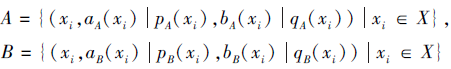
为定义在X上的2个PDHFS, 则A、B之间的相关性系数为
K1(A, B)=
其中
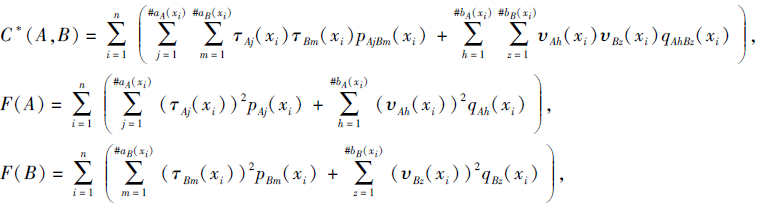
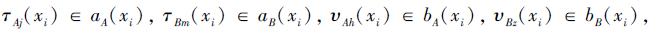
pAj(xi)、pBm(xi)、qAh(xi)、qBz(xi)分别为τ Aj(xi)、τ Bm(xi)、υ Ah(xi)、υ Bz(xi)的关联概率,
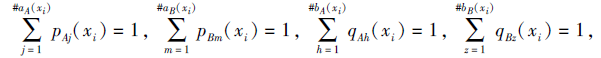
pAjBm(xi)为利用西北角法则得到的τ Aj(xi)和τ Bm(xi)的联合概率, qAhBz(xi)为利用西北角法则得到的υ Ah(xi)和υ Bz(xi)的联合概率.#aA(xi)、#aB(xi)、#bA(xi)、#bB(xi)分别为集合aA(xi)、aB(xi)、bA(xi)、bB(xi)中的元素个数.
例1 给定集合X={x1, x2}上的3个PDHFS,
A={(x1, ({0.1|1}, {0.4|0.2, 0.6|0.8})), (x2, ({0.2|0.9, 0.8|0.1}, {0.2|1}))},
B={(x1, ({0.3|0.9, 0.7|0.1}, {0.25|1})), (x2, ({0.06|1}, {0.1|0.4, 0.9|0.6}))},
D={(x1, ({0|1}, {0.4903|0.8312, 1|0.1688})),
(x2, ({0.4943|0.5672, 0.6084|0.4328}, {0.3916|1}))},
则根据K1计算相关性系数,
C* (A, B)=0.1× 0.3× 0.9+0.1× 0.7× 0.1+0.4× 0.25× 0.2+0.6× 0.8× 0.25+0.2× 0.9× 0.06+
0.06× 0.8× 0.1+0.1× 0.2× 0.4+0.2× 0.9× 0.6=0.3056,
C* (B, D)=0.25× 0.4903× 0.8312+0.25× 0.1688+0.06× 0.4943× 0.5672+0.06× 0.6084× 0.4328+
0.3916× 0.1× 0.4+0.3916× 0.9× 0.6=0.4038,
F(A)=0.12× 1+0.42× 0.2+0.62× 0.8+0.22× 0.9+0.82× 0.1+0.22× 1=0.47,
F(B)=0.32× 0.9+0.72× 0.1+0.252× 1+0.062× 1+0.12× 0.4+0.92× 0.6=0.6861,
F(D)=0.49032× 0.8312+1× 0.1688+0.49432× 0.5672+0.60842× 0.4328+0.39162× 1=0.8208,
则K1(A, B)=K1(B, D)=0.5382.
例1中的A、D是2个完全不同的PDHFS, A和D与B的相关性系数却相同, 这与直觉违背.此外, 0≤ K1≤ 1, 也就是说, Garg等[37]提出的相关性系数只能显示概率对偶犹豫模糊信息间的相关强度, 不能反映相关的极性.鉴于此种情况, 本文提出改进的概率对偶犹豫模糊信息相关性系数定义.
定义5 设X={x1, x2, ···, xn}为一个非空集合,
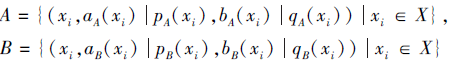
为定义在X上的2个PDHFS, 将A、B之间的相关性测度定义为
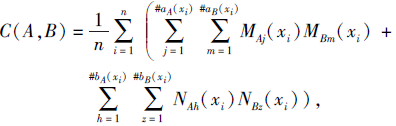 |
其中,
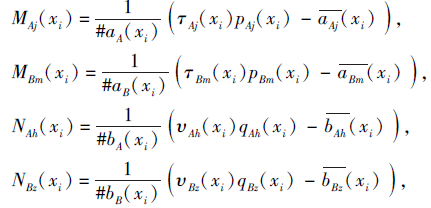
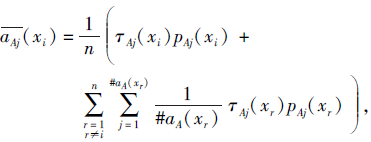
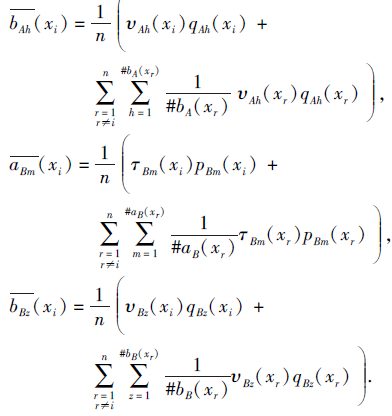
定理1 设
X={x1, x2, ···, xn}
为一个非空集合,
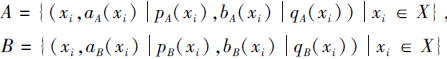
为定义在X上的2个PDHFS, 则A、B之间的相关性测度C(A, B)满足如下性质:
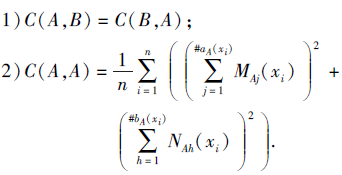
证明 根据式(6)可知, 性质1)显然成立,
下面证明性质2).由式(6)可得
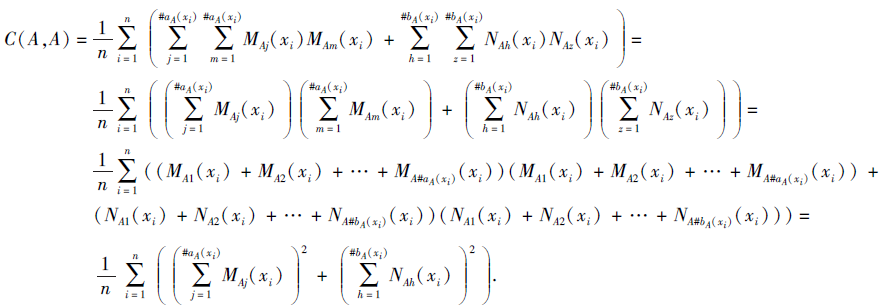
基于定义5提出的概率对偶犹豫模糊信息相关性测度, 下面给出改进的概率对偶犹豫模糊信息相关性系数公式.
定义6 设
X={x1, x2, ···, xn}
为一个非空集合,
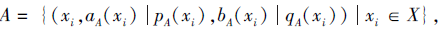
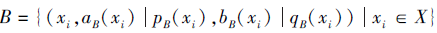
为定义在X上的2个PDHFS, A、B之间的相关性系数为
ρ(A, B)=
例2 对于例1中的3个PDHFS A、B、D, 根据ρ计算相关性系数如下:
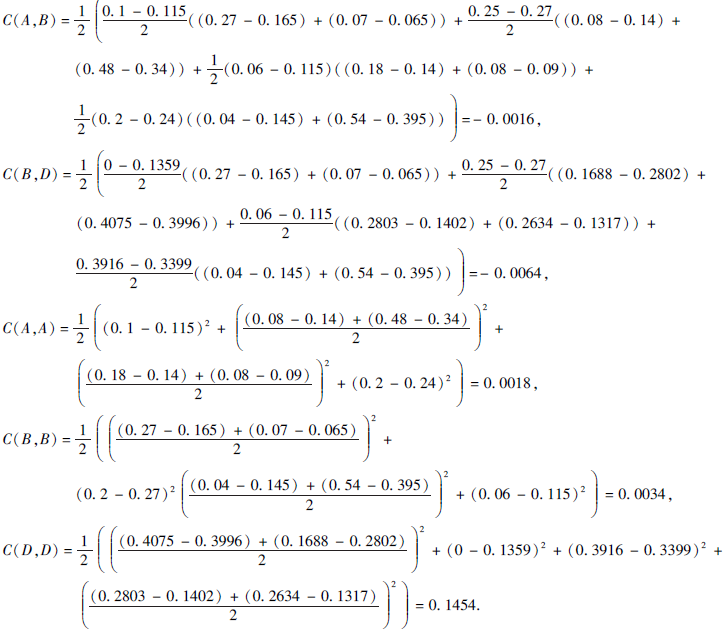
根据式(7)可得
ρ(A, B)=-0.6468, ρ(B, D)=-0.7486.
通过例2看出:对于2个完全不同的PDHFS A、D, 根据ρ计算的相关性系数
ρ(A, B)≠ ρ(B, D),
符合直觉.此外,
ρ(A, B)< 0, ρ(B, D)< 0.
因此, 本文提出的相关性系数能反映相关的极性, 与传统相关系数的定义符合.
定理2 设
X={x1, x2, ···, xn}
为一个非空集合,
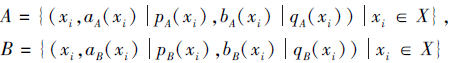
为定义在X上的2个PDHFS, A、B之间的相关性系数ρ(A, B)满足如下性质:
1)ρ(A, A)=1,
2)ρ(A, B)=ρ(B, A),
3)-1≤ ρ(A, B)≤ 1.
证明 根据定义5和定义6可知, 性质1)、2)显然成立.下面证明性质3).
由式(6)可得
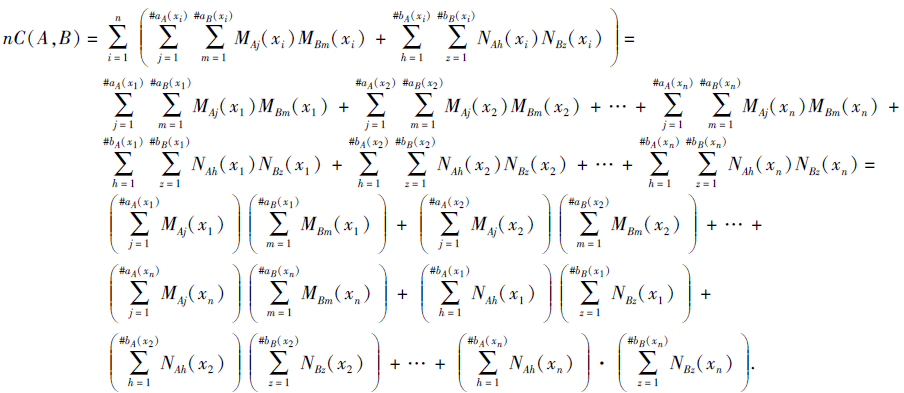
利用Cauchy-Schwarz不等式, 得
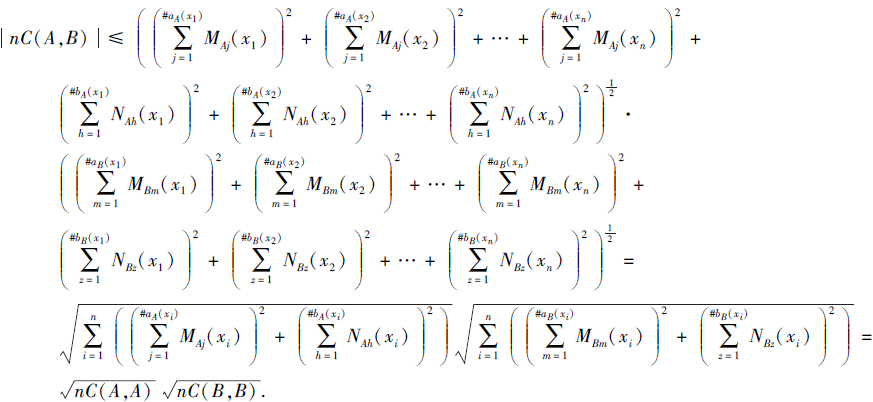
因此,
|ρ(A, B)|=
下面根据元素xi∈ X(i=1, 2, ···, n)的相对重要性给出相关性测度C(A, B)和相关性系数ρ(A, B)的加权形式.
定义7 设X={x1, x2, ···, xn}为一个非空集合,
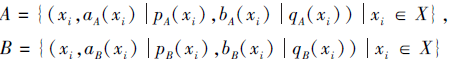
为定义在X上的2个PDHFS, 元素xi∈ X(i=1, 2, ···, n)的权重为ωi, 满足
0≤ ωi≤ 1,
则A、B之间的加权相关性测度为
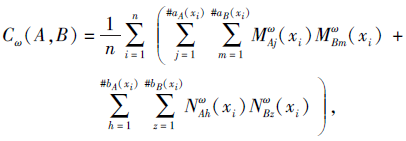 |
其中,
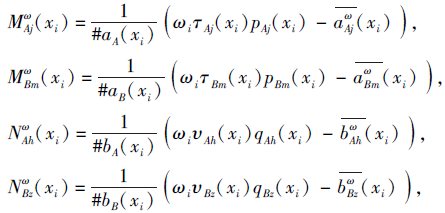
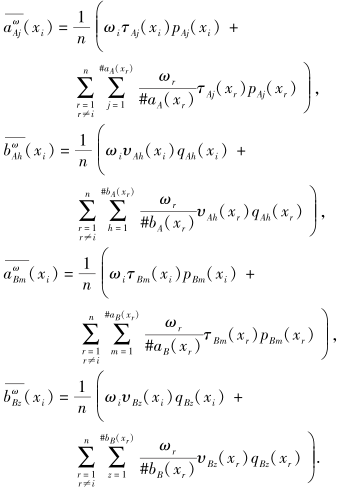
定义8 设X={x1, x2, ···, xn}为一个非空集合,
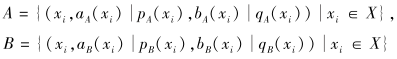
为定义在X上的2个PDHFS, 元素xi∈ X(i=1, 2, ···, n)的权重为ωi, 满足
0≤ ωi≤ 1,
则A、B之间的加权相关性系数为
ρω(A, B)=
其中,
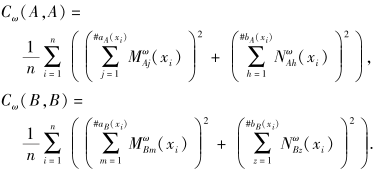
定理3 设X={x1, x2, ···, xn}为一个非空集合,
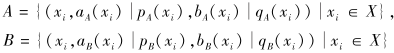
为定义在X上的2个PDHFS, A、B之间的加权相关性系数为ρω(A, B), 满足如下性质:
1)ρω(A, A)=1,
2)ρω(A, B)=ρω(B, A),
3)-1≤ ρω(A, B)≤ 1.
证明 根据定义7和定义8可知, 性质1)、2)显然成立.下面证明性质3).
由式(8)可得
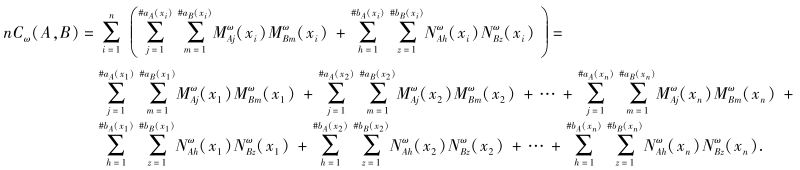
利用Cauchy-Schwarz不等式, 得
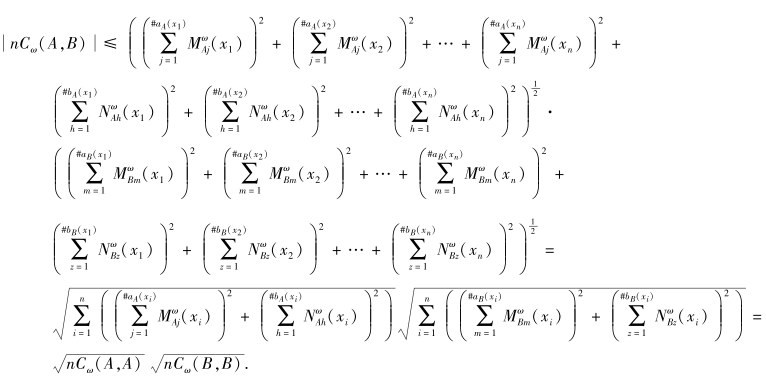
因此
|ρω(A, B)|=
设
E={E1, E2, ···, El}
表示l个决策者,
N={N1, N2, ···, No}
表示o个备选方案,
S={S1, S2, ···, Sn}
表示n个属性, 属性
Si∈ S, i=1, 2, ···, n
的权重为ωi, 满足
0≤ ωi≤ 1,
一般来说, 属性分为效益型属性和成本型属性两种, 且
S=Sbe∪ Sco, Sbe∩ Sco=Ø ,
其中, Sbe表示效益型属性组成的集合, Sco表示成本型属性组成的集合.
决策专家利用PDHFS表示评价信息, 记
s=1, 2, ···, l, i=1, 2, ···, o, j=1, 2, ···, n,

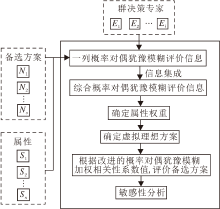
基于改进的PDHFS的相关性系数, 本节提出概率对偶犹豫模糊多属性决策方法, 整体流程如图1所示.
方法具体步骤如下.
1)标准化概率对偶犹豫模糊决策矩阵.无特殊说明, 本文以效益型属性为准, 根据Zhao等[41]的方法统一所有属性的评估值, 将决策专家Es的评价信息
Ts=
标准化为
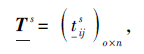
其中
2)利用定义3的PDHFA算子集结标准化后的概率对偶犹豫模糊决策矩阵
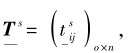
得到综合决策矩阵
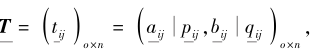
其中
$\underline{T}=P D H F A\left(\underline{{T}^{1}}, \underline{{T}^{2}}, \cdots, {T}^{l}\right)=\bigoplus_{s=1}^{l} \frac{1}{n} {T}^{s}$
3)由决策专家设定参数δ(0≤ δ≤ 1), 运用式(4)确定属性权重.
4)根据定义2给出的得分函数确定虚拟理想方案的评价值N* ={
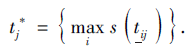
5)利用式(9)计算备选方案Ni与虚拟理想方案N* 的加权相关性系数ρω(Ni, N* ).
6)根据相关性系数ρω(Ni, N* )的大小对方案进行排序, 进而得到最优方案.
近年来, 我国工业化与城镇化的发展举世瞩目.但是, 长期的粗放式发展模式也付出巨大的环境代价. 2021年初, 我国东部地区出现大面积雾霾天气.
雾霾天气不仅威胁人们的健康, 而且对经济、社会产生消极影响.雾霾天气成为21世纪以来我国最大的环境污染问题之一.频发的雾霾天气已引起国家的高度关注, 2019年3月全国政协十三届二次会议指出, 环境治理的任务还很艰巨, 雾霾天气会有反复, 但是环境治理必须坚定地往前走.因此, 在雾霾污染事件频发的局势下, 亟需对雾霾进行有效的治理.
利用本文方法, 由来自环境保护相关部门的3位专家E={E1, E2, E3}组成决策群体, 对4个雾霾治理措施N={N1, N2, N3, N4}, 在如下4个指标下进行选优和评价, 即S1表示治理措施对二次颗粒物(气溶胶)形成的影响, S2表示治理措施对颗粒物的“ 吸湿作用” 的影响, S3表示治理措施对PM2.5排放水平的影响和, S4表示治理措施对扬尘与颗粒物区域传输的影响.3名决策专家的评估矩阵如表1~表3所示.
| 表1 专家E1给出的概率对偶犹豫模糊评估信息 Table 1 Probabilistic dual hesitant fuzzy evaluation information provided by decision-maker E1 |
| 表2 专家E2给出的概率对偶犹豫模糊评估信息 Table 2 Probabilistic dual hesitant fuzzy evaluation information provided by decision-maker E2 |
| 表3 专家E3给出的概率对偶犹豫模糊评估信息 Table 3 Probabilistic dual hesitant fuzzy evaluation information provided by decision-maker E3 |
利用本文方法对雾霾治理方案的效果排序, 下面给出具体的决策步骤.
1)由于所有考虑的属性都是效益型属性, 因此, 不需要对概率对偶犹豫模糊决策矩阵
Ts=
进行标准化.
2)利用PDHFA算子集结每位决策者的评价值, 得到综合决策矩阵
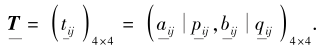
由于空间有限, 仅列出

3)确定属性权重.首先, 决策专家给出属性主观权重ω1=(0.23, 0.19, 0.35, 0.23).其次, 根据式(2)计算4个属性的熵值:
I1=0.4692, I2=0.3942,
I3=0.4865, I4=0.3085.
根据式(3)得到属性客观权重:
最后, 令δ=0.5, 根据式(4)得到属性权重:
ω1=0.2283, ω2=0.2243,
ω3=0.2847, ω4=0.2627.
4)基于定义2确定虚拟理想方案:

5)利用式(9)得到雾霾治理方案Ni(i=1, 2, 3, 4)与虚拟理想方案N* 的加权相关性系数ρω(Ni, N* ):
ρω(N1, N* )=0.2822, ρω(N2, N* )=0.3060,
ρω(N3, N* )=0.3680, ρω(N4, N* )=0.7975.
6)根据相关系数ρω(Ni, N* )的大小得到雾霾治理方案的排序结果:
N4> N3> N2> N1,
进而确定最优的雾霾治理方案是N4.
参数δ(0≤ δ≤ 1)反映决策者的主观偏好.当δ< 0.5时, 表明决策者更关注评价信息中属性指标包含的信息量; 当δ=0.5时, 表明决策者按照协商共识机制进行决策; 当δ> 0.5时, 表明决策者更重视决策专家的经验.
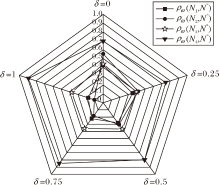
改变δ的取值, 计算雾霾治理方案Ni(i=1, 2, 3, 4)与虚拟理想方案N* 的加权相关性系数ρω(Ni, N* ), 分析雾霾治理方案优先序的变化情况.以0.25为间隔, 依次取δ=0, 0.25, 0.5, 0.75, 1, 进行实验.
敏感性分析结果如图2所示.由图可看出:当δ< 0.5时, 得到的排序结果为
N4> N2> N3> N1;
当δ=0.5时, 得到的排序结果为
N4> N3> N2> N1;
当δ> 0.5时, 得到的排序结果为
N4> N3> N1> N2.
因此, 本文方法能根据决策者的不同主观偏好得到不同的排序结果, 体现本文方法的灵活性和可用性.此外无论δ怎样变化, 方案N4均是决策过程中的最优方案, 体现本文方法的鲁棒性.
为了说明本文方法的可行性和有效性, 将本文方法与文献[31]和文献[37]中的多属性决策方法进行对比分析.
文献[37]提出基于PDHFS的相关性系数的多属性决策方法.运用文献[37]中的多属性决策方法处理雾霾治理方案排序问题, 相应步骤如下.
1)利用文献[37]中算法1获得综合决策矩阵
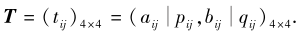
由于空间有限, 仅列出T中的部分元素:
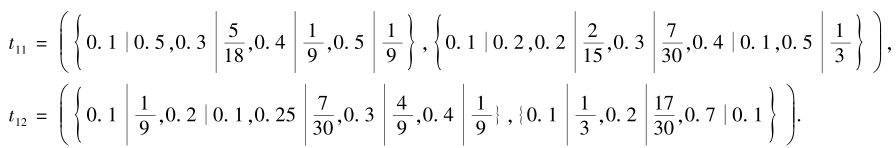
2)利用文献[38]中式(15)确定理想方案:

3)利用文献[37]中的相关性系数式(10)和式(11), 计算雾霾治理方案Ni(i=1, 2, 3, 4)与虚拟理想方案N* 的相关性系数K1(Ni, N* )和K2(Ni, N* ), 计算结果见表4.
| 表4 雾霾治理方案与理想方案之间的不同相关性系数值 Table 4 Different correlation coefficient values between alternatives of haze governance and ideal alternative |
同时, 文献[37]中的属性权重是决策者主观给出的, 为了便于与本文方法进行对比, 令文献[38]中的属性权重为
ω1=0.2283, ω2=0.2243,
ω3=0.2847, ω4=0.2627.
利用文献[37]中的加权相关性系数式(12)和式(13)计算治理方案Ni与虚拟理想方案N* 的加权相关性系数K3(Ni, N* )和K4(Ni, N* ), 计算结果见表4.
4)利用文献[37]中式(10)计算概率对偶犹豫模糊相关性系数K1, 得到4个雾霾治理方案的排序为
N2> N3> N4> N1.
利用文献[37]中式(11)和式(12)计算概率对偶犹豫模糊相关性系数K2和K3, 得到4个雾霾治理方案的排序为
N3> N2> N4> N1.
利用文献[37]中式(13)计算概率对偶犹豫模糊相关性系数K4, 得到4个雾霾治理方案的排序为
N3> N4> N2> N1.
当PDHFE的隶属度和非隶属度的概率值相同时, PDHFE退化为对偶犹豫模糊元, 将文献[31]的决策方法用于雾霾治理方案的排序, 相应步骤如下.
1)将决策专家给出的概率对偶犹豫模糊评估矩阵
Ts=(
转换为相应的对偶犹豫模糊评估矩阵
Ds=(
由于所有考虑的属性都是效益型属性, 因此不需要对Ds进行标准化.
2)利用对偶犹豫模糊平均算子集结每位决策者的评价值, 得到综合决策矩阵
D* =(
由于空间有限, 仅列出D* 中的部分元素:
0.3196}, {0.2466, 0.2714, 0.3107, 0.342}),
0.3196}, {0.1587, 0.241}).
3)为了便于与本文方法进行对比, 令文献[32]中的属性权重为
ω1=0.2283, ω2=0.2243,
ω3=0.2847, ω4=0.2627.
利用文献[31]中式(16)和式(17)计算雾霾治理方案Ni与虚拟理想方案
N+= {({1}, {0}), ({1}, {0}), ({1}, {0}), ({1}, {0})}
的加权相关性系数C
4)依据加权相关性系数C
| 表5 运用不同的相关性系数公式得到的决策结果 Table 5 Decision results with different correlation coefficient formulas |
1)在本文方法中, 雾霾治理方案的排序与决策者的主观偏好程度δ(0≤ δ≤ 1)相关.此外, 决策者的主观偏好程度δ(0≤ δ≤ 1)并未影响雾霾治理最佳方案的选择.这说明本文的概率对偶犹豫模糊决策方法具有较好的灵活性和鲁棒性.
2)与文献[37]中的多属性决策方法对比发现:首先, 利用文献[37]中算法1, 获得综合决策矩阵
T=(tij)4× 4=(aij|pij, bij|qij)4× 4,
其中,
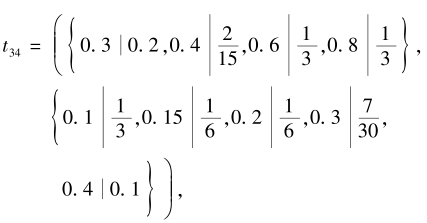
max{0.3, 0.4, 0.6, 0.8}+max{0.1, 0.15, 0.2, 0.3, 0.4}=1.2> 1.
因此, PDHFE t34不满足定义1, 利用文献[37]中算法1获得综合决策矩阵是不合理的, 进而使得最终的决策结果缺乏可信度, 而本文方法中的综合决策偏好信息值都满足定义1.其次, 文献[37]中的多属性决策方法只能处理属性权重已知情形, 而本文方法考虑决策者的主观偏好程度, 给出主/客观属性权重结合的属性权重确定方法, 能有效处理属性权重未知的决策情形.最后, 文献[37]提出的概率对偶犹豫模糊相关性系数介于0和1之间, 此相关性系数只能显示概率对偶犹豫模糊信息间的相关强度, 不能反映相关的极性, 而本文提出改进的概率对偶犹豫模糊信息相关性系数属于[-1, 1]区间.综上所述, 本文提出的决策方法比文献[37]的决策方法更可靠.
3)利用文献[31]中的多属性决策方法得到的方案排序与利用本文方法得到的排序结果不同.造成这种不同的主要原因在于:一方面, 运用文献[31]中的多属性决策方法, 需要将原始的概率对偶犹豫模糊信息转换为相应的对偶犹豫模糊信息, 造成原始信息的丢失, 而本文方法是直接运用原始的概率对偶犹豫模糊信息进行计算, 能更充分体现决策者的原始决策偏好.另一方面, 文献[31]中的多属性决策方法只能针对单个决策者的决策情形, 而本文方法可解决多个决策者的群体决策问题, 从而克服单个决策者自身知识能力与主观经验的局限性.综上所述, 本文方法比文献[31]的决策方法更有效.
本文在属性权重未知情形下, 提出基于概率对偶犹豫模糊信息相关性系数的多属性决策方法.首先, 构建同时考虑PDHFS的平均差异度和平均犹豫度的概率对偶犹豫模糊信息熵, 并提出属性主观权重和利用熵权法确定的属性客观权重结合的属性权重确定方法, 得到合理、全面的属性权重信息.其次, 针对现有概率对偶犹豫模糊相关性系数的局限性, 定义概率对偶犹豫模糊环境下一种相关性系数和加权相关性系数, 并探讨该相关性系数具有的优良性质.最后, 基于提出的属性权重确定方法和相关性系数, 设计一种概率对偶犹豫模糊环境下的多属性决策方法, 并将提出的决策方法用于雾霾治理方案的选择.实验表明本文方法的鲁棒性和有效性.
本文研究的多属性决策方法仅考虑决策专家给出的概率对偶犹豫模糊信息是完全可知的情况.针对专家难以给出PDHFE发生概率的情形未进行研究, 即如何解决概率未知的概率对偶犹豫模糊决策问题尚有待进一步研究.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|
| [19] |
|
| [20] |
|
| [21] |
|
| [22] |
|
| [23] |
|
| [24] |
|
| [25] |
|
| [26] |
|
| [27] |
|
| [28] |
|
| [29] |
|
| [30] |
|
| [31] |
|
| [32] |
|
| [33] |
|
| [34] |
|
| [35] |
|
| [36] |
|
| [37] |
|
| [38] |
|
| [39] |
|
| [40] |
|
| [41] |
|