引用本文
陈鸿杰, 何玉林, 黄哲学, 尹剑飞. 基于候选中心融合的多观测点I-nice聚类算法. 模式识别与人工智能, 2022,35(4): 348-362
CHEN Hongjie, HE Yulin, HUANG Zhexue, YIN Jianfei. Multi-observation I-nice Clustering Algorithm Based on Candidate Centers Fusion. PATTERN RECOGNITION AND ARTIFICIAL INTELLIGENCE, 2022,35(4): 348-362.  
Doi: 10.16451/j.cnki.issn1003-6059.202204005
Permissions
Copyright©2022, 《模式识别与人工智能》编辑部
《模式识别与人工智能》编辑部
基于候选中心融合的多观测点I-nice聚类算法
陈鸿杰1,2, 何玉林1,2, 黄哲学1,2, 尹剑飞1,2
1.深圳大学 计算机与软件学院 大数据技术与应用研究所 深圳 518060
2.深圳大学 大数据系统计算技术国家工程实验室 深圳 518060
通讯作者:

何玉林,博士,副研究员,主要研究方向为数据挖掘、机器学习、大数据处理与分析、大数据近似计算技术、多样本统计分析理论与方法等.E-mail:yulinhe@szu.edu.cn.

作者简介:

陈鸿杰,硕士研究生,主要研究方向为数据挖掘、大数据处理与分析、大数据系统计算技术.E-mail:chenhongjie2016@email.szu.edu.cn.

黄哲学,博士,教授,主要研究方向为数据挖掘、机器学习、大数据处理与分析、大数据系统计算技术等.E-mail:zx.huang@szu.edu.cn.

尹剑飞,博士,副教授.主要研究方向为大数据处理与分析、机器学习、数据挖掘、数值优化等.E-mail:yjf@szu.edu.cn.

收稿日期: 2021-10-25 接受日期: 2022-04-10
资助项目: 国家自然科学基金面上项目(No.61972261)、深圳市基础研究项目(No.JCYJ20210324093609026,JCYJ20200813091134001)
摘要

伴随着问题场景数据在规模上的快速增长和构成上的复杂化,精确估计簇的个数和簇的中心点是当下聚类算法处理和分析复杂大规模数据的重要挑战.簇数及簇心的精确估计对于部分有参聚类算法、数据集整体复杂性度量和数据简化表示等都十分关键.文中在深入分析I-nice的基础上,提出基于候选中心融合的多观测点I-nice聚类算法.在原多观测点投影分治框架上采用混合高斯模型(Gaussian Mixture Model, GMM),结合粗细粒度最佳GMM搜索策略,实现数据子集的精确划分.此外,基于候选中心点分别到各观测点的距离值及最佳GMM,构造候选中心点的GMM构件向量,并设计一组闵可夫斯基距离对进行候选中心点间的相异度度量,实现基于GMM构件向量相异度的多观测点I-nice候选中心融合.不同于现有聚类算法,文中算法联合优化分治环节数据子集划分和候选中心集成这两个关键过程,实现成百上千个簇的精确高效估计.在真实数据集和仿真数据集上的一系列实验表明,文中算法能精确估计簇数和簇中心,具备较高的聚类精度.实验同时验证算法的有效性及在各类数据场景下的稳定性.

关键词: 无监督学习; 观测点; I-nice; 无参聚类; 高斯混合模型
中图分类号:TP301
Multi-observation I-nice Clustering Algorithm Based on Candidate Centers Fusion
CHEN Hongjie1,2, HE Yulin1,2, HUANG Zhexue1,2, YIN Jianfei1,2
1. Big Data Institute, College of Computer Science and Software Engineering, Shenzhen University, Shenzhen 518060
2. National Engineering Laboratory for Big Data System Computing Technology, Shenzhen University, Shenzhen 518060
Corresponding author:
HE Yulin, Ph.D., associate professor. His research interests include data mining, machine learning, big data processing and analysis, big data approximate computing, and theories and methods of multi-sample statistics.

About Author:
CHEN Hongjie, master student. His research interests include data mining, big data processing and analysis, and big data system computing techno-logy.
HUANG Zhexue, Ph.D., professor. His research interests include data mining, machine learning, big data processing and analysis, and big data system computing technology.
YIN Jianfei, Ph.D., associate professor. His research interests include big data processing and analysis, machine learning, data mining and numerical optimization.

Fund:National Natural Science Foundation of China(No.61972261), Basic Research Foundations of Shenzhen(No.JCYJ20210324093609026,JCYJ20200813091134001)
Abstract

With the rapid growth of data scale and composition complexity in the real-world applications, it is an important challenge for current clustering algorithms to estimate the number and the centers of clusters accurately in processing and analyzing the complex and large-scale data. The accurate estimation of cluster number and cluster centers is crucial for partial parametric clustering algorithm, complexity measurement and simplified representation of dataset. In this paper, grounded on the in-depth analysis of I-nice, a multi-observation I-nice clustering algorithm based on candidate centers fusion(I-niceCF) is proposed. Based on the original multi-observation projection divide-and-conquer framework, Gaussian mixture model(GMM) is combined with the coarse-to-fine optimal mixture model search strategy to partition data subsets exactly. In addition, GMM component vectors of candidate centers are constructed based on the distance of candidate centers from each observation point and optimal GMMs. A Minkowski distance pair is designed to measure the dissimilarity between candidate centers. Finally, the candidate centers are fused based on the mixture component vectors. Different from the existing clustering algorithms, I-niceCF is jointly optimized by data subset partitioning of divide-and-conquer process and candidate centers fusion. Consequently, accurate and efficient estimation for hundreds of clusters is achieved. A series of experiments on real and synthetic datasets show that I-niceCF can estimate cluster number and cluster centers more accurately with higher clustering accuracy and its stability under various data scenarios is verified.

Key words: Key Words Unsupervised Learning; Observation Point; I-nice; Parameter-Free Clustering; Gaussian Mixture Model

本文责任编委 陈恩红

Recommended by Associate Editor CHEN Enhong

簇信息是用于理解、归纳和划分数据群体的重要统计信息, 是度量数据群体复杂性的一种量化指标.在簇信息中, 簇的个数和簇的中心是最核心的元素.例如, 在已知两者的情况下, 可使用K-means[1]等聚类算法估计数据集上簇的成员关系、离散量化误差等信息.在仅知道簇个数的情况下, 可使用谱聚类[2]等聚类算法估计簇的成员关系、数据点图的拉普拉斯矩阵特征值等信息.簇的成员关系信息又可进一步驱动数据处理的下游任务, 如监督分类和半监督分类.因此簇的个数和簇的中心点通常是许多聚类算法关键的先验参数, 需要提前设定两者或其一的聚类算法, 称为有参聚类算法, 如K-means和谱聚类等.簇数和初始中心点设定的好坏对于聚类算法的精度和效率都有很大的影响[3].

为了提升聚类算法的自动化能力, 必须解决簇的个数和簇的中心点的估计问题, 目前也存在一些研究成果[4, 5, 6, 7, 8], 然而精确估计复杂大规模数据集所含簇个数和簇中心是一项富有挑战性的任务.因为簇的信息是关于数据群体的统计信息, 通常能得到的是关于这个数据群体的某些样本数据集, 从样本数据集出发, 估计关于数据群体的信息存在固有的不确定性和偏置性.另一个原因是, 簇的成员关系存在多样性, 即用于判定一个数据点是否隶属于某个簇依赖于数据点之间的距离定义, 而高维空间的距离定义千差万别, 常用的有欧氏距离、闵可夫斯基距离、正态分布距离、积分距离、Wasserstein距离等.

另外, 当面对较大复杂数据集时, 现有的估计簇的个数和簇的中心点的聚类算法存在如下不足.

1)准确估计簇个数的能力有限.基于贝叶斯非参的方法[9, 10]通过迪利克雷随机过程枚举各个维度的隐藏变量, 建立随机过程模型, 只能有效识别300多个簇.Elbow[11]被广泛用于估计数据中的簇数, 计算簇心和对应簇内对象的平均距离和, 观察以簇数为自变量、平均距离和为因变量的曲线, 随着簇数增加, 平均距离和逐渐降低, 其中曲线存在“ 肘部” , 对应簇数值即为结果.缺点在于曲线“ 肘部” 的确定存在模糊性, 一些数据集会出现没有“ 肘部” 曲线特征的情况.Silhouette[12]针对数据集中每个对象, 计算簇不相似度与对象i到同簇其它对象的平均距离, 即对象i到异簇内对象的平均距离.两者的差值即为轮廓系数, 平均轮廓系数越小表示聚类效果越优.Silhouette和Elbow均仅可识别10多个簇.

2)估计簇个数和初始中心点的质量较差.现有的无监督的簇个数估计算法, 如Silhouette和Elbow, 在10个簇内存在至少一位数的偏差.Tibshirani等[13]提出Gap Statistic, 简称为Gap统计量, 用于确定数据集中的簇数, 在簇数K取不同值时, 度量其簇内离散值的对数值与相应数学期望的差值Gap, 进行簇数的合理选择, 差值最大时的K值为最佳的簇数.但Gap统计量容易导致簇数的过高估计[14], 在一些情况下差值Gap呈单调递增.另外这种方法无法较好地应用于源自指数分布的数据集[15].Mohajer等[16]在原本的Gap统计量的基础上进行修改, 提出Gap* 统计量, 去除Gap值的对数操作, 处理原Gap统计量中簇数过高估计的问题, 但在簇间发生重叠的数据集上表现不如Gap统计量, 并且在Gap统计量中差值单调递增的数据集上也并不保证在Gap* 统计量中得到合理结果, 而是得出过小的簇数估计值.Sugar等[15]提出Jump method, 度量每个维度上每个观测值与其最近的簇中心之间的平均距离, 确定簇数.Jump method在计算上较高效, 并且在一系列实验中得到验证, 但其畸变曲线容易出现单调情况, 导致计算全局最优无法获得一个合理的估计值.通过交叉验证能在一定程度上解决该问题, 但需付出昂贵的计算成本.此外, Yang等[17]提出M-means(Mountain Means Clustering Algorithm), 在数据集的样本数超过500时, 无法正确估计簇的个数.另外, 在数据集具有高维特征且簇数较多的情况下, 聚类算法往往需要人工介入、设计与观察各种渐进统计数据, 如平均Silhouette宽度, 才能获得较优的聚类结果.Maitra[3]寻找数据中的大量局部模式, 选取分离程度最大的点作为初始中心点, 在一系列实验上均取得可观结果.但当数据存在大量坐标(特征数)时, 奇异值分解计算过程变难, 阻碍在高维数据上的应用.

3)计算复杂度较高, 不利于大规模数据应用场景.例如, 基于谱聚类的算法[18]需要求解图拉普拉斯矩阵的特征根, 计算复杂度为O(N2K), 其中, N为样本点数量, K为簇数.狄利克雷过程混合模型[19]采用狄利克雷过程作为聚类参数的先验分布, 在较大范围内搜索簇的个数K, 并对整个数据集进行多次扫描, 估计参数的后验概率, 时间复杂度很高, 不适用于大规模数据聚类场景[20].此类算法对于大规模数据处理而言是计算不可行的.对于一些基于图神经网络的聚类算法[21], 由于需要计算每对数据点之间的距离及断开阈值, 计算复杂度也较高, 同时算法一般需要监督信息, 较适用于半监督场景[22].一些基于密度的聚类算法可直接进行聚类而无需输入簇数或初始中心作为参数[23, 24], 但往往受较高计算复杂度或空间复杂度限制, 难以在大规模或高维数据集上应用.

I-nice(Identifying the Number of Clusters and Initial Cluster Centres)[25]是一种基于观测点投影机制和混合伽马模型数据子集划分的无参聚类算法, 可有效估计数据集的簇数和簇中心点并聚类.I-niceSO(I-nice with a Single Observation)和I-niceMO(I-nice with Multiple Observations)分别为I-nice的两种基本模式, I-niceSO基于单观测点投影.I-niceMO基于多观测点投影形成分治聚类框架, 得出若干候选中心, 集成后得到最终簇数和簇心结果.实验表明I-nice具有比Elbow和Silhouette更优的簇数估计精度, I-niceMO表现最佳.但在面对如下场景时, I-nice的效果与性能明显变差.

1)当数据集的簇之间样本量差异较大时, 混合伽马模型无法对不平衡数据集进行较好地拟合, 导致数据子集划分质量较差, 进而影响候选中心点的选取.

2)当簇数规模较大时, 遍历搜索最佳高斯混合模型(Gaussian Mixture Model, GMM)的过程十分耗时.

3)当簇之间的相对距离差异较大时, 数据集得出的候选中心之间的距离关系更复杂, 无法简单基于候选中心之间的空间距离实现正确集成.

上述场景在实际应用中经常出现, 如何使算法能在不同的数据集上保持稳定的聚类效果及性能, 是一个非常关键的主题.因此, 本文提出基于候选中心融合的多观测点I-nice聚类算法(Multi-obser-vation I-nice Clustering Algorithm Based on Candidate Centers Fusion, I-niceCF), 实现在各种数据集上的簇数和中心点的准确估计.首先沿用I-niceMO多观测点投影机制.然后基于GMM构件进行数据子集划分, 提出粗细粒度结合的搜索策略, 快速划分数据子集.在识别子集候选中心后, 采用基于GMM构件归属向量的融合方法, 对来自多个子集的簇候选中心进行集成, 最终得到数据集的簇数和簇中心点.在合成数据集和真实数据集上进行一系列实验, 结果表明I-niceCF能正确估计各类数据集的簇数和簇中心点, 聚类效果较优.

1 基于候选中心融合的多观测点I-nice聚类算法
1.1 多观测点投影及数据子集划分

本文沿用I-nice, 使用多观测点机制对高维数据集进行投影, 得到对应的距离数组.然后使用GMM拟合距离数组, 实现数据集的划分.

计算数据集的全部N个样本点到某一观测点的距离, 得到对应的距离数组

X=(x1, x2, ···, xn),

定义对应GMM为

p(x|θ)= ∑j=1Mπjg(x|θj),

其中, M为GMM的构件数(或称模型分量数), πj为GMM中第j个构件的权重, g(· )为构件的密度函数, 即高斯函数, θj表示第j个构件高斯函数的均值μj和方差 σj2.通过最大化

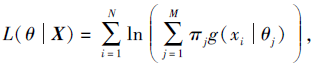
求解GMM参数, 其中

πj= 1N∑i=1Np(Zi=j|xi, θn),

μj= ∑i=1Nxip(Zi=j|xi, θn)∑i=1Np(Zi=j|xi, θn),

σj2= ∑i=1Np(Zi=j|xi, θn)(xi-μj)2∑i=1Np(Zi=j|xi, θn),

Zi=j表示xi属于GMM的第j个构件, θn表示第n次迭代估计的参数.求解参数, 得到拟合后的GMM, 并对数据集进行划分.

通过单观测点得到的GMM进行数据划分, 容易出现不同簇被归为同一子集中的现象.设置多个不同的观测点, 分别基于其到数据集全部样本点的距离数组拟合求解, 得到多个GMM, 每个GMM对数据集进行不同的划分.

1.2 最佳混合模型搜索策略

在进行距离的子集划分前, 最佳混合概率模型的搜索有助于对数据集进行更合理的划分, 不当的数据划分将导致候选中心的质量不佳, 从而影响最终聚类结果.最佳混合模型的搜索除了需要确定1.1节中提到的参数πj, μj, σj2以外, 最关键的是确定GMM中的构件个数.本文使用二阶赤池信息准则(Second-Order Variant of Akaike Information Cri-terion, AICc)[26, 27]评估混合高斯模型的拟合程度.

在I-nice中, 设M∈ [Mmax-Δ 1, Mmax+Δ 2], 逐个遍历求解得到M取不同值时的多个GMM, 选取其中具有最小AICc值的混合模型为最佳模型GMMbest, 构件数为Mbest.Mmax是通过核密度估计(Kernel Density Estimation, KDE)拟合距离数组计算密度函数曲线的波峰个数得到, 当数据集上簇数较多时, KDE估计的Mmax和最佳模型构件个数Mbest之间的偏差也会较大, Δ 1和Δ 2需要足够大才能保证Mbest∈ [Mmax-Δ 1, Mmax+Δ 2], 从而使遍历搜索过程能得到最佳混合模型.具体而言, 遍历搜索最佳模型所需时间与数据集簇数之间存在超线性关系.根据实验, 可设

Mmax=(1-α )Mbest,

误差率α 为实数区间内定值, 对于遍历搜索策略, 需

Δ 1=Δ 2=α Mbest

才能使Mbest落在遍历区间内.对于大小为N的数据集, 每个GMM的求解复杂度[25]为O(NM), 遍历搜索策略需求解2Δ +1个混合模型, 即I-nice的最佳GMM遍历搜索策略的计算复杂度为O(NMbest2).

本文提出粗细粒度结合的最佳GMM模型搜索策略, 具体见算法1.

算法1 粗细粒度结合的最佳GMM搜索策略

输入 数据集Y对应观测点p的距离数组X

输出 近似最佳混合模型GMMbest

阶段1 粗粒度搜索

for m=1; m< N/2; m=2m do

通过EM(Expectation-Maximization)算法求解GMMm(X);

计算AICcm;

if AIC c2-2m≤ AIC c2-3m&

AIC c2-2m≤ AIC c2-1m≤ AICcm then

break

end for

阶段2 细粒度搜索

h=(2-3m-2-1m)/12

for m'=2-3m+h; m'< 2-1m; m'=m'+h do

通过EM算法求解GMMm'(X);

计算AICcm';

if AIC c2-2m'≤ AIC c2-3m'&

AIC c2-2m'≤ AIC c2-1m'≤ AICcm' then

break

end for

GMMbest=GM M2-2m'

按两个阶段进行最佳混合模型的搜索, 第1个阶段进行粗粒度搜索, GMM构件数以底数为2的幂快速增长, 粗粒度搜索的第i步求解GMM的构件数为2i, 搜索可确定Mbest的近似区间.第2阶段在近似区间内进行一定步长的细粒度搜索.在2个搜索阶段中, 均以AICc的“ 山谷” 趋势作为搜索的结束特征.“ 山谷” 趋势定义为AICc下降一次, 然后连续增加两次的阶段, 即

AICci≤ AICci-1, AICci≤ AICci+1≤ AICci+2.

粗粒度搜索阶段需进行Mbest次求解, 该阶段总复杂度为

$N \sum_{i=1}^{\left\lceil\log _{2} M_{\text {best }}+1\right\rceil} 2^{i}=N\left(2^{\left\lceil\log _{2} M_{\text {best }}\right\rceil+2}-2\right)$;

细粒度搜索阶段在$\left(2^{\left\lfloor\log _{2} M_{\text {best }}\right\rfloor}, 2^{\left\lceil\log _{2} M_{\text {best }}\right\rceil}\right)$区间进行, 设搜索步长为区间长度的1/12, 则细粒度搜索阶段复杂度为

$\frac{11}{2} N\left(2^{\left\lfloor\log _{2} M_{\text {best }}\right\rfloor}+2^{\left\lceil\log _{2} M_{\text {best }}\right\rceil}\right) .$

综上所述, 该搜索策略总计算复杂度为O(NMbest), 搜索所需时间随簇数呈线性增加趋势, 以线性效率高效搜索求解近似最佳混合模型, 显著优于I-nice的遍历搜索策略, 便于I-niceCF在大规模数据集上的应用.

1.3 基于GMM构件向量相异度的候选中心融合

本文提出基于候选中心融合的多观测点I-nice聚类算法(I-niceCF), 准确集成来自多个观测点的候选中心.

经过多观测点投影及最佳GMM进行距离子集划分后, 将分别针对各个子集内距离值对应的原始样本点执行聚类任务.每个子集任务内可通过k近邻法确定高密度区域, 进一步选取k近邻最大的数据点作为候选中心; 或采用密度峰值聚类算法(Density Peak Clustering, DPC)[24]进行聚类, 得出高密度点作为候选中心.每个子集均得到若干候选中心, 最终需进行集成任务, 即集成来自全部观测点对应的最佳GMM的各个构件所得的候选中心.

I-nice通过基于候选中心距离度量的方法进行候选中心集成, 即通过候选中心之间的空间距离度量候选中心之间的冗余度, 距离越小表示冗余度越高, 更应将其合并以消除簇心冗余.

I-nice的缺点是只考虑候选中心的相对距离, 忽略数据集的原始分布情况.在簇间距离较均匀时, 已验证是有效的, 但当簇间距离差异较大时, 容易出现错误合并或漏合并候选中心的情况, 使得到的集成结果较差, 直接导致整个算法得出错误的簇数和簇中心.

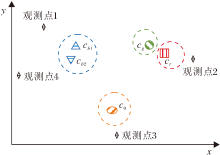
图1为在包含4个簇的数据集上得出的5个候选中心, 虚线区域为对应各簇样本点的分布情况, 5个填充点为待集成的候选中心, cb1、cb2归属于同个真实簇Gb, 3个候选中心co、cg、cr分别归属于3个真实簇Go、Gg、Gr.候选中心cg、cr之间的距离小于候选中心cb1、cb2之间的距离, 因此基于候选中心相对距离的集成方式无法同时保证合并cb1、cb2且保留cg、cr.按照I-niceMO, 基于候选中心的相对距离进行集成, 会出现两种错误.第1种为过度合并, cb1、cb2合并, cg、cr合并, co保留, 虽然成功消除真实簇Gb的候选中心冗余, 但也错误合并来自不同簇的cg、cr候选中心, 最终得出簇数为3的错误结果.第2种为合并不充分, 所设候选中心合并的距离阈值过小, 图1中5个候选中心全部保留, 导致最终得出簇数为5的错误结果.

图1 待集成的候选中心Fig.1 Candidate centers to be integrated

I-niceMO这类集成方法仅考虑候选中心之间的相对距离, 忽视数据集中各簇整体的分布情况, 在簇间距离差异较大时, 集成操作容易出现错误, 因此有必要提出更合理的候选中心集成方法.

本文提出I-niceCF, 可准确度量候选中心之间的冗余度.对于每个候选中心ci, 有构件向量Ψi=[ζ 1, ζ 2, ···, ζ P], 记录其分别在P个观测点的混合模型中对应的构件索引ζ .并结合曼哈顿距离和切比雪夫距离设计闵可夫斯基距离对:

$D_{M C}(X, Y)=\left\langle\sum_{i=1}^{P}\left|x_{i}-y_{i}\right|, \left(\sum_{i=1}^{P}\left|x_{i}-y_{i}\right|^{\infty}\right)^{\frac{1}{\infty}}\right\rangle$, (1)

度量不同候选中心构件向量之间的相异度, 相异度越小表明冗余度越高.简而言之, DMC的取值越小表明更多观测点将该两个候选中心划分为相同的子集或相邻的子集, 这意味着它们在原始高维空间更趋向属于同一个簇.

相对设定的4个观测点, 图1的5个候选中心可计算对应的构件向量, 过程如图2所示.

图2 4个观测点样本距离值分布和混合模型概率密度曲线Fig.2 Distance distribution and probability density curves of GMMs of samples on 4 observation points

每个观测点基于其到数据集所有点的距离数组, 可解出对应的混合高斯分布, 图2中虚线轮廓的填充区域对应的是图1中各真实簇内样本到观测点的距离数组构成的概率密度分布, 各子图横轴下5个候选中心图标的位置对应它们到观测点的距离值.因为对于某特定观测点, 存在多个真实簇位于同一距离区间, 因此求解的最佳GMM的构件个数常不等于真实簇个数, 会存在多个真实簇(对应距离值)包含在求解GMM的单个构件中, 也会存在单个真实簇的各部分(对应距离值)分别被包含在GMM的不同构件中.

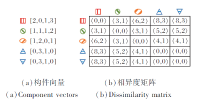对照图2可得出图3(a)的5个候选中心对应的构件向量, 如候选中心cr的构件向量Ψr=[2, 0, 1, 3], 表明cr到观测点1的距离值在对应GM Mbest1中归属于索引为2的高斯构件.类似地, 分别在观测点2~观测点4的混合模型GM Mbest2, GM Mbest3, GM Mbest4中归属于索引为0, 1, 3的构件.

图3 5个候选中心点的混合模型构件向量及相异度矩阵Fig.3 Mixed model component vectors and dissimilarity matrix of 5 candidate centers

图3(b)为基于DMC求解的5个候选中心的相异度矩阵.I-nice错误合并cg和cr, 在此处计算得出

DMC(Ψg, Ψr)=< 3, 1> ,

而候选中心cb1、cb2的相异度

DMC(Ψb1, Ψb2)=< 0, 0> .

显而易见, 2个冗余的候选中心cb1、cb2之间的相异度与其它候选中心之间的相异度差距明显, 可容易设定标准以融合相异度小于一定范围的候选中心点对.具体地, 设定

Tm= P2, Tc=max Ψ2,

其中P为观测点数量.当2个候选中心的相异度DMC同时满足

DMC[0]< Tm, DMC[1]< Tc,

则这2个候选中心应进行融合.

总之, 对于全部候选中心计算相异度矩阵, 矩阵元素满足上述两个条件, 表明对应的两个候选中心存在可融合连接.最终构成以全部候选中心为节点、以可融合连接为边的无向图, 计算其连通分量, 得出最终的簇数和簇心.基于GMM构件向量的候选中心融合方法步骤详见算法2.

算法2 基于GMM构件向量的候选中心融合方法

输入 候选中心c1, c2, ···, cm, 观测点O1, O2, ···, OP,

最佳模型GMM1(M1, π1, θ1), ···,

GMMP(MP, πP, θP)

输出 融合中心c'1, c'2, ···

step 1 对于c1, c2, ···, cm, 求各自对应的构件向量

Ψi=[ ζ1i, ζ2i, ···, ζPi], 1≤ i≤ m,

其中

ζvi=arg max0≤k< Mv( πkvg( civ| θkv)), 1≤ v≤ P,

Mv表示GMMv的构件个数, πkv、 θkv分别表示GMMv第k个构件的权重和高斯函数参数, civ表示候选中心ci相对观测点Ov的距离.

step 2 基于式(1)计算相异度矩阵

Φ =[DMC(Ψi, Ψj)]m× m, 1≤ i≤ m, 1≤ j≤ m.

step 3 Tm= P2, Tc= 12max(Ψ).

step 4 计算矩阵

[boolean(ϕ ij< < Tm, Tc> )]m× m,

并生成对应无向图G.

step 5 求解得到连通分量CC1, CC2, ···

step 6 计算每个连通分量所含候选中心样本点的均值, 得到融合后的中心c'1, c'2, ···

在全部观测点对应GMM的各个构件的候选中心集成之后, 将得到最终的簇数和融合后的候选中心称为初始中心点.将簇数及初始中心点作为先验参数传给K-means算法, 得到数据集的聚类结果.

1.4 本文算法流程及复杂度分析

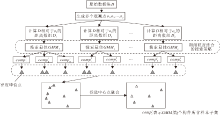
I-niceCF流程如图4所示.

图4 I-niceCF流程图Fig.4 Flowchart of I-niceCF

设数据集D的样本数为N, 特征数为D', 真实簇数为K, 观测点数量为P.按照算法流程分步分析其时间复杂度.

1)计算P个观测点到数据集D的全部样本点距离的时间复杂度为O(PND').

2)对于P组距离数组, 分别进行近似最佳GMM搜索, 设Mbest为距离数组对应的最佳GMM构件数量, 1.2节中已推导得出搜索过程时间复杂度为O(NMbest), 则该步骤总时间复杂度为O(PNMbest).

3)对P个最佳GMM的每个构件包含样本进行候选中心点的选择, 具体采用DPC选取密度峰值点作为候选中心点.对于样本为n的数据集, 若直接计算距离矩阵, 时间复杂度为O(n2), 通过R* -Tree[28]可快速计算与邻近点的距离, DPC时间复杂度为O(n log2n).每个构件平均包含样本数为N/Mbest, 则该步骤总时间复杂度为

$O\left(P M_{\text {best }}\left(\frac{N}{M_{\text {best }}}\right) \log _{2}\left(\frac{N}{M_{\text {best }}}\right)\right) \text {, }$

即

$O\left(P N \log _{2}\left(\frac{N}{M_{b e s t}}\right)\right) .$

4)候选中心点个数为β K, β ∈ [1, P], 计算全部候选中心点的构件分量的时间复杂度为O(β KP), 计算相异度矩阵, 得出对应融合无向图的时间复杂度为O(β 2K2), 求解对应连通分量的时间复杂度为O(β K), 则总时间复杂度为O(P2K2).

5)融合后的初始中心点作为输入参数进行K-means聚类, 时间复杂度为O(KD'N).

I-niceCF所需观测点数量P最多为D'+1, 且Mbest∈ [1, K].综合上述步骤, I-niceCF的平均时间复杂度为O(N log2N), 最差时间复杂度为O(N2).相比其它不需输入簇数作为先验参数的传统聚类算法, 时间复杂度与DBSCAN(Density Based Spatial Clustering of Applications with Noise)[23]、点排序识别聚类结构的聚类算法[29]、基于分布的大型空间数据库聚类算法[30]相同, 具有较优的计算效率.该算法时间复杂度显著优于围绕中心划分的聚类算法[31]的O(N2K3)及谱聚类的O(N2K), 差于K-means算法和BIRCH(Balanced Iterative Reducing and Clustering Using Hierarchies)[32]等需簇数作为参数的算法的时间复杂度, 其中K-means算法时间复杂度为O(tKN), t表示K-means算法的迭代次数, BIRCH的时间复杂度为O(N).

2 实验及结果分析
2.1 实验设置

本文实验在真实场景数据集和合成数据集上进行.真实数据集来自加州大学欧文分校机器学习库(http://archive.ics.uci.edu/ml)及开源手写字体库[33], 实验前均剔除时间戳字段并进行归一化, 具有多标签的数据集只选用单个字段作为标签, Anuran数据集使用Species作为标签字段.合成数据集采用多个高斯分布生成.真实数据集与合成数据集的具体信息分别见表1和表2.

表1 真实数据集信息 Table 1 Information of real-world datasets
表2 合成数据集信息 Table 2 Information of synthetic datasets

本文选择如下2个指标进行聚类结果的评价:调整兰德系数(Adjusted Rand Index, ARI)[34]和标准化互信息(Normalized Mutual Information, NMI)[35].

ARI计算公式如下:

$A R I=\frac{\sum_{i j}\left(0.5 n_{i j}\right)-\frac{2}{N} \sum_{i}\left(0.5 n_{i}\right) \sum_{j}\left(0.5 n_{j}\right)}{\frac{1}{2}\left[\sum_{i}\left(0.5 n_{i}\right)+\sum_{j}\left(0.5 n_{j}\right)\right]-\frac{2}{N} \sum_{i}\left(0.5 n_{i}\right) \sum_{j}\left(0.5 n_{j}\right)} .$

设C={C1, C2, ···, Cr}表示N个样本到r个簇的一个划分, Y={Y1, Y2, ···, Ys}表示N个样本到s个类的一个划分.nij=|Ci∩ Yj|, 表示2个划分中同时位于簇Ci和类Yj的样本个数, ni表示簇Ci的总样本个数, nj表示类Yj的总样本个数.NMI计算公式如下:

NMI(Y, C)= 2I(Y; C)H(Y)+H(C),

其中, C表示簇标签, Y表示类标签, H(· )表示熵, I(Y; C)表示其互信息.

ARI和NMI的指标值越大, 表示聚类结果越优.

实验主机处理器信息为Intel Core i7-10700 CPU@2.90 GHz×16, 内存容量为15.4 GB, 操作系统为ubuntu 16.04LTS 64-bit.实验涉及程序均运行于Python 3.5.实验进行时对I-niceMO和I-niceCF共有的参数赋予相同值, 若无特别说明, 观测点数量均设为5, 过滤系数设为(1, 0.1).此外两种算法分治环节的各构件(或子集)内的聚类任务均采用DPC.

2.2 合理性验证

本节评估I-niceCF的簇数估计效果, 与Elbow[11]、Silhouette[12]、Gap统计量[13]、Jump me-thod[15]、I-niceMO[25]进行对比.在5个真实数据集和5个合成数据集上进行实验, 结果如表3所示.

表3 各算法在不同数据集上的簇数估计效果对比 Table 3 Comparison of cluster number estimation results of different algorithms on different datasets

由表3可知, I-niceCF簇数估计效果明显优于包括I-niceMO在内的其它算法.当数据集簇数低于10时, Elbow和Silhouette存在约1~2的估计误差.数据集簇数超过10时, Elbow开始失效, 估计结果偏差很大或曲线无“ 肘部” 特征, Silhouette估计结果误差也逐渐增大.当数据集簇数达到1 000时, 估计误差已达到202, 而Gap统计量在数据集簇数超过10时已失效, 曲线呈上涨趋势.Jump method在5个簇数较大的合成数据集上的估计效果显著优于Elbow、Silhouette和Gap统计量, 但在5个真实数据集上表现不佳.I-niceMO受维度较高和数据集不平衡的困扰, 在真实数据集上存在个别误差, 在合成数据集上明显优于Elbow和Silhouette, 但在簇数达到1 000时, I-niceMO无法在合理时间内得出结果.I-niceCF几乎准确估计全部数据集的簇数, 仅在面对具有1 000个簇的SID5数据集时, 存在簇数估计偏差为3, I-niceCF估计出997个簇, 此时其余算法除Jump method之外均已无法发挥作用, 由此验证I-niceCF的簇数估计效果.

2.3 可行性验证

本节测试I-niceCF在不同数据集上的表现, 验证本文针对I-nice候选中心融合方法的改进对I-niceMO的提升, 以及验证I-niceCF在多种场景下的可行性.

考虑数据集的5个因素, 分别为数据集的簇数K、单簇样本量CN、数据集的维度D、簇心距离差异程度σncd、数据集平衡度S.其中簇心距离差异程度和数据集平衡度是评估的重点, 此处分别定义2个指标如下:

$\sigma_{n c d}=\operatorname{std}\left(d\left(c_{i}, c_{n e a r e s t(i)}\right)_{i=1}^{K}\right)$,

$S=-\sum_{k=1}^{K} \pi_{k} \log _{2} \pi_{k}$,

σncd计算每个簇的簇心ci与对应最近簇心cnearest(i)的距离di, 求得d1, d2, ···, dK的标准差为σncd.簇数相同时, σncd越大表示对应数据集的各簇心之间距离差异越大.S表示数据集的平衡程度, 计算每个簇包含样本数占数据集样本总数的比例π1, π2, ···, πK, 计算得出对应的熵, 以此度量数据集平衡程度.簇数相同时, S越小表示数据集越不平衡, 即不同簇所含样本数差异越大.

图5和图6分别表示σncd和S取不同值时数据集情况.

图5 σncd不同时数据集的簇中心点图Fig.5 Cluster centers of datasets with different σncd

图6 S不同时数据集情况Fig.6 Datasets with different S

基于这5个因素, 每组分别生成4个合成数据集, 5组共20个数据集, 详见表4.

表4 I-niceMO和I-niceCF在20个合成数据集上的簇数估计结果对比 Table 4 Comparison of cluster number estimation results of I-niceMO and I-niceCF on 20 synthetic datasets

因素K生成的4个数据集簇数分别为5, 15, 25, 50, 每个数据集内各簇样本数相同, 单簇样本数均为100, 数据维度(即特征数)均为2.因素CN生成的数据集均为2维5簇, 单簇样本从100逐步增至2 000, 每个数据集内各簇大小相同.因素D生成的4个数据集维度逐步增加.因素σncd生成的4个数据集对应σncd分别为2.786, 19.06, 78.03, 142.9.因素S生成的4个数据集的平衡度依次减少, 分别为2.322, 1.914, 1.635, 1.213.

在20个合成数据集上使用I-niceMO和I-niceCF进行簇数估计, 结果如表4所示.由表可知, 在5组数据中, 单簇样本量CN、维度D的变动对于I-niceMO和I-niceCF性能无影响, 10个数据集均能准确估计簇数.

簇数K增加至50时, I-niceMO性能出现一定波动, 估计簇数为44, 与真实簇数相差为6, I-niceCF估计簇数为51.在σncd影响下, 尽管Std3、Std4数据集上真实簇数仅为5, 但I-niceMO错误估计簇数为6和9, 这是因为σncd(Std3)=78.03, σncd(Std4)=142.9, 簇心距离差异较大, 导致存在冗余的候选中心未被合并.

图7为I-niceCF对Std1~Std4数据集的候选中心融合情况, I-niceCF准确合并属于同个真实簇的候选中心.

图7 I-niceCF在4个数据集上的候选中心融合情况Fig.7 Candidate center fusion for I-niceCF on 4 datasets

如图7(d)所示, I-niceCF在簇间距离差异很大时仍保持候选中心的正确融合, 准确估计σncd生成的4个数据集的簇数, 验证针对候选中心的融合方法的有效性.在S影响下, I-niceMO伴随着数据集平衡度的减小, 性能出现下降, 在数据集簇数仅为5时, 分别做出簇数为8和11的错误估计, 而I-niceCF对于S1~S4数据集均做出正确簇数估计.相比I-niceMO, I-niceCF在全部5个因素的20个数据集上始终保持稳定准确的簇数估计效果, 验证I-niceCF在面对多种类型数据集时的稳定性能.

2.4 有效性验证

本节通过计算ARI、NMI值, 评估I-niceCF的聚类结果, 并对比其它聚类算法, 包括1)同类型的I-niceMO[25], 2)无需簇数作为先验参数的DBSCAN[23]和DPC[24], 3)需要预先输入正确簇数作为参数的FCM(Fuzzy C-mean)[36, 37]和K-means算法[1].

在实验过程中, I-niceMO和I-niceCF的设置将遵照2.1节实验设置, 另外将真实簇数作为先验参数赋予FCM和K-means.K-means算法重复10次实验, 每次均随机生成对应数量的初始中心点, 取10次结果的ARI和NMI值的平均值作为K-means算法的最终结果.DBSCAN和DPC将以不同参数多次运行, 取得最佳结果的一次用于对比, 即

maxi(min(ARIi, NMIi)).

具体地, DBSCAN的参数minPts在1至50内多次选择, 参数eps在dn至50dn的范围内[38]多次选择, 其中dn表示数据集每个样本点到对应的最近样本点的平均距离.

各算法聚类实验的ARI和NMI值如表5所示, 表中黑体数字表示最优值.除了在USP40、WDBC数据集上I-niceCF的精度与输入正确簇数的FCM和K-means的精度持平, 在其余数据集上I-niceCF精度均优于FCM和K-means.I-niceCF在全部数据集上都得到最高的ARI、NMI值, 优于包含I-niceMO在内的其它对比算法, 由此验证I-niceCF的有效性.

表5 各算法的聚类结果对比 Table 5 Comparison of clustering results by different algorithms
2.5 参数敏感性评估

本节考察I-niceCF的参数敏感性, I-niceCF的主要参数为观测点数量P及过滤系数(fkde, fdpc).fkde表示在对各构件所含样本进行高密度点(候选中心)选择前, 对构件内样本的过滤比例.具体是通过KDE拟合构件对应的距离数组得到对应的密度值, 保留较高密度值对应的距离值, 保留比例为fkde.该设置主要是在大规模数据上可通过过滤一定比例的低密度点, 减少后续进行高密度点寻找的代价.本文的实验环节均设置fkde=1.0, 即全部保留.fdpc的取值则影响使用DPC对每个GMM构件对应样本进行高密度点识别时的截断距离dc, 具体为

dc=disasc[ddpc· Len(disasc)],

其中disasc为升序排序的样本点间距离数组.DPC对应于dc取值的鲁棒性已得到说明[39], 因此, 本文重点考察I-niceCF关于参数观测点数量P的敏感性.

对于D维空间中的2个不同样本点a、b, 必有多个观测点o1, o2, ···, oD+1, 满足

[ d1a, d2a, ···, dD+1a]≠ [ d1b, d2b, ···, dD+1b],

其中 dia, dib分别表示样本点a、b到观测点oi的距离.另一方面, 由于聚类任务不仅需要考察单个样本点之间的距离, 还需要兼顾数据空间中各个团簇的分布情况, 因此要达到聚类效果还需增加观测点数量.但上述分析是理论临界情况, I-nice在生成多个观测点时会确保相互之间的距离, 且观测点位置均选择在数据集样本点分布空间的外缘, 以此显著降低观测点之间的冗余度.因此在聚类时, I-niceCF并无必要设置D+1个观测点以保证算法在高维数据集上的计算效率.

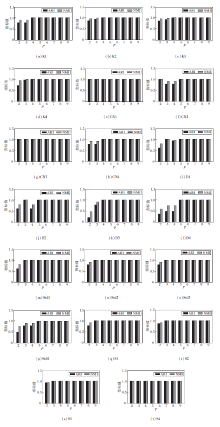
在20个不同数据集(数据集详情见表4)上测试I-niceCF在不同观测点数量时的聚类效果, ARI、NMI值如图8所示.在(a)~(d)子图中, 当P=2时, I-niceCF在4个数据集上均未取得正确结果, 随着观测点的增加, I-niceCF的聚类性能变优, P=4时已全部正确聚类.(e)~(h)、(q)~(t)子图中的聚类表现类似, 都能在P≤ 5时实现正确聚类.在(i)~(p)子图中, D、σncd生成的8个数据集的ARI、NMI值上涨趋势慢于其余12个数据集, 尤其是在(k)~(l)子图中, 它们对应的D3、D4数据集的特征数(维度)分别达到50和500, 但最终也都在P≤ 5时实现正确聚类.由图8可知, 较少的观测点数量P即可实现在不同数据集上的准确聚类任务, 包括高维数据集.

图8 I-niceCF参数敏感性测试结果Fig.8 Results of parameter sensitivity analysis for I-niceCF

2.6 算法效率评估

本节测试I-niceCF和I-niceMO在不同规模数据集上的运行时间, 结果如图9所示.

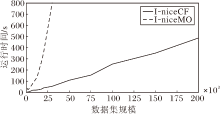图9 I-niceCF和I-niceMO在不同规模数据集上的运行时间对比Fig.9 Running time comparison of I-niceCF and I-niceMO on datasets of different scales

I-niceCF平均时间复杂度为O(N log2N), 而I-niceMO的时间复杂度为O(N2), 运行时间增长趋势显著快于I-niceCF.此外数据规模大于30 000时, I-niceMO的运行时间和内存占用非常大.I-niceMO的最佳GMM遍历搜索策略不适应于较大规模的数据, 计算复杂度与数据集上真实簇数的平方成正比.I-niceCF的粗细粒度结合的搜索策略大幅降低算法的运行时间.

上述为单机情况下算法的效率评估, 此外, I-niceCF的计算流程(见图4)使其在当下分布式平台上更容易部署且更高效.

3 结束语

本文提出基于候选中心融合的多观测点聚类算法(I-niceCF), 改进I-niceMO的聚类效果.I-niceMO在数据集内簇大小不平衡或簇心距离差异过大时聚类性能出现波动.为了解决这些问题, 本文提出粗细粒度结合的混合模型搜索策略, 使I-niceCF可快速求解最佳混合高斯模型, 并进行子集划分, 提升I-niceCF在不平衡数据集上的拟合精度和效率.基于GMM构件向量, 提出候选中心融合方法, 进行I-nice候选中心之间的相异度度量与集成.

在真实数据集和合成数据集上评估I-niceCF的簇数估计效果, 并基于5个因素(簇数、单簇样本量、维度、数据集平衡度和簇心距离差异程度)验证I-niceCF在不同数据集上的合理性, 克服I-niceMO的缺点.此外, 进行聚类精度对比实验, 结果表明I-niceCF的聚类效果较优.I-nice多观测点投影机制适合在分布式环境下工作, 结合候选中心融合方法, 今后将探究如何将该方式应用于其它聚类算法的分布式部署和集成.

参考文献
[1] MACQUEEN J. Some Methods for Classification and Analysis of Multivariate Observations // Proc of the 5th Berkeley Symposium on Mathematical Statistics and Probability. Berkeley, USA: University of California, 1967: 281-297. [本文引用:2]
[2] NG A Y, JORDAN M I, WEISS Y. On Spectral Clustering: Analysis and an Algorithm // DIETTERICH T G, BECKER S, GHAHRAMANI Z, eds. Advances in Neural Information Processing Systems 14. Cambridge, USA: The MIT Press, 2002: 849-856. [本文引用:1]
[3] MAITRA R. Initializing Partition-Optimization Algorithms. IEEE/ACM Transactions on Computational Biology and Bioinformatics, 2009, 6(1): 144-157. [本文引用:2]
[4] HU Q B, XIE S H, LIN S Y, et al. Clustering Embedded Approaches for Efficient Information Network Inference. Data Science and Engineering, 2016, 1: 29-40. [本文引用:1]
[5] RAY S, TURI R H. Determination of Number of Clusters in k-means Clustering and Application in Colour Image Segmentation // Proc of the 4th International Conference on Advances in Pattern Re-cognition and Digital Techniques. Berlin, Germany: Springer, 1999: 137-143. [本文引用:1]
[6] DE AMORIM R C, HENNIG C. Recovering the Number of Clusters in Data Sets with Noise Features Using Feature Rescaling Factors. Information Sciences, 2015, 324: 126-145. [本文引用:1]
[7] HENNIG C, LIAO T F. How to Find an Appropriate Clustering for Mixed-Type Variables with Application to Socio-Economic Stratification. Journal of the Royal Statistical Society(Applied Statistics), 2013, 62(3): 309-369. [本文引用:1]
[8] FORGEY E. Cluster Analysis of Multivariate Data: Efficiency vs. Interpretability of Classification. Biometrics, 1965, 21(3): 768-769. [本文引用:1]
[9] MILLER J W, HARRISON M T. Mixture Models with a Prior on the Number of Components. Journal of the American Statistical Association, 2018, 113(521): 340-356. [本文引用:1]
[10] AYED F, CARON F. Nonnegative Bayesian Nonparametric Factor Models with Completely Rand om Measures for Community Detection. Statistics and Computing, 2019, 31(5). DOI: 10.1007/s11222-021-10037-3. [本文引用:1]
[11] THORNDIKE R L. Who Belongs in the Family? Psychometrika, 1953, 18(4): 267-276. [本文引用:2]
[12] ROUSSEEUW P J. Silhouettes: A Graphical Aid to the Interpretation and Validation of Cluster Analysis. Journal of Computational and Applied Mathematics, 1987, 20: 53-65. [本文引用:2]
[13] TIBSHIRANI R, WALTHER G, HASTIE T. Estimating the Number of Clusters in a Data Set via the Gap Statistic. Journal of the Royal Statistical Society(Statistical Methodology), 2001, 63(2): 411-423. [本文引用:2]
[14] DUDOIT S, FRIDLYAND J. A Prediction-Based Resampling Me-thod for Estimating the Number of Clusters in a Dataset. Genome Biology, 2002, 3(7). DOI: 10.1186/gb-2002-3-7-research0036. [本文引用:1]
[15] SUGAR C A, JAMES G M. Finding the Number of Clusters in a Dataset: An Information-Theoretic Approach. Journal of the American Statistical Association, 2003, 98(463): 750-763. [本文引用:3]
[16] MOHAJER M, ENGLMEIER K H, SCHMID V J. A Comparison of Gap Statistic Definitions with and without Logarithm Function[C/OL]. [2021-09-26]. https://arxiv.org/pdf/1103.4767v1.pdf. [本文引用:1]
[17] YANG M S, WU K L. A Modified Mountain Clustering Algorithm. Pattern Analysis and Applications, 2005, 8(1): 125-138. [本文引用:1]
[18] SHARMA K K, SEAL A. Multi-view Spectral Clustering for Uncertain Objects. Information Sciences, 2021, 547: 723-745. [本文引用:1]
[19] MA Z Z, LAI Y P, XIE J Y, et al. Dirichlet Process Mixture of Generalized Inverted Dirichlet Distributions for Positive Vector Data with Extended Variational Inference. IEEE Transactions on Neural Networks and Learning Systems, 2021. DOI: 10.1109/TNNLS.2021.3072209. [本文引用:1]
[20] DINARI O, YU A, FREIFELD O, et al. Distributed MCMC Infe-rence in Dirichlet Process Mixture Models Using Julia // Proc of the 19th IEEE/ACM International Symposium on Cluster, Cloud and Grid Computing. Washington, USA: IEEE, 2019: 518-525. [本文引用:1]
[21] WANG C, PAN S R, HU R Q, et al. Attributed Graph Clus-tering: A Deep Attentional Embedding Approach // Proc of the 28th International Joint Conference on Artificial Intelligence. San Francisco, USA: IJCAI, 2019: 3670-3676. [本文引用:1]
[22] ZHU X J. Semi-Supervised Learning Literature Survey. Technical Report, 1530. Madison, USA: University of Wisconsin-Madison, 2005. [本文引用:1]
[23] ESTER M, KRIEGEL H P, SANDER J, et al. A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise // Proc of the 2nd International Conference on Knowledge Discovery and Data Mining. New York, USA: ACM, 1996: 226-231. [本文引用:3]
[24] RODRIGUEZ A, LAIO A. Clustering by Fast Search and Find of Density Peaks. Science, 2014, 344(6191): 1492-1496. [本文引用:3]
[25] MASUD M A, HUANG J Z, WEI C H, et al. I-nice: A New Approach for Identifying the Number of Clusters and Initial Cluster Centres. Information Sciences, 2018, 466: 129-151. [本文引用:4]
[26] HURVICH C M, TSAI C L. Regression and Time Series Model Selection in Small Samples. Biometrika, 1989, 76(2): 297-307. [本文引用:1]
[27] SUGIURA N. Further Analysts of the Data by Akaike's Information Criterion and the Finite Corrections: Further Analysts of the Data by Akaike's. Communications in Statistics-Theory and Methods, 1978, 7(1): 13-26. [本文引用:1]
[28] BECKMANN N, KRIEGEL H P, SCHNEIDER R, et al. The R*-Tree: An Efficient and Robust Access Method for Points and Rectangles. ACM SIGMOD Record, 1990, 19(2): 322-331. [本文引用:1]
[29] ANKERST M, BREUNIG M M, KRIEGEL H P, et al. OPTICS: Ordering Points to Identify the Clustering Structure. ACM Sigmod Record, 1999, 28(2): 49-60. [本文引用:1]
[30] XU X W, ESTER M, KRIEGEL H P, et al. A Distribution-Based Clustering Algorithm for Mining in Large Spatial Databases // Proc of the 14th International Conference on Data Engineering. Wa-shington, USA: IEEE, 1998: 324-331. [本文引用:1]
[31] KAUFMAN L, ROUSSEEUW P J. Finding Groups in Data: An Introduction to Cluster Analysis. New York, USA: John Wiley & Sons, 2009. [本文引用:1]
[32] ZHANG T, RAMAKRISHNAN R, LIVNY M. BIRCH: An Efficient Data Clustering Method for Very Large Databases. ACM Sigmod Record, 1996, 25(2): 103-114. [本文引用:1]
[33] HULL J J. A Database for Hand written Text Recognition Research. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1994, 16(5): 550-554. [本文引用:1]
[34] HUBERT L, ARABIE P. Comparing Partitions. Journal of Classification, 1985, 2(1): 193-218. [本文引用:1]
[35] VINH N X, EPPS J, BAILEY J. Information Theoretic Measures for Clusterings Comparison: Variants, Properties, Normalization and Correction for Chance. Journal of Machine Learning Research, 2010, 11: 2837-2854. [本文引用:1]
[36] DUNN J C. A Graph Theoretic Analysis of Pattern Classification via Tamura's Fuzzy Relation. IEEE Transactions on Systems, Man, and Cybernetics, 1974, 4(3): 310-313. [本文引用:1]
[37] BEZDEK J C. Objective Function Clustering // BEZDEK J C, ed. Pattern Recognition with Fuzzy Objective Function Algorithms. Berlin, Germany: Springer, 1981: 43-93. [本文引用:1]
[38] WANG S L, LI Q, ZHAO C F, et al. Extreme Clustering-A Clustering Method via Density Extreme Points. Information Sciences, 2021, 542: 24-39. [本文引用:1]
[39] HE Y L, WU Y Y, QIN H L, et al. Improved I-nice Clustering Algorithm Based on Density Peaks Mechanism. Information Sciences, 2021, 548: 177-190. [本文引用:1]