姚宏亮,博士,副教授,主要研究方向为机器学习、数据挖掘.E-mail:dmicyhl@163.com.
作者简介:

贾虹宇,硕士研究生,主要研究方向为机器学习、数据挖掘.E-mail:1551688132@qq.com.

杨 静,博士,副教授,主要研究方向为人工智能、数据挖掘.E-mail:jsjyj0801@163.com.

俞 奎,博士,教授,主要研究方向为机器学习、因果发现.E-mail:yukui@hfut.edu.cn.
当前研究者主要通过对历史交易数据的学习生成预测模型,由于影响市场的因素动态可变,因此训练好的模型在实际应用中预测效果远不及预期.针对现有预测模型适应力较弱的问题,文中提出基于分层动态贝叶斯网络的股市趋势扰动推理算法,对股市趋势进行实时预测.首先,针对稳定性较高的均线数据,通过马尔可夫毯对均线特征进行融合,提取为均线能量,得到均线的量化特征.由于多根均线之间存在结构关系,这种结构关系具有较强的抗噪能力和稳定性,因此利用分层动态贝叶斯网络对单根均线内部结构和多均线之间结构关系进行建模.然后,对顶层网络中多结点状态进行扰动,通过动态灵敏性分析实时计算结点状态变化对于股市趋势影响力.最后,基于灵敏分析的结果,利用联合树对股市趋势进行动态推理.在实际数据上的实验证明文中算法的有效性.
YAO Hongliang, Ph.D., associate professor. His research interests include machine learning and data mining.
About Author:
JIA Hongyu, master student. His research interests include machine learning and data mining.
YANG Jing, Ph.D., associate professor. Her research interests include artificial intelligence and data mining.
YU Kui, Ph.D., professor. His research interests include machine learning and causal discovery.
The current research mainly focuses on the forecasting models generated by the learning of historical transaction data. Due to the dynamic variation of the factors affecting the market, the forecasting effect of the trained model in practical applications is much worse than the expected. To solve the problem of weak adaptability of the existing forecasting models, a disturbance inference algorithm based on hierarchical dynamic Bayesian network(DA-NEC) is proposed to predict stock market trends in real time. Firstly, for the moving average data with high stability, the energy of the moving average is extracted through the Markov blanket fusion of the moving average features, and the quantitative characteristics of the moving average are generated. Since the structural relationship among multiple moving averages possesses strong anti-noise ability and stability, the hierarchical dynamic Bayesian network is employed to model the internal structure of a single moving average and the structural relationship among multiple moving averages. Then, the state of multiple nodes in the top-level network is disturbed, and the state changes of the nodes are calculated in real time through dynamic sensitivity analysis. In the end, based on the results of sensitive analysis, the junction tree is applied for dynamic inference on the stock market trend. Experimental results on actual data show the effectiveness of the proposed algorithm.
本文责任编委 高 阳
Recommended by Associate Editor GAO Yang
股票市场是一个复杂的非线性动态系统, 受政治、经济和交易者等众多因素的影响.股市历史数据量较大、非平稳、高噪声[1], 导致直接使用历史数据进行模型学习生成的模型适应力较弱, 模型在实际应用中效果不及预期.因此, 从历史信息中选取稳定性较高的数据, 并从中提取与系统趋势变化更密切的特征, 动态分析特征量变化对于趋势的影响, 是研究股市趋势演化的一种基本思路.
股市趋势预测是当前人工智能领域的一个研究热点, 主要研究工作有:将收盘价数据或多个技术指标作为输入训练神经网络[2, 3], 通过数据拟合寻找模型最优解进行趋势预测.Zhao等[4]提取股市特征, 结合时间序列临近时间点的重要性, 提出Time-Weighted Long Short-Term Memory(LSTM) Model, 性能较优.Qin等[5]针对多个技术指标, 使用支持向量机(Support Vector Machine, SVM)训练趋势预测模型, 使用粒子群优化算法(Particle Swarm Optimiza-tion, PSO)优化组合系数, 组合多个模型, 提升预测精度.Chandrika等[6]结合隐马尔可夫模型(Hidden Markov Model, HMM)和ARIMA(Autoregressive Inte-grated Moving Average Model), 考虑股市数据特征之间的因果关系.Wen等[7]通过MDTW(Modified Dy-namic Time Warping)[8]提取数据的模式特征, 并通过卷积神经网络(Convolutional Neural Network, CNN)预测股市趋势.
上述股市趋势预测研究工作主要存在如下问题:1)模型学习选取的数据平稳性较低且高噪声, 导致学习生成的模型适应性较差; 2)在动态系统中, 由于历史数据对于系统趋势的影响, 会受到新因素扰动, 导致学习生成的模型适应性不高; 3)由于股市趋势变化因素的影响力会随时间变化, 导致利用直接历史数据进行趋势预测的精度不高.
移动平均线(Moving Average, MA)[9]表示在不同时间周期上对于收盘价的移动平均、相对交易数据和指标数据, 均线数据稳定性较高、抗噪音能力较强.基础性的交易数据多变且波动较大, 趋势性的指标数据(如MACD(MA Convergence and Diver-gence))容易出现指标背离和钝化的现象, 导致股市趋势表达能力较弱[10].当系统内部结构发生改变时, 从能量交换和能量传递的角度可分析状态变化对系统未来的影响[11].均线的方向、斜率、平滑性等都具有能量特性, 均线能量更能体现股市系统真实状态, 因此可从均线能量出发, 研究均线结构关系.
动态贝叶斯网络(Dynamic Bayesian Networks, DBNs)是结构建模和自动推理的一种有力工具, 广泛应用于多变量系统的时序关系分析.Lewis等[12]构建动态贝叶斯网络, 对大型工程中不同模块及模块与系统之间的关联进行动态分析.Li等[13]利用动态贝叶斯网络模拟各地区的股市, 揭示全球股市市场之间的关联.分层动态贝叶斯网络[14]是动态贝叶斯网络的一种特殊结构, 具有多个层级, 并且各层级之间具有关联关系.研究者们利用分层动态贝叶斯网络对具有多层次的系统进行更深入分析, Chen等[15]将人类运动的全局特征和局部特征进行建模, 分析人类运动过程.Amiri等[16]利用分层动态贝叶斯网络对人类身体各组织特征进行多尺度分析, 研究癌症疾病产生的内因.因此, 可利用分层动态贝叶斯网络, 对股市中的单根均线内部结构和多根均线之间的结构关系进行整体建模.
灵敏性分析(Sensitivity Analysis, SA)在系统的特性分析和异常特征发现方面具有广泛应用, 其通过改变证据和推理传播过程[17], 考察对目标对象产生的影响, 从而对系统参数和结构的重要性进行分析.Mitrophanov等[18]针对HMM, 提出计算动态灵敏性分析方法, 对于每个时间片, 构建关于当前时间片中状态变量灵敏性函数的系数填充矩阵, 当一个时间片内有多个状态变量时, 难以计算系数填充矩阵.Low等[19]利用马尔可夫链蒙特卡洛方法(Markov Chain Monte Carlo, MCMC)分析网络中结点的内在关系.姚宏亮等[20]将动态贝叶斯网络转化成联合树, 在联合树上通过信息传播的推理实现动态灵敏性函数的求解, 给出可处理一般动态网络的单结点灵敏性分析方法.Chai等[21]结合Go-Flow, 评估动态贝叶斯网络中不同结点的影响程度.因此, 在已有研究工作的基础上, 通过对动态网络中多个结点进行动态灵敏性分析, 可更有效地推断系统演化趋势.
影响股市的要素动态多变, 因此, 本文提出基于分层动态贝叶斯网络的股市趋势扰动推理算法.首先, 引入均线能量概念, 从能量角度提取均线数据的内在特征, 提升数据的容噪能力.基于多根均线的结点关系, 给出利用分层动态贝叶斯网络的建模方法.进而, 通过对网络中单结点和多结点的扰点, 发现影响趋势的关键要素.最后, 通过联合树推理预测股市趋势.
均线状态对于股市的走势具有重要影响, 多根均线结构关系对于股市的走势具有更强的影响.相对基本交易数据和技术指标数据, 均线数据的信息量更大, 容噪能力更强.
定义1 均线[9] 均线即股票价格的移动平均线.使用统计分析的方法, 将一定时间周期内的证券价格加以平均, 并连接不同时间点的平均值.
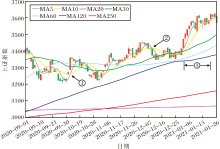
从时间周期由短到长, 将均线分成7根.如图1所示, MA5、MA10、MA20、MA30、MA60、MA120、MA250可依次使用M1, M2, ···, M7表示.7根均线作为股市的基础指标, 包含股市不同周期的价值信息, 反映股市趋势变化的本质, 广泛应用于股市研究工作中.
股市的均线具有方向、斜率、位置关系等多个特征, 这些特征结构关系决定均线趋势和趋势力度, 均线趋势的力度可理解为均线能量.均线趋势主要有三种:上行、横盘和下行.
定义2 均线能量 设均线的特征集合X={X1, X2, ···, Xn}, 集合中要素之间的结构关系决定均线维持当前趋势的能力大小, 称为均线能量(用Y表示), 则有Y=f(X1, X2, ···, Xn), 其中函数f为一种映射关系.
定义3 马尔可夫毯[22] 在一个贝叶斯网络中, 一个结点Xi的马尔可夫毯由Xi的父结点、子结点和子结点的父结点组成, 结点Xi与贝叶斯网中所有非马尔可夫毯结点条件独立.结点Xi的马尔可夫毯使用MB(Xi)表示, 关系式为
P(Xi|MB(Xi))=P(Xi|Z, MB(Xi)),
其中Z为贝叶斯网络中所有非马尔可夫毯结点.
令S表示均线趋势, MB(S)表示均线趋势的马尔可夫毯, 满足Xi∈ MB(S), 利用条件概率P(S|X1, X2, ···, Xn)计算均线能量, 均线能量用Y表示.条件概率P(S|X1, X2, ···, Xn)表示当前均线内部特征组合为X1, X2, ···, Xn时, 均线趋势为S的概率.它结合均线趋势和均线内部特征, 反映均线趋势与均线特征组合之间的关联, 体现均线对自身趋势的维持能力.具体可表示为
$\begin{aligned} Y=& P\left(S=s_{j} \mid X_{1}, X_{2}, \cdots, X_{n}\right)=\\ & \frac{P\left(X_{1}, X_{2}, \cdots, X_{n} \mid S=s_{j}\right) P\left(S=s_{j}\right)}{P\left(X_{1}, X_{2}, \cdots, X_{n}\right)} \end{aligned}$ (1)
其中, 1≤ j≤ 3, s1、s2、s3分别表示均线的上行、横盘和下行三种状态, Y表示sj状态时的均线能量.通过马尔可夫毯融合的均线能量满足0≤ Y≤ 1, 对于不同均线, 根据均线对自身趋势的维持能力将其分为难以维持自身趋势、基本维持自身趋势和较好维持自身趋势3个状态, 分别离散化成-1、0和1这3个值.
多根均线之间的排列关系形成均线结构, 均线之间不同的位置关系对股市价格走势的影响力不同, 在时间上这种位置关系也会不断变化.基本的结构关系如下.
1)均线交叉.两根不同均线存在交叉关系, 时间周期较短的均线自下而上地穿过周期较长的均线, 形成均线金叉关系, 对任两根均线值, Mi> Mj, 其中1≤ i< j≤ 7, 金叉支持股市价格向上运行.均线死叉形成过程与金叉相反, 死叉结构:Mi< Mj, 其中1≤ i< j≤ 7, 死叉支持股市价格向下运行.图1中①箭头所指位置表示两根均线金叉, ②箭头所指位置表示两根均线死叉.
2)均线排列.均线根据周期长短, 从小到大有序排列, 形成多头结构; 否则, 从大到小有序排列, 形成空头结构.如图1中③箭头所指位置为均线多头结构.多头结构表示均线结构支持股市价格的能量较大; 空头结构表示均线结构支持股市价格下行的能量较大.均线多头结构中每根均线值的大小关系描述为M1< M2< M3< M4< M5< M6< M7.
3)均线杂乱结构.不同周期均线之间相互穿插、缠绕, 杂乱无章, 形成杂乱结构.杂乱结构表示均线结构支持股市横盘态势.
均线之间的结构关系在时间上的变化对股市趋势产生重要影响, 因此, 可利用动态贝叶斯网络建模多均线之间的结构关系.
单根均线对于股市价格走势有影响, 多根均线的结构关系对于股市价格走势的影响力更大, 且这种影响关系是动态的.因此, 利用分层动态贝叶斯网络表示均线结构与股市价格趋势之间的作用关系.
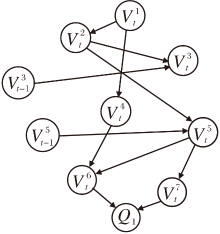
图2表示有t个时间片的分层动态贝叶斯网络.底层网络利用先验知识确定结点顺序并结合K2算法[23]学习网络结构, 每个底层网络对应一根均线.顶层网络中的每个结点对应一个底层网络.
顶层网络的学习分为3步:1)利用最大期望算法(Expectation Maximization, EM)[24]学习初始网络条件概率参数; 2)利用动态规划算法(Dynamic Programming, DP)[25]学习时间片间的转移网络, 利用EM学习条件概率参数; 3)合并1)、2)结果, 生成一个动态贝叶斯网络, 即顶层网络.
每根均线都对应一个底层网络, 不同均线的底层网络结构和内部参数具有一定差异.令
分层动态贝叶斯网络的结构关系可描述如下.
1)底层网络.在t时间片内, 顶层网络结点V
MB(
利用式(1)对结点进行特征融合:
Y=P(
2)顶层网络.在t时间片内, 顶层网络中的观测变量集为{V
P(Qt, Vt)=P(Qt|V0:t)P(Vt|Pa(Vt)).
设顶层的动态贝叶斯网络满足一阶马尔可夫性假设, 有
P(Qt|Q0:(t-1), V0:t)=P(Qt|Qt-1, Vt).
给定状态结点的转移概率分布P(Qt|Qt-1, Vt)和观测变量的概率分布P(Vt|Vt-1), 则t时刻状态变量的先验概率分布为
P(Qt|V0:(t-1))=
利用马尔可夫毯融合不同均线底层网络, 并将融合的均线能量离散化作为顶层网络中结点的取值.当底层网络的信息作为证据添加给顶层网络后, 通过证据分发和证据收集进行信息传播, 预测目标结点.
在顶层动态贝叶斯网络中, 不同结点的状态变化对股市价格趋势的影响程度不同, 动态灵敏性分析可实时度量均线状态变化对于趋势的影响.
动态灵敏性分析是研究非目标结点的扰动对目标结点条件概率产生的影响, 其中灵敏性函数[26]是非目标结点和目标结点之间的条件概率函数.对于已给定的分层动态贝叶斯网络, 参数
θ=P(Vi=vi|Pa(Vi)=pa(Vi)),
vi表示Vi结点的一个取值, pa(Vi)表示Vi结点父结点的某一组取值.
目标结点Qt为股市当前趋势,
P(Qt=qt|E1=e1, E2=e2, ···, ET=et)
表示证据变量E在不同时间片时的取值为e1, e2, ···, et; 变量Qt表示取值为qt的后验概率, 可表示为P(qt|e1, e2, ···, et).目标概率P(qt|e1, e2, ···, et)对于参数θ的灵敏性可用灵敏性函数P(qt|e1, e2, ···, et)(θ)表示[20, 26], 具体描述如下:
P(qt|e1, e2, ···, et)(θ)=
其中, α 、β 、γ 、σ 表示常量, P(qt, e1, e2, ···, et)(θ)表示q和e关于θ联合概率分布, 对于∀ θ, 满足
P(e1, e2, ···, et)(θ)表示e关于θ的先验概率.
定义4 接口[20] 接口是包含一个时间片内所有的向下一个时间片发出弧的结点集合, 时间片t的接口表示为It.
定义5 势[20] 势是一个非负的实函数, 将变量或变量集的概率分布映射到一个与每个实例对应的非负实函数, 表示为ϕ .设C为一个团, 则C的概率势函数可表示为
ϕ C=
设对于∀ Ci, 有
P(V)=
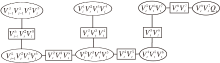
对于任意2个相邻时间片t-1和t的网络, 接口It-1可将这2个时间片进行有向分隔.保留It-1的结点, 再和t时间片的网络结合, 如图3所示, 包含接口It-1={V
通过正规化、三角化等操作, 可生成联合树JTt, 如图4所示, JTt通过接口It-1和接口It进行前向或后向信息传递.构造联合树JTt仅考虑相邻时间片的证据et-1和当前时间片证据et即可, 当顶层网络满足一阶马尔可夫性和齐次性时, 单个结点的灵敏性函数可表示为
P(qt|et-1, et)(θ)=
其中, 目标结点Qt的状态qt仅与t和t-1时间片的非目标结点有关, 且对于∀ θ, 满足0≤ θ≤ 1.
利用定义5对非目标结点所在团进行边缘化操作, 用于求解势函数, 并通过证据分发和证据收集确定该结点的灵敏性函数的具体形式.灵敏性函数表示目标结点条件概率对于非目标结点状态变化的灵敏性, 判别参数变化对目标结点条件概率产生影响的常用方法[17]是对灵敏函数进行求导, 求导结果的绝对值越大, 表明灵敏性越高.结合网络中非目标结点、目标结点和证据结点, 任意单个结点的影响程度可表示为
$\operatorname{IM}\left(V^{i}\right)=\frac{1}{r w} \sum_{p} \sum_{q_{t}, e}\left|\frac{P\left(q_{t} \mid e_{t-1}, e_{t}\right)(\theta)}{\partial \theta}\right|$, (3)
其中, r表示趋势qt的取值个数, w表示e的取值个数, p表示结点Vi中参数的个数, IM(Vi)表示结点Vi能量的影响程度.
在股市的分层动态贝叶斯网络中, 通常多个因素同时对于股市走势产生重要影响, 因而需要对多个结点同时进行扰动分析.
定理1 对分层动态贝叶斯网络中k个结点{V1, V2, ···, Vk}进行扰动分析, {θ1, θ2, ···, θ k}是对应结点表示的参数, {V1, V2, ···, Vk}中任意两个结点不在同一个团中, 则多结点动态灵敏性分析公式可表示为
$P\left(q_{t} \mid e_{t-1}, e_{t}\right)\left(\theta_{1}, \theta_{2}, \cdots, \theta_{k}\right)=\prod_{i=1}^{k}\left(\frac{\alpha_{i} \theta_{i}+\beta_{i}}{\gamma_{i} \theta_{i}+\sigma_{i}}\right)$ .(4)
证明 1)当k=1时, 即分析单个结点Vi.在单个结点情况下, 只存在一个参数θ i, et-1和et表示证据, qt表示目标结点某个状态, 有
$P\left(q_{t} \mid e_{t-1}, e_{t}\right)\left(\theta_{i}\right)=\frac{P\left(q_{t}, e_{t-1}, e_{t}\right)\left(\theta_{i}\right)}{P\left(e_{t-1}, e_{t}\right)\left(\theta_{i}\right)}=\frac{\alpha \theta_{i}+\beta}{\gamma \theta_{i}+\sigma}$
2)当k=2时, 即分析2个结点V1和V2.当V1和V2属于不同的2个团时, 则V1和V2被多个已知结点进行有向分隔, 动态灵敏性分析公式为
$P\left(q_{t} \mid e_{t-1}, e_{t}\right)\left(\theta_{1}, \theta_{2}\right)=\left(\frac{\alpha_{1} \theta_{1}+\beta_{1}}{\gamma_{1} \theta_{1}+\sigma_{1}}\right)\left(\frac{\alpha_{2} \theta_{2}+\beta_{2}}{\gamma_{2} \theta_{2}+\sigma_{2}}\right)$
因此, 当选择的2个结点在不同团中时, 灵敏性函数成立.
3)对于k(k> 2)个不同的结点{V1, V2, ···, Vk}, 由于选择的结点分别属于不同的团, 则选择的k个结点相互独立, 因此多结点动态灵敏性分析等式成立, 即
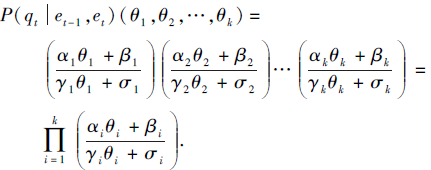
4)对选择的结点要求不在同一个团的条件进行分析, 假设选择的结点同存一个团中.
(1)V1和V2同存于一个团且有直接边相连, 灵敏性函数展开为
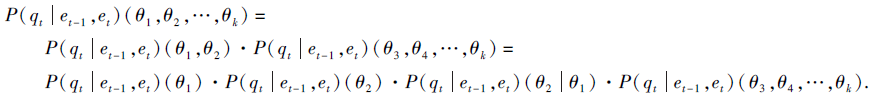
灵敏性函数分解式中包含
P(qt|et-1, et)(θ2|θ1),
则θ1与θ2存在依赖关系, 对θ1进行灵敏性分析时θ2会同步改变, 此时再对θ2进行灵敏性分析, 会隔断θ1与θ2的依赖关系, 导致V1与V2信息不一致, 因此不满足同时进行灵敏性分析的条件[27].
(2)V1和V2存于同一个团且具有公共子结点, 灵敏性函数展开为
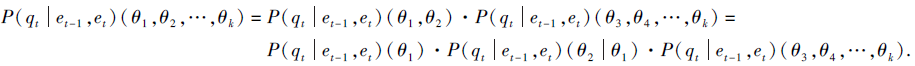
灵敏性函数分解式中同样包含
P(qt|et-1, et)(θ2|θ1),
不满足条件.
由上可知, 当扰动的多个结点不在同一个团时, 定理1成立. 证毕.
对单个结点和多个结点的状态进行动态灵敏性分析, 研究结点不同状态对于系统趋势的影响情况.扰动结点的选取描述如下.对结点集合
V={V1, V2, ···, Vk},
通过式(3)计算结点影响力, 选取V中影响程度最大的结点Vi, 并在集合中删除Vi结点.保持选取的Vi结点与已选择结点不同存于一个团中, 重复对结点集V进行操作, 直至为空.
针对顶层网络, 从t=1开始对顶层网络构建联合树JTt, 初始化JTt中所有团和分割团的条件概率表.令Dt为包含It-1={V
根据时间片t从中提取Ct-1的概率分布, 边缘化Ct-1, 得到It-1的概率分布, 吸收证据得到先验分布
其中, E1:t-1表示证据, 并将该先验概率分布作为Dt的概率分布, 将Ct作为根结点, 在JTt中执行收集证据的操作.
使JTt从JTt+1中吸收概率, 实现对JTt的概率分布进行更新, 边缘化Dt+1得到It的联合概率分布:
吸收JTt+1中Dt+1的概率分布, 更新JTt中Dt的概率分布, 由式(2)可得
当整个顶层网络趋于一致后, 对于预测目标结点Qt+1所在的团或分割团, 给定证据E, 计算Qt+1的后验概率P(Qt+1|E).
算法 基于分层动态贝叶斯网络的股市趋势扰动推理算法
输入 均线数据对应数据集Dataset
输出 股市未来的趋势Qt+1
step 1 收集A股板块指数的均线数据, 将实验数据划分为训练数据和测试数据.
step 2 对每根均线构建底层网络后, 利用马尔可夫毯提取并融合为均线能量Y.
step 3 将均线能量离散化后作为输入数据构建顶层网络, 设顶层网络一共有T个时间片.
step 4 对顶层网络构建联合树JTt, 从t=1开始, 通过证据分发和证据收集进行信息传播.
step 5 t=t+1, 若t< T, 返回step 4.
step 6 当t=T时, 通过4.1节方法对JTt进行扰动结点的选取.
step 7 对已选择的结点进行动态灵敏性分析, 若Qt趋势不发生改变, 判断未来趋势继续延续当前趋势, 否则, 计算 P(Qt+1|E), 进行预测.
本文算法由构建底层网络、构建顶层网络和联合树推理三部分组成.底层网络由K2算法进行学习, K2算法的时间复杂度为O(mu2n2r), 其中, m表示实例样本个数, u表示父结点个数, n表示网络中结点个数, r表示每个结点的取值个数.顶层网络中主要时间花费是DP算法, DP算法时间复杂度约为O(h2h+hkm), 其中, h表示顶层网络结点的数量, k表示父结点的最大个数, m表示实例样本个数.联合树推理算法的时间复杂度约为O(ct), 其中, c表示结点的最大取值数, t表示所有团的最大结点数.因此, 算法总体时间复杂度为
O(mu2n2r+h2h+hkm+ct).
从沪深A股软件通达信中收集行业板块指数, 选取2015-01-01至2020-12-31出现的约18 000多个均线汇聚样本, 样本中包含行业指数的均线数据及收盘价. 2015-01-01至2018-12-31之间的约70%样本作为训练数据, 2019-01-01至2020-12-31之间的约30%样本作为测试数据.其中, 2019-01-01至2019-08-31时间段包含2 000个测试数据, 该阶段样本指数的波动性较大, 不确定程度较高.2019-01-01至2020-12-31时间段包含5 000个测试数据, 该阶段样本环境复杂, 种类丰富.每个样本在均线汇聚发生后收盘价的五日涨跌幅为所要预测的趋势:期间涨幅大于5%, 表示趋势是上行; 期间涨跌幅在-5%至5%之间, 表示趋势是横盘; 当跌幅大于5%时, 趋势是下行.
为了验证本文算法的有效性, 利用真正类率(True Positive Rate, TPR)和假正类率(False Posi-tive Rate, FPR)评价预测效果, 具体公式如下:
TPR=
其中, TP表示预测为正的正样本, TN表示预测为负的负样本, FP表示预测为正的负样本, FN表示预测为负的正样本.
动态灵敏性分析针对单个或多个均线能量变化, 分析变化后的均线能量对当前趋势的影响.由于进行灵敏性分析的结点数不同, 因此对动态灵敏性函数求解k次平均, 衡量多个结点对趋势的综合影响, 其中k表示需要扰动分析的结点个数.使用灵敏性均值函数表示为
G(θ1, θ2, ···, θ k)=
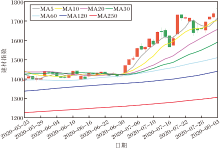
板块指数880344(建材2020-06-30)均线结构如图5所示, 当前指数的趋势为横盘.
设前一日的MA60状态为基本维持当前趋势, 即
P(V
当日MA5状态为基本维持当前趋势, 即
P(V
当日MA30状态为难以维持当前趋势, 即
P(V
根据式(4)计算结点能量影响由大至小为V
下面对影响力最大结点、随机分析两个结点及动态选取结点这3种情况进行分析.
1)仅分析影响程度最高的结点.3个结点中影响程度最高的结点为V
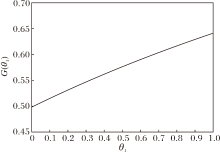
G(θ1)=
灵敏性均值G(θ1)和灵敏性均值θ1的曲线关系如图6所示.由图可知, G(θ1)随θ1增大而增大, G(θ1)最小为0.5, 最大可达到0.64, 说明前一日MA60基本维持当前趋势, 在当日趋势为横盘的情况下, 未来趋势大概率是横盘.
2)分析随机2个结点.当扰动结点为V
G(θ1, θ2)=
灵敏性均值和两个参数的曲面关系如图7所示.当θ1和θ2变化时, 灵敏性均值分布在0.46与0.58之间, 说明前一日MA60状态为基本维持当前趋势, 当日MA5状态为基本维持当前趋势, 当日趋势为横盘情况下, 趋势大概率不变.
 | 图7 灵敏性均值G(θ1, θ2)随θ1和θ2的变化曲面Fig.7 Surface of average value of sensitivity G(θ1, θ2) varying with θ1 and θ2 |
3)动态选取影响程度较高的2个结点.动态灵敏性分析转化为对V
G(θ1, θ3)=
当θ1和θ3变化时, 灵敏性均值的点分布在0.40与0.525之间, 表示前一日MA60状态为基本维持当前趋势, 当日MA30状态为难以维持当前趋势, 当日趋势为横盘情况下, 趋势大概率发生变化.
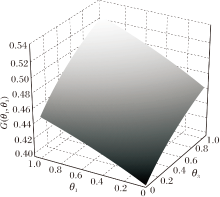 | 图8 灵敏性均值G(θ1, θ3)随θ1和θ3变化曲面Fig.8 Surface of average value of sensitivity G(θ1, θ3) varying with θ1 and θ3 |
已知当前θ1=0.448, θ2=0.423, θ3=0.518, 计算出灵敏性均值G(θ1)=0.754, G(θ1, θ2) =0.516, G(θ1, θ3)=0.472.基于单结点时和随机两个结点时的灵敏性分析, 由于信息量有限, 难以有效反映趋势变化.动态灵敏性分析通过分析一些影响度较高的结点, 更好地体现均线内在特性.
本节选用如下对比算法:T-LSTM-R(Time-Weighted LSTM Model with Trend Retracement)[4]、HOI-CNN(High Order Information Based on CNN)[8]、LSTM[28].LSTM和T-LSTM-R针对均线数据, HOI-CNN直接利用均线的基础数据收盘价.
4种算法的实验结果如表1所示.在表中, 2 000表示2019-01-01至2019-08-31时间段的2 000个测试数据, 5 000表示2019-01-01至2020-12-31时间段的5 000个测试数据.
| 表1 各算法在2种测试样本上的实验结果 Table 1 Experimental results of different algorithms on 2 kinds of test samples % |
由表1可知, 对于2 000个测试样本, 进行2个结点灵敏性分析或3个结点灵敏性分析后再进行预测都具有较优结果, 而仅对单结点灵敏性分析效果不理想.这是由于单结点信息价值有限, 而多结点灵敏分析能利用更多的有用信息.其中, 基于3个结点的本文算法精确率明显高于对比算法, 在召回率和F1值上, 也有明显优势, 说明引入均线能量的动态灵敏性分析, 比仅考虑价格走势和组合特征, 在预测精度和稳定性方面都更有优势.
对于5 000个测试样本, LSTM的波动性较少, 但总体指标表现一般.T-LSTM-R总体上有所上升.HOI-CNN在预测上行和横盘趋势能力上有所下降, 在预测下行趋势能力上有所上升.本文算法具有较小的波动, 仍具有较优效果.由此可见, 当采用不同分布的测试数据时, 本文算法都具有较强的适应性.
表1说明本文算法结合灵敏性分析与联合树推理, 效果较优.为了进一步判断灵敏性对实验结果的影响, 通过对灵敏性均值阈值的动态选取, 计算TPR和FPR, 得到灵敏性分析后的ROC(Receiver Opera-ting Characteristic)曲线[29].
AUC(Area Under Curve)定义为ROC曲线右下方的面积.基于TPR和FPR, 对上行、横盘和下行趋势进行分析, 结果如图9所示.
图9(a)表示对上行趋势的分析结果, 3个结点的AUC值明显大于单结点和2个结点, 而单结点的AUC值最小, 说明3个结点的灵敏性分析效果最优, 单结点的灵敏性分析效果最差.(b)表示对横盘趋势的分析结果, 3个结点的灵敏性分析和2个结点的灵敏性分析结果接近.(c)表示对下行趋势的分析结果, 3个结点的灵敏性分析同样优于单结点和2个结点.在3种趋势中, 单结点灵敏性分析由于考虑的信息过少, 效果一直较差.
图9的灵敏性分析结果与表1对应, 表明灵敏性分析能有效提升预测精度, 且多个结点的灵敏性分析预测效果更优.
股市数据挖掘是机器学习和人工智能领域的一个研究热点.股市是一个动态复杂系统, 数据具有非欧性, 因此采用动态结构建模方法进行分析.同时, 股市数据噪声较多, 通过数据选取和数据融合, 可降低数据噪声.针对使用机器学习方法训练的模型在实际应用中适应性较差的问题, 本文提出基于分层动态贝叶斯网络的股市趋势扰动推理算法.采用动态灵敏性分析方法实时调整模型数据.为了更有效地预测股市趋势变化, 将单结点的动态灵敏分析扩展到多结点情况.今后将考虑使用动态灵敏性分析研究主力资金的行为对股市趋势变化的影响.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|
| [19] |
|
| [20] |
|
| [21] |
|
| [22] |
|
| [23] |
|
| [24] |
|
| [25] |
|
| [26] |
|
| [27] |
|
| [28] |
|
| [29] |
|