引用本文
李金海, 周新然. 多粒度决策形式背景的属性约简. 模式识别与人工智能, 2022,35(5): 387-400
LI Jinhai, ZHOU Xinran. Attribute Reduction in Multi-granularity Formal Decision Contexts. PATTERN RECOGNITION AND ARTIFICIAL INTELLIGENCE, 2022,35(5): 387-400.  
Doi: 10.16451/j.cnki.issn1003-6059.202205001
Permissions
Copyright©2022, 《模式识别与人工智能》编辑部
《模式识别与人工智能》编辑部
多粒度决策形式背景的属性约简
李金海1,2, 周新然1,2
1.昆明理工大学 数据科学研究中心 昆明 650500
2.昆明理工大学 理学院 昆明 650500
通讯作者：

李金海,博士,教授,主要研究方向为认知计算、粒计算、大数据分析、概念格、粗糙集.E-mail:jhlixjtu@163.com.

作者简介:

周新然,硕士研究生,主要研究方向为形式概念分析、粒计算、粗糙集.E-mail:xrzhou101@163.com.

收稿日期: 2022-01-10 接受日期: 2022-03-04
资助项目: 国家自然科学基金项目(No.11971211,12171388)资助
摘要

针对现有的决策形式背景属性约简方法不能处理多粒度数据的问题,文中提出3种多粒度决策形式背景的属性约简方法,目的是通过删除每个协调粒度层下相同类别的类属性块,实现信息系统的属性约简.首先从信息粒的角度出发,在多粒度决策形式背景中引入协调粒度层的信息熵及条件信息熵,利用它们进一步度量属性重要度.然后,在多粒度决策形式背景中基于平均条件信息熵、最粗协调决策形式背景条件信息熵及最细协调决策形式背景条件信息熵,提出协调粒度约简方法、最粗协调粒度约简方法、最细协调粒度约简方法及其实现算法.最后,通过实验验证文中提出的3种属性约简方法的有效性,对比这3种方法得到的属性约简集,发现协调粒度约简方法的约束条件较严,相比之下,最粗协调粒度约简方法和最细协调粒度约简方法约束条件相对宽松.

关键词: 形式概念分析; 多粒度决策形式背景; 条件信息熵; 属性重要度; 属性约简
中图分类号:TP18
Attribute Reduction in Multi-granularity Formal Decision Contexts
LI Jinhai1,2, ZHOU Xinran1,2
1. Data Science Research Center, Kunming University of Science and Technology, Kunming 650500
2. Faculty of Science, Kunming University of Science and Technology, Kunming 650500
Corresponding author:
LI Jinhai, Ph.D., professor. His research interests include cognitive computing, granular computing, big data analysis, concept lattice and rough set.

About Author:
ZHOU Xinran, master student. Her research interests include formal concept analysis, granular computing and rough set.

Fund:National Natural Science Foundation of China(No.11971211,12171388)
Abstract

The existing attribute reduction methods for formal decision contexts cannot deal with multi-granularity data. Therefore, three attribute reduction methods are put forward in multi-granularity formal decision contexts to realize attribute reduction of an information system by removing the class-attribute blocks from the same category under each consistent granularity layer. Firstly, from the perspective of information granules, information entropy and conditional information entropy of the consistent granularity layer are introduced in the multi-granularity formal decision contexts to further measure the significance of attributes. Secondly, based on the average conditional information entropy and conditional information entropy in the coarsest and finest consistent formal decision contexts, the consistent granularity attribute reduction method and the coarsest and finest consistent granularity attribute reduction methods are proposed in multi-granularity formal decision contexts, and their corresponding implementation algorithms are developed. Finally, the experimental results show that the proposed attribute reduction methods are effective. In addition, it is concluded that the constraint of the consistent granularity attribute reduction method is too strict. Instead, the constraints of the coarsest and finest consistent granularity attribute reduction methods are relatively weaker.

Key words: Formal Concept Analysis; Multi-granularity Formal Decision Context; Conditional Information Entropy; Significance of Attribute; Attribute Reduction

本文责任编委 张燕平

Recommended by Associate Editor ZHANG Yanping

Wille[1]提出概念格, 成为形式概念分析的核心数据结构, 该方法通过形式化的方式表现组成概念的对象、属性及其结构关系等信息.随着相关研究的深入, 一些学者将粒计算[2, 3, 4, 5, 6]、多粒度[7, 8, 9]及粗糙集[10]等理论与形式概念分析紧密结合.同时, 概念格也被应用到机器学习[11]、数据挖掘[12]及知识发现[13, 14, 15, 16]等具有广阔应用前景的领域[17, 18, 19, 20].

形式概念分析通过引入诱导算子、定义概念的内涵和外延作为基础, 研究诱导算子性质、数据拆分合并关系、概念知识代数结构、概念格构造、概念格规则提取及消除冗余属性等问题.属性约简作为形式概念分析研究的主要内容之一, 已受到越来越多学者的关注.张文修等[21, 22]借鉴粗糙集理论中的属性约简思想, 在概念格中引入可辨识属性矩阵及在协调近似表示空间上给出属性协调集的判定定理, 实现概念格的属性约简.Wu等[23]基于信息粒协调结构关系, 提出粒约简与粒规则的概念.魏玲等[24]在决策形式背景中进一步建立概念格属性约简理论, 研究基于强协调决策形式背景和弱协调决策形式背景的属性约简.Li等[25]在决策形式背景中构造可辨识矩阵及布尔函数, 在非冗余规则提取意义下实现知识约简.李进金等[26]引入交并可约元的概念, 完成形式背景的属性约简.

Shannon等[27]提出信息熵的概念, 解决度量信息不确定性问题.粗糙集理论中广泛利用各种信息熵研究目标对象的近似质量、信息的刻画精度及属性的重要性程度等问题, 学者们通过这些有用的工具又研究信息系统的知识约简[28, 29, 30, 31, 32, 33], 主要侧重于约简集的快速计算.因为各种度量方法被提出, 启发式搜索属性约简集更容易实现.王国胤等[34]在粗糙集中基于条件信息熵, 提出决策表知识约简的快速实现算法.此外, 信息熵在形式概念分析中也得到重视.陈东晓等[35]在协调决策形式背景中利用条件信息熵研究属性约简问题, 具体是通过其约简过程中引起互信息的变化, 以此计算属性约简集.Li等[36]和Singh等[37]给出基于信息熵的加权概念格属性约简方法.

但是, 上述研究都是在单一粒度层下进行的数据分析及属性约简, 随着形式概念分析研究逐渐发展到多层次、多维度、多粒度的复杂环境, 出现多粒度决策形式背景的属性约简方法.基于上述讨论, 本文以现有的单粒度决策形式背景的属性约简方法为基础, 基于条件信息熵, 讨论多粒度决策形式背景的属性约简.具体地, 本文在多粒度决策形式背景中定义信息熵和条件信息熵, 度量属性重要度.根据删除冗余类属性块的不同需求, 提出3种多粒度决策形式背景属性约简方法, 即协调粒度约简方法、最粗协调粒度约简方法和最细协调粒度约简方法, 并通过实验说明它们的有效性.

1 相关知识

为了给出多粒度决策形式背景的有关概念, 下面先介绍形式背景及其概念诱导算子.

定义1[1] 三元组K=(G, A, I)称为形式背景, 其中G=(g1, g2, …, gp)为一个非空有限对象集, A=(a1, a2, …, aq)为一个非空有限属性集, I为笛卡尔积G× A上的二元关系.(g, a)∈ I表示对象g拥有属性a, 记为gIa.

定义2[1] 在形式背景K=(G, A, I)中, 对于X⊆G, B⊆A, 定义算子:

$\begin{aligned}& X^{* }=\{a \in A \mid \forall g \in X, g I a\}, \\ & B^{* }=\{g \in G \mid \forall a \in B, g I a\} .\end{aligned}$

如果X* =B, B* =X, 称序对(X, B)为形式概念, X为概念的外延, B为概念的内涵.

定义3[38] 设(G, A, I)和(G, D, J)为形式背景且A∩ D=Ø , 称五元组F=(G, A, I, D, J)为决策形式背景, 其中, A为条件属性, D为决策属性, (G, A, I)为F的条件子背景, (G, D, J)为F的决策子背景.

例1 表1给出一个信息系统C=(G, A), 其中G={g1, g2, g3, g4, g5, g6}, gi(i=1, 2, …, 6)表示某高校的6名即将毕业的大四学生, A={a1, a2, a3}, a1表示综合平均绩点, a2表示六级成绩, a3表示数学建模比赛获奖情况, 其中综合平均绩点和六级成绩的单位均为分数, 属性a1、a2、a3的取值形成多值集合.

表1 信息系统C=(G, A) Table 1 Information system C=(G, A)

先把信息系统转换成多个单粒度形式背景, 再并置且添加决策属性, 得到多粒度决策形式背景, 详见表2.具体地, 将信息系统中的多值属性a1分成2个子类:b1为综合平均绩点3.5分及以上, b2为综合平均绩点3.5以下; 将多值属性a2分成2个子类:b3为六级成绩425分及以上, b4为六级成绩425分以下; 将多值属性a3分成2个子类:b5为参加数学建模比赛且获奖, b6为参加数学建模比赛并未获奖.D={d1, d2}, d1表示获得国家级或省级奖学金, d2表示获得研究生推免资格.在该数据集中, 数字1表示该学生符合所在列的条件, 0表示不符合.

表2 决策形式背景(G, A1, I1, D, J) Table 2 Formal decision context(G, A1, I1, D, J)

定义4[23] 设F=(G, A, I, D, J)为决策形式背景, 对于∀ g∈ G, 若存在g* A* A⊆g* D* D, 称F为协调决策形式背景.

定义5[23] 设F=(G, A, I, D, J)为协调决策形式背景且B⊆A, 对于∀ g∈ G, 若存在g* B* B⊆g* D* D, 称B为F的协调集.进一步, 若∀ E⊂B, 存在g∈ G, 使得g* E* E⊄g* D* D, 称B为F的约简集.

定义6[23] 设F=(G, A, I, D, J)为协调决策形式背景, 对于∀ g∈ G, 称g* A→ g* D为F的一条粒规则.

定义7[24] 设F=(G, A, I, D, J)为协调决策形式背景, {Bi|Bi是约简集, i∈ τ }(τ 为指标集)为F的全体约简集, 记

1)绝对必要属性(核心属性):

$ M_{c}=\operatorname{Core}(A)=\bigcap_{i \in \tau} B_{i}$

2)相对必要属性:

$ M_{n}=\bigcup_{i \in \tau} B_{i}-\bigcap_{i \in \tau} B_{i}$

3)绝对不必要属性:

$ M_{u}=A-\bigcup_{i \in \tau} B_{i}$

2 多粒度决策形式背景的条件信息熵

信息熵在粗糙集中被广泛应用于度量属性的重要性[34, 39, 40], 本节参考形式背景的信息熵, 提出多粒度决策形式背景的条件信息熵.

2.1 多粒度决策形式背景

定义8[8] 设K=(G, A, I)为形式背景,

M={a1, a2, …, am}⊆A,

若每个属性ai(i∈ {1, 2, …, m})拥有的对象组成的集合为Iai, 全体Iai(ai∈ M)构成G的一个划分, 且M中所有的布尔属性在语义上属于同一类别, 则称M为(G, A, I)的一个类属性块.

上述定义说明类属性块实质上是一些同类布尔属性组成的集合, 它们构成论域G的划分, 换言之, 每个对象在不同类属性块下取值可能相同, 但在同一类属性块下取值必唯一.

例2 以表2中的条件子背景K=(G, A1, I1)为例, 因为{Ib1, Ib2}构成G的一个划分, 且都是综合平均绩点的布尔属性, 所以M11={b1, b2}为(G, A1, I1)的一个类属性块.同理, M12={b3, b4}, M13={b5, b6}也是(G, A1, I1)的类属性块.

定义9[8] 设(G, A1, I1)和(G, A2, I2)为2个不同粒度的形式背景, 属性集分别划分为M11, M12, …, M1s和M21, M22, …, M2s, 若单粒度类属性块M2k的布尔属性由M1k合并产生, 则称M1k比M2k的粒度细, 记作M1k≺M2k.若对∀ k∈ {1, 2, …, s}, 都有M1k≺M2k, 则称(G, A1, I1)比(G, A2, I2)的粒度细, 记作(G, A1, I1)≺(G, A2, I2).

定义10[8] 对于n个单粒度形式背景(G, Ai, Ii)(i∈ {1, 2, …, n}), 假设Ai的类属性块为Mi1, Mi2, …, Mis, 其中M1k, M2k, …, Mnk(k∈ {1, 2, …, s})为不同粒度下的同类别类属性块, 若

Mnk≺ M(n-1)k≺…≺M1k,

则称

$\Phi =\underset{i=1}{\overset{n}{\mathop{U}}}\,(G,{{A}_{i}},{{I}_{i}})$

为多粒度形式背景.

实际上, 现实中得到多粒度形式背景的方法很多, 如属性粒化[7]、乐观悲观分类[41].

定义11[42] 设

$\Phi =\underset{i=1}{\overset{n}{\mathop{U}}}\,(G,{{A}_{i}},{{I}_{i}})$

为多粒度形式背景, Mi1, Mi2, …, Mis为Ai的划分, M1k, M2k, …, Mnk (k∈ {1, 2, …, s})同属一个类别且它们内部的布尔属性的子类个数均为$\lambda_{k}$, Mik1, Mik2, …, Mikλk为Mik的划分,

$ M_{k}=\bigcup_{r=1}^{\lambda_{k}} M_{n_{r^{k}}}^{r}, N_{k}=\bigcup_{r=1}^{\lambda_{k}} M_{n_{r}^{\prime} k}^{r}$

为Φ 的第k个类别下的2个多粒度类属性块.如果对∀ r∈ {1, 2, …, λ k}, 有nr≤ n'r, 则称多粒度类属性块Nk比Mk的粒度细, 记作Nk≺Mk.

进一步, 将多粒度形式背景与单粒度决策背景进行并置, 可引入多粒度决策形式背景.

定义12[8] 设

$\Phi =\underset{i=1}{\overset{n}{\mathop{U}}}\,(G,{{A}_{i}},{{I}_{i}})$

为多粒度形式背景, (G, D, J)为单粒度形式背景, 则称

$\Pi =(\underset{i=1}{\overset{n}{\mathop{U}}}\,~(G,{{A}_{i}},{{I}_{i}}),D,J)$

为一个多粒度决策形式背景.

如果多粒度决策形式背景Π 中存在某一粒度层, 使得(G, Ai, Ii, D, J)是协调的, 那么称Π 是部分协调的.下文主要讨论部分协调的多粒度决策形式背景, 因为完全不协调的多粒度决策形式背景毫无全局协调性可言, 而本文关注的又是全局协调性意义下的属性约简, 所以暂不考虑完全不协调的情况.

例3 将表2中的属性进一步细化.首先, 将属性b1分为2个子属性:c1为综合平均绩点4.0分及以上, c2为综合平均绩点介于3.5分到3.9分之间; 将属性b3也分为2个子属性:c4为六级成绩介于425分到450分之间, c5为六级成绩451分及以上; 将属性b5分为2个子属性:c7为数学建模比赛获得国奖, c8为数学建模比赛获得省奖, c3、c6、c9分别与b2、b4、b6保持一致.那么, 表2又可转化为如表3所示的决策形式背景(G, A2, I2, D, J).

表3 决策形式背景(G, A2, I2, D, J) Table 3 Formal decision context(G, A2, I2, D, J)

令

M21={c1, c2, c3}, M22={c4, c5, c6}, M23={c7, c8, c9},

则M21、M22、M23构成A2的一个划分, 均为(G, A2, I2)的类属性块.由定义9及例3的讨论可知, M13和M23同属数学建模比赛获奖情况这一类别, 但M13比M23粒度更粗.

同理, 也能分析其它类属性块之间的粒度粗细关系, 并得到类似结论.因此, 由定义10可知, ( ⋃i=12(G, Ai, Ii), D, J)构成一个多粒度决策形式背景.容易验证, 它是完全不协调的:因为在第1粒度层下, g2* A1* A1⊄ g2* D* D; 在第2粒度层下, g2* A2* A2⊄ g2* D* D.因此, 需要进一步细化才能得到部分协调的多粒度决策形式背景.

2.2 多粒度决策形式背景的条件信息熵

文献[43]给出单粒度(决策)形式背景的信息熵(条件信息熵), 本节将其推广到多粒度决策形式背景, 讨论属性约简问题.

定义13 对于多粒度决策形式背景

$\Pi =(\underset{i=1}{\overset{n}{\mathop{U}}}\,~(G,{{A}_{i}},{{I}_{i}}),D,J),$

第i粒度层Ki=(G, Ai, Ii)的信息粒度定义为

$I G\left(A_{i}\right)=\frac{1}{|G|} \sum_{g \in G}\left(\frac{\left|g^{* A_{i} * A_{i}}\right|}{|G|}\right)$.

定义14 对于多粒度决策形式背景

$\Pi =(\underset{i=1}{\overset{n}{\mathop{U}}}\,~(G,{{A}_{i}},{{I}_{i}}),D,J),$

第i粒度层Ki=(G, Ai, Ii)的信息熵定义为

$ \operatorname{IE}\left(A_{i}\right)=\frac{1}{|G|} \sum_{g \in G}\left(1-\frac{\left|g^{* A_{i} * A_{i}}\right|}{|G|}\right)$.

定义15 对于多粒度决策形式背景

$\Pi =(\underset{i=1}{\overset{n}{\mathop{U}}}\,~(G,{{A}_{i}},{{I}_{i}}),D,J),$

决策子背景(G, D, J)关于第i粒度层下的条件子背景(G, Ai, Ii)的条件信息熵定义为

$ \begin{aligned} & \operatorname{CIE}\left(D \mid A_{i}\right)=\frac{1}{|G|} \sum_{g \in G}\left(\frac{\left|g^{* A_{i} * A_{i}}\right|-\left|g^{* A_{i} * A_{i}} \cap g^{* D * D}\right|}{|G|}\right) .\end{aligned}$

性质1 对于多粒度决策形式背景

$\Pi =(\underset{i=1}{\overset{n}{\mathop{U}}}\,~(G,{{A}_{i}},{{I}_{i}}),D,J),$

Bi⊆Ai, 则Bi为第i粒度层(G, Ai, Ii, D, J)的协调集当且仅当CIE(D|Bi)=0.

证明 充分性.由于Bi为(G, Ai, Ii, D, J)的协调集, 所以决策形式背景(G, Bi, IBi, D, J)是协调的, 那么根据定义4可知, 对于∀ g∈ G, 有

${{g}^{\text{*}{{B}_{i}}\text{*}{{B}_{i}}}}\subseteq {{g}^{*D*D}},$

故由定义15可得CIE(D|Bi)=0.

必要性.若CIE(D|Bi)=0, 则对于∀ g∈ G, 有

${{g}^{\text{*}{{B}_{i}}\text{*}{{B}_{i}}}}\subseteq {{g}^{*D*D}},$

因此由定义5可得, Bi为(G, Ai, Ii, D, J)的协调集.

也就是说, 部分协调的多粒度决策形式背景必存在某一粒度层, 使决策子背景关于该粒度层条件子背景的条件信息熵为零.需要指出的是, 多粒度决策形式背景的信息熵或条件信息熵与单粒度的情况是类似的, 推广到多粒度环境是为了进一步研究协调粒度层的平均条件信息熵及属性约简问题.

3 部分协调的多粒度决策形式背景的属性约简

本节针对部分协调的多粒度决策形式背景, 基于平均条件信息熵、最粗协调决策形式背景条件信息熵及最细协调决策形式背景条件信息熵, 提出3种属性约简方法, 并给出相应的实现算法.

3.1 基于平均条件信息熵的属性约简

定义16 设

$\Pi =(\underset{i=1}{\overset{n}{\mathop{U}}}\,~(G,{{A}_{i}},{{I}_{i}}),D,J)$

为部分协调的多粒度决策形式背景, 协调粒度层有h个, 各协调粒度层下的条件信息熵为CIE(D|Ai)

(i=1, 2, …, h), 则Π 的协调粒度层平均条件信息熵定义为

CIEave(D| ∑i=1hAi)= 1h∑i=1hCIE(D|Ai).

定义17 设

$\Pi =(\underset{i=1}{\overset{n}{\mathop{U}}}\,~(G,{{A}_{i}},{{I}_{i}}),D,J)$

为部分协调的多粒度决策形式背景, 协调粒度层有h个, 在每个协调粒度层下, 均存在Bi⊆Ai, 使得协调粒度层平均条件信息熵

CIEave(D| ∑i=1hBi)=CIEave(D| ∑i=1hAi),

则称(B1, B2, …, Bh)为多粒度决策形式背景Π 的协调粒度层协调集; 进一步, 若∀ i∈ {1, 2, …, h}, 有Ei⊆Bi, 且存在Ej⊂Bj使得

CIEave(D| ∑i=1hEi)≠ CIEave(D| ∑i=1hAi),

则称(B1, B2, …, Bh)为Π 的协调粒度层约简集.

需要指出的是, 具体进行约简时, Bi相对于Ai(i=1, 2, …, h)被约掉的信息需为同一类别的类属性块, 从而实现在每一粒度层下去掉相同的冗余类属性块信息.这样做的目的是可解决信息系统的属性约简问题, 即被约掉的类属性块在每一粒度层下都是冗余的.

性质2 设

$\Pi =(\underset{i=1}{\overset{n}{\mathop{U}}}\,~(G,{{A}_{i}},{{I}_{i}}),D,J)$

为部分协调的多粒度决策形式背景, Bi⊆Ai, 则(B1, B2, …, Bh)为Π 的协调粒度层协调集当且仅当在各协调粒度层下Bi均为(G, Ai, Ii, D, J)的协调集.

证明 充分性.若(B1, B2, …, Bh)为多粒度决策形式背景Π 的协调粒度层协调集, 则

$ \begin{aligned}\operatorname{CIE}_{\text {ave }}\left(D \mid \sum_{i=1}^{h} B_{i}\right)=& \frac{1}{h} \sum_{i=1}^{h} \operatorname{CIE}\left(D \mid B_{i}\right)= C I E_{\text {ave }}\left(D \mid \sum_{i=1}^{h} A_{i}\right)=0 .\end{aligned}$

由于条件信息熵CIE(D|Bi)≥ 0, 所以CIE(D|Bi)=0, 根据性质1可得在各粒度层下Bi均为(G, Ai, Ii, D, J)的协调集.

必要性.若在各粒度层下Bi均为(G, Ai, Ii, D, J)的协调集, 则由性质1可得CIE(D|Bi)=0, 因此

$\begin{aligned}\operatorname{CIE}_{\mathrm{ave}}\left(D \mid \sum_{i=1}^{h} B_{i}\right)=& \frac{1}{h} \sum_{i=1}^{h} \operatorname{CIE}\left(D \mid B_{i}\right)=CIE_{\text {ave }}\left(D \mid \sum_{i=1}^{h} A_{i}\right)=0, \end{aligned}$

即(B1, B2, …, Bh)为多粒度决策形式背景Π 的协调粒度层协调集.

定义18 设

$\Pi =(\underset{i=1}{\overset{n}{\mathop{U}}}\,~(G,{{A}_{i}},{{I}_{i}}),D,J)$

为部分协调的多粒度决策形式背景, 协调粒度层有h个, C1, C2, …, Ch分别为各协调粒度层下的属性真子集, 则在每一粒度层下Mi⊆Ai-Ci相对于Ci的外重要度记为

SIGouterAi(Mi|Ci)=CIE(D|Ci)-CIE(D|Ci∪ Mi),

那么在多粒度决策形式背景Π 中这些新添加属性集的协调粒度层平均外重要度定义为

SIG¯outer( ∑i=1h(Mi|Ci))= 1h∑i=1hSIGouterAi(Mi|Ci).

定义19 设

$\Pi =(\underset{i=1}{\overset{n}{\mathop{U}}}\,~(G,{{A}_{i}},{{I}_{i}}),D,J)$

为部分协调的多粒度决策形式背景, A1, A2, …, Ah为各协调粒度层下的属性全集, Mi为第i粒度层下的属性集Ai中任一属性子集, 则每一粒度层下Mi相对于Ai的内重要度记为

SIGinnerAi(Ai|Mi)= CIE(D|Ai-Mi))-CIE(D|Ai),

那么在多粒度决策形式背景Π 中这些被删除属性集的协调粒度层平均内重要度定义为

SIG¯inner( ∑i=1h(Ai|Mi))= 1h∑i=1hSI GinnerAi(Ai|Mi).

在实际应用中, 通常删除和添加属性集都是以类属性块为单位进行的, 在此前提下当这些类属性块同属一个类别时, 即可实现信息系统的属性约简.下文使用Coreave(A1, A2, …, Ah)表示所有核心类属性块组成的集合, 即使得协调粒度层平均内重要度大于零的那些类属性块.

例4 将表3中的六级分数及数学建模获奖情况进一步细分, 具体将c5分为2个子属性:e5为六级分数介于451~480分之间, e6为六级分数在481分及以上; 将c7分为2个子属性:e8为获得数学建模比赛国家级一等奖, e9为获得数学建模比赛国家级二等奖, e1、e2、e3、e4、e7、e11分别与c1、c2、c3、c4、c6、c8、c9保持一致.那么, 表3可转化为如表4所示的决策形式背景(G, A3, I3, D, J).

表4 决策形式背景(G, A3, I3, D, J) Table 4 Formal decision context(G, A3, I3, D, J)

此时,

$(\underset{i=1}{\overset{3}{\mathop{U}}}\,~(G,{{A}_{i}},{{I}_{i}}),D,J)$

构成一个部分协调的多粒度决策形式背景, 即第3粒度层下的决策形式背景(G, A3, I3, D, J)是协调的.对于第1位学生g1, 对应的粒规则e1e5e9→ d1d2, 语义解释为:如果某学生综合平均绩点4.0分及以上、六级成绩介于451~480分之间且数学建模比赛获得国家级二等奖, 那么该学生获得国家级奖学金且具有研究生推免资格.

为了更好地利用平均条件信息熵得到多粒度决策形式背景的协调粒度层约简集, 将表4进一步细分, 具体将属性e5分为2个子属性: f5为六级成绩在451~465分之间, f6为六级成绩在466~480分之间; 将属性e6分为2个子属性: f7为六级成绩在481~500分之间, f8为六级成绩在501分及以上, f1、 f2、 f3、 f4、 f9、 f10、 f11、 f12、 f13分别与e1、e2、e3、e4、e7、e8、e9、e10、e11保持一致.那么决策形式背景(G, A3, I3, D, J)可转化为表5所示的数据集.

表5 决策形式背景(G, A4, I4, D, J) Table 5 Formal decision context(G, A4, I4, D, J)

不难发现, 第4粒度层下的决策形式背景(G, A4, I4, D, J)也是协调的, 即

$(\underset{i=1}{\overset{4}{\mathop{U}}}\,~(G,{{A}_{i}},{{I}_{i}}),D,J)$

也构成一个部分协调的多粒度决策形式背景.

接下来, 由定义15计算多粒度决策形式背景中各协调粒度层的条件信息熵, 得到约简集, 并判断通过平均条件信息熵得到的约简集是否有效.由于本文基于平均条件信息熵计算约简集时, 需要将原平均条件信息熵与去掉任一类属性块后的平均条件信息熵进行对比, 所以原决策形式背景记为(G, Ai, Ii, D, J), 去掉任一类属性块Mij后的决策形式背景记为(G, AiMij, IiMij, D, J), 其中, i表示粒度层的序号, j表示类属性块的序号.

例5 计算表2~表5组成的部分协调多粒度决策形式背景

$\Pi =(\underset{i=1}{\overset{4}{\mathop{U}}}\,~(G,{{A}_{i}},{{I}_{i}}),D,J)$

的协调粒度层约简集.具体过程如下:根据例3和例4的讨论, Π 的第1粒度层和第2粒度层是不协调的, 但在第3粒度层和第4粒度层下均是协调的.因此

CIE(D|A3)=0, CIE(D|A4)=0.

在决策子背景 K¯=(G, D, J)中, 它的信息粒满足

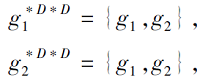
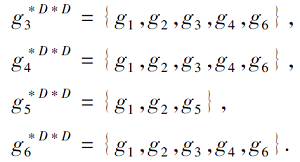
当去掉第3粒度层下形式背景K3=(G, A3, I3)中的类属性块M31={e1, e2, e3}后, 条件子背景

$K{{'}_{3}}=(G,A_{3}^{{{e}_{1}}{{e}_{2}}{{e}_{3}}},I_{3}^{{{e}_{1}}{{e}_{2}}{{e}_{3}}})$

的信息粒满足

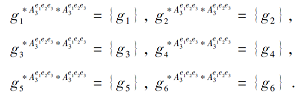
根据条件信息熵的定义可知, 去掉类属性块M31后, 决策子背景 K¯关于条件子背景

$K{{'}_{3}}=(G,A_{3}^{{{e}_{1}}{{e}_{2}}{{e}_{3}}},I_{3}^{{{e}_{1}}{{e}_{2}}{{e}_{3}}})$

的条件信息熵为

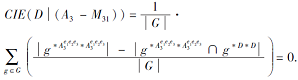
同理, 当去掉类属性块M41={f1, f2, f3}后, 决策子背景 K¯关于条件子背景

$K{{'}_{4}}=(G,A_{4}^{{{f}_{1}}{{f}_{2}}{{f}_{3}}},I_{4}^{{{f}_{1}}{{f}_{2}}{{f}_{3}}})$

的条件信息熵为

CIE(D|(A4-M41))=0.

因此, 决策子背景 K¯关于去掉类属性块M31和M41后的条件子背景的平均条件信息熵为0.

当去掉类属性块M32={e4, e5, e6, e7}后, 决策子背景 K¯关于条件子背景

$K'{{'}_{3}}=(G,A_{3}^{{{e}_{4}}{{e}_{5}}{{e}_{6}}{{e}_{7}}},I_{3}^{{{e}_{4}}{{e}_{5}}{{e}_{6}}{{e}_{7}}})$

的条件信息熵为

CIE(D|(A3-M32))=0;

去掉类属性块

M42={f4, f5, f6, f7, f8, f9}

后, 决策子背景 K¯关于条件子背景

$K'{{'}_{4}}=(G,A_{4}^{{{f}_{4}}{{f}_{5}}{{f}_{6}}{{f}_{7}}{{f}_{8}}{{f}_{9}}},I_{4}^{{{f}_{4}}{{f}_{5}}{{f}_{6}}{{f}_{7}}{{f}_{8}}{{f}_{9}}})$

的条件信息熵为

CIE(D|(A4-M42))=0.

因此, 去掉类属性块M32和M42后, 决策子背景 K¯关于条件子背景的平均条件信息熵为0.

当去掉第3粒度层下形式背景K3=(G, A3, I3)

中的类属性块M33={e8, e9, e10, e11}后, 条件子背景

$K''{{'}_{3}}=(G,A_{3}^{{{e}_{8}}{{e}_{9}}{{e}_{10}}{{e}_{11}}},I_{3}^{{{e}_{8}}{{e}_{9}}{{e}_{10}}{{e}_{11}}})$

的信息粒满足

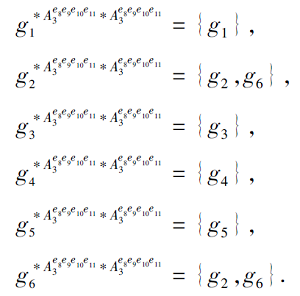
根据条件信息熵的定义可知, 去掉类属性块M33后, 决策子背景 K¯关于

$K''{{'}_{3}}=(G,A_{3}^{{{e}_{8}}{{e}_{9}}{{e}_{10}}{{e}_{11}}},I_{3}^{{{e}_{8}}{{e}_{9}}{{e}_{10}}{{e}_{11}}})$

的条件信息熵为

CIE(D|(A3-M33))= 136.

同理, 去掉类属性块

M43={f10, f11, f12, f13}

后, 决策子背景 K¯关于条件子背景

$K''{{'}_{4}}=(G,A_{4}^{{{f}_{10}}{{f}_{11}}{{f}_{12}}{{f}_{13}}},I_{4}^{{{f}_{10}}{{f}_{11}}{{f}_{12}}{{f}_{13}}})$

的条件信息熵为

CIE(D|(A4-M43))=0.

因此, 去掉类属性块M33和M43后, 决策子背景 K¯关于条件子背景的平均条件信息熵为 172.

综上可知, 去掉类属性块M31和M41(或M32和M42)后, 决策子背景 K¯关于条件子背景的平均条件信息熵与决策子背景 K¯关于原条件子背景的平均条件信息熵相等.因此, (M32∪ M33, M42∪ M43)和(M31∪ M33, M41∪ M43)均为多粒度决策形式背景Π 的协调粒度层约简集(相当于通过添加决策属性d1和d2, 可约简表1中的信息系统的属性a1或a2).注意, 通过约掉不重要的类属性块, 可使提取的粒规则更简洁.例如, 利用约简集(M32∪ M33, M42∪ M43), 可将第3粒度层下第1位学生g1对应的粒规则e1e5e9→ d1d2精简为e5e9→ d1d2, 语义解释为:如果六级成绩介于451~480分之间且数学建模比赛获得国家级二等奖, 那么该学生获得国家级奖学金且具有研究生推免资格.

3.2 最粗(细)协调决策形式背景下属性约简的判定

下面讨论的多粒度决策形式背景提及的最粗协调决策形式背景, 意指比它粒度更粗的决策形式背景均是不协调的; 最细的决策形式背景是指多粒度决策形式背景中最细的粒度层.

定义20 在部分协调的多粒度决策形式背景

$\Pi =(\underset{i=1}{\overset{n}{\mathop{U}}}\,~(G,{{A}_{i}},{{I}_{i}}),D,J)$

中, 若存在Bcor⊆Acor, 使得在最粗协调决策形式背景

Fcor=(G, Acor, Icor, D, J)

中的条件信息熵满足

CIE(D|Bcor)=CIE(D|Acor),

则称Bcor为多粒度决策形式背景Π 的最粗协调粒度层协调集; 进一步, 若对于∀ Ecor⊂Bcor, 有

CIE(D|Ecor)≠ CIE(D|Acor),

则称Bcor为多粒度决策形式背景Π 的最粗协调粒度层约简集.

定义21 在部分协调的多粒度决策形式背景

$\Pi =(\underset{i=1}{\overset{n}{\mathop{U}}}\,~(G,{{A}_{i}},{{I}_{i}}),D,J)$

中, 设在最粗协调粒度层

Fcor=(G, Acor, Icor, D, J)

下去掉任一属性集M⊆Acor后, 得到的决策形式背景为

F'cor=(G, AcorM, IcorM, D, J),

定义属性集M在Π 中的内重要度为

SIGinnercor(Acor|M)= CIE(D|Acor-M))-CIE(D|Acor).

定义22 在部分协调的多粒度决策形式背景

$\Pi =(\underset{i=1}{\overset{n}{\mathop{U}}}\,~(G,{{A}_{i}},{{I}_{i}}),D,J)$

中, 若存在Bfin⊆Afin, 使得在最细协调决策形式背景中的条件信息熵满足

CIE(D|Bfin)=CIE(D|Afin),

则称Bfin为多粒度决策形式背景Π 的最细协调粒度层协调集; 进一步, 若对于∀ Efin⊂Bfin, 有

CIE(D|Efin)≠ CIE(D|Afin),

则称Bfin为多粒度决策形式背景Π 的最细协调粒度层约简集.

定义23 在部分协调的多粒度决策形式背景

$\Pi =(\underset{i=1}{\overset{n}{\mathop{U}}}\,~(G,{{A}_{i}},{{I}_{i}}),D,J)$

中, 设在最细协调粒度层

Ffin=(G, Afin, Ifin, D, J)

下去掉任一属性集M⊆Afin后得到的决策形式背景为

F'fin=(G, AfinM, IfinM, D, J),

定义属性集M在Π 中的内重要度为

SIGinnerfin(Afin|M)= CIE(D|Afin-M))-CIE(D|Afin).

性质3 设

$\Pi =(\underset{i=1}{\overset{n}{\mathop{U}}}\,~(G,{{A}_{i}},{{I}_{i}}),D,J)$

为部分协调的多粒度决策形式背景, { Mcor1, Mcor2, …, Mcors}为最粗协调决策形式背景下条件属性集Acor的划分, { Mfin1, Mfin2, …, Mfins}为最细协调决策形式背景下条件属性集Afin的划分.令Bcor为Acor的最粗协调粒度层约简集, 记为 ⋃k=1r{ Mcork}, Bfin为Afin的最细协调粒度层约简集, 记为 ⋃l=1t{ Mfinl}.若 Mcork、 Mfinl同属一个类别, 它们内部的布尔属性的子类个数均为λ k, Mcork, 1, Mcork, 2, …, Mcork, λk为 Mcork的划分, Mfinl, 1, Mfinl, 2, …, Mfinl, λk为 Mfinl的划分, 则存在v∈ {1, 2, …, λ k}, 使得通过拆分 Mcork, v中的布尔属性块得到 Mfinl, v.

性质3给出最粗协调粒度层约简集与最细协调粒度层约简集之间在特定条件下相互转化的规律, 进一步揭示这两种协调粒度层约简集之间的关系.另外, 最粗协调粒度层约简集和最细协调粒度层约简集均是协调粒度层约简集的2种具体形式, 对于同一数据集, 协调粒度约简方法的约束条件比最粗协调粒度约简方法和最细协调粒度约简方法的约束条件更严格.

3.3 多粒度决策形式背景的属性约简算法

为了给出部分协调的多粒度决策形式背景的属性约简算法, 先讨论如下性质.下文将影响决策形式背景协调性的类属性块称为核心类属性块, 否则称为非核心类属性块.

性质4 设

$\Pi =(\underset{i=1}{\overset{n}{\mathop{U}}}\,~(G,{{A}_{i}},{{I}_{i}}),D,J)$

为部分协调的多粒度决策形式背景,

Fcor=(G, Acor, Icor, D, J)

为最粗协调决策形式背景, 则对于∀ M⊆Acor, M为Π 的核心类属性块当且仅当

SIGinnercor(Acor|M)> 0.

证明 充分性.若M为Π 的核心类属性块, 则

SIGinnercor(Acor|M)> 0,

否则

SIGinnercor(Acor|M)=0,

即

CIE(D|(Acor-M))-CIE(D|Acor)=0.

因为Fcor是协调的, 所以

CIE(D|Acor)=0,

那么

$CIE(D|({{A}_{cor}}-M))=\frac{1}{\left| G \right|}\cdot \underset{g\in G}{\mathop{\sum }}\,(\frac{\left| {{g}^{\text{*}A_{\text{cor}}^{M}\text{*}A_{\text{cor}}^{M}}}\left| - \right|{{g}^{\text{*}A_{\text{cor}}^{M}\text{*}A_{\text{cor}}^{M}}}\cap {{g}^{\text{*}D\text{*}D}} \right|}{\left| G \right|})=0.$

也就是说, 对于∀ g∈ G, 有 g* AcorM* AcorM⊆g* D* D, 由定义5可知Acor-M为Fcor的协调集.因此, 属性集M不是核心类属性块, 与已知矛盾, 故

SIGinnercor(Acor|M)> 0.

必要性.当

SIGinnercor(Acor|M)> 0

时, 可得

CIE(D|(Acor-M))-CIE(D|Acor)> 0.

因为在最粗粒度层下的决策形式背景Fcor是协调的, 故

CIE(D|Acor)=0,

所以

CIE(D|(Acor-M))= 1|G|· ∑g∈G( |g* AcorM* AcorM|-|g* AcorM* AcorM⋂g* D* D||G|)> 0.

也就是说, 存在某个对象g0, 使得不等式

| g0* AcorM* AcorM|-| g0* AcorM* AcorM∩ g0* D* D|> 0,

那么

g0* AcorM* AcorM⊄ g0* D* D,

故Acor-M不是Fcor的协调集.换言之, 删除属性集M改变Fcor的协调性, 所以M为核心类属性块.

类似地, 性质4对于最细协调决策形式背景也是成立的.为了方便, 将影响最粗协调决策形式背景和最细协调决策形式背景的所有核心类属性块组成的集合分别记为Corecor(Acor)和Corefin(Afin), 那么通过性质4可计算所有的核心类属性块.

此外, 类似于协调粒度层平均外重要度, 在最粗(细)协调决策形式背景中引入外重要度的概念.

定义24 设

$\Pi =(\underset{i=1}{\overset{n}{\mathop{U}}}\,~(G,{{A}_{i}},{{I}_{i}}),D,J)$

为部分协调的多粒度决策形式背景, Bj⊂Aj, 则Mj⊆Aj-Bj相对于Bj的最粗(细)协调粒度层外重要度定义为

SIGoutercor(fin)(Mj|Bj)= CIE(D|Bj)-CIE(D|Bj∪ Mj).

需要指出的是, 通过内重要度和外重要度可得到协调粒度层的约简集, 具体如下:首先计算内重要度得到多粒度决策形式背景的所有核心类属性块Ci(一般不是约简集); 再计算各个候选类属性块的外重要度, 将外重要度最大的类属性块不断添加到Ci中, 直至得到协调粒度层协调集Ei为止; 最后, 利用内重要度去掉协调集Ei中的冗余类属性块, 得到协调粒度层约简集Bi.

为了叙述清楚, 分2种算法给出多粒度决策形式背景的属性约简过程, 详见算法1和算法2.

算法1 基于协调粒度层平均条件信息熵的约简

输入 多粒度决策形式背景Π 及其协调粒度层

（ ⋃i=1h(G, Ai, Ii), D, J）

输出 约简集(B1, B2, …, Bh)

step 1 初始化(B1, B2, …, Bh)=(Ø , Ø , …, Ø ).

step 2 计算多粒度决策形式背景Π 中协调粒度层的平均条件信息熵CIEave(D| ∑i=1hAi).

step 3 遍历协调粒度层下的各个属性集Ai, 计算去掉类属性块M1j, M2j, …, Mhj后的多粒度决策形式背景的平均条件信息熵

CIEave(D| ∑i=1h(Ai-Mij)).

step 4 若

CIEave(D| ∑i=1h(Ai-Mij))≠ CIEave(D| ∑i=1h(Ai)),

则Bi← Bi∪ Mij.

step 5 若j小于类属性块个数, 返回step 3; 否则转step 7.

step 6 若Mit⊆Ai-Bi且

SIG¯outer( ∑i=1h(Mit|Bi))= maxMij⊆Ai-Bi{ SIG¯outer( ∑i=1hMij|Bi)}

则Bi← Bi∪ Mit.

step 7 若

CIEave(D| ∑i=1hBi)≠ CIEave(D| ∑i=1hAi),

返回step 6, 直至

CIEave(D| ∑i=1hBi))=CIEave(D| ∑i=1hAi)

为止.

step 8 遍历协调集(B1, B2, …, Bh), 计算各个类属性块Mij的内重要度.

step 9 若

SIG¯inner( ∑i=1h(Bi|Mij))=0,

则Bi← Bi-Mij.

step 10 输出约简集(B1, B2, …, Bh).

算法2 最粗协调决策形式背景下的约简

输入 多粒度决策形式背景中的最粗协调决策形

式背景Fcor=(G, Acor, Icor, D, J)

输出 约简集Bcor

step 1 初始化Corecor(Acor)=Ø .

step 2 遍历属性集Acor中每个类属性块Mj, 计算其内重要度.

step 3 若 SIGinnercor(Acor|Mj)> 0, 则

Corecor(Acor)← Corecor(Acor)∪ Mj.

step 4 设Acor-Corecor(Acor)中包含的类属性块为M1, M2, …, Mr, 令Bcor=Corecor(Acor).

step 5 若

SIGoutercor(Mt|Bcor)= maxMj⊆Acor-Corecor(Acor){ SIGoutercor(Mj|Bcor)},

则 Bcor← Bcor∪ Mt.

step 6 若

CIE(D|Bcor)≠ CIE(D|Acor),

返回step 5, 直至

CIE(D|Bcor)=CIE(D|Acor)

为止.

step 7 遍历协调集Bcor, 计算每类属性块Mj的内重要度.

step 8 若

SIGinnercor(Bcor|Mj)=0,

则Bcor← Bcor-Mj.

step 9 输出约简集Bcor.

注意, 算法2也适用于计算多粒度决策形式背景在最细协调决策形式背景下的约简集, 只需将上下标涉及cor的字母全部替换为上下标为fin的字母即可.

4 实验及结果分析
4.1 实验数据集

为了验证本文提出的属性约简方法的性能, 从UCI数据集(http://archive.ics.uci.edu/ml/index.php)中选取5个公开数据集, 分别为Bank Marketing、Forest Fires、Wine Quality、Estimation of Obesity Levels Based on Eating Habits and Physical Condition(简称EOL)和Chess(King-Rook vs.King).详细信息如表6所示.

表6 实验数据集 Table 6 Experimental datasets

由于原始数据集的属性不是标准的0-1布尔值形式, 为了得到实验中所需的部分协调的多粒度决策形式背景, 首先将实验中的5个数据集均转化为决策形式背景, 核心思想是根据原始数据集的不同形式, 采取不同方法将其转化为0-1布尔值属性.具体操作如下.1)若原始数据集的属性取值是连续的, 进行分段处理, 每个分段区间被看作一个新的布尔属性, 实验中针对不同数据集的属性取值, 分段方式会有所不同.如在[0, 20]区间上连续取值的情形, 可将其分为[0, 5), [5, 10), [10, 15), [15, 20].2)若原始数据集的属性并非连续型, 而是多值属性, 则将每个属性取值看作一个新的布尔属性.在此基础上, 将每个类属性块下的相邻属性进行适当合并, 把实验中的5个数据集均处理成包含4个粒度层的部分协调决策形式背景, 其中前4个数据集的后2层为协调决策形式背景, 最后一个数据集的最后一层为协调决策形式背景.具体地, 每个数据集上任一粒度层下的类属性块记为A(1, 2, …, j), 其中大写英文字母表示每个数据集中的各个类属性块, 每类属性块下的各个布尔属性依次使用正整数表示, 那么将该粒度层下的相邻布尔属性进行适当合并得到更粗粒度的决策形式背景, 对应的类属性块记为A(1-i, (i+1)-t, …, k-j), 这里的区间1-i, (i+1)-t, …, k-j构成{1, 2, …, j}的一个划分.

为了方便讨论, 将Bank Marketing、Forest Fires、Wine Quality、EOL、Chess(King-Rook vs.King)数据集经过上述预处理后得到的数据集记为数据集1~数据集5, 具体的属性预处理过程如表7所示, 预处理后得到的数据集见表8.

表7 属性预处理过程 Table 7 Process of attribute preprocessing
表8 预处理后的数据集 Table 8 Datasets after preprocessing

最后, 根据本文算法分别对数据集1~数据集5的最粗粒度层和最细粒度层进行属性约简, 找出它们的冗余属性.同时, 计算5个数据集的协调粒度层平均条件信息熵, 得到它们的协调粒度层约简集, 并对约简集结果进行对比分析.

4.2 实验结果

在多粒度决策形式背景的最粗(细)协调粒度层Fcor=(G, Acor, Icor, D, J)(或 Ffin=(G, Afin, Ifin, D, J))中, 对于同一属性集Acor(Afin), 对象集G的属性约简集为B1, B2为扩展对象集G'(G⊆G')的属性约简集, 且B2是B1通过添加类属性块后再去掉冗余类属性块得到的属性约简集.本文在计算G'的属性约简集时, 尽可能保留B1中的类属性块.这种做法是为了观察对象变化后属性约简集之间存在的关联, 进一步评估约简方法的灵敏性.

计算平均条件信息熵进行属性约简的结果如表9所示.

表9 基于平均条件信息熵的属性约简结果 Table 9 Results of attribute reduction based on average conditional information entropy

由表9可看出, 在多粒度决策形式背景中, 计算平均条件信息熵可得到属性约简集, 这种约简方法是有效的.具体地, 对于实验中的数据集1, 在属性不变的情况下, 取不同范围的对象可实现有包含关系的属性约简.对于实验中的数据集2~数据集5, 虽然也可实现属性约简, 但在取不同范围的对象时, 属性约简集基本保持不变, 说明这种约简方法的约束条件太强.

在多粒度决策形式背景中基于最粗(细)协调粒度层计算属性重要度, 得到属性约简集的情况, 如表10和表11所示.由表10和表11可看出, 基于多粒度决策形式背景的最粗(细)协调粒度层的属性约简结果较理想, 当取不同范围的对象时基本都实现有包含关系的属性约简, 说明这2种约简方法是有效的, 约束条件相对宽松.因此, 从属性约简条件的宽松与否而言, 最粗协调粒度约简方法和最细协调粒度约简优于协调粒度约简方法.

表10基于最粗粒度层的属性约简结果 Table 10Results of attribute reduction based on the coarsest granularity layer
表11基于最细粒度层的属性约简结果 Table 11Results of attribute reduction based on the finest granularity layer

此外, 通过表9~表11还可得到如下结论.

1)根据删除冗余布尔属性的强度, 最细协调粒度层约简方法优于最粗协调粒度层约简方法, 而最粗协调粒度层约简方法又优于协调粒度层约简方法.

2)多粒度决策形式背景中的对象个数越多, 属性约简集包含的属性个数越多.

3)对于对象个数较多的多粒度决策形式背景, 其属性约简集可包含对象个数较少的多粒度决策形式背景的属性约简集, 这3种属性约简方法删除的类属性块实际上是在每一粒度层下去掉相同的块信息.

5 结束语

对于概念格属性约简, 现有研究都是基于单粒度形式背景的信息熵或保持代数结构进行研究, 本文是基于多粒度决策形式背景的条件信息熵探讨属性约简, 具体在多粒度决策形式背景中基于平均条件信息熵及最粗(细)协调粒度层的条件信息熵计算属性约简集, 并对提出的3种属性约简方法进行对比分析.本文是在多粒度决策形式背景中通过删除各协调粒度层下的类属性块的方式实施属性约简, 当这些类属性块来源于同一类别时, 可实现信息系统的属性约简.相比现有方法, 基于类属性块的属性约简将粒计算的多粒度思想应用于形式概念分析, 能从多个水平研究多粒度数据的属性冗余问题.此外, 本文的结果有助于今后对多粒度决策形式背景的属性约简进行进一步研究.

尽管本文为探究多粒度决策形式背景的属性约简提出协调粒度约简方法、最粗协调粒度约简方法和最细协调粒度约简方法, 但仍存在一些不足:1)本文讨论的属性约简是在假定各多粒度类属性块的重要程度均等的情况下进行的, 即不考虑类属性块的权重因素, 但实际应用中某些属性会被特殊对待, 所以类属性块代价敏感问题值得继续探讨.2)由于多粒度决策形式背景中会存在多个属性约简集的情况, 所以如何找到最优的约简集也是一个有意义的研究课题, 特别是设计快速高效的实现算法.3)多粒度决策形式背景的属性约简能否像单粒度决策形式背景那样, 研究如何得到合适的类属性块以提升数据分类精度也是一个重要的问题.

参考文献
[1] WILLE R. Restructuring Lattice Theory: An Approach Based on Hie-rarchies of Concepts // RIVAL I, ed. Ordered Sets. Berlin, Germany: Springer, 1982: 445-470. [本文引用:3]
[2] 张玲, 张钹. 基于商空间的问题求解: 粒度计算的理论基础. 北京: 清华大学出版社, 2014.
(ZHANG L, ZHANG B. Quotient Space Based Problem Solving: A Theoretical Foundation of Granular Computing. Beijing, China: Tsinghua University Press, 2014. ) [本文引用:1]
[3] MULKAR-MEHTA R, HOBBS J, HOVY E. Granularity in Natural Language Discourse // Proc of the 9th International Conference on Computational Semantics. Stroudsburg, USA: ACL, 2011: 360-364. [本文引用:1]
[4] WEI L, WAN Q. Granular Transformation and Irreducible Element Judgment Theory Based on Pictorial Diagrams. IEEE Transactions on Cybernetics, 2016, 46(2): 380-387. [本文引用:1]
[5] YAO Y Y. Three-Way Decisions with Probabilistic Rough Sets. Information Sciences, 2010, 180(3): 341-353. [本文引用:1]
[6] 苗夺谦, 张清华, 钱宇华, 等. 从人类智能到机器实现模型——粒计算理论与方法. 智能系统学报, 2016, 11(6): 743-757.
(MIAO D Q, ZHANG Q H, QIAN Y H, et al. From Human Inte-lligence to Machine Implementation Model: Theories and Applications Based on Granular Computing. CAAI Transactions on Intelligent Systems, 2016, 11(6): 743-757. ) [本文引用:1]
[7] 曾望林, 折延宏. 面向对象的多粒度形式概念分析. 计算机科学, 2018, 45(10): 51-53, 63.
(ZENG W L, SHE Y H. Object-Oriented Multigranulation Formal Concept Analysis. Computer Science, 2018, 45(10): 51-53, 63. ) [本文引用:2]
[8] 李金海, 吴伟志, 邓硕. 形式概念分析的多粒度标记理论. 山东大学学报(理学版), 2019, 54(2): 30-40.
(LI J H, WU W Z, DENG S. Multi-scale Theory in Formal Concept Analysis. Journal of Shand ong University(Natural Science), 2019, 54(2): 30-40. ) [本文引用:5]
[9] 李金海, 李玉斐, 米允龙, 等. 多粒度形式概念分析的介粒度标记方法. 计算机研究与发展, 2020, 57(2): 447-458.
(LI J H, LI Y F, MI Y L, et al. Meso-Granularity Labeled Method for Multi-granularity Formal Concept Analysis. Journal of Computer Research and Development, 2020, 57(2): 447-458. ) [本文引用:1]
[10] PAWLAK Z. Rough Sets. International Journal of Computer and Information Sciences, 1982, 11(5): 341-356. [本文引用:1]
[11] KUZNETSOV S O. Machine Learning on the Basis of Formal Concept Analysis. Automation and Remote Control, 2001, 62(10): 1543-1564. [本文引用:1]
[12] 李金海, 魏玲, 张卓, 等. 概念格理论与方法及其研究展望. 模式识别与人工智能, 2020, 33(7): 619-642.
(LI J H, WEI L, ZHANG Z, et al. Concept Lattice Theory and Method and Their Research Prospect. Pattern Recognition and Artificial Intelligence, 2020, 33(7): 619-642. ) [本文引用:1]
[13] KUMAR C A, SRINIVAS S. Mining Associations in Health Care Data Using Formal Concept Analysis and Singular Value Decomposition. Journal of Biological Systems, 2010, 18(4): 787-807. [本文引用:1]
[14] LI J H, MEI C L, CHERUKURI A K, et al. On Rule Acquisition in Decision Formal Contexts. International Journal of Machine Learning and Cybernetics, 2013, 4(6): 721-731. [本文引用:1]
[15] POELMANS J, IGNATOV D I, KUZNETSOV S O, et al. Formal Concept Analysis in Knowledge Processing: A Survey on Applications. Expert Systems with Applications, 2013, 40(16): 6538-6560. [本文引用:1]
[16] SINGH P K, KUMAR C A. Bipolar Fuzzy Graph Representation of Concept Lattice. Information Sciences, 2014, 288: 437-448. [本文引用:1]
[17] TAN A H, LI J J, LIN G P. Connections between Covering-Based Rough Sets and Concept Lattices. Informational Journal of Approximation Reasoning, 2015, 56(A): 43-58. [本文引用:1]
[18] WANG L D, LIU X D. Concept Analysis via Rough Set and AFS Algebra. Information Sciences, 2008, 178(21): 4125-4137. [本文引用:1]
[19] YAO Y Y. Concept Lattices in Rough Set Theory // Proc of the IEEE Annual Meeting of the Fuzzy Information. Washington, USA: IEEE, 2004, II: 796-801. [本文引用:1]
[20] ZHANG W X, MA J M, FAN S Q. Variable Threshold Concept Lattices. Information Sciences, 2007, 177(22): 4883-4892. [本文引用:1]
[21] 张文修, 魏玲, 祁建军. 概念格的属性约简理论与方法. 中国科学(信息科学), 2005, 35(6): 628-639.
(ZHANG W X, WEI L, QI J J. Attribute Reduction Theory and Approach to Concept Lattice. Science in China(Information Sciences), 2005, 35(6): 628-639. ) [本文引用:1]
[22] 张文修, 仇国芳, 吴伟志. 粗糙集属性约简的一般理论. 中国科学(信息科学), 2005, 35(12): 1304-1313.
(ZHANG W X, QIU G F, WU W Z. Generalized Theory of Attribute Reduction in Rough Sets. Science in China(Information Sciences), 2005, 35(12): 1304-1313. ) [本文引用:1]
[23] WU W Z, LEUNG Y, MI J S. Granular Computing and Knowledge Reduction in Formal Contexts. IEEE Transaction on Knowledge and Data Engineering, 2009, 10(21): 1461-1474. [本文引用:4]
[24] 魏玲, 祁建军, 张文修. 决策形式背景的概念格属性约简. 中国科学(信息科学), 2008, 38(2): 195-208.
(WEI L, QI J J, ZHANG W X. Attribute Reduction of Concept Lattice in Decision Formal Context. Science in China(Information Sciences), 2008, 38(2): 195-208. ) [本文引用:2]
[25] LI J H, MEI C L, LÜ Y J. Knowledge Reduction in Decision Formal Contexts. Knowledge-Based Systems, 2011, 24(5): 709-715. [本文引用:1]
[26] 李进金, 张燕兰, 吴伟志, 等. 形式背景与协调决策形式背景属性约简与概念格生成. 计算机学报, 2014, 37(8): 1768-1774.
(LI J J, ZHANG Y L, WU W Z, et al. Attribute Reduction for Formal Context and Consistent Decision Formal Context and Con-cept Lattice Generation. Chinese Journal of Computers, 2014, 37(8): 1768-1774. ) [本文引用:1]
[27] SHANNON C E, WEARER W. The Mathematical Theory of Communication. Champaign, USA: University of Illinois Press, 1971. [本文引用:1]
[28] DAI J H, HU H, ZHENG G J, et al. Attribute Reduction in Interval-Valued Information Systems Based on Information Entropies. Frontiers of Information Technology & Electronic Engineering, 2016, 17(9): 919-928. [本文引用:1]
[29] ZHANG X, MEI C L, CHEN D G, et al. Active Incremental Feature Selection Using a Fuzzy-Rough-Set-Based Information Entropy. IEEE Transactions on Fuzzy Systems, 2020, 28(5): 901-915. [本文引用:1]
[30] ZHANG X, MEI C L, CHEN D G, et al. Feature Selection in Mixed Data: A Method Using a Novel Fuzzy Rough Set-Based Information Entropy. Pattern Recognition, 2016, 56: 1-15. [本文引用:1]
[31] THUY N N, WONGTHANAVASU S. On Reduction of Attributes in Inconsistent Decision Tables Based on Information Entropies and Stripped Quotient Sets. Expert Systems with Applications, 2019, 137: 308-323. [本文引用:1]
[32] WANG F, LIANG J Y, QIAN Y H. Attribute Reduction: A Dimension Incremental Strategy. Knowledge-Based Systems, 2013, 39: 95-108. [本文引用:1]
[33] HU Q H, XIE Z X, YU D R. Hybrid Attribute Reduction Based on a Novel Fuzzy-Rough Model and Information Granulation. Pa-ttern Recognition, 2007, 40(12): 3509-3521. [本文引用:1]
[34] 王国胤, 于洪, 杨大春. 基于条件信息熵的决策表属性约简. 计算机学报, 2002, 25(7): 759-766.
(WANG G Y, YU H, YANG D C. Decision Table Reduction Based on Conditional Information Entropy. Chinese Journal of Computers, 2002, 25(7): 759-766. ) [本文引用:2]
[35] 陈东晓, 李进金, 林荣德, 等. 基于信息熵的形式背景属性约简. 模式识别与人工智能, 2020, 33(9): 786-798.
(CHEN D X, LI J J, LIN R D, et al. Attribute Reductions of Formal Context Based on Information Entropy. Pattern Recognition and Artificial Intelligence, 2020, 33(9): 786-798. ) [本文引用:1]
[36] LI J L, HE Z Y, ZHU Q L, et al. An Entropy-Based Weighted Concept Lattice for Merging Multi-source Geo-Ontologies. Entropy, 2013, 15(6): 2303-2318. [本文引用:1]
[37] SINGH P K, CHERUKURI A K, LI J H. Concepts Reduction in Formal Concept Analysis with Fuzzy Setting Using Shannon Entropy. International Journal of Machine Learning and Cybernetics,2017, 8(1): 179-189. [本文引用:1]
[38] 张文修, 仇国芳. 基于粗糙集的不确定决策. 北京: 清华大学出版社, 2005.
(ZHANG W X, QIU G F. Uncertain Decision Making Based on Rough Set. Beijing, China: Tshinghua University Press, 2005. ) [本文引用:1]
[39] 梁吉业, 钱宇华. 信息系统中的信息粒与熵理论. 中国科学(信息科学), 2008, 38(12): 2048-2065.
(LIANG J Y, QIAN Y H. Information Granularity and Entropy Theory in Information systems. Science in China(Information Sciences), 2008, 38(12): 2048-2065. ) [本文引用:1]
[40] 苗夺谦, 胡桂荣. 知识约简的一种启发式算法. 计算机研究与发展, 1999, 36(6): 681-684.
(MIAO D Q, HU G R. A Heuristic Algorithm for Reduction of Knowledge. Journal of Computer Research and Development, 1999, 36(6): 681-684. ) [本文引用:1]
[41] 高乐, 王振, 魏玲, 等. 基于属性分类的悲观概念格与乐观概念格. 模式识别与人工智能, 2021, 34(8): 701-711.
(GAO L, WANG Z, WEI L, et al. Pessimistic Concept Lattices and Optimistic Concept Lattices Based on Attribute Classification. Pattern Recognition and Artificial Intelligence, 2021, 34(8): 701-711. ) [本文引用:1]
[42] 李金海, 贺建君, 吴伟志. 多粒度形式概念分析的类属性块优化. 山东大学学报(理学版), 2020, 55(5): 1-12.
(LI J H, HE J J, WU W Z. Optimization of Class-Attribute Block in Multi-granularity Formal Concept Analysis. Journal of Shand ong University(Natural Science), 2020, 55(5): 1-12. ) [本文引用:1]
[43] HUANG C C, LI J H, DIAS S M. Attribute Significance, Consistency Measure and Attribute Reduction in Formal Concept Analysis. Neural Network World, 2016, 26(6): 607-623. [本文引用:1]