1.1.1 改进潜在因子模型的推荐

SVD为常用的矩阵分解方法, 但由于需要将稀疏矩阵稠密化, 计算量和存储量都较大.相比SVD, LFM可较好地缓解这一问题, 避免填充原始稀疏矩阵的操作, 直接将原始矩阵分解为两个低维的特征矩阵的乘积, 降低计算量和存储量.本文定义P为用户特征矩阵, Q为项目特征矩阵, 利用ReLU激活函数随机初始赋值P和Q.重构的预测评分矩阵R=P^TQ.本文设定F为隐因子数量, u为用户编号, i为项目编号, 矩阵中所有个体

${{\hat{r}}_{u, i}}=\sum\limits_{f=1}^{F}{{{p}_{u, f}}{{q}_{i, f}}.}$

至此, 初步模型建立.

本文将已有的评分数据集随机划分为训练集和测试集, 在训练集上, 不断训练模型以优化P、Q, 然后取其乘积R, 最小化真实评分值r_{u, i}和预测评分值${{\hat{r}}_{u, i}}$的差值, 目标优化函数为:

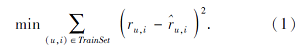
同时, 考虑到用户或项目本身的固有属性可能会对预测评分产生一定的影响, 在目标优化函数中加入偏差项, 消除评分的差异性.加入用户偏差项b_u、项目偏差项b_i和全局平均分s的评分计算函数:

将上式代入式(1), 可得

min∑(u, i)∈TrainSet(ru, i-∑f=1Fpu, fqi, f-bu-bi-s)2.

本文除了考虑用户对项目的显式评分以外, 也考虑社交行为关系.针对微博用户, 用户的社交行为信息主要有评论、转发、点赞等交互.参照文献[27]定义:

p_u=p_u+ S(u)α1∑k∈S(u)y_k+ A(u)α2∑k∈A(u)y_k,

其中:S(u)表示用户关注对象的集合; A(u)表示用户可能发生的行为集合; α ₁=α ₂=-0.5, 表示在最初的情况下, 这两个集合对用户的预测偏好具有相同影响; y_k表示用户的反馈信息.最终评分预测为:

${{\hat{r}}_{u, i}}=\sum\limits_{f=1}^{F}{\left( \left( {{p}_{u, f}}+{{\left| S(u) \right|}^{{{\alpha }_{1}}}}\sum\limits_{k\in S(u)}{{{y}_{k}}+{{\left| A(u) \right|}^{{{\alpha }_{2}}}}\sum\limits_{k\in A(u)}{{{q}_{i, f}}}} \right) \right)+{{b}_{u}}+{{b}_{i}}+s}.$

再通过全局目标优化函数不断进行多次迭代优化:

$\begin{aligned} C(p, q)=& \sum_{(u, i) \in \text { TrainSet }}\left(r_{u, i}-\hat{r}_{u, i}\right)^{2}=\sum_{(u, i) \in \text { TrainSet }}\left(r_{u, i} \mid-\sum_{f=1}^{F} p_{u, f} q_{i, f}\right)^{2} . \end{aligned}$ (2)

为了防止过拟合, 提高模型的泛化能力, 在式(2)中加入正则化约束, 可得

$C(p, q)=\sum_{(u, i) \in \text { TrainSet }}\left(r_{u, i}-\hat{r}_{u, i}\right)^{2}+\lambda\left(\left|p_{u}\right|^{2}+\left|q_{i}\right|^{2}\right)$

采用Adam(Adaptive Moment Estimation)对目标函数进行最小化求解.

1.1.2 基于神经网络的多层感知机模型

人工神经网络是一种利用多个线性单元组合以解决非线性问题的神经元组合, 它使用多层多神经元的结构分割非线性相关样本空间, 完成定义的预测任务.MLP是一种应用广泛的人工神经网络, 由于其在非线性表示学习上的优势而被广泛应用到各种连续的评分及预测任务中^[1].因此, 本文选择MLP处理输入层的用户交互, 选择合适的神经元激活函数对输入的隐式特征进行表示学习和评分预测.

本文构建MLP, 学习获取用户潜在特征向量p_u、q_i之间的非线性交互关系, 替代原有的MF中对用户特征矩阵和项目特征矩阵进行内积处理的操作.本文构建的MLP定义如下:

其中, W_X表示第X层隐层的权重矩阵, b_X表示第X层隐层的偏置向量, a_X表示第X层隐层的激活函数, σ 表示输出层激活函数.

对于激活函数的选择, MLP可选取Sigmoid、tanh、ReLU等激活函数.由于Sigmoid函数限制每个神经元取值范围为(0, 1), 收敛速度较慢, 可能会限制模型的性能, 所以本文不采用此激活函数.对于tanh、ReLU, 在实验部分, 本文进行相应的对比实验.

为了使最终预测的评分无限逼近真实有效评分, 采用Adam对目标函数进行最小化求解.Adam基于历史梯度计算一阶和二阶动量, 调整不同参数的学习速率, 减少学习速度调整的痛苦度, 因此收敛速度快于SGD(Stochastic Gradient Descent).

1.1.3 融合改进潜在因子和多层感知机的协同过滤推荐

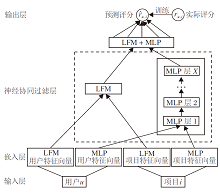
基于1.1.1节中改进的LFM获取用户和项目之间的线性交互关系, 依据1.1.2节中的MLP使用非线性内核捕捉用户和项目之间的非线性交互关系.为了获取用户和项目之间更多的交互特征, 本文融合LFM和MLP, 构建混合模型, 简记为LFM-MLP, 兼顾保留LFM和MLP的优势.LFM-MLP框图如图1所示.

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 LFM-MLP框图Fig.1 Framework of LFM-MLP

在模型融合方式的选择方面, 一般采取的方式是共享输入层和嵌入层, 然后融合LFM和MLP的评分输出.但是这种方式要求两个模型的潜在向量空间的维度相同, 如果两个模型在不同尺寸的嵌入层得到最优解, 混合后的模型就无法获得最优解.因此, 为了避免这一问题, 本文对两个模型分别灵活采用独立的嵌入层, 在LFM和MLP的输出层加入一个全连接层, 直至需要输出评分时, 结合两个模型的评分提取特征:

其中, puL、 qiL分别表示LFM上用户特征矩阵和项目特征矩阵的嵌入层, puM、 qiM分别表示MLP上用户特征矩阵和项目特征矩阵的嵌入层, ϕ ^LFM表示LFM输出的评分预测值, ϕ ^MLP表示MLP输出的评分预测值, ${{\hat{r}}_{u, i}}$表示LFM-MLP输出的预测评分值, α 表示权衡超参数, 当α =0.5时, 表明初始状态下LFM和MLP对LFM-MLP的影响度相同.

对于模型的优化, 鉴于LFM-MLP的非凸性, 使用SGD优化方法就可找到局部最优解.在模型初始化阶段, 本文使用LFM和MLP的预训练模型进行LFM-MLP的初始化, 预训练阶段仍利用基于动量的Adam方法进行优化.预训练完成后, 本文将训练完成的参数传送至LFM-MLP, 再采用基于梯度的SGD优化方法优化LFM-MLP, 达到最佳的优化效果, 同时节省内存空间.

1.2.1 传统偏好融合策略

群组推荐算法在获得个体用户对推荐项目的预测得分的基础上, 整合个体用户的预测评分, 实现群组用户的预测得分, 使推荐结果满足群组需求.文献[4]中介绍如下3种传统的基于满意度的融合策略.

1)最大满意策略.对某个项目进行评分时, 选取最喜欢该项目的成员的偏好值作为群组整体的偏好, 定义如下:

G_j= maxui∈Gr_ij,

其中, G_j表示群组G对项目j的评分值, r_ij表示群组成员用户u_i对项目j的评分值.

2)最小痛苦策略.对一个项目评分时, 取整个组中评分最低值作为群组偏好, 定义如下:

G_j= minui∈Gr_ij.

3)均值策略.为了平衡最大满意策略和最小痛苦策略, 对某个项目评分时, 选取整个群组预测分数的平均值作为群组偏好, 定义如下:

G_j= averageui∈Gr_ij= 1n∑i=1nr_ij .

这三种融合策略都属于单一融合策略, 主要依据群组成员对项目满意度的高低获取群组对该项目的偏好值.

1.2.2 纳什均衡偏好融合策略

一个群组内用户之间偏好的差异需要一定的权衡, 从而形成群组的最高满意度.博弈论是研究多方在一定条件下的博弈中, 利用相关各方的策略实施相应策略的理论^{[21, 28]}.本文考虑使用非合作博弈论的方法以最大化群组成员的平均满意度, 并将群组成员作为博弈参与者.项目的预测得分是游戏玩家的策略选择.在策略组合中, 所有参与者在不改变策略的情况下确保自己的策略最优, 即为纳什均衡.因此, 达到最佳群组满意度的问题可看作是纳什均衡的求解问题.尽管用户会有自己的选择, 但总会存在不止一种的纳什均衡.

文中设集合G为至少有两位成员的群组集合, 所有成员都来自用户集U, u为集合G中的用户成员,

|G| = 2^k-k-1,

表示集合G中的成员数量, N为群组推荐的未被组内成员评分过的项目集合:

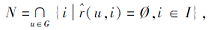
其中$\hat{r}(u, i)$表示用户u对项目i的预测评分值.

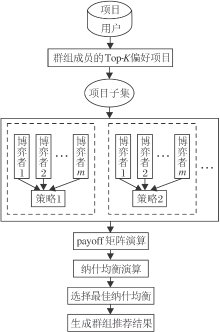
本文将群组推荐问题建模为一个非合作博弈, 向群组推荐的项目均为纳什均衡中的项目, 具体示意图如图2所示.

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 纳什均衡策略示意图Fig.2 Flow chart of Nash equilibrium strategy

常见博弈为元组(m, A, f).m为玩家(小组成员)的数目.A为玩家一组博弈动作的集合(可能的项目评分值), a_j∈ A, 为博弈动作.f为计算玩家收益值(payoff)的函数.

将一组可能的动作填充到动作集RA中, 供玩家使用, 即

RA= ⋃j=1ma_j.

这些动作都是具有较高预测值的项.

收益函数用于计算成员u的预测满意度, 通过给定的博弈策略下所有玩家选择的行动进行计算, 即

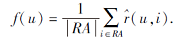
纳什均衡是一种稳定的群组策略, 认为其他参与者不会改变自己的满意度, 因此当前参与者没有动力去改变自己的满意度.而当该群组存在多个纳什均衡时, 本文定义获得收益的最佳方式, 即调和均值函数:

ha(x)=n( ∑i=1n1xi)^-1,

其中, x_i表示该群组成员对纳什均衡中每个项目的偏好值, n表示项目数.考虑到倒数平均数值越大, 方差越小, 这也意味着该策略越公平, 因此优先选取方差值较小的集合, 也就是调和平均值最高的动作集.

为了更直观地理解本文的纳什均衡策略, 现举例说明.如表1所示, 本文考虑一组中2位成员对5个项目的偏好.表2为正常博弈下的收益矩阵.

表1

Table 1

表1(Table 1)

表1 群组成员偏好 Table 1 Group member preference A B C D E 成员1 10 4 3 8 6 成员2 1 9 8 5 4

表1 群组成员偏好 Table 1 Group member preference

表2

Table 2

表2(Table 2)

表2 成员1和成员2正常博弈下的收益矩阵 Table 2 Payoff matrix of member 1 and member 2 in normal game B C D A (7.0, 5.0) (6.5, 4.5) (9.0, 3.0) D (6.0, 6.5) (3.5, 6.5) (8.0, 5.0) E (5.0, 6.5) (4.5, 6.0) (7.0, 4.5)

表2 成员1和成员2正常博弈下的收益矩阵 Table 2 Payoff matrix of member 1 and member 2 in normal game

由表1可看出, 成员1对项目A、D、E的评分较高, 这3个项目可能被其选择为博弈的对象项目.同样地, 成员2可能会选择B、C、D作为博弈的对象.可看出, 该收益矩阵只具有一个纳什均衡策略(A, B), 其中, A表示成员1将要选择的动作的项, B表示成员2将要选择的动作的项.因此, 7.0是成员1的收益值, 5.0是成员2的收益值.原因如下:如果成员1选择A, 成员2将不会从B改变为C或D, 因为收益会减少.同样地, 考虑到成员2选择行动B, 成员1如果将选择从A改为D或E, 也没好处.因此, 如果存在其它纳什均衡, 则使用调和均值函数.

本文提出基于纳什均衡策略的群组推荐算法, 步骤如算法1所示.

算法1 基于纳什均衡策略的群组推荐算法

输入 群组成员对项目的评分记录ratings

输出 群组推荐结果R

按照item-feature的内容把用户划分成组, 得到群组集合G;

for u in U: //用户集合U

for i in I: // 项目集合I

获取每位用户对项目的偏好评分pre_rat;

取top-K个预测评分项目添至ItemSet;

end for

end for

for tactic in ItemSet: //计算收益值并建立收益矩阵

payoff = f(tactic);

end for

从payoff中获取纳什均衡;

if 存在多个纳什均衡:

选择调和均值最大的纳什均衡;

end if

R= max(group_rat);

//在群组预测评分中取top-K项目, 形成群组推荐 项目集合R

Return R

设用户数为m, 项目数为n, 算法1的时间复杂度为O(mn).

本文所有实验的数据集都来自KDD CUP 2012 Track1中的腾讯微博数据集.选取时间段为2011.11.11至2011.12.11, 共30天的微博记录, 包含1 392 973名用户对4 710个项目的73 209 277个历史评分记录, 数据集的大小约为3.8 G.数据集内容包括社会关系和用户项特征等信息, 所有的个人数据中与用户相关的信息都加密保护, 如使用数字代替用户名和项目名.实验数据集文件列表如表3所示.

表3

Table 3

表3(Table 3)

表3 数据集文件统计 Table 3 Statistics of dataset files 文件名 大小 rec_log_train.txt 1.99G item.txt 1.18M user_profile.txt 55.8M user_action.txt 217M user_sns.txt 740M user_key_word.txt 182M

表3 数据集文件统计 Table 3 Statistics of dataset files

在表3的6个文件中, rec_log_train.txt中的评分值表示推荐结果, 即用户在该项上的显式得分.数据格式为UserId、ItemId、Result、Unix-timestamp, 分数有3种:1表示接受, -1表示拒绝, 0表示未知.通过实验数据需求获取user-item-score 三元组信息.

在评分数据集(rec_log_train.txt)上, 用户接受的记录数只有5 253 828条, 而总记录数为73 209 277条, 包含大量负样本, 还有大量的项目未被用户发现或接受, 相当多的用户不是很活跃.因此, 将用户的社交行为引入预测分数中, 解决数据的稀疏性, 提高推荐的准确性.累计用户行为数据集(user_action.txt)上记录用户行为权重(user@、转发数、评论数), 最后对用户行为权重进行由大到小的排序, 过滤活跃用户, 共有61 083人的活跃程度大于180.最后, 在原始的得分数据集上, 对这些活跃用户的得分进行筛选和测试, 总共有6 741 799条记录.

本文将数据集按照1∶ 4的比例随机划分为测试集与训练集, 采用交叉验证方式, 将每个模型计算5次后取其平均值作为最终的实验结果.

群组推荐实验通过数据集上item.txt文件中的用户分类信息查找同组用户, 本文取不同级种类的级别, 分别标记为级别1~级别4, 将同种中的用户划分为一个个小群组, 得到该组的集合G.

本文采用均方根误差(Root Mean Square Error, RMSE)作为评价指标, RMSE表示测试集中所有预测得分和真实得分之间的平方差之和的平方根与测试集数量之比, RMSE越小, 推荐越准确.RMSE计算公式如下:

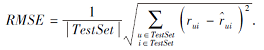
本文实验主要分为两部分:1)针对个体的推荐模型开展性能对比实验, 验证LFM-MLP的有效性; 2)面向群组, 通过不同融合策略的效果对比实验, 验证纳什均衡策略的有效性.

2.4.1 不同推荐模型性能对比

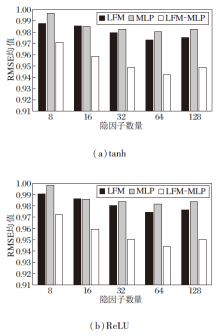
为了验证LFM-MLP的有效性, 先分析不同激活函数对模型的影响, 选择tanh、ReLU激活函数, LFM、MLP、和LFM-MLP在不同隐因子数量下的RMSE均值如图3所示.

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 不同激活函数对推荐模型的影响Fig.3 Effect of different activation functions on recommendation model

由图3可清晰看出, 当隐因子数量为8, 16, 32, 64时, 随着隐因子数量的增加, RMSE均值减小, 精度提高, 推荐性能变优.本文采用的数据集的值的特点(即数据评分为-1, 0, 1)导致对于不同的激活函数有不同的敏感性, 通过对比实验可看出, 选择tanh为激活函数时效果优于ReLU.因此本文选择tanh为网络的激活函数.另外, 在限定隐因子数量的条件下, LFM-MLP推荐性能最优, 在准确率上, LFM-MLP比优化后的LFM提升3.17%.

为了验证LFM-MLP的优势, 选择具有代表性的NeuMF(Neural Matrix Factorization)^[15] 、LFM和M-LP.在具体的网络参数设定时, 将NeuMF的隐层网络层数设为3, 即和LFM-MLP采用相同的隐层网络层数.

本文设置不同的潜在特征空间, 在不同数量的隐因子条件下, 随着隐因子数量的变化, 评估对比模型的性能.为了保障实验公平性, 隐因子数量为8、16、32、64、128.

不同推荐模型随隐因子数量变化的RMSE均值如表4所示.由表可看出, LFM-MLP的RMSE均值最小, 当隐因子数量为128时, 相比LFM-MLP, NeuMF误差增大0.78%, 表明LFM-MLP的推荐效果更优.这主要是因为LFM-MLP保留LFM和MLP的优势, 也说明本文使用线性内核和非线性内核分别捕捉用户和项目之间的线性交互和非线性交互的方法是可行的.MLP的推荐性能最差, 这可能主要与MLP的隐层层数有关, 过深的隐层虽然可获取更多的非线性交互信息, 也可能导致过拟合现象的发生.

表4

Table 4

表4(Table 4)

表4 隐因子数量不同时各模型的RMSE均值对比 Table 4 RMSE average comparison of all models with different number of latent factors 模型 隐因子数量 8 16 32 64 128 LFM 0.98726 0.98415 0.97934 0.97301 0.97496 MLP 0.99628 0.98549 0.98242 0.98035 0.98214 NeuMF 0.97628 0.96293 0.95224 0.94735 0.95605 LFM-MLP 0.97061 0.95836 0.94859 0.94213 0.94867

表4 隐因子数量不同时各模型的RMSE均值对比 Table 4 RMSE average comparison of all models with different number of latent factors

2.4.2 不同融合策略效果对比

本节的群组推荐实验主要对比基于满意度的融合策略(最大满意策略、最小痛苦策略和均值策略)^[4]、UL融合策略^[22]、AwU融合策略^[24]和本文的纳什均衡策略.UL融合策略考虑评分偏差, 并与均值、认可投票方法^[23]结合.AwU融合策略是利用信息熵分析组成员评分分布的一种增强的偏好聚合技术.

针对群组协同过滤推荐, 本文采用两种方法进行对比实验:

1)分组协同过滤, 先对用户分组, 再使用混合模型求解用户在组中项目集合的预测分数, 进行群组推荐;

2)全局协同过滤, 对所有个体完成推荐预测后再对用户进行分组, 使用全局预测评分矩阵进行计算.这两种方法都是将K个项目推荐给该组, 生成一个推荐列表Top-K以计算RMSE均值.

全局协同过滤和分组协同过滤方式下不同群组融合策略的效果对比如图4所示.

图4

Fig.4

	Figure Option ViewDownloadNew Window
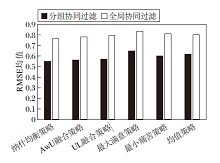	图4 不同协同过滤方式对群组融合策略性能的影响Fig.4 Effect of different collaborative filtering methods on the performance of group fusion strategies

由图4可知, 无论采用哪一种融合策略, 采用分组协同过滤方式的推荐效果都优于使用全局协同过滤方式.在不同级别的类中进行分组后, 如果群组成员之间的偏好相似度较高, 说明成员之间的兴趣偏好更相似, 接受的概率更大, 因此采用分组协同过滤方式的群组推荐效果更优.

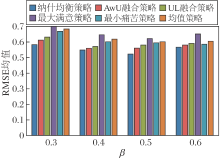
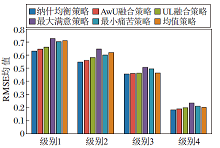
对于预测值, 本文定义阈值β , 若预测值大于β , 表示群组在真实情况下接收推送该项目的推荐, 否则表示此项目的推荐不被接受.β 对不同融合策略的影响如图5所示.本文取item.txt文件中的用户分类信息确定同组用户, 同时取不同级种类的级别, 分别标记为级别1~级别4, 将同一种类中的用户划分为一个个小群组, 得到该组的集合G.

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 β 对群组融合策略性能的影响Fig.5 Effect of β values on the performance of different group fusion strategies

由图5可知, 调整β 值的大小, 在一定范围内可提升三种基于满意度的推荐融合策略性能.在三种基于满意度的策略中, 最小痛苦策略一直保持最优的推荐效果.由于在均值的基础上考虑评分偏差, 所以UL融合策略性能优于三种基于满意度的融合策略.相比UL融合策略, AwU融合策略也是基于认可投票, 但是由于混合附加效用与认可投票方法, 并在此基础上利用信息熵分析组成员评分的分布, 所以性能优于UL融合策略.本文的纳什均衡策略性能最优, 在β =0.5时, 取得最优性能, RMSE均值最低.

不同群组分组级别下群组融合策略的性能对比如图6所示.由图可知, 不同群组分组级别中分类精细度也不同, 分类级别越高, 分类越细化.对比融合策略在群组推荐中同样取得良好性能.本文的纳什均衡策略在级别4(分类精细度最高)上RMSE均值最低, 取得最优效果.这也说明纳什均衡策略在用户相似度较高、分类细化度较高时推荐效果更精确.

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 不同群组分组级别对群组融合策略的影响Fig.6 Effect of different group levels on group fusion strategies

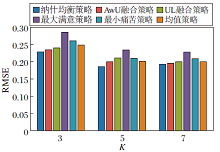
不同群组融合策略的性能对比如图7所示.由图可知, 当用户选取具有个人偏好的5个对象(K=5)而形成推荐集合ItemSet时, 纳什均衡策略获得最优数目, 推荐性能最优.同时, 随着K值的不断增加, UL融合策略和AwU融合策略的推荐效果逐步接近纳什均衡策略.由于纳什均衡策略主要是在固定两个项目的分布中体现分布之间的差异, 当用户与其他用户的组发生变化时, 项目的组合也会发生变化, 导致项目分布发生变化, 纳什均衡的结果也发生变化.

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 K值对群组融合策略的影响Fig.7 Effect of K values on group fusion strategies