引用本文
吴兴宇, 江兵兵, 吕胜飞, 王翔宇, 陈秋菊, 陈欢欢. 基于马尔科夫边界发现的因果特征选择算法综述. 模式识别与人工智能, 2022,35(5): 422-438
WU Xingyu, JIANG Bingbing, L#cod#x000dc; Shengfei, WANG Xiangyu, CHEN Qiuju, CHEN Huanhuan. A Survey on Causal Feature Selection Based on Markov Boundary Discovery. PATTERN RECOGNITION AND ARTIFICIAL INTELLIGENCE, 2022,35(5): 422-438.  
Doi: 10.16451/j.cnki.issn1003-6059.202205004
Permissions
Copyright©2022, 《模式识别与人工智能》编辑部
《模式识别与人工智能》编辑部
基于马尔科夫边界发现的因果特征选择算法综述
吴兴宇1, 江兵兵2, 吕胜飞3, 王翔宇1, 陈秋菊4, 陈欢欢1
1.中国科学技术大学 计算机科学与技术学院 合肥 230027
2.杭州师范大学 信息科学与工程学院 杭州 311121
3.南洋理工大学 计算机科学与工程学院 新加坡 639798
4.中国科学技术大学 信息科学技术学院 合肥 230026
通讯作者：

陈欢欢,博士,教授,主要研究方向为神经网络、贝叶斯推断、演化计算.E-mail:hchen@ustc.edu.cn.

作者简介：

吴兴宇,博士研究生,主要研究方向为因果学习、特征选择、机器学习.E-mail:xingyuwu@mail.ustc.edu.cn.

江兵兵,博士,讲师,主要研究方向为贝叶斯学习、半监督学习.E-mail:jiangbb@hznu.edu.cn.

吕胜飞,博士,主要研究方向为关系抽取.E-mail:shengfei.lyu@ntu.edu.sg.

王翔宇,博士研究生,主要研究方向为知识图谱.E-mail:sa312@mail.ustc.edu.cn.

陈秋菊,博士,副研究员,主要研究方向为信号与信息处理(电子对抗信息处理)、知识融合的智能计算.E-mail:qqchern@ustc.edu.cn.

收稿日期: 2021-12-20 接受日期: 2022-03-24
资助项目: 国家科技创新2030——“新一代人工智能”重大项目(No.2021ZD0111700)、国家自然科学基金项目(No.62137002,62006065)、安徽省重点研发计划项目(No.202104a05020011)、安徽省科技重大专项项目(No.202103a07020002)、中央高校基本科研业务费专项资金(No.WK2150110019,WK2100000027)资助
摘要

因果特征选择算法(也称为马尔科夫边界发现)学习目标变量的马尔科夫边界,选择与目标存在因果关系的特征,具有比传统方法更好的可解释性和鲁棒性.文中对现有因果特征选择算法进行全面综述,分为单重马尔科夫边界发现算法和多重马尔科夫边界发现算法.基于每类算法的发展历程,详细介绍每类的经典算法和研究进展,对比它们在准确性、效率、数据依赖性等方面的优劣.此外,进一步总结因果特征选择在特殊数据(半监督数据、多标签数据、多源数据、流数据等)中的改进和应用.最后,分析该领域的当前研究热点和未来发展趋势,并建立因果特征选择资料库(http://home.ustc.edu.cn/~xingyuwu/MB.html),汇总该领域常用的算法包和数据集.

关键词: 马尔科夫边界; 特征选择; 因果学习; 因果特征选择; 贝叶斯网络; 马尔科夫毯
中图分类号:TP391
A Survey on Causal Feature Selection Based on Markov Boundary Discovery
WU Xingyu1, JIANG Bingbing2, LÜ Shengfei3, WANG Xiangyu1, CHEN Qiuju4, CHEN Huanhuan1
1. School of Computer Science and Technology, University of Science and Technology of China, Hefei 230027
2. School of Information Science and Technology, Hangzhou Normal University, Hangzhou 311121
3. School of Computer Science and Engineering, Nanyang Technological University, Singapore 639798 Singapore
4. School of Information Science and Technology, University of Science and Technology of China, Hefei 230026
Corresponding author:
CHEN Huanhuan, Ph.D., professor. His research interests include neural networks, Bayesian inference and evolutionary computation.

About Author:
WU Xingyu, Ph.D. candidate. His research interests include causal learning, feature selection and machine learning.
JIANG Bingbing, Ph.D., lecturer. His research interests include Bayesian learning and semi-supervised learning.
LÜ Shengfei, Ph.D. His research inte-rests include relation extraction.
WANG Xiangyu, Ph.D. candidate. His research interests include knowledge graph.
CHEN Qiuju, Ph.D., associate professor. Her research interests include signal and information processing for electronic countermeasures, and know-ledge fusion for intelligent computing.

Fund:National Key R&D Program of China(No.2021ZD0111700), National Natural Science Foundation of China(No.62137002,62006065), Key Research and Development Program of Anhui Province(No.202104a05020011), Key Science and Technology Special Project of Anhui Province(No.202103a07020002), Fundamental Research Funds for the Central Universities(No.WK2150110019,WK2100000027)
Abstract

Causal feature selection methods,also known as Markov boundary discovery methods, select features by learning the Markov boundary(MB) of the target variable. Hence, causal feature selection methods possess better interpretability and robustness than the traditional methods. In this paper, the existing causal feature selection methods are reviewed comprehensively. The methods are divided into two types, single MB discovery algorithms and multiple MB discovery algorithms. Based on the development history of each type, the typical algorithms as well as the recent advances are introduced in detail, and the accuracy, efficiency and data dependency of the algorithms are compared. Moreover, the extended MB discovery algorithms for special applications, including semi supervised learning, multi-label learning, multi-source learning and streaming data learning, are summarized. Finally, the current hotspots and the research directions in the future of causal feature selection are analyzed. Additionally, a toolbox for causal feature selection is developed(http://home.ustc.edu.cn/~xingyuwu/MB.html), where the commonly used packages and datasets are provided.

Key words: Markov Boundary; Feature Selection; Causal Learning; Causal Feature Selection; Bayesian Network; Markov Blanket

本文责任编委 于 剑

Recommended by Associate Editor YU Jian

高维数据为真实世界的机器学习任务带来诸多挑战, 如计算资源和存储资源的消耗、数据的过拟合, 学习算法的性能退化[1], 而最具判别性的信息仅被一部分相关特征携带[2].为了降低数据维度, 避免维度灾难, 特征选择研究受到广泛关注.大量的实证研究[3, 4, 5]表明, 对于多数涉及数据拟合或统计分类的机器学习算法, 在去除不相关特征和冗余特征的特征子集上, 通常能获得比在原始特征集合上更好的拟合度或分类精度.此外, 选择更小的特征子集有助于更好地理解底层的数据生成流程[6].

传统的特征选择算法主要分为封装法、过滤法和嵌入法三类[7].封装法[8]为不同的特征子集训练一个学习器, 评估其在该特征子集上的表现, 决定所选特征子集.过滤法[9]使用一个评估函数, 为特征评分并选择分数较高的特征, 因此不依赖额外的分类器, 更高效.嵌入法[10]将特征选择过程嵌入学习过程中, 同时搜索特征选择空间和学习器参数空间, 获得特征子集.

传统的特征选择算法根据特征和目标变量之间的相关性寻找相关特征子集[11].然而, 相关关系只能反映目标变量和特征之间的共存关系, 而无法解释决定目标变量取值的潜在机制[12, 13].一些研究表明[12, 13], 因果关系具有更好的可解释性和鲁棒性.例如, 将吸烟与肺癌患者数据集上“ 肺癌” (例子中变量取值均为“ 是” 、“ 否” )作为目标变量, “ 黄手指” 和“ 吸烟” 作为特征变量.由于“ 吸烟” 可用来解释“ 肺癌” , 而长期吸烟手指会受到焦油的污染, 因此“ 黄手指” 和“ 吸烟” 与“ 肺癌” 之间存在相关关系, 而只有“ 吸烟” 与“ 肺癌” 之间存在因果关系.当一些吸烟者为了隐藏吸烟习惯而去除手指上的黄渍时, 基于“ 黄手指” 的预测模型将失效, 而基于“ 吸烟” 的预测模型更鲁棒.

为了寻找更鲁棒的因果特征, 近年来, 因果特征选择算法被广泛研究.该类算法通过学习目标变量的马尔科夫边界(Markov Boundary, MB)[14]以寻找关键特征, 因此又被称为MB发现算法.具体地, MB的概念来源于因果贝叶斯网络, 在满足忠实性假设的贝叶斯网络中, 一个变量的MB集合是唯一的, 包含该目标变量的父节点、子节点及配偶节点(子节点的其它父节点)[14].因此, MB反映目标变量周围的局部因果关系, 给定目标变量的MB作为条件集合, 其它特征条件独立于目标变量[14].基于此属性:Tsamardinos等[15]证明在分类问题中, 类别变量的MB是具有最大预测性的最小特征子集; Pellet等[16]证明类别变量的MB集合是特征选择的最优解.因此, 因果特征选择算法通常具有可靠的理论保证.

作为一种算法思路, 基于因果关系的特征选择算法促进特征选择的可解释性和鲁棒性.近年来, 因果特征选择算法不断发展, 不仅提升单/多重马尔科夫边界发现算法的搜索精度和计算效率, 在半监督数据、流数据、多源数据、多标签数据等特殊场景下也不断发展.这些算法无需学习包含所有特征的完整贝叶斯网络结构, 即可挖掘目标变量周围的因果特征.本文对现有因果特征选择方法进行较全面的研究和综述.

1 基本原理与现有方法分类
1.1 问题定义与基础理论

本节介绍MB相关的基本定义和基础理论.本文使用U表示特征集合, T表示目标变量(标签).MB的概念来源于人工智能基础模型之一的贝叶斯网络.

定义 1 贝叶斯网络[14] 对于三元组< U, G, P> , U表示变量集合, G表示U上的有向无环图(Directed Acyclic Graph, DAG), P表示U上的概率分布.对于∀ X∈ U, 将X在G中的父变量作为条件集合, 如果任意X的非后代变量在P中都条件独立于X, 那么< U, G, P> 为贝叶斯网络.

贝叶斯网络表征一个变量集合中的因果关系.在有向无环图中, 对于一对直接相连的父子变量, 父变量是子变量的直接原因, 子变量是父变量的直接结果[14].忠实性是贝叶斯网络的基础假设之一, 定义如下.

定义 2 忠实性[14] 给定贝叶斯网络< U, G, P> , G忠实于P当且仅当P中的每个条件独立性关系都是由G和马尔科夫条件决定的.P忠实于G当且仅当存在一个G的子图忠实于P.

MB的概念是基于忠实的贝叶斯网络而提出的, 定义如下.

定义 3 马尔科夫边界[14] 在满足忠实性的贝叶斯网络中, 一个节点的马尔科夫边界包含该节点的父节点、子节点和配偶节点(子节点的其它父节点)[14].

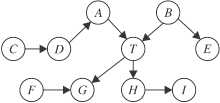
根据定义3, 一个节点的MB可直接从忠实的贝叶斯网络中“ 读” 出来.如图1所示, 节点T的MB为{A, B, G, H, F}, 包含父节点A、B, 子节点G、H, 配偶节点F.从因果图的角度分析, MB提供变量周围的局部因果结构, 父节点、子节点、配偶节点分别对应目标变量的直接原因、直接结果、直接结果的其它原因.MB发现算法通过挖掘变量的局部因果结构, 无需学习完整的贝叶斯网络即可找到变量的MB.而变量的MB集合有一个特殊的统计特性, 见定理1.

图1 马尔科夫边界的例子Fig.1 An example of Markov boundary

定理 1 对于变量X∈ U, X的马尔科夫边界MB⊆U, 满足:∀ Y∈ U-MB-{X}, X⊥Y|MB, 且MB为满足该统计特性的最小变量集.

定理1中阐述MB的最小性, MB的超集通常称为马尔科夫毯(Markov Blanket).根据定理1, 以MB集合为条件, 目标变量会条件独立于其它特征.因此, MB中的特征携带所有关于目标变量的预测信息, 并且其“ 最小性” 保证MB可作为特征选择问题的最优解, 见定理2.

定理 2 在满足忠实性假设的数据中, 目标变量的MB是唯一的, 并且为特征选择的最优解[15, 16].

定理2为MB发现算法解决特征选择问题提供理论保证, 由于MB发现算法根据数据中的因果关系选择特征, 并且特征包含目标变量的因果信息, 因此使用MB发现算法选择特征的过程称为因果特征选择.

1.2 现有马尔科夫边界学习方法分类及其基本原理

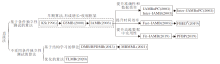
图2给出本文对现有MB发现算法的分类.常规数据中的MB发现算法主要分为单重MB发现算法和多重MB发现算法, 这两类算法的应用场景取决于训练数据是否满足忠实性假设.根据定理2, 在满足忠实性的条件下, 目标变量的MB是唯一的, 当真实数据并不完全满足忠实性条件时, 目标变量可能存在多个等价的MB.因此, 一部分现有算法假设数据满足忠实性, 并且试图寻找目标变量的唯一MB, 该类算法称为单重MB发现算法.另一部分算法考虑忠实性假设被违反的情况, 这些算法可挖掘目标变量的多个等价MB, 该类算法称为多重MB发现算法.特殊数据中的MB发现算法作为一类单独介绍, 其中包括半监督数据MB发现算法、流数据MB发现算法、多源数据MB发现算法、多标签数据MB发现算法.本文按照上述分类介绍现有算法的特点.

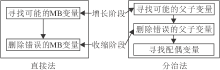
图2 现有MB发现算法的分类Fig.2 Categories of existing MB discovery algorithms

单重MB发现算法假设目标变量有唯一的MB, 输出的MB集合可直接作为特征选择的结果.该类算法主要分为两类:直接的MB发现算法(直接法)和分治的MB发现算法(分治法).主要区别是:直接法根据MB的性质(定理1)直接学习MB变量, 而分治法分别学习父子变量和配偶变量.主要理论依据为定理3和定理4.

定理 3 在U上的贝叶斯网络中, 如果节点X和Y满足:任意变量子集Z⊆U-{X, Y}, X⊥Y|Z不成立, 那么X和Y是一对父子变量[17].

定理 4 在U上的贝叶斯网络中, 如果不相连的节点X和Y均与T相连, 如果存在变量子集Z⊆U-{X, Y, T}, 使得X⊥Y|Z成立但X⊥Y|Z∪ {T}不成立, 那么X和Y是一对配偶变量[17].

定理3和定理4分别给出父子变量和配偶变量的判别条件, 基于上述定理, 分治的MB发现算法可通过条件独立性测试分别搜索父子和配偶变量.

如图3所示, 单重MB发现算法通常使用增长阶段和收缩阶段搜索MB变量或父子变量.增长阶段用于识别并添加可能的真变量, 而收缩阶段检测并删除增长步骤中找到的假变量.基于这一框架, 分治法需要进一步搜索配偶变量.直接法通常在时间效率上更优.但由于分治法在条件独立性测试中使用规模更小的条件集合, 因此通常分治法可达到比直接法更高的准确性.

图3 直接法和分治法的区别Fig.3 Difference between direct methods and divide-and-conquer methods

可用于MB发现算法的通用条件独立性测试方法有5种:1)λ 2测试、G2测试、互信息计算, 可用于离散数据[18]; 2)菲尔逊Z检验[19], 可用于带有高斯误差的线性关系的连续数据; 3)基于核的条件独立性测试方法[20], 可用于非线性、非高斯噪声的连续数据.

多重MB发现算法研究忠实性假设被违反的情况下一个变量的多个等价MB.理论上来说, 目标变量的多重MB携带等价的信息且具有相似的预测能力[21], 该类算法存在的意义是:1)由于实际应用中多个等价的MB适应的特定学习模型是不同的, 多重MB可用于解释学习模型的多样性现象; 2)实际应用中可能存在多个等价的MB, 但并非所有MB都适合作为特征子集建立学习模型.例如, 当不同变量的获取成本可能不同时, 多重MB算法可用于探索较低获取成本但具有相似预测性的替代解决方案(特征子集).

根据Statnikov等[21]的研究, 多重MB的本质原因是等价信息现象, 定义4和定理5如下.

定义 4 等价信息[21] 对变量集合X⊆U, Y⊆U及目标变量T∈ U, X和Y包含T的等价信息当且仅当X和Y与T相关且满足X⊥T|Y, Y⊥T|X.

定理 5 当且仅当没有发生信息等价时, 目标变量有一个唯一的MB集合[21].

根据定理5, 多重MB与等价信息现象是共存的, 因此寻找多个MB的过程也就是识别等价信息的过程[21].现有的多重MB发现算法通常遵循如下步骤:1)使用单重MB发现算法找到一个初始的MB; 2)在当前MB中选择特征子集, 将其从源数据分布中移除, 再在新的数据分布中找到新的MB; 3)测试新MB是否正确.

特殊数据的MB发现算法主要是面向近年来逐渐流行的一些特殊学习场景, 根据本文的调研, 目前主要包括但不限于:半监督数据MB发现算法、多标签数据MB发现算法、多源数据MB发现算法和流数据MB发现算法.这些算法大多对应某个单重MB发现算法, 考虑对应场景的特点, 将单重MB算法扩展应用到特殊数据中.

2 马尔科夫边界发现算法

本章介绍单重MB发现算法(分为直接法和分治法)和多重MB发现算法的研究现状, 以及现有算法在各方面性能上的优劣.

2.1 直接法的研究现状

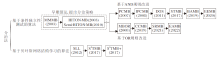
早期的MB发现算法均为直接法.直接法直接利用MB的性质(定理1)搜索MB变量.该类算法的发展脉络如图4所示.从Koller等[22]关注到MB在特征选择中的应用并提出第一个MB搜索的近似算法之后, 一些早期的直接法被相继提出, 这些算法大多采用增长-收缩的两阶段框架(如图3所示), 使用条件独立性测试搜索MB变量.该框架在GSMB(Growing-Shrinking Markov Blanket)[23]改进KS[22]之后正式确立, 并在IAMB(Incremental Asso-ciation Markov Blanket)[24]中得到完善.

图4 直接法的发展过程Fig.4 Development history of direct methods

Koller等[22]提出KS, 他们意识到MB在特征选择中的应用, 提出一个理论上合理的近似算法KS.KS使用基于后向选择的搜索策略, 即从特征的全集开始搜索, 不断最小化交叉信息熵的损失函数, 以此最小化在特征选择过程中丢失的预测信息.不同于KS, GSMB[23]的正确性可以被论证.GSMB基于两个假设:1)被研究的数据分布可使用忠实的贝叶斯网络建模; 2)条件独立性测试是可靠的.在这两个假设的条件下, GSMB开创性地提出增长-收缩框架, 增长阶段通过条件独立性测试找到可能的MB变量.由于变量遍历顺序的不同可能会引入一些错误的MB变量, 因此收缩阶段排查这一部分错误变量.使用的方法是:通过移除某个变量观察剩下的变量是否符合MB的定义.增长阶段和收缩阶段交替进行, 直到所选MB集合不发生改变.IAMB[24]在GSMB的基础上降低算法的数据依赖性, 继续使用GSMB中的增长-收缩框架, 主要改进GSMB的增长阶段, 采用“ 动态” 启发式过程, 在搜索可能的MB变量之前, 对候选变量进行重新排序.因此IAMB遍历变量的次序和GSMB不同, 变量的动态重排使IAMB在精度上更优.

在IAMB被提出后, 很多变形算法[24, 25, 26, 27, 28, 29, 30]通过改进IAMB而获得某一方面性能的提升.一些IAMB变形算法提升MB发现的数据依赖性和准确性.例如:Inter-IAMB[24]将IAMB中的增长阶段和收缩阶段整合到一次MB集合的更新迭代中, 并交错执行, 可及时消除当前MB中的错误变量, 尽量控制MB集合的规模.IAMBnPC[24]和Inter-IAMBnPC[24]使用PC[17]分别替代IAMB和Inter-IAMB的收缩阶段, PC可在收缩阶段只检查当前MB的子集而非整个MB集合, 通过缩小条件集合的规模, 提升准确性, 降低数据依赖.

一些IAMB变形算法提升MB发现的时间效率.例如:Fast-IAMB[25, 26]改进IAMB的增长阶段, 在每轮迭代中一次性添加多个变量到候选MB集合中, 减少迭代次数并提高效率.FBEDK(Forward-Backward Selection with Early Dropping)[27]发现IAMB的增长阶段(在寻找下一个最佳候选特征时)需要重新考虑所有剩余特征, 造成时间效率的损失.为了解决这一问题, FBEDK改进IAMB的增长阶段, 采用“ 早期下降” 策略.在每次迭代中, 如果一个特征在当前MB为条件下独立于目标变量, 则直接移除, 从而避免多次冗余的条件独立性测试.算法允许增长阶段被运行K次, 用于重新检测被删除的特征.通过这一改进, FBEDK可在保持准确性的同时提升MB搜索的时间效率.

此外, 一些IAMB变形算法提升MB发现算法在高维数据上的实用性.例如:Fit-IAMB(Three-Fast-Inter IAMB)[29]结合Inter-IAMB和Fast-IAMB的优势, 用于解决高维数据中样本不足的问题.PFBP(Parallel Forward-Backward with Pruning)[30]启发于IAMB和FBEDK, 进一步改进“ 早期下降” 策略.为了实现并行计算, PFBP分别按样本和特征划分数据, 并使用元分析技术结合本地计算的结果, 使算法可在数百万个特征和样本的数据集上学习变量的MB, 实现超线性的加速.

上述MB发现算法均基于条件独立性测试而设计.除此以外, 还有2种MB发现的思路:1)使用贝叶斯网络结构学习的方法; 2)使用优化的方法.DMB和RPDMB[31]采用基于评分的贝叶斯网络结构学习算法学习目标变量的MB, 避免条件独立性测试的级联错误带来的影响.DMB和RPDMB分别定义一个有约束的搜索子空间, 称为类聚焦有向无环图(CDAG)和类聚焦部分约束的有向无环图(CRPDAG).基于这两种图, 算法使用基于爬山的搜索算法从空图开始搜索, DMB在CDAG空间进行局部搜索, RPDMB在CRPDAG空间进行搜索, 直到评分函数达到最优.最后, 两种算法分别从得到的图中读取MB.MBMML(Markov Blanket Discovery Using Minimum Message Length)[32]利用最小信息长度作为评分函数, 实现性能提升.TLMB(Tolerant MB Discovery)[33]是优化法的代表, 该研究注意到条件独立性测试无法考虑多元相关关系, 通过条件协方差算子[34, 35]将特征空间和目标变量空间映射到一个可再生核希尔伯特空间, 度量特征携带的因果信息.该研究证明, 如果概率分布是严格为正的, 那么能最小化条件协方差算子的迹的特征子集就是目标变量的MB.基于这一理论, TLMB通过在希尔伯特空间中优化条件协方差算子的迹, 求出最优的MB集合.

2.2 直接法的特点对比与问题分析

从直接法的研究现状来看, 基于条件独立性测试的方法仍占据主导地位, 这是因为MB的概念来自于贝叶斯网络, 而贝叶斯网络是一个表征条件相关与独立的模型.但是, 随着该领域的不断发展, 基于条件独立性测试的方法在各方面性能都出现发展瓶颈, 表现不如分治法, 因此研究者寻求其它思路解决MB发现问题, 即贝叶斯网络结构学习法和优化法.

基于条件独立性测试的方法奠定该领域的研究基础.作为首个提出的MB发现算法, KS由于缺乏理论保证, 准确性不够稳定, 在大多数情况下的表现也不如后来提出的算法.KS需要预定义两个额外的参数:所选特征数量和条件独立性测试中条件集合的最大规模.这两个参数有利于降低算法的运行时间但牺牲正确性.GSMB是第一个可以在理论上被证明正确性的算法.相比KS, GSMB具有2个优势:可靠的理论保证和较高的时间效率(仅需O(n)次条件独立性测试).GSMB的缺点是:数据依赖性较强, 当样本太少或条件集合较大以致条件独立性测试不可靠时, 算法的准确性会受到很大影响.IAMB改善这一问题, 数据依赖性弱于GSMB.与此同时, 重新排序的改进策略确保配偶变量在增长阶段也被较早的找到, 从而减少更多的假MB变量进入候选集合, 提升条件独立性测试的可靠性, 避免更多级联错误的发生.值得一提的是, IAMB与GSMB的基本假设相同, 且理论上的正确性同样可被证明.正因为IAMB改善MB发现的各方面性能, 后来的大多数工作均在该算法上进行改进.

在IAMB的改进工作中, 准确性、时间效率和实用性均有所提升, 而这三方面具有代表性的算法是Inter-IAMB、FBEDK和PFBP, 它们在着重提升某一方面性能的同时在其它方面的损失也是不同的.然而, 尽管Inter-IAMB提升准确性, 但由于交错执行增长-收缩过程而在同一变量上耗时较多, 导致一定的时间效率损失.此外, 交叉两个阶段可能导致一个变量被多次添加到MB中或从MB中移除, 这也显著降低时间效率.在效率提升方面, FBEDK和PFBP均可在保持准确性的同时提升时间效率, 是适合于真实世界大规模高维数据的实用算法, 且PFBP在处理大规模数据时具有更显著的时间效率优势.

基于条件独立性测试的主要问题是有限的准确性和难以避免的级联错误.贝叶斯网络结构学习策略和优化的策略可在不同程度上解决这一问题, 但目前这两类方法的发展仍不够成熟.其中, 结构学习法DMB和RPDMB虽然避免条件独立性测试的弊端, 但是如果算法使用的有约束的搜索子空间规模较大时, 学习DAG的时间成本会很高.这导致该方法不具有其它直接法在时间效率上的优势, 在大规模数据中的实用性非常有限.相反, 优化法TLMB在提升准确性的同时并未过多地损失时间效率, 因为在求解优化问题之前, 首先使用基于条件协方差算子设计的评分函数过滤一部分冗余特征, 尽量缩小优化问题的解空间, 这在一定程度上节省运行时间.该方法面临的的新问题是:希尔伯特空间中优化条件协方差算子的迹没有理论上的解, 而对应的优化算法也不够有效.未来优化法的讨论和改进是直接法研究的趋势之一.

2.3 分治法的研究现状

尽管直接法已具有较高的效率和准确性, 但数据依赖性较强, 在小样本数据集中效果不理想.分治的MB发现算法的提出主要是为了解决这一问题, 其数据依赖性取决于目标变量周围的父子变量规模, 而非整个MB规模.该类算法以合理的时间效率牺牲换取准确性和数据依赖性的显著提高.分治法的发展脉络如图5所示.

图5 分治法的发展过程Fig.5 Development history of divide-and-conquer methods

分治策略是将MB发现问题分解为两个子问题:首先识别父子变量, 之后识别配偶变量.大多数算法的父子变量搜索过程遵循图3中增长-收缩框架, 而配偶变量的搜索可转化为子变量的父子变量的搜索, 因此在搜索配偶变量时也会调用父子变量搜索过程.

MMMB(Max-Min Markov Blanket)[36]是最早的分治算法.在搜索父子变量时, MMMB的增长阶段为每个候选特征找到一个特征子集, 使得在该子集为条件下, 对应特征与目标变量之间的相关性最小.在此情况下, 如果特征与标签之间相互独立, 根据定理3, 该特征不是MB变量而应被移除, 与此同时, 相关性最大的特征是可能性最大的MB变量而应被选入候选MB集合.父子变量搜索的收缩阶段会遍历当前MB的所有子集以检查选中的父子变量是否与目标变量相互独立, 根据定理3, 相互独立说明该变量不是MB变量而应被移除.MMMB的配偶搜索直接使用定理4中的准则, 搜索空间是每个父子变量集合的并集, 在搜索空间中找到配偶变量S和对应子变量C构成的V结构[36], 即S→ C← T.后来学者们提出的基于条件独立性测试的分治法均在MMMB的框架下进行改进.例如, HITON-Markov Blanket(HITON为Blanket的希腊语音译)[37]交错执行增长-收缩阶段, 使学习父子变量和删除错误变量在一次迭代中先后进行, 可较早识别错误的父子变量, 从而避免级联错误.Semi-HITON-MB[12]在HITON-MB的基础上进行改进, 在候选特征集为空之前只删除新添加的变量, 而在其为空之后执行考虑所有错误变量的删除.

由于分治法可找到变量之间的父子关系, 一些算法利用父子关系的对称性, 提升MB发现算法的准确性或实用性.考虑对称性的方法包括AND规则和OR规则.AND规则是指:对于一对变量, 只有当它们的父子变量集合均包含对方时, 才是一对父子变量.OR规则是指:对于一对变量, 只要其中一个的父子变量集合包含另一个变量, 那么它们就是一对父子变量.

第一个提出并使用AND规则的算法是PCMB(Parents-and-Children-Based MB)[38, 39].该算法沿用HITON-MB交错执行增长-收缩阶段, 并利用AND规则在父子变量之间进行对称检验, 避免一些非子变量的后代变量被误检测为子变量.由于避免这一错误, PCMB成为第一个被证明正确性的分治法.IPCMB(Iterative-PCMB)[40]则认为过滤错误变量比直接识别正确变量更容易, 基于这一考量, IPCMB采用PCMB的逆向过程, 即从完整的变量集合中删除错误变量, 直到恢复真正的MB集合.这一改进可尽早识别和去除错误的MB变量, 避免条件独立性测试中条件集合规模过大的问题及噪声的影响.DOS(Dynamic Ordering-Based Search)[41]基于IPCMB的思路, 提出2个改进策略:1)开展条件独立性测试的同时考虑候选集上的变量排序和条件集上的变量排序, 这一改进能在少量的条件独立性测试中有效检测假MB变量; 2)利用已知的条件独立性测试, 尽可能早地从候选集合中删除假MB变量, 提高时间效率.STMB(Simultaneous Markov Blanket)[42]主要关注算法效率.为了缓解AND规则中对称检验步骤效率低下的问题, STMB采用与PCMB相同的父子变量搜索方法, 再使用配偶变量辅助删除错误的父子变量, 融合两个过程, 提升时间效率.不同于上述算法着力于提升数据效率或时间效率, BAMB(Balanced Markov Blanket)[43]和EEMB(Efficient and Effective Markov Blanket Discovery)[44]通过父子变量和配偶变量的交替识别, 试图在数据效率和时间效率之间取得平衡.两者均采用类似于STMB的策略, 使用配偶变量辅助删除错误的父子变量, 同时在每个新的父子变量被找到时都会直接搜索其对应的配偶变量并删除错误的父子变量, 从而尽可能地限制候选集的规模.EEMB进一步改进BAMB中错误的父子变量可能导致错误的配偶变量级联增加的问题.

第一个使用OR规则的算法是MBOR(MB Sear-ch Using the OR Condition)[45, 46].该研究的主要目的是解决样本不足时MB发现算法失准的问题.由于数据不足时无法真实表达原始分布, 数据中的分布与真实分布可能存在偏差, 一些可能相关的特征被误以为是无关特征或冗余特征, 导致信息的损失.MBOR放弃AND规则而使用OR规则, 具体来说, MBOR使用一个弱MB学习器(原理正确但不够准确的算法)去产生一个强的MB学习器(更准确的算法).算法首先通过一些简单的条件独立性测试(条件集合包含1~2个变量), 找出目标变量的父子集合和配偶集合的超集; 再使用OR规则过滤这两个超集中的错误MB变量, 同时检测尚未被找到的真MB变量.CCMB(Cross-Check and Complement MB Discovery)[47]的研究直接关注上述MB算法查准率较高、查全率较低的缺陷, 从理论上分析父子变量违反OR规则的错误机理, 在此基础上, CCMB直接通过OR规则修复这类错误.相比MBOR, CCMB对OR规则的置信度更高, 这导致CCMB具有更高的查全率, 但同时查准率弱于其它算法.SRMB(Separation and Recovery MB Discovery)[48]与MBOR和CCMB动机相同, 引入两阶段发现策略:在分离阶段通过一个快速但不够准确的直接法得到MB的初始集合, 从中区分父子变量和配偶变量; 在恢复阶段, 基于OR规则和分治法的基本框架, 搜索父子变量和配偶变量.EAMB(Error-Aware Markov Blanket Learning)[49]提出一种宽松的R-AND规则, 其本质与OR规则接近.基于该规则, EAMB提出选择性策略, 在被丢弃的特征中找到由于条件独立性测试不准确而丢失的MB变量.此外该算法提出双重收缩策略, 同时减少条件集(当前选择的候选MB特征)和候选特征集(当前选择的候选MB特征之外的集合)的大小, 从而尽可能地减少不可靠的条件独立性测试.

上述算法均基于MMMB主导的框架, 利用条件独立性测试搜索MB.一些算法还尝试使用贝叶斯网络结构学习的方法分治学习父子变量和配偶变量, 如SLL(Score-Based Local Learning)[50]、S2TMB(Score-Based STMB)[51]和S2TMB+[51].这些算法通过学习目标变量周围的DAG, 从中读取目标变量的MB.SLL本质上是上述分治MB发现算法的一种变体, 采用贝叶斯网络结构学习算法而非条件独立性测试学习父子变量和配偶变量.为了识别其中的错误变量, SLL使用AND规则筛选错误的父子变量, 使用OR规则筛选错误的配偶变量.这一过程带来大量的对称检验, 因此当目标变量的MB集合规模较大时, SLL的计算开销会很大.为了解决效率问题, Gao等[51]提出S2TMB, 是STMB基于分数的变体.S2TMB不使用对称检查, 而是采用类似于STMB的方法, 即利用找到的配偶和父子变量去除错误的父子变量.S2TMB+是S2TMB的改进版本, 进一步提高计算效率.

2.4 分治法的特点对比与问题分析

由于直接法不区分父子变量和配偶变量并同时学习它们, 因此此类算法具有较低的时间复杂度, 但需要样本的数量与MB的规模呈指数关系, 这意味着样本不足可能影响算法性能.不同于直接法在时间效率上的优势, 分治法在准确性和数据依赖性方面表现更优.第一个分治法MMMB在这两方面均已有较好的表现(优于多数直接法), 之后提出的分治法几乎都在MMMB的框架下进行改进.早期的改进均为MMMB的修补, 如HITON-MB.

尽管MMMB具有很高的准确性, 但算法的输出无法保证正确性, 其中的一类错误在PCMB的研究中[38, 39]被关注到.在父子变量的搜索中, 如果特征X不是父子变量, MMMB和HITON-MB都认为必然存在一个父子变量子集作为条件集合, 那么X与T相互独立.然而, 如果X是T的后代(非子变量), 那么上述论断是错误的, 因此, 这两种算法(及其它不使用AND规则的算法)在后代链路较长的贝叶斯网络数据中精度较低.但是, 相对于MMMB, HITON-MB使用更简洁的启发式搜索策略, 因此也更高效.

MMMB和HITON-MB中的错误在PCMB中被基于AND规则的对称检验纠正.尽管规避一部分条件独立性测试无法解决的风险, 能在一定程度上提升MB发现算法的精度, 但对称检验有较大的时间开销, 必须对所有的父子变量再使用一次父子变量的搜索.STMB将对称检验融入配偶变量的搜索阶段, 相对其它基于AND规则设计的算法, 显著提高时间效率.但是, 由于在一些步骤中使用整个MB集合作为条件集而非穷举子集, 因此数据依赖性和直接法是相同的, 高于大多数分治法, 而弥补这一缺陷的方法是扩大数据集样本数.BAMB和EEMB在精度和效率上进行折衷处理.

尽管AND规则在理论上更合理, 但并不具有实用性.因为AND规则更关注精度(对应查准率(Precision)), 倾向于选择更少更精确的特征, 而OR规则更关注完整度(对应查全率(Recall)), 倾向于选择更多的特征且尽可能无遗漏.在真实世界的学习任务中, 保留尽量完整的特征信息显然更有利于学习器的训练, 因为大多数学习器可容忍少数冗余特征, 但丢失关键的相关特征会导致性能下降.因此, 过于苛求查准率的AND规则可能会导致重要特征的丢失, 尤其是在数据不足的情况下.OR规则在这种场景下更实用.因此MBOR等使用OR规则的算法更关注真实数据集上的数据有效性及准确性.然而, OR规则在效率上的损失大于AND规则, 因为需要检查更多变量的父子对称性, 到目前为止, 这一问题仍未有很好的解决方案.

2.5 多重马尔科夫边界发现算法研究现状

只有满足忠实性分布时, 目标变量具有唯一的MB, 而在其它分布下的数据集上, 目标变量可能有多个MB.真实世界应用领域中的数据分布常为后者, 因此, 从这些数据中诱导多个MB是重要的研究问题.多重MB发现算法的发展脉络如图6所示.多重MB发现算法通常会关联一个单重MB发现算法或其它基于互信息的特征选择算法, 多次调用关联算法, 提取多个MB集合.

图6 多重MB发现算法的发展过程Fig.6 Development history of multiple MB discovery methods

IR-HITON-PC(Iterative Removal HITON Parents and Children)[52]是最早考虑多重MB问题的研究, 关联的单重MB算法是Semi-HITON-PC.IR-HITON-PC在每次迭代后会将该次迭代找到的MB集合中的所有变量从变量总集合中移除, 下次迭代中从剩下的变量里寻找MB.因此, IR-HITON-PC具有较高的效率, 但输出的多重MB集合之间没有交集.

为了寻找更多的MB集合, 一些研究者尝试使用随机策略实现MB发现.KIAMB[39]重复运行IAMB, 获得不同的MB.其中, 参数K∈ [0, 1], 用于指定搜索中贪婪和随机性之间的权衡, 当K= 1时, KIAMB与IAMB等价且进行贪婪搜索, 当K=0时, KIAMB是完全随机的算法.当K∈ (0, 1)时, KIAMB使用IAMB贪婪地向MB候选集合中添加与目标变量最相关的节点, 然后根据K值选取MB的一个子集.因此, 不同于IAMB的贪婪选择, KIAMB输出的MB可能并不是最优的.但通过反复运行KIAMB, 可得到若干不同的MB, KIAMB将这些结果视为目标变量的多重MB.相似地, EGS-CMIM(Ensemble Gene Selection Method with CMIM)[53]和EGSNCM-IGS(Ensemble Gene Selection Method with NCM-IGS)[53]分别反复调用CMIM(Conditional Mutual Information Maximization)[54]和NCMIGS(Gene Selection Using Normalized Conditional Mutual Information)[53], 提取多个MB.但是, CMIM和NCMIGS并不是理论上可靠的MB发现算法, 它们只采用类似于IAMB增长阶段的贪婪前向选择策略, 并通过度量互信息测量变量和目标之间的条件相关关系.因此, CMIM和NCMIGS搜索的MB会存在错误变量, 这也导致EGS-CMIM和EGS-NCMIGS无法保证其输出MB的正确性.此外, 和其它随机算法一样, EGS-CMIM和EGS-NCMIGS无法保证找到所有的MB.

除了随机策略, 另一种脱离因果图的策略也被用于多重MB发现.EGSG(Ensemble Gene Selection by Grouping)[55]使用规范化的互信息度量变量之间的成对关联, 并划分为不相交的组.每个组将组中的第一个变量作为“ 质心” , 变量与质心的关联度高于目标变量时则入组, 否则作为质心并创建一个新的组.EGSG假设组内的变量包含关于目标变量的类似信息, 因此每组中选取一个变量即可构成一个MB集合.EGSG从每组中随机抽取与目标变量关联的最大变量, 形成一个MB集合, 通过多次重复这一过程, 获得多个MB集合.

第一个可在理论上证明正确性的算法是TIE* (Target Information Equivalence)[21].该研究给出多重MB现象发生的根本原因— — 信息等价[21].基于这一理论, TIE* 包括3个步骤:1)使用一个单重MB发现算法, 从数据集中学习目标变量的一个MB; 2)将MB的某些子集从源数据分布中移除, 消除可能的等价信息; 3)利用单重MB发现算法在新的数据中寻找MB, 而先前在1)中无法被发现的MB变量可重新被找到; 4)由于新的MB可能只是新数据集的MB而在原数据集中并不成立, 因此该步骤检验新的MB是否是源分布的MB.重复上述步骤, 直到遍历所有可能的MB子集为止.

一些研究者在TIE* 框架下提出改进实例.MB-DEA(Markov Boundaries from Distributed Feature Data)[56]扩展TIE* , 可在多变量集的数据中使用.TIE* 的一个典型实例是WLCMB(MB Discovery under the Weak Markov Local Composition Assumption)[28].WLCMB首先提出一个单重MB发现算法LRH(Lessen Swamping, Resist Masking, and Highlight the True Positives)[28], 改正条件独立性测试的不准确带来的错误, WLCMB利用LRH与搜索恢复过程相交织, 从而在LRH停止工作时, 搜索过程可重新开始.其中, 搜索恢复过程与TIE* 中的恢复过程相似, 都是通过去除现有MB的一个子集以重新发现MB.WLCMB本质上是TIE* 的一个实例.

2.6 多重马尔科夫边界发现算法的特点对比与问题分析

由于多重MB发现算法并不能直接作为特征选择技术而被应用, 因此算法数量远少于单重MB发现算法, 且该领域研究不够成熟, 每种算法都有一定的缺陷.IR-HITON-PC由于在每次迭代中都不会考虑之前的MB变量, 因此输出的MB之间没有交集, 这是与事实情况相悖的, 因此算法在准确性上较低, 但时间效率和数据效率均较高.KIAMB等随机算法并不具有理论保证, 无法确保输出的MB集合都是真正的MB, 但从理论上来说, 如果在算法的第一阶段中探索足够多次, 将不同的相关变量序列加入到当前的MB候选集合中, KIAMB可识别所有可能的MB.然而这种策略的计算效率很低, 因为其大部分的运行可能会产生先前已经确定的MB.因此, 为了产生完整的MB集合, 参数K和KIAMB的运行次数必须基于贝叶斯网络的拓扑结构和目标变量的MB具体数量确定, 然而, 两者都不是已知的.KIAMB的另一个缺点与IAMB相同, 具有很强的数据依赖性, 需要大量样本完成测试.

KIAMB等的大部分缺陷在TIE* 中得到解决, 但TIE* 主要存在3个问题:1)数据集的生成方法本质是一个变量筛选算法, 过程几乎遍历一个MB的所有子集, 与此同时新的MB也在产生, 又将会遍历更多的子集, 因此时间复杂度很高.2)新的MB是否在源数据分布中成立依赖于可靠的判别准则, 但文献[21]中给出的两个判别准则都各有缺陷.其中一种使用MB的定义进行条件独立性测试, 该准则需要以先前找到的MB作为条件集合, 并测试目标变量和新MB之间的相关关系, 运算涉及到两个规模庞大的集合, 导致算法数据依赖性较强, 依赖于大量数据样本才能完成测试; 另一种方法使用一些学习算法和性能指标评估新MB的预测(分类或回归)性能, 若高于之前的MB, 认为它也是MB, 这显然是不够可靠的, 并且由于不同的MB被找到的先后顺序是不确定的, 因此对比MB之间的预测性是不合理的.3)TIE* 不够鲁棒, 当某一步骤产生错误, 会产生大量的级联错误, 而由于问题1)、2)导致这种级联错误容易发生.作为TIE* 的一个实例也具有相似的问题, 都依赖大量的样本确保准确性.

3 马尔科夫边界发现算法在特殊数据中的应用

单重MB发现算法可直接作为特征选择算法, 对一般应用场景中的单标签高维数据进行降维, 但无法直接应用到复杂学习场景中.为了解决这一问题, 学者们扩展出一些针对特殊学习场景的MB发现算法.

1)半监督数据特征选择.许多真实世界应用通常难以获取有标签的样本, 但容易收集无标签数据.为了同时利用无标签和有标签数据学习MB, 学者们提出一些半监督MB发现算法, 包括分治法BASSUM(Bayesian Semi-Supervised)[57]和直接法Semi-IAMB[58, 59].BASSUM使用一个基于半监督数据改进的G2检验, 使有标签和无标签数据中的信息可同时用于判断变量之间的条件独立关系.此外, 文献[57]中提出有效特征集的概念, 利用该子集, BASSUM可不访问有标签数据中的类别信息而删除错误的父子变量.因此, 相比普通的MB学习算法, BASSUM在半监督数据中更有效.但是, BASSUM在理论上不可靠, 因为无法保证修改后的G2统计量服从卡方分布, 同时, 当有标签数据较少时, 表现会受到很大影响.为了改进这一缺陷, Sechidis等[58, 59]提出部分标签样本的条件独立性测试, 假设所有无标签均属于正类或负类, 文献[58]提出一个用于半监督数据假设检验的代理类变量和代理测试, 并应用于包含少量有标签样本和大量无标签样本的半监督数据中.由于Semi-IAMB是基于上述理论贡献而提出的算法, 因此主要缺陷与代理测试的缺陷相似:1)只能用于二分类问题; 2)为了减少假负例, 算法依赖于更多的数据或额外的先验知识.

2)流特征与流数据特征选择.在真实世界中, 很多学习场景是实时系统, 在这些系统中, 高维流数据的生成速度非常快, 数据样本不断产生, 特征也不断增加.针对这一问题, 一些算法研究流数据(假设训练数据以单个实例或数据块的形式顺序到达而特征数量不变)[60]和流特征(假设特征按顺序到达但训练样本的数量是固定的)[61]中的MB发现问题.OMBSF(Online Markov Blanket Discovery with Strea-ming Features)[62]是一个面向流特征的MB发现算法, 属于分治法.算法首先检查新特征与目标变量之间的相关性(条件集合为空集), 如果是相关的, 判断其是否为父子变量, 如果独立, 判断其是否为配偶变量.其识别原理与其它分治法相同, 该过程可快速识别冗余变量, 尽量保证条件独立性测试的准确性.值得注意的是, 存在一些使用MB进行流特征选择的算法[62, 63, 64, 65, 66, 67], 如OSFS(Online Streaming Feature Selection)[63]、Fast-OSFS(Fast Online Streaming Feature Selection)[65]和OFSVMB(Online Streaming Features Selection via Markov Blanket)[67], 由于这些算法只搜索MB中的子集(只搜索父子变量作为特征子集), 因此本文没有详细介绍这些算法.SDMB(Streaming Data-Based MB)[68]是一个面向流数据的MB发现算法, 属于直接法.算法利用AD-Tree[69]的数据结构, 用于存储流数据中的条件相关和条件独立信息, 利用存储空间的损失提升时间效率.SDMB使用动态AD-Tree记录历史数据, 使用IAMB的思路针对AD-Tree中的数据计算变量之间的条件相关关系, 从而学习目标的MB.然而, SDMB并未从理论上讨论MB在流数据中的性质, 算法本质是将流数据进行存储并在所有流数据形成的数据块上进行MB变量搜索, 未从根本上解决流数据MB发现问题.

3)多源数据特征选择.在真实世界的应用中, 数据的来源更丰富, 可能一个标签的信息来自于多个不同的数据源.为了实现对不同分布的多个数据集的稳定预测, MIMB(Multiple Interventional Markov Blanket)[70]和MCFS(Multi-source Causal Feature Selection)[71]被提出, 用于解决多源MB学习问题.Yu等[70]系统研究多个数据集上MB变量和父子变量的性质, 提出分治的MB学习算法MIMB, 算法由两个子过程组成:1)使用MIPC从多个干预数据集上发现目标变量的父子变量; 2)根据父子变量的结果, 从多个干预数据集中识别目标变量的配偶变量.基于文献[70]的理论贡献, 并受到因果不变性概念[72]的启发, Yu等[71]提出MCFS, 算法将多个数据集上的稳定预测问题定义为跨不同数据集搜索不变集.该工作证实在具有不同分布的多源数据集上进行特征选择时, 最优且最稳定的不变集是目标变量的父变量集合而不是目标变量的MB集合.同时为了加快搜索速度, Yu等分析不变集的上界和下界, 使MCFS能在一定范围内学习最佳的不变集.

4)多标签数据特征选择.常见的MB发现算法通常只关注单个目标变量的MB集合, 近年的一些工作关注多目标变量的MB发现问题, 包括:MIAMB(Multivariate IAMB)[73]、MKIAMB(Multivariate KI-AMB)[73]、MB-MCF(MB-Based Multi-label Causal Fea-ture selection)[74]、CLCD(Common and Label-Specific Causal Variables Discovery)[75]和CLCD-FS(CLCD-Based Feature Selection)[75].Liu等[73]证明在局部Intersection假设下, 只需取每个目标变量的MB的并集, 并将所有目标变量排除在并集之外, 就可构造多类变量的MB.根据这一理论, Liu等[73]提出MIAMB和MKIAMB, 将多目标变量的MB学习问题转化为单目标变量的多个MB学习问题.相比直接将单标签算法分别作用于多个标签, MIAMB和MKIAMB具有更高的准确性和更低的时间复杂度, 但是MIAMB和MKIAMB在真实世界数据的特征选择任务上表现一般.Wu等[74]认为, 多标签数据中特征选择不仅应找到所有的因果特征, 还应指出一个因果特征影响哪几个标签变量.Wu等[74]提出一个可解释的MB-MCF以解决此问题, 但缺乏可靠的理论保证.Wu等[75]指出, 在不满足忠实性假设的数据中, 多重MB可能会导致更多的共有因果变量.因此, 考虑忠实性被违反的情况下单个目标变量可能拥有多个MB的情况, 并研究等价信息是如何影响多目标变量下的MB学习.Wu等[75]证明只有标签上的等价信息会导致更多的共有因果变量, 并讨论每种等价信息情况下共有因果变量和特有因果变量的性质.根据理论研究, Wu等[75]提出, CLCD不仅可找出多个目标变量的MB集合, 还可解释多个目标变量的共有特征和单个目标变量的特有特征. CLCD-FS[75]是CTCD在真实世界多标签特征选择问题上的应用.Wu等[75]从理论上证明CLCD-FS选择的特征子集具有最小的冗余性和最多的相关性, 为多标签特征选择提供理论依据.

4 因果特征选择与传统方法的异同

MB发现算法与因果特征选择算法在概念和功能上都是等价的[76], MB集合就是所选特征集合, 其中的特征就是算法选择的因果特征, 因此本文提到的所有单重MB发现算法都可直接用于因果特征的选择.但多重MB发现算法会选择多个特征子集, 需要进一步选择最合适的特征子集.一般会根据特征集合的规模、特征获取的难易程度和成本等因素考虑最终使用哪个MB集合.基于上述MB发现算法的综述, 本节介绍因果特征选择与传统特征选择之间的联系和差异.

按照传统算法的分类, 因果特征选择属于过滤法[9], 该类方法时间效率较高, 对过拟合问题更鲁棒[76].传统过滤法通常利用评分函数评估特征与目标变量之间的关联性, 并根据分数排序特征并选择相关特征, 而评分函数通常基于条件互信息的概念而设计, 这与MB发现算法中条件独立性测试的本质是一致的.但是, 传统过滤法与MB发现算法对条件互信息的度量精确程度不同, 这可从互信息度量中条件集合的规模进行评价.

以三个经典的过滤法为例.MIM(Mutual Infor-mation Maximization)[77]只关注备选特征和目标变量之间的互信息, 而mRMR(Max-Relevance and Min-Redundancy)[78]不仅关注备选特征和目标变量之间的相关性, 同时关注备选特征与已选特征之间的相关性以评价其冗余度, 这两种算法在度量互信息时涉及的条件集合均为空集.JMI(Joint Mutual Infor-mation for Feature Selection)[79]除了关注上述互信息以外, 还额外考虑以目标变量为条件的备选特征与已选特征之间的相关性, 所以JMI使用的条件互信息为单变量条件集.大多数传统过滤法与上述算法类似, 在度量条件互信息时, 条件集合的规模只精确到1或2个变量, 这意味着传统过滤法假设数据中的条件独立于条件相关关系只涉及到有限规模的条件集合, 不涉及更复杂的条件相关或独立关系.

不同于这些算法, MB发现算法具有可靠的理论保证, 无论是直接法挖掘的MB变量还是分治法挖掘的父子变量和配偶变量, MB发现算法对这些变量的度量标准(定理3和定理4)均考虑变量全集的所有可能子集.因此, MB发现算法的基本假设要比传统过滤法更宽泛, 也正是这个原因, MB发现算法具有可靠的理论保证, 能证明MB集合是最优的特征子集, 而传统过滤法并未在理论上给出最优特征子集的标准解.不同过滤法对互信息的利用精度有所区别, 均无法在算法进程中智能决定条件独立性的层次级别, 未形成一套具有理论保证的方法框架.理论上来说, 如果训练数据足够充分, MB发现算法可实现更优性能.

从上述分析可看出, MB发现算法考虑的互信息层级比传统算法更深入, 可度量更精确的条件相关和独立关系.因此, 在样本足够多时, MB发现算法可在任意规模的条件集合下度量一对变量之间的互信息, 从而实现更优的性能.精确的条件互信息也提升MB发现算法的鲁棒性和稳定性, 但这些优势是以牺牲时间效率和数据效率为代价.MB发现算法涉及大量的条件互信息计算, 对训练数据的规模要求较高, 同时MB学习比普通特征子集选择耗时更多, 尤其是分治MB算法对条件子集的考虑导致指数级的时间复杂度, 这极大影响该类算法的实用性.从数据集的特性上考虑, 当数据中的变量关系较简单时, 传统的过滤法更有效, 可实现和MB发现算法相当的精度, 时间效率更高.而在变量关系更复杂的数据集上, MB发现算法可实现比传统过滤法更优的性能.此外, MB发现算法是基于结构因果模型理论而设计的, 相对于传统特征选择算法(不限于过滤法)只考虑相关关系, MB发现算法选择的特征与目标变量同时具有相关关系和因果关系.其中, 分治的MB发现算法不仅可选择特征用于完成学习任务, 同时可得到这些特征与目标变量之间的因果关系骨架, 是因果发现的第一步.因此, MB发现算法更接近于系统的机理, 相比传统特征选择, 具有更好的因果可解释性.

5 数据集与工具包

由于MB发现算法是基于贝叶斯网络模型的概念而提出的, 因此, 该类算法首先需要在标准的贝叶斯网络数据集上被检验.通常这类数据集上每个变量的MB集合是已知的, 通过让MB发现算法搜索每个变量的MB并测试精度(包括查全率和查准率)和效率, 评估算法性能.此外, 作为特征选择方法, MB发现算法同时需要在真实数据集上被检验, 考察算法在特征选择任务上的有效性(通常以某个分类器在特征子集上的分类精度为依据).

常用的标准贝叶斯网络数据集主要来自真实的决策支持系统, 这些系统涵盖医学、农业、天气预报、金融建模和动物养殖等不同的应用领域.例如:小规模网络ASIA[80]、CANCER[81]、SURVEY[82]; 中等规模网络ALARM[83]、INSURANCE[84]、CHILD[85]; 大规模网络ANDES[86]、LINK[87]、HEPAR2[88]等.此外, Tsamardinos等[89]使用平铺算法创建几个较小网络的大规模版本, 创建的贝叶斯网络包含3个、5个或10个原始网络的副本[89].标准贝叶斯网络数据集从这些网络中采样若干训练样本而得到.针对特征选择任务通常使用真实数据, 例如UCI社区中的数据集(https://archive.ics.uci.edu/ml/datasets.ph/).

一些早期的MB发现算法被包含在贝叶斯网络学习工具包中.例如:“ bnlearn” R语言工具包[90]中包含 GSMB、IAMB、Inter-IAMB、Fast-IAMB、MMPC(Max-Min Parents and Children)、HITON-PC(HITON Parents and Children), 该算法包利用这些算法实现贝叶斯网络的学习, 并基于贝叶斯网络完成推理和分类的任务.“ Causal Explorer” MATLAB工具包[91]中包含KS、GSMB、IAMB、IAMBnPC、Inter-IAMB、Inter-IAMBnPC、HITON-MB、MMMB, 该算法包[92]利用这些算法实现局部因果结构的发现.“ CausalFS” C++语言工具包中包含大多数MB发现算法, 该算法包利用这些算法进行因果特征选择.一些其它工具包还包括:R语言工具包“ PGM” [93]和“ PC-ALG” [94]、Matlab工具包“ BNT” [95]、JAVA语言工具包“ tetrad” [96].本文建立在线的因果特征选择的资料库(http://home.ustc.edu.cn/~xingyuwu/MB.html), 汇总因果特征选择领域经典算法的不同语言工具包(如C/C++、Python、Matlab、R语言等)以及用于测试该类算法的标准贝叶斯网络数据集.

6 研究热点与发展趋势

MB这一概念的提出为传统的特征选择问题找到理论依据, MB发现算法基于数据中的因果关系, 提升特征选择的鲁棒性和可解释性.经过十几年的发展, 学者们对MB发现问题展开研究, 并在效率、准确性、数据依赖性、实用性等多个方面改进MB学习方法.本文回顾当前该领域的经典算法和最新算法, 并进行归纳和分类讨论, 包括常规数据中的MB发现算法和特殊数据中的MB发现算法.结合每类算法的发展脉络, 分析异同并对比算法在效率、准确性及数据依赖性等方面的优劣.

6.1 当前研究热点

经过几十年的发展, 单重MB发现算法在理论和方法上都趋于完备, 由于直接法和分治法的优势不同, 这两类方法在近几年的研究趋势也有所差异.基于条件独立性测试的方法是单重MB发现研究的主力, 近年的研究也保持着活力.基于条件独立性测试的分治法研究仍着眼于提升该类方法的准确性.随着大数据的发展, 研究者们关注真实数据中的效率和实用性问题.因此, 一些研究者提出BAMB[43]和EEMB[44], 用于确保准确性的同时提升效率.而另一些研究者注意到算法在标准数据集和真实数据集上的性能差异, 提出CCMB[47]和SRMB[48], 更好地发挥OR规则在真实数据中的实用性.与分治法不同, 直接法本身就具有效率上的优势, 因此在大数据时代更受欢迎.但是, 基于条件独立性测试的直接法在高维数据中的性能短板更明显, 因此, 新提出的算法都着眼于高维数据中的效率和实用性研究, 包括:FBEK[27]、Fit-IAMB[29]和PFBP[30].此外, 基于优化的直接法[33]在MB研究中是一种新的思路, 该项研究证明条件协方差算子与MB之间的关联, 但并未给出理论上的解, 这导致搜索最优解的效率不够高.未来应为该优化方法构建坚实的理论基础, 支撑其进一步发展和应用.

相比单重MB发现算法, 多重MB发现算法更关注理论的完备性, 而在应用层面上更窄.因为实际应用场景下常常只需要找到一个最优的特征子集, 而不是多个性能相似的特征子集, 因此, 该领域近年发展缓慢, 但是多重MB理论应用在多标签问题上是必要的.文献[73]~文献[75]中关于多标签因果特征选择的探讨都未忽略多重MB的影响, 并且其中的实证研究表明, 考虑多重MB对多标签因果特征选择具有实际意义, 尤其在定义多个标签的共有特征和单个标签的特有特征上[75].

由于因果特征选择在真实世界数据中的广泛应用, 特殊数据中的MB发现算法是近年的另一个研究热点, 如流特征[62]、流数据[68]、多源数据[70, 71]、多标签数据[73, 74, 75]等.这些算法基于单重MB算法的框架和理论, 完善和扩展特殊数据中的因果特征选择理论和方法.未来仍存在更多复杂的低质量数据场景, 有待被进一步被解决.

6.2 未来发展趋势

尽管目前基于因果关系的特征选择算法已被大量开发并广泛应用于大数据分析, 但在这一领域仍需要更多的努力以应对如下挑战.

1)由于直接法步骤中的条件独立性测试远少于分治法, 使得直接法在效率上具有天然优势, 因此是海量数据场景下MB算法的最佳选择.未来应尽可能地提升直接法在超高维数据中的准确性, 使该类算法能在大数据时代更实用.此外, 一些不适用条件独立性测试的直接法也应在理论上逐步完善, 在基于条件独立性测试的性能提升进入瓶颈时, 基于结构学习或基于优化的方法可能为问题的解决带来新的思路.其中基于优化的方法目前仍没有有效的方式获得理论最优解, 只能在较小的解空间下搜索最优解, 未来应在该优化框架的启发下进行更广泛的理论研究, 以促进单重MB发现算法获得更优性能.对于分治法, 尽管它们提升特征选择的鲁棒性和可解释性, 但探索因果关系的过程却需要耗费大量的时间.这一缺陷限制分治法在海量高维数据中的实用性.因此, 提升MB发现算法效率的同时保证算法的可解释性和鲁棒性优势是当前分治法研究的重要课题.直接法和分治法的结合是否能让两类方法形成优势互补, 是一个值得讨论的问题.此外, 一些深度学习技术可用于挖掘变量之间的因果关系, 并进一步构建MB.例如:图神经网络的表示能力已在多个领域被验证[97], 可表示对象之间的复杂关系, 未来可使用图神经网络模型构建变量之间的因果图, 获得目标变量的MB.

2)现有的多重MB发现算法存在很多问题.在效率上, 当前算法包含大量冗余的迭代和不必要的测试, 时间复杂度非常高; 在准确性上, 现有算法存在较多不可靠的步骤, 容易受到级联错误的影响; 在数据依赖性上, 现有算法的条件独立性测试都存在将整个马尔科夫边界作为条件集合的问题, 使数据依赖性非常高.因此, 多重MB发现算法的问题需要在效率、准确性及数据依赖性等多方面进行改进.此外, 多重MB发现算法在特征选择问题上的应用是一个值得研究的问题.当目标变量存在多个等价的MB, 意味着这些特征子集在理论上拥有等效的预测信息, 导致多重MB无法直接解决特征选择问题.然而实际应用中的特征子集之间在其它方面存在差异, 如特征集合的规模、特征获取的难易程度和成本、特征在特定学习模型中的有效性、特征在不同学习模型中的稳定性及在不同设置下的鲁棒性等.因此, 如何从多重MB中选取合适的特征子集是一个值得被应用领域研究的课题.

3)一些特殊数据中的MB发现问题仍未被解决, 包括不平衡类数据、在线学习数据、弱监督数据、具有缺失值(或噪声)的数据等.大多数现有的基于因果关系的方法不能处理这些场景的MB发现问题, 然而, 它们在许多真实世界的应用程序中是广泛存在.开发特定的因果特征选择方法解决这一问题非常重要.此外, MB发现算法当前主要的应用场景是鲁棒的特征选择、特征与标签之间因果关系的解释及特征因果关系图的构建.未来可继续研究特定应用领域的MB发现算法, 提升实用性.

参考文献
[1] LIU H, MOTODA H. Feature Selection for Knowledge Discovery and Data Mining. Berlin, Germany: Springer, 1998. [本文引用:1]
[2] ZEBARI R R, ABDULAZEEZ M A, ZEEBAREE D Q, et al. A Comprehensive Review of Dimensionality Reduction Techniques for Feature Selection and Feature Extraction. Journal of Applied Science and Technology Trends, 2020, 1(2): 56-70. [本文引用:1]
[3] BOLÓN-CANEDO V, ALONSO-BETANZOS A. Ensembles for Feature Selection: A Review and Future Trends. Information Fusion, 2019, 52: 1-12. [本文引用:1]
[4] SOLORIO-FERNÁNDEZ S, CARRASCO-OCHOA J A, MARTÍN-EZ-TRINIDAD J F. A Review of Unsupervised Feature Selection Methods. Artificial Intelligence Review, 2020, 53(2): 907-948. [本文引用:1]
[5] LI X P, WANG Y D, RUIZ R. A Survey on Sparse Learning Models for Feature Selection. IEEE Transactions on Cybernetics, 2022, 52(3): 1642-1660. [本文引用:1]
[6] SOLORIO-FERNÁNDEZ S, CARRASCO-OCHOA J A, MARTÍN-EZ-TRINIDAD J F. A Survey on Feature Selection Methods for Mixed Data. Artificial Intelligence Review, 2021. DOI: DOI:10.1007/s10462-021-10072-6. [本文引用:1]
[7] GUYON I, GUNN S, NIKRAVESH M, et al. Feature Extraction: Foundations and Applications. Berlin, Germany: Springer, 2006. [本文引用:1]
[8] LIU W, WANG J Y. Recursive Elimination Current Algorithms and a Distributed Computing Scheme to Accelerate Wrapper Feature Selection. Information Sciences, 2022, 589: 636-654. [本文引用:1]
[9] BOMMERT A, SUN X D, BISCHL B, et al. Benchmark for Filter Methods for Feature Selection in High-Dimensional Classification Data. Computational Statistics & Data Analysis, 2020, 143. DOI: DOI:10.1016/j.csda.2019.106839. [本文引用:2]
[10] JIANG B B, WU X Y, YU K, et al. Joint Semi-Supervised Feature Selection and Classification through Bayesian Approach // Proc of the 33rd AAAI Conference on Artificial Intelligence and 31st Innovative Applications of Artificial Intelligence Conference and 9th AAAI Symposium on Educational Advances in Artificial Intelligence. Palo Alto, USA: AAAI, 2019: 3983-3990. [本文引用:1]
[11] GUYON I, ELISSEEFF A. An Introduction to Variable and Feature Selection. The Journal of Machine Learning Research, 2003, 3: 1157-1182. [本文引用:1]
[12] ALIFERIS C F, STATNIKOV A, TSAMARDINOS I, et al. Local Causal and Markov Blanket Induction for Causal Discovery and Feature Selection for Classification Part I: Algorithms and Empirical Evaluation. The Journal of Machine Learning Research, 2010, 11: 171-234. [本文引用:3]
[13] ALIFERIS C F, STATNIKOV A, TSAMARDINOS I, et al. Local Causal and Markov Blanket Induction for Causal Discovery and Feature Selection for Classification Part II: Analysis and Exten-sions. The Journal of Machine Learning Research, 2010, 11: 235-284. [本文引用:2]
[14] PEARL J. Probabilistic Reasoning in Intelligent Systems: Networks of Plausible Inference. San Francisco, USA: Morgan Kaufmann Publishers, 2014. [本文引用:8]
[15] TSAMARDINOS I, ALIFERIS C F. Towards Principled Feature Selection: Relevancy, Filters and Wrappers[C/OL]. [2021-12-22]. http://proceedings.mlr.press/r4/tsamardinos03a/tsamardinos03a.pdf. [本文引用:2]
[16] PELLET J P, ELISSEEFF A. Using Markov Blankets for Causal Structure Learning. The Journal of Machine Learning Research, 2008, 9: 1295-1342. [本文引用:2]
[17] SPIRTES P, GLYMOUR C, SCHEINES R. Causation, Prediction, Search. Berlin, Germany: Springer, 1993. [本文引用:3]
[18] MCDONALD J H. Hand book of Biological Statistics. 2nd Edition. Baltimore, USA: Sparky House Publishing, 2014. [本文引用:1]
[19] PEÑA J M. Learning Gaussian Graphical Models of Gene Networks with False Discovery Rate Control // Proc of the European Confe-rence on Evolutionary Computation, Machine Learning and Data Mining in Bioinformatics. Berlin, Germany: Springer, 2008: 165-176. [本文引用:1]
[20] ZHANG K, SCHÖLKOPF B, SPIRTES P, et al. Learning Causality and Causality-Related Learning: Some Recent Progress. National Science Review, 2018, 5(1): 26-29. [本文引用:1]
[21] STATNIKOV A, LEMEIR J, ALIFERIS C F, et al. Algorithms for Discovery of Multiple Markov Boundaries. The Journal of Machine Learning Research, 2013, 14(1): 499-566. [本文引用:8]
[22] KOLLER D, SAHAMI M. Toward Optimal Feature Selection // Proc of the 13th International Conference on Machine Learning. San Francisco, USA: Morgan Kaufmann Publishers, 1996: 284-292. [本文引用:3]
[23] MARGARITIS D. Toward Provably Correct Feature Selection in Arbitrary Domains // Proc of the 22nd International Conference on Neural Information Processing Systems. Cambridge, USA: The MIT Press, 2009: 1240-1248. [本文引用:2]
[24] TSAMARDINOS I, ALIFERIS C F, STATNIKOV A, et al. Algorithms for Large Scale Markov Blanket Discovery // Proc of the 16th International Florida Artificial Intelligence Research Society Conference. Palo Alto, USA: AAAI, 2003: 376-380. [本文引用:6]
[25] YARAMAKALA S. Fast Markov Blanket Discovery. Master's Dissertation. Ames, USA: Iowa State University, 2004. [本文引用:2]
[26] YARAMAKALA S, MARGARITIS D. Speculative Markov Blanket Discovery for Optimal Feature Selection // Proc of the 5th IEEE International Conference on Data Mining. Washington, USA: IEEE, 2005. DOI: DOI:10.1109JZCOM.2005.134. [本文引用:2]
[27] BORBOUDAKIS G, TSAMARDINOS I. Forward-Backward Selection with Early Dropping. The Journal of Machine Learning Research, 2019, 20(1): 276-314. [本文引用:3]
[28] LIU X Q, LIU X S. Swamping and Masking in Markov Boundary Discovery. Machine Learning, 2016, 104(1): 25-54. [本文引用:3]
[29] YANG X L, WANG Y J, OU Y, et al. Three-Fast-Inter Incremental Association Markov Blanket Learning Algorithm. Pattern Recognition Letters, 2019, 122: 73-78. [本文引用:3]
[30] TSAMARDINOS I, BORBOUDAKIS G, KATSOGRIDAKIS P, et al. A Greedy Feature Selection Algorithm for Big Data of High Dimensionality. Machine Learning, 2019, 108(2): 149-202. [本文引用:3]
[31] ACID S, DE CAMPOS L M, FERNÁNDEZ M. Score-Based Me-thods for Learning Markov Boundaries by Searching in Constrained Spaces. Data Mining and Knowledge Discovery, 2013, 26(1): 174-212. [本文引用:1]
[32] LI Y, KORB K B, ALLISON L. Markov Blanket Discovery Using Minimum Message Length[C/OL]. [2021-12-22]. https://arxiv.org/pdf/2107.08140v1.pdf. [本文引用:1]
[33] WU X Y, JIANG B B, ZHONG Y, et al. Tolerant Markov Boun-dary Discovery for Feature Selection // Proc of the 29th ACM International Conference on Information and Knowledge Management. New York, USA: ACM, 2020: 2261-2264. [本文引用:2]
[34] BAKER C R. Joint Measures and Cross-Covariance Operators. Tran-sactions of the American Mathematical Society, 1973, 186: 273-289. [本文引用:1]
[35] FUKUMIZU K, BACH F R, JORDAN M I. Kernel Dimension Reduction in Regression. The Annals of Statistics, 2009, 37(4): 1871-1905. [本文引用:1]
[36] TSAMARDINOS I, ALIFERIS C F, STATNIKOV A. Time and Sample Efficient Discovery of Markov Blankets and Direct Causal Relations // Proc of the 9th ACM SIGKDD International Confe-rence on Knowledge Discovery and Data Mining. New York, USA: ACM, 2003: 673-678. [本文引用:2]
[37] ALIFERIS C F, TSAMARDINOS I, STATNIKOV A. HITON: A Novel Markov Blanket Algorithm for Optimal Variable Selection[C/OL]. [2021-12-22]. http://www.ccdlab.org/paper-pdfs/AMIA_2003.pdf. [本文引用:1]
[38] PEÑA J M, BJÖRKEGREN J, TEGNÉR J. Scalable, Efficient and Correct Learning of Markov Boundaries under the Faithfulness Assumption // Proc of the European Conference on Symbolic and Quantitative Approaches to Reasoning and Uncertainty. Berlin, Germany: Springer, 2005: 136-147. [本文引用:2]
[39] PEÑA J M, NILSSON R, BJÖRKEGREN J, et al. Towards Sca-lable and Data Efficient Learning of Markov Boundaries. International Journal of Approximate Reasoning, 2007, 45(2): 211-232. [本文引用:3]
[40] FU S K, DESMARAIS M C. Fast Markov Blanket Discovery Algorithm via Local Learning within Single Pass // Proc of the Confe-rence of the Canadian Society for Computational Studies of Intelligence. Berlin, Germany: Springer, 2008: 96-107. [本文引用:1]
[41] ZENG Y F, HE X, XIANG Y P, , et al. Dynamic Ordering-Based Search Algorithm for Markov Blanket Discovery // Proc of the 15th Pacific-Asia Conference on Advances in Knowledge Discovery and Data Mining. Berlin. Germany: Springer, 2011, II: 420-431. [本文引用:1]
[42] GAO T, JI Q. Efficient Markov Blanket Discovery and Its Application. IEEE Transactions on Cybernetics, 2017, 47(5): 1169-1179. [本文引用:1]
[43] LING Z L, YU K, WANG H, et al. BAMB: A Balanced Markov Blanket Discovery Approach to Feature Selection. ACM Transactions on Intelligent Systems and Technology, 2019, 10(5): 1-25. [本文引用:2]
[44] WANG H, LING Z L, YU K, et al. Towards Efficient and Effective Discovery of Markov Blankets for Feature Selection. Information Sciences, 2020, 509: 227-242. [本文引用:2]
[45] DE MORAIS S R, AUSSEM A. A Novel Scalable and Data Efficient Feature Subset Selection Algorithm // Proc of the European Conference on Machine Learning and Knowledge Discovery in Databases. Berlin, Germany: Springer, 2008, II: 298-312. [本文引用:1]
[46] DE MORAIS S R, AUSSEM A, CORBEX M. Hand ling Almost-Deterministic Relationships in Constraint-Based Bayesian Network Discovery: Application to Cancer Risk Factor Identification // Proc of the European Symposium on Artificial Neural Networks-Advances in Computational Intelligence and Learning Bruges. Berlin, Germany: Springer, 2008: 101-106. [本文引用:1]
[47] WU X Y, JIANG B B, YU K, et al. Accurate Markov Boundary Discovery for Causal Feature Selection. IEEE Transactions on Cybernetics, 2020, 50(12): 4983-4996. [本文引用:2]
[48] WU X Y, JIANG B B, YU K, et al. Separation and Recovery Markov Boundary Discovery and Its Application in EEG-Based Emotion Recognition. Information Sciences, 2021, 571: 262-278. [本文引用:2]
[49] GUO X J, YU K, CAO F Y, et al. Error-Aware Markov Blanket Learning for Causal Feature Selection. Information Sciences, 2022, 589: 849-877. [本文引用:1]
[50] NIINIMÄKI T, PARVIAINEN P. Local Structure Discovery in Ba-yesian Networks // Proc of the 28th Conference on Uncertainty in Artificial Intelligence. Arlington, USA: AUAI, 2012: 634-643. [本文引用:1]
[51] GAO T, JI Q. Efficient Score-Based Markov Blanket Discovery. International Journal of Approximate Reasoning, 2017, 80: 277-293. [本文引用:3]
[52] NATSOULIS G, EL GHAOUI L, LANCKRIET G R G, et al. Classification of a Large Microarray Data Set: Algorithm Comparison and Analysis of Drug Signatures. Genome Research, 2005, 15(5): 724-736. [本文引用:1]
[53] LIU H W, LIU L, ZHANG H J. Ensemble Gene Selection for Cancer Classification. Pattern Recognition, 2010, 43(8): 2763-2772. [本文引用:3]
[54] FLEURET F. Fast Binary Feature Selection with Conditional Mu-tual Information. The Journal of Machine Learning Research, 2004, 5: 1531-1555. [本文引用:1]
[55] LIU H W, LIU L, ZHANG H J. Ensemble Gene Selection by Grouping for Microarray Data Classification. Journal of Biomedical Informatics, 2010, 43(1): 81-87. [本文引用:1]
[56] YU K, WANG D W, DING W, et al. Tornado Forecasting with Multiple Markov Boundaries // Proc of the 21st ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York, USA: ACM, 2015: 2237-2246. [本文引用:1]
[57] CAI R C, ZHANG Z J, HAO Z F. BASSUM: A Bayesian Semi-Supervised Method for Classification Feature Selection. Pattern Recognition, 2011, 44(4): 811-820. [本文引用:2]
[58] SECHIDIS K, BROWN G. Markov Blanket Discovery in Positive-Unlabelled and Semi-Supervised Data // Proc of the European Conference on Machine Learning and Knowledge Discovery in Databases. Berlin, Germany: Springer, 2015, I: 351-366. [本文引用:3]
[59] SECHIDIS K, BROWN G. Simple Strategies for Semi-Supervised Feature Selection. Machine Learning, 2018, 107(2): 357-395. [本文引用:2]
[60] WANG J L, ZHAO P L, HOI S C H, et al. Online Feature Selection and Its Applications. IEEE Transactions on Knowledge and Data Engineering, 2014, 26(3): 698-710. [本文引用:1]
[61] WU X D, YU K, DING W, et al. Online Feature Selection with Streaming Features. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2013, 35(5): 1178-1192. [本文引用:1]
[62] YOU D L, LI R Q, SUN M M, et al. Online Markov Blanket Discovery with Streaming Features // Proc of the IEEE International Conference on Knowledge Graph. Washington, USA: IEEE, 2020: 92-99. [本文引用:3]
[63] WU X D, YU K, WANG H, et al. Online Streaming Feature Selection // Proc of the 27th International Conference on Machine Learning. New York, USA: ACM, 2010: 1159-1166. [本文引用:2]
[64] YU K, DING W, SIMOVICI D A, et al. Mining Emerging Patterns by Streaming Feature Selection // Proc of the 18th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York, USA: ACM, 2012, 60-68. [本文引用:1]
[65] YU K, WU X D, DING W, et al. Exploring Causal Relationships with Streaming Features. The Computer Journal, 2012, 55(9): 1103-1117. [本文引用:2]
[66] YU K, DING W, SIMOVICI D A, et al. Classification with Strea-ming Features: An Emerging-Pattern Mining Approach. ACM Transactions on Knowledge Discovery from Data, 2015, 9(4): 1-31. [本文引用:1]
[67] KHAN W, KONG L F, BREKHNA B, et al. Online Streaming Features Selection via Markov Blanket. Symmetry, 2022, 14(1). DOI: DOI:10.3390/sym14010149. [本文引用:2]
[68] LIU C F, YANG S, YU K. Markov Boundary Learning with Strea-ming Data for Supervised Classification. IEEE Access, 2020, 8: 102222-102234. [本文引用:2]
[69] ROURE J, MOORE A W. Sequential Update of ADtrees // Proc of the 23rd International Conference on Machine Learning. New York, USA: ACM, 2006: 769-776. [本文引用:1]
[70] YU K, LIU L, LI J Y. Learning Markov Blankets from Multiple Interventional Data Sets. IEEE Transactions on Neural Networks and Learning Systems, 2020, 31(6): 2005-2019. [本文引用:4]
[71] YU K, LIU L, LI J Y, et al. Multi-source Causal Feature Selection. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2020, 42(9): 2240-2256. [本文引用:3]
[72] PETERS J, BÜHLMANN P, MEINSHAUSEN N. Causal Inference by Using Invariant Prediction: Identification and Confidence Intervals. Journal of the Royal Statistical Society Series B(Statistical Methodology), 2016, 78(5): 947-1012. [本文引用:1]
[73] LIU X Q, LIU X S. Markov Blanket and Markov Boundary of Multiple Variables. The Journal of Machine Learning Research, 2018, 19(43): 1658-1707. [本文引用:6]
[74] WU X Y, JIANG B B, YU K, et al. Multi-label Causal Feature Selection. Proceeding of the AAAI Conference on Artificial Intelligence, 2020, 34(4): 6430-6437. [本文引用:4]
[75] WU X Y, JIANG B B, ZHONG Y, et al. Multi-label Causal Variable Discovery: Learning Common Causal Variables and Label-Specific Causal Variables[C/OL]. [2021-12-22]. https://arxiv.org/pdf/2011.04176.pdf. [本文引用:10]
[76] YU K, LIU L, LI J Y. A Unified View of Causal and Non-causal Feature Selection. ACM Transactions on Knowledge Discovery from Data, 2021, 15(4): 1-46. [本文引用:2]
[77] LEWIS D D. Feature Selection and Feature Extraction for Text Ca-tegorization // Proc of the Workshop on Speech and Natural Language, Stroudsburg, USA: ACL, 1992: 212-217. [本文引用:1]
[78] PENG H C, LONG F H, DING C. Feature Selection Based on Mutual Information Criteria of Max-Dependency, Max-Relevance, and Min-Redundancy. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2005, 27(8): 1226-1238. [本文引用:1]
[79] YANG H H, MOODY J. Data Visualization and Feature Selection: New Algorithms for Nongaussian Data // Proc of the 12th International Conference on Advances in Neural Information Processing Systems. San Diego, USA: NeurIPS, 1999: 687-702. [本文引用:1]
[80] LAURITZEN S L, SPIEGELHALTER D J. Local Computations with Probabilities on Graphical Structures and Their Application to Expert Systems. Journal of The Royal Statistical Society: Series B(Methodology), 1988, 50(2): 157-224. [本文引用:1]
[81] KORB K B, NICHOLSON A E. Bayesian Artificial Intelligence. 2nd Edition. Boca Raton, USA: CRC Press, 2011. [本文引用:1]
[82] SCUTARI M, DENIS J B. Bayesian Networks: With Examples in R. Boca Raton, USA: CRC Press, 2014. [本文引用:1]
[83] BEINLICH I A, SUERMONDT H J, CHAVEZ R M, et al. The ALARM Monitoring System: A Case Study with Two Probabilistic Inference Techniques for Belief Networks // Proc of the 2nd European Conference on Artificial Intelligence in Medicine. Berlin, Germany: Springer, 1989: 247-256. [本文引用:1]
[84] BINDER J, KOLLER D, RUSSELL S, et al. Adaptive Probabilis-tic Networks with Hidden Variables. Machine Learning, 1997, 29(2/3): 213-244. [本文引用:1]
[85] SPIEGELHALTER D J, COWELL R G. Learning in Probabilistic Expert Systems. Bayesian Statistics, 1992, 4: 447-465. [本文引用:1]
[86] CONATI C, GERTNER A S, VANLEHN K, et al. On-Line Stu-dent Modeling for Coached Problem Solving Using Bayesian Networks // Proc of the 6th International Conference on User Mode-ling. Berlin, Germany: Springer, 1997: 231-242. [本文引用:1]
[87] JENSEN C S, KONG A. Blocking Gibbs Sampling for Linkage Analysis in Large Pedigrees with Many Loops. The American Journal of Human Genetics, 1999, 65(3): 885-901. [本文引用:1]
[88] ONISKO A, DRUZDZEL M J, WASYLUK H. A Probabilistic Causal Model for Diagnosis of Liver Disorders[C/OL]. [2021-12-22]. https://sites.pitt.edu/~druzdzel/psfiles/malbork.pdf. [本文引用:1]
[89] TSAMARDINOS I, BROWN L E, ALIFERIS C F. The Max-Min Hill-Climbing Bayesian Network Structure Learning Algorithm. Machine Learning, 2006, 65(1): 31-78. [本文引用:2]
[90] SCUTARI M. Learning Bayesian Networks with the Bnlearn R Package[C/OL]. [2021-12-22]. https://arxiv.org/pdf/0908.3817.pdf. [本文引用:1]
[91] STATNIKOV A, TSAMARDINOS I, BROWN L E, et al. Causal Explorer: A Matlab Library of Algorithms for Causal Discovery and Variable Selection for Classification[C/OL]. [2021-12-22]. http://proceedings.mlr.press/v3/supplemental/Software_WCCI08_challenge.pdf. [本文引用:1]
[92] YU K, GUO X J, LIU L, et al. Causality-Based Feature Selection: Methods and Evaluations. ACM Computing Surveys, 2021, 53(5): 1-36. [本文引用:1]
[93] Mens X Machina. Probabilistic Graphical Model Toolbox[D/OL]. [2021-12-22]. http://mensxmachina.org/en/software/probabilistic-graphical-model-toolbox. [本文引用:1]
[94] KALISCH M, MÄCHLER M, COLOMBO D, et al. Causal Infe-rence Using Graphical Models with the R Package pcalg. Journal of Statistical Software, 2012, 47(11): 1-26. [本文引用:1]
[95] MURPHY K P. The Bayes Net Toolbox for Matlab. Computing Science and Statistics, 2001, 33: 1024-1034. [本文引用:1]
[96] SCHEINES R, SPIRTES P, GLYMOUR C, et al. The TETRAD Project: Constraint Based Aids to Causal Model Specification. Multivariate Behavioral Research, 1998, 33(1): 65-117. [本文引用:1]
[97] YU Y, CHEN J, GAO T, et al. DAG-GNN: DAG Structure Lear-ning with Graph Neural Networks[C/OL]. [2021-12-22]. http://proceedings.mlr.press/v97/yu19a/yu19a.pdf. [本文引用:1]