作者简介: 
黄心宏,硕士研究生,主要研究方向为粗糙集、模糊集.E-mail:1037517539@qq.com. 
张贤勇,博士,教授,主要研究方向为不确定分析、智能决策.E-mail:xianyongzh@sina.com. 
杨霁琳,博士,副教授,主要研究方向为粒计算、数据挖掘.
在复杂的不确定性环境中,粗糙集引入拓展要素,可增强模型强健性,因此,文中基于直觉模糊关系,在双论域上研究多粒度概率粗糙集.首先,利用直觉模糊关系与双论域背景,进行多粒度概率粗糙集建模,得到正向乐观、正向悲观、逆向乐观、逆向悲观4种模型及相关集成算法.然后,研究模型下上近似的数学性质,包括集合运算关系、概率参数极限、精度大小对比3方面.最后,采用医疗实例验证模型有效性与性质正确性,提供三支决策制定方案,并验证关于多粒度双论域直觉模糊概率粗糙集所得模型、算法、性质都具有深入的系统性、扩张性、应用性.
About Author:
HUANG Xinhong, master student. Her research interests include rough sets and fuzzy sets.
ZHANG Xianyong, Ph.D., professor. His research interests include uncertainty analysis and intelligent decision.
YANG Jilin, Ph.D., associate professor. Her research interests include granular computing and data mining.
In the complex uncertainty environment, extension factors are introduced into rough sets to enhance model robustness. Based on intuitionistic fuzzy relations, multi-granularity probability rough sets are investigated in two universes in this paper. Firstly, the intuitionistic fuzzy relations and two-universe background are utilized to model multi-granularity probabilistic rough sets, and four models and their integrated algorithms are acquired, including positive optimism, positive pessimism, inverse optimism and inverse pessimism. Then, mathematical properties of model lower and upper approximations are studied from the perspectives of set operation relation, probability parameter limitation and precision size comparison. Finally, the effectiveness and property correctness of the model are verified by a medical example, and the corresponding three-way decision making is provided. Regarding multi-granularity two-universe intuitionistic-fuzzy probability rough sets, systematicness, extension and applicability of the obtained models, algorithms and properties are confirmed in depth.
本文责任编委 张燕平
Recommended by Associate Editor Zhang Yanping
粗糙集是不确定性分析的基本数学工具, 广泛应用于人工智能和机器学习等领域.广义粗糙集模型构建能有效实现理论扩张, 应用于不确定性处理, 从而成为一个重要的研究主题.通过引入概率、多粒度、双论域三种拓展要素, 产生基本的概率粗糙集[1]、多粒度粗糙集[2]、双论域粗糙集[3, 4, 5, 6], 以及基于双要素的多粒度概率粗糙集[7]、双论域多粒度粗糙集[8]、双论域概率粗糙集[9].
基于三要素的粗糙集模型具有更好的适应性.Mandal等[10]构建双论域多粒度概率粗糙集, 进行三支决策制定, 但基于三要素的粗糙集模型的相关研究相对较少.特别地, 多粒度粗糙集是一类基础模型.李金海等[11]综述最新研究成果:模型扩展具有关系泛化、论域双化、其它理论结合化三方面的结果, 而相关前沿问题包括粒度结构、属性约简、规则提取、多源数据分析、动态知识更新等.
模糊是不确定性的一种基本形态, 其引入能强化粗糙集的不确定性处理能力.基于直觉模糊隶属与非隶属双刻画优势, 直觉模糊关系被广泛引入粗糙集中进行拓展建模, 获得多属性决策等应用.在多粒度要点上涌现各种多粒度直觉模糊粗糙集及对应决策制定[12, 13, 14].特别地, 高玲玲[15]聚焦多粒度、双论域, 提出双论域多粒度直觉模糊粗糙集, 郭智莲等[16]聚焦双论域、概率, 提出双论域直觉模糊概率粗糙集.事实上, 基于直觉模糊关系的粗糙集具有更好的抗噪性与鲁棒性, 但结合概率、多粒度、双论域三要素的综合模型还少见报道.
综上所述, 本文主要采用直觉模糊关系, 系统构建具备概率、多粒度、双论域的多粒度概率粗糙集, 即多粒度双论域直觉模糊概率粗糙集.具体建立正向乐观、正向悲观、逆向乐观、逆向悲观4种模型, 并得到相应的集成算法、数学性质、医疗决策.相关模型综合考虑模糊性、随机性、粗糙性等不确定性要素与对应概率、多粒度、双论域结构拓展要素, 呈现强健性, 改进文献[15]的多粒度模糊形式并推广文献[16]的单粒度粗糙形式, 有效引导不确定性分析与知识发现应用研究.
基于直觉模糊关系, 下面简要回顾双论域多粒度直觉模糊粗糙集[15]与双论域直觉模糊概率粗糙集[16].
定义非空有限论域U上的直觉模糊集
A={x, μ A(x), vA(x)},
其中, 元素x的隶属度
μ A(x)∶ U→ [0, 1],
和非隶属度
vA(x)∶ U→ [0, 1].
非空有限论域U、V上的直觉模糊关系为:
R={< (x, y), μ R(x, y), vR(x, y)> |(x, y)∈ U× V},
其中, 对象x、y具有关系R的隶属度
μ R(x, y)∶ U× V→ [0, 1],
和非隶属度
vR(x, y)∶ U× V→ [0, 1].
这里, 称(U, V, R)为双论域直觉模糊近似空间, 再加入概率测度P, 组建双论域直觉模糊概率近似空间(U, V, R, P).文献[16]的概率刻画还使用模糊截集参数λ 1、λ 2, 概率比较阈值α 、 β , 极限参数r, 其中, λ 1+λ 2∈ [0, 1], 0≤ β < α ≤ 1, r∈ (0, 1).
相关的多粒度构造主要涉及U× V上的直觉模糊关系族Rk, k=1, 2, …, m, 下面简单使用空间符号(U, V, Rk)或(U, V, Rk, P).此外, 双论域拓展还需要涉及落实于V× U的逆关系, 如R-1、
定义 1[15] 基于(U, V, Rk), 集合T⊆U的下上近似为
$\underline{\sum\nolimits_{k=1}^{m}{{{R}_{k}}}}(T)=\left\{ \left\langle y, {{\mu }_{\underline{\sum\nolimits_{k=1}^{m}{{{R}_{k}}}}(T)}}(y), \left. {{v}_{\underline{\sum\nolimits_{k=1}^{m}{{{R}_{k}}}}(T)}}(y) \right\rangle |y\in V \right. \right\}$
$\overline{\sum\nolimits_{k=1}^{m}{{{R}_{k}}}}(T)=\left\{ \left\langle y, {{\mu }_{\overline{\sum\nolimits_{k=1}^{m}{{{R}_{k}}}}(T)}}(y), \left. {{v}_{\overline{\sum\nolimits_{k=1}^{m}{{{R}_{k}}}}(T)}}(y) \right\rangle |y\in V \right. \right\}$ (1)
其中,
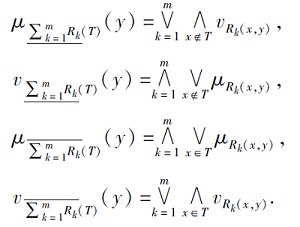
对称地, 集合X⊆V的下上近似为
$\underline{\sum\nolimits_{k=1}^{m}{{{R}_{k}}}}(X)=\left\{ \left\langle x, {{\mu }_{\underline{\sum\nolimits_{k=1}^{m}{{{R}_{k}}}}(X)}}(x), \left. {{v}_{\underline{\sum\nolimits_{k=1}^{m}{{{R}_{k}}}}(X)}}(x) \right\rangle |x\in U \right. \right\}$
$\overline{\sum\nolimits_{k=1}^{m}{{{R}_{k}}}}(X)=\left\{ \left\langle x, {{\mu }_{\overline{\sum\nolimits_{k=1}^{m}{{{R}_{k}}}}(X)}}(x), \left. {{v}_{\overline{\sum\nolimits_{k=1}^{m}{{{R}_{k}}}}(X)}}(x) \right\rangle |x\in U \right. \right\}$ (2)
定义 2[16] 基于(U, V, R, P)及参数λ 1、λ 2、α 、β , 集合X⊆V的下上近似为
${{\underline{PR}}_{({{\lambda }_{1}}, {{\lambda }_{2}}, \alpha )}}(X)=\left\{ x\in U|P(X|{{R}_{({{\lambda }_{1}}, {{\lambda }_{2}})}}(x))\ge \alpha , {{R}_{({{\lambda }_{1}}, {{\lambda }_{2}})}}(x)\ne \varnothing \right\}$
${{\overline{PR}}_{({{\lambda }_{1}}, {{\lambda }_{2}}, \beta )}}(X)=\left\{ x\in U|P(X|{{R}_{({{\lambda }_{1}}, {{\lambda }_{2}})}}(x))\ge \beta , {{R}_{({{\lambda }_{1}}, {{\lambda }_{2}})}}(x)\ne \varnothing \right\}\cup \left\{ x\in U|{{R}_{({{\lambda }_{1}}, {{\lambda }_{2}})}}(x)\ne \varnothing \right\}$ (3)
其中,

对称地, 采用逆关系R-1, 集合T⊆U的下上近似类似为
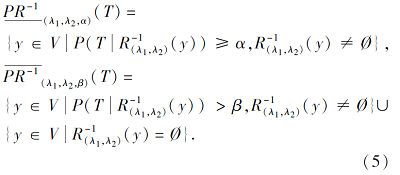
其中,
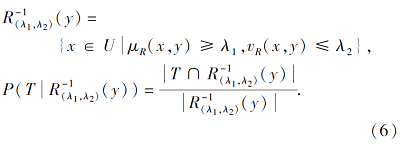
本节基于直觉模糊关系, 建立双论域多粒度概率粗糙集.具体考虑双论域正向关系、逆向关系与多粒度乐观视角、悲观视角的组合, 系统构建正向乐观、正向悲观、逆向乐观、逆向悲观4种模型, 并主要以正向乐观为例展开讨论.
下面将定义2的单粒度模型推广到多粒度模型, 近似空间从(U, V, R, P)变为(U, V, Rk, P).从多粒度视角上看, 阈值参数统一采用λ 1、λ 2、α 、β , 式(4)和式(6)的截集与概率首先更新为:
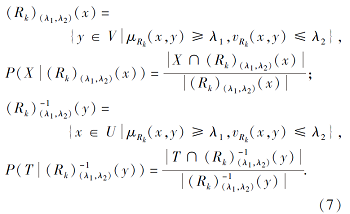
定义 3 正向乐观模型 在(U, V, Rk, P)中, 集合X⊆V的乐观多粒度下上近似为
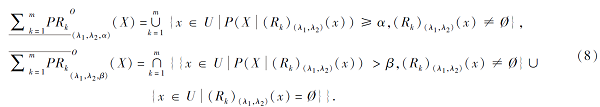
由于下近似不一定包含于上近似, 进而定义对应的正域、负域、上边界域、下边界域、边界域为
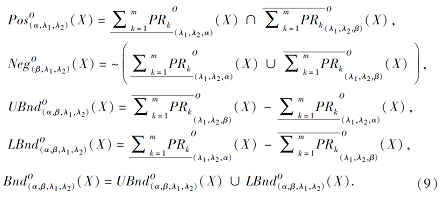
相应的精度与粗糙度如下:
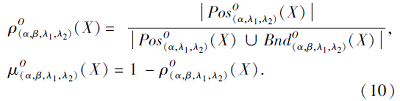
针对直觉模糊关系与双论域、概率双要点, 定义3依托并推进定义2的单粒度模型(式(3)), 建立多粒度粗糙集的正向乐观模型, 其中, 乐观融合采用常规多粒度模式下的集合运算[8].式(9)的正域、负域、上边界域、下边界域、边界域采用文献[5]的运算形式, 式(10)采用文献[6]的思路, 使用正域、边界域定义精度与粗糙度.该模型主要采用乐观多粒度视角与正向直觉模糊关系, 下面加入悲观视角与逆向关系, 类似建立正向悲观模型、逆向乐观模型、逆向悲观模型, 并以双近似刻画为主.特别地, 这4种模型共同组建多粒度双论域直觉模糊概率粗糙集, 具有系统关系, 也体现并行性与选择性.从特征上看, 正向与反向来源于双论域的两个不同方向:
定义 4 正向悲观模型 在(U, V, Rk, P)中, 集合X⊆V的悲观下上近似为
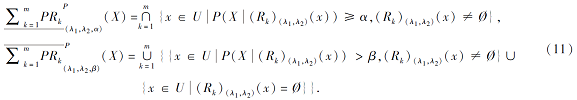
定义 5 逆向乐观模型 在(U, V, Rk, P)中, 集合T⊆U的乐观下上近似为
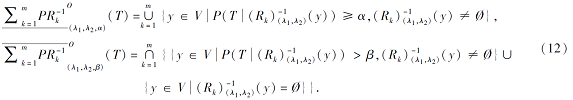
定义 6 逆向悲观模型 在(U, V, Rk, P)中, 集合T⊆U的悲观下上近似为
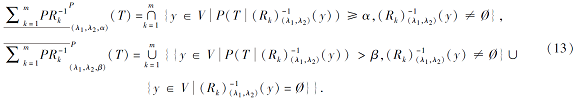
命题 1 正向与逆向悲观上近似具有如下公式:
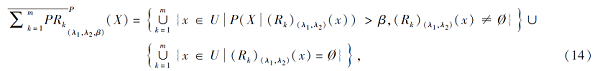
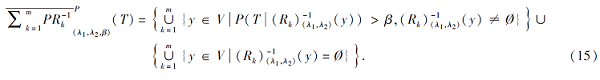
命题 2 关于下上近似之间的包含关系, 正向与逆向乐观模型不一定成立, 但正向与逆向悲观模型一定成立, 即:
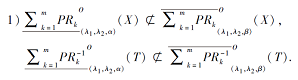
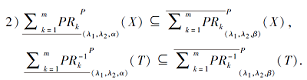
此外, 乐观模型与悲观模型的同向近似之间存在如下包含关系:

命题 3 4种粗糙集模型具有如下退化性:
1)若m=1, 该粗糙集为文献[16]的双论域直觉模糊概率粗糙集.
2)若m=1, α =1, β =0, 且Rk为分明二元关系, 则该粗糙集为文献[4]的双论域粗糙集.
3)若m=1且Rk是从U到V的集值映射, 则该粗糙集为文献[9]的双论域概率粗糙集.
4)若m=1, λ 1=1-λ 2, 且Rk是从U到V的模糊关系, 则该粗糙集为双论域模糊概率粗糙集.
5)若m=1且U=V, 则该粗糙集为(单论域)直觉模糊概率粗糙集.
根据定义3~定义6, 基于直觉模糊关系的双论域多粒度概率粗糙集获得4种模型, 即多粒度双论域直觉模糊概率粗糙集蕴含着正向乐观模型、正向悲观模型、逆向乐观模型、逆向悲观模型.这4种模型具有相似性、对称性与系统性, 都能进行精度与粗糙度的特征量化.
鉴于单粒度上近似具有并形式(如式(3)、式(5)), 命题1变形基于并集成的悲观上近似, 即采用并运算交换律将式(11)和式(13)分别变形为式(14)和式(15).对比地, 乐观上近似的式(8)和式(12)涉及到并交运算, 可使用并交分配律展开, 但会变复杂.命题2考虑构建乐观模型与悲观模型下上近似的包含关系, 1)、2)涉及同一模型内部, 3)、4)涉及乐观与悲观之间, 所有结果由相关定义可证.基于命题2中1)、2), 由于乐观模型式(8)和式(12)的下近似使用并运算, 而上近似使用交运算, 如此上近似不一定严格包含下近似, 还可能上近似包含于下近似.但悲观模型式(11)和式(13)的下上近似构造相反, 导致下上近似之间具有严格包含关系.
此外基于命题2中3)、4), 正向乐观模型与正向悲观模型的下(上)近似之间具有集合包含关系, 逆向乐观模型与逆向悲观模型的下(上)近似之间也具有集合包含关系.
总之, 命题2的研究呈现4类模型关系— — 正反向之间相对独立而乐观悲观之间呈现一定强弱, 该结果一致于相关的系统建模机制.进而根据命题3的退化分析, 4种模型一同扩张对应粗糙集[4, 9, 16].其中, 粒度个数m=1是向(单粒度)双论域直觉模糊概率粗糙集[16]退化的基本条件, 此时正向乐观模型等价于正向悲观模型, 而逆向乐观模型等价于逆向悲观模型.
对比文献[15]和文献[16]的模型发现, 三者都基于直觉模糊背景进行粗糙集建模, 但本文完全涉及概率、多粒度、双论域三要素的综合集成, 相关模型更适用于复杂环境的不确定性分析.文献[15]模型主要采用隶属函数与非隶属函数的逻辑最值运算, 相关结果更偏重于模糊集形式, 不仅复杂、费解, 也不好确定后续的不确定性度量(如精度、粗糙度).文献[16]将模糊信息进行截取粒化, 利用概率及阈值完成单粒度粗糙集的确定.通过拓展与深化, 本文采用集合交并运算进行多粒度集成, 相关结果是粗糙集常用的集合形式, 更具简单性与解释性, 也可自然定义后续的精度与粗糙度等不确定性度量.由此可见, 本文模型具有多粒度建模改进优势.在理论上, 本文模型更具有系统综合性、刻画深入性、优良扩张性; 在应用上, 相关结果具有广泛适应性与更强应用性, 有利于不确定性测量与多属性决策制定等应用.
综上所述, 本文4种模型具有理论扩张优势, 同时具有多粒度环境的实际应用性, 都适用于共同的直觉模糊、双论域、多粒度环境, 但具有不同的侧重点, 可根据实际情况进行选择.后面主要讨论正向乐观模型, 其余3种模型可得到类似结果.在这里, 算法1首先提供4种模型的集成计算, 主要通过单粒度近似[16]集成获取多粒度近似, 具有系统结构性与集成推进性的相关优势.算法引入4个单粒度近似, 即
用于多粒度信息集成.
算法 1 计算正向乐观模型、正向悲观模型、逆向乐
观模型、逆向悲观模型
输入 近似空间(U, V, Rk, P), k=1, 2, …, m,
集合X⊆V、, T⊆U, 参数λ 1、λ 2、α 、 β
输出 正向乐观近似、逆向乐观近似、
正向悲观近似、逆向悲观近似
1. for Rk∈ {R1, R2, …, Rm}do
2. for x∈ U do
3. 由式(7)计算(Rk
4. 由式(3)对应条件判别x
5. end for
6. 得到类似式(3)的单粒度近似
7. for y∈ V do
8. 由式(7)计算(Rk
9. 由式(5)对应条件判别y
10. end for
11. 得到类似式(5)的单粒度近似
12. end for
13. 由式(8)、式(11)~式(13), 采用集成运算得到4种多粒度双近似:
14. 返回13中4对公式结果.
在算法1中, 步骤1~12涉及外层多粒度循环, 包含2个并行内层循环:求正向单近似的论域U循环(步骤2~5)及求反向单近似的论域V循环(步骤7~10).步骤13采用式(16)集成计算4种多粒度双近似, 也可具体分入循环之中.选取求近似所需的模糊截取与概率测量作为基本运算, 可得时间复杂度为O(2m(|U|+|V|)).由此可见, 算法1具有有效性, 可系统得到4类模型的双近似, 具体结果还依赖于参数选择, 从而相关的优化确定成为一个问题.此外, 算法1还可修正到计算后续数量特征或只关注一个模型.
最后说明相关参数的设定.本文模型主要涉及4个参数λ 1、λ 2、α 、 β , 分为2类, 一般性设置讨论如下.
1)λ 1、λ 2为截集参数, 具有基本范围, λ 1∈ [0, 1], λ 2∈ [0, 1], λ 1+λ 2∈ [0, 1], 主要将直觉模糊关系的(非)隶属函数进行截取剖分, 建立基础的模糊粒化.因此, λ 1、λ 2可由(非)隶属函数特性确定, 也可由决策者的粒化需求设定.
2)α 、 β 为概率阈值参数, 通常约束范围是0≤ β ≤ 0.5≤ α ≤ 1, 主要将条件概率进行三支剖分, 支持粗糙近似集的提取.α 、 β 可由概率函数特性确定, 也可由专家经验与实验结果设定.作为补充, 这里提供2种合理的设定方案:(1)可模拟决策粗糙集建模方法, 引入决策风险代价与贝叶斯最优决策进行参数计算与确定; (2)可考虑条件概率排序与精度度量最大值, 通过算法极小化参数所属区间, 最后选取居中参数或偏好阈值.
文中上述建模(及算法)与下述性质都具有普适性, 不依赖于参数值或参数无需预先设定.但在后续实例中, 选取非极端的适中值进行说明, 这种设定可完成基本的有效性验证.在深入研究与实际应用中, 合理的参数设置更依赖于需求与经验、实验与优化等, 并可涉及参数灵敏性分析.
针对多粒度双论域直觉模糊概率粗糙集的4类模型, 本节研究下上近似的基本性质, 包括集合运算关系、概率参数极限、精度大小对比3方面.主要考虑正向乐观模型, 其余3个模型具有类似结果.从而, 基于性质的四类模型关系就成为一个平凡工作或额外问题.这些性质将文献[16]的相关单粒度性质进行多粒度扩展, 具有机制性与扩张性.基于多粒度的并交集成机制(如式(16))在多粒度环境下的性质自然具有集成性、传递性、正确性.因此, 性质证明中通常只选取一个代表作为示例.
性质 1 正向乐观模型的下上近似性质如下:
1)
2)若X⊆Y, 则
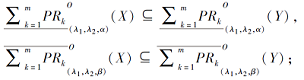

5)若0< α 1≤ α 2≤ 1, 0≤ β 1≤ β 2< 1, 则
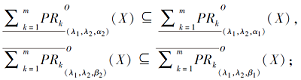
6)
α > 0.5, β < 0.5.
证明 性质1可由基本定义3(即式(8))证明.作为示范, 下面证明2)~4).
∀ x∈
由定义3, 存在k, 使得

若X⊆Y, 则对于上述k, 有
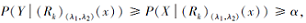
所以
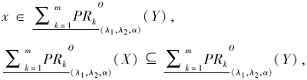
即2)成立.
X∩ Y⊆X, Y⊆X∪ Y,
则由2)可直接推出3)与4)成立. 证毕
性质1聚焦近似算子的运算性质, 得到正向乐观模型近似的并交补运算关系.相关结果在系统上类似于文献[16]的对应性质, 但有多粒度提升性.
性质 2 正向乐观模型近似算子极限刻画为
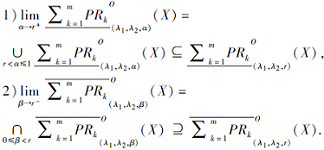
进而, 若Rk是一个串行的直觉模糊关系, 即
∀ x∈ U,
则上述⊆、⊇关系能够被强化为= .
证明 下面仅证一种情况.根据性质1中5), 有

根据定义3, 若α > r, 则
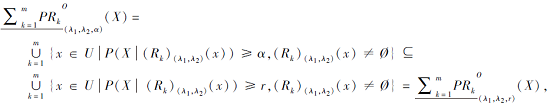
这就意味着
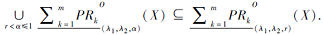
进而, Rk串行的性质导致
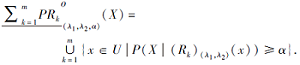
从而
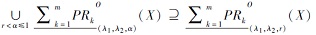
的证明类似于文献[16]中定理3的相应证明. 证毕
性质 3 若Rk是一个串行的直觉模糊关系, 则
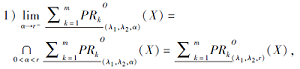
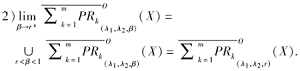
性质2与性质3聚焦正向乐观模型近似的概率参数极限, 性质2主要讨论下近似右极限与上近似左极限, 而性质3提供对称的下近似左极限与上近似右极限.基于串行直觉模糊关系, 相关极限体现对于概率参数的双近似连续性, 一致于并深化文献[16]的对应结果.
性质 4 设Ø ≠ X⊆Y⊆V, 如下3条成立:
1)若
则
2)若
则
3)若
则
进而, 对于
X≠ Ø , Y⊆V,
有如下2条成立:
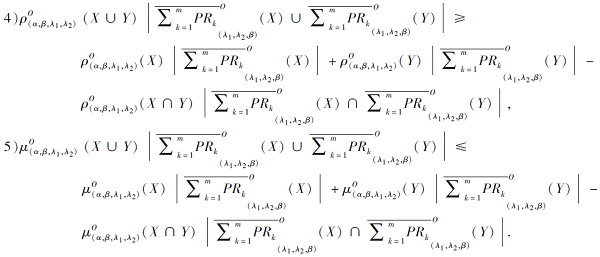
证明 由定义3的精度、粗糙度(式(10))和性质1中2)可证明1)~3). 4)、5)的证明与文献[16]定理6的证明类似. 证毕
性质4呈现正向乐观模型近似的度量大小关系, 主要是基于子集关系与并交运算的精度(粗糙度)大小刻画, 其中精度与粗糙度具有对称性.相关结果关联并深化文献[16]的对应结果.
本节采用一个医疗实例, 说明本文模型的计算算法、决策制定、数学性质.
论域U={x1, x2, …, x5}为病人集, 论域V={y1, y2, …, y5}收集发烧、头痛、胃痛、咳嗽、肌痛5种症状.
假设4位专家对患者及症状进行相应的关联诊断, 相关结果使用U× V上的模糊关系Rk(xi, yj), i=1, 2, …, 5, j=1, 2, …, 5, k=1, 2, 3, 4表示.具体如表1所示.
| 表1 病人与症状之间的直觉模糊关系 Table 1 Intuitionistic fuzzy relations between patients and symptoms |
假设决策者根据实际情况, 设置截集粒化参数λ 1=0.3, λ 2=0.5.基于概率分布与精度优化, 初步确定概率阈值参数所属范围α ∈ (0.5, 1], β ∈ [0.25, 0.33), 由此选定α =0.77, β =0.32进行基本计算与有效验证.考虑症状子集
X={y3, y4}⊆V,
其在(U, V, Rk, P)空间中的关系截集
| 表2 关系截集与条件概率 Table 2 Relational cut-set and conditional probability |
下面先考虑正向乐观模型.基于定义3(或修正算法1)可得如下的下上近似、三支区域、测评度量的计算结果:
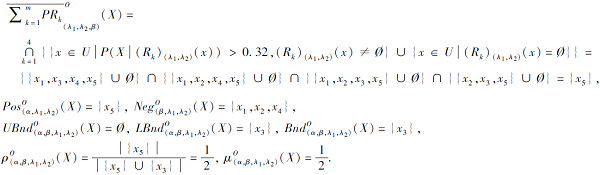
根据上述三支区域结果, 可得正向乐观模型的决策制定策略, 主要实施如下三支决策方案:
1)正域患者x5被判断感染关联X的疾病, 需要相关治疗;
2)负域患者x1、x2、x4未感染X相关疾病, 不需要治疗;
3)边界域患者x3可能感染也可能没有感染X相关疾病, 需要进一步观测与评估.
其余3种模型可类似计算.
表3给出正向和逆向情况下的单粒度模型[16]与多粒度模型的相关结果, 正向模型考虑
X={y3, y4}⊆V,
| 表3 单粒度模型与多粒度模型的实例结果 Table 3 The results of instances of single-granularity and multi-granularity models |
而逆向模型考虑T={x2, x5}⊆U, 并且涉及4个粒度R1、R2、R3、R4.
基于表3的实例结果, 可揭示新建四类模型的关系, 如容易验证命题2的研究结果.类似上述正向乐观模型, 其余3种模型的语义或决策也可进行相应解释.由此可见, 4种模型已将文献[16]的单粒度模型拓展到多粒度环境及其综合应用, 相关的三支决策仍然具有可调机制以控制误诊风险.此外, 临床诊断更期待高精度, 这意味着更多的确诊患者与更少的不确诊患者.
由表3可见, 在相同阈值情况下, 正向乐观模型的精度高于4个正向单粒度模型的精度, 而逆向乐观模型的精度不低于4个逆向单粒度模型的精度, 这也说明本文模型对文献[16]单粒度模型决策效果的改进性.
对比文献[15]发现, 本文模型引入概率度量以获取多粒度建模改进.在本例中, 定义1模型[15]呈现如下近似结果:

由此对比可见, 文献[15]模型的模糊集表达更复杂与费解, 而本文模型的粗糙集表达更直接多样并具可解释性, 并更利于后续的度量构造与决策制定.
在医疗实例中, 专家针对医治病人与疾病症状的关联, 提供直觉模糊关系.一般地, 根据医学机理, 这种模糊关系的隶属值与非隶属值更倾向于在特定范围内合理摆动, 即专家们意见可能不同, 但容易具有较一致的定性机制或总体方向, 具体的把握程度可能会有所不同.
本例专家数据(如表1)具有较好的一致性, 从而多粒度集成融合呈现合理的系统结果, 能说明相关模型及性质的有效性.此外, 在实际情况中, 专家们也可能出现较大分歧(包括在定性方面或定量方面), 特别是针对一些特殊病人或疑难病症.此时, 可考虑一致性判断或特异性删除, 避免专家意见冲突, 更好地进行统计分析与医疗决策.
本节验证构建模型的性质, 主要聚焦正向乐观模型, 重点是其中一些代表结果.首先采用
λ 1=0.3, λ 2=0.5, α =0.77, β =0.32, X={y3, y4}
的基本假设与结果.
考察性质1.
1)
2)取Y={y1, y3, y4, y5}⊇X,
3)设Y={y1, y2, y4}, 则
(
(X
4)设Y={y1, y2, y4}, 则
(
(X
5)取α 1=0.6, β 1=0.2, 则
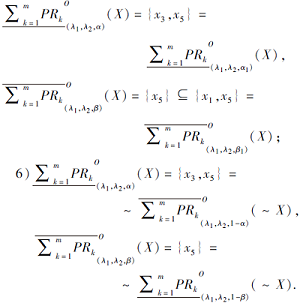
综合1)~6)可知性质1成立.特别指出, 3)、4)及表3结果可说明命题2.
性质2与性质3涉及到概率参数极限, 可通过阈值单调序列进行近似验证.该理论性质也可使用性质1中5)说明, 即5)的参数大小验证也提供这里的一个支撑验证, 即本例的4个直觉模糊关系(R1、R2、R3、R4)都是串行的.
最后说明性质4, 主要是其中的精度部分, 从而粗糙度结果自然成立.首先, 选取
Y={y1, y3, y4, y5}⊇{y1, y3, y4}=X,
考虑1)~3), 此时
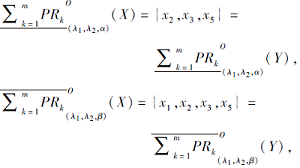
进而, 选取Y={y1, y2, y4}, 考虑4)、5), 此时
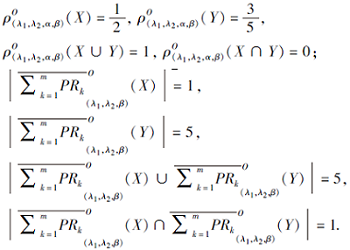
综上所述, 相关数值结果容易验证性质4.
本文基于直觉模糊关系, 并综合考虑概率、双论域、多粒度的泛化因素, 构建正向乐观、正向悲观、逆向乐观、逆向悲观4种多粒度双论域直觉模糊概率粗糙集模型, 得到相关的计算算法、数学性质、决策分析.文中主要以正向乐观模型为主.针对模糊、粗糙、随机等不确定性复杂情况, 利用概率度量方法改善文献[15]的模型复杂性与测量困难性, 将文献[16]的单粒度模型推进到多粒度集成处理, 在理论上扩张文献[4]、文献[9]、文献[16]相应模型与性质.本文模型具有有效融合性、优良扩张性、广泛适应性, 适用于复杂环境, 增强模型强健性, 有利于不确定性分析与多属性决策制定.
鉴于本文模型的有效不确定性刻画能力, 后续的数据分析与知识发现还值得深入研究.特别地, 基于文献[11]的论述, 本文模型有利于多粒度数据分析, 在相关的属性约简、规则提取、决策制定等方面都具有研究空间与应用前景.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|


