引用本文
王浩, 汪京, 方宝富. 稀疏奖励场景下基于个体落差情绪的多智能体协作算法. 模式识别与人工智能, 2022,35(5): 451-460
WANG Hao, WANG Jing, FANG Baofu. Multi-agent Cooperation Algorithm Based on Individual Gap Emotion in Sparse Reward Scenarios. PATTERN RECOGNITION AND ARTIFICIAL INTELLIGENCE, 2022,35(5): 451-460.  
Doi: 10.16451/j.cnki.issn1003-6059.202205006
Permissions
Copyright©2022, 《模式识别与人工智能》编辑部
《模式识别与人工智能》编辑部
稀疏奖励场景下基于个体落差情绪的多智能体协作算法
王浩1,2, 汪京1,2, 方宝富1,2
1.合肥工业大学 计算机与信息学院 合肥230601
2.合肥工业大学 情感计算与先进智能机器安徽省重点实验室 合肥 230601
通讯作者：

方宝富,博士,副教授,主要研究方向为多机器人/ 智能体系统、情感智能体、强化学习.E-mail:fangbf@hfut.edu.cn.

作者简介：

王 浩,博士,教授,主要研究方向为人工智能、机器人.E-mail:jsjxwangh@hfut.edu.cn.

汪 京,硕士研究生,主要研究方向为多智能体强化学习、情感智能体.E-mail:wangj@mail.hfut.edu.cn.

收稿日期: 2021-09-06 接受日期: 2022-01-17
资助项目: 国家自然科学基金项目(No.61872327)、民航飞行技术与飞行安全重点实验室开放基金项目(No.FZ2020KF07)资助
摘要

针对在多智能体环境中强化学习面临的稀疏奖励问题,借鉴情绪在人类学习和决策中的作用,文中提出基于个体落差情绪的多智能体协作算法.对近似联合动作值函数进行端到端优化以训练个体策略,将每个智能体的个体动作值函数作为对事件的评估.预测评价与实际情况的差距产生落差情绪,以该落差情绪模型作为内在动机机制,为每个智能体产生一个内在情绪奖励,作为外在奖励的有效补充,以此缓解外在奖励稀疏的问题.同时内在情绪奖励与具体任务无关,因此具有一定的通用性.在不同稀疏程度的多智能体追捕场景中验证文中算法的有效性和鲁棒性.

关键词: 稀疏奖励; 多智能体协作; 强化学习; 个体落差情绪; 内在情绪奖励
中图分类号:TP181
Multi-agent Cooperation Algorithm Based on Individual Gap Emotion in Sparse Reward Scenarios
WANG Hao1,2, WANG Jing1,2, FANG Baofu1,2
1. School of Computer Science and Information Engineering,Hefei University of Technology, Hefei 230601
2. Anhui Province Key Laboratory of Affective Computing and Advanced Intelligent Machine, Hefei University of Technology, Hefei 230601
Corresponding author:
FANG Baofu, Ph.D., associate professor. His research interests include multirobot/agent systems, emotion agent and reinforcement learning.

About Author:
WANG Hao, Ph.D., professor. His research interests include artificial intelligence and robots.
WANG Jing, master student. His research interests include multi-agent reinforcement learning and emotion agent.

Fund:National Natural Science Foundation of China(No.61872327), Open Fund of Key Laboratory of Flight Techniques and Flight Safety of CAAC(No.FZ2020KF07)
Abstract

To address the sparse reward problem confronted by reinforcement learning in multi-agent environment, a multi-agent cooperation algorithm based on individual gap emotion is proposed grounded on the role of emotions in human learning and decision making. The approximate joint action value function is optimized end-to-end to train individual policy, and the individual action value function of each agent is taken as an evaluation of the event. A gap emotion is generated via the gap between the predicted evaluation and the actual situation. The gap emotion model is regarded as an intrinsic motivation mechanism to generate an intrinsic emotion reward for each agent as an effective supplement to the extrinsic reward. Thus, the problem of sparse extrinsic rewards is alleviated. Moreover, the intrinsic emotional reward is task-independent and consequently it possesses some generality. The effectiveness and robustness of the proposed algorithm are verified in a multi-agent pursuit scenario with different sparsity levels.

Key words: Sparse Reward; Multi-agent Cooperation; Reinforcement Learning; Individual Gap Emotion; Intrinsic Emotional Reward

本文责任编委 陈松灿

Recommended by Associate Editor CHEN Songcan

强化学习(Reinforcement Learning, RL)以试错机制与环境进行交互, 通过最大化累积奖励学习完成目标任务的最优策略.RL主要用于解决序贯决策问题, 广泛应用于交通控制[1]、机器人控制[2]、游戏博弈[3]等领域.然而在面对一些真实场景下的复杂决策问题时, 单智能体系统的决策能力有限, 需要多个决策者之间相互协作共同完成任务.因此将强化学习与多智能体系统交叉融合形成的多智能体强化学习(Multi-agent RL, MARL)[4]成为人工智能领域中的重要研究方向.

在强化学习中, 奖励具有引导智能体学习方向的作用[5], 智能体依赖奖励进行策略优化.在训练开始阶段, 智能体采用随机策略探索环境, 需要经过一系列复杂的操作才能获得奖励, 导致智能体训练困难.缺乏外在奖励信息导致智能体学习缓慢甚至无法学习到有效策略, 这就是稀疏奖励问题(Sparse Reward Problem)[6].在多智能体系统中, 多位决策者需要相互协作共同完成目标任务才能获得奖励, 因此稀疏奖励问题在多智能体系统中普遍存在.在一定程度上解决稀疏奖励问题, 有助于提高多智能体强化学习算法的样本利用率, 加快策略学习的速度.

针对稀疏奖励问题, 一种直观的解决方法是利用先验知识人工设计密集的奖励函数.通过人为设计的密集奖励, 引导智能体完成目标任务, 简化训练过程.但是人工设计的奖励函数与任务密切相关, 缺乏通用性.针对奖励设计困难的问题, Hussein等[7]提出模仿学习方法, 使用示例数据进行监督学习, 使智能体快速掌握示例策略, 加快智能体训练速度, 但是模仿不可能精确复制示范动作, 又由于强化学习是序列决策问题, 因此将累积误差.

此外, 解决稀疏奖励问题的另一个研究方向是将内在动机引入强化学习, 外在奖励结合内在奖励共同指导智能体学习.Pathak等[8]学习环境的状态转移, 使用预测误差作为内在奖励, 促进智能体的探索.Strouse 等[9]使用目标与状态或行动之间的交互信息作为内在奖励, 加快智能体的收敛速度.上述内在动机方法引入额外的网络计算内在奖励, 并引入额外的偏差, 在一定程度上影响智能体训练.

在人类行为塑造中, 情绪起到关键作用.人类和其它动物在学习和探索过程中也会使用情绪传达关于个体内部状态的信息, 这种方式与语言无关[10], 具有一定的通用性.另一方面, 情绪通过提供对过去、现在和未来情况的反馈塑造行为[11], 这种反馈在影响行为选择时, 总是使行为偏向某个特定方向.当智能体选择并执行一个动作, 到达新的状态时, 如果奖励高于预期或情况优于预期, 智能体将产生积极情绪, 从而指导智能体在该状态下更多地选择这一动作.情绪的加入使智能体能感受到自身行动的优劣, 通过为其增加内在奖励的方式, 帮助智能体调整行为策略, 缓解稀疏奖励问题.

借鉴情绪对决策的重要作用, 本文提出基于个体落差情绪的多智能体协作算法(Multi-agent Cooperative Algorithm Based on Individual Gap Emo-tion, IGE).遵循CTDE(Centralized Training with Decentralized Execution)[12]框架, 学习一个集中但分解的评论家, 将集中式评论家分解为以自身观测为条件的单个评论家的加权线性组合.集中式策略梯度估计器直接优化整个联合动作空间, 加强智能体间策略的协调.综合考虑多智能体系统中全局奖励对每个智能体的不同影响, 将个体动作值函数映射为落差情绪.该落差情绪直接与RL的学习过程关联, 把智能体的个体落差情绪作为内在情绪奖励反馈到每个智能体.该奖励在每个时间步分别刺激相应的智能体, 促进智能体行为的多样性, 同时缓解稀疏奖励问题.在不同稀疏程度的多智能体追捕任务上评估IGE, 实验表明, IGE在追捕成功率和收敛步数上均较优, 能在奖励稀疏的环境中更快地学会协作策略.

1 相关工作
1.1 多智能体深度确定性策略梯度算法

多智能体深度确定性策略梯度算法(Multi-agent Deep Deterministic Policy Gradient, MADDP-G)[13]将深度确定性策略梯度算法(Deep Determi-nistic Policy Gradient, DDPG)扩展到多智能体系统, 使用CTDE范式学习连续动作空间的确定性策略.为每个智能体建立一个中心化的评论家(Critic)网络, 在训练阶段使用所有智能体的信息而非仅使用个体信息, 以此缓解多智能体系统的非平稳问题.而在执行阶段策略(Actor)网络仅根据当前智能体的局部观测信息oi选择动作ai.

在MADDPG中, 集中式Critic网络通过全局状态s和所有智能体的动作{a1, a2, …, an}估计联合动作值函数Qi, 由φ i参数化.最小化损失

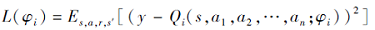
以训练集中式Critic网络, 其中

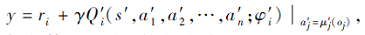
ri为智能体i 收到的外在奖励, {μ '1, μ '2, …, μ 'n}为智能体的目标策略集合, φ 'i为目标Critic网络Q'i的参数.

MADDPG单独计算策略梯度

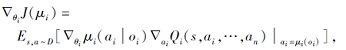
以更新每个智能体的策略μ i(oi|θ i).

1.2 内在奖励

内在动机是心理学中一个被广泛研究的领域, 它关注由内在满足而不是结果驱动的行为[14].通过内在动机计算额外的内在奖励以支持智能体训练, 促进智能体的探索.

Tang等[15]提出基于计数(Count-Based)、可泛化到高维状态空间的探索策略.使用状态的访问频率衡量状态的不确定性, 访问次数越少的状态具有越强的新颖性.通过Hash函数将状态映射到Hash表进行计数, 以与计数成反比的方式为智能体提供内在奖励, 实现在高维状态空间中应用基于计数的探索方法, 取得较优效果.

Pathak等[8]提出ICM(Intrinsic Curiosity Mo-dule), 学习有效的观测表示.使用逆环境模型获取状态的特征表示, 去除环境模型中与动作无关的部分.通过前向动态模型的预测误差作为鼓励其好奇心的内在奖励, 促进智能体的探索.

Badia等[16]提出NGU(Never Give Up), 基于智能体最近经验的k近邻构建基于情景记忆的内在奖励, 并通过长期新颖性模块使智能体保持持久好奇心, 以此训练定向探索策略, 鼓励智能体访问其环境中的所有状态.

1.3 情绪与强化学习

情绪在学习中扮演着重要的角色, 通过激发生理信号, 使行为偏向于奖励最大化和惩罚最小化.

目前也有学者将情绪结合RL.Horio等[17]通过基于蒙特卡洛方法的学习调整情绪, 根据自己的位置与他人位置之间的关系, 选择要执行的协作动作, 并结合由强化学习获得的战略决策训练智能体.Salichs等[18]提出基于价值的情绪激发方法, 对特定状态的恐惧建模为与该状态相关的最糟糕的历史动作值, 建立的模型会记住它应该害怕的特定坏位置.上述方法仅适用于离散动作空间且状态空间较小, 难以泛化到高维连续动作空间.

针对情绪在多智能体复杂决策中的应用, 方宝富等[19]侧重考虑智能体的异构性, 根据智能体自身的个性特点建立情感模型, 经历衰减和刺激后生成具有自身个性特征的情感值, 基于情感值生成智能体的内在奖励.但是, 该方法需要事先设定每个智能体的个性特征, 不同的个性将导致不同的策略方案, 缺乏对环境的通用性, 并且也未充分考虑总体奖励对每个智能体的不同影响.

2 基于个体落差情绪的多智能体协作算法

情绪是智能体的一种内在属性, 与智能体行为选择机制密切相关.受此启发, 综合考虑全局团队奖励对多智能体系统中每个智能体的不同影响, 提出基于个体落差情绪的多智能体协作算法(IGE).为每个智能体建立落差情绪模型, 作为内在动机机制, 该情绪模型仅以自身观测信息作为条件, 以每个智能体产生不同的内在情绪奖励作为外在奖励的有效补充, 以此缓解稀疏奖励问题, 并促进智能体行为多样化.

2.1 个体落差情绪

情绪是对外部事件或内部事件的反应, 事件是一种状态变化[20].这一变化是否具有象征意义并不重要, 重要的是, 生物体能推断出相比之前情况发生的变化.在大多数认知情绪理论中, 情绪与状态变化有关[21].由于情绪是对事件的反应, 这意味着情绪总是包含对状态变化的积极评估和消极评估.

基于上述特点, 本文提出落差情绪概念, 基于个体相关性, 由预期结果与实际情况之间的差异产生落差情绪, 这里的预期是指对未来可能状态的预测.落差情绪定义如下:

Eg=Φ '(s)-Φ (s),

其中, Φ '、Φ 分别表示对事件的预期评价与实际评价, s表示状态信息.

本文中的情绪并不意味着智能体应该“ 了解自己的情绪” .情绪更多来自于RL学习过程的各方面(如价值函数), 且在学习趋同后也可能持续存在[22].因此, 在强化学习中, 可通过价值函数衡量预期评价与实际评价.落差情绪通过预期评价与实际评价之间差值的正负, 反映个体对事件积极评价和消极评价.通过落差情绪提供的反馈信息, 个体可调整未来的行为趋势.

2.2 基于落差情绪的内在情绪奖励

将情绪引入强化学习中并进行量化分析, 智能体根据量化的情绪模型将感知的状态信息映射为相应的情绪值, 将情绪值进行加权处理, 作为最终的内在情绪奖励信号.

在RL中量化落差情绪时, 若采用状态值函数, 则意味着状态本身导致情绪的产生, 类似人类的状态评估, 当处于绝境时, 会直接影响心情的好坏.而采用动作值函数量化情绪, 更侧重于动作选择的影响.综合考虑后, 本文采用动作值函数量化落差情绪.强化学习中动作值函数表示智能体在当前状态下采取行动获得的预期累积奖励, 以此作为对当前状态的评价.

在多智能体系统中, 联合动作空间会随着智能体数目呈指数增长, 难以单纯学习以全局状态和联合动作为条件的集中式情感模型, 会造成过大偏差, 并且该集中式情感模型未充分体现多智能体系统中个体之间的差异.因此, 本文学习集中但分解的Critic网络, 通过个体Critic建模情绪, 充分考虑个体间的差异性, 同时缓解状态空间和动作空间增长造成的难训练问题.在AC(Actor-Critic)框架中采用值分解方法, 相比基于价值的值分解方法, 集中式Critic网络的设计不受约束[23].所有智能体共享一个集中式Critic网络, 联合动作值函数Qtot被分解为

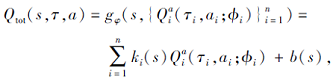
其中, τ i表示每个智能体的行为观测历史, ϕ i表示每个智能体的局部动作值 Qia的参数, gφ 表示以全局状态信息为条件的线性混合网络, 其中通过超网络产生线性权重, ki和b由混合网络生成.

集中但分解的Critic网络通过最小化

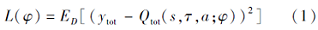
进行训练, 其中

ytot=rex+γ Q'tot(s', τ ', a'; φ '),

rex表示智能体收到的团队奖励, D表示经验缓冲区, φ '表示目标混合网络的参数.通过依赖于外在奖励的全局时间差分(Temporal-Difference, TD)误差以学习个体评论家 Qia, 即 Qia是隐式学习的, 而不是从任何特定于智能体i的奖励中学习的.此时, 多智能体系统中个体评论家包含总体奖励对个体的影响.

落差情绪中预期结果与实际情况的差值可由TD误差计算.强化学习中TD根据当前获得的奖励和对未来奖励的预测, 估计情境变得更好或更坏的程度, 通过TD误差可反映智能体对事件的积极评价和消极评价.

但是, 生物往往通过奖励而非惩罚学习新技能, 频繁的惩罚只会使学习者因为恐惧而停止[20].受此启发, 本文在落差情绪定义的基础上, 通过实际结果与预期评价之间的相对距离计算落差情绪值, 以此反映个体对环境的掌控力度, 鼓励智能体提高积极情绪.并且引入最大控制力常量ξ , 若相对差值大于ξ , 表明情绪波动较大, 对环境的掌控力较弱, 给予消极评价, 反之亦然.本文以上述方式对事件进行积极评价和消极评价.

基于上述分析, 本文建立个体情绪模型, 将个体动作值函数映射为落差情绪.该情绪模型只需智能体的局部观测信息, 缓解多智能体扩展性问题.同时, 通过混合网络的分解架构综合考虑全局奖励对个体的不同影响.个体落差情绪通过动作值函数 Qia的变化表示为

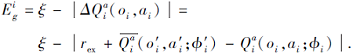
其中:ξ 为预先设定的控制常量, 表示情绪差异的最大阈值; Qia¯为目标动作值函数, φ 'i为目标网络参数.

个体落差情绪反映个体对其能力的主观评价, 表明个体对环境模型的控制力度(即对环境变化的预测能力), 对环境模型预测越准确, 意味着个体对环境的控制力越强.每次更新时Q值变化越大, 意味着智能体在该“ 状态-动作” 下的策略越不稳定, 离到达收敛越远, 即控制力越小, 而随着智能体的学习, 控制力会逐渐提高.

将个体落差情绪映射到内在情绪奖励, 对落差情绪值进行加权, 得到每个智能体的内在情绪奖励:

rini=ω Egi.(2)

2.3 基于内在情绪奖励的多智能体算法

基于个体落差情绪的内在情绪奖励可准确分配给特定的智能体, 因此单独最大化内在奖励比联合最大化所有智能体的内在奖励总和更有效[24].

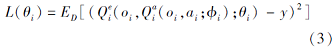
在分解架构中, 每个智能体都有一个单独的动作值函数 Qia, 所有单独的动作值函数通过混合网络组合成联合动作值函数Qtot.向个体动作值函数 Qia引入内在落差情绪奖励, 每个智能体i通过内在情绪网络(Intrinsic Emotional Network, IEN)学习一个内在情绪函数 Qie, 将观测信息oi和个体动作值函数 Qia作为输入, 通过最小化损失

更新 Qie(θ i)的参数θ i, 其中

y= rini+γ Qie¯(o'i, Qia¯(o'i, a'i; ϕ 'i); θ 'i),

Qia¯、 Qie¯为目标动作值函数, D为经验缓冲区, rini为由式(2)产生的内在情绪奖励.

然后采用辅助梯度的方式引入内在奖励的影响, 通过最大化E[ Qie(oi, Qia(ϕ i))]及最小化联合动作值函数Qtot的TD误差δ tot更新个体动作值函数[25] Qia(ϕ i)的参数:

∇ϕiJ(ϕ i)= ∂δtot∂ϕi-α ∂Qie(oi, Qia(oi, ai; ϕi))∂Qia(oi, ai; ϕi)∂Qia(oi, ai; ϕi)∂ϕi. (4)

以此提高全局奖励和内在情绪奖励, 而非直接将内在情绪奖励加入联合动作值函数的TD 误差中, 该辅助梯度方式不会导致原来的TD 误差增加.同时混合网络参数仍通过原有联合动作值函数的TD误差δ tot进行更新.由于未引入内在奖励的影响, 因此不会因为引入内在情绪奖励导致过高的TD误差, 从而影响智能体的训练.

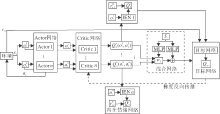
本文算法(IGE)整体框架如图1所示, 每个智能体具备负责自身决策的Actor网络, Critic网络根据自身观测和Actor网络选择的动作计算个体动作值 Qia, 通过式(2)得到相应的内在情绪奖励, 将其与个体动作值一起输入内在情绪网络中, 学习内在情绪函数 Qie.再将所有个体动作值通过混合网络计算联合动作值函数Qtot.最后通过目标网络得出联合动作值函数的TD误差δ tot.根据梯度式(4)更新智能体的Critic网络.

图1 IGE整体架构Fig.1 Overall architecture of IGE

在更新智能体策略网络时, IGE使用一个集中式梯度估计器优化整个动作空间, 而非分别优化每个智能体的动作空间, 以此实现智能体间策略的更好协调.集中式策略梯度

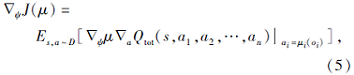
其中,

μ ={μ 1(o1; ψ 1), μ 2(o2; ψ 2), …, μ n(on; ψ n)}

为所有智能体的当前策略集合,

ψ ={ψ 1, ψ 2, …, ψ n}

为智能体策略参数集合, D为经验缓冲池.

本文方法是异策略(Off-Policy)算法, 环境的外在奖励存放在经验缓冲区中, 因为个体动作值函数在智能体学习过程中不断改变, 所以在每次更新之前, 需要在采样批次中重新计算内在情绪奖励.

IGE完整训练过程如算法1所示.

算法 1 IGE

初始化 智能体网络的权重参数ψ ,

价值网络的权重参数ϕ ,

内在情绪网络的权重参数θ ,

混合网络的权重参数φ , 经验池D,

对应目标网络的权重参数

ϕ '=ϕ , ψ '=ψ , θ '=θ , φ '=φ .

for t=1 to T do

对于每个智能体i, 选择动作ai~μ i(oi)+ε .

执行动作a=(a1, a2, …, an), 得到奖励r及下一个状态s'.

在经验池D中存储(s, a, r, s').

s← s'.

以均匀分布在D中采样N条记录.

for agent i=1 to n do

通过式(2)计算每个智能体的内在情绪奖励 rini.

最小化损失函数(3)以更新内在情绪网络的权重参数θ i.

根据式(4)计算的策略梯度更新价值网络的权重参数ϕ i.

end for

通过最小化损失函数(1)更新混合网络gφ .

通过集中式策略梯度(5)更新智能体网路 μψi.

更新目标网络:

ϕ '=τ ϕ +(1-τ )ϕ ', ψ '=τ ψ +(1-τ )ψ ', θ '=τ θ +(1-τ )θ ', φ '=τ φ +(1-τ )φ '.

end for

3 实验及结果分析

本文以多智能体追捕任务为实验场景, 在3种不同稀疏程度的追捕环境中进行实验, 包括单目标追捕、多目标追捕和协作追捕.在这些环境中将IGE与多种基线方法进行对比.

3.1 实验环境

多智能体追捕环境改编自Lowe等[13]原始 Predator-Prey 环境, 引入追捕半径同时允许智能体死亡, 取消根据距离人为设置的密集奖励, 以此验证多智能体稀疏奖励问题.

追捕环境设置为:在一个二维世界中, 有n位追捕者(研究主体)和m位逃跑者(任务目标), 只能控制追捕者, 逃跑者是随机智能体.所有智能体可出现在二维世界中任意位置, 并向任意方向移动.追捕者的目标是协调以尽可能少的步骤捕获逃跑者.每位追捕者的状态包括当前位置和速度、其它智能体的相对位置及逃跑者的速度, 追捕者的动作空间是二维连续动作空间, 取值范围为[-1, 1].追捕者的追捕半径为0.15, 当逃跑者与追捕者的距离小于追捕半径时逃跑者被捕获, 被捕获的逃跑者会死亡.

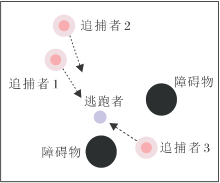
实验环境如图2所示.有3位追捕者(红色)和一位逃跑者(紫色).黑色圆形表示障碍物, 可以阻碍双方的行动.浅红色圆圈表示该追捕者的追捕范围, 追捕范围的数值可控.

图2 实验环境Fig.2 Experimental environment

本文共设计3组实验, 分别从目标数量和追捕条件的角度对环境中奖励稀疏级别进行分级, 如表1所示.

表1 实验环境稀疏等级 Table 1 Sparse level of experimental environment

1)单目标追捕.逃跑者数量为单人, 所有追捕者合围逃跑者, 仅当追捕到逃跑者时全局奖励+5, 同时任务结束, 中间其它时间步不获得奖励.

2)多目标追捕.逃跑者数量为多人, 追捕到其中一位逃跑者不获得奖励, 仅当所有逃跑者都被捕获时才获得全局奖励.相比单目标追捕, 多目标环境的奖励稀疏程度更高, 同时随着智能体数目的增加, 训练难度也相应提高.

3)协作追捕.考虑多智能体间的协作, 设置追捕者处于弱势, 需要两位及以上追捕者同时追到逃跑者, 该逃跑者才会被捕获.若逃跑者只被一个追捕者追到, 捕获失败, 无法获得全局奖励.相比只需一位追捕者就能成功捕获的情况, 协作追捕环境需要更强的协作能力, 同时减弱环境的随机性, 稀疏程度相应增加.

3.2 对比方法和评价指标

在3种不同稀疏程度的追捕实验中选择如下对比算法:1)使用原始架构的MADDPG[13], 使用内在奖励解决稀疏问题的算法; 2)ICM[8], 使用前向动态模型的预测误差作为鼓励好奇心的内在奖励; 3)NGU[16], 通过长期新颖模块和情节内新颖模块计算内在奖励; 4)基于计数的算法(简记为Count)[15], 使用状态的访问频率衡量状态的不确定性.

在实验中, 为了保持相对的公平性, 所有多智能体算法的策略和评论网络都由MLP(Multilayer Perceptron)参数化, 折扣因子γ 设置为0.97, 所有模型都由自适应矩估计(Adaptive Moment Estimation, Adam)优化器训练[26], 学习率设置为1e-3.最大时间步设置为25.当所有逃跑者都被追捕成功或达到最大时间步后, 一个情节终止.每100个情节后暂停训练并独立运行10个情节进行评估.目标网络采用软更新方式, 更新率τ =0.001.

每组实验分别从测试胜率和收敛步数进行分析对比.测试胜率指追捕者在一定时间内追捕到所有逃跑者的情节数占总测试情节数的百分比, 平均追捕步数指在总测试情节中, 追捕到所有逃跑者所需

的平均时间步.

3.3 实验结果

在3种不同稀疏程度的追捕场景中对每种算法进行评估, 每个场景中每种算法按照不同的随机种子运行5次, 本节所有实验图中实线表示5次运行结果的均值, 误差带表示5次运行结果的95%置信区间.

3.3.1 单目标追捕

在本次实验中, 设置追捕者数量为3, 逃跑者数量为1, 即设定一个3追1的单目标追逃场景.只有最终追到逃跑者时追捕者才获得全局奖励, 其余中间时间步均不获得奖励.

在单目标追捕环境中不同方法的性能对比如图3所示.

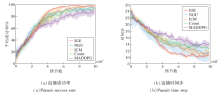图3 单目标追捕环境中各算法性能对比Fig.3 Performance comparison of different algorithms in single target pursuit environment

由图3可知, IGE在追捕成功率和追捕步数上均最优.相比基于内在奖励的算法, IGE收敛速度更快, 表明内在奖励的设置有利于提高算法的学习效率, 缓解稀疏奖励问题.而MADDPG在单目标追捕中也有相当胜率, 原因在于单目标追捕中奖励稀疏程度较弱, 通过随机方式也能探索到正向奖励, 以此更新策略逐渐提升得到奖励的概率直至收敛.

3.3.2 多目标追捕

为了增加环境中奖励的稀疏程度, 设置逃跑者数量为2, 即设置一个3追2的多目标追捕场景.相比单目标追捕环境, 此时只有两位逃跑者都被追到时, 才会获得全局奖励, 因此外在奖励更稀疏, 同时智能体数量的增加也进一步增加状态空间的维度, 智能体训练的难度更大.

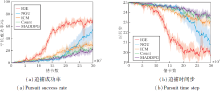
各算法在多目标追捕中的性能对比如图4所示.由图可知, 相比基于内在奖励的算法(ICM、Count), NGU在追捕胜率和收敛时间步上具有一定提升, 这表明NGU能缓解内在奖励算法随着训练进行, 环境状态不再新颖, 导致无法提供内在奖励的问题.而本文的内在情绪奖励直接与强化学习过程关联, 也进一步避免知识衰退这一问题.

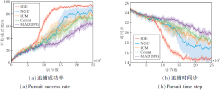图4 多目标追捕环境中各算法的性能对比Fig.4 Performance comparison of different algorithms in multi-target pursuit environment

相比单目标追捕场景, 其它基线算法的追捕成功率和追捕所需步数均产生明显下降, 分析原因如下.一方面, 多目标环境的奖励更稀疏, 基于内在奖励的基线方法通过额外的网络计算内在奖励, 引入一定偏差.另一方面, 基线算法均采用集中式Critic网络, 简单地将所有智能体的观测连接到一个单一的输入向量中, 学习联合动作值函数, 使学习一个好的集中式Critic网络变得更困难.而相比之下, IGE性能下降较小, 仍能达到90%以上的胜率, 同时在追捕所需步数上也明显最优.这是因为IGE的个体情绪奖励与动作值函数关联, 直接优化强化学习的学习过程, 引入的偏差较小.相比其它基线方法, IGE的内在情绪奖励仅需个体的观测信息, 缓解集中式的扩展性问题, 同时分解架构也未忽略总体奖励对个体的影响.

3.3.3 协作追捕

从多智能体间协作的角度出发, 进一步增加环境中奖励的稀疏程度, 需要两位及以上追捕者同时追到逃跑者, 该逃跑者才会死亡, 即设置一个4追2协作追捕环境, 该环境需要智能体间更高的协作能力.

各算法在协作追捕中的性能对比如图5所示.由图可知, IGE在追捕成功率和收敛步数上仍最优, 而基于内在奖励的基线算法的性能优于MADDPG, 说明内在奖励算法对智能体训练有一定的促进作用, 但对于智能体间协作能力的提升作用有限.相比ICM和Count, NGU在训练后期有较明显的提升, 这是由于NGU能克服上述两种算法因持续训练而导致无法及时提供内在奖励的问题.相比之下, IGE在收敛速度上具有明显提升, 能更好地完成协作任务.通过集中但分解的评论家, 将全局奖励进行隐式分配, 个体情绪奖励分别刺激不同智能体, 促进智能体间的探索, 并优化整个联合动作空间, 避免陷入局部最优, 以此促进智能体间的协作.

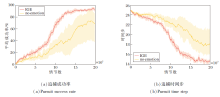
图5 协作追捕环境中各算法的性能对比Fig.5 Performance comparison of different algorithms in cooperative pursuit environment

3.4 消融实验

本节将对IGE进行进一步的消融研究, 验证加入个体落差情绪奖励的有效性.选择在3追2多目标追捕环境中进行实验.IGE取消内在情绪奖励模块后记作no-emotion, 并与IGE在3追2多目标追捕环境中进行分析对比, 以此反映情绪对多智能体训练的影响.

具体消融实验结果如图6所示.图中两种算法按照不同的随机种子运行8次, 误差带表示8次运行结果的95%置信区间.由图可知, no-emotion误差带较宽, 反映算法结果波动较大, 原因在于未加入情感模块, 算法通过随机方式探索环境, 存在一定的随机误差, 导致训练困难甚至失败.通过内在情绪奖励, 可在一定程度上指导智能体的训练方向, 促进智能体更稳定的训练, 同时在一定程度上提高智能体的学习效率.

图6 多目标追捕环境中的消融实验结果Fig.6 Result comparison of ablation experiment in multi-target pursuit environment

4 结束语

针对多智能体系统中的稀疏奖励问题, 本文结合情绪与强化学习, 提出基于个体落差情绪的多智能体协作算法.基于个体的落差情绪生成智能体的内在情绪奖励, 可分别刺激不同智能体, 促进智能体产生多样性的行为, 加强智能体间的协作.以该内在情绪奖励作为外在稀疏奖励的有效补充, 缓解稀疏奖励问题.在不同稀疏程度的追捕环境中验证算法的有效性和鲁棒性.今后将研究抽象级别更高的情绪维度, 丰富情绪的表示形式.

参考文献
[1] MA J M, WU F. Feudal Multi-agent Deep Reinforcement Learning for Traffic Signal Control // Proc of the 19th International Confe-rence on Autonomous Agents and Multiagent Systems. New York, USA: ACM, 2020: 816-824. [本文引用:1]
[2] KOBER J, PETERS J. Reinforcement Learning in Robotics: A Survey // WIERING M, VAN DTTERLO M, eds. Reinforcement Learning: Start-of-the-Art. Berlin, Germany: Springer, 2012: 519-610. [本文引用:1]
[3] VINYALS O, BABUSCHKIN I, CZARNECKI W M, et al. Grand master Level in StarCraft II Using Multi-agent Reinforcement Lear-ning. Nature, 2019, 575: 350-354. [本文引用:1]
[4] 孙长银, 穆朝絮. 多智能体深度强化学习的若干关键科学问题. 自动化学报, 2020, 46(7): 1301-1312.
(SUN C Y, MU C X. Important Scientific Problems of Multi-agent Deep Reinforcement Learning. Acta Automatica Sinica, 2020, 46(7): 1301-1312. ) [本文引用:1]
[5] LI Y X. Deep Reinforcement Learning: An Overview[C/OL]. [2021-09-18]. https://arxiv.org/pdf/1701.07274.pdf. [本文引用:1]
[6] RIEDMILLER M, HAFNER R, LAMPE T, et al. Learning by Playing-Solving Sparse Reward Tasks from Scratch // Proc of the 35th International Conference on Machine Learning. San Diego, USA: JMLR, 2018: 4344-4353. [本文引用:1]
[7] HUSSEIN A, GABER M M, ELYAN E, et al. Imitation Learning: A Survey of Learning Methods. ACM Computing Surveys, 2018, 50(2): 1-35. [本文引用:1]
[8] PATHAK D, AGRAWAL P, EFROS A A, et al. Curiosity-Driven Exploration by Self-Supervised Prediction // Proc of the 34th International Conference on Machine Learning. San Diego, USA: JMLR, 2017: 488-499. [本文引用:3]
[9] STROUSE D J, KLEIMAN-WEINER M, TENENBAUM J, et al. Learning to Share and Hide Intentions Using Information Regularization // Proc of the 32nd International Conference on Neural Information Processing Systems. Cambridge, USA: The MIT Press, 2018: 10270-10281. [本文引用:1]
[10] BROEKENS J, CHETOUANI M. Towards Transparent Robot Lear-ning through TDRL-Based Emotional Expressions. IEEE Transactions on Affective Computing, 2019, 12(2): 352-362. [本文引用:1]
[11] BAUMEISTER R F, VOHS K D, NATHAN DEWALL C, et al. How Emotion Shapes Behavior: Feedback, Anticipation, and Reflection, Rather Than Direct Causation. Personality and Social Psychology Review, 2007, 11(2): 167-203. [本文引用:1]
[12] SON K, KIM D, KANG W J, et al. QTRAN: Learning to Factorize with Transformation for Cooperative Multi-Agent Reinforcement Learning[C/OL]. [2021-08-21]. https://arxiv.org/pdf/1905.05408v1.pdf. [本文引用:1]
[13] LOWE R, WU Y, TAMAR A, et al. Multi-agent Actor-Critic for Mixed Cooperative-Competitive Environments // Proc of the 31st International Conference on Neural Information Processing Systems. Cambridge, USA: The MIT Press, 2017: 6380-6391. [本文引用:3]
[14] ZHENG Z Y, OH J, HESSEL M, et al. What Can Learned Intrinsic Rewards Capture? // Proc of the 37th International Conference on Machine Learning. San Diego, USA: JMLR, 2020: 11436-11446. [本文引用:1]
[15] TANG H R, HOUTHOOFT R, FOOTE D, et al. #Exploration: A Study of Count-Based Exploration for Deep Reinforcement Learning // Proc of the 31st International Conference on Neural Information Processing Systems. Cambridge, USA: The MIT Press, 2017: 2750-2759. [本文引用:2]
[16] BADIA A P, SPRECHMANN P, VITVITSKYI A, et al. Never Give Up: Learning Directed Exploration Strategies[C/OL]. [2021-09-18]. https://arxiv.org/pdf/2002.06038.pdf. [本文引用:2]
[17] HORIO K, MATSUDA A. The Decision Making Method Added Emotion Judgment // Proc of the World Automation Congress. Washington, USA: IEEE, 2010: 1-6. [本文引用:1]
[18] SALICHS M A, MALFAZ M. Using Emotions on Autonomous Agents. The Role of Happiness, Sadness and Fear[C/OL]. [2021-09-18]. http://roboticslab.uc3m.es/publications/Salichs06.PDF. [本文引用:1]
[19] 方宝富, 马云婷, 王在俊, 等. 稀疏奖励下基于情感的异构多智能体强化学习. 模式识别与人工智能, 2021, 34(3): 223-231.
(FANG B F, MA Y T, WANG Z J, et al. Emotion-Based Heterogeneous Multi-agent Reinforcement Learning with Sparse Reward. Pattern Recognition and Artificial Intelligence, 2021, 34(3): 223-231. ) [本文引用:1]
[20] BROEKENS J. A Temporal Difference Reinforcement Learning Theory of Emotion: Unifying Emotion, Cognition and Adaptive Behavior[C/OL]. [2021-09-18]. https://arxiv.org/ftp/arxiv/papers/1807/1807.08941.pdf. [本文引用:2]
[21] MOORS A, ELLSWORTH P C, SCHERER K R, et al. Appraisal Theories of Emotion: State of the Art and Future Development. Emotion Review, 2013, 5(2): 119-124. [本文引用:1]
[22] MOERLAND T M, BROEKENS J, JONKER C M. Emotion in Reinforcement Learning Agents and Robots: A Survey. Machine Learning, 2018, 107: 443-480. [本文引用:1]
[23] PENG B, RASHID T, DE WITT C A S, et al. FACMAC: Factored Multi-agent Centralised Policy Gradients[C/OL]. [2021-09-18]. https://arxiv.org/pdf/2003.06709.pdf. [本文引用:1]
[24] HUGHES E, LEIBO J Z, PHILLIPS M G, et al. Inequity Aversion Improves Cooperation in Intertemporal Social Dilemmas[C/OL]. [2021-09-18]. https://arxiv.org/pdf/1803.08884.pdf. [本文引用:1]
[25] JIANG J C, LU Z Q. The Emergence of Individuality[C/OL]. [2021-09-18]. https://arxiv.org/pdf/2006.05842.pdf. [本文引用:1]
[26] KINGMA D P, BA J L. Adam: A Method for Stochastic Optimization[C/OL]. [2021-09-18]. https://arxiv.org/pdf/1412.6980v3.pdf. [本文引用:1]