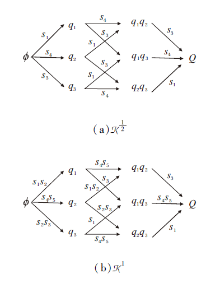李进金,博士,教授,主要研究方向为信息技术、不确定性的数学理论与方法.E-mail:jinjinlimnu@126.com.
作者简介: 
杨桃丽,硕士研究生,主要研究方向为知识空间理论.E-mail:yangtaoli2019@163.com. 
李招文,博士,教授,主要研究方向为拓扑及其应用、粗糙集、模糊集、信息系统.E-mail:lizhaowen8846@126.com. 
金 铭,硕士研究生,主要研究方向为粗糙集.E-mail:jinming149@163.com. 
周银凤,硕士研究生,主要研究方向为知识空间理论.E-mail:j_jenifer@126. com. 
林艺东,博士,副教授,主要研究方向为知识空间理论、形式概念分析、认知概念学习.E-mail:yidong_lin@yeah.net.
在现存构建知识结构的模型中,以同一知识结构评价个体的知识掌握情况并不合理.为此,文中主要针对如下两个问题展开研究:技能映射通过析取模型、合取模型与能力模型诱导知识结构的条件过于宽松或苛刻,不同技能子集在同一模型下可能诱导相同知识状态.首先,介绍技能包含度和能力包含度的概念,建立构建知识结构的变精度 α-模型和变精度 α-能力模型.再讨论诱导良级知识结构时技能映射需满足的条件,得到良好技能映射诱导的知识结构均为良级知识结构的结果.然后,针对技能映射和技能函数存在等价技能子集的情况,分别考虑保持知识结构不变的技能子集约简及学习路径选择的问题,并给出获取极小技能子集族和知识结构的算法.最后,在6个数据集上的实验验证文中算法的可行性和有效性.
LI Jinjin, Ph.D., professor. His research interests include information technology, mathematical theories and methods of uncertainty.
About Author:
YANG Taoli, master student. Her research interests include knowledge space theory.
LI Zhaowen, Ph.D., professor. His research interests include topology and its applications, rough set, fuzzy set and information systems.
JIN Ming, master student. Her research interests include rough set.
ZHOU Yinfeng, master student. Her research interests include knowledge space theory.
LIN Yidong, Ph.D., associate professor. His research interests include knowledge space theory, formal concept analysis and cognitive concept learning.
It is unreasonable to evaluate the knowledge mastery of different individuals by a same knowledge structure in the existing models of constructing knowledge structures. In this paper, two problems are mainly discussed. The conditions of knowledge structure delineated via disjunctive model, conjunctive model and competency model by a skill map are too loose or harsh, and the same knowledge state may be delineated by different skill subsets on the same model. Firstly, the concepts of skill inclusion degree and competency inclusion degree are introduced, and the variable precision α-model and variable precision α-competency model for constructing knowledge structures are established. Secondly, the conditions that a skill map should satisfy while delineating well-graded knowledge structures are discussed, and the result that the knowledge structures delineated by well-skill maps are well-graded knowledge structures is obtained. Then, in view of equivalent skill subsets existing in skill maps and skill functions, skill subset reduction keeping knowledge structure unchanged and learning path selection are studied, respectively. Algorithms for acquiring the family of minimal skill subsets and knowledge structures are given. Finally, experiments on 6 datasets show the feasibility and effectiveness of the proposed algorithms.
知识空间理论(Knowledge Space Theory, KS-T)[1, 2, 3]是一种用于评估个体知识水平和指导进一步学习的数学心理框架, 目前, 已应用在ALEKS系统和自适应辅导系统[4], 并在其它领域具有潜在的应用价值[2].
知识状态是KST的基本概念之一.在非空有限的问题域中, 个体的知识状态表示为个体在理想状态下能正确解决问题的集合[1, 2].在很多情况下, 可从个体对不同问题的回答中推断个体的知识状态, 即通过检测个体对问题的回答情况, 评估个体的知识掌握情况.知识结构是评估个体知识水平的重要工具, 表示为序对(Q, K).其中K是至少包含Ø 和全集Q的知识状态的集合, 一般地, 习惯直接使用K表示知识结构.
构建一个准确的知识结构的方法是知识空间理论的重要研究内容.围绕这一问题, 学者们结合其它学科以构建知识结构.形式概念分析(Formal Con-cept Analysis, FCA)可与KST结合.Rusch等[5]讨论由形式背景构建知识结构的方法, 为概念知识的获取提供一种新的途径.李进金等[6]基于知识基, 提出由形式背景构建知识结构的方法, 进一步加强FCA与KST之间的联系.受粗糙集近似思想的启发, Yao等[7]利用粗糙集理论(Rough Set Theory, RST)中的近似思想构建知识结构, 有效地在同一环境下研究RST与KST.
特别地, 在Doignon[15]提出的析取模型、合取模型和能力模型中, 由技能映射诱导知识结构的条件过于宽松或苛刻.这是因为, 在析取模型中, 一旦个体掌握与解决问题有关的某个技能, 便足以解决该问题, 这将导致无论个体掌握多少个与解决问题相关的技能, 最终个体的知识结构都是相同的.在合取模型中, 个体需掌握与解决问题有关的所有技能, 才能解决该问题.实际上, 个体不一定要掌握所有技能才有能力解决相应的问题.在能力模型中, 对于解决问题的所有能力, 个体掌握其中某个能力就足以解决该问题, 而一个能力是由多种技能形成的, 即个体需掌握这个能力中的所有技能才能解决此问题.因此, 这些评价个体知识情况的方法都集中于个体所能解决的问题, 无法解释不同个体解决相同问题背后却有不同知识结构的现象.
然而, 在解决问题的所有方法中, 可能会存在冗余的技能.为此, Dü ntsch等[8]研究技能多映射的极小形式, 定义技能函数和问题函数的概念.孙晓燕等[18]基于项目状态转移函数, 将问题空间推广到多分情形.Xu等[19]结合粗糙集属性约简的方法, 寻找极小技能集.Sun等[20]提出极小模糊技能映射的概念.Heller等[9]指出技能函数具有两种特殊的情形, 即析取技能函数和合取技能函数.在现实生活中, 不同的个体具有不同的技能或能力, 不同的技能或能力可能解决相同的问题, 于是出现等价的技能或能力.基于上述考虑的问题, 可根据个体的知识状态规划其下一步需要学习的技能.
总之, 由技能映射或技能函数构建知识结构是KST的热点研究问题, 在教育教学方面具有较大的应用前景和理论研究价值.因此, 本文引入技能包含度和能力包含度的概念, 建立构建知识结构的变精度α -模型和变精度α -能力模型.再讨论诱导良级知识结构时技能映射需满足的条件, 得到良好技能映射诱导的知识结构均为良级知识结构的结果.然后, 针对技能映射和技能函数存在等价技能子集的情况, 分别考虑保持知识结构不变的技能子集约简及学习路径选择的问题, 并给出获取极小技能子集族和知识结构的算法.最后, 在6个数据集上的实验验证本文算法的可行性和有效性.
本文仅在理想状态下考虑非空有限的问题域和非空有限的技能域. 这里的理想状态是指个体在回答问题时没有粗心答错或侥幸答对的情况.
知识结构是KST的重要概念之一.个体知识状态的集合是一个知识结构(Q, K).若知识结构K保持并封闭, 即对K中的任意两个元素Ki和Kj, 有Ki∪ Kj∈ K, 则称K是一个知识空间.若知识结构K保持交封闭, 即对K中的任意两个元素Ki, Kj, 有Ki∩ Kj∈ K, 则称K是一个简单闭包空间.若知识结构K同时保持交、并封闭, 则称K是一个拟序空间.
设(Q, K)是一个知识结构, 对q∈ Q, Kq是知识结构K中包含问题q的所有知识状态的集合.对q∈ Q,
$[q]=\{p\in Q|{{\mathcal{K}}_{q}}={{\mathcal{K}}_{p}}\}$
表示与q同时出现在某些知识状态中的问题集合.若对∀ q∈ Q, [q]为单点集, 则称(Q, K)是一个可辨识的知识结构.若一个拟序空间(Q, K)是可辨识的, 则称(Q, K)是一个序空间.
定义1[2] 三元组(Q, S, τ )称为一个技能映射, 其中, Q为非空有限问题集, S为非空有限技能集, τ 为由Q到2S\{Ø }的映射.
在问题集和技能集给定的情况下, 直接称τ 为一个技能映射.
设(Q, S, τ )为一个技能映射, 对T⊆S, 定义
$K=\{q\in Q|\tau (q)\bigcap T\ne \varnothing \}$
称K是由T通过析取模型诱导的知识状态.当T取遍S的所有子集时, 所得知识状态的集合K称为由技能映射τ 通过析取模型诱导的知识空间.对T⊆S, 定义
$K=\{q\in Q|\tau (q)\subseteq T\}$
称K是由T通过合取模型诱导的知识状态.当T取遍S的所有子集时, 所得知识状态的集合K称为由技能映射τ 通过合取模型诱导的简单闭包空间.
定义2[8] 三元组(Q, S, μ )称为一个技能多映射, 其中, Q为非空有限问题集, S为非空有限技能集, μ 为由Q到${{2}^{{{2}^{S}}\backslash \{\varnothing \}}}\backslash \{\varnothing \}$的映射.
在技能多映射(Q, S, μ )中, 对∀ q∈ Q, 若满足
1)μ (q)≠ Ø ,
2)对∀ M∈ μ (q), M≠ Ø ,
3)μ (q)中的能力关于集合的包含关系两两不可比较, 则称(Q, S, μ )为一个技能函数.
在问题集和技能集给定的情况下, 直接称μ 为一个技能函数.此时, 对∀ q∈ Q, 称C∈ μ (q)为解决问题q的一个极小能力.
对T⊆S, 定义
$K=\{q\in Q|\exists C\in \mu (q):C\subseteq T\}$
称K是由T通过技能函数μ 诱导的知识状态.当取遍S的所有子集时, 所得知识状态的集合K称为由μ 诱导的知识结构.
技能函数有两种特殊的类型, 即析取技能函数和合取技能函数.
设(Q, S, μ )为一个技能函数, 若对∀ q∈ Q, 有μ (q)={M}, 其中Ø ⊂M⊆S, 则称(Q, S, μ )为一个合取技能函数.若对∀ q∈ Q, 有
μ (q)={{s}∶ s∈ M},
其中Ø ⊂M⊆S, 则称(Q, S, μ )为一个析取技能函数.合取技能函数为每个问题分配一个非空的技能子集, 诱导的知识结构保持交封闭, 是一个简单闭包空间.析取技能函数为每个问题分配单点的技能子集, 诱导的知识结构保持并封闭, 是一个知识空间.
定义3[2] 设F是一个有限的集族, 若对
∀ K∈ F, L∈ F,
存在有限序列
K=K0, K1, …, Kn=L,
使得
$d({{K}_{i}}, {{K}_{i+1}})=|{{K}_{i}}\vartriangle {{K}_{i+1}}|=|({{K}_{i}}\backslash {{K}_{i+1}})\bigcup ({{K}_{i+1}}\backslash {{K}_{i}})|=1$
其中, i∈ [0, n-1], d(K, L)=n, 则称F是良级的.
满足定义3的有限序列
K=K0, K1, …, Kn=L
称为由K到L的紧路径.
定义4 设(Q, S, τ )为一个技能映射.对q∈ Q, T⊆S, 称
D(T/τ (q))=
为关于q和T的技能包含度.为了方便起见, 将D(T/τ (q))记为
$D(\tau )=\{\tau _{q}^{T}|q\in Q, T\subseteq S\}$
为τ 的技能包含度集.对q∈ Q, 将
$D({{\tau }_{q}})=\{\tau _{q}^{T}|T\subseteq S\}$
称为关于问题q的技能包含度集.
推论1 设(Q, S, τ )为一个技能映射.对q∈ Q,
$D({{\tau }_{q}})=\{\tau _{q}^{T}|T\subseteq S\}$
为关于问题q的技能包含度集, 则有
$D(\tau )=\bigcup\limits_{q\in Q}{D({{\tau }_{q}})}$.
由技能包含度的定义可知, 对于两个不相交的技能子集Ti⊆S, Tj⊆S和T⊆S, 不难验证它们的技能包含度满足可加性和互补性, 即
$\tau _{q}^{{{T}_{i}}}+\tau _{q}^{{{T}_{j}}}=\tau _{q}^{{{T}_{i}}\bigcup {{T}_{j}}}, \tau _{q}^{T}+\tau _{q}^{S\backslash T}=1$
如果T={si, sj}, 可将技能包含度简单记为
定义5 设(Q, S, τ )为一个技能映射, 对q∈ Q, T⊆S,
$K_{T}^{\alpha }=\{q\in Q|\tau _{q}^{T}\ge \alpha \}$.
对α ∈ (0, 1], 根据定义5, 显然有
$K_{\varnothing }^{\alpha }=\varnothing $, $K_{S}^{\alpha }=Q$.
遍历S的子集T, 通过变精度α -模型诱导的所有知识状态的集合构成知识结构
${{\mathcal{K}}^{\alpha }}=\{K_{T}^{\alpha }|T\subseteq S\}$.
为了方便起见, 不妨将技能包含度集记为
D(τ )={β 1, β 2, …, β n},
其中
0=β 1< β 2< …< β n =1.
假设
α ∈ (β i, β i+1], i=1, 2, …, n-1,
在β i和β i+1之间没有别的技能包含度, 所以技能映射在这样一个区间诱导的知识结构就是在区间右端点诱导的知识结构, 即Kα =
若一个技能映射(Q, S, τ )确定的技能包含度集为D(τ )={β 1, β 2, …, β n}, 除了β 1以外, 对于β 2, β 3, …, β n, 技能映射(Q, S, τ )通过变精度α -模型可诱导n-1个知识结构.容易验证, 对α ∈ (β 1, β 2], 变精度α -模型为析取模型, 技能映射(Q, S, τ )通过变精度α -模型诱导的知识结构是一个知识空间.对α ∈ (β n-1, β n], 变精度α -模型为合取模型, 技能映射(Q, S, τ )通过变精度α -模型诱导的知识结构是一个简单闭包空间.
下面考虑更一般的情形, 即结合技能函数与包含度, 讨论构建知识结构的另一种方法.
定义6 设(Q, S, μ )为一个技能函数.对q∈ Q, C∈ μ (q), T⊆S, 称
D(T/C)=
为问题q关于C和T的能力包含度.为了方便起见, 将D(T/C)记为
D(μ )={
称为μ 的能力包含度集.对q∈ Q,
D(μ q)={
称为关于问题q的能力包含度集.
推论2 设(Q, S, μ )为一个技能函数.对q∈ Q,
D(μ q)={
为关于问题q的能力包含度集, 则有
$D(\mu )= \bigcup\limits_{q\in Q}{D({{\mu }_{q}})}$.
同样地, 由能力包含度的定义可知, 对于两个不相交的技能子集Ti⊆S, Tj⊆S和T⊆S, 它们的能力包含度满足可加性和互补性.于是可得如下命题 1.
命题1 设(Q, S, μ )为一个技能函数.对∀ q∈ Q, C∈ μ (q), T1⊆S, T2⊆S, T1∩ T2=Ø , 则有
证明 由定义6, 对q∈ Q, C∈ μ (q), T1⊆S, T2⊆S, T1∩ T2=Ø , 有
$\mu _{{{C}_{q}}}^{{{T}_{1}}\bigcup {{T}_{2}}}=\frac{|{{C}_{q}}\bigcap ({{T}_{1}}\bigcup {{T}_{2}})|}{|{{C}_{q}}|} \text{=}\frac{|{{C}_{q}}\bigcap {{T}_{1}}|+|{{C}_{q}}\bigcap {{T}_{2}}|}{|{{C}_{q}}|} =\frac{|({{C}_{q}}\bigcap {{T}_{1}})\bigcup ({{C}_{q}}\bigcap {{T}_{2}})|}{|{{C}_{q}}|} =\mu _{{{C}_{q}}}^{{{T}_{1}}}+\mu _{{{C}_{q}}}^{{{T}_{2}}}$
命题2 设(Q, S, μ )为一个技能函数, 则有如下性质:
1)对q∈ Q, C∈ μ (q), T⊆S, 有$\mu _{{{C}_{q}}}^{T}=\sum\limits_{s\in T}{\mu _{{{C}_{q}}}^{s}}$;
2)对q∈ Q, C∈ μ (q), T⊆S, 有
证明 由定义6和命题1即证.
由于D(μ )为一个有限集, 为了方便起见, 不妨将能力包含度集表示为D(μ )={β 1, β 2, …, β n}, 其中
0=β 1< β 2< …< β n=1, β i+β n-i+1=1.
令
即
命题3 设(Q, S, μ )为一个技能函数, 其中Q={q1, q2, …, qm}.设D(μ )={β 1, β 2, …, β n}为能力包含度集, 则下述成立:
1)对qi∈ Q, i=1, 2, …, m, $|D({{\mu }_{{{q}_{i}}}})|$为偶数当且仅当
2)对qi∈ Q, i=1, 2, …, m, $|D({{\mu }_{{{q}_{i}}}})|$为奇数当且仅当
3)对∀ qi∈ Q, i=1, 2, …, m, 若$|D({{\mu }_{{{q}_{i}}}})|$为偶数, 则
$|D(\mu )|=|\bigcup\limits_{i=1}^{m}{D({{\mu }_{{{q}_{i}}}})}|$
为偶数;
4)若存在qi∈ Q, i=1, 2, …, m, 使得$|D({{\mu }_{{{q}_{i}}}})|$为奇数, 则
$|D(\mu )|=|\bigcup\limits_{i=1}^{m}{D({{\mu }_{{{q}_{i}}}})}|$
为奇数.
证明 先证1).对qi∈ Q, 设
D(
若$|D({{\mu }_{{{q}_{i}}}})|$为偶数, 由
ε j+ε n-j+1=1, j=1, 2, …, n,
当j=
于是
即
这与假设矛盾, 因此$|D({{\mu }_{{{q}_{i}}}})|$为偶数.
再证2).类似于1), 容易证明2)是成立的.
再证3).对∀ qi∈ Q, 若$|D({{\mu }_{{{q}_{i}}}})|$为偶数, 由1)可得
$D(\mu )=\bigcup\limits_{i=1}^{m}{D({{\mu }_{{{q}_{i}}}})}$
于是有
$\tfrac{1}{2}\notin \bigcup\limits_{i=1}^{m}{D({{\mu }_{{{q}_{i}}}})}$,
即
最后证明4).若存在qi∈ Q, 使得$|D({{\mu }_{{{q}_{i}}}})|$为奇数, 从而有
$\tfrac{1}{2}\in \bigcup\limits_{i=1}^{m}{D({{\mu }_{{{q}_{i}}}})}=D(\mu )$,
故D(μ )为奇数.
定义7 设(Q, S, μ )为一个技能函数.对q∈ Q, C∈ μ (q), T⊆S,
$K_{T}^{\alpha }=\{q\in Q|\exists C\in \mu (q):\mu _{{{C}_{q}}}^{T}\ge \alpha \}$.
注意到, 因为
$\mu _{{{C}_{q}}}^{\varnothing }=\frac{|{{C}_{q}}\bigcap \varnothing |}{|{{C}_{q}}|}=0\ngeqslant \alpha $,
所以T=Ø 诱导的知识状态为
故T=S诱导的知识状态为
定义8 设(Q, S, μ )为一个技能函数.对α ∈ (0, 1], 称
${{\mathcal{K}}^{\alpha }}=\{K_{T}^{\alpha }|T\subseteq S\}$
为由μ 通过变精度α -能力模型诱导的知识结构.
定理1 设(Q, S, μ )为一个技能函数.
D(μ )= {β 1, β 2, …, β n}
为μ 的能力包含度集.对α ∈ (β i, β i+1], i=1, 2, …, n-1, 有Kα =
证明 对α ∈ (β i, β i+1], 设Kα 为由技能函数μ 通过变精度α -能力模型诱导的知识结构.对∀ T⊆S, 有
$K_{T}^{\alpha }=\{q\in Q|\exists C\in \mu (q):\mu _{{{C}_{q}}}^{T}\ge \alpha \}=\{q\in Q|\exists C\in \mu (q):\mu _{{{C}_{q}}}^{T}> {{\beta }_{i}}\}$.
由于β i与β i+1之间不存在其它的能力包含度, 因此
$K_{T}^{\alpha }=\{q\in Q|\exists C\in \mu (q): \mu _{{{C}_{q}}}^{T}\ge {{\beta }_{i+1}}\}=K_{T}^{{{\beta }_{i+1}}}$,
故${{\mathcal{K}}^{\alpha }}={{\mathcal{K}}^{{{\beta }_{i+1}}}}$.
定理2 设(Q, S, μ )为一个技能函数,
D(μ )= {β 1, β 2, …, β n}
为μ 的能力包含度集.对α ∈ (β n-1, β n], 由μ 通过变精度α -能力模型诱导的知识结构是由μ 通过能力模型诱导的知识结构.
证明 因为有Kα =
$K_{T}^{{{\beta }_{n}}}=\{q\in Q| \exists C\in \mu (q):\mu _{C}^{T}\ge {{\beta }_{n}}=1\}$.
因为
所以有C⊆T, 即
$K_{T}^{{{\beta }_{n}}}=\{q\in Q|\exists C\in \mu (q):C\subseteq T\}$.
于是
由于技能函数具有析取技能函数和合取技能函数两种特殊情形, 可对这两种特殊情形进行讨论.
推论3 设(Q, S, μ )为一个析取技能函数, 则D(μ )={0, 1}.对α ∈ (0, 1], 技能函数μ 通过变精度α -模型诱导的知识结构是由μ 通过能力模型诱导的知识结构.
当(Q, S, μ )为合取技能函数时, 此时变精度α -能力模型退化为变精度α -模型.需要注意的是在技能映射(Q, S, τ )中,
τ (q)=C∈ μ (q),
于是有定理3.
定理3 设(Q, S, μ )为一个合取技能函数, (Q, S, τ )为一个技能映射, 且对q∈ Q,
$\mu (q)=\{C| \varnothing \subset C\subseteq S\}$.
对α ∈ (β i, β i+1], 由μ 通过变精度α -能力模型诱导的知识结构是由技能映射(Q, S, τ )通过变精度α -模型诱导的知识结构.
证明 设(Q, Kα )是由μ 通过变精度α -能力模型诱导的知识结构.对∀ T⊆S, 由定义7可得
$K_{T}^{\alpha }=\{q\in Q|\exists C\in \mu (q):\mu _{{{C}_{q}}}^{T}\ge \alpha \}$.
由于合取技能函数中只为每个问题q分配一个能力且τ (q)=C, 于是
$K_{T}^{\alpha }=\{q\in Q|\mu _{{{C}_{q}}}^{T}\ge \alpha \}=\{q\in Q|\tau _{q}^{T}\ge \alpha \}$.
变精度α -模型包括析取模型和合取模型, 而技能函数的变精度α -能力模型包含能力模型和变精度α -模型, 于是本文的变精度α -能力模型比文献[15]中的能力模型适用性更广.下面继续讨论合取技能函数下变精度α -能力模型诱导的知识结构的一些性质.
定理4 设(Q, S, μ )为一个合取技能函数, D(μ )={β 1, β 2, …, β n}为μ 的技能包含度集, 则由μ 通过变精度α -能力模型诱导的知识结构
证明 设(Q,
$K_{T}^{{{\beta }_{i+1}}}=\{q\in Q| \exists C\in \mu (q):\mu _{{{C}_{q}}}^{T}\ge {{\beta }_{i+1}}\}$.
由于μ 为合取技能函数, 于是
$K_{T}^{{{\beta }_{i+1}}}=\{q\in Q|\mu _{{{C}_{q}}}^{T}\ge {{\beta }_{i+1}}\}$.
故
$Q\backslash K_{T}^{{{\beta }_{i+1}}}=Q\backslash \{q\in Q|\mu _{{{C}_{q}}}^{T}\ge {{\beta }_{i+1}}\} =\{q\in Q|\mu _{{{C}_{q}}}^{T}< {{\beta }_{i+1}}\} =\{q\in Q|1-\mu _{{{C}_{q}}}^{T}> 1-{{\beta }_{i+1}}\} =\{q\in Q|\mu _{{{C}_{q}}}^{S\backslash T}> 1-{{\beta }_{i+1}}\}$.
由于在能力包含度1-β i+1和1-β i之间不存在其它的能力包含度, 从而
$Q\backslash K_{T}^{{{\beta }_{i+1}}}=\{q\in Q|\mu _{{{C}_{q}}}^{S\backslash T}\ge 1-{{\beta }_{i}}\}$.
又
β i+β n-i+1=1,
则
$Q\backslash K_{T}^{{{\beta }_{i+1}}}=\{q\in Q|\mu _{{{C}_{q}}}^{S\backslash T} \ge {{\beta }_{n-i+1}}\}=K_{S\backslash T}^{{{\beta }_{n-i+1}}}\in {{\mathcal{K}}^{{{\beta }_{n-i+1}}}}$
于是知识结构
例1 设(Q, S, μ )为一个合取技能函数, 其中
Q={q1, q2, q3, q4}, S={s1, s2, s3},
μ (q1)={{s1, s2}}, μ (q2)={{s3}},
μ (q3)={{s2, s3}}, μ (q4)={{s2}}.
根据定义6, 对q∈ Q, T⊆S, 可得到能力包含度
| 表1 例1中能力包含度 |
为了简单起见, 将技能子集{sl, sm}简记为slsm, μ (qi)中的能力记为
由表1可得, 能力包含度集
$D(\tau )=\{0, \tfrac{1}{2}, 1\}$.
| 表2 例1中知识状态 |
显然, 对$\alpha \in (0, \tfrac{1}{2}]$, 由合取技能函数μ 诱导的知识结构是知识空间; 对$\alpha \in (\tfrac{1}{2}, 1]$, 由μ 诱导的知识结构为简单闭包空间.
一个技能映射通过变精度α -模型诱导的所有知识结构中不一定存在拟序空间.如例1中的两个知识结构都不能同时满足交、并封闭.本节讨论在满足什么条件下, 技能映射通过变精度α -模型诱导的所有知识结构都是拟序空间.
Spoto等[21]指出在技能函数中, 对某个问题存在专属技能和专属能力.
定义9[22] 设(Q, S, τ )为一个技能映射.对q∈ Q, 若如下条件成立:
1)对所有p∈ Q\{q}, 有s∉τ (p),
2)s∈ τ (q),
则技能s∈ S称为一个专属技能.
定义10 设(Q, S, τ )为一个技能映射.对q∈ Q, 若s为问题q的专属技能, 则记为s▷q.
命题4 设(Q, S, τ )为一个技能映射.对不同的q∈ Q, q'∈ Q, 若τ (q)⊂τ (q'), 则不存在s▷q.若
τ (q)⊄τ (q'), τ (q')⊄τ (q),
则存在
t∈ τ (q)\τ (q'), u∈ τ (q')\τ (q),
使得t▷q, u▷q'.
证明 由定义10显然得证.
定义11 设(Q, S, τ )为一个技能映射.若τ 满足下面两个条件:
1)至少存在一个q∈ Q, 有s▷q,
2)存在q∈ Q, q'∈ Q, 有
$\tau (q)\subset \tau ({q}') |\tau ({q}')\backslash \tau (q)|=1$,
则称τ 为良好的技能映射.
例2 设(Q, S, τ )为一个技能映射, 其中
Q= {q1, q2, q3, q4, q5}, S={s1, s2, s3, s4, s5},
τ (q1)={s2}, τ (q2)={s4}, τ (q3)={s1, s2},
τ (q4)={s3, s4}, τ (q5)={s1, s2, s5}.
根据定义11, 对∀ q∈ Q, 有s3▷q4, s5▷q5, 且有
τ (q1)⊂τ (q3)⊂τ (q5), τ (q2)⊂τ (q4).
可发现
$|\tau ({{q}_{3}})\backslash \tau ({{q}_{1}})|=|\tau ({{q}_{5}})\backslash \tau ({{q}_{3}})|=|\tau ({{q}_{4}})\backslash \tau ({{q}_{2}})|=1$,
于是τ 为一个良好的技能映射.
定理5 设(Q, S, τ )为一个技能映射.对α ∈ (0, 1], (Q, Kα )为由(Q, S, τ )通过变精度α -模型诱导的知识结构.(Q, Kα )为拟序空间, 当且仅当τ 为一个良好的技能映射.
证明 假设对α ∈ (0, 1], (Q, Kα )为拟序空间, 则对∀
于是T1∪ T2诱导的知识状态为
T1∩ T2诱导的知识状态为
若T1⊄T2, 则
${{T}_{1}}\bigcap {{T}_{2}}=\varnothing $, $|({{T}_{1}}\bigcup {{T}_{2}})\backslash ({{T}_{1}}\bigcap {{T}_{2}})|> 1$.
若T1⊂T2, 则
$|({{T}_{1}}\bigcup {{T}_{2}})\backslash ({{T}_{1}}\bigcap {{T}_{2}})|\ge 1$.
不妨设
τ (q)=T1∩ T2, τ (q')=T1∪ T2,
存在s∈ τ (q')\τ (q), 使得
$|\tau ({q}')\backslash \tau (q)|=|s|=1$,
于是s▷q'.
反过来, 令
$\mathcal{K}=\{K_{T}^{\alpha }|T\subseteq S\}\subseteq {{\mathcal{K}}^{\alpha }}$,
其中α ∈ (0, 1].对∀ q∈ Q,
诱导的知识状态为
于是对∀ K⊆Kα , 有
∩ K∈ Kα , ∪ K∈ Kα ,
故Kα 为一个拟序空间.
推论4[2] 任意有限的序空间是学习空间, 而学习空间是良级的知识结构.
由推论3, 有如下定理6.
定理6 设(Q, S, τ )为一个技能映射.对α ∈ (0, 1], (Q, Kα )是由(Q, S, τ )通过变精度α -模型诱导的知识结构, (Q, Kα )为拟序空间当且仅当(Q, Kα )是良级的.
证明 因为对∀ τ (q)⊂τ (q'), 有
$|\tau ({q}')\backslash \tau (q)|=1$,
则有Kq≠ Kq', 于是由技能映射(Q, S, τ )通过变精度α -模型诱导的知识结构均是可辨识的, 即(Q, Kα )是序空间.故由定理5和推论3可知, (Q, Kα )是良级的.
反之, 由定理5显然得证.
定理7 设(Q, S, τ )为一个技能映射.对α ∈ (0, 1], (Q, Kα )是由(Q, S, τ )通过变精度α -模型诱导的知识结构, (Q, Kα )是良级的当且仅当τ 是一个良好的技能映射.
证明 由定理5和定理6可证.
例3 设
Q={q1, q2, q3, q4}, S={s1, s2, s3, s4, s5}
τ (q1)={s2, s3}, τ (q2)={s3, s5},
τ (q3)={s1, s2, s3}, τ (q4)={s3, s4, s5}.
通过计算可得到τ 的技能包含度集为
$D(\tau )=\{0, \tfrac{1}{3}, \tfrac{1}{2}, \tfrac{2}{3}, 1\}$,
且由技能映射(Q, S, τ )通过变精度α -模型诱导的知识结构分别为
K1={Ø , {q1}, {q2}, {q1, q2}, {q1, q3}, {q2, q4}, {q1, q2, q3}, {q1, q2, q4}, Q}.
可发现所有的知识结构都是满足交并封闭的, 于是为良级的知识结构.
例4 设
Q={q1, q2, q3}, S={s1, s2, s3, s4, s5},
定义技能映射τ :
τ (q1)={s1, s2, s5}, τ (q2)={s1, s3, s4}, τ (q3)={s2, s4}.
τ 的技能包含度集为
$D(\tau )= \{0, \tfrac{1}{3}, \tfrac{1}{2}, \tfrac{2}{3}, 1\}$.
显然, τ 不满足良好技能映射的条件2).对α ∈ (β i, β i+1], i=1, 2, 3, 4, 由τ 通过变精度α -模型诱导的知识结构分别为
K1={Ø , {q1}, {q2}, {q3}, {q1, q3}, {q2, q3}, Q}.
通过上述知识结构可发现, 由τ 诱导的所有知识结构中至少有一个不为拟序空间.
在现实生活中, 不同个体具有不同的技能或能力, 不同的技能或能力可能解决相同问题, 于是出现等价的技能或能力, 可根据个体的知识状态对其下一步需要学习的技能进行规划.从概念认知[23, 25]的角度上看, 个体学习技能是一种概念认知更新的过程, 即使在学习某个技能的过程中没有使个体的知识状态发生改变, 但个体的认知是有细微更新的.因此, 若要对个体的学习进行指导, 对其技能学习的缩减和学习路径的规划尤为重要.
给定一个技能映射(Q, S, τ ), 对∀ q∈ Q, 若∃Ti⊆S, Tj⊆S, 使得
定义12 设(Q, S, τ )为一个技能映射, 对T⊆S, T'⊆S, q∈ Q, 若有
$[T]=\{{T}'\subseteq S|\forall q\in Q, \tau _{q}^{T}=\tau _{q}^{{{T}'}}\}$
是T的一个等价类.对任意[T], 任取一个T'∈ [T], 所有T'构成的集族Y被称为关于技能映射τ 的一个极小技能子集族.
需要注意的是, 对Ti⊆S, Tj⊆S, ∀ q∈ Q, 若有
即
对于技能映射(Q, S, τ ), 对∀ q∈ Q, 取遍Y中元素计算得到的技能包含度集记为
${D}'(\tau )=\{\tau _{q}^{{{T}_{i}}}| q\in Q, {{T}_{i}}\in Y\}$.
对q∈ Q的技能包含度集记为
${D}'({{\tau }_{q}})=\{\tau _{q}^{{{T}_{i}}}|{{T}_{i}}\in Y\}$,
显然
D'(τ )=∪ D'(τ q).
例5 设(Q, S, τ )为一个技能映射, 其中
Q={q1, q2, q3}, S={s1, s2, s3, s4, s5}, τ (q1)={s1, s2}, τ (q2)={s4, s5}, τ (q3)={s2, s3}.
根据定义4可得到技能包含度
| 表3 例5中技能包含度 |
由表3和定义4可知, 技能包含度集
$D(\tau )= \{0, \tfrac{1}{2}, 1\}$.
对∀ q∈ Q, 有
根据定义12和表3, 显然可将2S分为21个等价类, 从而关于τ 的一个极小技能子集族为
Y={Ø , {s1}, {s2}, {s3}, {s4}, {s1, s2}, {s1, s4}, {s2, s3}, {s2, s4}, {s3, s4}, {s4, s5}, {s1, s2, s3}, {s1, s2, s4}, {s1, s4, s5}, {s2, s3, s4}, {s2, s4, s5}, {s3, s4, s5}, {s1, s2, s3, s4}, {s1, s2, s4, s5}, {s2, s3, s4, s5}, S}.
该极小技能子集族的技能包含度
| 表4 例5中极小技能子集族的技能包含度 |
由表4可知, 技能包含度集
${D}'(\tau )=D(\tau )=\{0, \tfrac{1}{2}, 1\}$,
因此约去冗余的技能子集, 对技能包含度集并不产生影响.根据表4和定义2, 对α =β i+1, i=1, 2, 由技能映射τ 通过变精度α -模型诱导的知识结构分别为
K1={Ø , {q1}, {q2}, {q3}, {q1, q2}, {q1, q3}, {q2, q3}, Q}.
定理8 设(Q, S, τ )为一个技能映射, Y为关于τ 的一个极小技能子集族. 若对q∈ Q, 取遍Y中元素计算得到的技能包含度集为D'(τ ), 则
D'(τ )= D(τ ).
证明 对∀ q∈ Q, 存在T⊆S, T'⊆S, 使得
${D}'({{\tau }_{q}})=\{\tau _{q}^{T}|T\subseteq S\}=D({{\tau }_{q}})$,
即
${D}'(\tau )= \bigcup\limits_{q\in Q}{{D}'({{\tau }_{q}})}=\bigcup\limits_{q\in Q}{D({{\tau }_{q}})}=D(\tau )$.
定理9 设(Q, Kα )为由技能映射(Q, S, τ )通过变精度α -模型诱导的知识结构,
D'(τ )={β 1, β 2, …, β n}
为Y的技能包含度集, 其中Y为关于τ 的一个极小技能子集族.对于α ∈ (β i, β i+1], i=1, 2, …, n-1, 由τ 通过变精度α -模型诱导的知识结构为(Q, Kα ).
证明 由定理2可知, 对∀ q∈ Q, 存在T⊆S, T'⊆S, 使得
$K_{T}^{\alpha }=\{q\in Q|\tau _{q}^{T} \ge \alpha \}=\{q\in Q|\tau _{q}^{{{T}'}}\ge \alpha \}=K_{{{T}'}}^{\alpha }$.
于是对任意[T], 任取一个T'∈ [T], Y是由所有的T'构成的技能子集族, α ∈ (β i, β i+1], 技能映射(Q, S, τ )通过变精度α -模型诱导的知识结构为Kα .
推论5 设(Q, S, τ )为一个技能映射, 则保持Kα 不变的技能子集的约简必是保持D(τ )不变的技能子集的约简.
下面讨论保持技能包含度集不变的技能子集的约简是否是保持知识结构不变的技能子集的约简, 二者之间是否存在一一对应的关系.给定技能映射(Q, S, τ ), 对于q∈ Q, 由于
$D(\tau )=\bigcup\limits_{q\in Q}{D({{\tau }_{q}})}$,
于是可保持D(τ q)不变, 进而保持D(τ )不变.
例如, 在例5中,
$D({{\tau }_{{{q}_{1}}}})=\{0, \tfrac{1}{2}, 1\}$,
对于
[Ø , {s3}, {s4}, {s3, s4}, {s4, s5}, {s3, s4, s5}],
[{s1}, {s2}, {s2, s4}, {s2, s3}, {s2, s4}, {s1, s4, s5},
{s2, s3, s4}, {s2, s4, s5}, {s2, s3, s4, s5}],
[{s1, s2}, {s1, s2, s3}, {s1, s2, s4}, {s1, s2, s3, s4},
{s1, s2, s4, s5}, S],
则对任意[T], 任取一个T'∈ [T], 计算所得技能包含度集的极小技能子集族为
Y1={Ø , {s1}, {s1, s2}},
其中由Ø 确定的技能包含度为0, {s1}确定的技能包含度为
$D({{\tau }_{{{q}_{2}}}})= \{0, \tfrac{1}{2}, 1\}$, ${{Y}_{2}}=\{\varnothing , \{{{s}_{4}}\}, \{{{s}_{4}}, {{s}_{5}}\}\}$
$D({{\tau }_{{{q}_{3}}}})=\{0, \tfrac{1}{2}, 1\}$, ${{Y}_{3}}=\{\varnothing , \{{{s}_{2}}\}, \{{{s}_{1}}, {{s}_{3}}\}\}$.
于是
$D(\tau )=\bigcup\limits_{i=1, 2, 3}{D({{\tau }_{{{q}_{i}}}})}$,
$Y= \bigcup\limits_{i=1, 2, 3}{{{Y}_{i}}}=\{\varnothing , \{{{s}_{1}}\}, \{{{s}_{2}}\}, \{{{s}_{4}}\}, \{{{s}_{1}}, {{s}_{2}}\}, \{{{s}_{1}}, {{s}_{3}}\}, \{{{s}_{4}}, {{s}_{5}}\}\}$.
因为Y中没有包含全集S, 遍历Y中的元素, 由τ 确定的并不是知识结构, 从而保持技能包含度集不变的技能子集的约简并不一定是保持知识结构不变的技能子集的约简.
根据上述结果, 下面给出寻找极小技能子集族及获取知识结构的算法.
算法1 基于技能映射, 获取极小技能子集族及知
识结构
输入 技能映射(Q, S, τ )
输出 关于τ 的极小技能子集族Y,
知识结构(Q, Kα )
step 1 令D(τ )=Ø , Y=Ø , Kα =Ø , ta=Ø ;
step 2 计算B=2S, 其中B为S的幂集;
step 3 遍历问题集Q的问题q和S的幂集B中的元素T;
step 4 根据定义4计算技能包含度
D(τ )← D(τ )∪
对D(τ )进行去重并按从小到大排列;
step 5 遍历问题集Q的问题q和S的幂集B中的元素T;
step 6 若
Y← Y∪ (B-B(t));
step 7 令β =D(τ )(2∶ end);
step 8 遍历β 中的元素α 和Y中的元素T';
step 9 根据定义5计算知识状态
Kα ← Kα ∪
step 10 根据上述获得邻接表ta并生成知识结构图.
算法1寻找技能映射的极小技能子集族的步骤是一个启发式搜索过程.step 3和step 4为找到技能包含度集, step 5和step 6为获取一个极小技能子集族, step 8~step 10为生成知识结构.step 3和step 4的时间复杂度及空间复杂度最大为($O(|Q| |{{2}^{S}}|)$O), step 5和step 6的时间复杂度及空间复杂度最大为O(|Q| |2S|), step 8~step 10的时间复杂度及空间复杂度最大为O(|Q| |2S| |Y|).因此, 算法1的最大时间复杂度和空间复杂度均为
O(|Q| |2S| |Y|).
接下来讨论关于技能函数μ 的极小技能子集族.类似于技能映射的情况, 可将2S进行分类.设(Q, S, μ )为一个技能函数, 对∀ qi∈ Q,
定义13 设(Q, S, μ )为一个技能函数, 对于q∈ Q, C∈ μ (q), 存在T⊆S, T'⊆S, 使得
$[T]=\{{T}'\subseteq S|\forall q\in Q, C\in \mu (q), \mu _{C}^{T}=\mu _{C}^{{{T}'}}\}$
是T的一个等价类.对任意[T], 任取一个T'∈ [T], 所有T'构成的集族M称为关于技能函数μ 的一个极小技能子集族.
设(Q, S, μ )为一个技能函数, 对每个qi∈ Q, 取遍M中元素计算得到的能力包含度集记为
${D}'(\mu )=\{\mu _{C_{i}^{j}}^{T}|C_{i}^{j}\in \mu ({{q}_{i}}), T\in M\}$.
对某个问题qi∈ Q的能力包含度集记为
${D}'({{\mu }_{{{q}_{i}}}})=\{\mu _{C_{i}^{j}}^{T}|C_{i}^{j}\in \mu ({{q}_{i}}), T\in M\}$,
显然
${D}'(\mu )=\bigcup\limits_{{{q}_{i}}\in Q}{{D}'({{\mu }_{{{q}_{i}}}})}$.
定理10 设(Q, S, μ )为一个技能函数, M为一个极小技能子集族.若对q∈ Q, 取遍M中元素计算得到的技能包含度集为D'(μ ), 则D'(μ )= D(μ ).
证明 类似于定理8即证.
定理11 设(Q, Kα )是由技能函数(Q, S, μ )通过变精度α -能力模型诱导的知识结构,
D'(μ )= {β 1, β 2, …, β n}
为M的能力包含度集, 其中M为关于μ 的一个极小技能子集族.对α ∈ (β i, β i+1], i=1, 2, …, n-1, 由μ 通过变精度α -能力模型诱导的知识结构为(Q, Kα ).
证明 类似于定理9即证.
推论6 设(Q, S, μ )为一个技能函数, 则保持Kα 不变的技能子集的约简必是保持D(μ )不变的技能子集的约简, 反之不成立.
基于上述结论, 下面给出获取极小技能子集族和知识结构的算法.
算法2 基于技能函数, 获取极小技能子集族和知
识结构
输入 技能函数(Q, S, μ )
输出 关于μ 的极小技能子集族M,
知识结构(Q, Kα )
step 1 令D(μ )=Ø , M=Ø , Kα =Ø , ta=Ø ;
step 2 计算B=2S, 其中B为S的幂集;
step 3 遍历每个μ (q)中的能力C和B中的元素T;
step 4 根据定义6计算能力包含度
D(μ )← D(μ )∪
对D(μ )进行去重并按从小到大进行排列;
step 5 遍历每个μ (q)中的能力C和B中的元素T;
step 6 若
M← M∪ (B-B(U));
step 7 令β =D(μ )(2∶ end);
step 8 遍历β 中的元素α 和M中的元素T', 根据定义8计算知识状态
Kα ← Kα ∪
step 9 根据上述步骤获得邻接表ta并生成知识结构图.
算法2寻找技能函数的极小技能子集族的步骤也是一个启发式搜索过程.step 3和step 4为获得一个能力包含度集, step 5和step 6为获得一个极小技能子集族, step 8和step 9为生成知识结构.step 3和step 4的时间复杂度及空间复杂度最大为
$O(|{Q}'| |\mu (q)| |{{2}^{{{S}'}}}|)$,
step 5和step 6的时间复杂度及空间复杂度最大为
$O(|{Q}'| |\mu (q)| |{{2}^{{{S}'}}}|)$,
step 8和step 9的时间复杂度及空间复杂度最大为
$O(|{Q}'| |\mu (q)|\times |{{2}^{{{S}'}}}| |M|)$.
因此, 算法2的最大时间复杂度和空间复杂度均为
$O(|{Q}'| |\mu (q)| |{{2}^{{{S}'}}}| |M|)$.
例6 设(Q, S, μ )为一个技能函数, 其中,
Q= {q1, q2, q3}, S={s1, s2, s3, s4},
μ (q1)={{s2, s4}}, μ (q2)={{s1, s3}, {s2, s4}},
μ (q3)={{s1, s2, s3}, {s2, s4}}.
根据算法2中的step 2可得到能力包含度
| 表5 例6中能力包含度 |
由表5可发现,
$\mu _{C_{i}^{j}}^{{{s}_{1}}}=\mu _{C_{i}^{j}}^{{{s}_{3}}}$, $\mu _{C_{i}^{j}}^{{{s}_{1}}{{s}_{2}}}=\mu _{C_{i}^{j}}^{{{s}_{2}}{{s}_{3}}}$,
$\mu _{C_{i}^{j}}^{{{s}_{1}}{{s}_{4}}}=\mu _{C_{i}^{j}}^{{{s}_{3}}{{s}_{4}}}$, $\mu _{C_{i}^{j}}^{{{s}_{1}}{{s}_{2}}{{s}_{4}}}=\mu _{C_{i}^{j}}^{{{s}_{2}}{{s}_{3}}{{s}_{4}}}$
于是由step 3从2S中删去技能子集{s3}, {s2, s3}, {s3, s4}, {s2, s3, s4}, 得到一个极小技能子集族
M={Ø , {s1}, {s2}, {s4}, {s1, s2}, {s1, s3}, {s1, s4}, {s2, s4}, {s1, s2, s3}, {s1, s2, s4}, {s1, s3, s4}, S}.
由M计算得到的技能包含度集
$D(\mu )=\{0, \tfrac{1}{3}, \tfrac{1}{2}, \tfrac{2}{3}, 1\}$.
根据step 4, 对于
α =β i+1, i=1, 2, 3, 4,
技能函数μ 通过变精度α -能力模型诱导的知识结构分别为
${{\mathcal{K}}^{\tfrac{1}{3}}}=\{\varnothing , \{{{q}_{2}}, {{q}_{3}}\}, Q\}$,
${{\mathcal{K}}^{\tfrac{1}{2}}}=\{\varnothing , \{{{q}_{2}}\}, \{{{q}_{2}}, {{q}_{3}}\}, Q\}$,
${{\mathcal{K}}^{\tfrac{2}{3}}}=\{\varnothing , \{{{q}_{3}}\}, \{{{q}_{2}}, {{q}_{3}}\}, Q\}$,
${{\mathcal{K}}^{1}}=\{\varnothing , \{{{q}_{2}}\}, \{{{q}_{2}}, {{q}_{3}}\}, Q\}$.
不同的个体在学习过程中对新的信息或知识具有不同的接受能力, 有的接受能力较强, 有的接受能力较弱, 但这不是绝对而言的.在寻找极小技能子集族时, 涉及到技能选择的问题.如例4中, 对于$\alpha \in (0, \tfrac{1}{2}]$, 要解决问题q1、q3, 个体需学会技能s2或s1和s3.从个体的角度来说, 如何实现较高效的学习是它们所需的学习方式.
定义14 给定技能映射(Q, S, τ )或技能函数(Q, S, μ ).对∀ [Ti], [Tj], 取T'∈ [Ti], T″∈ [Tj]且T'⊂T″, 则称T'⊂T″⊂…为有效技能学习链.
一个技能映射或技能函数有多条有效技能学习链, 例如, 在例6中, 对于
若个体在[{s1}, {s3}]中选择学习{s1}, 则在[{s1, s2}, {s2, s3}]中选择学习{s1, s2}, 依此类推.
根据定义14, 针对个体的学习情况, 可规划个体的学习路径, 即从Ø 到Q的一条学习路径所需学习的技能子集都具有包含关系.
例7 对于例5中的知识结构,
K1={Ø , {q1}, {q2}, {q3}, {q1, q2}, {q1, q3}, {q2, q3}, Q}.
根据上述描述规划个体的学习路径, 如图1所示.在图中:将知识状态{q1}简记为q1, 其它知识状态也是如此; 箭头表示知识状态之间的包含关系, 一个把知识状态K和K'连接起来并指向K'的箭头表示K⊂K', 并且不存在K″, 使得K⊂K″⊂K'成立.当从图的左边往右看时, 它表示一种学习路径:一个个体开始时什么都不知道, 即知识状态为Ø , 通过某一条学习路径可从某一状态向另一个状态转移, 最终可达到知识状态Q.
由图1可发现, 同一知识结构不管个体选择哪条学习路径学习, 其知识状态从Ø 到Q所需学习的技能都是一样的, 只是学习的先后顺序不一样.因此, 根据个体的学习路径图, 可通过个体知识状态的变化趋势指导下一步需要学习的技能.
为了验证本文两种算法的有效性, 在6个数据集上进行实验分析.
所有实验运行环境为Windows 7操作系统, 硬件环境为Inter(R)Core(TM) i7-6700 CPU @3.40 GHz和8.00 GB内存, 软件环境为MATLAB(R2013a)和RStudio(1.1.463).
从UCI数据库(http://archive.ics.uci.edu/ml/datasets.php)中选取Shuttle-landing-control、Adult、Lenses、StoneFlakes、Hayes、Post这6个数据集进行实验, 具体如表6所示.
| 表6 实验数据集 Table 6 Experimental datasets |
根据本文讨论的问题, 将对象视为问题, 将属性视为技能.首先, 对表6中的数据集进行离散化处理, 得到全新的数据集, 并分别将其表示为技能映射(Qi, Si, τ i)和技能函数(Qi', Si', μ i), 其中i=1, 2, 3.关于技能映射(Qi, Si, τ i)和技能函数(Qi', Si', μ i)的详细描述如表7~表12所示.
| 表7 技能映射(Q1, S1, τ 1) Table 7 Skill map (Q1, S1, τ 1) |
| 表8 技能映射(Q2, S2, τ 2) Table 8 Skill map (Q2, S2, τ 2) |
| 表9 技能映射(Q3, S3, τ 3) Table 9 Skill map (Q3, S3, τ 3) |
根据算法1, 可求出每个技能映射的技能包含度和知识结构, 如表13所示.根据算法2, 可求出每个技能函数的能力包含度和知识结构, 如表14所示.
| 表13 不同技能映射的技能包含度和知识结构 Table 13 Skill inclusion degrees and knowledge structures of different skill maps |
| 表14 不同技能函数的能力包含度和知识结构 Table 14 Competence inclusion degrees and knowledge structures of different skill functions |
由表13和表14可知, 根据本文算法, 技能子集得到明显缩减.技能映射和技能函数通过极小技能子集族获得知识结构, 相对于遍历所有技能子集, 分别减少32, 4, 28, 32, 4, 88个技能子集.这不仅为求解知识结构的过程提供很大的便利, 还可根据个体的自身情况帮助其缩小学习范围, 降低大脑的存储成本.
对于技能映射(Qi, Si, τ i):当α =β 2时, 由τ i通过变精度α -模型诱导的知识结构与由τ i通过析取模型诱导的知识结构对应; 当α =β n时, 由τ i通过变精度α -模型诱导的知识结构与由τ i通过合取模型诱导的知识结构对应.而当α ≠ β 1, β 2, β n时, 在由τ i通过变精度α -模型诱导的知识结构中, 至少存在一个知识结构包含
{q21, q22, q24, q25, q26, q28}, {q21, q23, q24, q25, q27, q28}, {q21, q24, q25, q26, q27, q28}, {q22, q23, q24, q26, q27, q28},
{q23, q24, q25, q26, q27, q28}, {q21, q22, q24, q25, q26, q27, q28}, {q21, q23, q24, q25, q26, q27, q28},
{q22, q23, q24, q25, q26, q27, q28}, Q2},
{q22, q23, q24, q26, q27}, {q21, q23, q24, q25, q27, q28}, {q21, q24, q25, q26, q27, q28}, {q22, q23, q24, q26, q27, q28},
{q23, q24, q25, q26, q27, q28}, {q21, q22, q24, q25, q26, q27, q28}, {q21, q23, q24, q25, q26, q27, q28},
{q22, q23, q24, q25, q26, q27, q28}, Q},
K1={Ø , {q21}, {q22}, {q23}, {q21, q22}, {q21, q25}, {q22, q23}, {q22, q26}, {q23, q27}, {q21, q23, q24},
{q21, q22, q23, q24}, {q21, q22, q25, q26}, {q22, q23, q26, q27}, {q21, q23, q24, q25, q27, q28}, Q}.
由上述描述可知,
因此, 变精度α -模型和变精度α -能力模型均克服诱导知识结构过于宽松或苛刻的条件, 使得对于不同的个体, 知识结构更合理.
为了使结果更可观, 使用(a)~(c)表示技能映射的变精度α -模型与析取模型和合取模型的关系, (d)~(f)表示技能函数的变精度α -能力模型与能力模型的关系.
由图2可知, 变精度α -模型既包含析取模型, 又包含合取模型, 并具有析取模型和合取模型不能诱导的知识结构.而变精度α -能力模型包含能力模型, 并具有能力模型不能诱导的知识结构.由此说明本文算法可解决文献[15]中存在条件过于宽松或苛刻的问题.
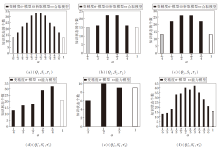 | 图2 不同模型下诱导的知识结构中知识状态个数Fig.2 Number of knowledge states in knowledge structures delineated via different models |
根据算法1, 获得(Q1, S1, τ 1)通过变精度α -模型(α =
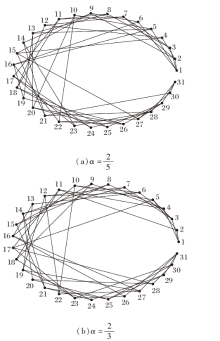 | 图3 τ 1通过变精度α -模型诱导的知识结构图Fig.3 Knowledge structures delineated by τ 1 via variable precision α -models |
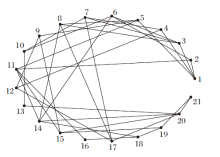 | 图4 μ 1通过变精度α -能力模型(α =1)诱导的知识结构图Fig.4 Knowledge structures delineated by μ 1 via variable precision α -competency model (α =1) |
在图3和图4中, 节点均表示知识状态.图3中节点“ 1” 表示知识状态为Ø , 节点“ 31” 表示知识状态为Q.图4中节点“ 1” 也表示知识状态为Ø , 节点“ 21” 表示知识状态为Q.连接2个节点的边表示大的节点包含小的节点.
本文将技能映射和技能函数与包含度结合, 研究技能映射和技能函数诱导知识结构的另一种方法, 还讨论技能映射在满足什么条件时, 通过变精度α -模型可诱导拟序空间.为了降低构建知识结构的复杂度, 考虑对技能子集进行约简, 得到技能集S的一个极小技能子集族.遍历极小技能子集族中的元素, 技能映射(技能函数)通过变精度α -模型(变精度α -能力模型)诱导的知识结构保持不变.本文提出两种算法:1)基于技能映射, 寻找极小技能子集族和生成知识结构的算法; 2)基于技能函数, 寻找极小技能子集族和生成知识结构的算法.UCI数据集上的实验表明对技能子集的约简算法是可行的, 这不仅使诱导知识结构的复杂度得以降低, 还涉及到个体技能选择和知识评估的问题.Sun等[20]将模糊集的思想融入技能映射中, 研究个体技能的熟练程度, 为评估个体的知识掌握情况提供另一种思路.因此, 在今后的研究中:一方面考虑把文献[20]中模糊技能映射结合到本文考虑的问题中, 继续研究个体的技能选择与知识评估的问题; 另一方面将考虑技能映射通过变精度α -模型诱导的知识结构中至少存在一个拟序空间的条件.
本文责任编委 王士同
Recommended by Associate Editor WANG Shitong
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|
| [19] |
|
| [20] |
|
| [21] |
|
| [22] |
|
| [23] |
|
| [24] |
|
| [25] |
|