基于适应度分组的多策略人工蜂群算法

引用本文

周新宇, 胡建成, 吴艳林, 钟茂生, 王明文. 基于适应度分组的多策略人工蜂群算法. 模式识别与人工智能, 2022,35(8): 688-700
ZHOU Xinyu, HU Jiancheng, WU Yanlin, ZHONG Maosheng, WANG Mingwen. A Multi-strategy Artificial Bee Colony Algorithm Based on Fitness Grouping. PATTERN RECOGNITION AND ARTIFICIAL INTELLIGENCE, 2022,35(8): 688-700. 复制到剪切板

Doi: 10.16451/j.cnki.issn1003-6059.202208002
Permissions

《模式识别与人工智能》编辑部

基于适应度分组的多策略人工蜂群算法

周新宇¹, 胡建成¹, 吴艳林¹, 钟茂生¹, 王明文¹

1.江西师范大学计算机信息工程学院南昌 330022

通信作者:

王明文,博士,教授,主要研究方向为进化计算及其应用、中文信息处理、信息检索、机器学习.E-mail:mwwang@jxnu.edu.cn.

作者简介:

周新宇,博士,副教授,主要研究方向为进化计算及其应用.E-mail:xyzhou@jxnu.edu.cn.

胡建成,硕士研究生,主要研究方向为进化计算及其应用.E-mail:hujiancheng@jxnu.edu.cn.

吴艳林,硕士,主要研究方向为进化计算及其应用.E-mail:yanlin_wu@jxnu.edu.cn.

钟茂生,博士,教授,主要研究方向为进化计算及其应用、机器学习、数据挖掘(大数据)、自然语言处理.E-mail:zhongmaosheng@sina.com.

收稿日期: 2022-05-05 接受日期: 2022-08-19

资助项目: 国家自然科学基金项目(No.61966019,61876074,61866017)、江西省自然科学基金项目(No.20192BAB207030)、江西省教育厅研究生创新基金项目(No.YC2021-S309)资助

摘要

多策略机制是改进人工蜂群算法的有效手段,但是现有的很多相关工作未考虑种群中不同个体的特点,一视同仁地分配解搜索方程,导致多策略机制的有效性受到限制.为此,文中提出基于适应度分组的多策略人工蜂群算法,既考虑种群中的优秀个体,又照顾较差个体.首先,根据个体适应度把种群划分为三组,每组个体都有自己的特点,能在勘探和开采之间有所侧重.然后,为每组设计具备不同搜索能力的解搜索方程,使各组能相互分工与合作,更好地平衡整体种群的勘探和开采能力.最后,为了继续维持观察蜂阶段的原有作用,设计融合全局最优个体和精英个体的解搜索方程,充分发挥优秀个体在搜索过程中的引导作用.在CEC2013、CEC2015测试集上的实验表明文中算法竞争力较强.

关键词: 人工蜂群; 适应度分组; 搜索能力; 精英个体

中图分类号:TP301

A Multi-strategy Artificial Bee Colony Algorithm Based on Fitness Grouping

ZHOU Xinyu¹, HU Jiancheng¹, WU Yanlin¹, ZHONG Maosheng¹, WANG Mingwen¹

1. School of Computer and Information Engineering, Jiangxi Normal University, Nanchang 330022

Corresponding author:
WANG Mingwen, Ph.D., professor. His research interests include evolutionary computation and its applications, Chinese information processing, information retrieval and machine lear-ning

About Author:
ZHOU Xinyu, Ph.D., associate profe-ssor. His research interests include evolutio-nary computation and its applications.
HU Jiancheng, master student. His research interests include evolutionary computation and its applications.
WU Yanlin, master. His research interests include evolutionary computation and its app-lications.
ZHONG Maosheng, Ph.D., professor. His research interests include evolutionary computation and its applications, machine learning, data mining(big data), and natural language processing.

Fund:National Natural Science Foundation of China(No.61966019,61876074,61866017), Natural Science Foundation of Jiangxi Province(No.20192BAB207030), Postgraduate Innovation Fund of Education Department of Jiangxi Province(No.YC2021-S309)

Abstract

The multi-strategy mechanism is an effective way to improve the performance of artificial bee colony algorithm(ABC). However, characteristics of different individuals in the population are not considered in the existing methods, and the strategies are typically assigned to individuals without distinction. Consequently, the effectiveness of the multi-strategy mechanism is limited. Therefore, a multi-strategy ABC algorithm based on fitness grouping is proposed in this paper with consideration of both excellent individuals and poor individuals. Firstly, the population is divided into three groups according to fitness value of the individuals. Thus, the individuals of each group hold their own characteristics and preferences for exploration or exploitation. Then, solution search equations with distinct search capabilities are designed for three groups respectively to achieve division and cooperation among the groups and balance exploration and exploitation of the whole population. Finally, a solution search equation integrating the global best individual and some elite individuals is specially designed to further maintain the original role of the onlooker bee phase. In this scenario, the superior individuals can guide the search procedure. Experimental results on CEC2013 and CEC2015 datasets indicate the strong competitiveness of the proposed algorithm.

Key words: Key Words Artificial Bee Colony; Fitness Grouping; Search Capability; Elite Individual

文章图片

在科学研究和工程应用中, 很多实际问题可转化为优化问题进行求解, 但其中大部分问题都是高度复杂的, 通常有非凸、多峰、强约束等特点, 致使一些经典的最优化方法往往难以求解^{[1, 2]}.近年来, 一些基于进化优化的方法表现出良好的求解性能, 它们对优化问题的数学性质要求不高, 甚至可作为一类黑盒优化工具直接使用.在这类方法中, 进化算法是核心, 它通过模拟自然界中的生物进化行为实现寻优.作为一类算法, 进化算法包含多种不同的算法范例, 常见的有:遗传算法(Genetic Algorithm, GA)^[3]、粒子群优化算法(Particle Swarm Optimiza-tion, PSO)^[4]、差分进化算法(Differential Evolution, DE)^[5]、人工蜂群算法(Artificial Bee Colony, ABC)^[6]等.

ABC模拟自然界中蜂群的智能采蜜行为, 通过不同种类蜜蜂的分工协作寻找含量最多的蜜源地, 即找到优化问题的最优解.相比GA、PSO、DE, ABC的性能相当, 具有竞争力^[7], 并且结构简单、控制参数较少.近年来, ABC受到相关领域中众多研究人员的密切关注, 相继提出很多关于ABC的算法改进和应用方面的研究工作.目前, ABC已成功应用于求解多种不同的实际优化问题, 包括:流水车间调度问题^[8]、服务计算优化问题^[9]、投资组合优化问题^[10]、人群疏散路径规划问题^[11]、特征选择问题^[12]、图像分割问题^[13]、网络负载均衡问题^[14]等.

然而, ABC在求解复杂优化问题时, 性能受到严重挑战, 主要表现为求解精度不高、收敛速度较慢.为此, 研究人员提出很多相关改进策略, 并指出导致ABC性能受限的一个主要原因是其解搜索方程的勘探能力过强, 而开采能力不足.这些相关改进策略可大致分为两类:1)如何利用种群中的最优个体或精英个体设计新的解搜索方程.Zhu等^[15]提出GABC(Gbest-Guided ABC, GABC), 在解搜索方程中把种群的最优个体Gbest添加为引导项.周新宇等^[16]提出邻域搜索的ABC, 在环形邻域拓扑结构中选择最优个体进行开采, 利用邻域信息引导算法搜索.Cui等^[17]设计基于精英个体引导的解搜索方程, 把具有较好适应度的若干个体视为精英个体, 再从中任选一个精英个体作为解搜索方程的目标个体.2)如何利用不同的解搜索方程设计多策略机制.Wang等^[18]提出多策略集成的改进ABC, 采用3种不同的解搜索方程, 用于构建策略候选池, 在初始化阶段为个体随机分配一种解搜索方程, 再根据子代个体质量动态选择不同的解搜索方程.Xiang等^[19]提出ABCG, 在雇佣蜂阶段引入引力模型, 选择引力最大的邻域个体生成后代个体, 而在观察蜂阶段采用随机引导方式、反向学习、重新初始化三种策略.Chen等^[20]将3种解搜索方程集成到ABC中, 提出自适应多策略机制, 每个个体可自适应地选择其中的一种策略.

上述两类策略可有效提高ABC性能, 并为设计新的策略提供有益借鉴, 但这些工作还存在一定的局限性:1)虽然利用精英个体引导搜索可加快算法的收敛速度, 但未考虑种群中占多数的非精英个体, 在一定程度上容易导致种群陷入局部最优; 2)大部分的多策略机制是以算法的历史经验选择策略, 即把以往迭代的策略成功率作为后续策略选择的概率, 但当问题的适应度地形非常崎岖时, 这种历史经验往往不准确.因此, 本文提出基于适应度分组的多策略ABC算法(Multi-strategy ABC Based on Fitness Grouping, MABC-FG).一方面, 在利用精英个体引导搜索的同时, 考虑种群中占多数的非精英个体, 设计4种精英个体与非精英个体结合的解搜索方程; 另一方面, 从个体层次出发选择策略, 根据适应度对种群进行分组, 为不同分组的个体分配具备不同搜索能力的解搜索方程, 使不同个体产生不同的搜索行为, 平衡算法的勘探能力和开采能力, 达到有效提高ABC性能的目的.为了验证本文算法性能, 在CEC2013 (2013 IEEE Congress on Evolutionary Computation)、CEC2015 (2015 IEEE Congress on Evolu- tionary Computation)测试集及调频声波合成问题上进行实验, 结果表明本文算法性能较优.

1 经典人工蜂群算法

经典ABC^[21]是根据蜜蜂寻找蜜源的搜索过程提出的一种进化算法.在算法中有3种蜜蜂:雇佣蜂、观察蜂、侦察蜂, 这3种蜜蜂相互分工和合作, 寻找更好的蜜源.首先, 雇佣蜂负责在蜜源周围搜索新的蜜源, 并且完成搜索后将蜜源位置、蜜量等信息分享给观察蜂.然后, 观察蜂根据雇佣蜂分享的信息按照一定的概率选择某一个蜜源继续进行开采, 如果该蜜源的蜜量越多, 被选择的概率越高.最后, 如果某一蜜源连续limit次仍未更新, 该蜜源就会被抛弃, 侦察蜂负责重新随机搜索一个新的蜜源代替被抛弃的蜜源.值得注意的是, 雇佣蜂的数目、观察蜂的数目和蜜源的数目是相同的, 侦察蜂只有一只, 蜜源对应优化问题的候选解, 蜜源的蜜量对应优化问题的适应度值.

经典ABC采用随机初始化种群开始迭代搜索, 设蜜源的规模为SN, 其中, 蜜源

X_i=(x_i_{, 1}, x_i_{, 2}, …, x_i_,_D)

表示一个候选解, 第i个蜜源的第j个维度

x_i_,_j= $x_{j}^{\min}$ +rand· ( $x_{j}^{\max}$ - $x_{j}^{\min}$ ), (1)

其中, i=1, 2, …, SN, j=1, 2, …, D, $x_{j}^{\max}$ 表示第j维上界, $x_{j}^{\min}$ 表示第j维下界, rand表示[0, 1]之间均匀分布的随机数.在初始化过程中, 使用式(1)产生每个蜜源的所有维度值.在种群初始化之后, 整个种群进入雇佣蜂、观察蜂、侦察蜂搜索阶段, 循环迭代这3个阶段直至达到算法终止条件.3个阶段具体情况如下.

1)雇佣蜂阶段.在该阶段, 每只雇佣蜂在对应的蜜源X_i处, 根据

v_i_,_j=x_i_,_j+ϕ _i_,_j(x_i_,_j-x_r_,_j)

产生一个新的蜜源V_i=(v_i_{, 1}, v_i_{, 2}, …, v_i_,_D), 其中, X_r表示种群中随机选择的一个蜜源, r=1, 2, …, SN, 满足i≠ r, ϕ _i_,_j表示[-1, 1]内均匀分布的随机数.依据贪婪选择机制, 当候选蜜源V_i的蜜量更多, 即适应度值更优, 替换蜜源X_i.

2)观察蜂阶段.所有雇佣蜂完成搜索后, 观察蜂根据收到的信息, 选择一个蜜源继续进行开采.第i个蜜源被选择的概率为:

p_i=$\frac{fit_{i}}{\sum\limits_{j=1}^{SH}fit_{j}}$, (2)

其中, fit_i表示第i个蜜源的适应度,

fit_i= $\{\begin{array}{l} \frac{1}{1 + f_{i}}, & fi t_{i} \geq 0 \\ 1 + | f_{i} |, & 其它 \end{array}$ (3)

f_i表示第i个解的目标函数值.适应度越高的蜜源被选择的概率越大.

3)侦察蜂阶段.在上面两个阶段完成之后, 如果某一蜜源连续limit次开采仍未更新, 说明该蜜源已被开采耗尽.在这种情况下, 该蜜源将被舍弃, 并根据式(1)产生一个新的蜜源替换它.

2 基于适应度分组的多策略人工蜂群算法

2.1 适应度分组机制

从多策略集成的ABC的相关研究中, 本文发现这些算法通常对种群中的每个个体都一视同仁, 但是从个体层次上看, 个体之间存在优劣差异, 这种差异可根据适应度值衡量, 这种差异也可粗略地在适应度地形的位置分布上得到体现.一般而言, 较好的个体可能离局部最优解或全局最优解更近, 而较差的个体可能离局部最优解或全局最优解更远.因此, 较好的个体更适合进行开采, 而对于较差的个体应更注重勘探.因此, 本文从个体层次出发, 在设计多策略机制时, 根据适应度将种群分成3个具有不同特性的组.具体地, 本文按照个体的适应度对种群排序, 适应度最好的个体排在第一位, 适应度最差的个体排在最后一位.将种群中前三分之一的个体划分到A组, 三分之一到三分之二的个体划分到B组, 最后三分之一的个体划分到C组.此过程如图1所示.

	Figure Option View Download New Window
	图1 种群划分示意图Fig.1 Illustration of population division

根据上述种群划分过程可得出如下结论:1)A组中个体的适应度值均优于其它两组中个体, 此时A组中的个体很可能离局部最优解或全局最优解更近, 因此A组应注重开采; 2)C组中个体的适应度值均差于其它两组中的个体, 相对而言, C组的个体很可能离局部最优解或全局最优解更远, 因此C组应注重勘探; 3)B组中个体的适应度值比A组差, 但比C组好, 因此对于B组中的个体而言, 应注重开采与勘探的平衡.综合来看, A组注重开采, B组注重开采与勘探的平衡, C组更注重勘探.通过这种划分方式, 不同分组中的个体可表现出不同的搜索行为, 对于整个种群而言也能有效平衡勘探与开采.需要注意的是, 考虑到观察蜂是负责开采更好蜜源的这一特性, 在观察蜂阶段不使用适应度分组机制, 而继续只使用具有较强开采能力的解搜索方程.为了完成这一目标, 本文为观察蜂阶段专门设计一个解搜索方程.

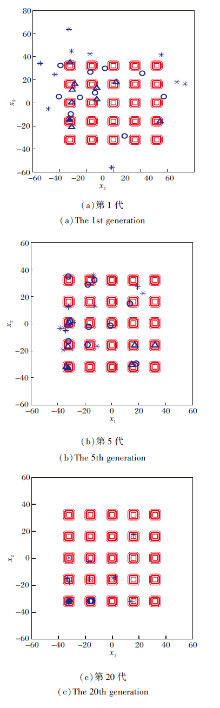
为了更直观地说明各组成员的位置分布特点, 以二维的Shekel's Foxholes函数为例具体说明.该函数有24个局部极值点和1个全局最优点

f(-32, -32)=0.998,

搜索范围为[-65.536, 65.536]², 具体定义可参考文献[22].此例中种群规模为30.

图2分别表示算法第1、5、20代的种群分布图, 图中△ 表示A组个体, ▲表示整个种群的最优个体, ○表示B组个体, * 表示C组个体.由图可看出, 在第1代, 3组个体在搜索空间中随机分布.第5代后, 算法已找到全局最优解, 大多数A组个体和B组个体已靠近极值点, C组也聚集在极值点附近.在第20代, A组个体已全部聚集在全局最优点, C组个体仍分散在各个极值点, 使整个种群保持较好的勘探能力.

	Figure Option View Download New Window
	图2 种群分布示意图Fig.2 Illustration of population distribution

通过该例可知, A组能快速找到最有潜力的搜索区域, B组跟随A组进行细粒度搜索, C组负责在全局区域搜索, 这三组相互配合、缺一不可.

2.2 多策略机制

针对每个分组的不同特性, 本文引入多策略的思想, 为不同分组的个体设计具备不同搜索能力的解搜索方程, 具体操作如下.

针对A组个体注重开采的特性, 设计的解搜索方程如下:

v_i_,_j=x_i_,_j+α (x_best_,_j-x_i_,_j)+α · rand· (x_i_,_j-x_r_1,_j). (4)

其中:α 表示新引入的扰动参数,

α = $\frac{MaxFEs - FEs}{MaxFEs}$ ∈ [0, 1],

MaxFEs表示适应度函数的最大评价次数(Maximum Number of Function Evaluations), FEs表示已使用的评价次数; X_best表示全局最优个体, X_r₁表示随机选择的一个个体,

i∈ A, r₁=1, 2, …, SN, i≠ r₁≠ best;

rand为[0, 1]内均匀分布的随机数; j=1, 2, …, D为随机选择的一个维度.式(4)的目的是使搜索范围集中在精英个体周围, 并且为了防止陷入局部最优, 在种群中随机选择一个个体作为扰动个体, 提供一定的多样性.与此同时, 引入扰动参数α , 目的是为了在进化过程中动态平衡勘探与开采.在算法初始阶段, α 值接近于1, 此时个体的搜索范围较大, 适合进行全局搜索, 可增加种群多样性.随着迭代次数的增加, 搜索范围会适当减小, 有利于加快种群收敛.但注意到, 当α 接近于0时, 会使V_i接近于X_i, 即父代几乎将全部信息遗传给子代, 不利于种群进化.因此, 为了保证个体在算法后期的搜索范围不至于过小, 本文将α 的最小值设置为0.1.

针对B组中的个体兼顾勘探与开采的特性, 解搜索方程如下:

v_i_,_j= $\{\begin{array}{l} \begin{array}{l} x_{i, j} + α (x_{elite 1, j} - x_{i, j}) + \\ α \cdot rand \cdot (x_{r 1, j} - x_{r 2, j}), \end{array} \begin{array}{l} rand < CR or \\ j = j_{rand} \end{array} \\ x_{i, j}, 其它 \end{array}$ (5)

其中, X_elite₁∈ A, X_r₂=1, 2, …, SN, i≠ r₁≠ r₂≠ elite₁, j_rand表示随机选择的一个维度, α 表示扰动参数, CR表示控制参数.式(5)中引入A组中的个体引导搜索.

此外, 为了使B组具有更好的全局搜索能力, 在种群中随机选择两个个体作为扰动项, 引入控制参数CR, 使个体每次迭代以一定的概率更新多个维度.显然相对A组的解搜索方程, 该解搜索方程更偏向于勘探.

针对C组中的个体注重全局勘探的特性, 解搜索方程设计如下:

$v_{i, j} = x_{i, j} + rand ∙ (x_{elite 1, j} - x_{i, j}) + α ∙ rand ∙ (x_{elite 2, j} - x_{w, j}),$ (6)

其中, X_elite₁∈ A, X_elite₂∈ A, X_w∈ C, i≠ w≠ elite₁≠ elite₂, α 表示扰动参数, 与式(4)相同.为了更有效地利用劣势个体的信息, C组中每个个体每次迭代均会更新所有维度, 同时为了防止后期收敛过慢, 还引入A组中的个体引导搜索.

ABC中雇佣蜂主要负责勘探新的蜜源, 观察蜂负责针对适应度较好的蜜源进行局部开采, 它们具有不同的分工.在经典ABC中, 这两个阶段使用同一解搜索方程.在经典解搜索方程中, 受随机选择的个体影响, 种群在搜索过程中具有很强的随机性, 影响算法的整体性能.为了克服该缺点, 本文在观察蜂阶段设计解搜索方程, 引入全局最优个体和精英个体, 有利于目标个体移动到适应度更好的搜索区域, 具体如下:

$v_{i, j} = x_{i, j} + rand ∙ (x_{elite, j} - x_{i, j}) + rand ∙ (x_{best, j} - x_{r 1, j})$ , (7)

各个变量含义同上, 需要注意的是

elite≠ best≠ r1≠ i.

为了加强观察峰阶段的局部开采能力, 引入全局最优个体和精英个体作为扰动个体引导搜索, 使目标个体向精英个体和全局最优个体所在区域移动, 加强对适应度值较好的区域进行搜索, 并且为了防止算法太过于贪婪, 引入随机个体, 增加一定的多样性.

总之, 在观察蜂阶段, 通过全局最优个体、精英个体和随机个体这3种不同个体之间的协同合作, 增强算法的局部开采能力, 同时也确保算法具有一定的全局勘探能力.

2.3 算法步骤

本文算法的伪代码如下.

算法 MABC-FG

输入种群规模SN, 控制参数limit,

维度控制参数CR,

适应度函数的最大评估次数MaxFEs

输出全局最优个体X_best

对输入参数进行初始化.

由式(1)产生初始种群, 计算每个个体的适应度值.

令trial_i=0, FEs=SN.

while (FEs< =MaxFEs) do

//雇佣蜂阶段

根据个体的适应度值将种群划分为3组.

for i=1 to SN do

根据个体X_i所在的分组, 选择式(4)~式(6), 产生候选个体V_i.

如果f(V_i)< f(X_i), 令X_i=V_i, trial_i=0,

否则, 令trial_i=trial_i+1.

end for

FEs=FEs+SN.

//观察蜂阶段

按式(2)和式(3)计算个体被选中的概率p_i.

for i=1 to SN do

if p_i> rand(0, 1) then

根据式(7)产生候选个体V_i.

如果f(V_i)< f(X_i), 令X_i=V_i, trial_i=0,

否则, 令trial_i=trial_i+1.

end if

end for

FEs=FEs+SN.

//侦察蜂阶段

for i=1 to SN do

if trial_i> limit then

根据式(1)重新生成X_i, 令trial_i=0.

FEs=FEs+1.

end if

end for

end while

3 实验及结果分析

在测试函数方面, 本文选取2套权威的测试函数:CEC2013测试集^[23]和CEC2015测试集^[24].这两套测试函数都是求解难度较高的测试集, 涵盖偏移、旋转和复合等多种复杂测试问题, 常用于验证优化算法的性能.

为了公平起见, 本文将各算法中用到的公共参数进行统一设置, 其余参数均参照相应算法的原始文献设置.实验参数设置如下:测试函数的维度D=30, 50, 对应的两套测试函数的最大评价次数MaxFEs=10000D.在所有实验中, 每种算法独立运行30次, 给出30次运行的平均结果和标准差.实验结果分析采用Wilcoxon秩和检验和Friedman检验, 显著性水平均设置为0.05.

3.1 参数敏感性分析

在本文提出的多策略机制中, 针对B组个体的特性, 引入参数CR控制子代个体可更新维度.一般而言, 越小的CR值会使子代个体可更新的维度越少, 从父代个体中获取越多的信息.但越大的CR值会使子代可更新的维度越多, 搜索范围也会越大.因此, CR值的选取会对算法性能具有一定影响.

本节选取CR=0.1, 0.3, 0.5, 0.7, 0.9这5个典型值进行测试, 均在CEC2015测试集上进行实验, 测试函数维度设置为30.实验结果如表1所示, 表中黑体数字表示最优值, Best表示最优值的数量, 同时给出Friedman检验的结果.

表1 CR不同时本文算法在CEC2015测试集上的实验结果 Table 1 Experimental results of different CR values of the proposed algorithm on CEC2015 dataset

由表1可看到, 当CR=0.1和CR=0.7时, 算法性能最优.但是:当CR=0.1时, 算法在7个函数上取得最优值; 当CR=0.7时, 算法只在3个函数上取得最优值.可能的原因是, 当CR=0.1时, B组中个体可从父代中继承更多的维度, 而B组中个体都是适应度值相对较好的个体, 有较好的引导作用, 能使算法的性能更优.综合考虑下, 本文设置CR=0.1.

种群规模的大小也影响算法性能, 种群规模越大, 越适合全局勘探; 反之种群规模越小, 越适合局部开采.因此, 选择一个合适的种群规模至关重要.一般而言, 不同的改进ABC通常会采用不同的SN, 本文选择SN=20, 30, 40, 50, 100这5个典型值.具体实验结果如表2所示, 表中黑体数字表示最优值.

表2 SN不同时本文算法在CEC2015测试集上的实验结果 Table 2 Experimental results of different SN values of the proposed algorithm on CEC2015 dataset

由表2可看出, SN=50时, 算法在10个函数上取得最优且综合排名也是最优, 而SN=20和SN=100时, 算法只在1个函数和3个函数上表现最优.这是因为当种群规模过大时, 算法会过度偏向于勘探, 而种群规模过小时, 算法会过度偏向于开采, 使算法性能下降.当SN=50时, 种群规模适中, 有利于平衡算法的勘探与开采.综上所述, 本文设置SN=50.

参数limit控制侦察蜂阶段的执行频率, limit越大, 侦察蜂阶段的执行频率越低, 种群越容易陷入局部最优.limit越小, 侦察蜂阶段的执行频率越高, 影响算法的收敛.所以limit取值对算法性能也会有一定的影响.与种群规模SN类似, 不同的改进ABC通常会采用不同的limit, 本文设定limit=100, 200, SN· D.具体实验结果如表3所示, 表中黑体数字表示最优值.由表可知, 当limit=200时, 算法在8个函数上取得最优, 当limit=100和limit=SN· D时, 算法分别在7个函数和5个函数上取得最优.从结果上看, 当limit=100和limit=200时, 算法整体性能相当, 但是在F06~F15复杂函数上, 当limit=200时, 算法取得7个最优值, 而当limit=100时, 算法取得5个最优值.这说明当limit过小时, 侦察蜂阶段执行的频率过高, 会破坏算法已获得的搜索经验算法, 降低算法求解复杂问题的性能.从整体的排名上看, limit=200时排名第一, 说明limit=200使算法的整体性能更优, 因此, 本文设置limit=200.

表3 limit不同时本文算法在CEC2015测试集上的实验结果 Table 3 Experimental results of different limit values of the proposed algorithm on CEC2015 dataset

3.2 策略有效性验证

相比ABC, 本文主要提出两点改进:在雇佣蜂阶段采用基于适应度分组的多策略机制; 在观察蜂阶段采用基于全局最优个体与精英个体的解搜索方程.为了分别验证这两点改进之处对算法性能的影响, 设计如下对比算法:1)在ABC的基础上, 仅将基于适应度分组的多策略机制引入雇佣蜂阶段, 而其它部分与ABC保持相同, 该对比算法记为MABC-FG-1; 2)在ABC的基础上, 仅将基于全局最优个体和精英个体的解搜索方程引入观察蜂阶段, 而其它部分与ABC保持相同, 该对比算法记为MABC-FG-2.此外, ABC作为对比基准也加入对比实验.

实验在CEC 2015测试集上进行, 测试函数维度设置为30.结果如表4所示, 表中符号“ +” 、“ -” 、“ ≈ ” 分别表示MABC-FG优于、弱于、相似于对比算法.由表可看出, MABC-FG-1没有在一个函数上优于MABC-FG, 这是因为MABC-FG-1的观察蜂阶段仍使用经典解搜索方程, 不能确保随机选择的个体好坏, 使MABC-FG-1在3个函数上弱于MABC-FG.MABC-FG在9个函数优于MABC-FG-2.由此说明, 适应度分组机制能显著提高种群的搜索效率.注意到MABC-FG-2的总体表现不如ABC, 这是由于观察蜂阶段的主要作用是开采精英个体, 而MABC-FG-2的雇佣蜂阶段依旧使用经典解搜索方程产生候选个体, 随机性较强, 找到的个体往往适应度不好.

表4 策略有效性验证结果 Table 4 Verification results of strategy effectiveness

总之, MABC-FG的综合表现优于仅有一点改进之处的对比算法, 这也说明MABC-FG的两点改进之处是一个整体、缺一不可.尽管上述实验可验证本文策略的有效性, 但还不足以说明MABC-FG性能较优.

3.3 实验结果对比

本节选择近年来提出的5个相关改进ABC作为对比算法:1)LL-ABC^[10].基于方向信息和精英机制的ABC.2)ABCG^[19].基于引力模型的ABC.3)iqABC(Improved Quick ABC)^[25].4)MGABC^[26].基于多精英引导的ABC.5)ECABC^[27].基于精英群引导和广度-深度搜索结合的ABC.LL-ABC、iqABC、MGABC都涉及对解搜索方程进行改进, ECABC、ABCG都融入多策略的思想.

当D=30, 50时, 各算法在CEC2013测试集上的实验结果如表5和表6所示.由表5可看出, 当D=30时, MABC-FG在绝大多数函数上的性能最优.从Freidman测试结果可看出, MABC-FG的综合表现排名第一.具体来说, 在F01~F05单峰函数上, MABC-FG在F05上弱于MGABC、ABCG和ECABC, 在F01和F02上弱于MGABC.这是因为MGABC在侦察蜂阶段完成之后, 增加一个对全局最优个体进行邻域搜索的过程, 有效提高算法的开采能力.而MABC-FG利用不同组之间的分工合作进行搜索, 并未完全依赖于全局最优个体.客观来说MABC-FG的开采能力稍弱于MGABC.对于单峰函数, 因为函数只有一个全局最优解, 适应度地形较平滑, 使MGABC在该类问题上表现较优.在F06~F20多峰函数中, MABC-FG在F07、F09、F12、F13、F15、F20函数上最优, 在其余的函数上也有较优性能.在F21~F28组合函数上, MABC-FG在F23、F24、F25函数上最优, 在其余的函数上也表现不错.这是因为MABC-FG中的基于适应度分组机制发挥重要作用, 在该机制中C组个体的作用主要是进行勘探, 可提高算法跳出局部最优解的能力, 并且A组的个体专注于开采, 有利于提高算法的开采能力.所以在多峰问题和复杂问题上, MABC-FG具有较优性能.总之, MABC-FG在这三种类型的函数上都具有很强的竞争力.

表5 D=30时各算法在CEC2013测试集上的实验结果 Table 5 Experimental results of different algorithms on CEC2013 dataset with D=30

函数	MGABC	ABCG	ECABC	LL-ABC	iqABC	MABC-FG
F01	0.000e+00± 0.000e+00^-	2.274e-13± 0.000e+00⁺	9.095e-14± 1.114e-13^≈	5.002e-13± 1.083e-13⁺	4.851e-13± 7.729e-14⁺	1.288e-13± 1.127e-13
F02	8.770e+05± 3.641e+05^-	2.509e+07± 2.481e+06⁺	1.475e+07± 3.071e+06⁺	8.203e+06± 2.892e+06⁺	9.079e+06± 2.365e+06⁺	2.012e+06± 1.095e+06
F03	2.694e+08± 3.341e+08⁺	1.126e+09± 6.055e+08⁺	2.572e+08± 1.823e+08⁺	3.172e+08± 2.190e+08⁺	4.175e+08± 2.531e+08⁺	2.526e+06± 3.635e+06
F04	8.000e+03± 1.791e+03⁺	5.614e+04± 5.011e+03⁺	6.895e+04± 6.032e+03⁺	7.338e+04± 8.589e+03⁺	7.219e+04± 8.597e+03⁺	3.105e+03± 1.417e+03
F05	1.061e-13± 2.836e-14^-	2.312e-13± 2.041e-14^-	1.251e-13± 3.411e-14^-	6.632e-13± 7.240e-14⁺	7.465e-13± 6.998e-14⁺	3.297e-13± 2.261e-13
F06	2.765e+01± 2.586e+01^-	2.306e+01± 1.777e+01^-	2.125e+01± 1.255e+01^-	1.213e+01± 4.294e+00^-	1.400e+01± 3.588e+00^-	4.872e+01± 2.837e+01
F07	6.335e+01± 1.686e+01⁺	8.574e+01± 6.505e+00⁺	9.611e+01± 1.167e+01⁺	1.040e+02± 1.132e+01⁺	1.056e+02± 1.236e+01⁺	5.459e+00± 4.305e+00
F08	2.095E01± 4.612e-02^≈	2.095e+01± 4.643e-02^≈	2.096e+01± 4.097e-02^≈	2.093e+01± 5.544e-02^≈	2.096e+01± 4.690e-02^≈	2.095e+01± 4.281e-02
F09	2.220e+01± 4.107e+00⁺	3.064e+01± 1.556e+00⁺	2.909e+01± 1.621e+00⁺	3.020e+01± 1.232e+00⁺	2.989e+01± 1.661e+00⁺	1.266e+01± 3.322e+00
F10	2.649e-01± 1.199e-01^≈	2.692e-01± 1.305e-01^≈	9.918e-01± 2.428e-01⁺	1.089e+00± 2.353e-01⁺	1.693e+00± 3.372e-01⁺	3.188e-01± 2.832e-01
F11	1.137e-14± 2.274e-14^≈	5.874e-14± 1.020e-14^≈	1.895e-15± 1.020e-14^-	5.684e-14± 0.000e+00⁺	1.042e-13± 2.118e-14⁺	1.330e-14± 2.400e-14
F12	1.066e+02± 2.478e+01⁺	2.115e+02± 1.350e+01⁺	9.836e+01± 1.966e+01⁺	2.295e+02± 4.088e+01⁺	2.519e+02± 3.579e+01⁺	2.478e+01± 5.688e+00
F13	1.621e+02± 2.628e+01⁺	2.019e+02± 1.010e+01⁺	1.461e+02± 2.285e+01⁺	2.966e+02± 3.924e+01⁺	3.026e+02± 2.683e+01⁺	4.124e+01± 1.523e+01
F14	1.531e-01± 5.603e-02^-	6.796e+01± 2.270e+01⁺	4.252e+00± 2.263e+00⁺	1.951e+00± 9.169e-01^≈	2.095e+00± 1.258e+00^≈	1.606e+00± 1.106e+00
F15	3.222e+03± 5.711e+02⁺	6.124e+03± 3.031e+02⁺	4.630e+03± 3.951e+02⁺	3.641e+03± 4.010e+02⁺	3.625e+03± 3.359e+02⁺	2.797e+03± 4.048e+02
F16	2.264e+00± 2.466e-01⁺	2.250e+00± 2.719e-01⁺	2.003e+00± 2.612e-01⁺	1.461e+00± 1.590e-01^≈	1.316e+00± 1.931e-01^≈	1.381e+00± 2.599e-01
F17	3.045e+01± 2.196e-02^-	3.043e+01± 7.502e-04^-	3.048e+01± 6.453e-02^-	3.049e+01± 2.650e-02^≈	3.054e+01± 3.805e-02⁺	3.049e+01± 1.853e-02
F18	1.134e+02± 2.603e+01⁺	3.000e+01± 2.406e-14^≈	3.000e+01± 3.193e-14^≈	2.953e+01± 2.531e+00^≈	2.999e+01± 5.556e-02^≈	3.000e+01± 2.554e-14
F19	1.369e+00± 4.608e-01⁺	2.487e+00± 2.311e-01⁺	5.885e-01± 2.198e-01^-	3.515e-01± 8.884e-02^-	4.283e-01± 1.371e-01^-	9.483e-01± 1.921e-01
F20	9.512e+00± 6.642e-01⁺	1.188e+01± 2.051e-01⁺	1.212e+01± 2.481e-01⁺	1.198e+01± 3.036e-01⁺	1.198e+01± 2.525e-01⁺	7.890e+00± 5.388e-01
F21	3.200e+02± 5.999e+01^≈	2.702e+02± 4.553e+01^-	3.270e+02± 4.934e+01⁺	1.789e+02± 3.052e+01^-	1.737e+02± 3.245e+01^-	3.033e+02± 4.068e+01
F22	1.001e+02± 3.023e+01^-	9.268e+01± 9.306e+01^-	1.148e+02± 3.872e+01⁺	3.643e+01± 3.048e+01^-	2.996e+01± 2.036e+01^-	1.142e+02± 2.621e+01
F23	4.124e+03± 5.568e+02⁺	6.777e+03± 4.011e+02⁺	5.636e+03± 3.689e+02⁺	4.875e+03± 4.650e+02⁺	4.616e+03± 4.446e+02⁺	3.120e+03± 4.146e+02
F24	2.304e+02± 1.010e+01⁺	2.424e+02± 4.387e+00⁺	2.721e+02± 4.997e+00⁺	2.853e+02± 5.116e+00⁺	2.834e+02± 6.179e+00⁺	2.059e+02± 3.974e+00
F25	2.787e+02± 1.061e+01⁺	2.960e+02± 1.941e+01⁺	3.035e+02± 4.525e+00⁺	3.097e+02± 6.314e+00⁺	3.091e+02± 5.584e+00⁺	2.422e+02± 2.176e+01
F26	2.179e+02± 4.560e+01⁺	2.006e+02± 1.093e-01^-	2.007e+02± 1.644e-01^-	2.005e+02± 1.336e-01^-	2.006e+02± 1.409e-01^-	2.037e+02± 1.958e+01
F27	7.457e+02± 9.091e+01⁺	4.000e+02± 1.280e-13^≈	4.116e+02± 4.231e+01^≈	4.000e+02± 5.734e-02^≈	4.001e+02± 1.894e-01^≈	4.090e+02± 7.717e+01
F28	2.800e+02± 6.000e+01^≈	3.000e+02± 2.255e-13^≈	3.000e+02± 2.012e-13^≈	2.226e+02± 7.939e+01^-	1.990e+02± 8.170e+01^≈	3.000e+02± 2.269e-13
+/-/≈	16/7/5	16/6/6	17/6/5	16/6/6	17/5/6	-
Friedman	3.0000	3.9286	3.5871	3.6429	3.9286	2.6429

表5 D=30时各算法在CEC2013测试集上的实验结果 Table 5 Experimental results of different algorithms on CEC2013 dataset with D=30

表6 D=50时各算法在CEC2013测试集上的实验结果 Table 6 Experimental results of different algorithms on CEC2013 dataset with D=50

函数	MGABC	ABCG	ECABC	LL-ABC	iqABC	MABC-FG
F01	2.046e-13± 6.821e-14^-	5.533e-13± 1.127e-13⁺	2.274e-13± 0.000e+00^-	1.152e-12± 1.430e-13⁺	1.069e-12± 1.332e-13⁺	2.653e-13± 8.474e-14
F02	9.625e+05± 3.362e+05^-	3.334e+07± 6.893e+06⁺	2.792e+07± 6.546e+06⁺	1.266e+07± 2.780e+06⁺	1.260e+07± 2.993e+06⁺	3.734e+06± 1.484e+06
F03	1.829e+08± 2.176e+08⁺	1.305e+10± 2.607e+09⁺	3.041e+09± 1.379e+09⁺	1.331e+09± 8.911e+08⁺	1.572e+09± 9.117e+08⁺	3.012e+07± 3.705e+07
F04	2.295e+04± 3.140e+03⁺	7.687e+04± 5.019e+03⁺	1.259e+05± 1.356e+04⁺	1.376e+05± 9.092e+03⁺	1.251e+05± 1.045e+04⁺	5.429e+03± 1.750e+03
F05	1.137e-13± 0.000e+00^-	4.623e-13± 4.081e-14^-	3.411e-13± 5.084e-14^-	1.410e-12± 1.196e-13^-	1.603e-12± 1.617e-13^-	3.721e-12± 1.765e-12
F06	6.052e+01± 2.483e+01^≈	4.447e+01± 1.249e+00^-	4.461e+01± 1.173e+00^-	4.010e+01± 5.538e+00^-	4.254e+01± 2.855e+00^-	5.058e+01± 1.370e+01
F07	7.610e+01± 1.352e+01⁺	1.130e+02± 4.854e+00⁺	1.357e+02± 8.389e+00⁺	1.479e+02± 1.020e+01⁺	1.466e+02± 1.039e+01⁺	2.603e+01± 7.576e+00
F08	2.112e+01± 4.736e-02^≈	2.113e+01± 3.732e-02^≈	2.113e+01± 3.820e-02^≈	2.112e+01± 3.320e-02^≈	2.112e+01± 3.873e-02^≈	2.113e+01± 3.458e-02
F09	4.474e+01± 5.944e+00⁺	5.870e+01± 2.032e+00⁺	5.787e+01± 2.352e+00⁺	5.884e+01± 2.765e+00⁺	5.853e+01± 1.707e+00⁺	2.601e+01± 3.317e+00
F10	2.058e-01± 7.760e-02^-	2.676e-01± 1.576e-01^-	1.646e+00± 4.585e-01^-	1.491e+00± 2.969e-01^-	2.192e+00± 4.462e-01^≈	2.551e+00± 1.012e+00
F11	8.623e-01± 1.578e+00⁺	1.326e-13± 2.680e-14⁺	4.169e-14± 2.514e-14^-	1.326e-13± 3.055e-14⁺	2.558e-13± 7.591e-14⁺	5.680e-14± 0.000e+00
F12	2.029e+02± 2.949e+01⁺	4.049e+02± 1.717e+01⁺	3.587e+02± 3.510e+01⁺	6.337e+02± 6.062e+01⁺	6.503e+02± 7.116e+01⁺	6.465e+01± 1.321e+01
F13	2.857e+02± 3.538e+01⁺	4.317e+02± 2.089e+01⁺	4.375e+02± 3.761e+01⁺	7.186e+02± 5.041e+01⁺	7.212e+02± 5.276e+01⁺	1.332e+02± 2.704e+01
F14	9.208e-01± 6.834e-01^-	9.968e+02± 1.180e+02⁺	1.128e+01± 4.378e+00⁺	5.292e+00± 1.544e+00^≈	6.279e+00± 1.735e+00^≈	5.681e+00± 2.302e+00
F15	7.313e+03± 6.602e+02⁺	1.236e+04± 3.610e+02⁺	9.662e+03± 4.600e+02⁺	7.668e+03± 3.948e+02⁺	7.705e+03± 4.091e+02⁺	6.846e+03± 5.894e+02
F16	2.984e+00± 2.810e-01⁺	3.203e+00± 2.807e-01⁺	2.827e+00± 2.877e-01⁺	1.976e+00± 2.209e-01⁺	1.957e+00± 1.810e-01⁺	1.714e+00± 2.942e-01
F17	5.082e+01± 4.914e-02^-	5.230e+01± 9.743e-01⁺	5.089e+01± 1.013e-01^-	5.029e+01± 3.614e+00^≈	5.104e+01± 6.164e-02⁺	5.097e+01± 4.240e-02
F18	2.024e+02± 3.794e+01⁺	5.017e+01± 5.071e-14^≈	5.017e+01± 4.685e-14^≈	5.017e+01± 5.996e-14^≈	5.017e+01± 8.477e-14^≈	5.017e+01± 1.331e-13
F19	2.512e+00± 6.262e-01⁺	6.209e+00± 6.219e-01⁺	8.261e-01± 1.990e-01^-	8.039e-01± 1.667e-01^-	1.112e+00± 2.464e-01^-	1.760e+00± 3.634e-01
F20	1.822e+01± 7.338e-01⁺	2.117e+01± 2.739e-01⁺	2.140e+01± 2.466e-01⁺	2.092e+01± 4.093e-01⁺	2.103e+01± 3.345e-01⁺	1.497e+01± 9.147e-01
F21	3.533e+02± 4.989e+01⁺	2.100e+02± 2.999e+01^-	3.167e+02± 3.727e+01^≈	2.464e+02± 4.672e+01^-	2.296e+02± 3.578e+01^-	3.133e+02± 4.269e+01
F22	2.665e+01± 3.375e+01⁺	8.390e+02± 1.905e+02⁺	3.661e+01± 5.328e+01⁺	2.174e+01± 2.613e+00^-	2.737e+01± 3.149e+00⁺	2.625e+01± 3.779e+01
F23	8.403e+03± 8.770e+02⁺	1.356e+04± 4.264e+02⁺	1.149e+04± 6.700e+02⁺	9.742e+03± 6.655e+02⁺	9.822e+03± 6.264e+02⁺	6.816e+03± 6.301e+02
F24	2.864e+02± 1.953e+01⁺	2.834e+02± 6.310e+00⁺	3.515e+02± 7.899e+00⁺	3.680e+02± 6.185e+00⁺	3.682e+02± 6.543e+00⁺	2.285e+02± 1.139e+01
F25	3.527e+02± 1.701e+01⁺	4.067e+02± 4.836e+00⁺	4.113e+02± 6.362e+00⁺	4.193e+02± 7.470e+00⁺	4.230e+02± 8.274e+00⁺	3.080e+02± 8.587e+00
F26	2.404e+02± 8.080e+01⁺	2.022e+02± 3.081e-01^-	2.024e+02± 4.536e-01^-	2.016e+02± 3.052e-01^-	2.016e+02± 2.390e-01^-	2.446e+02± 6.755e+01
F27	1.387e+03± 2.053e+02⁺	4.000e+02± 1.827e-13^-	1.344e+03± 6.865e+02^≈	8.588e+02± 6.978e+02⁺	8.789e+02± 7.082e+02⁺	8.168e+02± 1.326e+02
F28	8.517e+02± 1.153e+03⁺	4.000e+02± 1.438e-13^≈	4.000e+02± 4.151e-13^≈	4.000e+02± 3.791e-13^≈	4.000e+02± 3.575e-07^≈	4.000e+02± 6.398e-10
+/-/≈	19/7/2	18/7/3	16/7/5	15/8/5	18/5/5	-
Friedman	3.0357	4.1071	3.8929	3.3929	4.0000	2.5714

表6 D=50时各算法在CEC2013测试集上的实验结果 Table 6 Experimental results of different algorithms on CEC2013 dataset with D=50

由表6可看出, 当D=50时, MABC-FG综合表现依旧排名第一, 即在绝大多数函数上仍保持领先.此外, 从Freidman测试结果可看出, MGABC综合性能排名第二.MGABC使用多精英引导机制, 具有较强的开采能力, 在高维问题上性能较优.LL-ABC综合性能排名第三, 这可能是由于方向信息能明确种群个体每步移动的优劣, 判断下一步个体走向, 特别在高维问题上表现明显.

为了进一步验证MABC-FG的性能, 在CEC2015测试集上继续实验, 当D=30, 50时的实验结果如表7和表8所示.

表7 D=30时各算法在CEC2015测试集上的实验结果 Table 7 Experimental results of different algorithms on CEC2015 dataset with D=30

函数	MGABC	ABCG	ECABC	LL-ABC	iqABC	MABC-FG
F01	5.294e+05± 2.581e+05^≈	8.431e+06± 2.170e+06⁺	2.774e+06± 1.091e+06⁺	2.421e+06± 7.084e+05⁺	2.478e+06± 9.088e+05⁺	6.907e+05± 3.485e+05
F02	3.041e+03± 3.234e+03^≈	1.355e+03± 1.326e+03^≈	1.991e+03± 2.199e+03^≈	6.560e+02± 5.591e+02^-	4.798e+02± 3.223e+02^-	1.883e+03± 2.134e+03
F03	2.041e+01± 4.087e-02⁺	2.043e+01± 3.710e-02⁺	2.033e+01± 3.640e-02⁺	2.026e+01± 2.921e-02^≈	2.024e+01± 3.135e-02^≈	2.024e+01± 6.104e-02
F04	4.509e+01± 1.165e+01⁺	8.236e+01± 4.982e+00⁺	2.869e+01± 4.797e+00⁺	7.409e+01± 1.070e+01⁺	7.309e+01± 9.290e+00⁺	1.939e+01± 2.859e+00
F05	1.819e+03± 3.452e+02⁺	3.776e+03± 1.816e+02⁺	2.198e+03± 2.699e+02⁺	1.871e+03± 2.364e+02⁺	1.907e+03± 2.470e+02⁺	1.549e+03± 2.636e+02
F06	1.096+E05± 6.981e+04⁺	6.515e+05± 2.684e+05⁺	1.419e+06± 8.262e+05⁺	1.239e+06± 4.538e+05⁺	1.025e+06± 4.331e+05⁺	5.620e+04± 4.319e+04
F07	8.323e+00± 2.410e+00⁺	9.247e+00± 4.346e-01⁺	8.794e+00± 1.232e+00⁺	7.036e+00± 9.906e-01^≈	6.519e+00± 8.230e-01^≈	6.892e+00± 1.044e+00
F08	4.086e+04± 2.358e+04⁺	9.900e+04± 5.455e+04⁺	2.517e+05± 1.287e+05⁺	2.399e+05± 1.097e+05⁺	2.420e+05± 1.128e+05⁺	2.164e+04± 1.002e+04
F09	1.023e+02± 1.562e-01⁺	1.042e+02± 2.063e-01⁺	1.038e+02± 2.574e-01⁺	1.043e+02± 3.393e-01⁺	1.044e+02± 3.510e-01+	1.021e+02± 1.475e-01
F10	8.942e+04± 5.227e+04⁺	3.792e+05± 1.545e+05⁺	6.401e+05± 2.880e+05⁺	5.059e+05± 2.613e+05⁺	5.971e+05± 2.800e+05⁺	5.743e+04± 3.944e+04
F11	5.047e+02± 1.365e+02⁺	3.539e+02± 1.858e+01^≈	3.209e+02± 5.827e+00^≈	3.189e+02± 5.696e+00^≈	3.206e+02± 4.639e+00^≈	3.521e+02± 5.344e+01
F12	1.040e+02± 3.891e-01⁺	1.069e+02± 4.453e-01⁺	1.056e+02± 2.287e-01⁺	1.059e+02± 2.926e-01⁺	1.062e+02± 3.668e-01⁺	1.026e+02± 3.609e-01
F13	9.592e+01± 4.652e+00⁺	1.163e+02± 2.889e+00⁺	9.672e+01± 2.693e+00⁺	1.014e+02± 2.743e+00⁺	1.014e+02± 3.761e+00⁺	8.537e+01± 5.291e+00
F14	3.310e+04± 1.019e+03⁺	3.145e+04± 5.840e+03^-	3.178e+04± 6.602e+02^≈	3.025e+04± 5.412e+03^-	3.126e+04± 9.687e+01^-	3.200e+04± 7.847e+02
F15	1.000e+02± 7.105e-14^≈	1.000e+02± 8.527e-14^≈	1.000e+02± 2.070e-13^≈	1.000e+02± 2.607e-13^≈	1.000e+02± 3.208e-13^≈	1.000e+02± 2.359e-13
+/-/≈	12/0/3	11/1/3	11/0/4	9/2/4	9/2/4	-
Friedman	3.2333	4.6333	4.2333	3.3667	3.5667	1.9667

表7 D=30时各算法在CEC2015测试集上的实验结果 Table 7 Experimental results of different algorithms on CEC2015 dataset with D=30

表8 D=50时各算法在CEC2015测试集上的实验结果 Table 8 Experimental results of different algorithms on CEC2015 dataset with D=50

函数	MGABC	ABCG	ECABC	LL-ABC	iqABC	MABC-FG
F01	7.085e+05± 1.877e+05^-	3.255e+07± 5.762e+06⁺	1.217e+07± 2.938e+06⁺	8.662e+06± 3.142e+06⁺	8.465e+06± 2.447e+06⁺	3.094e+06± 1.503e+06
F02	3.731e+03± 3.503e+03^≈	4.312e+03± 2.141e+03^≈	7.139e+03± 5.899e+03⁺	2.904e+03± 2.691e+03^≈	2.329e+03± 1.681e+03^≈	3.978e+03± 3.815e+03
F03	2.058e+01± 3.019e-02⁺	2.060e+01± 4.327e-02⁺	2.048e+01± 3.313e-02⁺	2.037e+01± 3.520e-02^≈	2.038e+01± 2.880e-02^≈	2.035e+01± 7.675e-02
F04	1.511e+02± 2.702e+01⁺	2.079e+02± 1.006e+01⁺	7.474e+01± 9.299e+00⁺	1.836e+02± 1.786e+01⁺	1.785e+02± 1.890e+01⁺	4.773e+01± 6.444e+00
F05	3.679e+03± 6.744e+02⁺	7.605e+03± 3.414e+02⁺	4.484e+03± 3.412e+02⁺	3.824e+03± 2.736e+02⁺	3.770e+03± 1.914e+02⁺	3.084e+03± 2.928e+02
F06	4.246e+05± 2.007e+05^≈	2.492e+06± 7.712e+05⁺	3.823e+06± 1.206e+06⁺	2.842e+06± 1.051e+06⁺	3.034e+06± 7.238e+05⁺	4.526e+05± 2.533e+05
F07	3.069e+01± 2.701e+01^≈	4.878e+01± 9.292e+00^≈	3.278e+01± 1.746e+01^-	1.519e+01± 1.343e+00^-	1.554e+01± 1.686e+00^-	4.233e+01± 1.696e+01
F08	2.086e+05± 1.007e+05^-	2.817e+06± 8.369e+05⁺	3.323e+06± 1.080e+06⁺	2.770e+06± 1.060e+06⁺	2.897e+06± 8.092e+05⁺	3.553e+05± 2.105e+05
F09	1.040e+02± 1.671e-01⁺	1.071e+02± 3.352e-01⁺	1.061e+02± 3.974e-01⁺	1.073e+02± 4.315e-01⁺	1.076e+02± 3.377e-01⁺	1.035e+02± 1.243e-01
F10	2.048e+04± 1.354e+04^≈	8.363e+05± 2.318e+05⁺	1.185e+06± 5.656e+05⁺	7.037e+05± 3.845e+05⁺	9.850e+05± 3.227e+05⁺	1.957e+04± 1.914e+04
F11	8.395e+02± 1.171e+02⁺	3.765e+02± 1.021e+01^-	4.186e+02± 1.826e+02^-	3.220e+02± 7.410e+00^-	3.260e+02± 1.071e+01^-	4.552e+02± 3.963e+01
F12	1.065e+02± 5.604e-01⁺	1.103e+02± 3.913e-01⁺	1.082e+02± 2.308e-01⁺	1.084e+02± 3.688e-01⁺	1.090e+02± 4.193e-01⁺	1.044e+02± 5.767e-01
F13	1.807e+02± 5.428e+00⁺	2.126e+02± 2.849e+00⁺	1.844e+02± 2.900e+00⁺	1.912e+02± 4.941e+00⁺	1.925e+02± 3.654e+00⁺	1.648e+02± 6.098e+00
F14	5.813e+04± 1.161e+04^≈	4.953e+04± 2.318e+00^-	5.160e+04± 5.688e+03^-	4.953e+04± 1.938e+00^-	4.953e+04± 4.427e+00^-	5.720e+04± 1.091e+04
F15	1.000e+02± 0.000e+00^≈	1.000e+02± 1.524e-13^≈	1.000e+02± 2.81e-13^≈	1.000e+02± 3.235e-13^≈	1.000e+02± 2.055e-12^≈	1.000e+02± 1.059e-10
+/-/≈	7/2/6	10/2/3	11/3/1	9/3/3	9/3/3	-
Friedman	2.8333	4.7000	4.3000	3.1000	3.7000	2.3667

表8 D=50时各算法在CEC2015测试集上的实验结果 Table 8 Experimental results of different algorithms on CEC2015 dataset with D=50

由表7可看出, MABC-FG的综合排名依旧第一, 在F01和F02单峰函数上, MABC-FG在F01函数上除了与MGABC性能相当, 优于另外四种算法, 在F02函数上, MABC-FG弱于LL-ABC和iqABC.在F03~F05多峰函数上, MABC-FG的实验结果全部优于或相似于其它算法.在F06~F15复杂函数上, MABC-FG也具有较优性能, 仅在F14函数上弱于ABCG、LL-ABC和iqABC.此外, ECABC和MGABC没有在一个函数上优于MABC-FG.这是因为MABC-FG是从个体层面上设计多策略机制, 不同分组都具有不同特性, 在处理复杂问题时, 不同分组分工明确、相互合作, 提升性能.

由表8可看出, MABC-FG在D=50时依旧保持领先地位.Friedman检验结果中MABC-FG综合表现排名第一, 即随着问题维度的提升, MABC-FG依然具有较好性能.

由表5~表8的统计结果可看出, 无论是在单峰函数上还是多峰函数上, MABC-FG综合表现最优, 尤其在CEC2015测试集上更明显.这说明雇佣蜂阶段使用的基于适应度分组的多策略机制和在观察蜂阶段设计的由全局最优个体和精英个体引导的解搜索方程相互配合, 能明显提升ABC的性能.

总之, 上述实验验证MABC-FG的性能具有较强的竞争力, 原因如下:1)雇佣蜂阶段将种群按照适应度分为A、B和C组, A组负责寻找优秀个体, B组负责使种群向精英群体移动, C组负责全局勘探并逐步向A组移动, 同时C组能有效增加种群多样性, 三组分工明确、相互配合, 能有效平衡勘探与开采.2)观察蜂阶段使用全局最优个体和精英个体引导种群搜索, 这些个体由于具有良好的适应度, 因此其区域具有很高的开采价值, 在这些区域搜索能提高搜索效率.

3.4 运行时间对比

相比ABC, MABC-FG主要是在雇佣蜂阶段对种群中的个体进行排序, 会消耗一定的计算资源.为了更准确地评估MABC-FG的运行时间, 本节给出算法的时间复杂度和实际CPU运行时间.设种群规模为SN, 问题维度为D, 在一次迭代过程中, 对种群个体进行适应度排序的时间复杂度为O(SN· log(SN)).因为ABC的时间复杂度为O(SN· D), 所以MABC-FG的整体时间复杂度为

O(SN· log(SN)+SN· D).

考虑到D通常情况下会远大于log(SN), 则MABC-FG和ABC的时间复杂度均为O(SN· D).

进一步分析MABC-FG的运行时间, 记录其在CEC2013测试集上的实际CPU运行时间, 并与3.3节的五种算法进行对比.为了确保公平对比, 所有算法均在每个测试函数上独立运行30次, 以平均CPU运行时间作为最终结果.

算法运行平台的配置信息如下:CPU Inter(R)Core i7-10700H, 内存16 GB, 操作系统Microsoft Windows 10 Professional, 编程语言Java.

各算法的CPU运行时间如表9所示, 表中Avg.为算法在28个测试函数上的总体平均时间, 最后一行为总体平均时间的排名情况.由表可得, MABC-FG、iqABC、ECABC排在前三位, 而LL-ABC、MGABC、ABCG排在后三位.从实验结果可知, MABC-FG无论在单峰函数、多峰函数、复杂函数上运行时间都较短, 并且这种优势在复杂函数上更明显.这是因为MABC-FG并未引入过多的造成额外计算开销的操作.综上可知, MABC-FG在运行时间上同样也具有竞争力.

表9 D=30时各算法的CPU运行时间 Table 9 CPU running time of different algorithms on CEC2013 dataset with D=30 s

3.5 在调频声波合成问题上的应用

本节选择一个实际优化问题测试MABC-FG.调频(Frequency Modulation, FM)声波合成在音乐领域中具有重要作用, 调频合成器是一个6维高度复杂的多峰优化问题, 数学表达式如下:

$y (t) = a_{1} \sin \sin (ω_{1} tθ + a_{2} \sin \sin (ω_{2} t θ + a_{3} \sin \sin (ω_{3} t θ)))$ ,

$y_{0} (t) = 1.0 \sin \sin (5.0 tθ - 1.5 \sin \sin (4.8) tθ + 2.0 \sin \sin (4.9 tθ))$

其中, θ =2π /100, X={a₁, ω ₁, a₂, ω ₂, a₃, ω ₃}为问题的决策向量, a_i和ω _i的取值范围为[-6.4, 6.35], i=1, 2, 3.

该问题优化的目标是y(t)尽可能接近y₀(t), 适应度函数为:

$f (X) = \sum_{t = 0}^{100} {(y (t) - y_{0} (t))}^{2}$ .

可以看出, 函数的最优解f(X_best)=0.在本次实验中, D=6, 其余的参数设置和3.3节相同, 记录30次运行结果.具体实验结果如表10所示, 表中黑体数字表示最优值.由表可看到, MABC-FG的平均误差最小, 综合表现最优.

表10 D=50时各算法在FM问题上的实验结果 Table 10 Experimental results of different algorithms for FM problems with D=50

4 结束语

为了克服经典ABC仅采用一种解搜索方程和对所有个体都一视同仁的缺点, 本文提出基于适应度分组的多策略人工蜂群算法(MABC-FG).首先, 根据个体适应度的大小将种群分为三组, 针对每组特性, 为每组个体设计不同特征的解搜索方程, 更好地平衡整个种群的勘探和开采能力.此外, 适应度较差的分组还兼有保持种群多样性的作用, 各组之间并非相互独立, 在勘探或开采的同时也向更优个体学习.与此同时, 观察蜂阶段使用全局最优个体和精英个体引导种群快速向适应度值较好的区域移动, 确保该区域被充分开采.为了验证MABC-FG的性能, 设计5组不同的实验, 验证本文策略的有效性, 并通过对比实验验证本文算法具有较强的竞争力.今后将考虑把本文算法应用于求解更多的实际优化问题, 如图像分割问题等.

本文责任编委付俊

Recommended by Associate Editor FU Jun

参考文献

文献选项

[1]	周新宇, 吴志健, 王明文. 基于正交实验设计的人工蜂群算法. 软件学报, 2015, 26(9): 2167-2190. (ZHOU X Y, WU Z J, WANG M W. Artificial Bee Colony Algorithm Based on Orthogonal Experimental Design. Journal of Software, 2015, 26(9): 2167-2190. ) [本文引用:1]
[2]	CUI L Z, ZHANG K, LI G H, et al. Modified Gbest-Guided Artificial Bee Colony Algorithm with New Probability Model. Soft Computing, 2018, 22(7): 2217-2243. [本文引用:1]
[3]	AHN C W, RAMAKRISHNA R S. Elitism-Based Compact Genetic Algorithms. IEEE Transactions on Evolutionary Computation, 2003, 7(4): 367-385. [本文引用:1]
[4]	李笠, 王万良, 徐新黎, 等. 基于网格排序的多目标粒子群优化算法. 计算机研究与发展, 2017, 54(5): 1012-1023. (LI L, WANG W L, XU X L, et al. Multi-objective Particle Swarm Optimization Based on Grid Ranking. Journal of Computer Research and Development, 2017, 54(5): 1012-1023. ) [本文引用:1]
[5]	XIA X W, TONG L, ZHANG Y L, et al. NFDDE: A Novelty-Hybrid-Fitness Driving Differential Evolution Algorithm. Information Sciences, 2021, 579: 33-54. [本文引用:1]
[6]	YAVUZ G, DURMUŞ B, AYDIN D. Artificial Bee Colony Algorithm with Distant Savants for Constrained Optimization. Applied Soft Computing, 2022, 116. DOI: DOI:10.1016/j.asoc.2021.108343. [本文引用:1]
[7]	KARABOGA D, BASTURK B. On the Performance of Artificial Bee Colony(ABC) Algorithm. Applied Soft Computing, 2008, 8(1): 687-697. [本文引用:1]
[8]	PAN Q K, WANG L, LI J Q, et al. A Novel Discrete Artificial Bee Colony Algorithm for the Hybrid Flowshop Scheduling Problem with Makespan Minimisation. Omega, 2014, 45: 42-56. [本文引用:1]
[9]	徐晓飞, 刘志中, 王忠杰, 等. S-ABC——面向服务领域的人工蜂群算法范型. 计算机学报, 2015, 38(11): 2301-2317. (XU X F, LIU Z Z, WANG Z J, et al. S-ABC-Service Domain-Oriented Artificial Bee Colony Algorithm Paradigm. Chinese Journal of Computers, 2015, 38(11): 2301-2317. ) [本文引用:1]
[10]	GAO W F, SHENG H L, WANG J, et al. Artificial Bee Colony Algorithm Based on Novel Mechanism for Fuzzy Portfolio Selection. IEEE Transactions on Fuzzy Systems, 2019, 27(5): 966-978. [本文引用:2]
[11]	LIU H, XU B, LU D J, et al. A Path Planning Approach for Crowd Evacuation in Buildings Based on Improved Artificial Bee Colony Algorithm. Applied Soft Computing, 2018, 68: 360-376. [本文引用:1]
[12]	WANG X H, ZHANG Y, SUN X Y, et al. Multi-objective Feature Selection Based on Artificial Bee Colony: An Acceleration Approach with Variable Sample Size. Applied Soft Computing, 2020, 88. DOI: DOI:10.1016/j.asoc.2019.106041. [本文引用:1]
[13]	GUPTA S, DEEP K. Hybrid Sine Cosine Artificial Bee Colony Algorithm for Global Optimization and Image Segmentation. Neural Computing and Applications, 2020, 32(13): 9521-9543. [本文引用:1]
[14]	XING H L, SONG F H, YAN L S, et al. A Modified Artificial Bee Colony Algorithm for Load Balancing in Network-Coding-Based Multicast. Soft Computing, 2019, 23(15): 6287-6305. [本文引用:1]
[15]	ZHU G P, KWONG S. Gbest-Guided Artificial Bee Colony Algorithm for Numerical Function Optimization. Applied Mathematics and Computation, 2010, 217(7): 3166-3173. [本文引用:1]
[16]	周新宇, 吴志健, 邓长寿, 等. 一种邻域搜索的人工蜂群算法. 中南大学学报(自然科学版), 2015, 46(2): 534-546. (ZHOU X Y, WU Z J, DENG C S, et al. Neighborhood Search-Based Artificial Bee Colony Algorithm. Journal of Central South University(Science and Technology), 2015, 46(2): 534-546. ) [本文引用:1]
[17]	CUI L Z, LI G H, LIN Q Z, , et al. A Novel Artificial Bee Colony Algorithm with Depth-First Search Framework. A Novel Artificial Bee Colony Algorithm with Depth-First Search Framework and Elite-Guided Search Equation. Information Sciences, 2016, 367/368: 1012-1044. [本文引用:1]
[18]	WANG H, WU Z J, RAHNAMAYAN S, et al. Multi-strategy Ensemble Artificial Bee Colony Algorithm. Information Sciences, 2014, 279: 587-603. [本文引用:1]
[19]	XIANG W L, MENG X L, LI Y Z, et al. An Improved Artificial Bee Colony Algorithm Based on the Gravity Model. Information Sciences, 2018, 429: 49-71. [本文引用:2]
[20]	CHEN X, TIANFIELD H, LI K J. Self-Adaptive Differential Artificial Bee Colony Algorithm for Global Optimization Problems. Swarm and Evolutionary Computation, 2019, 45: 70-91. [本文引用:1]
[21]	KARABOGA D. An Idea Based on Honey Bee Swarm for Numerical Optimization. Technical Report, TR06. Kayseri, Türkiye: Erciyes University, 2005. [本文引用:1]
[22]	YAO X, LIU Y, LIN G M. Evolutionary Programming Made Faster. IEEE Transactions on Evolutionary Computation, 1999, 3(2): 82-102. [本文引用:1]
[23]	LIANG J J, QU B Y, SUGANTHAN P N, et al. Problem Definitions and Evaluation Criteria for the CEC 2013 Special Session on Real-Parameter Optimization. Technical Report, 201212. Zhengzhou, China: Zhengzhou University, 2013. [本文引用:1]
[24]	LIANG J J, QU B Y, SUGANTHAN P N, et al. Problem Definitions and Evaluation Criteria for the CEC 2015 Competition on Learning-Based Real-Parameter Single Objective Optimization. Technical Report, 201411A. Zhengzhou, China: Zhengzhou University, 2014. [本文引用:1]
[25]	ASLAN S, BADEM H, KARABOGA D. Improved Quick Artificial Bee Colony(iqABC) Algorithm for Global Optimization. Soft Computing, 2019, 23(24): 13161-13182. [本文引用:1]
[26]	ZHOU X Y, LU J X, HUANG J H, et al. Enhancing Artificial Bee Colony Algorithm with Multi-elite Guidance. Information Sciences, 2021, 543: 242-258. [本文引用:1]
[27]	KONG D P, CHANG T Q, DAI W J, , et al. An Improved Artificial Bee Colony Algorithm Based on Elite Group Guidance. An Improved Artificial Bee Colony Algorithm Based on Elite Group Guidance and Combined Breadth-Depth Search Strategy. Information Sciences, 2018, 442/443: 54-71. [本文引用:1]

2015

0.0

... 在科学研究和工程应用中,很多实际问题可转化为优化问题进行求解,但其中大部分问题都是高度复杂的,通常有非凸、多峰、强约束等特点,致使一些经典的最优化方法往往难以求解^[1,2] ...

2018

0.0

2003

0.0

... 作为一类算法,进化算法包含多种不同的算法范例,常见的有:遗传算法(Genetic Algorithm, GA)^[3]、粒子群优化算法(Particle Swarm Optimiza-tion, PSO)^[4]、差分进化算法(Differential Evolution, DE)^[5]、人工蜂群算法(Artificial Bee Colony, ABC)^[6]等 ...

2017

0.0

2021

0.0

2022

0.0

2008

0.0

... 相比GA、PSO、DE,ABC的性能相当,具有竞争力^[7],并且结构简单、控制参数较少 ...

2014

0.0

... 目前,ABC已成功应用于求解多种不同的实际优化问题,包括:流水车间调度问题^[8]、服务计算优化问题^[9]、投资组合优化问题^[10]、人群疏散路径规划问题^[11]、特征选择问题^[12]、图像分割问题^[13]、网络负载均衡问题^[14]等 ...

2015

0.0

2019

0.0

... 3 实验结果对比本节选择近年来提出的5个相关改进ABC作为对比算法:1)LL-ABC^[10] ...

2018

0.0

2020

0.0

2020

0.0

2019

0.0

2010

0.0

... Zhu等^[15]提出GABC(Gbest-Guided ABC, GABC),在解搜索方程中把种群的最优个体Gbest添加为引导项 ...

2015

0.0

... 周新宇等^[16]提出邻域搜索的ABC,在环形邻域拓扑结构中选择最优个体进行开采,利用邻域信息引导算法搜索 ...

2016

0.0

... Cui等^[17]设计基于精英个体引导的解搜索方程,把具有较好适应度的若干个体视为精英个体,再从中任选一个精英个体作为解搜索方程的目标个体 ...

2014

0.0

... Wang等^[18]提出多策略集成的改进ABC,采用3种不同的解搜索方程,用于构建策略候选池,在初始化阶段为个体随机分配一种解搜索方程,再根据子代个体质量动态选择不同的解搜索方程 ...

2018

0.0

... Xiang等^[19]提出ABCG,在雇佣蜂阶段引入引力模型,选择引力最大的邻域个体生成后代个体,而在观察蜂阶段采用随机引导方式、反向学习、重新初始化三种策略 ...

... 2)ABCG^[19] ...

2019

0.0

... Chen等^[20]将3种解搜索方程集成到ABC中,提出自适应多策略机制,每个个体可自适应地选择其中的一种策略 ...

2005

0.0

... 1 经典人工蜂群算法经典ABC^[21]是根据蜜蜂寻找蜜源的搜索过程提出的一种进化算法 ...

1999

0.0

... 536]²,具体定义可参考文献[22] ...

2013

0.0

... 3 实验及结果分析在测试函数方面,本文选取2套权威的测试函数:CEC2013测试集^[23]和CEC2015测试集^[24] ...

2014

0.0

... 3 实验及结果分析在测试函数方面,本文选取2套权威的测试函数:CEC2013测试集^[23]和CEC2015测试集^[24] ...

2019

0.0

... 3)iqABC(Improved Quick ABC)^[25] ...

2021

0.0

... 4)MGABC^[26] ...

2018

0.0

... 5)ECABC^[27] ...