引用本文
郭瑞泽, 魏巍, 崔军彪, 冯凯. 图自适应原型网络的小样本节点分类方法. 模式识别与人工智能, 2022,35(8): 743-753
GUO Ruize, WEI Wei, CUI Junbiao, FENG Kai. Few-Shot Node Classification Method of Graph Adaptive Prototypical Networks. PATTERN RECOGNITION AND ARTIFICIAL INTELLIGENCE, 2022,35(8): 743-753.  
Doi: 10.16451/j.cnki.issn1003-6059.202208005
Permissions
Copyright©2022, 《模式识别与人工智能》编辑部
《模式识别与人工智能》编辑部
图自适应原型网络的小样本节点分类方法
郭瑞泽1, 魏巍1,2, 崔军彪1, 冯凯1,2
1.山西大学 计算机与信息技术学院 太原 030006
2.山西大学 计算智能与中文信息处理教育部重点实验室 太原 030006
通信作者:

魏 巍,博士,教授,主要研究方向为数据挖掘、机器学习.E-mail:weiwei@sxu.sdu.cn.

作者简介:

郭瑞泽,硕士研究生,主要研究方向为机器学习.E-mail:1669612095@qq.com.

崔军彪,博士研究生,主要研究方向为数据挖掘、机器学习.E-mail:945546899@qq.com.

冯 凯,博士,副教授.主要研究方向为互连网络与图.E-mail:fengkai@sxu.edu.cn.

收稿日期: 2022-03-21 接受日期: 2022-08-31
资助项目: 国家自然科学基金项目(No.61976184,61772323)资助
摘要

小样本节点分类旨在让机器从少量节点中学习到快速认知和分类的能力,现有小样本节点分类模型的分类性能容易受到图编码器提取的节点特征不够准确和子任务中支撑集实例的类内异常值的影响.为此,文中提出图自适应原型网络(Graph Adaptive Prototypical Networks, GAPN)的小样本节点分类方法.首先,将图中的节点通过图编码器嵌入度量空间中.然后,将全局重要度和局部重要度的融合结果作为支撑集实例的权重计算类原型,使查询集实例能自适应地学习更鲁棒的类原型.最后,计算自适应任务的类原型与查询集实例之间距离产生的分类概率,最小化分类概率和真实标签间的正间隔损失,反向更新网络参数,学习到更有判别性的节点特征.在常用图数据集上的实验表明,文中方法具有较优的节点分类性能.

关键词: 小样本学习; 节点分类; 图神经网络; 原型网络
中图分类号:TP391
Few-Shot Node Classification Method of Graph Adaptive Prototypical Networks
GUO Ruize1, WEI Wei1,2, CUI Junbiao1, FENG Kai1,2
1. School of Computer and Information Technology, Shanxi University, Taiyuan 030006
2. Key Laboratory of Computational Intelligence and Chinese Information Processing of Ministry of Education, Shanxi University, Taiyuan 030006
Corresponding author:
WEI Wei, Ph.D., professor. His research interests include data mining and machine learning.

About Author:
GUO Ruize, master student. Her research interests include machine learning.
CUI Junbiao, Ph.D. candidate. His research interests include data mining and machine learning.
FENG Kai, Ph.D., associate professor. His research interests include interconnection network and graph.

Fund:National Natural Science Foundation of China(No.61976184,61772323)
Abstract

Few-shot node classification aims to make machines recognize and classify quickly from a small number of nodes. Existing few-shot node classification models are easily affected by the inaccurate node features extracted by encoders and the intra-class outliers of query set instances in sub-tasks. Therefore, a graph adaptive prototypical networks(GAPN) model is proposed. Firstly, the nodes are embedded into the metric space by the graph encoder. Then, prototypes are computed by fusing the global importance and the local importance as weight of support set instances, and thus more robust prototypes can be learned adaptively for query set instances. Finally, the distance between the class prototypes of the adaptive task and the query set instance is calculated to generate the classification probability. By minimizing the positive marginal feedback loss between the classification probability and the true label, network parameters are updated backward and more discriminative node features can be learned. Experimental results on common graph datasets show that GAPN model yields better node classification performance.

Key words: Key Words Few Shot Learning; Node Classification; Graph Neural Networks; Prototypical Networks

电子商务网络[1]、引文网络[2]和社交网络[3] 等属性网络广泛存在于现实世界中.节点分类作为这类网络的关键任务之一, 可预测用户对于商品的购买意图、论文主题及帖子的归属社区.图表示学习可学习保留图数据的拓扑结构和语义信息的低维表征, 为节点分类等下游任务创造条件[4, 5, 6].因此, 利用图表示学习方法进行节点分类已成为现阶段研究热点, 受到学者们的广泛关注.

节点分类任务通常为监督学习问题或半监督学习问题[7], 依赖一定数量有标记节点实现图神经网络(Graph Neutral Networks, GNN)的训练[8].但对于许多现实应用中的属性网络, 标记节点的数量通常很少[2], 传统的GNN因标记节点不足产生过拟合问题, 泛化能力显著下降.因此, 研究属性网络上的小样本节点分类问题具有重要的科学意义和应用价值[8, 9, 10].

元学习[10]可快速学习适应新任务的可迁移知识, 已成功应用于图像和文本的小样本学习[11, 12, 13, 14, 15].基于元学习的小样本学习模型是基于优化方法的模型, 如基于长短期记忆网络的元学习器(Meta-Learner Based on Long Short-Term Memory, Meta-Learner LSTM)[16]和模型无关的元学习器(Model-Agnostic Meta-Learning, MAML)[10], 均是通过梯度下降法得到优化后的参数.

此外, 基于度量的小样本学习也是一类重要的方法[17], 该类方法尝试学习跨越不同任务的查询集实例和支撑集实例间可推广的度量关系, 如孪生网络(Siamese Neural Networks, SN)[11]、匹配网络(Matching Networks, MN)[12]、原型网络(Prototypical Networks, PN)[13]和关系网络(Relation Networks, RN)[14].

目前, 已有的小样本节点分类的工作大多属于基于元学习的方法, 主要通过基类(大量节点的类别)组成的元训练任务学习可转移的先验知识, 进而应用于新类(少量节点的类别), 实现元测试任务.但传统的小样本学习模型无法捕获图数据的拓扑结构, 得到的节点特征不含结构信息, 会导致节点分类的精度较差.

为此, 研究者提出一些图小样本学习方法, 致力于减少方法对标记节点数量的依赖[18].Yao等[19]提出GFL(Graph Few-Shot Learning), 用于标签集共享的图小样本节点分类任务, 利用辅助图的先验知识提高目标图的分类精度.但这种方法在测试阶段未考虑未见类, 不能直接用于小样本节点分类任务.Zhou等[7]提出MAML-GNN(GNN with Meta-Lear-ning), 结合GNN与元学习的MAML, 应用到节点分类任务.Wang等[20]提出AMM-GNN(Attribute Ma-tching Meta-Learning GNN), 是MAML-GNN的改进版本, 利用属性级别的注意力机制捕获每个元任务的不同重要信息.Ding等[21]提出GPN(Graph Prototypical Networks), 结合GNN与度量学习的PN, 应用到节点分类任务.

之后, 学者们对图编码器进行优化, 得到更好的面向节点分类任务的特征表示, Liu等[22]提出RALE(Relative and Absolute Location Embedding), 为节点分配基于图的绝对位置和基于任务的相对位置, 获得更好的特征表示, 实现节点分类任务.因此, 通过图卷积网络(Graph Convolutional Network, GCN)提取的节点特征对于小样本节点的分类性能至关重要.另外, 由于子任务中查询集实例数量极少, 现有的小样本节点分类模型均容易受到查询集实例类内异常值的影响.

为了解决上述问题, 本文提出图自适应原型网络(Graph Adaptive Prototypical Networks, GAPN)的小样本节点分类方法, 采用GCN提取图数据的节点特征, 加权计算支撑集中的实例, 得到类原型, 可有效减少类内异常值对类原型的影响, 使查询集实例自适应地学习更鲁棒的类原型.加权融合全局重要度和局部重要度, 得到支撑集实例的权重.支撑集实例的全局重要度基于其对应节点在图中的重要程度定义; 局部重要度基于子任务中支撑集实例与查询集实例的重构误差定义.在常用的图数据集上的实验表明, 在小样本节点分类任务上, 本文方法具有一定的优越性.

1 问题定义

在图数据上进行小样本节点分类任务, 形式上, 输入图可表示为

G=(A, X, C).

其中:A={0, 1}|V|× |V|表示邻接矩阵, 代表图的拓扑结构, A中元素为1时表示节点间存在边; X∈ R|V|×dX表示特征矩阵, dX表示特征维数; C表示节点所属类别的集合.

在小样本节点分类设置中,

C=Cb∪ Cn,

其中, Cb表示基类, Cn表示新类, 基类Cb中有足够数量的标记节点被用于训练模型, 随后, 给定N个新类Cn的任意子集, 目标是为新类Cn训练每类只有K个(K通常取3, 5)标记节点的分类器, 可预测N类中剩余未标记节点的标签, 这被称为N-way K-shot节点分类问题.

采用元学习范式处理小样本节点分类问题.基类Cb作为元训练集, 新类Cn作为元测试集,

Cb∩ Cn=Ø .

Cb和Cn都被表述为一系列的任务(Episodes).

从基类Cb中采样N类构造元训练任务t, t由支持集St和查询集Qt组成, St由类别N中每类随机抽取的K个节点组成, 表示为

St={(v1, y1), (v2, y2), …, (vN× K, yN× K)},

Qt由N类中每类抽取Q个剩余节点组成, 表示为

Qt={( v1* , y1* ), ( v2* , y2* ), …, ( vN×Q* , yN×Q* )}.

支持集St为任务t中被标记的节点, 每个元训练任务的目标都是最小化查询集Qt的预测概率和真实标签之间的分类损失.

给定一系列的元训练任务, 其目标是学习一个可应用于元测试任务中含有可转移先验知识的分类器模型.

类似的N-way K-shot, 在新类Cn中对元测试任务t'采样, t'由支持集St'和查询集Qt'组成, 通过分类器模型可预测查询集Qt'的标签[21].

下文中的符号说明如表1所示.

表1 主要符号及相关说明 Table 1 Main symbols and related descriptions
2 图自适应原型网络的小样本节点分类方法

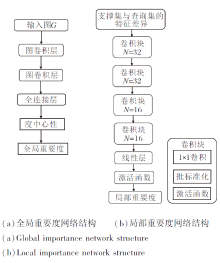
本节提出自适应原型网络(GAPN)的小样本节点分类方法, 主要包括图编码器、自适应原型网络、小样本节点分类, 框架如图1所示.

图1 本文方法框架图Fig.1 Framework of the proposed method

1.1 图编码器

为了从网络中学习节点的嵌入表示, 本文使用图编码器捕获图数据的节点特征和拓扑结构.具体地, 图编码器使用GNN提取节点特征, 每个节点被转换为低维的特征表示.GNN由2个GCN层组成, 每层GCN均遵循邻域聚合的准则, 通过递归组合和聚合邻居节点更新中心节点的特征, 并递归组合和聚合邻居节点, 更新中心节点特征.GCN层定义为[20]

$\begin{align} & h_{i}^{l}=\operatorname{C}\text{OM}BIN{{E}^{l}}\left( h_{i}^{l-1}, h_{{{\mathcal{N}}_{i}}}^{l} \right) \\ & h_{{{\mathcal{N}}_{i}}}^{l}=\text{ AGGREGATE}{{\text{ }}^{l}}\left( \left\{ h_{j}^{l-1}\mid \forall j\in {{\mathcal{N}}_{i}}\cup {{v}_{i}} \right\} \right) \\ \end{align}$

其中, hil表示层l中节点i的表示, Ni表示节点i相邻节点的集合.

组合和聚合是GCN的两个关键过程.通过两层GCN, 得到的节点特征已捕获远距离的节点依赖关系, 最终学习网络节点的特征表示:

$z\text{=}\widetilde{A}\operatorname{ReLU}\left( \widetilde{A}XW_{0}^{{}} \right)W_{1}^{{}}$ (1)

其中, W0∈ RdX×F表示GNN第1层参数, W1∈ RF×dM表示GNN第2层参数,

$\widetilde{A}={{\widetilde{D}}^{-\frac{1}{2}}}\widetilde{A}{{\widetilde{D}}^{-\frac{1}{2}}}$

表示正则化后的拉普拉斯矩阵,

$\widetilde{A}=A+I, \widetilde{D}=D+I$.

在本文中, fθ ∶ RdX→ RdM表示图编码器.

1.2 自适应原型网络

利用图编码器函数 fθ ∶ RdX→ RdM得到子任务内部支撑集实例和查询集实例的dM维嵌入表示, 一个类原型由这个类所有的支撑集实例在度量空间中的特征向量求平均得到, 计算类原型

pc= 1Stc∑i∈Stczi∈ RdM, (2)

其中, Stc表示c类的支撑集实例子集, zi表示节点i的最终特征表示.

式(2)将支撑集实例的平均向量作为类原型, 但它忽略支撑集实例的重要性差异, 而小样本模型在样本有限时对支撑集实例异常值非常敏感.为了应对此问题, 本文提出图自适应原型网络(GAPN), 将全局重要度和局部重要度的融合结果作为支撑集实例的权重, 实现原型的计算, 可有效降低类内异常值对类原型的影响, 使每个查询集实例自适应学习更鲁棒的原型.在本文中:基于支撑集实例对应节点在图中的重要程度定义为全局重要度, 由节点的特征向量与度中心性结合得到; 基于子任务中支撑集实例与查询集实例的重构误差定义为局部重要度, 由两个特征向量的相似度度量网络作为重构误差表达式计算得到.

全局重要度与局部重要度的定义如下.

将节点i的特征输入两层GCN并更新, 再输入全连接层FC, 得到节点i的全局重要度:

${{\hat{\alpha} }_{i}}\text{=FC}\left( \text{ReLU}\left( \operatorname{ReLU}\left( \widetilde{A}XW_{2}^{{}} \right)W_{3}^{{}} \right) \right)$,

其中, W2∈ RdX×F, W3∈ RF×dM为GCN的参数.

由于节点在图中的重要程度与节点的度中心性呈正相关, 故最终图节点的全局重要度定义为 α︿i与节点度Cen(i)的结合:

α˜i=sigmoid(Cen(i)· α︿i),
Cen(i)=ln(degree(i)).

使用gφ (· )表示全局重要度网络, 具体结构为图2(a)所示.

图2 融合重要度网络结构Fig.2 Fusion importance network structure

在计算每个支撑集实例i的全局重要度 α˜i后, 使用Softmax函数得到归一化后的全局重要度:

α i= exp(α˜i)∑k∈Stcexp(α˜k). (3)

在子任务内部, 支撑集实例表示为{v1, v2, …, vN× K}, 之后通过度量网络计算针对每个查询集实例的局部重要度:

β i= exp(hλ(abs(z* -zi)))∑k∈Stcexp(hλ(abs(z* -zk))), (4)

其中, abs(· )表示绝对值函数, z* 表示单个查询集实例v* 的节点表征, hλ 表示计算相似度分数的度量网络.

局部重要度网络结构如图2(b)所示.该网络是由4个卷积块组成的卷积神经网络, 卷积块为1× 1卷积.

通过查询集实例与支撑集实例的重构误差定义局部重要度, 可使与查询集实例较远的支撑集实例获得较小的注意力, 并且重构误差的表达式由神经网络组成.可根据预测结果对网络进行参数更新.

将支撑集实例在图中的全局重要度α i和其针对查询集实例v* 的局部重要度β i融合, 得到针对查询集实例v* 的融合重要度:

γ i= exp(μβi+(1-μ)αi)∑k∈Stcexp(μβk+(1-μ)αk), (5)

其中, μ 为全局重要度和局部重要度比例的超参, 定义μ =0.5.

然后, 对于每类c, 为每个查询集实例v* 定义基于该查询集实例v* 的自适应原型:

pc= 1Stc∑i∈Stcγ izi, (6)

可为每个查询集实例获得更适应和鲁棒的原型.

1.3 小样本节点分类

在Episodic training的元学习范式下, 随机采样一个由N-way K-shot组成的子任务, 每个元训练任务的目标均是最小化查询集实例预测概率与真实标签间的分类损失.利用查询集实例v* 计算得到自适应原型pc, pc与查询集实例v* 的距离函数d产生v* 属于类c的概率分布:

$\begin{align} & p\left( c\mid v_{{}}^{* } \right)= \\ & \frac{\exp \left( -dis\left( z_{{}}^{* }, {{p}_{c}} \right) \right)}{\text{e}xp\left( -dis\left( z_{{}}^{* }, {{p}_{c}} \right) \right)\text{+}\sum\limits_{{{c}^{\prime }}\varsubsetneq c}{\exp }\left( -dis\left( z_{{}}^{* }, {{p}_{{{c}^{\prime }}}} \right) \right)\text{+}m} \\ \end{align}$

其中, dis∶ RdM× RdM→ [0, +¥ )表示平方欧氏距离.学习判别性的嵌入空间的直观想法是在异类支撑集实例和查询集实例之间增加正间隔距离m, 这有助于增加度量空间中的类间距离, 迫使嵌入为异类的实例提取更多可区分的节点特征.

最后通过随机梯度下降(Stochastic Gradient Descent, SGD)最小化负对数概率, 对于图编码器fθ ∶ RdX→ RdM, 参数更新如下:

L=- 1Qt∑(v* , y* )∈Qtln p(c|v* ). (7)

在元测试的子任务中, 一个新的分类任务与一个元训练基础分类任务是类似的, 将带有标签的支撑集实例和未标记的查询集实例输入训练好的模型, 将预测分类结果作为输出, 即

p(c|v* )= exp(-dis(z* , pc))∑c'exp(-dis(z* , pc')).

综上所述, 图自适应原型网络的小样本节点分类方法步骤如算法1所示.

算法1 图自适应原型网络的小样本节点分类方法

输入 图G=(A, X, C), 子任务数量T, 元测试的小样本节点分类任务T={St', Qt'}

输出 预测元测试查询集节点Q的标签

While t< T

t=t+1;

// 元训练的过程

采样元训练子任务Tt={St, Qt};

根据式(1)计算St和Qt的节点嵌入;

根据式(3)和式(4)计算支撑集实例的全局重要度和局部重要度;

根据式(5)和式(6)计算自适应原型pc;

根据式(7)最小化元训练的损失;

// 元测试的过程

计算St'和Qt'的节点嵌入和自适应原型;

预测元测试查询集节点Qt'的标签;

End

2 实验及结果分析

为了验证本文方法在小样本节点分类任务上的有效性, 在4个图数据集上进行实验, 并与经典方法进行对比.同时进行参数敏感度分析和消融实验.

2.1 实验数据集

本文选择在Amazon-Clothing[1]、Amazon-Elec-tronics[1]、DBLP[2]、Reddit[3]这4个具有大量节点类的数据集上评估方法的节点分类性能, 数据集的基本信息如表2所示.

表2 实验数据集基本信息 Table 2 Basic information of experimental datasets

Amazon-Clothing、Amazon-Electronics数据集上均是产品网络, 产品作为节点, “ 共同查看” 和“ 一起购买” 的关系作为边.DBLP数据集是引文网络, 论文作为节点, 论文间的引用关系作为边.Reddit数据集是社交网络, 帖子作为节点, 当两个帖子被同个用户评价时存在边.

2.2 实验设置

在PyTorch框架中实现本文方法, 具体地, 图编码器由2个维度分别为32和16的GCN层组成, 最终得到网络中的节点特征为16维.本文方法使用Adam(Adaptive Moment Estimation)优化器进行训练, 学习率最初在不同的数据集上设置不同, 权重衰减为0.000 5.全局重要度和局部重要度比例μ =0.5.正间隔距离m=1.0.

本文选择如下8种经典方法进行对比.

1)图节点嵌入方法:(1)DeepWalk[3].在获得随机游走的路径后, 可学习到节点嵌入.(2)Node2Vec[23].通过偏置获得随机游走的路径, 学习到节点嵌入后, 使用逻辑回归分类器进行多标签节点分类.(3)GCN[24].通过分层聚合和更新节点的特征进行节点分类.(4)GraphSAGE[2].通过分层采样聚合和更新节点的特征进行节点分类.

2)传统的小样本方法:(1)MN[12].基于度量的小样本学习方法, 目标是学习注意力加权的最近邻分类器.(2)PN[13].获取支撑集实例的平均向量, 计算每类的原型, 从而对查询集实例进行分类.(3)GNN-FSL(Graph Neutral Networks for Few-Shot Learning)[25].通过GNN进行信息传递, 然后进行分类.(4)DPGN(Distribution Propagation Graph Net-work)[26].通过分布图和实例图的双重网络对查询集实例进行节点分类.

3)小样本节点分类方法:(1)MAML-GNN[7].通过GNN将MAML扩展到图数据集上, 解决小样本节点分类问题.(2)GPN[21].通过GNN将原型网络扩展到图数据集上, 并学习到更多可迁移的知识进行节点分类.

2.3 对比实验结果

在4个小样本节点分类任务上, 即5-way 3-shot、5-way 5-shot、10-way 3shot、10-way 5-shot, 评估方法性能.查询集实例数目为15.实验采用广泛的准确率用于评估性能, 共运行1 000个迭代周期, 最终结果为平均10次随机抽样的50个元测试任务(共100个元测试任务)的结果, 具体准确率对比如表3~表6所示.

表3 各方法在Amazon-Clothing数据集上的准确率对比 Table 3 Accuracy comparison of different methods on Amazon-Clothing dataset %
表4 各方法在Amazon-Electronics数据集上的准确率对比 Table 4 Accuracy comparison of different methods on Amazon-Electronics dataset %
表5 各方法在DBLP数据集上的准确率对比 Table 5 Accuracy comparison of different methods on DBLP dataset %
表6 各方法在Reddit数据集上的准确率对比 Table 6 Accuracy comparison of different methods on Reddit dataset %

从综合的角度上进行分析, 结论如下.

1)图节点嵌入方法在小样本节点分类任务上的性能较差, 因其需要使用学习的节点表示训练监督分类器, 而这些节点表示依赖于大量标记数据以获得良好的性能.

2)传统的小样本方法虽在小样本图像分类任务上取得成功, 但在小样本节点分类上均表现很差, 主要原因是这些方法不能捕获图数据节点间的拓扑关系, 并用于学习节点表示.

3)MAML-GNN和GPN将GNN与元学习、度量学习结合进行小样本节点分类, 但GPN仅将支撑集实例对应的节点在图中的全局重要度作为权重计算原型, 忽略一次子任务中支撑集实例针对查询集实例的局部重要度, 得到的原型不够准确.

4)本文方法在4个图数据集的不同任务设置上均取得不错的分类结果.

2.4 参数敏感性分析

本节分析本文方法对支撑集类别数(N-way)、支撑集实例数(K-shot)和查询集实例数(Q-query)的敏感性.

实验还包括GPN-naive和GPN[21], 其中, GPN-naive仅使用原型网络执行节点分类任务.

N表示支撑集类别数, 设置N=5, 6, …, 9, 固定K=5, 在4个数据集上观察3种方法的准确率, 具体如图3所示.由图可观察到:

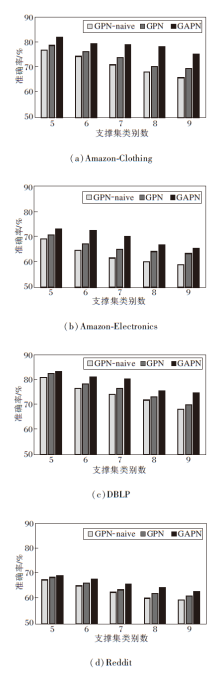图3 支撑集类别数对各方法准确率的影响Fig.3 Effect of the number of support set classes on accuracy of different methods

1)从综合角度上看, 不同方法的性能均随着支撑集类别数目的增加而降低, 这是因为更多的类别会导致更广泛的节点类被预测, 增加小样本节点分类的难度.

2)当N相同时, 可进一步观察到, GAPN始终优于GPN和GPN-naive, GPN-naive由平均支撑集实例的向量计算原型, 对类内异常值特别敏感, GPN的加权权重不够准确.由此表明本文方法为每个查询集实例生成的自适应原型可得到代表性的原型, 这说明方法的鲁棒性.

K表示支撑集实例数, 设置K=2, 3, …, 6, 固定N=5, 各方法在4个数据集上的准确率如图4所示.

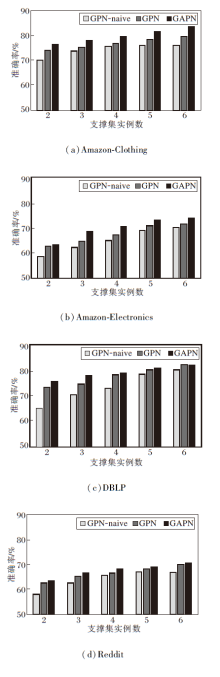图4 支撑集实例数对各方法准确率的影响Fig.4 Effect of the number of support set instances on accuracy of different methods

由图4可观察到:

1)不同方法的性能均随着K的增加而增加, 表明每类中更多的实例数目可产生更优的分类结果.

2)当K相同时, 相比GPN, 本文方法在大部分情况下都表现良好, 这表明为每个查询集实例得到自适应原型使节点分类结果更准确.

考虑训练阶段和测试阶段查询集实例数(Q)对实验结果的影响, 以5-way 5-shot节点分类任务为例, 设置Q=5, 10, 15, 各方法准确率变化情况如图5所示.

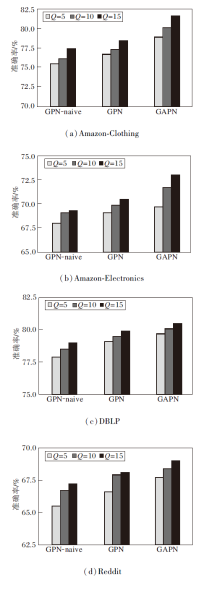图5 查询集实例数对各方法准确率的的影响Fig.5 Effect of the number of query set instances on accuracy of different methods

由图5可观察到:

1)训练过程中增加查询集实例数可在所有模型上实现性能增益, 较大的查询集实例数可学习更好的元训练任务的知识, 得到更好的泛化能力.

2)当Q相同时, 本文方法预测准确率最高, 此结果得益于由全局重要度和局部重要度融合得到的自适应原型可提高小样本节点分类的准确率.

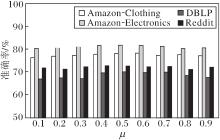
另外, 在4个数据集上分析全局重要度和局部重要度参数μ 对准确率的影响, 以5-way 5-shot为例, 准确率对比如图6所示.

图6 μ 对准确率的影响Fig.6 Effect of parameter μ on accuracy

由图6可知, 在μ 在0.5左右时, 全局重要度和局部重要度的共同调和, GAPN可取得相对较高的准确率.

2.5 消融实验结果

为了验证本文方法中全局重要度和局部重要度在小样本节点分类上的有效性, 设置小样本节点变体GAPN-G和GAPN-L, GAPN-G仅包含方法中的全局重要度, GAPN-L仅包含方法中的局部重要度.

以5-way 3-shot、5-way 5-shot、10-way 3-shot和10-way 5-shot节点分类任务为例, GAPN-G、GAPN- L、GAPN在3个数据集上计算准确率, 具体数值对比如表7所示.

表7 各方法在4个数据集上的准确率对比 Table 7 Accuracy comparison of different methods on 4 datasets %

由表7可得, GAPN-G和GAPN-L的准确率均比本文方法降低约1%~2%, 本文方法融合全局重要度和局部重要度作为支撑集实例的权重计算原型, 减少类内异常值对原型的影响, 得到更准确的原型用于节点分类任务.

GAPN-G仅使用全局重要度, 准确率低于仅使用局部重要度的GAPN-L, 由此可知支撑集实例对应的节点在图中的全局重要度在针对子任务时不够准确, 在全局重要度和局部重要度调和下可为查询集实例自适应地学习更鲁棒的原型.

此外, 为了验证正间隔距离m对于准确率的影响, 构造变体GAPN-W/O margin, 即本文方法中不包含正间隔距离.

以5-way 5-shot节点分类任务为例, 在4个数据集上的准确率对比如表8所示.

表8 正间隔距离对各方法准确率的影响 Table 8 Effect of positive marginal distances on accuracy of different methods %

由表8可知, 正间隔距离有助于增加度量空间中的类间距离, 迫使嵌入为异类的实例提取更多可区分的节点特征, 缓解节点特征准确与否对分类性能的制约.

3 结束语

本文提出图自适应原型网络(GAPN)的小样本节点分类方法, 将图中的节点通过图编码器嵌入度量空间中, 全局重要度和局部重要度的融合结果作为支撑集实例的权重计算类原型, 使查询集实例能自适应地学习更鲁棒的类原型.此外, 训练时在度量空间的异类支撑集实例和查询集实例间加入正间隔距离, 使学到的节点特征具有判别性.4个通用图数据集上的实验表明, 在不同设置的小样本节点分类任务中, 本文方法性能较优.今后可考虑结合子任务进行图编码器优化, 从而提高小样本节点分类的准确率.

本文责任编委 陈松灿

Recommended by Associate Editor CHEN Songcan

参考文献
[1] MCAULEY J, PANDEY R, LESKOVEC J. Inferring Networks of Substitutable and Complementary Products // Proc of the 21st ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York, USA: ACM, 2015: 785-794. [本文引用:3]
[2] SINHA A, SHEN Z H, SONG Y, et al. An Overview of Microsoft Academic Service(MAS) and Applications // Proc of the 24th International Conference on World Wide Web. New York, USA: ACM, 2015: 243-246. [本文引用:4]
[3] PEROZZI B, AL-RFOU R, SKIENA S. DeepWalk: Online Lear-ning of Social Representations // Proc of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York, USA: ACM, 2014: 701-710. [本文引用:3]
[4] SCARSELLI F, GORI M, TSOI A C, et al. The Graph Neural Network Model. IEEE Transactions on Neural Networks, 2009, 20(1): 61-80. [本文引用:1]
[5] HAMILTON W L, YING R, LESKOVEC J. Inductive Representation Learning on Large Graphs // Proc of the 31st International Conference on Neural Information Processing Systems. Cambridge, USA: The MIT Press, 2017: 1025-1035. [本文引用:1]
[6] VELIČKOVIĆ P, CUCURULL G, CASANOVA A, et al. Graph Attention Networks[J/OL]. [2022-03-21]. https://arxiv.org/pdf/1710.10903.pdf. [本文引用:1]
[7] ZHOU F, CAO C T, ZHANG K P, et al. Meta-GNN: On Few-Shot Node Classification in Graph Meta-Learning // Proc of the 28th ACM International Conference on Information and Knowledge Ma-nagement. New York, USA: ACM, 2019: 2357-2360. [本文引用:3]
[8] KIPF T N, WELLING M. Semi-Supervised Classification with Graph Convolutional Networks[J/OL]. [2022-03-21]. https://arxiv.org/pdf/1609.02907.pdf. [本文引用:2]
[9] QIAO L M, SHI Y M, LI J, et al. Transductive Episodic-Wise Adaptive Metric for Few-Shot Learning // Proc of the IEEE/CVF International Conference on Computer Vision. Washington, USA: IEEE, 2019: 3602-3611. [本文引用:1]
[10] YOON J, KIM T, DIA O, et al. Bayesian Model-Agnostic Meta-Learning // Proc of the 32nd International Conference on Neural Information Processing Systems. Cambridge, USA: The MIT Press, 2018: 7343-7353. [本文引用:3]
[11] KOCH G, ZEMEL R, SALAKHUTDINOV R, et al. Siamese Neural Networks for One-Shot Image Recognition[C/OL]. [2022-03-21]. https://www.cs.utoronto.ca/~rsalakhu/papers/oneshot1.pdf. [本文引用:2]
[12] VINYALS O, BLUNDELL C, LILLICRAP T, et al. Matching Networks for One Shot Learning // Proc of the 30th International Conference on Neural Information Processing Systems. Cambridge, USA: The MIT Press, 2016: 3637-3645. [本文引用:3]
[13] SNELL J, SWERSKY K, ZEMEL R S. Prototypical Networks for Few-Shot Learning // Proc of the 31st International Conference on Neural Information Processing Systems. Cambridge, USA: The MIT Press, 2017: 4077-4087. [本文引用:3]
[14] SUNG F, YANG Y X, ZHANG L, et al. Learning to Compare: Relation Network for Few-Shot Learning // Proc of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2018: 1199-1208. [本文引用:2]
[15] 代磊超, 冯林, 尚兴林, 等. 基于深度网络的快速少样本学习算法. 模式识别与人工智能, 2021, 34(10): 941-956.
(DAI L C, FENG L, SHANG X L, et al. Fast Few-Shot Learning Algorithm Based on Deep Network. Pattern Recognition and Artificial Intelligence, 2021, 34(10): 941-956. ) [本文引用:1]
[16] RAVI S, LAROCHELLE H. Optimization as a Model for Few-Shot Learning[C/OL]. [2022-03-21]. https://openreview.net/pdf?id=rJY0-Kcll. [本文引用:1]
[17] 刘鑫, 周凯锐, 何玉琳, 等. 基于度量的小样本分类方法研究综述. 模式识别与人工智能, 2021, 34(10): 909-923.
(LIU X, ZHOU K R, HE Y L, et al. Survey of Metric-Based Few-Shot Classification. Pattern Recognition and Artificial Intelligence, 2021, 34(10): 909-923. ) [本文引用:1]
[18] SUN K, LIN Z C, ZHU Z X. Multi-stage Self-Supervised Learning for Graph Convolutional Networks on Graphs with Few Labeled Nodes. Proceedings of the AAAI Conference on Artificial Intelligence, 2020, 34(4): 5892-5899. [本文引用:1]
[19] YAO H X, ZHANG C X, WEI Y, et al. Graph Few-Shot Learning via Knowledge Transfer. Proceedings of the AAAI Conference on Artificial Intelligence, 2020, 34(4): 6656-6663. [本文引用:1]
[20] WANG N, LUO M N, DING K Z, et al. Graph Few-Shot Learning with Attribute Matching // Proc of the 29th ACM International Conference on Information and Knowledge Management. New York, USA: ACM, 2020: 1545-1554. [本文引用:2]
[21] DING K Z, WANG J N, LI J D, et al. Graph Prototypical Networks for Few-Shot Learning on Attributed Networks // Proc of the 29th ACM International Conference on Information and Knowledge Management. New York, USA: ACM, 2020: 295-304. [本文引用:4]
[22] LIU Z M, FANG Y, LIU C H, et al. Relative and Absolute Location Embedding for Few-Shot Node Classification on Graph. Proceedings of the AAAI Conference on Artificial Intelligence, 2021, 35(5): 4267-4275. [本文引用:1]
[23] GROVER A, LESKOVEC J. Node2vec: Scalable Feature Learning for Networks // Proc of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York, USA: ACM, 2016: 855-864. [本文引用:1]
[24] BRUNA J, ZAREMBA W, SZLAM A, et al. Spectral Networks. Spectral Networks and Locally Connected Networks on Graphs[J/OL]. [2022-03-21]. https://arxiv.org/pdf/1312.6203.pdf. [本文引用:1]
[25] GARCIA V, BRUNA J. Few-Shot Learning with Graph Neural Net-works[J/OL]. [2022-03-21]. https://arxiv.org/pdf/1711.04043.pdf. [本文引用:1]
[26] YANG L, LI L L, ZHANG Z L, et al. DPGN: Distribution Propagation Graph Network for Few-Shot Learning // Proc of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2020: 13387-13396. [本文引用:1]