引用本文
楼嘉琪, 叶海良, 杨冰, 李明, 曹飞龙. 双分支多交互的深度图卷积网络. 模式识别与人工智能, 2022,35(8): 754-763
LOU Jiaqi, YE Hailiang, YANG Bing, LI Ming, CAO Feilong. Deep Graph Convolutional Network with Dual-Branch and Multi-interaction. PATTERN RECOGNITION AND ARTIFICIAL INTELLIGENCE, 2022,35(8): 754-763.  
Doi: 10.16451/j.cnki.issn1003-6059.202208006
Permissions
Copyright©2022, 《模式识别与人工智能》编辑部
《模式识别与人工智能》编辑部
双分支多交互的深度图卷积网络
楼嘉琪1, 叶海良1, 杨冰1, 李明2, 曹飞龙1
1.中国计量大学 理学院 应用数学系 杭州 310018
2.浙江师范大学 浙江省智能教育技术与应用重点实验室 金华 321004
通信作者:

叶海良,博士,讲师,主要研究方向为深度学习及其应用、图神经网络、机器学习及其应用.E-mail:yhl575@163.com.

作者简介:

楼嘉琪,硕士研究生,主要研究方向为深度学习、图神经网络等.E-mail:18757511013@163.com.

杨 冰,博士,讲师,主要研究方向为深度学习、图像处理.E-mail:bingyang0517@163.com.

李 明,博士,教授,主要研究方向为深度学习、图神经网络等.E-mail:mingli@zjnu.edu.cn.

曹飞龙,博士,教授,主要研究方向为深度学习、图像处理等.E-mail:feilongcao@gmail.com.

收稿日期: 2022-05-23 接受日期: 2022-08-31
资助项目: 国家自然科学基金项目(No.62006215,62176244,62172370)、浙江省自然科学基金项目(No.LQ20F030016)资助
摘要

图神经网络在节点分类任务中表现较优,然而,如何充分获取图数据的高阶语义特征并防止过平滑现象,仍是影响节点分类准确性的关键问题之一.为此,文中构造双分支多交互的深度图卷积网络,用于增强节点获取高阶语义特征的能力.首先,根据节点的特征信息对图结构进行重构.然后,利用原始图结构和构造重构图结构,建立一个双分支的网络架构,充分提取不同的高阶语义特征.同时,设计一个通道信息交互机制,学习不同分支的信息交互,进一步增强节点特征的多样性.最后,在多个基准数据集上的实验表明,文中网络可有效提升半监督节点分类任务的精度,并缓解过平滑现象.

关键词: 深度学习; 图神经网络; 特征提取; 节点分类
中图分类号:TP391
Deep Graph Convolutional Network with Dual-Branch and Multi-interaction
LOU Jiaqi1, YE Hailiang1, YANG Bing1, LI Ming2, CAO Feilong1
1. Department of Applied Mathematics, College of Sciences, China Jiliang University, Hangzhou 310018
2. Key Laboratory of Intelligent Education Technology and Application of Zhejiang Province, Zhejiang Normal University, Jinhua 321004
Corresponding author:
YE Hailiang, Ph.D., lecturer. His research interests include deep learning and its application, graph neural networks, machine learning and its application.

About Author:
LOU Jiaqi, master student. His research interests include deep learning and graph neural networks.
YANG Bing, Ph.D., lecturer. His research interests include deep learning and image processing.
LI Ming, Ph.D., professor. His research interests include deep learning and graph neural networks.
CAO Feilong, Ph.D., professor. His research interests include deep learning and image processing.

Fund:National Natural Science Foundation of China(No.62006215,62176244,62172370), Natural Science Foundation of Zhejiang Province(No.LQ20F030016)
Abstract

Graph neural networks show excellent performance in node classification tasks. However, how to fully obtain high-order semantic features of graph data and prevent over-smoothing is one of the key issues affecting the accuracy of node classification. Therefore, deep graph convolutional network with dual-branch and multi-interaction is constructed to enhance the ability to acquire high-order semantic features of nodes. Firstly, the graph structure is reconstructed according to the feature information of the nodes. Then, a dual-branch network architecture is established by both the original and the constructed graph structures to fully extract different high-order semantic features. A channel information interaction mechanism is designed to increase the diversity of node features by learning the information interaction of different branches. Finally, experiments on multiple benchmark datasets demonstrate that the proposed method improves the accuracies of the semi-supervised node classification tasks and alleviates the over-smoothing phenomenon effectively.

Key words: Key Words Deep Learning; Graph Neural Network; Feature Extraction; Node Classification

图神经网络(Graph Neural Networks, GNNs)[1]是一类有效处理图结构数据的方法, 现已成为推荐系统[2]、计算机视觉[3]、交通预测[4]和生物医学[5]等诸多领域中广泛使用的工具之一.特别地, 通过借鉴卷积神经网络(Convolutional Neural Network, CNN)[6]的思想, Bruna等[7]构造图上的卷积操作, 将卷积运算从欧氏空间数据推广至非欧图结构数据.之后, 学者们又提出一系列基于图卷积的神经网络模型[8, 9].这些方法的主要目标是通过卷积操作聚合图中节点及其邻居节点的信息, 为图数据的每个节点学习一个低维的表示向量.之后, 该节点表示向量可应用于图上的诸多下游任务, 如节点分类[10]、节点补全[11]、图分类[12]、链接预测[13]等.

事实上, 图卷积网络(Graph Convolutional Net-work, GCN)可分为两类:基于频域的谱图卷积和基于空域的空间图卷积.谱图卷积操作通常在傅里叶空间完成, 通过傅里叶变换将图信号从空域转化到频域.为了减少图卷积的计算量, Defferrard等[14]提出使用Chebyshev算子代替原始的卷积核.之后, 为了适应图上的半监督学习任务, Kipf等[15]进一步限制邻域宽度并运用归一化技巧, 提出图卷积网络.Li等[16]分析现有图卷积的局限性, 提出图高斯卷积网络(Graph Gaussian Convolution Networks, G2CN), 其中的3个属性解耦使网络结构变得更灵活, 适用于不同的图数据.

空间图卷积操作旨在将图中节点的多阶邻居信息聚合为新的节点表示.为了适应大规模的图数据, Hamilton等[17]提出基于归纳式的节点嵌入算法, 对部分节点邻居采样后进行聚合操作, 得到节点新的表示.为了关注更有价值的节点和边, Veli cˇkovi c'等[18]提出图注意力网络(Graph Attention Network, GAT), 通过自注意力机制[19]确定各邻居节点的权重, 聚合邻居节点的特征信息.为了解决图上的邻居爆炸问题, Zeng等[20]引入基于图采样的归纳学习模型, 并在子图上构建GCN, 加速训练过程.

虽然上述图神经网络取得一定效果, 但浅层架构的特点限制其从高阶邻居节点中获取信息的能力.而深度图神经网络可利用节点较远的聚合范围, 提取相对丰富的高阶语义特征.然而, 简单叠加多个图卷积层的深度网络往往存在一些固有的缺陷, 如产生过平滑现象[21].过平滑现象是指图节点信息经过多次图卷积操作后会趋于一致, 丧失节点特征多样性.He等[22]利用深度残差网络(Deep Residual Network), 解决计算机视觉中的网络退化问题, 有效提升训练深层网络的可行性.基于该工作, Kipf等[15]在GCN中引入残差连接, 一定程度上缓解过平滑现象.进一步, Rong等[23]使用随机丢弃部分节点之间的边(DropEdge), 减轻过平滑现象的影响.

尽管随着网络深度的增加, 上述2种方法都可延缓性能下降, 但对于半监督的节点分类任务, 深层模型的性能仍不如某些浅层模型.为此, 在网络架构层面, Chen等[24]对GCN进行两个有效的修改, 即引入恒等映射和初始残差连接, 设计GCNII(GCN with Initial Residual and Identity Mapping), 使深层模型的性能超越浅层模型.

在图卷积操作层面, Zhu等[25]使用改进的马尔可夫扩散核构造GCN的变体— — S2GC(Simple Spectral Graph Convolution), 捕获节点的局部与全局上下文信息, 进而限制过平滑现象的产生.此外, Chamberlain等[26]将图深度学习作为一个连续扩散过程, 并将图神经网络视为基础偏微分方程的离散化情形, 提出GRAND(Graph Neural Diffusion).进一步, Thorpe等[27]提出GRAND++(Graph Neural Diffu-sion with a Source Term), 用于低标签率的图深度学习.作为一类新式的GNN, 图神经扩散也能在一定程度上缓解过平滑现象.

尽管上述方法增加图卷积网络的深度, 但忽略图卷积操作固有的缺陷:基于GCN学习的节点表示往往会破坏原始特征空间的节点相似性[28].事实上, 节点相似性在许多场景中发挥至关重要的作用, 这一结果会大幅影响捕获的节点表示的有效性, 并阻碍其下游任务的性能.此外, 真实世界中的图结构数据往往存在长尾分布的现象, 即图中的大多数节点只存在少量的邻居节点, 这些尾节点往往不能在聚合操作时获得足够的信息, 这一现象影响网络获取节点表示的准确性.

因此, 本文提出双分支多交互的深度图卷积网络, 有效改善节点分类任务的性能.首先, 利用K近邻算法对图数据结构进行重构, 学习具有节点相似性的重构图, 由于重构的图结构中节点具有较平衡的邻居数量, 可避免长尾分布带来的影响.然后, 利用原始图和重构图构造双分支深度图卷积网络, 既保留原始图的结构信息, 又考虑节点间的相似性信息, 充分提取高阶语义特征.设计通道信息交互机制, 建立对不同分支信息的多次交互, 增加特征的多样性, 进一步增强网络获取高阶语义特征的能力, 避免过平滑现象.最后, 将不同分支的特征进行融合以获得分类结果.实验表明本文网络在多个数据集上取得较优性能.

1 相关工作

对于一个无向图G=(V, E, X), 其中V={v1, v2, …, vn}为n个节点的集合, E={e1, e2, …, em}为m条边的集合, X={x1, x2, …, xn}∈ Rn× d为节点特征矩阵, d为每个节点的特征维数, A∈ {0, 1}n× n为大小为n× n的邻接矩阵, D为A的对角度矩阵.

A˜=A+In

为添加自连接的邻接矩阵, In为n阶单位矩阵,

D˜=D+In.

节点标签表示为一组one-hot向量.

Kipf等[15]提出用于半监督节点分类的GCN, 只考虑一阶邻居, GCN的特征提取过程可表示为

${{H}_{l+1}}=\sigma ({{\tilde{D}}^{-1/2}}\tilde{A}{{\tilde{D}}^{-1/2}}{{H}_{l}}{{W}_{l}})$,

其中, Hl为第l层的输出, H0=X, Wl为第l层的权重矩阵, σ (· )为激活函数, 通常取修正线性单元(Rectified Linear Unit, ReLU), 即

σ (x)=max(0, x).

最近, Chen等[24]指出, 上述GCN固定的多项式系数限制其加深网络深度的表达能力, 导致过平滑现象的产生.若要将网络扩展到深层, 需要GCN能使用任意系数表示的K阶多项式滤波器.这可由两个简单的操作实现:初始残差连接和恒等映射.为此, Chen等[24]提出GCNII, 特征提取过程可表示为

${{H}_{l+1}}=\sigma (((1-\alpha )\tilde{P}{{H}_{l}}+\alpha {{H}_{0}}){{\hat{W}}_{l}})$,

其中

${{\hat{W}}_{l}}=(1-{{\beta }_{l}}){{I}_{n}}+{{\beta }_{l}}{{W}_{l}}$,

$\tilde{P}={{\tilde{D}}^{-1/2}}\tilde{A}{{\tilde{D}}^{-1/2}}$,

α > 0, β l> 0为超参数.注意, 初始残差连接借鉴APPNP(Approximate Personalized Propagation of Neural Predictions)[29], 融合部分初始特征信息.之后又借鉴深度残差网络[22]加入恒等映射, 即在参数Wl和In之间进行加权求和, 比例系数β l随着层数的加深而减少.通过该恒等映射可加快网络收敛速度, 减少有效信息的损失.

2 双分支多交互的深度图卷积网络
2.1 网络架构

本文设计双分支多交互的深度图卷积网络, 具体框架如图1所示.网络可分为4部分:初始特征变换、基于图结构信息的深度图卷积网络分支、基于节点相似性信息的深度图卷积网络分支、特征融合.

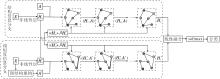图1 双分支多交互的深度图卷积网络框架图Fig.1 Architecture of deep graph convolutional network with dual branches and multi-interaction

首先, 将原始数据X={xi }i=1n分别输入两个不同的非线性全连接层, 得到图结构分支的初始特征H'0和节点相似性分支的初始特征H'0, 作为深度图卷积模块及通道信息交互机制的初始输入.整个过程表示为

H0=σ (f1(X)), H'0=σ (f2(X)),

其中f1(· )、 f2(· )为两个线性变换.这是由于图节点的特征维度往往较大, 若不对其进行限制, 会大幅增加网络的参数量, 影响计算效率.通过非线性变换层可将初始特征X的维度压缩到一个较小的值, 在不影响分类精度的前提下, 大幅减少网络的参数量.

其次, 构造双分支网络, 分别为基于图结构信息的深度图卷积网络分支与基于节点相似性信息的深度图卷积网络分支.显然, 想要获得精确的节点表示, 不仅需要考虑图的结构信息, 也需要注重图中节点的特征信息.为此:基于图结构信息的分支, 利用原始图的邻接矩阵A, 通过深度图卷积操作, 充分提取高阶语义特征; 节点相似度信息的分支利用新构造的邻接矩阵A', 弥补原始结构信息分支中可能存在的高阶邻居信息提取不充分的问题.此外, 针对过平滑现象, 为每个分支加入残差连接及恒等映射.同时, 为了增加节点特征的多样性, 设计通道信息交互机制, 对不同分支进行多次交互.最终形成双分支多交互网络.相比相同深度的单通道深度图卷积网络, 能有效提取更丰富的高阶语义特征, 并进一步降低过平滑问题的风险.

最后, 在经过双分支多交互的深度图卷积操作后, 获得两组新的节点表示, 进行特征融合, 得到最终的节点表示, 再利用softmax函数对节点进行分类.

2.2 图结构重构

GCN、GCNII等方法仅考虑图的拓扑结构, 往往存在一些缺陷, 即图中的许多节点是低维度的.这意味着它只有很少的邻居节点, 在特征聚合过程中无法得到足够的信息, 导致获取的节点表示不理想.另一方面, 受限于图卷积操作低通滤波器的特点, 在经过多次图卷积操作后, 相似节点之间的结构信息被破坏, 这可能导致节点属性趋于一致, 丧失节点特征的多样性.因此, 本文考虑利用节点自身的特征, 重新构造图的邻接矩阵.利用K近邻算法, 根据节点特征之间的相似度, 判定相似的节点连接.

事实上, 有许多不同的相似度计算方式, 考虑到节点特征的性质, 本文选择余弦相似度作为衡量指标.具体流程如下:对于图上的一个节点vi(i=1, 2, …, n), 其与另一节点vj(j=1, 2, …, i-1, i+1, …, n)的原始节点特征xi与xj之间的余弦相似度为

sij= xTixj‖xi‖2‖xj‖2.

每个节点都会与其最相似的k个节点连接, 可得到一个新的图结构, 邻接矩阵可表示为A'.

原始图结构的邻接矩阵A和新构造的邻接矩阵A'将分别用于两个不同的网络分支.利用A', 节点相似度信息分支弥补原始图结构信息分支在经过深度图卷积操作后节点相似性被破坏的问题, 允许网络扩展到更深的层次, 提取更高阶的语义特征, 得到更精确的节点表示.

2.3 通道信息交互机制

图信号经过一次图卷积操作后会更平滑, 在进行多次图卷积操作后, 图信号会越来越趋同, 导致节点的区分性越来越差, 丧失节点特征的多样性.为了保持节点特征的多样性, 本文提出通道信息交互机制.引入分支间的残差连接, 每次图卷积操作不仅获取原分支的初始图信号, 也会获取另一分支的初始图信号, 增强不同分支特征的交互.注意到, 此处的初始图信号并非原始特征, 而是2.1节中提到的H0和H'0.在总层数为L的网络中, 第l(l=1, 2, …, L)层的具体操作如下:

${{H}_{l}}=\sigma (((1-\alpha )P{{H}_{l-1}}+\alpha {{H}_{0}}+\beta {{{H}'}_{0}}){{\hat{W}}_{l}})$,

${{{H}'}_{l}}=\sigma (((1-\alpha ){P}'{{{H}'}_{l-1}}+\alpha {{{H}'}_{0}}+\beta {{H}_{0}}){{\hat{W}}_{l}}^{\prime })$,

其中,

${{\hat{W}}_{l}}=(1-{{\gamma }_{l}}){{I}_{n}}+{{\gamma }_{l}}{{W}_{l}}$,

${{{\hat{W}}'}_{l}}=(1-{{\gamma }_{l}}){{I}_{n}}+{{\gamma }_{l}}{{{W}'}_{l}}$,

$P={{\tilde{D}}^{-1/2}}\tilde{A}{{\tilde{D}}^{-1/2}}$,

${P}'={{\tilde{{D}'}}^{-1/2}}{\tilde{A}}'{{{\tilde{D}}'}^{-1/2}}$,

α 为初始残差连接系数, β 为通道信息交互系数, 这两个超参数可在一个经验性的范围内通过网格搜索得到, γ 1为随网络层数递增的一个参数,

$\gamma_{1}=ln\lgroup \frac{\theta}{l}+1 \rgroup$,

θ 为超参数, 用于控制γ 1递增的速度, 经验性地取0.5.

D˜'=D'+In,

D'为A'对应的度矩阵, Wl与W'l分别为两个分支中第l层的权重矩阵.

在深度图卷积网络中, 低层次的特征更具有多样性, 而高层次的特征聚合更多高阶邻居的特征.本文在双分支网络中, 每次图卷积操作都加入通道信息交互机制, 允许网络在充分提取高阶语义特征的同时保持特征的多样性, 得到更精确的节点表示.值得注意的是, 在本文网络下, 令β =0, 则每个分支退化成GCNII, 因此, 本文网络是GCNII的进一步推广.

2.4 通道特征融合

经过双分支深度图卷积网络后, 可得到两组基于不同图结构聚合方式的节点特征, 为了更合理地融合代表两种信息的特征, 本文设计线性特征融合方式, 将两组特征分别经过一个线性变换后进行相加.通过此方式, 网络可自适应地将结构信息特征与相似性信息特征融合为新的节点表示.整个过程的表达式为

out=f3(HL)+f4(H'L),

其中f3(· )和f4(· )为两个线性变换.

2.5 损失函数

本文的目的是从测试集中预测未标记节点的类别, 通过softmax函数获得模型的输出向量:

Y︿=softmax(out).

Y︿={ ŷi}i=1n为预测节点vi在类别概率.然后采用交叉熵损失[30]:

L= 1NT∑vi∈NTyiln( ŷi),

其中, NT为用于训练的节点, yi为真实节点标签.

3 实验及结果分析
3.1 实验环境

各网络均在NVIDIA RTX 2080Ti GPU上训练, 使用PyTorch[31]实现.使用Adam(Adaptive Moment Estimation)[32]优化算法进行训练, 设置初始学习率为0.01, 权重衰减为0.01, 丢弃率为0.6, 训练轮数为1 500, 同时设置训练的耐心值为100, 即当训练损失在100次循环后都未下降时, 停止训练.其它对比方法涉及到的超参数, 如学习率和丢弃率等, 都取自相应文章或代码中默认使用的值.

对于超参数α 和β 的选取, 本文使用网格搜索的方法, 经验性地定在[0, 0.2]区间内, 选取其中表现最好的一组以确定α 和β 的取值.

此外, 参照文献[23]、文献[24]、文献[32]等的设置, 重复多次实验, 选取其中最优结果作为最终结果.本文网络的各层参数如表1所示, 表中N表示图节点个数, F表示节点特征的维度.

表1 网络各层参数设置 Table 1 Parameter settings of each layer of network

本文选取Cora、PubMed、CiteSeer这3个标准的引文网络数据集[33]作为实验数据集, 表2为数据集具体信息.在Cora、CiteSeer数据集上, 节点对应论文, 边对应论文的引用, 节点特征是每篇论文的词袋表示, 使用0、1表示论文有无此主题.在PubMed数据集上, 节点特征为论文中每个单词的词频-逆文档频率(Term Frequency-Inverse Document Fre-quency, TF-IDF).

表2 实验数据集 Table 2 Experimental datasets

本文遵循广泛使用的半监督学习设置[15, 24, 25], 对3个数据集采用标准固定的训练集、验证集、测试集, 从每类中选取20个带标签的节点(其余节点仅使用特征信息)用于训练, 500个节点用于验证, 1 000个节点用于测试.

3.2 分类性能对比

本文选择如下对比网络:GCN[15]、GAT[18]、GCNII[24]、 S2GC[25]、 GRAND[26]、 GRAND++[27]、APPNP[29]、DGCN(Dual Graph Convolutional Net-works)[34]、 JK-Nets(Jumping Knowledge Networks)[35].

各网络在3个数据集上的最高分类精度如表3所示, 表中括号里的数字对应模型的层数.

表3 各网络在3个数据集上的分类精度 Table 3 Classification accuracies of different networks on 3 datasets

由表3可看出, 在Cora、CiteSeer数据集上, 本文网络的分类精度最高, 相比GCN等浅层模型, 本文网络的分类精度提升超过5.5%, 这主要是因为双分支深度网络具有更大的聚合范围, 可获得更丰富的高阶语义特征.相比GCNII等深层模型, 本文网络至少提升1.1%的分类精度, 并且分类精度可凭借相对较浅的层数超越对比方法更深层数的结果.这得益于多分支的信息交互机制, 在同样的网络深度下, 本文网络可获取更高阶的语义特征, 进一步避免出现过平滑现象.在PubMed数据集上, 本文网络同样取得最优结果, 对比次优的GCNII、S2GC, 在相同的网络深度下仍有0.5%的提升.上述结果皆证实本文网络可提取更充分高阶语义特征, 获得更精确的节点表示.

3.3 不同层数下的分类性能对比

各网络在不同层数下的分类精度对比如表4所示, 表中黑体数字表示最优值.

表4 各网络在不同层数下的分类精度 Table 4 Classification accuracies of networks with different layers

在Cora、CiteSeer数据集上, 本文网络在各层数都达到最优值, 随着深度的增加, 本文网络的分类精度也在不断提高.在PubMed数据集上, 本文网络在8层及更高的层数上都取得最优值, 并且随着深度的增加仍保持良好性能.上述结果主要归因于通道信息交互机制及双分支网络结构, 同时本文网络缓解原始图数据中存在的长尾分布问题, 使所有节点都能获取足够的语义特征.另一方面, GCN在深度增加时, 分类精度出现迅速下降, JK-Nets在一定程度上抑制过平滑, 但深度模型的性能仍不如浅层模型, 这意味着这些方法仍存在过平滑问题.这主要是由于节点的相似性信息在图卷积操作时遭到破坏.

总之, 由于设计的信息交互机制及网络结构, 本文网络可通过深度图卷积网络提取更充分的高阶语义特征, 并防止过平滑现象.

3.4 超参数分析

本节讨论3个重要超参数:重构图结构时k近邻的数量, 控制初始残差连接权重的α 、 β .其它实验设置在测试时保持不变.

首先, 通过实验判断不同数量的邻居个数的影响.邻居数量k=2, 4, 8, 16, 32, 64.k不同时本文网络在3个数据集上的平均分类精度如表5所示, 表中黑体数字表示最优值.由表可看出, 在Cora、PubMed数据集上, 随着k的增加, 分类精度总体呈上升趋势.在CiteSeer数据集上, 当k=4时取得最优值, 而k继续增大时没有进一步的提升.总之, k值会影响分类精度, 本文网络在Cora、CiteSeer、PubMed数据集上最优的邻居数量k分别为64, 4, 64.由于Cora、PubMed数据集上节点的特征维度相对较低, 需要聚合更多的邻居以获取充足的信息, 而CiteSeer数据集上节点的特征维度相对较高, 无需大量的邻居也能获得足够信息.

表5 k不同时本文网络的分类精度 Table 5 Classification accuracies of the proposed network with different k

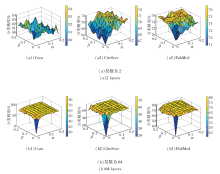
下面验证α 、 β 对分类精度的影响.α 、 β 取值不同时, 本文网络在3个数据集上的分类精度如图2所示, 同时控制每个数据集上表现最优的邻居数量k的选取.选取具有代表性的层数:2层、64层, 分别表示浅层网络及深层网络.当α 或β 为0时, 分别表示未使用初始残差连接和通道信息交互.由图2可见, 对于浅层网络, 分类精度总体表现出“ 边缘低中心高” 的特点, 这表明当α 和β 在合理范围内时, 通过本文网络可得到更好的节点表示.而对于深层网络, 当α 或β 趋向于0时, 分类精度严重下滑, 原因是此时出现过平滑现象, 这表明通过本文网络可有效防止过平滑现象.

图2 α 、 β 不同时本文网络的分类精度Fig.2 Classification accuracy of the proposed network with different α and β

总之, 本文网络中α 、 β 的取值都在0.1左右时取得相对较高的精度, 这是因为过小的取值会抑制通道交互, 出现过平滑现象, 而过大的取值会影响聚合高阶语义特征的效率, 导致网络在相同的深度下获取更少的信息.

3.5 消融实验结果

在本文网络中, 有两个核心模块:通道信息交互机制以及图结构重构.为了评估模块的有效性, 设计如下的消融实验.1)网络A:本文网络, 即同时应用通道信息交互机制及重构图结构.2)网络B:无通道信息交互机制的网络.3)网络C:未使用重构的结构的网络.不同模块对分类精度的影响如表6所示, 各网络均使用3.4节中最佳超参数设置.由表可得:

表6 不同模块对分类精度的影响 Table 6 Influence of different modules on classification accuracy

1)由于通道信息交互机制具有保持节点特征多样性的特点, 当没有采样通道信息交互机制时, 分类性能在3个数据集上都会下降, 这说明通道信息交互机制的有效性.

2)由余弦相似度构造的重构图结构在Cora、CiteSeer数据集上对节点分类起到重要作用, 这表明余弦相似度更有利于词袋属性数据集上的节点分类.而在PubMed数据集上网络A同样在16层时取得最高的分类精度, 这表明本文网络可充分提取高阶语义特征.此外, 由于重构的图结构中每个节点都具有数量相似的邻居节点, 降低原始图结构中长尾分布带来的负面影响.总之, 上述实验结果皆验证本文网络的有效性.

3.6 可视化分析

t-SNE(t-Distributed Stochastic Neighbor Embe-dding)[36]是一种高维数据可视化的工具, 本文以Cora数据集为例, 对单支网络(GCNII)、双分支无交互网络、双分支通道交互网络输出进行可视化, 结果如图3所示.由图可看到, 3种设置都具有可观的分类效果, 但双分支通道交互网络明显具有更精确的聚类效果.由于网络获得更准确的节点表示, 同类的样本点之间更紧凑, 而通道信息交互机制带来的特征多样性又能使不同类别的节点更有区分性, 具体表现为图中不同类别的样本点更分离、边界更分明.这也进一步说明本文的双分支结构及通道信息交互机制能明显改善分类结果.

图3 t-SNE可视化结果Fig.3 t-SNE visualization results

4 结束语

本文提出双分支多交互的深度图卷积网络.核心思想在于设计通道信息交互的机制, 构造采用多邻接矩阵的双分支网络结构.通过通道信息交互机制, 节点特征的多样性得到增强, 网络得以扩展到更深的层次, 并进一步解决过平滑问题.另一方面, 利用节点特征相似度重构图结构, 可同时考虑图的结构信息与节点相似度信息, 解决图卷积操作后节点特征相似性被破坏的问题.基于这两个核心思想, 在相同的深度下, 本文网络可提取更充分的高阶语义特征.实验表明, 本文网络有效提高半监督节点分类精度, 并抑制过平滑问题的出现.

总之, 本文网络能学习到一组准确的节点表示并用于下游任务.针对不同数据集的特性, 后续工作可设计更多相似度计算方式, 构造更多不同的图结构, 在更多数据集上获得更优结果.另一方面, 本文的图结构重构相当于提取图的部分先验信息.因此, 后续可尝试对节点标签极少的图数据开展节点分类任务.

本文责任编委 于剑

Recommended by Associate Editor YU Jian

参考文献
[1] GORI M, MONFARDINI G, SCARSELLI F. A New Model for Learning in Graph Domains // Proc of the IEEE International Joint Conference on Neural Networks. Washington, USA: IEEE, 2005, II: 729-734. [本文引用:1]
[2] YU J L, YIN H Z, LI J D, et al. Enhancing Social Recommendation with Adversarial Graph Convolutional Networks. IEEE Transactions on Knowledge and Data Engineering, 2022, 34(8): 3727-3739. [本文引用:1]
[3] HONG D F, GAO L R, YAO J, et al. Graph Convolutional Networks for Hyperspectral Image Classification. IEEE Transactions on Geoscience and Remote Sensing, 2021, 59(7): 5966-5978. [本文引用:1]
[4] 冯宁, 郭晟楠, 宋超, 等. 面向交通流量预测的多组件时空图卷积网络. 软件学报, 2019, 30(3): 759-769.
(FENG N, GUO S N, SONG C, et al. Multi-component Spatial-Temporal Graph Convolution Networks for Traffic Flow Forecasting. Journal of Software, 2019, 30(3): 759-769. ) [本文引用:1]
[5] SONG X G, LI H M, GAO W W, et al. Augmented Multicenter Graph Convolutional Network for COVID-19 Diagnosis. IEEE Transactions on Industrial Informatics, 2021, 17(9): 6499-6509. [本文引用:1]
[6] LECUN Y, BENGIO Y. Convolutional Networks for Images, Speech, and Time Series // ARBIB M A, ed. The Hand book of Brain Theory and Neural Networks. Cambridge, USA: MIT Press, 1998: 255-258. [本文引用:1]
[7] BRUNA J, ZAREMBA W, SZLAM A, , et al. Spectral Networks and Deep Locally Connected Networks on Graphs [C/OL]. [2022-05-10]. https://arxiv.org/pdf/1312.6203.pdf. [本文引用:1]
[8] SPINELLI I, SCARDAPANE S, UNCINI A. Adaptive Propagation Graph Convolutional Network. IEEE Transactions on Neural Networks and Learning Systems, 2021, 32(10): 4755-4760. [本文引用:1]
[9] WU F, ZHANG T Y, DE SOUZA JR A H, et al. Simplifying Graph Convolutional Networks // Proc of the 36th International Conference on Machine Learning. San Diego, USA: JMLR, 2019: 6861-6871. [本文引用:1]
[10] LI K J, YE W J. Semi-Supervised Node Classification via Graph Learning Convolutional Neural Network. Applied Intelligence, 2022. DOI: DOI:10.1007/s10489-022-03233-9. [本文引用:1]
[11] 刘臣, 李自然, 周立欣. 基于图卷积神经网络的网络节点补全算法. 模式识别与人工智能, 2021, 34(6): 532-540.
(LIU C, LI Z R, ZHOU L X. Network Node Completion Based on Graph Convolutional Network. Pattern Recognition and Artificial Intelligence, 2021, 34(6): 532-540. ) [本文引用:1]
[12] BAI L, CUI L X, JIAO Y H, et al. Learning Backtrackless Aligned-Spatial Graph Convolutional Networks for Graph Classification. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2022, 44(2): 783-798. [本文引用:1]
[13] ZEB A, SAIF S, CHEN J D, et al. Complex Graph Convolutional Network for Link Prediction in Knowledge Graphs. Expert Systems with Applications, 2022, 200. DOI: DOI:10.1016/j.eswa.2022.116796. [本文引用:1]
[14] DEFFERRARD M, BRESSON X, VANDERGHEYNST P. Convolutional Neural Networks on Graphs with Fast Localized Spectral Filtering // Proc of the 30th International Conference on Neural Information Processing Systems. Cambridge, USA: MIT Press, 2016: 3844-3852. [本文引用:1]
[15] KIPF T N, WELLING M. Semi-Supervised Classification with Graph Convolutional Networks[C/OL]. [2022-05-10]. https://openreview.net/pdf?id=SJU4ayYgl. [本文引用:5]
[16] LI M J, GUO X J, WANG Y F, et al. G2CN: Graph Gaussian Convolution Networks with Concentrated Graph Filters // Proc of the 39th International Conference on Machine Learning. San Diego, USA: JMLR, 2022: 12782-12796. [本文引用:1]
[17] HAMILTON W L, YING R, LESKOVEC J. Inductive Representation Learning on Large Graphs // Proc of the 31st International Conference on Neural Information Processing Systems. Cambridge, USA: MIT Press, 2017: 1025-1035. [本文引用:1]
[18] VELIČKOVIĆ P, CUCURULL G, CASANOVA A, et al. Graph Attention Networks[C/OL]. [2022-05-10]. https://openreview.net/pdf?id=rJXMpikCZ. [本文引用:2]
[19] VASWANI A, SHAZEER N, PARMAR N, et al. Attention Is All You Need // Proc of the 31st International Conference on Neural Information Processing Systems. Cambridge, USA: MIT Press, 2017: 6000-6010. [本文引用:1]
[20] ZENG H Q, ZHOU H K, SRIVASTAVA A, et al. GraphSAINT: Graph Sampling Based Inductive Learning Method[C/OL]. [2022-05-10]. https://openreview.net/pdf?id=BJe8pkHFwS. [本文引用:1]
[21] LI Q M, HAN Z C, WU X M. Deeper Insights into Graph Convolutional Networks for Semi-Supervised Learning. Proceedings of the AAAI Conference on Artificial Intelligence, 2018, 32(1): 3538-3545. [本文引用:1]
[22] HE K M, ZHANG X Y, REN S Q, et al. Deep Residual Learning for Image Recognition // Proc of the IEEE Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2016: 770-778. [本文引用:2]
[23] RONG Y, HUANG W B, XU T Y, et al. DropEdge: Towards Deep Graph Convolutional Networks on Node Classification[C/OL]. [2022-05-10]. https://openreview.net/pdf?id=Hkx1qkrKPr. [本文引用:2]
[24] CHEN M, WEI Z W, HUANG Z F, et al. Simple and Deep Graph Convolutional Networks // Proc of the 37th International Confe-rence on Machine Learning. New York, USA: ACM, 2020: 1725-1735. [本文引用:6]
[25] ZHU H, KONIUSZ P. Simple Spectral Graph Convolution[C/OL]. [2022-05-10]. https://openreview.net/pdf?id=CYO5T-YjWZV. [本文引用:3]
[26] CHAMBERLAIN B P, ROWBOTTOM J, GORINOVA M, et al. GRAND: Graph Neural Diffusion // Proc of the 38th International Conference on Machine Learning. San Diego, USA: JMLR, 2021: 1407-1418. [本文引用:2]
[27] THORPE M, XIA T D, NGUYEN T, et al. GRAND++: Graph Neural Diffusion with a Source Term[C/OL]. [2022-05-10]. https://openreview.net/pdf?id=EMxu-dzvJk. [本文引用:2]
[28] JIN W, DERR T, WANG Y Q, et al. Node Similarity Preserving Graph Convolutional Networks // Proc of the 14th ACM International Conference on Web Search and Data Mining. New York, USA: ACM, 2021: 148-156. [本文引用:1]
[29] GASTEIGER J, BOJCHEVSKI A, GÜNNEMANN S. Predict Then Propagate: Graph Neural Networks Meet Personalized PageRank[C/OL]. [2022-05-10]. https://openreview.net/pdf?id=H1gL-2A9Ym. [本文引用:2]
[30] DE BOER P T, KROESE D P, MANNOR S, et al. A Tutorial on the Cross-Entropy Method. Annals of Operations Research, 2005, 134(1): 19-67. [本文引用:1]
[31] PASZKE A, GROSS S, MASSA F, et al. PyTorch: An Imperative Style, High-Performance Deep Learning Library // Proc of the 33rd International Conference on Neural Information Processing Systems. Cambridge, USA: MIT Press, 2019: 8026-8037. [本文引用:1]
[32] KINGMA D P, BA J L. Adam: A Method for Stochastic Optimization[C/OL]. [2022-05-10]. https://arxiv.org/pdf/1412.6980.pdf. [本文引用:2]
[33] SEN P, NAMATA G, BILGIC M, et al. Collective Classification in Network Data. AI Magazine, 2008, 29(3): 93-106. [本文引用:1]
[34] ZHUANG C Y, MA Q. Dual Graph Convolutional Networks for Graph-Based Semi-Supervised Classification // Proc of the World Wide Web Conference. New York, USA: ACM, 2018: 499-508. [本文引用:1]
[35] XU K Y L, LI C T, TIAN Y L, et al. Representation Learning on Graphs with Jumping Knowledge Networks[C/OL]. [2022-05-10]. https://arxiv.org/pdf/1806.03536.pdf. [本文引用:1]
[36] VAN DER MAATEN L, HINTON G. Visualizing Data Using t-SNE. Journal of Machine Learning Research, 2008, 9: 2579-2605. [本文引用:1]