鲁明羽,博士,教授,主要研究方向为数据挖掘、自然语言处理.E-mail: lumingyu@dlmu.edu.cnss.
鲁明羽,博士,教授,主要研究方向为数据挖掘、自然语言处理.E-mail: lumingyu@dlmu.edu.cnss.
作者简介: 庞阔,博士研究生,主要研究方向为机器学习、智能信息处理、形式概念分析.E-mail:pangkuo_p@dlmu.edu.cn.
庞阔,博士研究生,主要研究方向为机器学习、智能信息处理、形式概念分析.E-mail:pangkuo_p@dlmu.edu.cn.
 周爱,博士研究生,主要研究方向为自然语言处理、作者身份识别.E-mail:zhouai9070@dlmu.edu.cn.
周爱,博士研究生,主要研究方向为自然语言处理、作者身份识别.E-mail:zhouai9070@dlmu.edu.cn.
 杨鑫冉,硕士研究生,主要研究方向为智能信息处理、多值逻辑、形式概念分析.E-mail:yangxinrancn@163.com.
杨鑫冉,硕士研究生,主要研究方向为智能信息处理、多值逻辑、形式概念分析.E-mail:yangxinrancn@163.com.
 李楠,硕士研究生,主要研究方向为智能信息处理、形式概念分析.E-mail:linan123cn@163.com.
李楠,硕士研究生,主要研究方向为智能信息处理、形式概念分析.E-mail:linan123cn@163.com.
 邹丽,博士,教授,主要研究方向为数据挖掘、智能信息处理、形式概念分析.E-mail:zoulicn@163.com.
邹丽,博士,教授,主要研究方向为数据挖掘、智能信息处理、形式概念分析.E-mail:zoulicn@163.com.
在形式概念分析中,属性偏序结构图作为一种数据可视化工具,可有效解决用户认知过载的问题.在现实生活中,人们往往通过模糊语言值表达偏好信息,会产生大量的模糊语言值数据.为了解决在模糊语言环境下的属性约简问题,文中提出模糊语言属性偏序结构图的逐层属性约简算法.首先,基于模糊语言值形式背景构建模糊语言属性偏序结构图,将模糊语言值数据嵌入属性偏序结构图中.通过语言真值格蕴涵代数作为模糊语言值表示模型,表达模糊语言值间的序关系和不可比关系.然后,为了获取保持模糊语言值形式背景区分能力不变的最小属性子集,结合模糊语言值属性偏序结构图,搜索未与底层节点建立边的节点.在保证模糊语言值属性偏序结构图类等价的前提下,计算该节点及其子节点间的差别属性,并构造相应的逐层属性约简模型.最后,通过实例与对比实验验证文中算法的有效性和实用性.
Author:PANG Kuo, Ph.D. candidate. His research interests include machine learning, intelligent information processing and formal concept analysis.
ZHOU Ai, Ph.D. candidate. Her research interests include natural language processing and author identification.
YANG Xinran, master student. Her research interests include intelligent information processing, multivalued logic and formal concept analysis.
LI Nan, master student. His research inte-rests include intelligent information processing and formal concept analysis.
ZOU Li, Ph.D., professor. Her research interests include data mining, intelligent information processing and formal concept ana-lysis.
As a data visualization tool, attribute partial order structure diagram can solve the problem of user cognitive overload in formal concept analysis effectively. People often express preference information through fuzzy linguistic values in real life,and thus a large amount of fuzzy linguistic-valued data is generated. To solve the problem of attribute reduction in fuzzy linguistic environment, a layer-by-layer attribute reduction algorithm for fuzzy linguistic attribute partial order structure diagram is proposed in this paper. Firstly, the fuzzy linguistic attribute partial order structure diagram is constructed based on the fuzzy linguistic-valued formal context, and the fuzzy linguistic-valued data is embedded into the attribute partial order structure diagram. The order relation and the incomparable relation between fuzzy linguistic values are expressed by the linguistic truth-valued lattice implication algebra acting as the representation model of the fuzzy linguistic values. Secondly, the fuzzy linguistic attribute partial order structure diagram is employed and the nodes that do not form edges with the underlying nodes are searched to obtain the minimum attribute subset with the fuzzy linguistic-valued formal context discrimination ability unchanged. On the premise of ensuring the class equivalence of the fuzzy linguistic attribute partial order structure diagram, the difference attribute between the node and its child nodes is calculated, and the corresponding layer-by-layer attribute reduction model is constructed. Finally, examples and comparative experiments verify the effectiveness and practicability of the proposed method.
形式概念分析(Formal Concept Analysis, FCA)理论, 也称概念格理论[1], 是知识表示与发现的一种有效数学工具.FCA的输入是一个二元表, 其中, 行表示对象, 列表示属性, 称为形式背景.主要输出是在形式背景中挖掘的对象与属性的特定集群与其层次结构, 称为概念格.目前, FCA被广泛应用于机器学习[2, 3, 4, 5]、专家系统[6]、推荐系统[7, 8, 9]及数据挖掘[10, 11, 12]等领域.
在现实生活中, 人们常通过模糊语言值描述定性的信息.如何利用人类认知对模糊语言值数据进行分析和可视化, 从模糊语言值数据中获取有价值的模糊语言偏好知识, 已成为当前FCA研究的热点.学者们对使用概念格处理模糊语言值数据进行深入研究, 并取得重要成果.Zou等[11, 13, 14]基于语言术语集和语言值格蕴涵代数构造相应的语言概念格, 并完成规则提取、属性约简和不确定性推理等任务.Pei等[15]基于 FCA 探索模糊语言值集的层次结构, 并通过模糊语言值刻画对象的适用性, 进一步研究模糊语言值的推理.
在现实世界中, 概念往往不满足严格数学意义下的内涵与外延的充要关系.偏序形式结构分析(Partial Order Formal Structure Analysis, POFSA)[16]是从FCA理论基础上发展而来, 从认知事物的角度出发, 挖掘形式背景中对象、属性及属性与对象之间的关系, 构建一种以发掘属性间关系和区分对象为基本目的的数学结构.在POFSA中存在2种知识结构:属性偏序结构(Attribute Partial Ordered Structure, APOS)[17]与对象偏序结构(Object Partial Ordered Structure, OPOS)[18].APOS与OPOS的可视化结构图分别称为属性偏序结构图(APOS Diagram, AP-OSD)与对象偏序结构图(OPOS Diagram, OPOSD).目前APOSD在中医药数据挖掘、中医诊断的模式识别分类及自然语言处理等相关研究中取得较好的应用效果[19, 20, 21, 22].由于APOSD的构建效率高于概念格, 并且相比概念格, APOSD层次分明, 可读性较强, 在进行下游任务时, 选择APOSD不仅可提高构建效率, 还能提高结果的可解释性.然而, 目前还未发现将模糊语言值数据嵌入APOSD的方法.因此, 如何将模糊语言值嵌入APOSD中是一个值得研究的问题.
近年来, 随着词计算(Computing with Words, CW)[23, 24, 25]的不断发展, 学者们在模糊语言值信息处理方面也取得较大成就.目前, 模糊语言值表示的工作主要集中于模糊集[26, 27]、语言项集[28, 29]和语言真值格蕴涵代数[30, 31].语言真值格蕴涵代数可处理模糊语言值间的可比性和不可比性, 丰富的蕴涵操作更适合计算机利用模糊语言进行不同的下游任务.
概念格约简是概念格理论研究中的核心问题之一.概念格约简是在保持特定信息不变的前提下避免对象、属性或概念的冗余.概念格约简主要分为对象约简、属性约简和概念约简.概念格中的属性约简是一个保持形式背景或概念格某种特性不发生改变以计算极小属性子集的过程[32].学者们在这一方面进行深入研究, 张文修等[33]系统研究保持概念格结构不变的属性约简理论与方法, 引入可辨识属性矩阵实现属性约简, 并进一步研究概念格属性特征.Wei等[34]利用图论结合概念格与有向图, 对属性进行约简.Dias等[35]给出不同特性的概念格约简方法, 同时有效去除系统中不相关的属性信息.
在形式概念分析约简理论中, 大多数属性约简方法属于保持概念格结构不变的属性约简[36, 37, 38, 39].此后, 学者们扩展经典概念格的属性约简方法, 研究其它不同类型的概念格属性约简问题.Wang等[40]提出4种基于不同准则的近似概念格属性约简方法, 并讨论4种属性约简之间的关系.Lin等[41]基于粒度矩阵, 通过粒度协调集, 提出模糊形式背景的知识约简方法.模糊语言值作为人们定性表达的工具, 在属性约简的过程中考虑模糊语言值可避免数值转化为语言值造成的信息损失, 更贴近人类的思维模式.针对含有模糊语言值信息的形式背景, 通过APOSD适当弱化概念, 从而保持某种特定要求不变的属性约简方法也是一个有意义的研究问题.
在理想情况下, 属性约简集中的每个属性及属性组合都能起到区分对象的作用.结合模糊语言属性偏序图为每个结点都向底层结点建立边, 基于语言真值格蕴涵代数与模糊语言值形式背景, 提出模糊语言属性偏序结构图的逐层属性约简算法(Layer-by-Layer Attribute Reduction Algorithm for Fuzzy Linguistic APOSD, LLAR).在属性约简过程中嵌入模糊语言值数据的同时, 还得到保持属性偏序结构图区分能力不变的最小属性子集, 并以层次化视图显示简明区分对象的过程, 可加强用户与数据的交互, 减轻大数据情况下用户的认知过载问题.本文提出模糊语言属性偏序结构图(Fuzzy Linguistic APOSD, FL-APOSD), 逐层分析模糊语言属性偏序图中未向底层结点建立边的结点及其子结点对应的属性, 根据定义在模糊语言属性偏序图中的类等价, 判断属性是否可约, 把属性约简问题转化为在模糊语言属性偏序图中的搜索问题.对比实验表明本文算法的有效性.
定义1[1] 称K=(U, A, I)为一个形式背景, 其中, U为对象集, A为属性集, I为U和A之间的二元关系, I⊆U× A.若x∈ U, a∈ A, (x, a)∈ I, 说明对象x具有属性a, 记为xIa.
定义2[1] 在形式背景K=(U, A, I)中, 对∀ X⊆U, B⊆A, 定义
f(X)={a∈ A | ∀ x∈ X, (x, a)∈ I}, g(B)={x∈ U | ∀ a∈ B, (x, a)∈ I},
其中, f(X)表示X中所有对象共同拥有的属性组成的集合, g(B)表示B中所有属性的对象组成的集合.
对于形式背景(U, A, I), 对于∀ X⊆U, B⊆A, 若满足f(X)=B且g(B)=X, 称(X, B)为一个概念, 其中, X称为概念的外延, B称为概念的内涵.
所有概念的集合形成一个完备格, 称为(U, A, I)的概念格, 表示为L(U, A, I).
在各种下游任务中, 概念往往不能满足严格意义上的内涵与外延的协调统一.因此, 在弱化概念的前提下, Hong等[16]提出近似概念的定义.
定义3[16] 设K=(U, A, I)为一个形式背景, (X, B)为K上的一个概念.假设存在(X1, B1), 满足X1⊆X或B1⊆B, 称(X1, B1)为(X, B)的一个近似概念, 其中, X1为近似概念的外延, B1为近似概念的内涵.
定义4[16] 假设(X1, B1)、(X2, B2)为形式背景(U, A, I)上2个近似概念, 满足X1⊆X2, 称(X1, B1)为(X2, B2)的子概念, (X2, B2)为(X1, B1)的超概念, 记作(X1, B1)≤ (X2, B2).关系≤ 表示概念间基于属性的序.形式背景(U, A, I)所有近似概念用这种序组成的集合表示为R(U, A, I), 称为形式背景(U, A, I)上的属性偏序结构图.
定义5[16] 在形式背景K=(U, A, I)中, 若属性a∈ A满足g(a)=U, 则称属性a为形式背景K的最大共有属性.
定义6[16] 在形式背景K=(U, A, I)中, 若属性a0∈ A, a1∈ A, …, ak∈ A满足
g(at)⊆g(a0), t=1, 2, …, k, k≥ 2,
则称在形式背景K中, 属性a0为属性集合{a1, a2, …, ak}的共有属性.
定义7[16] 在形式背景K=(U, A, I)中, 若属性a∈ A满足|g(a)|=1, 则称属性a为形式背景K的独有属性, 其中|g(a)|表示具有集合g(a)的基数.
最大共有属性、共有属性和独有属性及其关系是构造属性偏序结构图的关键, 基于这3种基本属性特征和基本关系类型的属性偏序结构图构建方法在文献[16]中有详细介绍.下面通过例1直观说明属性偏序结构图.
例1 表1为一个形式背景(U, A, I), 其中, 对象集U={1, 2, …, 6}, 属性集
A={a, b, c, d, e, f, g},
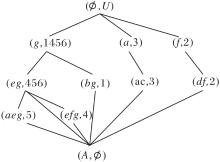
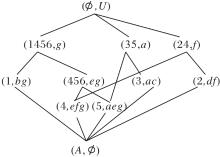
表中× 表示对象具有某属性.根据表1, 构建属性偏序结构图R(U, A, I), 如图1所示, 生成的概念格L(U, A, I)如图2所示.
| 表1 形式背景(U, A, I) Table 1 formal context(U, A, I) |
对比图1与图2可知, 概念格与APOSD都属于偏序结构, 都是从FCA发展而来.不同之处在于概念格是以概念的外延偏序由大到小建立的偏序结构, 而APOSD是以属性覆盖概念的程度为偏序.在同一形式背景中, 概念格一般会有边的交叉, 而APOSD中边与边之间不交叉.由于两种图形依据的原理和节点定义不同, 在不同的应用问题上具有各自的优势.相比在概念格下进行属性约简任务, 在APOSD下进行属性约简任务不仅可提高构建效率, 而且可在每个属性约简步骤中提供约简图, 从而提高属性约简方法的可解释性.
定义8[30] 设一个带有逆序对和运算“ '” 的有界格(L, ∨ , ∧ , O, I), L的最大元为I, 最小元为O, 若存在
1)x→ (y→ z)=y→ (x→ z);
2)x→ x=I;
3)x→ y=y'→ x';
4)如果x→ y=y→ x=I, 那么x=y;
5)(x→ y)→ y=(y→ x)→ x;
6)(x∨ y)→ z=(x→ z)∨ (y→ z);
7)(x∧ y)→ z=(x→ z)∧ (y→ z);
那么有界格(L, ∨ , ∧ , ', → , O, I)称为一个格蕴涵代数.
定义9[30] 设ADn={h1, h2, …, hn}为含有n个语气算子的集合, h1< h2< …< hn, MT={c1, c2}为具有一对相反意义的语言真值的集合, c1< c2, 令
LV(n× 2)=ADn× MT,
则称
LV(n× 2)=(LV(n× 2), ∧ , ∨ , ', → , (hn, c1), (hn, c2))
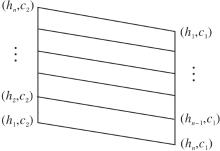
为由ADn和MT生成的语言真值格蕴涵代数.LV(n× 2)哈斯图如图3所示.
定义10[11] 称(U, A,
其中(hi, cj)∈ LV(n× 2).
定义11[11] 设(U, A,
其中
注 λ 所取的模糊语言值(hi, cj)与决策者的风险偏好有关.
对于模糊语言值形式背景(U, A,
所有模糊语言值分层概念的集合形成一个完备格, 称为(U, A,
由于人们在对客观事物进行评价或决策时往往存在主观不确定性.对于评价结果, 人们往往通过模糊语言值描述.因此, 有必要对APOSD中的模糊语言值数据进行处理.本节根据粒计算(Granular Computing, GrC)的思想, 从模糊语言值粒度的角度研究模糊语言属性偏序结构图的构造方法.
定义12 设(U, A,
1)模糊语言值λ 下的最大共有属性am:
2)模糊语言值λ 下的共有属性an:
3)模糊语言值λ 下的独有属性ao:
|
am、an、ao统称为模糊语言值约束下的属性特征.在模糊语言值约束下的特征属性的基础上, 模糊语言属性偏序结构图(FL-APOSD)的构建模型如下.
1)初始化语言真值格蕴涵代数LV(n× 2)与模糊语言值形式背景(U, A,
2)计算模糊语言值λ 下的最大共有属性am与其对应的节点N0.若不存在am, 则增加(Ø , U)作为顶节点.
3)在am的约束下计算模糊语言值λ 下的特征属性集{a11, a12, …, a1k}与其对应的节点{N11, N12, …, N1k}, 再建立与N0连接的边.
若节点间的关系满足
转至4).当不满足式(1), 在最底层节点与N0间建立l条边:
l=|
4)在上层每个模糊语言值λ 下的共有属性{Nl1, Nl2, …, Nlr}下, 计算模糊语言值λ 下的共有属性和独有属性集
{a(l+1)1, a(l+1)2, …, a(l+1)q}
与其对应的节点
{N(l+1)1, N(l+1)2, …, N(l+1)q}.
若其上层节点{Nl1, Nl2, …, Nlr}与模糊语言值λ 下的共有属性和独有属性节点满足
其中Ext(Nlj)表示第l层第j个节点的对象集, 转至5).若不满足式(2), 在最底层节点与Nlj节点间建立L条边:
L=|Ext(Nlj)-
5)当模糊语言值λ 下的共同属性或独有属性下无法生成新节点时停止, 否则转3).
相比属性偏序结构图, 从如下3个角度说明FL-APOSD的优势.
1)出发点.属性偏序结构图的出发点为形式背景, 而FL-APOSD的出发点为模糊语言值形式背景.相比形式背景, 模糊语言值形式背景直接描述对象与属性间的模糊语言值关系, 减少由模糊语言值转化为数值造成的信息损失.
2)构造方法.属性偏序结构图直接根据特征属性的计算或论域划分生成, 而FL-APOSD从粒度的角度, 通过选取不同的模糊语言值信任度λ 生成不同的FL-APOSD, 满足不同决策者的不同需要, 随着模糊语言值信任度λ 的增大, 构建速度也会加快.
3)背景知识.属性偏序结构图直接通过对象与属性间的布尔关系进行构造, 而FL-APOSD需要引入语言真值格蕴涵代数, 得到模糊语言值间的序关系与不可比关系.
例2 表2表示一个模糊语言值形式背景(U, A,
| 表2 模糊语言值形式背景(U, A, |
设语气算子的集合
AD3={h1=有点, h2=一般, h3=极},
元语言真值集
MT={c1=坏, c2=好}.
可得到模糊语言值集
LV(3× 2)={(h1, c1), (h2, c1), (h3, c1), (h1, c2), (h2, c2), (h3, c2)},
由定义9可容易得到一个六元语言真值格蕴涵代数:
LV(3× 2)=(LV(3× 2), ∨ , ∧ , ', → , (h3, f), (h3, t)),
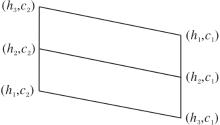
哈斯图如图4所示.
由图4可容易获得模糊语言值的序关系与不可比关系:
(h3, c1)< (h1, c2)< (h2, c2)< (h3, c2), (h2, c1)< (h2, c2), (h1, c1)< (h3, c2), (h3, c1)< (h2, c1)< (h1, c1), (h1, c1)‖ (h2, c2), (h2, c1)‖ (h1, c2), (h1, c1)‖ (h1, c2).
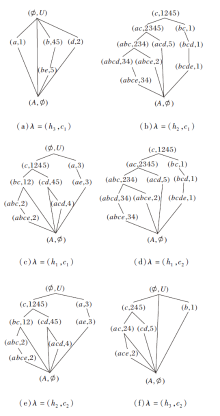
可根据不同的模糊语言值信任度得到同个模糊语言值形式背景的不同的FL-APOSD R(U, A,
由图5可知, 当模糊语言值信任度λ 1=(h2, c1)和λ 2=(h1, c2)时, 模糊语言值形式背景(U, A,
对于模糊语言值λ 3=(h1, c1)和λ 2=(h1, c2), 虽然它们之间不可比, 但是存在λ 3> λ 1和λ 1‖ λ 2, 所以λ 3=(h1, c1)和λ 2=(h1, c2)对应的FL-APOSD表示不同, 即当λ 3=(h1, c1) 和 λ 2=(h1, c2) 时, (U, A,
由于模糊语言属性偏序结构图构建效率高于模糊语言值分层概念格, 可反映模糊语言形式背景下属性约简的过程, 可解释性较强.因此, 本节以模糊语言属性偏序结构图为基础, 研究模糊语言值形式背景下的属性约简理论.
定义13 设(U, A,
h∶ P→ 2U,
h((Bm, n, Xm, n))=Xm, n-
其中, (Bm, n, Xm, n)∈ P表示第m层第n个节点, Xm+1, n表示(Bm, n, Xm, n)第n个下层节点对应的对象集合, 称映射h为R (U, A,
U/h={
称为R(U, A,
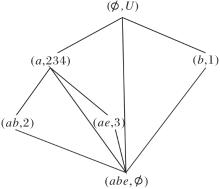
例3 以图5(e)中λ =(h2, c2)的属性偏序结构图R(U, A,
P={(abce, 2), (bc, 12), (cd, 45), (acd, 4), (ae, 3)}.
(bc, 12)节点拥有2个下层节点:(abc, 2)和(A, Ø ).(cd, 45)节点拥有2个下层节点:(acd, 4)和(A, Ø ).其余3个节点的下层节点都为(A, Ø ).容易得到R(U, A,
U/h={{1}, {2}, {3}, {4}, {5}}.
定义14 设
(U, A1, (
为2个模糊语言值形式背景, λ 1、λ 2为模糊语言值信任度,
R(U, A1,
为2个模糊语言属性偏序结构图, U/h1、U/h2为其对应的对象划分集合.对于∀ X∈ U/h1, 总存在X∈ U/h2, 则称R (U, A1,
类等价, 记作
R (U, A1,
定义15 设(U, A,
定理1 在模糊语言值形式背景(U, A,
证明 充分性.设R(U, A,
必要性.若在模糊语言值形式背景(U, A,
R (U, Di,
且Di⊆A-{e}, 所以存在
R (U, A-{e},
得证.
定理2 在模糊语言值形式背景(U, A,
R (U, A-{e},
则一定存在属性集B⊂A, 使得
证明 假设对于∀ B⊂A, 存在e∈ A-B, 使得
因为对于∀ B⊂A, 存在e∈ A-B, 使得
当模糊语言值形式背景(U, A,
由模糊语言属性偏序结构图的构图步骤可知, 在模糊语言值形式背景(U, A,
Cm, n=(Am, n, Um, n)
与其子节点集合
Φ ={Φ (j)=Cm+1, j|j=1, 2, …, M}
满足关系
节点Cm, n与最底层节点建立边, Cm, n表示R(U, A, I)中第m层第n个节点.若节点
Cm, n=(Am, n, Um, n)
未向底层节点建立边, 为建边需得到
可删除Cm, n=(Am, n, Um, n)及其子节点集合
Φ ={Φ (j)=Cm+1, j|j=1, 2, …, M}
中对应属性的差别属性Am+1, j-Am, n.
因此本文的模糊语言属性偏序结构图的逐层属性约简算法(LLAR)的思想是:在保持与FL-APOSD类等价的情况下, 分析删减FL-APOSD中未向底层节点建立边的节点
Cm, n=(Am, n, Um, n)
及其子节点集合
Φ ={Φ (j)=Cm+1, j|j=1, 2, …, M}
中对应属性的差别属性Am+1, j-Am, n.简化FL-APOSD, 直至删除任意属性后的更新图都不与原FL-APOSD类等价, 这样保留的属性组成的集合即为属性约简集.
根据上述分析, LLAR步骤如算法1所示.
算法1 LLAR
输入 模糊语言值形式背景(U, A,
模糊语言值信任度λ
输出 约简图R(U, D,
属性约简集D
构造模糊语言属性偏序结构图R(U, A,
Γ ={Γ (s)=Cm, n|s=1, 2, …, N};
令s = 1;
while Γ ≠ Ø
Γ (s)=Cm, n;
A'← A-(Am+1, j-Am, n);
R(U, A',
if R(U, A',
根据R (U, A',
else
if j≤ M
j++;
else
Γ (s)=Ø ;
end if
end if
end while
return R (U, D,
算法1的运行时间主要包括如下2部分.
1)R(U, D,
2)约简图与R(U, D,
LLAR的输出结果为约简图
R (U, D,
与属性约简集D, 根据定理1, 当删除核心属性时, 会造成R(U, D,
通过上述分析可知, 通过遍历所有节点的属性信息以删除节点中的非核心属性信息得到的属性约简集是保持模糊语言属性偏序结构图区分能力不变的最小属性子集.
例4(续例2) 以表2作为LLAR的输入, 并设置模糊语言值信任度λ =(h2, c2), 构造模糊语言属性偏序结构图R (U, A,
1)按照由上到下、由左到右的顺序扫描
R(U, A,
发现首个未向底层节点建立边的节点为(Ø , U), 子节点为(c, 1245)、(a, 3), 由于构图时属性a、c左右位置可能不同, 所以属性集A中可删除属性a或c.
当属性集A删除属性a时, 更新
R(U, A,
为
R(U, A-{a},
模糊语言属性偏序结构图如图6所示.在图中
R (U, A-{a},
的对象划分集合为
U/h1={{1}, {2}, {3}, {4, 5}}.
由定义14可知
R (U, A-{a},
与R (U, A,
当删除属性c时, 更新R(U, A,
R (U, A-{c},
如图7所示.在图中, R (U, A-{c},
2)扫描R(U, A-{c},
R(U, A-{c},
为
R(U, A-{a, c},
模糊语言属性偏序结构图如图8所示.
在图8中R (U, A-{a, c},
可得
R (U, A-{a, c},
与R (U, A,
R (U, A-{c},
发现节点(a, 234)的子节点为(ae, 23)、(ad, 4), 可删除属性为e或d.
3)当删除属性e时, 更新
R(U, A-{c},
为
R(U, A-{c, e},
模糊语言属性偏序结构图如图9所示.在图中
R(U, A-{c, e},
的对象划分集合为
U/h4={{1}, {2}, {3}, {4}, {5}},
因此, R (U, A,
R (U, A-{c, e},
类等价, 确认删除属性e.
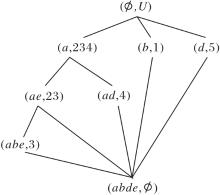
扫描
R (U, A-{c, e},
除顶层节点以外, 未发现未向底层节点建立边的节点, 算法结束.输出属性约简集D1={a, b, d}, 模糊语言属性偏序结构图如图9所示.
当删除属性d时, 更新
R (U, A-{c},
为
R (U, A-{c, d},
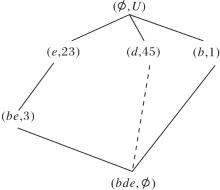
模糊语言属性偏序结构图如图10所示.在图中
R (U, A-{c, d},
的对象划分集合为
U/h5={{1}, {2}, {3}, {4}, {5}},
因此, 与R(U, A,
R (U, A-{c, d},
未发现未向底层节点建立边的节点, 算法结束.输出属性约简集D2={a, b, e}.
由上述步骤可知, 属性约简集为{a, b, d}和{a, b, e}, 对比R(U, A-{c, d},
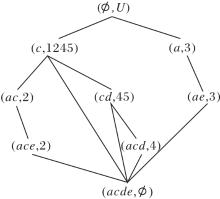
当在算法中设置(Ø , U)∉Γ 时, 属性约简步骤如下.
1)按照由上到下、由左到右的顺序扫描
R(U, A,
首个发现未向底层节点建立边的节点为(c, 1245), 其子节点有(bc, 12), (cd, 45), 可选择删除属性b或d.
2)当删除属性b时, 更新
R(U, A,
为
R(U, A-{b},
模糊语言属性偏序结构图如图11所示.在图中,
R(U, A-{b},
的对象划分集合为
U/h1={{1}, {2}, {3}, {4}, {5}},
因此
R(U, A-{b},
与R(U, A,
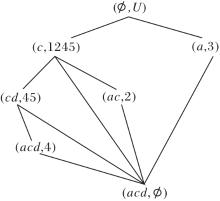
3)扫描
R(U, A-{b},
R(U, A-{b},
为
R(U, A-{b, e},
模糊语言属性偏序结构图如图12所示.在图中
R(U, A-{b, e},
的对象划分集合为
U/h2={{1}, {2}, {3}, {4}, {5}},
R(U, A-{b, e},
与R(U, A,
4)扫描
R(U, A-{b, e},
除顶层节点外, 未发现未向底层节点建立边的节点, 算法结束.输出属性约简集D3={a, c, d}及其约简图R(U, D3,
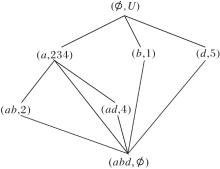
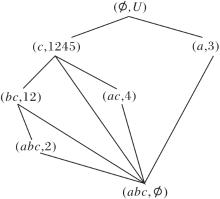
同理, 当删除属性d时, 最终得到的属性约简结果为D4={a, b, c}, 模糊语言属性偏序结构图如图13所示.
本节通过在真实数据集上实现模糊语言属性偏序结构图在不同模糊语言值信任度λ 上的构建及属性约简, 进而验证LLAR的有效性.
实验环境如下:CPU为Intel(R)Core(TM) i5-10400FCPU@2.90 GHz, 16 GB内存, 软件环境为Windows10下的python 3.9.
使用UCI数据集上的Iris、Glass Identification、Ionosphere、Winequality-Red这4个真实数据集评估LLAR.为了说明LLAR的有效性, 将这4个数据集进行转置, 使其属性数量增多, 更明显表现LLAR的效果.具体数据集信息如表3所示.
| 表3 实验数据集 Table 3 Experimental datasets |
LLAR可以处理不确定性环境中的多个模糊语言值.将表3中的原始数据集通过模糊语言值信任度λ 转化为模糊语言值形式背景(U, A,
| 表4 模糊语言值形式背景(U, A, |
在4个不同的模糊语言值形式背景(U, A,
不同模糊语言值信任度λ 下模糊语言属性偏序结构图的指标值变化情况如表5所示.由表可看出, 在模糊语言值形式背景(U, A,
| 表5 不同λ 对模糊语言属性偏序结构图的影响 Table 5 Influence of different λ on FL-APOSD |
为了验证LLAR在属性约简方面的有效性与实用性, 在4个数据集上进行实验, 并记录不同模糊语言值信任度λ 下LLAR的属性约简数量、约简率及运行时间, 具体如表6所示.由表可看出, 在不同模糊语言值形式背景(U, A,
| 表6 不同λ 对LLAR属性约简结果的影响 Table 6 Influence of different λ on LLAR attribute reduction results |
本文提出LLAR, 删除冗余属性的同时保证R(U, D,
本文选择如下属性约简算法进行实验对比:概念格约简方法(Concept Lattice Reduction Approach, CLR)[33]、SE-ISIAR(Attribute Reduction of SE-ISI Concept Lattices)[40] 、DM-methods[39]、DMSRC(Reduct Construction Method Based on Discernibility Matrix Simplification)[42]、MGLCR(Multi-granularity Linguistic Concept Reduction)[13] .各算法对比结果如表7所示.
本文在如下4方面上进行对比分析.
1)出发点.相比其它属性约简方法, 只有LLAR是以模糊语言属性偏序结构图为基础进行的属性约简.存在3个模型是以概念格为基础进行的属性约简.在形式背景(U, A, I)中, 构造属性偏序结构图的时间复杂度为O(|A|2), 构造概念格的时间复杂度为O(|U||A|2), 属性偏序结构图的生成效率高于概念格, 更适合应用于属性约简.
SE-ISIAR在三支概念格下进行属性约简, 可同时考虑正面信息与负面信息, 但是构建效率低于概念格.
CLR、SE-ISIAR、DM-methods、DMSRC都无法表达模糊语言值数据, MGLCR与LLAR可表达模糊语言值信息, 但MGLCR使用的模糊语言值会随着属性数量的增多而产生维度爆炸的问题, 并且MGLCR嵌入的模糊语言值数据是语义序关系, 无法表达模糊语言值的不可比性.
LLAR使用的FL-APOSD是由模糊语言值形式背景构建的, 模糊语言值数据通过语言真值格蕴涵代数表示, 可同时处理模糊语言值的可比信息与不可比信息.此外, FL-APOSD的构建效率与可解释性都优于语言概念格.
2)约简原理.由于LLAR是在FL-APOSD下进行的属性约简, 因此, 得到的属性约简结果是保持对象的区别能力不变的最小属性子集.而其它方法是在不同种类的概念格下进行属性约简, 得到的是保持其概念结构不变的最小属性子集.
3)约简图.仅有LLAR可产生约简图, 从而可直接观察对象之间的区分方式, 明确属性约简结果中每个属性的作用. 每个约简过程产生的约简图方便人工纠正约简信息, 提高LLAR的鲁棒性.相比其它基于辨识矩阵的方法, 属性偏序结构图能更完整地表达信息, 有利于部分对象的识别.
4)背景知识.CLR、SE-ISIAR、DM-methods、DM-SRC未使用背景知识.MGLCR将模糊语言值的语义序作为背景知识, 指导语言概念格下的属性约简工作.LLAR在约简每个属性时都充分利用FL-APOSD的节点, 保持与FL-APOSD类等价.在模糊语言值形式背景中, 使用语言真值格蕴涵代数作为模糊语言值的表示模型, 引入模糊语言值的序关系与不可比关系作为背景知识.
此外, 在同个模糊语言值形式背景中, 选取的模糊语言值信任度λ 不同, 产生的FL-APOSD不同.因此, LLAR得到的属性约简结果也不同.可通过选择模糊语言值信任度满足不同风险偏好的决策者对于同一模糊语言值形式背景属性约简结果的不同需要.
| 表7 各算法结果对比 Table 7 Result comparison analysis of different methods |
本文利用模糊语言属性偏序结构图能发掘属性间关系和区分对象及嵌入模糊语言值数据的特征, 提出基于模糊语言属性偏序结构图的逐层属性约简算法.对比分析和实例表明, LLAR可有效地为模糊语言值形式背景提供可解释性属性约简, 同时动态展示每个属性的约简过程, 鲁棒性较强.LLAR在模糊语言属性偏序结构图下进行属性约简, 不但可提高效率, 而且保存搜索路径, 容易追溯约简的依据, 以直观方式展现属性约简的过程, 可解释性较强.此外, 将模糊语言值数据嵌入形式背景中, 可减少数值转化为语言值造成的信息缺失, 更贴近人类的思维模式.LLAR体现数据动态更新过程, 在处理带有属性偏好关系的模糊语言值形式背景属性约简问题上具有一定优势.可通过语言真值格蕴涵代数表示模糊语言值信息, 有效利用模糊语言值的序关系与不可比关系的背景知识.
随着语言真值格蕴涵代数中元数的增加, FL-APOSD的构建效率会逐渐降低, 如何在语言真值格蕴涵代数全局结构下设计FL-APOSD构造算法, 并在此基础上研究新的属性约简方法是一个值得研究的方向.本文只对FL-APOSD的构建模型与属性约简方法进行初步探索, 今后可考虑将FL-APOSD应用于不同领域的知识发现任务中.此外, 今后也将考虑研究动态模糊语言信息系统约简问题, 并设计带偏好的属性约简算法.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|
| [19] |
|
| [20] |
|
| [21] |
|
| [22] |
|
| [23] |
|
| [24] |
|
| [25] |
|
| [26] |
|
| [27] |
|
| [28] |
|
| [29] |
|
| [30] |
|
| [31] |
|
| [32] |
|
| [33] |
|
| [34] |
|
| [35] |
|
| [36] |
|
| [37] |
|
| [38] |
|
| [39] |
|
| [40] |
|
| [41] |
|
| [42] |
|
| [43] |
|
| [44] |
|
| [45] |
|