吴伟志,博士,教授,主要研究方向为粗糙集、粒计算、数据挖掘、人工智能.E-mail:wuwz@zjou.edu.cn.
吴伟志,博士,教授,主要研究方向为粗糙集、粒计算、数据挖掘、人工智能.E-mail:wuwz@zjou.edu.cn.
作者简介: 张嘉茹,硕士研究生,主要研究方向为粗糙集、粒计算.E-mail:1697628349@qq.com.
张嘉茹,硕士研究生,主要研究方向为粗糙集、粒计算.E-mail:1697628349@qq.com.
 杨烨,硕士研究生,主要研究方向为粗糙集、粒计算.E-mail:1523562213@qq.com.
杨烨,硕士研究生,主要研究方向为粗糙集、粒计算.E-mail:1523562213@qq.com.
决策多尺度信息系统是一类特殊的数据集,系统中的每个对象无论在条件属性集上还是在决策属性上都可取多个尺度的标记值,并且从细粒度标记属性值到粗粒度标记属性值有一个信息粒度变换.文中针对广义决策多尺度序信息系统的知识获取问题展开研究.首先,引入尺度选择概念,一个尺度选择对应一个单尺度的序决策系统,并将优势关系引入广义决策多尺度信息系统,给出在不同尺度选择下对象集的优势类和集合的下近似和上近似的定义及其性质.然后,在协调广义决策多尺度序信息系统中定义5种最优尺度选择的概念,证明实际上只有2种不同类型的最优尺度选择,即最优尺度选择、下近似最优尺度选择、信任最优尺度选择是等价的,而上近似最优尺度选择与似然最优尺度也是等价的.最后,给出协调广义决策多尺度序信息系统的辨识矩阵约简方法,并在最优尺度选择基础上给出蕴含在协调广义决策多尺度序信息系统中的序决策规则.
Author:ZHANG Jiaru, master student. Her research interests include rough set and granular computing.
YANG Ye, master student. Her research interests include rough set and granular computing.
A decision Multi-scale inforMation systeM is a sPecial tyPe of Multi-scale data set and each object under each attribute in the systeM froM either the condition attribute set or the decision attribute is rePresented by different scales at different levels of the granulations, holding a granular inforMation transforMation froM a finer to a coarser labelled value. To solve the ProbleM of knowledge acquisition in generalized decision Multi-scale ordered inforMation systeMs, the concePt of scale selection is firstly defined. Each scale selection is linked with a single-scale ordered decision systeM. DoMinance relations are also introduced into decision Multi-scale inforMation systeMs, rePresentations of inforMation granules as well as lower and uPPer aPProxiMations of sets under different scale selections are Presented, and their relationshiPs are exaMined. Then, five tyPes of oPtiMal scale selections in consistent generalized decision Multi-scale ordered inforMation systeMs are defined. It is Proved that there are indeed two different tyPes of oPtiMal scale selections. The notions of oPtiMal scale selection, lower aPProxiMation oPtiMal scale selection and belief oPtiMal scale selection are all equivalent, and a scale selection is uPPer aPProxiMation oPtiMal if and only if it is Plausibly oPtiMal. Finally, based on oPtiMal scale selections, a Method of discernibility Matrix attribute reduction and ordered decision rules hidden in consistent generalized decision Multi-scale ordered inforMation systeMs are exPlored.
粒计算(Granular CoMPuting, GrC) [1, 2, 3, 4]是人工智能领域活跃的研究方向之一.它模拟人类问题思考模式, 以粒(Granule)为基本计算单位, 通过信息粒化等手段达到简化复杂问题求解的主要目标.粒计算的研究主要集中在粒的描述、表示与构造, 粒的多层次合成与分解, 具有多层次或多粒度结构数据的信息粒的变换、最优粒度或尺度的选择, 蕴含在数据集上的粒与粒之间的IF-THEN规则的提取, 以及粒结构的不确定性分析等.目前, 粒计算已成为大数据挖掘与决策分析的一种重要研究方法[5, 6, 7, 8, 9].
粗糙集[10]是推动和发展粒计算研究的一个重要数据分析模型, 它以各种各样的信息系统(InforMation SysteMs)或决策系统(Decision SysteMs)为数据分析对象, 通过定义在数据样本集上的二元关系构造“ 粒” , 粒化论域或样本空间, 并通过属性约简方法挖掘蕴含在数据集上的决策规则集.传统粗糙集数据分析呈现的数据集大都是单尺度形式的, 即信息系统中每个对象在每个属性上只取唯一的值.然而, 在实际生活中, 人们可能需要在多粒度或多尺度环境下处理和分析数据, 要在不同尺度下对同一对象在同一属性下的数据进行观察、分析并做出相应决策.为此, Wu等[11]提出多尺度粗糙集数据分析模型, 处理的数据集称为多尺度信息系统, 系统中的每个对象在同个属性下根据不同的尺度呈现不同标记的值, 并且从细尺度的属性值到粗尺度的属性值都有相应的信息粒度变换.这种数据处理模型又称为Wu-Leung模型[12].在该模型中, 较细尺度对应的数据所含信息较详细, 但是意味着获取信息成本较高, 而较粗尺度对应的数据所含信息较少, 获取信息成本也较低.在实际问题研究中, 选取合适尺度去解决问题就显得至关重要.多尺度粗糙集数据分析的核心思想是:根据决策目标, 对每个属性选择一个合适的尺度或粒度(称为最优尺度), 构成一个新的单尺度信息系统, 再在保持相同目标约束要求下使用粗糙集方法给出属性约简, 做出最终的决策(如分类、聚类或排序决策等).因此, 多尺度信息系统或多尺度决策系统中的最优尺度选择是从该类数据集上获取知识的关键步骤, 现已成为多尺度粗糙集数据分析的一个重要研究方向[13, 14, 15, 16, 17, 18, 19, 20, 21].
经典Wu-Leung模型的一个基本假设是数据集上所有属性具有相同的尺度个数, 并且在数据分析时只能取同层尺度.然而在实际问题中, 数据集上不同属性可能具有不同的尺度个数, 为此, Li等[12]引入尺度组合的概念, 提出广义多尺度信息系统的知识获取模型.近年来, 针对各类广义多尺度信息系统的最优尺度组合及知识获取的研究受到相关研究人员的关注, 并取得重要进展[22, 23, 24, 25, 26, 27, 28, 29, 30].由于Li等[12]提出的广义多尺度决策表的决策属性是单尺度的, 在实际应用中, 同一对象的决策属性也可能根据不同尺度取不同的值.为此, Huang等[31]提出决策属性也是多尺度的广义多尺度信息系统(简称为广义决策多尺度信息系统)的数据分析模型, 研究协调广义决策多尺度信息系统的最优尺度选择方法.
证据理论, 又称DeMPster-Shafer证据理论[32](简称D-S证据理论), 是处理不精确和不确定性问题的数学工具之一.它的核心思想是通过由信任结构导出的一对信任函数与似然函数刻画概念的不确定性.粗糙集理论的下近似集与上近似集和证据理论的信任测度与似然测度可分别看作是对同个不确定概念(集合)的定性和定量不确定性表示, 因此, 两个理论具有很强的关联性.相关研究已证实, 由粗糙近似空间导出的集合的下近似概率和上近似概率一定是某个信任结构下的信任测度与似然测度, 反之, 任给一个信任结构及其导出的信任函数与似然函数, 一定可表示为某个粗糙近似空间下的下近似概率和上近似概率[33, 34, 35].基于这两个理论之间的关系, 学者们提出利用证据理论进行粗糙集数据分析, 取得很多重要成果[36].近几年, 使用证据理论刻画多尺度环境下的最优尺度选择也取得一些研究进展.
众所周知, 多属性决策或排序是粗糙集数据分析中一类重要的研究问题, 也是现实生活中较常见的数据处理问题.Greco等[37, 38, 39]定义序信息系统中属性(在序信息系统中又称为准则)子集导出的优势关系, 提出基于优势关系的粗糙集方法(DoMi-nance-Based Rough Set APProach, DRSA), 解决序信息系统或序决策系统的序IF-THEN规则的提取或排序问题.随后, 针对不同数据类型的DRSA也相继被提出[40, 41, 42, 43].Xu等[44]使用证据理论的信任函数与似然函数, 研究序信息系统的属性约简问题, 而Du等[45]使用证据理论的信任函数与似然函数, 讨论序决策系统的属性约简问题.
近年来, 针对多尺度环境下信息系统的多属性决策、排序等问题已受到相关领域研究人员的关注[46, 47, 48].Zheng等[20]研究Wu-Leung模型下多尺度序信息系统的最优尺度选择问题, 使用证据理论中的信任函数与似然函数等价刻画协调和不协调多尺度序决策系统中下近似最优尺度和上近似最优尺度的特征.
尽管多尺度环境下很多数据类型的最优尺度选择和知识获取方面的研究取得重要进展, 但迄今未有学者对决策属性也是多尺度的多尺度序信息系统(称为决策多尺度序信息系统)的知识获取方面展开研究.本文在文献[20]和文献[31]基础上, 探索研究协调决策多尺度序信息系统的最优尺度选择及其相应的序决策规则提取问题.
在本文中, 对于给定的非空有限集合U={x1, x2, …, xr}(也称为论域), 记P(U)为U的幂集.对于X∈ P(U), 记~X为X在U上的补集, 即
~X=U-X={x∈ U|x∉X}.
定义1[10] 称S=(U, A)为一个信息系统, 其中U={x1, x2, …, xr}为一个非空有限对象集, 称为论域, A={a1, a2, …, aM}为一个非空有限属性集, 对于∀ a∈ A, 有a∶ U→ Va, 即a(x)∈ Va, x∈ U, 其中
Va={a(x)|x∈ U}
为属性a的值域.
对于信息系统S=(U, A), B⊆A, 记
RB={(x, y)∈ U× U|a(x)=a(y), ∀ a∈ B},
RB为由属性子集B诱导的不可分辨关系, RB可将U中元素分成两两不相交的等价类, 即
[x]B={y∈ U|(x, y)∈ RB}, ∀ x∈ U,
它们构成U的一个划分, 即
U/RB={[x]B|x∈ U}.
对于X∈ P(U), X关于属性子集B的下近似和上近似定义如下:
定义2[31] 称S=(U, C∪ {d})为一个具有多尺度决策的广义多尺度信息系统, 简称为广义决策多尺度信息系统, 其中,
(U, C)=(U, {
为一个广义多尺度信息系统, d∉C为具有n个尺度的决策属性, S也可表示为
S=(U, C∪ {d})=(U, {
在广义决策多尺度信息系统
S=(U, C∪ {d})=(U, {
中,
即
称
使得
dt+1=
即
dt+1(x)=
称
定义3[31] 设
S=(U, C∪ {d})=(U, {
为一个广义决策多尺度信息系统, 若将条件属性aj(1≤ j≤ M)限制在该属性的第ij(1≤ ij≤ Ij)尺度下, 则
K=(i1, i2, …, iM)
称为S的条件属性的一个尺度组合, 记S的条件属性尺度组合全体为K.若在此基础上将决策属性d限制在第t(1≤ t≤ n)尺度下, 则
Q=(i1, i2, …, iM, t)
称为S的一个尺度选择.记S的尺度选择全体为Q, 则每个尺度选择
(i1, i2, …, iM, t)=Q∈ Q
形成一个单尺度决策表SQ=(U, CK∪ {dt}), 其中
CK={
定义4 设
S=(U, C∪ {d})=(U, {
为一个广义决策多尺度信息系统.对于两个尺度组合
K1=(
若对∀ j∈ {1, 2, …, M}, 都有
Q1=(
若对∀ j∈ {1, 2, …, M}, 都有
设
S=(U, C∪ {d})=(U, {
为一个广义决策多尺度信息系统, Q为S的尺度选择全体.对于
Q1=(
定义
Q1∧ Q2=(
Q1∨ Q2=(
其中,
且
t1∧ t2=Min{t1, t2}, t1∨ t2=Max{t1, t2},
则可验证
Q1≼Q2⇔ Q1∧ Q2=Q1⇔ Q1∨ Q2=Q2.
且(Q, ≼, ∧ , ∨ )为一个有界格, 其中(1, 1, …, 1, n)为最小元, (I1, I2, …, IM, 1)为最大元.
定义5 称二元组(L, ⩽)为一个全序集, 其中L≠ Ø 称为标记集, ⩽为L上的二元关系, 满足
1)自反性.对于∀ x∈ L, x⩽x.
2)传递性.对于∀ x∈ L, y∈ L, z∈ L, x⩽y, y⩽z蕴含x⩽z.
3)⩽是线性序.对于∀ x∈ L, y∈ L, 或x⩽y, 或y⩽x.
定义6 对于2个全序集(L1, ⩽1)和(L2, ⩽2), 若映射
g∶ (L1, ⩽1)→ (L2, ⩽2),
对∀ l∈ L1, s∈ L1, 有
l⩽1s⇒ g(l)⩽2g(s),
则称映射g为保序的.
不失一般性, 本文讨论序信息系统中的属性取值按照优先级递增排序.在信息系统S=(U, A)中, 若属性a的值域是全序集, 则称属性a为一个标准或准则.设a∈ A为一个准则, 在a的值域Va上建立偏序关系⩾a, 对于x∈ U, y∈ U, y⩾a x意为关于准则a, 对象y至少和对象x一样优, 或者说对象y支配对象x.若对于准则集B⊆A, y⩾B x, 意为对于∀ a∈ B, y⩾a x, 即对于B中的任意准则, 对象y至少和对象x一样优.
定义7[40] 设S=(U, A)为一个信息系统, 若S的条件属性集A={a1, a2, …, aM}中每个属性都是标准或准则, 则称S为一个序信息系统(Ordered InforMation SysteM, OIS).
在序信息系统中, 对于B⊆A, 记
称
[x
[x
U/
U/
对于X∈ P(U), B⊆A, X关于优势关系
定义8[40] 称S=(U, A∪ {d})为一个序决策系统(Ordered Decision SysteM, ODS), 若S=(U, A)为一个序信息系统, 决策属性d∉A也是标准或准则, 记
则
[x
[x
U/
U/
定义9[32] 设U为一个非空有限集合, 对于一个集合函数M∶ P(U)→ [0, 1], 若满足
M(Ø )=0,
则称M为一个Mass函数或一个基本概率指派.
对于一个集合X∈ P(U), 若M(X)> 0, 则称X为函数M的一个焦元.记
M={X∈ P(U)|M(X)> 0}
为M的全体焦元构成的集合, 则称序对(M, M)为U上的一个信任结构.
任何一个信任结构可导出一对信任函数与似然函数.
定义10[32] 设(M, M)为U上的一个信任结构, 在U上定义信任函数Bel∶ P(U)→ [0, 1]和似然函数Pl∶ P(U)→ [0, 1]如下:
Bel(X)=
可验证, 信任函数和似然函数是对偶的, 即
Bel(X)=1-Pl(~X), Pl(X)=1-Bel(~X),
其中~X为X在U中的补集.
粗糙集理论和D-S证据理论之间具有较强的联系, 已证实, 信息系统中每个属性子集导出的集合的下近似概率与上近似概率分别为该集合在某个信任结构下的信任度与似然度.
定理1[33] 设S=(U, A)为一个信息系统, 对于∀ X∈ P(U), B⊆A, 记
BelB(X)=P
其中,
P(X)=
|X|为X的基数, 则
Bel∶ P(U)→ [0, 1], Pl∶ P(U)→ [0, 1]
分别为U上的信任函数与似然函数, 对应的Mass函数为:
MB(X)=
定义11 设
S=(U, C∪ {d})=(U, {
为一个广义决策多尺度信息系统, 若对于
Q1=(1, 1, …, 1)∈ Q,
为一个序决策系统, 且对于每个条件属性aj(j∈ {1, 2, …, M})和每个尺度k∈ {1, 2, …, Ij-1}, 条件属性aj(j∈ {1, 2, …, M})的信息粒度变换
由定义11知, 只要
为序决策系统, 且条件属性的信息粒度变换和决策属性的信息粒度变换都是保序的, 则对于S的任意一个尺度选择
Q=(K, t)∈ Q, K∈ K,
对应的决策系统
SQ=(U, CK∪ {dt})
都是一个序决策系统.
定义12 设
S=(U, C∪ {d})=(U, {
为一个广义决策多尺度序信息系统,
K=(i1, i2, …, iM)∈ K,
记
[x
[x
U/
U/
对于∀ X∈ P(U), X关于
类似于文献[20], 可证明命题1成立.
命题1 设
S=(U, C∪ {d})=(U, {
为一个广义决策多尺度序信息系统,
X∈ P(U), Y∈ P(U), K∈ K, Q=(K, t)∈ Q,
则如下性质成立:
1)
2)
3)
4)
5)
6)若X⊆Y, 则
7)
8)若K'∈ K, K≼K', 则
9)若记
KMin=(1, 1, …, 1)∈ K, KMax=(I1, I2, …, IM)∈ K,
则对于∀ K∈ K, 有
定义13 设
S=(U, C∪ {d})=(U, {
为一个广义决策多尺度序信息系统,
∀ x∈ U, K∈ K, Q=(K, t)∈ Q,
记
[x
[x
U/
U/
∀ x∈ U, [x
决策属性dt关于
Po
类似于文献[20], 可得命题2.
命题2 设
S=(U, C∪ {d})=(U, {
为一个广义决策多尺度序信息系统, 对于
∀ x∈ U, K∈ K, K'∈ K, K≼K',
则
1)
2)
3)
4)
t∈ {1, 2, …, n-1},
5)Po
r(CK', dt)≤ r(CK, dt),
6)Po
r(CK, dt)≤ r(CK, dt+1),
t∈ {1, 2, …, n-1},
7)若KMin=(1, 1, …, 1)∈ K,
KMax=(I1, I2, …, IM)∈ K,
则对于∀ K∈ K, 都有
r(
类似于文献[44]和文献[45]可得, 广义决策多尺度序信息系统中每个尺度组合下集合的下近似集与上近似集的概率一定是某个信任结构下该集合的信任度与似然度.
定理2 设
S=(U, C∪ {d})=(U, {
为一个广义决策多尺度序信息系统, K∈ K, 对于X∈ P(U), 记
则
分别为U上一对对偶的信任函数与似然函数, 对应的Mass函数为:
其中,
推论1 设
S=(U, C∪ {d})=(U, {
为一个广义决策多尺度序信息系统, 对于K1∈ K, K2∈ K, K1≼K2, 则对于∀ X∈ P(U), 信任函数
尺度选择是从多尺度信息系统中知识获取的一个关键步骤, 在广义决策多尺度序信息系统中, 寻找最优尺度选择的目的是从系统中选择一个合适的单尺度序决策系统, 用于最终的决策规则提取.
定义14 设
S=(U, C∪ {d})=(U, {
为一个广义决策多尺度序信息系统,
K1=(1, 1, …, 1)∈ K
为条件属性集C的最细尺度组合.对于t∈ {1, 2, …, n}, 若
定义15 设
S=(U, C∪ {d})=(U, {
为一个广义决策多尺度序信息系统, 对于
K=(i1, i2, …, iM)∈ K,
对应一个具有多尺度决策的单尺度信息系统
SK=(U, CK∪ {d})=(U, {
对于t∈ {1, 2, …, n}, 若
定理3 设
S=(U, C∪ {d})=(U, {
为一个广义决策多尺度序信息系统, K∈ K, K'∈ K, 若K≼K', 且SK'是协调的, 则SK也是协调的.
证明 一方面, 由于SK'=(U, CK'∪ {d})是协调的, 因此
SK=(U, CK∪ {d})
也是协调的. 证毕.
定理4 设
S=(U, C∪ {d})=(U, {
为一个广义决策多尺度序信息系统,
Q1=(K1, t1)∈ Q, Q2=(K2, t2)∈ Q, Q1≼Q2,
若序决策系统
证明 由于
定义16 设
S=(U, C∪ {d})=(U, {
为一个协调广义决策多尺度序信息系统, 对于
Q=(K, t)∈ Q,
若满足
1)SQ是协调的, 即
2)对任意满足Q≺Q'的Q'=(K', t')∈ Q, SQ'是不协调的, 即
则称Q=(K, t)为S的一个最优尺度选择, 并称
SQ=(U, CK∪ {dt})
为S的一个最优协调序决策系统.
由定义16可见, 一个协调广义决策多尺度序信息系统S=(U, C∪ {d})的一个最优尺度选择
Q=(K, t)∈ Q
是Q中使SQ是协调的最粗的尺度选择, 因此, 寻求协调广义决策多尺度序信息系统的一个最优尺度选择问题可转化为求以下最优解问题:
Max
满足上述最优解问题的一个尺度选择Q就是S的一个最优尺度选择.
定义17 设
S=(U, C∪ {d})=(U, {
为一个协调广义决策多尺度序信息系统, K1=(1, 1, …, 1)∈ K, Q=(K, t)∈ Q,
则
1)若对于∀ x∈ U, 有
2)若对于∀ x∈ U, 都有
定义18 设
S=(U, C∪ {d})=(U, {
为一个协调广义决策多尺度序信息系统,
K1=(1, 1, …, 1)∈ K, Q=(K, t)∈ Q,
则
1)若对于∀ x∈ U, 都有
Be
则称SQ关于S是信任协调的; 若SQ关于S是信任协调的, 且对于任意满足Q≺Q'的
Q'=(K', t')∈ Q,
∃y∈ U, 使得Be
即SQ'关于S不是信任协调的, 则称Q=(K, t)是S的一个信任最优尺度选择.
2)若对于∀ x∈ U, 都有P
则称SQ关于S是似然协调的; 若SQ关于S是似然协调的, 且对于任意满足Q≺Q'的Q'=(K', t')∈ Q,
∃y∈ U, 使得
P
即SQ'关于S不是似然协调的, 则称Q=(K, t)是S的一个似然最优尺度选择.
定理5 设
S=(U, C∪ {d})=(U, {
为一个协调广义决策多尺度序信息系统,
Q=(K, t)∈ Q,
则
1)SQ关于S是下近似协调的当且仅当SQ关于S是信任协调的.
2)Q是S的下近似最优尺度选择当且仅当Q是S的信任最优尺度选择.
3)SQ关于S是上近似协调的当且仅当SQ关于S是似然协调的.
4)Q是S的上近似最优尺度选择当且仅当Q是S的似然最优尺度选择.
证明 先证1).充分性.设SQ关于S是下近似协调, 则对∀ x∈ U, 有
从而
P
即
Be
因此, SQ关于S是信任协调的.
必要性.若SQ关于S是信任协调的, 则对∀ x∈ U,
即
又由于
于是可得
因此, SQ关于S是下近似协调的.
再证2).由结论1)即得.
再证3)充分性.设SQ关于S是上近似协调的, 则对于∀ x∈ U, 有
从而
P
即
P
因此, SQ关于S是似然协调的.
必要性.若SQ关于S是似然协调的, 则对于∀ x∈ U, 有P
又由于
最后证明4).由结论3)即得. 证毕.
定理6 设
S=(U, C∪ {d})=(U, {
为一个协调广义决策多尺度序信息系统,
Q=(K, t)∈ Q,
则SQ是协调的当且仅当SQ关于S是信任协调的.
证明 充分性.设SQ是协调的, 则∀ x∈ U, 有
[x
由命题1知,
成立, 对于∀ y∈ [x
[y
由于SQ关于S是协调的, 即[y
[x
这样就证明
又由于K1=(1, 1, …, 1)是最细的尺度组合, 因此
[x
从而
[x
即序决策系统
成立, 于是
再由定理5知
Be
即SQ关于S是信任协调的.
必要性.设SQ是关于S信任协调的, 由定理5知, 对于∀ x∈ U, 有
反证, 假如SQ是不协调的, 即
定义19 设
S=(U, C∪ {d})=(U, {
为一个协调广义决策多尺度序信息系统,
K1=(1, 1, …, 1)∈ K,
对于t∈ {1, 2, …, n}, S的信任和Mt与似然和Nt分别定义为
Mt=
其中,
U/
为决策属性d在第t个尺度下决策优势类全体.
定理7 设
S=(U, C∪ {d})=(U, {
为一个广义决策多尺度序信息系统,
Q=(K, t)∈ Q,
则
1)SQ是协调的当且仅当
2)Q=(K, t)∈ Q为S的最优尺度选择当且仅当
且对任意满足Q≺Q'的
Q'=(K', t)∈ Q,
有
证明 由定理6和推论1即证明1).由结论1)即证明2). 证毕.
定理8 设
S=(U, C∪ {d})=(U, {
为一个协调广义决策多尺度序信息系统, Q=(K, t)∈ Q,
则
1)SQ是似然协调的当且仅当
2)Q=(K, t)∈ Q是S的似然最优尺度选择当且仅当
证明 类似于定理7的证明. 证毕.
由上述结论可见, 保持序决策系统是协调的最粗尺度选择(即最优尺度选择)与下近似最优尺度选择和信任最优尺度选择都是等价的, 而上近似最优尺度选择与似然最优尺度选择也是等价的.因此, 定义16~定义18给出的5种类型的最优尺度选择概念实际上只有2种不同的类型.
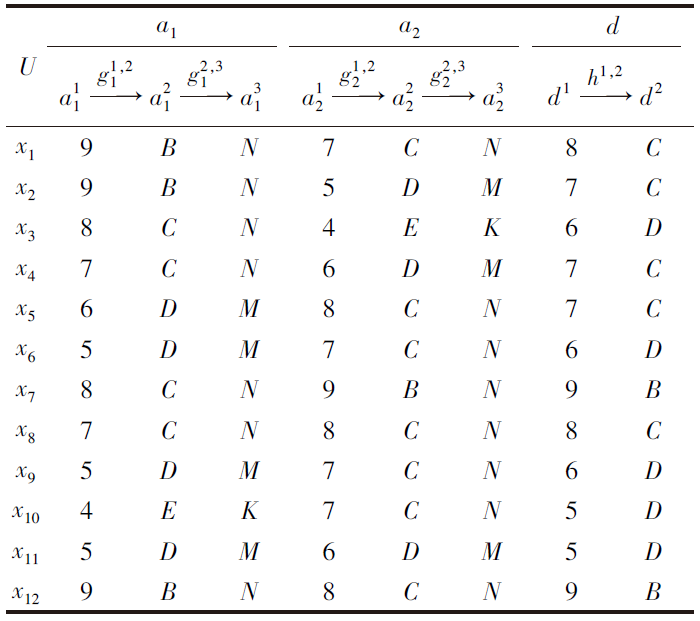
例1 表1为一个广义决策多尺度序信息系统
S=(U, C∪ {d})=(U, {
其中,
U={x1, x2, x3, x4, x5, x6, x7, x8, x9, x10, x11, x12}, C={a1, a2}.
条件属性a1、a2都有3个尺度, 决策属性d有2个尺度.条件属性a1、a2和决策属性
d={dt|t=1, 2}
的信息粒度变换分别如下.对于x∈ U:
1)
2)
3)h1, 2∶
其中, 数值型值域
B> C> D> E, N> M> K.
| 表1 一个广义决策多尺度序信息系统 Table 1 A generalized decision Multi-scale ordered inforMation systeM |
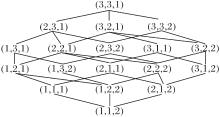
图1为S的全体尺度选择的格结构.
1)判断S是否是协调的; 2)确定S的最优尺度选择; 3)确定S的上近似最优尺度选择、下近似最优尺度选择、信任最优尺度选择和似然协调最优尺度选择.
解:1)对于K1=(1, 1), 即
[x1
[x2
[x3=
[x4={
[x5={x
[x6={x1
[x7
[x8
[x10=
[x11={
[x12={x
即
U/
{x1, x4, x7, x8, x11}, {x5, x7, x8, x12},
{x1, x5, x6, x7, x8, x9, x12}, {x7}, {x7, x8, x12},
{x1, x5, x6, x7, x8, x9, x10, x12},
{x1, x4, x5, x6, x7, x8, x9, x11, x12}, {x12}}.
对于d1, 有
[x1
[x2
[x3
[X7
[x10
则
U/
对于d2, 有
[x1
[x3
U=[x6
[x7
即
U/
易见U/
2)设K2=(1, 2), 即
U/
{x1, x2, x4, x7, x8, x12}, {x1, x5, x7, x8, x12},
{x1, x5, x6, x7, x8, x9, x12}, {x7},
{x1, x7, x8, x12},
{x1, x5, x6, x7, x8, x9, x10, x12},
{x1, x2, x4, x5, x6, x7, x8, x9, x11, x12}},
因此
U/
设K3=(2, 1), 即
U/
{x1, x2, x3, x4, x7, x8, x12}, {x1, x4, x7, x8, x12},
{x5, x7, x8, x12}, {x1, x5, x6, x7, x8, x9, x12},
{x7}, {x7, x8, x12},
{x1, x5, x6, x7, x8, x9, x10, x12},
{x1, x4, x5, x6, x7, x8, x9, x11, x12}, {x12}},
因此
U/
设K4=(2, 2), 即
U/
{x1, x2, x3, x4, x7, x8, x12},
{x1, x2, x4, x7, x8, x12},
{x1, x5, x6, x7, x8, x9, x12}, {x7},
{x1, x7, x8, x12},
{x1, x5, x6, x7, x8, x9, x10, x12},
{x1, x2, x4, x5, x6, x7, x8, x9, x11, x12}},
因此
U/
所以S有唯一的最优尺度选择(2, 1, 1).
3)求S的下近似最优尺度选择.只需验证当t=1时的情况即可, 对于K1=(1, 1), 即
对于K2=(1, 2), 即
且对于x12, 有
对于K3=(2, 1), 即
成立.
对于K4=(2, 2), 即
且对于x12, 有
所以S有唯一的下近似最优尺度选择(2, 1, 1).
求S的上近似最优尺度选择.当t=1时, 对于K1=(1, 1), 即
对于K2=(1, 2), 则
同理, 对于K9=(3, 3), 即
所以(3, 3, 1)是S的上近似最优尺度选择.
求S的信任最优尺度选择.当t=1时,
当t=2时,
因此, (2, 1, 1)为S的信任最优尺度选择.
求S的似然最优尺度选择.由于(3, 3, 1)是S的上近似最优尺度选择, 只需验证K9=(3, 3)和t=1时即可.
有
(3, 3, 1)为S的似然最优尺度选择.
对于S, (2, 1, 1)为最优尺度选择、下近似最优尺度选择和信任最优尺度选择, (3, 3, 1)为上近似最优尺度选择和似然最优尺度选择.
定义20 设
S=(U, C∪ {d})=(U, {
为一个协调广义决策多尺度序信息系统,
K∈ K, Q=(K, t)∈ Q,
若对于B⊆C, 有
定理9 设
S=(U, C∪ {d})=(U, {
为一个协调广义决策多尺度序信息系统,
K1∈ K, K2∈ K, K1≺K2, Q1=(K1, t)∈ Q, Q2=(K2, t)∈ Q.
若B是S的Q2-尺度协调集, 则B是S的一个Q1-尺度协调集.
证明 由定义20与定理3可证. 证毕.
定义21 设
S=(U, C∪ {d})=(U, {
为一个协调广义决策多尺度序信息系统,
K=(i1, i2, …, iM)∈ K, Q=(K, t)∈ Q,
定义
Dt={(x, y)∈ U× U|dt(x)< dt(y)},
其中
称
定义22 设
S=(U, C∪ {d})=(U, {
为一个协调广义决策多尺度序信息系统,
B⊆C, K∈ K, Q=(K, t)∈ Q,
定义
为S在尺度选择Q上的可辨识函数, 其中, ∧ 为合取, ∨ 为析取.
类似于文献[37]~文献[39], 将上式给出的合取式转化为极小析取范式, 则该极小析取范式中每个合取式中的属性集合就是系统的一个Q-尺度约简.
获取
本节在最优尺度选择约简的基础上给出蕴含在广义决策多尺度序信息系统中的序决策规则.
定义23 设
S=(U, C∪ {d})=(U, {
为一个广义决策多尺度序信息系统, 对于B⊆C,
K=(i1, i2, …, iM)∈ K,
蕴含在决策信息系统中的命题知识可使用决策规则的形式表示: t→ s, 其中, t为规则的前件, s为规则的后件, 表示由t可得出s.对同时满足规则的前件和后件的对象, 称为支持这条规则.
对于协调广义决策多尺度序信息系统, 结合原子公式的概念, 类似于Greco等[37, 38, 39]提出序决策规则, 可得蕴含在系统中基于优势关系的确定性序决策规则如下:
(
例2 (接例1) 由于S的最优尺度选择为Q=(2, 1, 1), 则可得到在尺度选择Q下S的可辨识矩阵如表2所示.
由于
于是, S在尺度选择Q=(2, 1, 1)下唯一的属性约简为{
序决策规则如下:
该规则支持的对象为x1, x7, x8, x12.
该规则支持的对象为x1, x2, x4, x5, x7, x8, x12.
该规则支持的对象为x1, x2, x3, x4, x5, x6, x7, x8, x9, x12.
该规则支持的对象为U.
| 表2 尺度选择Q下S的可辨识矩阵 Table 2 Discernibility Matrix of S under scale selection Q |
最优尺度选择是多尺度信息系统知识获取的一个关键步骤, 最优尺度选择的作用是从多尺度信息系统中找到一个符合目标条件的最优子表用于最终的决策(如聚类、分类或排序).本文针对协调广义决策多尺度序信息系统中的知识获取问题, 分别使用粗糙集理论和证据理论定义下近似最优尺度选择与上近似最优尺度选择、信任最优尺度选择与似然最优尺度选择的概念, 证明保持序决策系统是协调的最粗尺度选择(即最优尺度选择)与下近似最优尺度选择和信任最优尺度选择都是等价的, 而上近似最优尺度选择与似然最优尺度选择也是等价的.并在最优尺度选择基础上, 进一步使用粗糙集辨识矩阵方法给出属性约简, 最终获得蕴含在协调广义决策多尺度序信息系统中的序决策规则集.在后续研究中:一方面, 可进一步研究在协调和不协调广义决策多尺度序信息系统中局部最优尺度选择及规则提取问题; 另一方面, 其它更复杂数据类型(如不完备广义决策多尺度序信息系统等)的最优尺度选择及序决策规则提取也是值得研究的问题.
粒计算(Granular CoMPuting, GrC) [1, 2, 3, 4]是人工智能领域活跃的研究方向之一.它模拟人类问题思考模式, 以粒(Granule)为基本计算单位, 通过信息粒化等手段达到简化复杂问题求解的主要目标.粒计算的研究主要集中在粒的描述、表示与构造, 粒的多层次合成与分解, 具有多层次或多粒度结构数据的信息粒的变换、最优粒度或尺度的选择, 蕴含在数据集上的粒与粒之间的IF-THEN规则的提取, 以及粒结构的不确定性分析等.目前, 粒计算已成为大数据挖掘与决策分析的一种重要研究方法[5, 6, 7, 8, 9].
粗糙集[10]是推动和发展粒计算研究的一个重要数据分析模型, 它以各种各样的信息系统(InforMation SysteMs)或决策系统(Decision SysteMs)为数据分析对象, 通过定义在数据样本集上的二元关系构造“ 粒” , 粒化论域或样本空间, 并通过属性约简方法挖掘蕴含在数据集上的决策规则集.传统粗糙集数据分析呈现的数据集大都是单尺度形式的, 即信息系统中每个对象在每个属性上只取唯一的值.然而, 在实际生活中, 人们可能需要在多粒度或多尺度环境下处理和分析数据, 要在不同尺度下对同一对象在同一属性下的数据进行观察、分析并做出相应决策.为此, Wu等[11]提出多尺度粗糙集数据分析模型, 处理的数据集称为多尺度信息系统, 系统中的每个对象在同个属性下根据不同的尺度呈现不同标记的值, 并且从细尺度的属性值到粗尺度的属性值都有相应的信息粒度变换.这种数据处理模型又称为Wu-Leung模型[12].在该模型中, 较细尺度对应的数据所含信息较详细, 但是意味着获取信息成本较高, 而较粗尺度对应的数据所含信息较少, 获取信息成本也较低.在实际问题研究中, 选取合适尺度去解决问题就显得至关重要.多尺度粗糙集数据分析的核心思想是:根据决策目标, 对每个属性选择一个合适的尺度或粒度(称为最优尺度), 构成一个新的单尺度信息系统, 再在保持相同目标约束要求下使用粗糙集方法给出属性约简, 做出最终的决策(如分类、聚类或排序决策等).因此, 多尺度信息系统或多尺度决策系统中的最优尺度选择是从该类数据集上获取知识的关键步骤, 现已成为多尺度粗糙集数据分析的一个重要研究方向[13, 14, 15, 16, 17, 18, 19, 20, 21].
经典Wu-Leung模型的一个基本假设是数据集上所有属性具有相同的尺度个数, 并且在数据分析时只能取同层尺度.然而在实际问题中, 数据集上不同属性可能具有不同的尺度个数, 为此, Li等[12]引入尺度组合的概念, 提出广义多尺度信息系统的知识获取模型.近年来, 针对各类广义多尺度信息系统的最优尺度组合及知识获取的研究受到相关研究人员的关注, 并取得重要进展[22, 23, 24, 25, 26, 27, 28, 29, 30].由于Li等[12]提出的广义多尺度决策表的决策属性是单尺度的, 在实际应用中, 同一对象的决策属性也可能根据不同尺度取不同的值.为此, Huang等[31]提出决策属性也是多尺度的广义多尺度信息系统(简称为广义决策多尺度信息系统)的数据分析模型, 研究协调广义决策多尺度信息系统的最优尺度选择方法.
证据理论, 又称DeMPster-Shafer证据理论[32](简称D-S证据理论), 是处理不精确和不确定性问题的数学工具之一.它的核心思想是通过由信任结构导出的一对信任函数与似然函数刻画概念的不确定性.粗糙集理论的下近似集与上近似集和证据理论的信任测度与似然测度可分别看作是对同个不确定概念(集合)的定性和定量不确定性表示, 因此, 两个理论具有很强的关联性.相关研究已证实, 由粗糙近似空间导出的集合的下近似概率和上近似概率一定是某个信任结构下的信任测度与似然测度, 反之, 任给一个信任结构及其导出的信任函数与似然函数, 一定可表示为某个粗糙近似空间下的下近似概率和上近似概率[33, 34, 35].基于这两个理论之间的关系, 学者们提出利用证据理论进行粗糙集数据分析, 取得很多重要成果[36].近几年, 使用证据理论刻画多尺度环境下的最优尺度选择也取得一些研究进展.
众所周知, 多属性决策或排序是粗糙集数据分析中一类重要的研究问题, 也是现实生活中较常见的数据处理问题.Greco等[37, 38, 39]定义序信息系统中属性(在序信息系统中又称为准则)子集导出的优势关系, 提出基于优势关系的粗糙集方法(DoMi-nance-Based Rough Set APProach, DRSA), 解决序信息系统或序决策系统的序IF-THEN规则的提取或排序问题.随后, 针对不同数据类型的DRSA也相继被提出[40, 41, 42, 43].Xu等[44]使用证据理论的信任函数与似然函数, 研究序信息系统的属性约简问题, 而Du等[45]使用证据理论的信任函数与似然函数, 讨论序决策系统的属性约简问题.
近年来, 针对多尺度环境下信息系统的多属性决策、排序等问题已受到相关领域研究人员的关注[46, 47, 48].Zheng等[20]研究Wu-Leung模型下多尺度序信息系统的最优尺度选择问题, 使用证据理论中的信任函数与似然函数等价刻画协调和不协调多尺度序决策系统中下近似最优尺度和上近似最优尺度的特征.
尽管多尺度环境下很多数据类型的最优尺度选择和知识获取方面的研究取得重要进展, 但迄今未有学者对决策属性也是多尺度的多尺度序信息系统(称为决策多尺度序信息系统)的知识获取方面展开研究.本文在文献[20]和文献[31]基础上, 探索研究协调决策多尺度序信息系统的最优尺度选择及其相应的序决策规则提取问题.
在本文中, 对于给定的非空有限集合U={x1, x2, …, xr}(也称为论域), 记P(U)为U的幂集.对于X∈ P(U), 记~X为X在U上的补集, 即
~X=U-X={x∈ U|x∉X}.
定义1[10] 称S=(U, A)为一个信息系统, 其中U={x1, x2, …, xr}为一个非空有限对象集, 称为论域, A={a1, a2, …, aM}为一个非空有限属性集, 对于∀ a∈ A, 有a∶ U→ Va, 即a(x)∈ Va, x∈ U, 其中
Va={a(x)|x∈ U}
为属性a的值域.
对于信息系统S=(U, A), B⊆A, 记
RB={(x, y)∈ U× U|a(x)=a(y), ∀ a∈ B},
RB为由属性子集B诱导的不可分辨关系, RB可将U中元素分成两两不相交的等价类, 即
[x]B={y∈ U|(x, y)∈ RB}, ∀ x∈ U,
它们构成U的一个划分, 即
U/RB={[x]B|x∈ U}.
对于X∈ P(U), X关于属性子集B的下近似和上近似定义如下:
定义2[31] 称S=(U, C∪ {d})为一个具有多尺度决策的广义多尺度信息系统, 简称为广义决策多尺度信息系统, 其中,
(U, C)=(U, {
为一个广义多尺度信息系统, d∉C为具有n个尺度的决策属性, S也可表示为
S=(U, C∪ {d})=(U, {
在广义决策多尺度信息系统
S=(U, C∪ {d})=(U, {
中,
即
称
使得
dt+1=
即
dt+1(x)=
称
定义3[31] 设
S=(U, C∪ {d})=(U, {
为一个广义决策多尺度信息系统, 若将条件属性aj(1≤ j≤ M)限制在该属性的第ij(1≤ ij≤ Ij)尺度下, 则
K=(i1, i2, …, iM)
称为S的条件属性的一个尺度组合, 记S的条件属性尺度组合全体为K.若在此基础上将决策属性d限制在第t(1≤ t≤ n)尺度下, 则
Q=(i1, i2, …, iM, t)
称为S的一个尺度选择.记S的尺度选择全体为Q, 则每个尺度选择
(i1, i2, …, iM, t)=Q∈ Q
形成一个单尺度决策表SQ=(U, CK∪ {dt}), 其中
CK={
定义4 设
S=(U, C∪ {d})=(U, {
为一个广义决策多尺度信息系统.对于两个尺度组合
K1=(
若对∀ j∈ {1, 2, …, M}, 都有
Q1=(
若对∀ j∈ {1, 2, …, M}, 都有
设
S=(U, C∪ {d})=(U, {
为一个广义决策多尺度信息系统, Q为S的尺度选择全体.对于
Q1=(
定义
Q1∧ Q2=(
Q1∨ Q2=(
其中,
且
t1∧ t2=Min{t1, t2}, t1∨ t2=Max{t1, t2},
则可验证
Q1≼Q2⇔ Q1∧ Q2=Q1⇔ Q1∨ Q2=Q2.
且(Q, ≼, ∧ , ∨ )为一个有界格, 其中(1, 1, …, 1, n)为最小元, (I1, I2, …, IM, 1)为最大元.
定义5 称二元组(L, ⩽)为一个全序集, 其中L≠ Ø 称为标记集, ⩽为L上的二元关系, 满足
1)自反性.对于∀ x∈ L, x⩽x.
2)传递性.对于∀ x∈ L, y∈ L, z∈ L, x⩽y, y⩽z蕴含x⩽z.
3)⩽是线性序.对于∀ x∈ L, y∈ L, 或x⩽y, 或y⩽x.
定义6 对于2个全序集(L1, ⩽1)和(L2, ⩽2), 若映射
g∶ (L1, ⩽1)→ (L2, ⩽2),
对∀ l∈ L1, s∈ L1, 有
l⩽1s⇒ g(l)⩽2g(s),
则称映射g为保序的.
不失一般性, 本文讨论序信息系统中的属性取值按照优先级递增排序.在信息系统S=(U, A)中, 若属性a的值域是全序集, 则称属性a为一个标准或准则.设a∈ A为一个准则, 在a的值域Va上建立偏序关系⩾a, 对于x∈ U, y∈ U, y⩾a x意为关于准则a, 对象y至少和对象x一样优, 或者说对象y支配对象x.若对于准则集B⊆A, y⩾B x, 意为对于∀ a∈ B, y⩾a x, 即对于B中的任意准则, 对象y至少和对象x一样优.
定义7[40] 设S=(U, A)为一个信息系统, 若S的条件属性集A={a1, a2, …, aM}中每个属性都是标准或准则, 则称S为一个序信息系统(Ordered InforMation SysteM, OIS).
在序信息系统中, 对于B⊆A, 记
称
[x
[x
U/
U/
对于X∈ P(U), B⊆A, X关于优势关系
定义8[40] 称S=(U, A∪ {d})为一个序决策系统(Ordered Decision SysteM, ODS), 若S=(U, A)为一个序信息系统, 决策属性d∉A也是标准或准则, 记
则
[x
[x
U/
U/
定义9[32] 设U为一个非空有限集合, 对于一个集合函数M∶ P(U)→ [0, 1], 若满足
M(Ø )=0,
则称M为一个Mass函数或一个基本概率指派.
对于一个集合X∈ P(U), 若M(X)> 0, 则称X为函数M的一个焦元.记
M={X∈ P(U)|M(X)> 0}
为M的全体焦元构成的集合, 则称序对(M, M)为U上的一个信任结构.
任何一个信任结构可导出一对信任函数与似然函数.
定义10[32] 设(M, M)为U上的一个信任结构, 在U上定义信任函数Bel∶ P(U)→ [0, 1]和似然函数Pl∶ P(U)→ [0, 1]如下:
Bel(X)=
可验证, 信任函数和似然函数是对偶的, 即
Bel(X)=1-Pl(~X), Pl(X)=1-Bel(~X),
其中~X为X在U中的补集.
粗糙集理论和D-S证据理论之间具有较强的联系, 已证实, 信息系统中每个属性子集导出的集合的下近似概率与上近似概率分别为该集合在某个信任结构下的信任度与似然度.
定理1[33] 设S=(U, A)为一个信息系统, 对于∀ X∈ P(U), B⊆A, 记
BelB(X)=P
其中,
P(X)=
|X|为X的基数, 则
Bel∶ P(U)→ [0, 1], Pl∶ P(U)→ [0, 1]
分别为U上的信任函数与似然函数, 对应的Mass函数为:
MB(X)=
定义11 设
S=(U, C∪ {d})=(U, {
为一个广义决策多尺度信息系统, 若对于
Q1=(1, 1, …, 1)∈ Q,
为一个序决策系统, 且对于每个条件属性aj(j∈ {1, 2, …, M})和每个尺度k∈ {1, 2, …, Ij-1}, 条件属性aj(j∈ {1, 2, …, M})的信息粒度变换
由定义11知, 只要
为序决策系统, 且条件属性的信息粒度变换和决策属性的信息粒度变换都是保序的, 则对于S的任意一个尺度选择
Q=(K, t)∈ Q, K∈ K,
对应的决策系统
SQ=(U, CK∪ {dt})
都是一个序决策系统.
定义12 设
S=(U, C∪ {d})=(U, {
为一个广义决策多尺度序信息系统,
K=(i1, i2, …, iM)∈ K,
记
[x
[x
U/
U/
对于∀ X∈ P(U), X关于
类似于文献[20], 可证明命题1成立.
命题1 设
S=(U, C∪ {d})=(U, {
为一个广义决策多尺度序信息系统,
X∈ P(U), Y∈ P(U), K∈ K, Q=(K, t)∈ Q,
则如下性质成立:
1)
2)
3)
4)
5)
6)若X⊆Y, 则
7)
8)若K'∈ K, K≼K', 则
9)若记
KMin=(1, 1, …, 1)∈ K, KMax=(I1, I2, …, IM)∈ K,
则对于∀ K∈ K, 有
定义13 设
S=(U, C∪ {d})=(U, {
为一个广义决策多尺度序信息系统,
∀ x∈ U, K∈ K, Q=(K, t)∈ Q,
记
[x
[x
U/
U/
∀ x∈ U, [x
决策属性dt关于
Po
类似于文献[20], 可得命题2.
命题2 设
S=(U, C∪ {d})=(U, {
为一个广义决策多尺度序信息系统, 对于
∀ x∈ U, K∈ K, K'∈ K, K≼K',
则
1)
2)
3)
4)
t∈ {1, 2, …, n-1},
5)Po
r(CK', dt)≤ r(CK, dt),
6)Po
r(CK, dt)≤ r(CK, dt+1),
t∈ {1, 2, …, n-1},
7)若KMin=(1, 1, …, 1)∈ K,
KMax=(I1, I2, …, IM)∈ K,
则对于∀ K∈ K, 都有
r(
类似于文献[44]和文献[45]可得, 广义决策多尺度序信息系统中每个尺度组合下集合的下近似集与上近似集的概率一定是某个信任结构下该集合的信任度与似然度.
定理2 设
S=(U, C∪ {d})=(U, {
为一个广义决策多尺度序信息系统, K∈ K, 对于X∈ P(U), 记
则
分别为U上一对对偶的信任函数与似然函数, 对应的Mass函数为:
其中,
推论1 设
S=(U, C∪ {d})=(U, {
为一个广义决策多尺度序信息系统, 对于K1∈ K, K2∈ K, K1≼K2, 则对于∀ X∈ P(U), 信任函数
尺度选择是从多尺度信息系统中知识获取的一个关键步骤, 在广义决策多尺度序信息系统中, 寻找最优尺度选择的目的是从系统中选择一个合适的单尺度序决策系统, 用于最终的决策规则提取.
定义14 设
S=(U, C∪ {d})=(U, {
为一个广义决策多尺度序信息系统,
K1=(1, 1, …, 1)∈ K
为条件属性集C的最细尺度组合.对于t∈ {1, 2, …, n}, 若
定义15 设
S=(U, C∪ {d})=(U, {
为一个广义决策多尺度序信息系统, 对于
K=(i1, i2, …, iM)∈ K,
对应一个具有多尺度决策的单尺度信息系统
SK=(U, CK∪ {d})=(U, {
对于t∈ {1, 2, …, n}, 若
定理3 设
S=(U, C∪ {d})=(U, {
为一个广义决策多尺度序信息系统, K∈ K, K'∈ K, 若K≼K', 且SK'是协调的, 则SK也是协调的.
证明 一方面, 由于SK'=(U, CK'∪ {d})是协调的, 因此
SK=(U, CK∪ {d})
也是协调的. 证毕.
定理4 设
S=(U, C∪ {d})=(U, {
为一个广义决策多尺度序信息系统,
Q1=(K1, t1)∈ Q, Q2=(K2, t2)∈ Q, Q1≼Q2,
若序决策系统
证明 由于
定义16 设
S=(U, C∪ {d})=(U, {
为一个协调广义决策多尺度序信息系统, 对于
Q=(K, t)∈ Q,
若满足
1)SQ是协调的, 即
2)对任意满足Q≺Q'的Q'=(K', t')∈ Q, SQ'是不协调的, 即
则称Q=(K, t)为S的一个最优尺度选择, 并称
SQ=(U, CK∪ {dt})
为S的一个最优协调序决策系统.
由定义16可见, 一个协调广义决策多尺度序信息系统S=(U, C∪ {d})的一个最优尺度选择
Q=(K, t)∈ Q
是Q中使SQ是协调的最粗的尺度选择, 因此, 寻求协调广义决策多尺度序信息系统的一个最优尺度选择问题可转化为求以下最优解问题:
Max
满足上述最优解问题的一个尺度选择Q就是S的一个最优尺度选择.
定义17 设
S=(U, C∪ {d})=(U, {
为一个协调广义决策多尺度序信息系统, K1=(1, 1, …, 1)∈ K, Q=(K, t)∈ Q,
则
1)若对于∀ x∈ U, 有
2)若对于∀ x∈ U, 都有
定义18 设
S=(U, C∪ {d})=(U, {
为一个协调广义决策多尺度序信息系统,
K1=(1, 1, …, 1)∈ K, Q=(K, t)∈ Q,
则
1)若对于∀ x∈ U, 都有
Be
则称SQ关于S是信任协调的; 若SQ关于S是信任协调的, 且对于任意满足Q≺Q'的
Q'=(K', t')∈ Q,
∃y∈ U, 使得Be
即SQ'关于S不是信任协调的, 则称Q=(K, t)是S的一个信任最优尺度选择.
2)若对于∀ x∈ U, 都有P
则称SQ关于S是似然协调的; 若SQ关于S是似然协调的, 且对于任意满足Q≺Q'的Q'=(K', t')∈ Q,
∃y∈ U, 使得
P
即SQ'关于S不是似然协调的, 则称Q=(K, t)是S的一个似然最优尺度选择.
定理5 设
S=(U, C∪ {d})=(U, {
为一个协调广义决策多尺度序信息系统,
Q=(K, t)∈ Q,
则
1)SQ关于S是下近似协调的当且仅当SQ关于S是信任协调的.
2)Q是S的下近似最优尺度选择当且仅当Q是S的信任最优尺度选择.
3)SQ关于S是上近似协调的当且仅当SQ关于S是似然协调的.
4)Q是S的上近似最优尺度选择当且仅当Q是S的似然最优尺度选择.
证明 先证1).充分性.设SQ关于S是下近似协调, 则对∀ x∈ U, 有
从而
P
即
Be
因此, SQ关于S是信任协调的.
必要性.若SQ关于S是信任协调的, 则对∀ x∈ U,
即
又由于
于是可得
因此, SQ关于S是下近似协调的.
再证2).由结论1)即得.
再证3)充分性.设SQ关于S是上近似协调的, 则对于∀ x∈ U, 有
从而
P
即
P
因此, SQ关于S是似然协调的.
必要性.若SQ关于S是似然协调的, 则对于∀ x∈ U, 有P
又由于
最后证明4).由结论3)即得. 证毕.
定理6 设
S=(U, C∪ {d})=(U, {
为一个协调广义决策多尺度序信息系统,
Q=(K, t)∈ Q,
则SQ是协调的当且仅当SQ关于S是信任协调的.
证明 充分性.设SQ是协调的, 则∀ x∈ U, 有
[x
由命题1知,
成立, 对于∀ y∈ [x
[y
由于SQ关于S是协调的, 即[y
[x
这样就证明
又由于K1=(1, 1, …, 1)是最细的尺度组合, 因此
[x
从而
[x
即序决策系统
成立, 于是
再由定理5知
Be
即SQ关于S是信任协调的.
必要性.设SQ是关于S信任协调的, 由定理5知, 对于∀ x∈ U, 有
反证, 假如SQ是不协调的, 即
定义19 设
S=(U, C∪ {d})=(U, {
为一个协调广义决策多尺度序信息系统,
K1=(1, 1, …, 1)∈ K,
对于t∈ {1, 2, …, n}, S的信任和Mt与似然和Nt分别定义为
Mt=
其中,
U/
为决策属性d在第t个尺度下决策优势类全体.
定理7 设
S=(U, C∪ {d})=(U, {
为一个广义决策多尺度序信息系统,
Q=(K, t)∈ Q,
则
1)SQ是协调的当且仅当
2)Q=(K, t)∈ Q为S的最优尺度选择当且仅当
且对任意满足Q≺Q'的
Q'=(K', t)∈ Q,
有
证明 由定理6和推论1即证明1).由结论1)即证明2). 证毕.
定理8 设
S=(U, C∪ {d})=(U, {
为一个协调广义决策多尺度序信息系统, Q=(K, t)∈ Q,
则
1)SQ是似然协调的当且仅当
2)Q=(K, t)∈ Q是S的似然最优尺度选择当且仅当
证明 类似于定理7的证明. 证毕.
由上述结论可见, 保持序决策系统是协调的最粗尺度选择(即最优尺度选择)与下近似最优尺度选择和信任最优尺度选择都是等价的, 而上近似最优尺度选择与似然最优尺度选择也是等价的.因此, 定义16~定义18给出的5种类型的最优尺度选择概念实际上只有2种不同的类型.
例1 表1为一个广义决策多尺度序信息系统
S=(U, C∪ {d})=(U, {
其中,
U={x1, x2, x3, x4, x5, x6, x7, x8, x9, x10, x11, x12}, C={a1, a2}.
条件属性a1、a2都有3个尺度, 决策属性d有2个尺度.条件属性a1、a2和决策属性
d={dt|t=1, 2}
的信息粒度变换分别如下.对于x∈ U:
1)
2)
3)h1, 2∶
其中, 数值型值域
B> C> D> E, N> M> K.
| 表1 一个广义决策多尺度序信息系统 Table 1 A generalized decision Multi-scale ordered inforMation systeM |
图1为S的全体尺度选择的格结构.
1)判断S是否是协调的; 2)确定S的最优尺度选择; 3)确定S的上近似最优尺度选择、下近似最优尺度选择、信任最优尺度选择和似然协调最优尺度选择.
解:1)对于K1=(1, 1), 即
[x1
[x2
[x3=
[x4={
[x5={x
[x6={x1
[x7
[x8
[x10=
[x11={
[x12={x
即
U/
{x1, x4, x7, x8, x11}, {x5, x7, x8, x12},
{x1, x5, x6, x7, x8, x9, x12}, {x7}, {x7, x8, x12},
{x1, x5, x6, x7, x8, x9, x10, x12},
{x1, x4, x5, x6, x7, x8, x9, x11, x12}, {x12}}.
对于d1, 有
[x1
[x2
[x3
[X7
[x10
则
U/
对于d2, 有
[x1
[x3
U=[x6
[x7
即
U/
易见U/
2)设K2=(1, 2), 即
U/
{x1, x2, x4, x7, x8, x12}, {x1, x5, x7, x8, x12},
{x1, x5, x6, x7, x8, x9, x12}, {x7},
{x1, x7, x8, x12},
{x1, x5, x6, x7, x8, x9, x10, x12},
{x1, x2, x4, x5, x6, x7, x8, x9, x11, x12}},
因此
U/
设K3=(2, 1), 即
U/
{x1, x2, x3, x4, x7, x8, x12}, {x1, x4, x7, x8, x12},
{x5, x7, x8, x12}, {x1, x5, x6, x7, x8, x9, x12},
{x7}, {x7, x8, x12},
{x1, x5, x6, x7, x8, x9, x10, x12},
{x1, x4, x5, x6, x7, x8, x9, x11, x12}, {x12}},
因此
U/
设K4=(2, 2), 即
U/
{x1, x2, x3, x4, x7, x8, x12},
{x1, x2, x4, x7, x8, x12},
{x1, x5, x6, x7, x8, x9, x12}, {x7},
{x1, x7, x8, x12},
{x1, x5, x6, x7, x8, x9, x10, x12},
{x1, x2, x4, x5, x6, x7, x8, x9, x11, x12}},
因此
U/
所以S有唯一的最优尺度选择(2, 1, 1).
3)求S的下近似最优尺度选择.只需验证当t=1时的情况即可, 对于K1=(1, 1), 即
对于K2=(1, 2), 即
且对于x12, 有
对于K3=(2, 1), 即
成立.
对于K4=(2, 2), 即
且对于x12, 有
所以S有唯一的下近似最优尺度选择(2, 1, 1).
求S的上近似最优尺度选择.当t=1时, 对于K1=(1, 1), 即
对于K2=(1, 2), 则
同理, 对于K9=(3, 3), 即
所以(3, 3, 1)是S的上近似最优尺度选择.
求S的信任最优尺度选择.当t=1时,
当t=2时,
因此, (2, 1, 1)为S的信任最优尺度选择.
求S的似然最优尺度选择.由于(3, 3, 1)是S的上近似最优尺度选择, 只需验证K9=(3, 3)和t=1时即可.
有
(3, 3, 1)为S的似然最优尺度选择.
对于S, (2, 1, 1)为最优尺度选择、下近似最优尺度选择和信任最优尺度选择, (3, 3, 1)为上近似最优尺度选择和似然最优尺度选择.
定义20 设
S=(U, C∪ {d})=(U, {
为一个协调广义决策多尺度序信息系统,
K∈ K, Q=(K, t)∈ Q,
若对于B⊆C, 有
定理9 设
S=(U, C∪ {d})=(U, {
为一个协调广义决策多尺度序信息系统,
K1∈ K, K2∈ K, K1≺K2, Q1=(K1, t)∈ Q, Q2=(K2, t)∈ Q.
若B是S的Q2-尺度协调集, 则B是S的一个Q1-尺度协调集.
证明 由定义20与定理3可证. 证毕.
定义21 设
S=(U, C∪ {d})=(U, {
为一个协调广义决策多尺度序信息系统,
K=(i1, i2, …, iM)∈ K, Q=(K, t)∈ Q,
定义
Dt={(x, y)∈ U× U|dt(x)< dt(y)},
其中
称
定义22 设
S=(U, C∪ {d})=(U, {
为一个协调广义决策多尺度序信息系统,
B⊆C, K∈ K, Q=(K, t)∈ Q,
定义
为S在尺度选择Q上的可辨识函数, 其中, ∧ 为合取, ∨ 为析取.
类似于文献[37]~文献[39], 将上式给出的合取式转化为极小析取范式, 则该极小析取范式中每个合取式中的属性集合就是系统的一个Q-尺度约简.
获取
本节在最优尺度选择约简的基础上给出蕴含在广义决策多尺度序信息系统中的序决策规则.
定义23 设
S=(U, C∪ {d})=(U, {
为一个广义决策多尺度序信息系统, 对于B⊆C,
K=(i1, i2, …, iM)∈ K,
蕴含在决策信息系统中的命题知识可使用决策规则的形式表示: t→ s, 其中, t为规则的前件, s为规则的后件, 表示由t可得出s.对同时满足规则的前件和后件的对象, 称为支持这条规则.
对于协调广义决策多尺度序信息系统, 结合原子公式的概念, 类似于Greco等[37, 38, 39]提出序决策规则, 可得蕴含在系统中基于优势关系的确定性序决策规则如下:
(
例2 (接例1) 由于S的最优尺度选择为Q=(2, 1, 1), 则可得到在尺度选择Q下S的可辨识矩阵如表2所示.
由于
于是, S在尺度选择Q=(2, 1, 1)下唯一的属性约简为{
序决策规则如下:
该规则支持的对象为x1, x7, x8, x12.
该规则支持的对象为x1, x2, x4, x5, x7, x8, x12.
该规则支持的对象为x1, x2, x3, x4, x5, x6, x7, x8, x9, x12.
该规则支持的对象为U.
| 表2 尺度选择Q下S的可辨识矩阵 Table 2 Discernibility Matrix of S under scale selection Q |
最优尺度选择是多尺度信息系统知识获取的一个关键步骤, 最优尺度选择的作用是从多尺度信息系统中找到一个符合目标条件的最优子表用于最终的决策(如聚类、分类或排序).本文针对协调广义决策多尺度序信息系统中的知识获取问题, 分别使用粗糙集理论和证据理论定义下近似最优尺度选择与上近似最优尺度选择、信任最优尺度选择与似然最优尺度选择的概念, 证明保持序决策系统是协调的最粗尺度选择(即最优尺度选择)与下近似最优尺度选择和信任最优尺度选择都是等价的, 而上近似最优尺度选择与似然最优尺度选择也是等价的.并在最优尺度选择基础上, 进一步使用粗糙集辨识矩阵方法给出属性约简, 最终获得蕴含在协调广义决策多尺度序信息系统中的序决策规则集.在后续研究中:一方面, 可进一步研究在协调和不协调广义决策多尺度序信息系统中局部最优尺度选择及规则提取问题; 另一方面, 其它更复杂数据类型(如不完备广义决策多尺度序信息系统等)的最优尺度选择及序决策规则提取也是值得研究的问题.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|
| [19] |
|
| [20] |
|
| [21] |
|
| [22] |
|
| [23] |
|
| [24] |
|
| [25] |
|
| [26] |
|
| [27] |
|
| [28] |
|
| [29] |
|
| [30] |
|
| [31] |
|
| [32] |
|
| [33] |
|
| [34] |
|
| [35] |
|
| [36] |
|
| [37] |
|
| [38] |
|
| [39] |
|
| [40] |
|
| [41] |
|
| [42] |
|
| [43] |
|
| [44] |
|
| [45] |
|
| [46] |
|
| [47] |
|
| [48] |
|