基于决策重要度的概念认知学习模型

引用本文

王启君, 林艺东, 林梦雷, 寇毅. 基于决策重要度的概念认知学习模型. 模式识别与人工智能, ,35(9): 816-826
WANG Qijun, LIN Yidong, LIN Menglei, KOU Yi. Concept-Cognitive Learning Model Based on Decision Significance. PATTERN RECOGNITION AND ARTIFICIAL INTELLIGENCE, ,35(9): 816-826. 复制到剪切板

Doi: 10.16451/j.cnki.issn1003-6059.202209005
Permissions

《模式识别与人工智能》编辑部所有

基于决策重要度的概念认知学习模型

王启君¹, 林艺东¹, 林梦雷^1,², 寇毅¹

1.闽南师范大学数学与统计学院漳州 363000

2.闽南师范大学数字福建气象大数据研究所漳州 363000

通信作者：

林梦雷,硕士,教授,主要研究方向为不确定性理论及其应用.E-mail:menglei36@126.com.

作者简介:王启君,硕士研究生,主要研究方向为粒计算、概念认知学习.E-mail:wqj_1106@163.com.
林艺东,博士,副教授,主要研究方向为不确定性理论及其应用.E-mail: yidong_lin@yeah.net.
寇毅,硕士研究生,主要研究方向为粒计算、机器学习.E-mail:ky20eku@163.com.

收稿日期: 2022-07-27 接受日期: 2022-09-26

资助项目: 国家自然科学基金项目(No.12201284)、福建省自然科学基金项目(No.2022J05169,B12127)、闽南师范大学校长基金项目(No.L22130) 资助

摘要

概念认知学习是模拟人类认知过程的概念学习方法,大多从概念相似性的角度出发,往往忽略先验决策信息的影响,造成有效信息的丢失. 因此,文中提取先验决策信息, 刻画决策重要性,提出基于决策重要度的概念认知学习模型,用于动态环境中的概念归类.首先,通过余弦相似度构造邻域粒,探讨概念认知的渐进过程.然后,面对动态环境,考虑到先验决策信息对后续学习的影响,进一步提出决策重要度和置信度,设计概念分类的计算方法.最后,通过仿真实验验证文中模型的有效性和优越性.

关键词: 概念认知学习; 模糊概念; 决策重要度; 渐进模糊概念

中图分类号:TP 182

Concept-Cognitive Learning Model Based on Decision Significance

WANG Qijun¹, LIN Yidong¹, LIN Menglei^1,², KOU Yi¹

1.School of Mathematics and Statistics, Minnan Normal University, Zhangzhou 363000

2.Institute of Meteorological Big Data-Digital Fujian, Minnan Normal University, Zhangzhou 363000

Corresponding author: LIN Menglei, master, professor. His research interests include uncertain theories and application.

Author：WANG Qijun, master student. Her research interests include granular computing and concept-cognitive learning.
LIN Yidong, Ph.D., associate professor. His research interests include uncertain theories and application.
KOU Yi, master student. His research interests include granular computing and machine learning.

Fund:Supported by National Natural Science Foundation of China(No.12201284), Natural Science Foundation of Fujian Province(No.2022J05169,B12127), President Foundation of Minnan Normal University(No.L22130)

Abstract

Concept-cognitive learning is a concept learning method that simulates human cognitive process based on formal concept analysis. Most of the current concept-cognitive learning methods only consider conceptual similarity and ignore the influence of prior decision information, resulting in the loss of practical details. To solve this problem, a concept-cognitive learning model based on decision significance is put forward for concept classification in a dynamic environment by extracting prior decision information to describe the significance of decision making. The neighborhood granule is constructed by cosine similarity, and the progressive process of concept cognition is discussed. For the dynamic environment, the decision significance and confidence degree are proposed to design the computational method of concept classification with the consideration of the validity of the a priori decision information. The effectiveness and superiority of the proposed method are verified by simulation experiments.

Key words: Key Words: Concept-Cognitive Learning; Fuzzy Concept; Decision Significance; Progressive Fuzzy Concept

文章图片

“ 概念” 一词来源于哲学, 是外延与内涵的统一.概念学习理论作为粗糙集理论的高度补充, 在规则提取、对象分类等领域具有广泛的应用价值^{[1, 2, 3, 4, 5]}.经典概念通过内涵和外延描述同类事物的本质特征, 为概念学习提供数学基础^{[6, 7, 8, 9, 10, 11, 12, 13]}.其中, 对象(外延)和属性(内涵)的关系是分明的, 即属性是否为对象所拥有.然而在实际应用中, 对象与属性之间的关系通常是模糊的、不确定的, 连续型数据只有通过离散化预处理才能进行经典概念学习, 这期间往往会造成信息丢失^{[8, 9, 10]}.

作为经典概念的扩展, 模糊概念能处理连续型数据, 通过把属性值转换为对象的隶属度以刻画概念, 不仅降低由于离散化产生的耗时, 并且保留原始信息^{[2, 5, 14, 15]}.目前, 已有许多学者在信息描述、模式识别与概念聚类等方面进行相关研究^{[2, 9, 12, 14]}.Cross等^[14]对比单边阈值方法和模糊闭包算子方法分别产生的模糊概念格, 发现前者概念的外延是后者外延的子集.Xu等^[11]基于粒计算提出双向概念认知模型, 能有效处理实际问题中的模糊知识.

随着科学技术的发展, 尤其是数据科技和人工智能的兴起, 概念认知学习理论(Concept-Cognitive Learning, CCL)逐渐成为认知科学、脑科学、计算机科学等领域的研究热点.CCL的主要思想是通过具体的认知模型从给定线索中进行概念学习, 揭示人脑概念学习的系统性规律.然而, 在自然条件下, 概念学习容易受到认知环境和个体认知水平等因素的影响^{[2, 16, 17, 18, 19]}.李金海等^[17]提出概念的渐进式认知理论与方法, 处理不完全认知条件下的概念获取问题.在概念认知学习理论的发展过程中, 李金海等^[18]对概念认知的公理化、概念认知系统、概念认知过程等问题进行进一步思考与研究.徐伟华等^[19]提出模糊三支算子, 用于讨论模糊三支概念的概念认知学习方法.

为了克服认知环境的限制, 一些学者研究基于进化计算的概念学习方法, 并通过实验验证其有效性^{[2, 3, 16, 20, 21, 22, 23, 24, 25, 26, 27, 28]}.Mukhopadhyay等^[20]提出多目标进化算法, 解决工程中的多目标问题.Dragoni^[21]基于概念域, 提出多域情感分析进化策略.为了提高概念学习的效率和灵活性, Li等^[8]从认知计算的角度讨论基于粒计算的概念学习.Mi等^[2]考虑个体认知水平和认知环境的限制, 从概念聚类角度阐述模糊概念.

大型数据集的时限性、多样性、复杂性等因素使高效计算概念空间成为必要.为了降低概念认知学习过程的复杂度, Shi等^[22]利用并行计算, 提高概念认知学习效率.Zhang等^[23]基于属性拓扑设计概念更新算法.Tsang等^[3]提出多层次认知机制.Wang等^[24]利用特征之间的相关性设计具有认知推理能力的分类模型.

概念的构建和概念空间的更新是概念认知学习中影响学习效率的两个重要因素.对于动态分类问题, Yan等^[25]基于三支偏序结构图, 提出增量概念认知学习方法.Mi等^[26]从概念认知计算系统的视角出发, 实现对数据的动态分类.Xu等^[27]考虑注意力对概念认知的影响, 提出多注意概念认知学习模型.为了去除一些不必要信息的影响, 根据概念内涵之间的差异性, Yuan等^[28]提出基于渐进模糊三支概念的增量学习机制, 却忽略先验决策信息对概念认知的影响, 导致部分有效信息的丢失.

受文献[28]的启发, 本文利用先验决策信息, 提出基于决策重要度的概念认知学习模型.首先, 引入余弦相似度构造邻域粒, 生成相应的模糊概念空间.考虑到个体认知的局限性和认知环境的不完全性, 进一步构建渐进模糊概念空间.由于不同决策对对象的影响程度不同, 通过渐进模糊概念的外延得到某一决策对该概念的决策重要度和置信度, 以此讨论概念分类, 并设计相似性度量指标.最后, 通过实验验证本文模型的有效性.

1 相关知识

本节主要回顾模糊形式背景和模糊概念的定义^[28].

定义1^[28] 设X={x₁, x₂, …, x_n}为非空有限对象集, A={a₁, a₂, …, a_m}为非空有限属性集, $\tilde{I}$ 为X和A之间的二元关系, 则称三元组X, A, $\tilde{I}$ 为一个模糊形式背景.

对于∀ x∈ X, a∈ A, 有 $\tilde{I}$ (x, a)∈ [0, 1]. $\tilde{I}$ (x, a)表示对象x关于属性a的隶属度或属性a被对象x的拥有程度.

若D为决策属性且E∶ X× D→ {0, 1}, 则称X, A, $\tilde{I}$ , D, E为模糊决策形式背景.若E(x, a)=1, 则对象x拥有属性a, 否则x不拥有a.

在形式概念分析中, 将概念定义为由内涵和外延组成的二元组.符合概念的全体对象的集合称为概念的外延, 此集合全体对象共有的属性称为概念的内涵.然而, 经典形式背景下只能判断一个对象是否具有某个属性.若具有, 为1; 否则为0.但现实生活中很多问题不能通过绝对真1和绝对假0来刻画, 而模糊形式背景可通过对象对属性的拥有程度处理模糊状态下的部分问题.

定义2^[28] 设X, A, $\tilde{I}$ 为一个模糊形式背景, L^A表示A上所有模糊集合.对∀ Q∈ P(X), $\tilde{B}$ ∈ L^A, 对象学习算子 $\tilde{G}$ ∶ P(X)→ L^A和属性学习算子 $\tilde{H}$ ∶ L^A→ P(X)定义如下:

$\tilde{G}$ (Q)(a)=X^*(a)= $\underset{x \in Q}{\land} \tilde{I}$ (x, a), a∈ A, $\tilde{H}(\tilde{B})={{\tilde{B}}^{* }}=\{x\in X|\widetilde{I}(x, a)\ge \tilde{B}(a)\} $.

若 $\tilde{G}$ (Q)= $\tilde{B}$ , ${\tilde{B}}^{*}$ =Q, 则(Q, $\tilde{B}$ )称为模糊概念, Q和 $\tilde{B}$ 分别为模糊概念的外延与内涵.若

(Q₁, ${\tilde{B}}_{1}$ ) ∈ L(X, A, $\tilde{I}$ ), (Q₂, ${\tilde{B}}_{2}$ ) ∈ L(X, A, $\tilde{I}$ ), (Q₁, ${\tilde{B}}_{1}$ ) ≤ (Q₂, ${\tilde{B}}_{2}$ ),

当且仅当Q₁⊆Q₂或( ${\tilde{B}}_{2}$ ⊆ ${\tilde{B}}_{1}$ ).若

(Q₁, ${\tilde{B}}_{1}$ )≤ (Q₂, ${\tilde{B}}_{2}$ ),

称(Q₁, ${\tilde{B}}_{1}$ )为(Q₂, ${\tilde{B}}_{2}$ )的子概念, (Q₂, ${\tilde{B}}_{2}$ )为(Q₁, ${\tilde{B}}_{1}$ )的超概念.

2 基于邻域粒的渐进模糊概念空间的构造

粒化是粒计算的基本问题.在模糊形式背景中, 对象的相似度通常使用其属性之间的距离进行刻画.本文利用相似度描述对象之间的邻域关系, 以此构造模糊概念空间.

定义3 设(X, A, $\tilde{I}$ )为模糊形式背景, 对∀ x_i∈ X, x_j∈ X, (x_i, a_s)和(x_j, a_s)相应的隶属度为 $\tilde{I}$ (x_i, a_s)和 $\tilde{I}$ (x_j, a_s), 称

cos(x_i, x_j)= $\frac{\overset{m}{\sum_{s}} \tilde{I} (x_{i}, a_{s}) \cdot \tilde{I} (x_{j}, a_{s})}{\sqrt[]{\overset{m}{\sum_{s}} \tilde{I} (x_{i}, a_{s})^{2}} \cdot \sqrt[]{\overset{m}{\sum_{s}} (\tilde{I} (x_{j}, a_{s})^{2}}}$

为对象x_i、x_j之间的余弦相似性.显然, cos(x_i, x_j)∈ [0, 1], 当对象的余弦相似性大于某值时, 认为它们相似度较高, 越趋近1, 表示两个对象的方向越接近.在本文中, 引入参数δ , 由此得到每个对象的邻域粒.

定义4 设(X, A, $\tilde{I}$ , D, $\tilde{E}$ )为模糊决策形式背景, 对x∈ X和a_j∈ A(j=1, 2, …, m), 它的邻域粒为:

$Q_{x}^{δ}$ ={y∈ X|cos(x, y)≥ δ }.

基于邻域粒 $Q_{x}^{δ}$ , 根据定义3, 可得到模糊概念.

若存在 $Q_{x_{1}}^{δ}$ ⊆ $Q_{x_{2}}^{δ}$ , 则称 $Q_{x_{1}}^{δ}$ 为 $Q_{x_{2}}^{δ}$ 的子邻域或 $Q_{x_{2}}^{δ}$ 为 $Q_{x_{1}}^{δ}$ 的超邻域.于是基于邻域粒的模糊概念空间的构造如下.

定义5 设(X, A, $\tilde{I}$ , D, $\tilde{E}$ )为模糊决策形式背景, 则关于 $Q_{x}^{δ}$ 的模糊概念空间为:

C_i={( $\tilde{H} \tilde{G}$ ( $Q_{x}^{δ}$ ), $\tilde{G}$ ( $Q_{x}^{δ}$ ))|x∈ X_i}.

模糊概念空间为C={C₁, C₂, …, C_l}, 每个C_i称为C的第i个子空间.同时, 注意到δ 值会影响邻域粒的大小, 不同对象集的最小隶属度会不同, 进而内涵会随外延变化而变化, 因此模糊概念会受到δ 值的影响.此外, 本文提出的对象分类机制是基于模糊概念的, 因此δ 将进一步影响模型目标分类性能.在算法1中给出模糊概念空间的构造过程.

算法1 构造模糊概念空间

输入模糊形式背景(X, A, $\tilde{I}$ , D, E), 参数δ

输出模糊概念空间C

令C_i← Ø ;

for x∈ X

计算x∈ X邻域粒 $Q_{x_{1}}^{δ}$ ;

得到模糊概念( $\tilde{H} \tilde{G}$ ( $Q_{x}^{δ}$ ), $\tilde{G}$ ( $Q_{x}^{δ}$ ));

C_i← ( $\tilde{H} \tilde{G}$ ( $Q_{x}^{δ}$ ), $\tilde{G}$ ( $Q_{x}^{δ}$ ));

end

例1 表1为包含10个对象和2个属性的模糊决策形式背景, 对象被b₁和b₂描述.

在模糊决策形式背景下, 令δ =0.95, 根据定义5, 得到相应邻域粒:

$Q_{{{x}_{1}}}^{\delta }=\{{{x}_{1}}, {{x}_{2}}, {{x}_{4}}\}$, $Q_{{{x}_{2}}}^{\delta }=\{{{x}_{1}}, {{x}_{2}}, {{x}_{4}}, {{x}_{5}}\}$, $Q_{{{x}_{3}}}^{\delta }=\{{{x}_{3}}, {{x}_{5}}, {{x}_{6}}\}$, $Q_{{{x}_{4}}}^{\delta }=\{{{x}_{2}}, {{x}_{3}}, {{x}_{5}}, {{x}_{6}}\}$, $Q_{{{x}_{5}}}^{\delta }=\{{{x}_{7}}, {{x}_{9}}\}$, $Q_{{{x}_{6}}}^{\delta }=\{{{x}_{8}}, {{x}_{9}}, {{x}_{10}}\}$, $Q_{{{x}_{7}}}^{\delta }=\{{{x}_{7}}, {{x}_{8}}, {{x}_{9}}, {{x}_{10}}\}$.

进而得到模糊概念子空间:

C₁=({x₁, x₂, x₄}, (0.04, 0.47)),

C 2₌({x1_,x2_,x4_,x5_}, (0.04, 0.47)),

C₃=({x₃, x₅, x₆}, (0.28, 0.47)),

C 4₌({x2_,x3_,x5_,x6_}, (0.11, 0.47)),

C 5=₍{x7, _x9}_,(0.68, 0.11)),

C 6=(_{x8, x₉, x₁0}_{, (}0.75, 0.32)),

C 7=({_x7, x8_,x9_,x1₀}, ₍₀.68, 0.11)).

模糊概念空间C={C₁, C₂, …, C₇}.

表1 模糊决策形式背景 Table1 Fuzzy formal decision context

在模糊概念空间中, 概念之间相互影响, 甚至存在大量的重复信息.与此同时, 由于个体认知的局限性和认知环境的不完全性, 概念认知通常是渐进的.因此, 为了提高认知的准确性, 在原有模糊概念空间的基础上构建对应的渐进模糊概念空间.

定义6^[17] 对于模糊概念( $Q_{1}^{δ}$ , $\tilde{G}$ ( $Q_{1}^{δ}$ ))∈ C_i, ( $Q_{2}^{δ}$ , $\tilde{G}$ ( $Q_{2}^{δ}$ ))∈ C_i, …, ( $Q_{u}^{δ}$ , $\tilde{G}$ ( $Q_{u}^{δ}$ ))∈ C_i, 若存在 $Q_{1}^{δ}$ ⊆ $Q_{2}^{δ}$ ⊆…⊆ $Q_{u}^{δ}$ , 则称( $Q_{u}^{δ}$ , $\tilde{G}$ ( $Q_{u}^{δ}$ ))为上确界概念.渐进概念定义如下:

Q_i= $Q_{1}^{δ}$ ∪ $Q_{2}^{δ}$ ∪ …∪ $Q_{u}^{δ}$ , G_i= $\frac{1}{2^{u - 1}}$ ( $\tilde{G} Q_{1}^{δ}$ + $\tilde{G} Q_{2}^{δ}$ +2 $\tilde{G} Q_{3}^{δ}$ +… +2^u-2 $\tilde{G} (Q_{u}^{δ})$ ),

称P_i=(Q_i, G_i)为渐进模糊概念空间.

在渐进概念的学习过程中, 不同子概念的内涵根据其相应外延大小被赋予不同的权重.子概念对新概念生成的影响随外延的增加而增大.同时, 所有概念的权重之和为1, 即总效应之和为1.因此, 在算法2中给出选择上确界概念和获取渐进模糊概念空间的详细过程.

算法2 构造渐进模糊概念空间

输入模糊概念空间C={C₁, C₂, …, C_l}

输出渐进模糊概念空间P={P₁, P₂, …, P_l}

for C_i∈ C

令上确界概念空间S={( $Q_{1}^{δ}$ , $\tilde{G}$ ( $Q_{1}^{δ}$ )}};

C_i∈ C_i-S;

for ( $Q_{i}^{δ}$ , $\tilde{G}$ ( $Q_{i}^{δ}$ ))∈ C_i,

( $Q_{j}^{δ}$ , $\tilde{G}$ ( $Q_{j}^{δ}$ ))∈ C_i-( $Q_{i}^{δ}$ , $\tilde{G}$ ( $Q_{i}^{δ}$ ))

if ( $Q_{j}^{δ}$ , $\tilde{G}$ ( $Q_{j}^{δ}$ ))为上确界概念 then

S=S, S_j=S_j∪ {( $Q_{j}^{δ}$ , $\tilde{G}$ ( $Q_{j}^{δ}$ ))};

C_i=C_i-( $Q_{j}^{δ}$ , $\tilde{G}$ ( $Q_{j}^{δ}$ ));

else

S=S_j∪ {( $Q_{j}^{δ}$ , $\tilde{G}$ ( $Q_{j}^{δ}$ ))},

S_j={( $Q_{j}^{δ}$ , $\tilde{G}$ ( $Q_{j}^{δ}$ ))};

end

if 存在( $Q_{j}^{δ}$ , $\tilde{G}$ ( $Q_{j}^{δ}$ ))的上确界概念

( $Q_{i}^{δ}$ , $\tilde{G}$ ( $Q_{i}^{δ}$ ))∈ S then

S=S-( $Q_{j}^{δ}$ , $\tilde{G}$ ( $Q_{j}^{δ}$ )), S=S_j∪ ( $Q_{j}^{δ}$ , $\tilde{G}$ ( $Q_{j}^{δ}$ ));

S_j=S_i∪ {( $Q_{j}^{δ}$ , $\tilde{G}$ ( $Q_{j}^{δ}$ ))}, 删除S_i;

C_i=C_i-( $Q_{j}^{δ}$ , $\tilde{G}$ ( $Q_{j}^{δ}$ ));

end

for ( $Q_{i}^{δ}$ , $\tilde{G}$ ( $Q_{i}^{δ}$ ))∈ S且令其对应的子概念为S_i

计算渐进模糊概念(Q_i, G_i);

P_i← (Q_i, G_i);

end

例2(接例1) 根据定义7, 由例1中模糊概念进一步得到渐进模糊概念:

P₁=({x₁, x₂, x₄, x₅}, (0.04, 0.47)),

P2=({x2_,x3_,x5_,x6_}, (0.195, 0.47)),

P3=({x7, _x8, _x9, _x10_},(0.6975, 0.1625)).

3 基于决策重要度的概念认知学习模型

面向动态环境, 如何基于概念空间识别新增对象的类标签是一个值得探讨的问题.为了解决此问题, 本文提出决策重要度和置信度, 再充分融合二者信息, 提出概念认知学习模型.

3.1 渐进概念的决策重要度和置信度

在动态环境中, 原有决策信息会对新增对象的学习产生影响, 然而这部分信息往往被人们忽略.因此, 为了充分利用先验决策信息, 在渐进概念的基础之上引入决策重要度和置信度, 用于刻画分类指标.

定义7 设(X, A, $\tilde{I}$ , D, E)为模糊决策形式背景, P={P₁, P₂, …, P_l}为渐进模糊概念空间, P_i=(Q_i, G_i)为渐进概念, d_j∈ D/E={d₁, d₂, …, d_t}, 其中d_j表示E对决策D的划分, 决策重要度定义如下:

sig(G_i, d_j)= $\frac{| G_{i}^{*} ⋂ d_{j} |}{| G_{i}^{*} |}$ ,

其中, $G_{i}^{*}$ 表示渐进概念的外延, 0≤ sig(G_i, d_j)≤ 1.若某类决策重要度越接近1, 说明该标签对对象的影响越大.

例3 (接例2) 根据定义1,

$\mathcal{G}_{1}^{* }=\{{{x}_{1}}, {{x}_{2}}, {{x}_{4}}, {{x}_{5}}\}$, $\mathcal{G}_{2}^{* }=\{{{x}_{2}}, {{x}_{3}}, {{x}_{5}}, {{x}_{6}}\}$, $\mathcal{G}_{3}^{* }=\{{{x}_{7}}, {{x}_{8}}, {{x}_{9}}, {{x}_{10}}\}$; $d_{1}^{* }=\{{{x}_{1}}, {{x}_{2}}, {{x}_{3}}, {{x}_{4}}\}$, $d_{2}^{* }=\{{{x}_{5}}, {{x}_{6}}, {{x}_{7}}\}$, $d_{3}^{* }=\{{{x}_{8}}, {{x}_{9}}, {{x}_{10}}\}$,

则

sig(G₁, d_j)=( $\frac{3}{4}$ , $\frac{1}{4}$ , 0), sig(G₂, d_j)=( $\frac{1}{2}$ , $\frac{1}{2}$ , 0), sig(G₃, d_j)=(0, 0, 1).

由于决策重要度有时会产生相等的情况, 导致无法确定对象的决策, 因此本文引进决策置信度对其进行进一步处理.

定义8 设(X, A, $\tilde{I}$ , D, E)为模糊决策形式背景, $Q_{x}^{δ}$ 为样本的邻域粒, d_j∈ D/E={d₁, d₂, …, d_t}, 其中d_j表示E对决策D的划分, 决策置信度定义如下:

con( $Q_{x}^{δ}$ , d_i)= $\frac{| Q_{x}^{δ} ⋂ d_{i}^{} |}{|Q_{x}^{δ}|}$ .

由于渐进模糊概念的初始邻域粒可能由多个子邻域组成, 多个邻域粒之间相互影响, 故需计算每个子邻域的决策置信度, 融合后得到最终决策置信度.具体融合方式如下.

若存在

$Q_{1}^{δ}$ ⊆ $Q_{2}^{δ}$ ⊆…⊆ $Q_{u}^{δ}$ ,

则

con( $Q_{x}^{δ}$ , d_i)= $\frac{1}{2^{u - 1}}$ (con( $Q_{x_{1}}^{δ}$ , d_i)+con( $Q_{x_{2}}^{δ}$ , d_i)+…+2u^-²^con( $Q_{x_{u}}^{δ}$ di)),

其中 $Q_{x}^{δ}$ 表示邻域粒中的所有样本集合, 显然有0< con( $Q_{x}^{δ}$ , d_i)≤ 1.若某个决策置信度越接近1, 说明该决策系统中不一致性越低, 即决策越可信.决策重要度的构造过程如算法3所示.

算法3 构造基于渐进概念决策重要度

输入模糊决策形式背景(X, A, $\tilde{I}$ , D, E),

渐进模糊概念空间P={P₁, P₂, …, P_l}

输出决策重要度sig(G_i, d_j)

for G_i∈ P

for x_i∈ X

计算G_i∈ P的外延 $G_{i}^{*}$ 和sig(G_i, d_j);

if sig(G'_i, d_j)中含有相等的数值

计算con( $Q_{x}^{δ}$ , d_i);

sig(G_i, d_j)← con( $Q_{x}^{δ}$ , d_i)· sig(G_i, d_j);

end

例4 (接例3) 根据定义8,

sig(G₂, d_j)=( $\frac{1}{2}$ , $\frac{1}{2}$ , 0),

其渐进模糊概念初始邻域粒为

$Q_{x_{1}}^{δ}$ ={x₃, x₅, x₆}, $Q_{x_{2}}^{δ}$ ={x₂, x₃, x₅, x₆},

则

$con(Q_{{{x}_{1}}}^{\delta }, {{d}_{i}})=(\frac{1}{3}, \frac{2}{3}, 0)$, $con(Q_{{{x}_{2}}}^{\delta }, {{d}_{i}})=(\frac{1}{2}, \frac{1}{2}, 0)$; $con(Q_{{{x}_{3}}}^{\delta }, {{d}_{i}})=(\frac{5}{12}, \frac{7}{12}, 0)$.

3.2 基于决策重要度的增量学习机制

本文结合分类机制与动态更新机制, 构建基于决策重要度渐进模糊概念的学习机制.首先对比新增对象与原渐进概念的信息, 寻找相似性最大的渐进概念, 再选取其决策重要度最大的决策更新新增对象的信息, 具体过程如算法4所示.

算法4 基于决策重要度的分类机制

输入渐进模糊概念空间P={P₁, P₂, …, P_l},

新增对象x_a

输出 x_a的类别

for P_i∈ P

计算cos(P_i, x_a);

得到s_i=index(ma $x_{\cos (P_{i}, x_{a})}$ );

for s_i∈ P_i

x_a的类别为max(sig(s_i, d_i));

end

当添加新对象x_a时, X'=X∪ {x_a}, 构造渐进模糊概念空间的时间成本很高.为了减少耗时, 本文设计决策重要度的动态更新机制(Incremental Lear-ning Mechanism for Fuzzy Concept Based on Decision Significance, FCDS).在此过程中, 只需计算x_a和C_i∈ C的相似度以更新模糊概念空间, 进而更新决策重要度, 而不需要计算与每个样本的相似度.决策重要度的动态更新过程如算法5所示.

算法5 决策重要度的动态更新机制

输入初始邻域粒 $Q_{x}^{δ}$ , 模糊概念空间C_i,

添加的对象x_a, 参数δ

输出决策重要度sig(G'_i, d_j)

for C_i∈ C

计算cos(x_a, C_i);

x_i=index(ma $x_{\cos (x_{a}, C_{i})}$ );

$Q_{x_{i}}^{δ'}$ = $Q_{x_{i}}^{δ}$ ∪ {x_a};

C'_i← ( $\tilde{H} \tilde{G}$ ( $Q_{x_{i}}^{δ'}$ ), $\tilde{G}$ ( $Q_{x_{i}}^{δ'}$ ));

更新渐进模糊概念空间P'_i;

更新决策重要度sig(G'_i, d_j);

end

动态更新算法与静态更新算法不同的关键在于新的渐进模糊概念空间的构造.假设新增对象为x_a, 则X'=X∪ {x_a}.当更新第i个模糊概念时, 首先需要计算x_a和C_i之间的相似度, 复杂度为O(l).通过原始概念计算新模糊概念的内涵 $\tilde{G}$ ( $Q_{x_{i}}^{δ'}$ ), 更新过程的时间复杂度为O(2l).同样根据原始概念的外延 $\tilde{H} \tilde{G}$ ( $Q_{x_{i}}^{δ'}$ )对新概念的外延进行更新, 因此复杂度为

O(l(|C_i|-| $\tilde{H} \tilde{G}$ ( $Q_{x_{i}}^{δ'}$ )|)).

由于 $|C_{i}|$ 为原始概念空间的个数, 算法总的时间复杂度为

O(l $\overset{| C_{i} |}{\sum_{i}}$ (1+2+2)|C_i|-| $\tilde{H} \tilde{G}$ ( $Q_{x_{i}}^{δ'}$ )|))),

即为动态更新决策重要度的时间复杂度.

4 实验及结果分析

4.1 实验环境

为了验证本文提出的决策重要度的动态更新机制(FCDS)的分类性能, 选择如下对比算法:ILMPFTC(Incremental Learning Mechanism Based on Progressive Fuzzy Three Way Concept)^[28]、KNN(k-Nearest Neighbor)、CART(Classification and Re-gression Trees)、NB(Naive Bayes)、DT(Decision Tree).

根据定义9的分析可知, 参数δ 是影响分类精度的一个重要参数.在实验中, FCDS和ILMPFTC根据添加对象的分类精度选择最佳δ , 选择范围为[0, 1], 步长为0.001.其它4种对比算法都具有相同的邻域参数k, 本文中k=3.

实验选择UCI机器学习库上的11个实验数据集, 详细信息如表2所示.

表2 数据集详情 Table 2 Dataset description

在预处理阶段, 对数据集进行归一化, 得到区间[0, 1]内的隶属度.本文使用文献[29]对这些数据集进行归一化:

R(x_i, a_j)= $\frac{f (x_{i}, a_{j}) - \min (f (a_{j}))}{\max (f (a_{j})) - \min (f (a_{j}))}$ , (1)

其中, f(x_i, a_j)表示属性a_j中x_i的值, max(f(a_j))和min(f(a_j))表示属性a_j中所有对象的最大值和最小值.在模糊决策形式背景中, R(x_i, a_j)反映(x_i, a_j)对a_j的隶属度.通常, 模糊集可理解为对象对属性的拥有程度.f(x_i, a_j)的值越大, x拥有属性a的程度越大.式(1)作为一种模糊化方法, 可将原始数值转换为模糊决策形式背景.

在每个数据集上, 70%的数据用于训练模型, 剩余数据均分为10份, 逐次添加至测试集上, 由此验证FCDS的分类性能和有效性.

所有算法均在Matlab 2021b上实现, 并在配置为Intel(R)Core(TM)i7-7700 CPU@3.60 GHz和8 GB内存的个人计算机上执行.

4.2 各算法分类性能的对比

各算法在11个数据集上添加对象时的分类精度对比如表3所示, 表中, t₁~t₁₀表示逐次添加测试数据的时间, 黑体数字表示最优值, -表示该算法在两周之内未输出结果.由表可见, 除了Breast数据集, FCDS的分类精度都大于或等于对比算法, 同时, FCDS在8个数据集上的平均分类精度最高, 这表明利用决策重要度可提高样本的分类性能, 由此验证FCDS的有效性.利用先验决策信息也可提高分类器性能, 使分类更准确.

表3 各算法添加新对象时的分类精度 Table 3 Classification accuracy of different algorithms while adding new objects %

数据集	算法	t₁	t₂	t₃	t₄	t₅	t₆	t₇	t₈	t₉	t₁₀	平均精度
Breast	FCDS ILMPFTC KNN CART NB DT	100.00 50.00 78.57 100.00 - 87.65	100.00 75.00 80.95 100.00 - 79.32	100.00 66.67 83.33 94.44 - 72.50	87.50 75.00 78.57 100.00 - 75.74	90.00 80.00 78.57 100.00 - 77.23	91.67 66.67 78.57 100.00 - 78.39	92.86 64.28 85.71 100.00 - 81.30	87.50 68.75 84.62 100.00 - 84.62	88.89 72.22 76.19 100.00 - 81.85	85.00 75.00 78.57 100.00 - 81.24	92.34± 5.72 69.36± 8.38 80.35± 3.13 99.44± 1.75 - 79.98± 4.36
Breast Cancer Coimbra	FCDS ILMPFTC KNN CART NB DT	66.67 66.67 54.31 73.14 78.70 71.39	66.67 83.33 53.44 73.14 78.70 71.39	77.78 77.78 56.07 73.14 76.32 71.39	83.33 75.00 50.80 73.14 78.70 71.39	86.67 73.33 54.31 73.14 77.25 69.16	88.89 66.67 60.45 65.74 77.42 62.13	90.476 61.90 57.82 66.25 73.76 56.89	91.67 54.17 55.19 62.39 72.25 59.48	92.60 48.15 56.07 61.02 71.08 58.48	83.33 50.00 56.07 60.76 67.30 56.23	82.81± 9.61 65.71± 2.04 55.45± 2.58 68.19± 5.50 75.15± 3.90 64.79± 6.69
Colonstd	FCDS ILMPFTC KNN CART NB DT	100.00 0.00 79.20 90.23 - 70.89	100.00 0.00 79.20 79.12 - 60.89	100.00 0.00 82.38 83.57 - 63.75	100.00 25.00 80.79 85.47 - 70.89	100.00 40.00 85.55 86.53 - 76.45	100.00 50.00 80.79 87.46 - 78.04	100.00 42.86 82.38 87.85 - 79.23	87.5 37.50 80.79 88.15 - 77.14	89.89 44.44 79.20 86.53 - 77.03	90.00 50.00 82.38 84.97 - 78.04	96.64± 5.44 28.98± 21.19 81.26± 1.98 85.99± 3.04 - 73.24± 6.45
Congressional Voting Records	FCDS ILMPFTC KNN CART NB DT	100.00 100.00 91.49 87.29 95.56 90.95	100.00 92.30 91.49 88.40 93.18 91.99	100.00 92.30 91.49 89.08 91.29 92.79	100.00 90.38 90.80 89.11 92.53 92.69	98.47 89.23 91.03 88.56 92.12 91.73	97.43 91.02 91.95 88.67 93.27 93.18	95.60 91.21 91.49 89.70 93.52 94.07	94.23 89.42 91.95 90.02 92.59 93.94	94.01 89.89 91.72 89.89 92.56 94.09	94.62 89.23 91.49 90.23 93.02 93.70	97.44± 2.59 91.40± 3.27 91.49± 0.35 89.10± 0.90 92.97± 1.11 92.92± 1.09
Dermatology	FCDS ILMPFTC KNN CART NB DT	100.00 100.00 94.26 91.38 90.28 86.56	100.00 100.00 93.98 94.16 95.95 96.09	96.67 100.00 93.71 97.96 98.62 93.23	97.50 100.00 94.26 98.38 97.89 92.61	98.00 92.00 94.80 98.68 98.05 92.81	98.33 93.33 94.26 98.82 96.77 91.64	98.57 94.28 95.35 98.90 97.79 93.79	98.75 93.75 94.80 98.66 97.88 93.14	98.89 92.22 94.26 99.09 97.03 93.05	99.00 93.00 93.16 98.88 98.05 92.78	98.57± 1.03 95.86± 3.62 94.28± 0.61 97.49± 2.59 96.83± 2.42 92.57± 2.40
Fea	FCDS ILMPFTC KNN CART NB DT	81.94 28.17 2.69 75.52 - 54.52	83.33 27.46 2.89 74.77 - 49.11	86.11 29.58 3.02 74.40 - 49.33	84.37 28.87 2.81 74.37 - 44.87	81.94 29.29 3.10 73.50 - 44.08	81.25 28.97 2.81 73.40 - 42.96	81.94 27.96 2.77 73.28 - 41.05	81.94 28.52 2.77 73.58 - 38.68	82.40 28.63 3.06 73.20 - 37.45	81.94 28.45 2.81 72.28 - 36.10	82.72± 1.48 28.58± 0.62 2.81± 0.13 73.83± 0.93 - 43.79± 5.81

表3 各算法添加新对象时的分类精度 Table 3 Classification accuracy of different algorithms while adding new objects %

表3 各算法添加新对象时的分类精度(续) Table 3 Classification accuracy of different algorithms while adding new objects(continued) %

数据集	算法	t₁	t₂	t₃	t₄	t₅	t₆	t₇	t₈	t₉	t₁₀	平均精度
Gearbox	FCDS ILMPFTC KNN CART NB DT	100.00 100.00 99.25 100.00 100.00 98.62	100.00 100.00 99.12 100.00 100.00 98.94	100.00 100.00 98.81 100.00 100.00 99.25	100.00 99.47 98.50 100.00 100.00 99.10	100.00 99.57 99.25 100.00 100.00 99.12	100.00 99.64 98.69 100.00 99.79 99.14	100.00 99.69 98.75 100.00 100.00 99.16	100.00 99.73 99.31 100.00 100.00 99.09	100.00 99.76 99.06 100.00 100.00 99.04	100.00 99.78 99.06 100.00 100.00 99.00	100.00± 0.00 99.77± 1.85 98.98± 0.27 100.00± 0.00 99.97± 0.06 99.04± 0.17
PIE10Pstd	FCDS ILMPFTC KNN CART NB DT	100.00 100.00 14.28 98.09 - 85.71	100.00 100.00 15.23 98.09 - 82.68	100.00 100.00 16.67 98.09 - 80.95	100.00 100.00 17.61 98.09 - 77.71	100.00 100.00 17.14 98.09 - 76.70	100.00 100.00 17.61 98.09 - 79.19	100.00 100.00 17.14 97.44 - 75.91	100.00 100.00 17.14 95.71 - 76.94	100.00 100.00 14.28 95.44 - 80.50	100.00 100.00 15.71 95.71 - 77.14	100.00± 0.00 100.00± 0.00 16.28± 1.30 97.28± 1.16 - 79.34± 3.12
Rice	FCDS ILMPFTC KNN CART NB DT	100.00 66.67 90.36 73.28 77.79 60.59	100.00 66.67 91.31 89.95 88.90 87.26	100.00 77.78 89.41 85.78 84.74 87.26	91.67 83.33 86.55 85.50 83.78 88.80	93.33 86.67 90.36 84.06 81.06 91.96	88.89 83.33 86.55 85.40 77.24 88.66	85.18 80.95 87.50 85.78 79.93 89.58	87.5 83.33 90.36 87.57 79.71 88.80	85.18 85.18 91.31 87.72 80.02 89.33	86.67 86.67 88.45 87.99 80.08 89.88	91.90± 6.12 80.05± 7.53 89.22± 1.84 85.30± 4.55 81.32± 3.53 86.21± 9.10
Wine	FCDS ILMPFTC KNN CART NB DT	100.00 100.00 89.88 98.24 94.74 85.41	100.00 100.00 92.71 94.91 89.98 93.49	100.00 100.00 89.88 98.24 94.74 94.86	100.00 100.00 93.27 96.57 92.89 93.75	100.00 100.00 91.01 95.57 93.41 94.22	100.00 96.67 90.45 96.22 88.68 94.56	100.00 91.43 92.71 95.61 90.57 94.86	97.50 92.50 91.58 96.76 93.29 95.01	97.78 93.33 93.84 96.93 92.78 94.56	98.00 94.00 93.27 96.45 93.55 95.33	99.33± 1.08 96.79± 3.63 91.86± 6.77 96.55± 3.07 92.46± 2.04 93.61± 2.93
Zoo	FCDS ILMPFTC KNN CART NB DT	100.00 100.00 97.05 98.98 59.62 64.64	100.00 100.00 95.09 98.98 92.95 97.97	100.00 100.00 97.05 95.65 86.28 97.97	100.00 100.00 97.05 96.42 92.95 86.86	100.00 100.00 96.07 98.98 92.95 86.86	100.00 100.00 99.01 98.98 92.95 88.17	100.00 100.00 95.09 98.98 92.95 92.71	100.00 100.00 96.07 96.32 92.95 92.42	100.00 100.00 97.05 96.76 91.80 96.86	100.00 100.00 96.07 97.02 91.97 96.99	100.00± 0.00 100.00± 0.00 96.56± 1.15 97.71± 1.38 88.74± 10.43 90.15± 10.01

表3 各算法添加新对象时的分类精度(续) Table 3 Classification accuracy of different algorithms while adding new objects(continued) %

分类精度虽然常用, 但不能满足所有任务需求.本节通过其它性能度量, 说明FCDS的有效性与优越性.

对于二分类问题, 可将样例根据其真实类别与学习器预测类别的组合划分为真正例(True Positive)、假正例(False Positive)、真反例(True Negative)、假反例(False Negative)4种情形, 令TP、FP、TN、FN分别表示其对应的样例数, 显然有

TP+FP+ TN+FN=样例总数.

查准率P与查全率R分别定义为

P= $\frac{TP}{TP + FP}$ , R= $\frac{TP}{TP + FN}$ .

为了更好地刻画学习器的分类效果, F1度量定义如下:

F1= $\frac{2 \times P \times R}{P + R}$ .

对于多个二分类混淆矩阵, 如执行多分类任务, 每两两类别的组合都对应一个混淆矩阵.本文先在各混淆矩阵上分别计算查准率和查全率, 再计算平均值, 得到宏查准率(macro-P)、宏查全率(macro-R)、相应的宏F1(macro-F1):

macro-P= $\frac{1}{n} \overset{n}{\sum_{i}}$ P_i, macro-R= $\frac{1}{n} \overset{n}{\sum_{i}}$ R_i, macro-F1= $\frac{2 \cdot macro-P \cdot macro-R}{macro-P + macro-R}$ .

各算法在11个数据集上的查准率和查全率对比如表4所示, 表中黑体数字表示最优值, -表示真正例和假反例或假正例和真反例的个数都为0.由表可知, FCDS在6个数据集上的查准率和查全率都大于或等于对比算法, 在Colonstd数据集上取得最大查准率.ILMPFTC只在Zoo数据集上取得最大查全率和查准率; CART在Breast、Gearbox数据集上取得最大查全率和查准率, 在Colonstd数据集上取得最大查全率, 在Rice数据集上取得最大查准率; DT在Congressional Voting Records数据集上取得最大查全率和查准率, 在Rice数据集上取得最大查准率; NB在Gearbox数据集上取得最大查准率和查全率.由此说明FCDS在分类效果上具有一定的优越性.

表4 各算法的查准率和查全率对比 Table 4 Precision and recall of different algorithms%

各算法在11个数据集上的F1度量如表5所示, 表中黑体数字表示最优值.由表可看出, FCDS在11个数据集中获得8次最大值, 说明FCDS在分类方面的优越性.

表5 各算法的F1度量对比 Table 5 F1 comparison of different algorithms %

4.3 统计检验

为了进一步验证分类算法是否性能相同, 本节选择常用的Friedman检验^[30], 验证算法是否存在显著差异.设N为数据集数, k为算法数目, R_i为所有数据集上第i个算法平均排名.F遵循自由度为k-1和(k-1)(N-1)的Fisher分布.Friedman检验定义如下:

$χ_{F}^{2}$ = $\frac{12 N}{k (k + 1)}$ （ $\overset{k}{\sum_{i}} R_{i}^{2}$ - $\frac{k {(k + 1)}^{2}}{4}$ ）, F= $\frac{(N - 1) χ_{F}^{2}}{N (k - 1) - χ_{F}^{2}}$ .

由于在NB中有部分数据未得出结果, 因此在本次检验中只考虑FCDS与其它四种算法的差异性.对5种算法的分类精度进行排序, 详细的排序结果如表6所示.

表6 算法的分类精度排名 Table 6 Classification accuracy rank of 5 algorithms

根据定义, 计算F=10.28, 大于临界值F=2.090, 因此可知这5种算法有一定差异.下面使用Bonfer-

roni-Dunn检验测试5种分类算法之间的统计差异^[32].当

k=5, N=11, α =0.1

时, q₀_.₁=2.459, 得到临界距离

CD_α=q_α $\sqrt[]{\frac{k (k + 1)}{6 N}}$ =1.11.

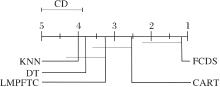
对于任意两种算法, 如果它们的距离超过CD_α, 说明这两种算法的性能具有显著不同.本文使用Bonferroni-Dunn测试图^[31]直观显示5种算法之间的统计学差异, 具体如图1所示.图中使用灰色线段绘制临界差CD_α=1.11, 然后连接距离小于1.11的分类算法, 越靠近1说明算法性能越优.由图可看出, FCDS与其它4种算法的平均排名的差值都大于临界差1.11, 说明FCDS的分类性能与其它算法具有显著差异.

	Figure Option View Download New Window
	图1 各算法Bonferroni-Dunn测试图对比Fig.1 Bonferroni-Dunn test graph of different algorithms

5 结束语

本文提出基于决策重要度的概念认知学习模型, 结合决策信息与渐进模糊概念, 获得更优的分类性能.随着更新后的概念被进一步学习, 概念空间包含新增对象的新信息, 因此通过先验决策信息和新信息的结合可提高分类精度.同时, 在11个公共数据集上的实验验证上述结论.在现实生活中, 只要能从概念思维上描述对象, FCDS就可用于解决其相应的分类问题, 如模式识别和人脸识别.同时, 增量学习的思想也可应用于动态增加的数据, 如时间序列数据.但是, 本文算法对数据集决策分布依赖较大, 当决策分布不均匀时, 分类效果无明显优势.因此, 今后将着重探讨决策分布不均匀时的分类方法.

参考文献

文献选项

[1]	LIN B Y, ZHANG X Y, XU W H, et al. Dynamically Updating Approximations Based on Multi-threshold Tolerance Relation in Incomplete Interval-Valued Decision Information Systems. Knowledge and Information Systems, 2020, 62(3): 1063-1087. [本文引用:1]
[2]	MI Y L, SHI Y, LI J H, et al. Fuzzy-Based Concept Learning Method: Exploiting Data with Fuzzy Conceptual Clustering. IEEE Transactions on Cybernetics, 2020, 52(1): 582-593. [本文引用:6]
[3]	TSANG E C C, FAN B J, CHEN D G, et al. Multi-level Cognitive Concept Learning Method Oriented to Data Sets with Fuzziness: A Perspective from Features. Soft Computing, 2020, 24(5): 3753-3770. [本文引用:3]
[4]	ZHANG Q, SHI C Y, NIU Z D, et al. HCBC: A Hierarchical Case-Based Classifier Integrated with Conceptual Clustering. IEEE Transactions on Knowledge and Data Engineering, 2018, 31(1): 152-165. [本文引用:1]
[5]	ZOU C F, DENG H F, WAN J F, et al. Mining and Updating Association Rules Based on Fuzzy Concept Lattice. Future Generation Computer Systems, 2018, 82: 698-706. [本文引用:2]
[6]	WILLE R. Restructuring Lattice Theory: An Approach Based on Hierarchies of Concepts // RIVAL I, ed. Ordered Sets. Berlin, Germany: Springer, 1982: 445-470. [本文引用:1]
[7]	GANTER B, WILLE R, FRANZKE C. Formal Concept Analysis: Mathematical Foundations. Berlin, Germany: Springer: 1999. [本文引用:1]
[8]	LI J H, MEI C L, XU W H, et al. Concept Learning via Granular Computing: A Cognitive Viewpoint. Information Sciences, 2015, 298: 447-467. [本文引用:3]
[9]	LONG B H, XU W H, ZHANG X Y, et al. The Dynamic Update Method of Attribute-Induced Three-Way Granular Concept in Formal Contexts. International Journal of Approximate Reasoning, 2020, 126: 228-248. [本文引用:3]
[10]	WEI L, LIU L, QI J J, et al. Rules Acquisition of Formal Decision Contexts Based on Three-Way Concept Lattices. Information Sciences, 2020, 516: 529-544. [本文引用:2]
[11]	XU W H, LI W T. Granular Computing Approach to Two-Way Lear-ning Based on Formal Concept Analysis in Fuzzy Datasets. IEEE Transactions on Cybernetics, 2016, 46(2): 366-379. [本文引用:2]
[12]	ZHAO Y X, LI J H, LIU W Q, et al. Cognitive Concept Learning from Incomplete Information. International Journal of Machine Learning and Cybernetics, 2017, 8(1): 159-170. [本文引用:2]
[13]	ZHI H L, LI J H. Granule Description Based Knowledge Discovery from Incomplete Formal Contexts via Necessary Attribute Analysis. Information Sciences, 2019, 485: 347-361. [本文引用:1]
[14]	CROSS V, KANDASAMY M. Fuzzy Concept Lattice Construction: A Basis for Building Fuzzy Ontologies // Proc of the IEEE International Conference on Fuzzy Systems. Washington, USA: IEEE, 2011: 1743-1750. [本文引用:3]
[15]	LI W T, PEDRYCZ W, XUE X P, et al. Fuzziness and Incremental Information of Disjoint Regions in Double-Quantitative Decision-Theoretic Rough Set Model. International Journal of Machine Learning and Cybernetics, 2019, 10(10): 2669-2690. [本文引用:1]
[16]	AVIGAD G, MOSHAIOV A. Interactive Evolutionary Multiobjective Search and Optimization of Set-Based Concepts. IEEE Transactions on Systems, Man, and Cybernetics(Cybernetics), 2009, 39(4): 1013-1027. [本文引用:2]
[17]	李金海, 米允龙, 刘文奇. 概念的渐进式认知理论与方法. 计算机学报, 2019, 42(10): 2233-2250. (LI J H, MI Y L, LIU W Q. Incremental Cognition of Concepts: Theories and Methods. Chinese Journal of Computers, 2019, 42(10): 2233-2250. ) [本文引用:3]
[18]	李金海, 闫梦宇, 徐伟华, 等. 概念认知学习的若干问题与思考. 西北大学学报(自然科学版), 2020, 50(4): 501-515. (LI J H, YAN M Y, XU W H, et al. Some Problems and Thoughts on Concept-Cognitive Learning. Journal of Northwest University(Natural Science Edition), 2020, 50(4): 501-515. ) [本文引用:2]
[19]	徐伟华, 杨蕾, 张晓燕. 模糊三支形式概念分析与概念认知学习. 西北大学学报(自然科学版), 2020, 50(4): 516-528. (XU W H, YANG L, ZHANG X Y. Fuzzy Three-Way Formal Concept Analysis and Concept-Cognitive Learning. Journal of Northwest University(Natural Science Edition), 2020, 50(4): 516-528. ) [本文引用:2]
[20]	MUKHOPADHYAY A, MAULIK U, BANDYOPADHYAY S, et al. A Survey of Multiobjective Evolutionary Algorithms for Data Mining: Part I. IEEE Transactions on Evolutionary Computation, 2014, 18(1): 4-19. [本文引用:2]
[21]	DRAGONI M. An Evolutionary Strategy for Concept-Based Multi-domain Sentiment Analysis. IEEE Computational Intelligence Magazine, 2019, 14(2): 18-27. [本文引用:2]
[22]	SHI Y, MI Y L, LI J H, et al. Concurrent Concept-Cognitive Learning Model for Classification. Information Sciences, 2019, 496: 65-81. [本文引用:2]
[23]	ZHANG T, LI H H, LIU M Q, et al. Incremental Concept-Cognitive Learning Based on Attribute Topology. International Journal of Approximate Reasoning, 2020, 118: 173-189. [本文引用:2]
[24]	WANG J H, ZHANG D P, LIANG L N. A Classification Model with Cognitive Reasoning Ability. Symmetry, 2022, 14(5). DOI: DOI:10.3390/sym14051034. [本文引用:2]
[25]	YAN E L, YU C G, LU L M, et al. Incremental Concept Cognitive Learning Based on Three-Way Partial Order Structure. Know-ledge-Based Systems, 2021, 220. DOI: DOI:10.1016/j.knosys.2021.106898. [本文引用:2]
[26]	MI Y L, QUAN P, SHI Y, et al. Concept-Cognitive Computing System for Dynamic Classification. European Journal of Operational Research, 2022, 301(1): 287-299. [本文引用:2]
[27]	XU W H, CHEN Y Q. Multi-attention Concept-Cognitive Learning Model: A Perspective from Conceptual Clustering. Knowledge-Based Systems, 2022, 252. DOI: DOI:10.1016/j.knosys.2022.109472. [本文引用:2]
[28]	YUAN K H, XU W H, LI W T, et al. An Incremental Learning Mechanism for Object Classification Based on Progressive Fuzzy Three-Way Concept. Information Sciences, 2022, 584: 127-147. [本文引用:7]
[29]	ELHADAD A, GHAREEB A, ABBAS S. A Blind and High-Capacity Data Hiding of DICOM Medical Images Based on Fuzzification Concepts. Alexand ria Engineering Journal, 2021, 60(2): 2471-2482. [本文引用:1]
[30]	FRIEDMAN M. A Comparison of Alternative Tests of Significance for the Problem of m Rankings. The Annals of Mathematical Statistics, 1940, 11(1): 86-92. [本文引用:1]
[31]	DEMŠAR J. Statistical Comparisons of Classifiers over Multiple Data Sets. Journal of Machine Learning Research, 2006, 7(1): 1-30. [本文引用:1]

2020

0.0

... 概念学习理论作为粗糙集理论的高度补充,在规则提取、对象分类等领域具有广泛的应用价值^[1,2,3,4,5] ...

2020

0.0

... 概念学习理论作为粗糙集理论的高度补充,在规则提取、对象分类等领域具有广泛的应用价值^[1,2,3,4,5] ...

... 作为经典概念的扩展,模糊概念能处理连续型数据,通过把属性值转换为对象的隶属度以刻画概念,不仅降低由于离散化产生的耗时,并且保留原始信息^[2,5,14,15] ...

... 目前,已有许多学者在信息描述、模式识别与概念聚类等方面进行相关研究^[2,9,12,14] ...

... 然而,在自然条件下,概念学习容易受到认知环境和个体认知水平等因素的影响^{[2,16,17,18,19]} ...

... 为了克服认知环境的限制,一些学者研究基于进化计算的概念学习方法,并通过实验验证其有效性^{[2,3,16,20,21,22,23,24,25,26,27,28]} ...

... Mi等^[2]考虑个体认知水平和认知环境的限制,从概念聚类角度阐述模糊概念 ...

2020

0.0

... 概念学习理论作为粗糙集理论的高度补充,在规则提取、对象分类等领域具有广泛的应用价值^[1,2,3,4,5] ...

... 为了克服认知环境的限制,一些学者研究基于进化计算的概念学习方法,并通过实验验证其有效性^{[2,3,16,20,21,22,23,24,25,26,27,28]} ...

... Tsang等^[3]提出多层次认知机制 ...

2018

0.0

... 概念学习理论作为粗糙集理论的高度补充,在规则提取、对象分类等领域具有广泛的应用价值^[1,2,3,4,5] ...

2018

0.0

... 概念学习理论作为粗糙集理论的高度补充,在规则提取、对象分类等领域具有广泛的应用价值^[1,2,3,4,5] ...

1982

0.0

... 经典概念通过内涵和外延描述同类事物的本质特征,为概念学习提供数学基础^{[6,7,8,9,10,11,12,13]} ...

1999

0.0

... 经典概念通过内涵和外延描述同类事物的本质特征,为概念学习提供数学基础^{[6,7,8,9,10,11,12,13]} ...

2015

0.0

... 经典概念通过内涵和外延描述同类事物的本质特征,为概念学习提供数学基础^{[6,7,8,9,10,11,12,13]} ...

... 然而在实际应用中,对象与属性之间的关系通常是模糊的、不确定的,连续型数据只有通过离散化预处理才能进行经典概念学习,这期间往往会造成信息丢失^[8,9,10] ...

... 为了提高概念学习的效率和灵活性,Li等^[8]从认知计算的角度讨论基于粒计算的概念学习 ...

2020

0.0

... 经典概念通过内涵和外延描述同类事物的本质特征,为概念学习提供数学基础^{[6,7,8,9,10,11,12,13]} ...

... 目前,已有许多学者在信息描述、模式识别与概念聚类等方面进行相关研究^[2,9,12,14] ...

2020

0.0

... 经典概念通过内涵和外延描述同类事物的本质特征,为概念学习提供数学基础^{[6,7,8,9,10,11,12,13]} ...

2016

0.0

... 经典概念通过内涵和外延描述同类事物的本质特征,为概念学习提供数学基础^{[6,7,8,9,10,11,12,13]} ...

... Xu等^[11]基于粒计算提出双向概念认知模型,能有效处理实际问题中的模糊知识 ...

2017

0.0

... 经典概念通过内涵和外延描述同类事物的本质特征,为概念学习提供数学基础^{[6,7,8,9,10,11,12,13]} ...

... 目前,已有许多学者在信息描述、模式识别与概念聚类等方面进行相关研究^[2,9,12,14] ...

2019

0.0

... 经典概念通过内涵和外延描述同类事物的本质特征,为概念学习提供数学基础^{[6,7,8,9,10,11,12,13]} ...

2011

0.0

... 目前,已有许多学者在信息描述、模式识别与概念聚类等方面进行相关研究^[2,9,12,14] ...

... Cross等^[14]对比单边阈值方法和模糊闭包算子方法分别产生的模糊概念格,发现前者概念的外延是后者外延的子集 ...

2019

0.0

2009

0.0

... 然而,在自然条件下,概念学习容易受到认知环境和个体认知水平等因素的影响^{[2,16,17,18,19]} ...

... 为了克服认知环境的限制,一些学者研究基于进化计算的概念学习方法,并通过实验验证其有效性^{[2,3,16,20,21,22,23,24,25,26,27,28]} ...

2019

0.0

... 然而,在自然条件下,概念学习容易受到认知环境和个体认知水平等因素的影响^{[2,16,17,18,19]} ...

... 李金海等^[17]提出概念的渐进式认知理论与方法,处理不完全认知条件下的概念获取问题 ...

... 定义6^[17] 对于模糊概念( Q1δ, G˜( Q1δ))#cod#x02208 ...

2020

0.0

... 然而,在自然条件下,概念学习容易受到认知环境和个体认知水平等因素的影响^{[2,16,17,18,19]} ...

... 在概念认知学习理论的发展过程中,李金海等^[18]对概念认知的公理化、概念认知系统、概念认知过程等问题进行进一步思考与研究 ...

2020

0.0

... 然而,在自然条件下,概念学习容易受到认知环境和个体认知水平等因素的影响^{[2,16,17,18,19]} ...

... 徐伟华等^[19]提出模糊三支算子,用于讨论模糊三支概念的概念认知学习方法 ...

2014

0.0

... 为了克服认知环境的限制,一些学者研究基于进化计算的概念学习方法,并通过实验验证其有效性^{[2,3,16,20,21,22,23,24,25,26,27,28]} ...

... Mukhopadhyay等^[20]提出多目标进化算法,解决工程中的多目标问题 ...

2019

0.0

... 为了克服认知环境的限制,一些学者研究基于进化计算的概念学习方法,并通过实验验证其有效性^{[2,3,16,20,21,22,23,24,25,26,27,28]} ...

... Dragoni^[21]基于概念域,提出多域情感分析进化策略 ...

2019

0.0

... 为了克服认知环境的限制,一些学者研究基于进化计算的概念学习方法,并通过实验验证其有效性^{[2,3,16,20,21,22,23,24,25,26,27,28]} ...

... 为了降低概念认知学习过程的复杂度,Shi等^[22]利用并行计算,提高概念认知学习效率 ...

2020

0.0

... 为了克服认知环境的限制,一些学者研究基于进化计算的概念学习方法,并通过实验验证其有效性^{[2,3,16,20,21,22,23,24,25,26,27,28]} ...

... Zhang等^[23]基于属性拓扑设计概念更新算法 ...

2022

0.0

... 为了克服认知环境的限制,一些学者研究基于进化计算的概念学习方法,并通过实验验证其有效性^{[2,3,16,20,21,22,23,24,25,26,27,28]} ...

... Wang等^[24]利用特征之间的相关性设计具有认知推理能力的分类模型 ...

2021

0.0

... 为了克服认知环境的限制,一些学者研究基于进化计算的概念学习方法,并通过实验验证其有效性^{[2,3,16,20,21,22,23,24,25,26,27,28]} ...

... 对于动态分类问题,Yan等^[25]基于三支偏序结构图,提出增量概念认知学习方法 ...

2022

0.0

... 为了克服认知环境的限制,一些学者研究基于进化计算的概念学习方法,并通过实验验证其有效性^{[2,3,16,20,21,22,23,24,25,26,27,28]} ...

... Mi等^[26]从概念认知计算系统的视角出发,实现对数据的动态分类 ...

2022

0.0

... 为了克服认知环境的限制,一些学者研究基于进化计算的概念学习方法,并通过实验验证其有效性^{[2,3,16,20,21,22,23,24,25,26,27,28]} ...

... Xu等^[27]考虑注意力对概念认知的影响,提出多注意概念认知学习模型 ...

2022

0.0

... 为了克服认知环境的限制,一些学者研究基于进化计算的概念学习方法,并通过实验验证其有效性^{[2,3,16,20,21,22,23,24,25,26,27,28]} ...

... 为了去除一些不必要信息的影响,根据概念内涵之间的差异性,Yuan等^[28]提出基于渐进模糊三支概念的增量学习机制,却忽略先验决策信息对概念认知的影响,导致部分有效信息的丢失 ...

... 受文献[28]的启发,本文利用先验决策信息,提出基于决策重要度的概念认知学习模型 ...

... 1 相关知识本节主要回顾模糊形式背景和模糊概念的定义^[28] ...

... 定义1^[28] 设X={x₁,x₂,…,x_n}为非空有限对象集,A={a₁,a₂,…,a_m}为非空有限属性集, I˜为X和A之间的二元关系,则称三元组X,A, I˜为一个模糊形式背景 ...

... 定义2^[28] 设X,A, I˜为一个模糊形式背景,L^A表示A上所有模糊集合 ...

... 1 实验环境为了验证本文提出的决策重要度的动态更新机制(FCDS)的分类性能,选择如下对比算法:ILMPFTC(Incremental Learning Mechanism Based on Progressive Fuzzy Three Way Concept)^[28]、KNN(k-Nearest Neighbor)、CART(Classification and Re-gression Trees)、NB(Naive Bayes)、DT(Decision Tree) ...

2021

0.0

... 本文使用文献[29]对这些数据集进行归一化: ...

1940

0.0

... 3 统计检验为了进一步验证分类算法是否性能相同,本节选择常用的Friedman检验^[30],验证算法是否存在显著差异 ...

2006

0.0

... 本文使用Bonferroni-Dunn测试图^[31]直观显示5种算法之间的统计学差异,具体如图1所示 ...