作者简介: 潘柏儒,硕士研究生,主要研究方向为数据挖掘、深度学习.E-mail:511170318@qq.com.
潘柏儒,硕士研究生,主要研究方向为数据挖掘、深度学习.E-mail:511170318@qq.com.
 鞠恒荣,博士,副教授,主要研究方向为粒计算、粗糙集、机器学习、知识发现.E-mail:juhengrong@ntu.edu.cn.
鞠恒荣,博士,副教授,主要研究方向为粒计算、粗糙集、机器学习、知识发现.E-mail:juhengrong@ntu.edu.cn.
 黄嘉爽,博士,讲师,主要研究方向为脑网络分析、深度学习.E-mail:hjshdym@163.com.
黄嘉爽,博士,讲师,主要研究方向为脑网络分析、深度学习.E-mail:hjshdym@163.com.
 程纯,博士,讲师,主要研究方向为社交网络、多智能体系统.E-mail:chengchun0912@163.com.
程纯,博士,讲师,主要研究方向为社交网络、多智能体系统.E-mail:chengchun0912@163.com.
 沈鑫杰,硕士研究生,主要研究方向为数据挖掘、深度学习.E-mail:2010310030@stmail.ntu.edu.cn.
沈鑫杰,硕士研究生,主要研究方向为数据挖掘、深度学习.E-mail:2010310030@stmail.ntu.edu.cn.
 耿宇,硕士研究生,主要研究方向为粒计算、机器学习、深度学习.E-mail:tian19981999@163.com.
耿宇,硕士研究生,主要研究方向为粒计算、机器学习、深度学习.E-mail:tian19981999@163.com.
图卷积神经网络在解决节点分类问题时,使用拓扑图刻画节点间关系,并根据该拓扑图进行节点特征更新.然而,传统的拓扑图只能刻画节点之间的确定关系(即连接边权重为固定值),忽略真实世界中广泛存在的不确定性.这些不确定性不仅影响节点之间的关系,同时影响模型最终的分类性能.为了克服该缺陷,文中提出基于粗糙图的图卷积神经网络算法.首先,使用上下近似理论和传统拓扑图的边理论构造粗糙边,在粗糙边中使用成对出现的最大-最小关系值刻画节点之间的不确定关系,从而构建粗糙图.然后,设计基于粗糙图的可端到端训练的神经网络架构,将使用粗糙权重系数训练后的粗糙图输入图卷积神经网络,使用这些不确定信息更新节点特征.最后,根据这些学习的节点特征进行节点分类.在真实数据上的实验表明,文中算法可提高节点分类的准确率.
Author:PAN Bairu, master student. Her research interests include data mining and deep lear-ning.
JU Hengrong, Ph.D., associate professor. His research interests include granular computing, rough sets, machine learning and know-ledge discovery.
HUANG Jiashuang, Ph.D., lecturer. His research interests include brain network analysis and deep learning.
CHENG hun,Ph.D., lecturer. His research interests include social networks and multi-agent systems.
SHEN Xinjie,master student. His research interests include data mining and deep lear-ning.
GENG Yu,master student. His research interests include granular computing, machine learning and deep learning.
A topology graph is utilized to portray the relationship between nodes and node features are updated on the basis of the topology graph, when the graph convolutional neural network is applied for solving node classification problems. However, traditional topology graph can only portray definite relationships between nodes, i.e. fixed values of connected edge weights, ignoring the widespread uncertainty in the real world. The uncertainty affects not only the relationship between nodes, but also the final classification performance of the model. To overcome this defect, a graph convolutional neural network algorithm based on rough graphs is proposed. Firstly, the rough edges are constructed via the upper-lower approximation theory and the edge theory of traditional topology graph, and the uncertain relationships between nodes are inscribed in rough edges using maximum-minimum relationship values coming in pairs to construct a rough graph. Then, an end-to-end trainable neural network architecture based on rough graphs is designed, the rough graphs trained with rough weight coefficients are fed into the graph convolutional neural network, and the node features are updated based on the uncertain information. Finally, nodes are classified according to the learned node features. The experiments on real dataset show that the proposed algorithm improves the accuracy of node classification.
近年来, 图卷积神经网络(Graph Convolutional Neural Network, GCN)在各领域都得到广泛应用.在交通流预测领域, Zhao等[1]提出时态图卷积神经网络, 使用GCN学习复杂的拓扑结构, 获取空间相关性, 并将网络应用于城市道路网的交通预测.Yu等[2]提出时空卷积网络, 使用的拓扑图可区分相邻道路连接的权重, 采用GCN进行交通预测.在社交分析领域, Ying等[3]结合随机游走和GCN, 将只适用于小规模用户群体的推荐系统扩充到适用于数亿用户的推荐系统.在疾病分类任务中, Parisot等[4]将受试者表示为一个稀疏图, 图的节点与基于图像的特征向量相关联.之后, Parisot等[5]构建稀疏图, 将受试者的特点和特征均整合到稀疏图中, 对它们之间的相互作用进行建模.
上述对于传统GCN的研究, 通常先构造一个拓扑图用于描述节点之间的联系, 再根据该拓扑图使用各种方法进行节点特征的更新.然而, 传统拓扑图只能表示确定性关系, 无法描述真实世界的不确定性关系.在社交网络中, Kipf等[6]将GCN应用于空手道俱乐部网络[7], 将该数据集建模为表示确定关系的拓扑图, 然后分类.Liu等[8]根据给定社会文本构建拓扑图, 利用GCN提取社会文本的情感特征.
目前, 研究人员尝试结合不确定性关系和传统拓扑图.Zadeh等[9]引入模糊集理论, 试图使用模糊集理论处理图中的不确定因素.Rosenfeld等[10]尝试使用模糊图刻画节点之间的不确定信息.特别是在节点分类任务中, Huang等[11]构造具有不确定性的图, 以此进行疾病预测, 提高对疾病预测的准确率和受试者人群的分类精度.Yao等[12]构建多个邻接矩阵表示拓扑图的不确定性, 并将基于注意力的特征聚合策略引入图卷积的计算中, 得到较高的分类精度.由此可看出, 引入不确定关系对提升GCN的分类准确率是有帮助的.
上述研究通常只适用于特定的图数据集, 如Cora、Citeseer、Pubmed数据集[13], 或适用于可简单转变成拓扑图结构的数据.在交通流预测中, Cui等[14]将地点建模成图节点, 将地点之间的距离建模成边权值.除了这种内容较单一、较好转换格式的数据集以外, 还存在一种医学图像数据集, 它同时包含成像数据和非成像数据.在这种医学图像数据集上:成像数据是指受试者的神经影像数据, 如功能性磁共振图像(Functional Magnetic Resonance Imaging, fMRI); 非成像数据是指受试者对应的表型属性, 包括每位受试者对应的年龄、性别、采集地点等, 这些数据是以表格形式呈现的固定信息, 而非fMRI医学影像的形式.
目前这种同时包含成像数据和非成像数据的医学图像数据集也广泛应用于构造图结构中, 一般情况下, 节点表示受试者(患者或健康对照组), 并伴有一组特征, 而图的边以直观方式结合主体之间的关联, 这种表示允许在疾病分类任务中同时结合丰富的成像信息和非成像信息及主体特征.以往用于疾病预测的基于图的方法只关注受试者之间的两两相似性, 依赖受试者特定的成像特征向量, 忽略个体特征, 未能对它们之间的相互作用建模.例如, Tong等[15]使用监督学习进行分类, Wolz等[16]、Brosch等[17]使用无监督任务进行分类, Parisot等[18]采用聚类进行人群分析, 均是因为它们有能力容纳复杂的成对互动, 并能整合非成像信息.Wang等[19]提出一种渐进的方法, 旨在从观察到的成像特征中学习亲和矩阵, 同时使用已知的表型标签对训练数据进行验证, 旨在使用表型信息增强成像.也就是说, 利用成像数据和非成像数据, 将受试者作为图节点, 并从成像数据中提取特征向量与其关联, 边权值从非成像数据(表型属性)中编码受试者和他们特征之间的成对相似性, 就可在一个单一框架中结合成像数据和非成像数据.
然而, 上述方法仍存在两点缺陷:1)采用模糊集理论刻画不确定关系时, 需要附加信息或先验知识, 但这些信息可能不容易得到; 2)刻画不确定性关系时需要使用固定的图数据集或可简单转变成拓扑图结构的数据, 而未涉及到同时包含成像数据和非成像数据的医学图像数据集.
为了解决上述问题, 本文提出基于粗糙图的图卷积神经网络算法(Graph Convolutional Neural Network Algorithm Based on Rough Graphs, RG-GCN).首先, 针对不确定性关系, 构造可表示这种不确定关系的拓扑图— — 粗糙图.由于Pawlak[20]提出的粗糙集可用于定量分析并处理不精确、不一致、不完整的信息与知识, 也不需要先验知识, 所以本文首先使用非成像数据刻画节点间的边, 并将这种传统拓扑图的边理论与粗糙集中的上下近似关系结合, 较好地表示不确定性关系, 把这种能表示节点间不确定关系的边定义为粗糙边, 从而得到粗糙图.然后, 基于该粗糙图更新节点特征, 利用粗糙权重系数训练粗糙图.最后, 把训练后的粗糙图作为GCN的输入, 采用半监督分类方式进行节点分类.
图是描述一组对象的结构, 其中某些对象对在某种意义上是“ 相关的” [21].给定一个无向图G={V, E}, 其中, V表示节点集, E表示边集, 节点集中的节点表示实际个体, 边集中的边表示个体和个体之间的关系.图G含有n个节点, vi表示图G中的第i个节点.图G的邻接矩阵W的大小为n× n, 邻接矩阵W的第i行第j列的数字Wij表示节点vi、vj之间的权重.当节点vi、vj之间无连接时, 设它们之间的权重为0.该拓扑图的构图方式为:若节点对(vi, vj)之间存在相同的属性M, 则该节点对(vi, vj)之间的权值增加1.
粗糙集理论基于不可分辨关系对数据进行划分, 利用上下近似集对目标进行描述[22].
假设连续值信息系统表示为
S=(U, AT=C∪ D, f, V),
其中:U={x1, x2, …, xn}表示非空有限对象集合, n表示系统中对象的个数; AT表示信息系统的属性集合, 包含条件属性集合C和决策属性集合D; V=
在粗糙集中可通过上、下近似集对目标概念X进行逼近.粗糙集在属性集合R⊆AT上对论域U的任意对象子集X⊆U中的对象进行上、下近似集的划分, 那么X基于属性集合R的上近似集
$\overline{R}(X)=\{x\in U|{{[x]}_{R}}\cap X\ne \varnothing \}$
$\underline{R}(X)=\{x\in U|{{[x]}_{R}}\subseteq X\}$
其中[x]R表示包含x∈ U的R等价类.集合X关于R的上近似
图卷积神经网络是用于图数据的神经网络模型.图卷积神经网络的传播规则如下[23]:
H(l+1)=σ (
其中,
在两层GCN中, A表示邻接矩阵, 在预处理步骤中, 首先计算
使模型更简洁, 而
Z=f(X, A)=softmax(
其中:W(0)∈ RC× H表示输入层到隐藏层的权重矩阵, 隐藏层有H个特征; W(1)=RH× F表示隐藏层到输出层的权重矩阵; X表示输入图信号, 对应图上就是点的输入特征; ReLU(· )和softmax(· )表示激活函数.
图提供一种直观的方式建模受试者(作为节点)及它们之间的关联或相似性(作为边).文献[15]~文献[18]均利用非成像数据构造节点间的边, 利用现有的互补性非成像数据描述图结构中主体之间的相似性.但是在此基础上构造的边是表示确定性关系的边, 边权值为固定值.为了更好地处理真实世界中的不确定关系, 本文提出基于粗糙图的GCN(RG-GCN), 结合粗糙集中表示不确定性关系的上下近似理论和传统拓扑图的边理论, 也就是说, 将使用非成像数据构造、表示确定性关系的边转换成可以表示不确定性关系的粗糙边, 即利用这种方式处理不确定性关系.
基于上述讨论, 为了能更好地表示具有不确定性的图数据, 并对这种具有不确定性的图数据进行分类, 本文提出基于粗糙图的图卷积神经网络, 实现对节点间不确定性关系的刻画, 以及对不确定性图结构的处理, 提高算法的运行效率和分类准确率.
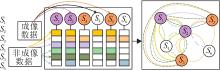
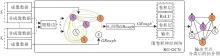
RG-GCN具体框图如图1所示.在图中, S表示图节点, GRough表示本文构造的粗糙图, GRough中的实线表示粗糙图的上近似边(
RG-GCN分类过程如下.首先, 从节点的成像数据中提取节点特征.再从节点的表型属性中选择较关键的表型属性, 根据其不确定程度把对应的属性划分成两组不同的非成像表型属性:上近似非成像表型属性集合Mmax={Mhmax}和下近似非成像表型属性集合Mmin={Mhmin}, 其中, Mhmax表示上近似非成像表型属性集合中的上近似非成像表型属性, Mhmin表示下近似非成像表型属性集合中的下近似非成像表型属性.并利用对应非成像表型属性的关系构造节点之间的粗糙边, 得到粗糙图GRough.然后, 利用节点间的粗糙权重系数α ij分别训练粗糙图对应的上近似图GMAX和下近似图GMIN, 得到训练后的粗糙图GRough'.最后, 将训练后的粗糙图GRough'作为GCN的输入, 通过式(1)对其进行训练, 输出经过GCN训练和优化的结果, 得到图节点的分类结果.
需要注意的是, 非成像互补数据可提供关键信息以解释受试者特征向量之间的关联, 因此选择最能解释成像数据之间相似性或受试者标签之间相似性的表型测量方法是必要的.本文通过粗糙集中能表示不确定性关系的上下近似理论分别划分上近似非成像数据和下近似非成像数据, 分别构造上近似边和下近似边.从粗糙集可知, 集合X关于R的上近似是那些可能属于X的对象组成的最小集合, 集合X关于R的下近似是肯定属于X的对象组成的最大集合, 即上近似类似取大的可能范围, 下近似类似取更精确、小的范围.所以, 本文使用上下近似理论将具有准确数值的非成像数据划分成如下两类.1)若非成像数据对应的数值的任何差别都可直接判别为完全不相同, 这类非成像数据划分为下近似非成像数据; 2)若非成像数据对应的数值虽然不相同, 但在相差很小的范围以内, 并不会有很大差别, 这类非成像数据划分为上近似非成像数据.
表型属性可提供关键信息, 解释节点和节点之间的关系.本文利用表型属性定义精确的邻域系统, 优化图卷积的性能.
为了克服传统拓扑图中边只能表示确定性关系的缺点, 结合传统拓扑图与粗糙集理论, 提出一种工具图— — 粗糙图.
根据定义可知, 上近似类似取大的可能范围, 下近似类似取更精确、小的范围, 所以利用粗糙集的上下近似理论, 将具有准确数值的非成像数据划分成下近似非成像数据和上近似非成像数据.根据这种划分对传统拓扑图的边理论进行一般化推广:使用上近似非成像数据划分上近似边, 使用下近似非成像数据划分下近似边.
定义1 给定节点集V={v1, v2, …, vv}, 根据上述非成像表型属性的划分标准, 该节点集对应非成像表型属性划分为一组上近似非成像表型属性Mmax={Mhmax}和一组下近似非成像表型属性Mmin={Mhmin}.对于Mmin, 如果两个节点在其对应的下近似表型属性中的对应数值相同, 且具有该特征的表型属性的个数为i1个, 则称两个节点之间存在i1条下近似边
定义2 给定节点集V={v1, v2, …, vv}, 根据上述非成像表型属性的划分标准, 该节点集对应非成像表型属性划分为一组上近似非成像表型属性Mmax={Mhmax}和一组下近似非成像表型属性Mmin={Mhmin}, 则该拓扑图根据不同的非成像表型属性对应的上近似邻接矩阵和下近似邻接矩阵分别为
Wmax(v, w)=Sim(Av, Aw)
Wmin(v, w)=Sim(Av, Aw)
其中, v、w表示节点集中不同的节点, Sim(Av, Aw)表示节点之间相似性的度量, 增加最相似图节点之间的边权值, γ max、γ min表示表型度量之间距离的度量.
相似性度量
Sim(Av, Aw)=exp(-
其中, ρ 表示相关距离, σ 表示核的宽度, x(v)表示从节点v成像数据中提取的特征向量.
根据Mmax和Mmin的不同, 分别定义γ max和γ min如下.γ max为一个单位阶跃函数:
γ max(Mhmax(v), Mhmax(w))=
其中θ 表示设置的阈值.
γ min为标准的克罗内克函数δ :
γ min(Mhmin(v), Mhmin(w))=
定义3 若给定粗糙图GRough, 其节点集V={v1, v2, …, vv}, 根据上述非成像表型属性的划分标准, 该节点集对应非成像表型属性划分为一组上近似非成像表型属性Mmax={Mhmax}和一组下近似非成像表型属性Mmin={Mhmin}.节点的上近似边集
如果节点之间存在相同属性Mhmin或等价属性Mhmax, 则对应的边权值加1.将得到的邻接矩阵A与相似性度量结合, 可得到该粗糙图的邻接矩阵ARough.最终根据节点集V、上近似边集
如果图中所有的边都为下近似边, 称该图为下近似图GMIN, 其下近似邻接矩阵为Wmin(v, w).如果图中所有的边都为上近似边, 称该图为上近似图GMAX, 其上近似邻接矩阵为Wmax(v, w).如果图中存在上近似边, 也存在下近似边, 该图称为粗糙图GRough, 即
GRough=GMAX+GMIN. (7)
粗糙图的邻接矩阵为:
ARough=Wmax(v, w)+Wmin(v, w). (8)
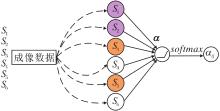
如图2所示, 根据定义2和定义3可知, 假如给定节点集S={S1, S2, …, S6}, 该节点集对应一组上近似非成像表型属性
Mmax={M1max, M2max, M3max}
和一组下近似非成像表型属性
Mmin={M1min, M2min, M3min}.
S1和S2之间具有等价的M1max和M3max, 具有相同的M1min和M2min, 可得S1和S2之间存在两条上近似边、两条下近似边, 且S1和S2之间上近似边权值为2, 下近似边权值也为2.S1和S3之间具有等价的M3max, 具有相同的M2min, 可得S1和S3之间存在一条上近似边、一条下近似边, 且S1和S3之间上近似边权值为1, 下近似边权值也为1.同理可得到其它任意两节点间上近似边、下近似边、上近似边权值和下近似边权值.若只关注两点间的上近似边(图中节点间为实线的边), 得到上近似图GMAX, 将得到的上近似边权值和节点间的γ max结合, 得到上近似邻接矩阵Wmax(v, w).若只关注两点间的下近似边(图中节点间为虚线的边), 得到下近似图GMIN, 将得到的下近似边权值和节点间的γ min结合, 得到下近似邻接矩阵Wmin(v, w).根据式(7)和已得到的上近似图GMAX、下近似图GMIN, 得到粗糙图GRough, 根据式(8)和已得到的上近似邻接矩阵Wmax(v, w)、下近似邻接矩阵Wmin(v, w), 得到粗糙图的邻接矩阵ARough.
若图G中包含n个节点, 使用一个n× n的方阵A, 并使每个节点都分别对应某行(列).既然图描述这些节点各自对应的属性之间的关系, 故可将任意一对节点v、w之间可能存在关系与矩阵A中对应的单元A[v, w]和A[w, v]对应.从邻接矩阵的定义上看, 若有S个图节点, 构造的下近似邻接矩阵Wmin(v, w)为一个S× S的方阵, 每个节点都分别对应于某行(列), 且下近似图描述这些节点各自对应属性之间的关系, 故可将任意一对节点v、w之间可能存在关系与矩阵Wmin(v, w)中对应的单元Wmin[v, w] 和Wmin[w, v]对应.结合定义3可知:每对节点间对应的下近似边的权值表示存在关系, 0表示不存在关系, 满足对称邻接矩阵的定义, 所以下近似矩阵Wmin(v, w)为对称的.同理, 构造的上近似邻接矩阵Wmax(v, w)为一个S× S的方阵, 每个节点都分别对应于某行(列), 且下近似图描述这些节点各自对应属性之间的关系, 故可自然地将任意一对节点v、w之间可能存在关系与矩阵Wmax(v, w)中对应的单元Wmax[v, w] 和Wmax[w, v]对应.结合定义3可知:每对节点间对应的上近似边的权值表示存在关系, 0表示不存在关系, 满足对称邻接矩阵的定义, 所以上近似矩阵Wmax(v, w)为对称的.根据式(8)可知粗糙图GRough对应的邻接矩阵为ARough.
基于上述讨论, 本文给出算法1.
算法1 粗糙图的生成
输入 拓扑图中的节点V={v1, v2, …, vv},
一组非成像上近似表型属性Mmax={Mhmax},
一组非成像下近似表型属性Mmin={Mhmin}
输出 粗糙图GRough
step 1 任取一对节点v、w, 判断该节点对之间在Mmin中是否具有相同属性, 如果有, 则说明该节点对之间存在下近似边
step 2 重复step 1, 直到该节点对中所有的Mmin都完成对比, 若该节点对在下近似属性集中具有完全相同的i1个属性个数, 则使用对应的i1个下近似边
step 3 重复step 2, 直到该图中任意两个节点对(v, w)的Mmin被对比完成为止.
step 4 得到原始下近似邻接矩阵Wmin0(v, w).
step 5 由式(4)得到相似性度量Sim(Av, Aw).
step 6 利用Sim(Av, Aw)对Wmin0(v, w)进行训练, 得到下近似矩阵Wmin(v, w).
step 7 任取一对节点vi、vj, 判断在一定规则下该节点对是否存在等价的上近似属性Mmax, 如果有, 则说明该节点对之间存在上近似边
step 8 重复step 7, 直到该节点对中所有的Mmax都完成对比, 若在一定规则下该节点对在Mmax中具有能被判断为等价的i2个属性个数, 则用对应的i2个上近似边
step 9 重复step 8, 直到该图中任意两个节点对(v, w)的上近似表型属性被对比完成为止.
step 10 得到原始上近似邻接矩阵Wmax0(v, w).
step 11 利用Sim(Av, Aw)对Wmax0(v, w)进行训练, 得到上近似矩阵Wmax(v, w).
step 12 通过式(8)构造粗糙图的邻接矩阵ARough, 得到对应的粗糙图GRough.
因为粗糙图GRough是由上近似图GMAX和下近似图GMIN共同构成的, 其中上近似图GMAX和下近似图GMIN具有不同的权重系数, 并且在构图时对粗糙图GRough的影响是不同的, 所以引入节点间的粗糙权重系数α ij, 对上近似图GMAX和下近似图GMIN进行训练.
节点间的粗糙权重系数为:
α ij=
其中, hi、hj、hk表示不同的节点特征, 函数a表示一个单层的前馈网络, W∈ RF'× F表示权重矩阵, F表示每个节点特征的数量, F'表示输出节点的特征维数, 维数由具体的参数设定, 与输入节点特征维数F相比, 可能存在维数不一致.
通过节点间的粗糙权重系数α ij, 对粗糙图GRough进行训练:
GRough'=α ijGMAX+(1-α ij)GMIN. (10)
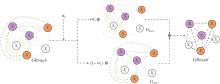
粗糙权重系数α ij的构造如图3所示.使用α ij训练粗糙图GRough的过程如图4所示.由于上近似图GMAX和下近似图GMIN在构造GRough时对其影响不同, 所以利用α ij训练上近似图GMAX, 利用1-α ij训练下近似图GMIN, 再结合两者训练后的结果, 得到训练后的粗糙图GRough'.
RG-GCN步骤如下所示.
算法2 RG-GCN
输入 拓扑图中的节点V={v1, v2, …, vv},
一组上近似非成像表型属性Mmax={Mhmax},
一组下近似非成像表型属性Mmin={Mhmin},
图节点特征h=(h1, h2, …, hv),
权重矩阵W
输出 节点的分类结果
step 1 由式(4)得到相似性度量Sim(Sv, Sw).
step 2 构造表型度量之间最大距离的度量, 由式(5)得到γ max.
step 3 构造表型度量之间最小距离的度量, 由式(6)得到γ min.
step 4 通过图节点集V和Mmax, 按照式(2)构造上近似图邻接矩阵Wmax(v, w), 得到上近似图GMAX.
step 5 通过图节点集V和Mmin, 按照式(3)构造下近似图邻接矩阵Wmin(v, w), 得到下近似图GMIN.
step 6 通过式(8)构造粗糙图邻接矩阵ARough, 得到粗糙图GRough.
step 7 由式(9)求得粗糙权重系数α ij.
step 8 由式(10)对粗糙图GRough进行训练.
step 9 得到训练后的粗糙图GRough'.
step 10 将训练后的粗糙图GRough'作为图卷积神经网络的输入, 通过式(1)对其进行训练.
step 11 得到GCN的输出结果.
本文选取ABIDE数据集[24, 25]进行实验, 该数据集包含受试者的信息, 可构成特定的粗糙图.ABIDE数据集收集来自不同国际采集站点的数据, 并公开分享1 112名受试者的神经成像(fMRI)和表型数据.本文选择Abraham等[26]使用的符合成像质量和表型信息标准的871名受试者的数据, 包括403名自闭症(Autistic Spectrum Disorder, ASD)患者和468名健康对照者, 具体信息如表1所示, 本文将健康对照者与ASD患者分开.
| 表1 ABIDE数据集信息 Table 1 Information of ABIDE dataset |
ABIDE数据库提供表型属性列表.本文选择数据较完整的6个不同的表型属性:性别(SEX)、年龄(AGE)、采集地点(SITE)、言语智商(VIQ)、操作智商(PIQ)、全量表智商(FIQ).对于Mmin, 选择SEX、AGE、SITE_ID作为3个下近似表型属性.对于Mmax, 选择VIQ、PIQ、FIQ作为3个上近似表型属性.
将ABIDE数据集上每个受试者作为一个节点, 选取受试者不同的表型属性, 进行表型属性之间关系的对比, 刻画节点之间的上近似边和下近似边, 得到一个粗糙图.
本文采用的实验平台为PC(Intel(R) Core(TM) i9-10900K CPU@3.70 GHz, 64GB RAM), NVIDIA RTX3090 GPU, Windows10操作系统, 开发工具为JetBrains PyCharm, 使用Python语言实现算法.
在训练过程中, 采用NLL(Negative Log-Likeli-hood)损失作为训练的损失函数, 迭代次数设置为10 000, 初始化学习率设置为0.005, 选择Adam(Adaptive Moment Estimation)优化器更新参数.
对比预测的标签值和真实的标签值, 可得到混淆矩阵中的真阳性TP、真阴性TN、假阳性FP、假阴性FN.其中, TP表示标签为“ 健康” 的受试者分为“ 健康” , TN表示标签为“ 患病” 的受试者分为“ 患病” , FP表示标签为“ 患病” 的受试者分为“ 健康” , FN表示标签为“ 健康” 的受试者分为“ 患病” .
为了评估分类性能, 本文使用如下6个评估指标:分类准确度(Accuracy, ACC)、敏感性(Sensi-tivity, SEN)、特异性(Specificity, SPE)、阳性预测值(Positive Predictive Value, PPV)、阴性预测值(Nega-tive Predictive Value, NPV)、平衡准确度(Balance Accuracy, BAC).ACC表示将受试者分类正确的概率, SEN表示将健康的人分类正确的概率, SPE表示将患者分类正确的概率, PPV表示预测为健康的人的样本中真正为健康的人所占的比例, NPV表示预测为患者的样本中真正为患者所占的比例.评估指标定义如下:
ACC=
SPE=
NPV=
为了验证本文方法的有效性, 实验中选取如下对比算法.
1)采用Linear中的岭回归器进行分类[27].该分类器使用最小二乘损失适应分类模型, 首先将二进制目标转换为{-1, 1}, 然后将问题视为回归任务, 优化二进制目标.
2)GNN(Graph Neural Network)[28].直接作用于图结构上的神经网络.利用GNN提取每个节点的特征向量, 用于预测每个节点的标签.
3)GAT(Graph Attention Network)[29].采用注意力机制对邻近节点特征加权求和, 邻近节点特征的权重完全取决于节点特征.
4)GCN.利用一小部分带有标签的节点进行半监督学习, 结合这部分节点的图结构和节点特征, 进行节点分类.GCN中这种结合邻近节点特征的方式和图的结构相关.
5)文献[4]算法(Graph Convolutional Networks for Brain Analysis in Populations).将受试者表示为一个稀疏图, 关联图的节点与基于图像的特征向量.
6)文献[5]算法.构建稀疏图, 将受试者的特点和特征均整合到稀疏图中, 对它们之间的相互作用进行建模.
本文采用ABIDE数据集上不相同的6个表型属性(SEX、SITE、AGE、FIQ、VIQ、PIQ)进行构图, 采用粗糙图的构图方式, 判断节点对中是否具有相同属性, 若具有相同属性, 节点对中对应的边权值加1, 由此得到拓扑图A.再使用Linear、GNN、GAT、GCN、文献[4]算法、文献[5]算法对其进行分类.选择SEX、SITE_ID、AGE作为下近似表型属性, 选择FIQ、VIQ、PIQ作为上近似表型属性, 构造粗糙图Arough.
各方法对传统拓扑图进行分类的指标值对比如表2所示, 表中黑体数字表示最优值.由表可看出:在ACC、SEN、SPE、BAC指标上, 深度学习方法明显好于Linear, Linear在PPV指标上略高于GAT, 但仍低于GNN、GCN、文献[4]算法、文献[5]算法; Linear在NPV指标上略高于GNN、文献[5]算法, 但仍低于GAT、GCN、文献[4]算法.这说明采用深度学习算法会得到较高的指标值, 因此本文选择深度学习算法是有效的.
| 表2 各算法在ABIDE数据集上的指标值结果对比 Table 2 Index value comparison of different algorithms on ABIDE dataset % |
为了验证粗糙图的分类效果, 本文把粗糙图Arough作为GCN的输入, 构成RG-GCN.由表2可看出, RG-GCN的ACC、SEN、SPE、PPV、BAC均明显高于其它算法, 只有NPV处于中等, 还有待提升.
RG-GCN可有效增加ACC, 这表明本文构造的粗糙图可准确刻画不确定性关系.这些结果表明, 基于粗糙图的GCN的分类算法有助于提高对潜在自闭症患者进行人群诊断的准确率.
构图方式的不同会影响算法的分类准确率.为了表现不同的构图方式对分类准确率的影响, 采用RG-GCN验证粗糙图的分类准确率.对于RG-GCN, 采取15种不同的构图方式, 对比不同的粗糙图结构在RG-GCN上的分类准确率.
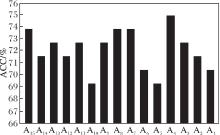
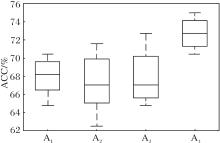
本文采用SEX、SITE、AGE构造下近似图A1; 采用FIQ、VIQ、PIQ构造上近似图A2; 采用SEX、SITE、AGE、FIQ构造粗糙图A3; 采用SEX、SITE、AGE、FIQ、VIQ、PIQ构造粗糙图A4; 采用SEX、SITE、AGE、PIQ构造粗糙图A5; 采用SEX、SITE、AGE、VIQ构造粗糙图A6; 采用SEX、SITE、AGE、PIQ、VIQ构造粗糙图A7; 采用SEX、SITE、AGE、PIQ、FIQ构造粗糙图A8; 采用SEX、SITE、AGE、VIQ、PIQ构造粗糙图A9; 采用SEX、FIQ、VIQ、PIQ构造粗糙图A10; 采用SITE、FIQ、VIQ、PIQ构造粗糙图A11; 采用AGE、FIQ、VIQ、PIQ构造粗糙图A12; 采用SEX、SITE、FIQ、VIQ、PIQ构造粗糙图A13; 采用SEX、AGE、FIQ、VIQ、PIQ构造粗糙图A14; 采用SITE、AGE、FIQ、VIQ、PIQ构造粗糙图A15.A3、A5~A9具有完全相同的下近似表型属性, A10~A15具有相同的上近似表型属性.
这15种不同结构的粗糙图在RG-GCN上的分类准确率如图5所示.由图可看出, 粗糙图A4的准确率最高, 可达到75%.
除ACC之外, 本文还给出其它相关指标的对比结果, 具体如表3所示, 表中黑体数字表示最优值.本文还把A3、A5~A9统称为下近似表型图Alower, 取A3、A5~A9各项指标的平均值作为下近似表型图的指标值; 把A10~A15统称为上近似表型图Aupper, 取A10~A15各项指标的平均值作为上近似表型图的指标值.由表3可见, 粗糙图A4在ACC、SEN、PPV上均取得最高值, 在BAC上仅略低于A14, 在SPE、NPV上的效果中等, 还有提升的空间, 所以粗糙图A4整体指标值较优, 因此本文选择粗糙图A4的构图方式是有效的.
| 表3 不同的粗糙图在RG-GCN上的指标值对比 Table 3 Comparison of metric values of different rough graphs on RG-GCN % |
为了进一步验证RG-GCN的有效性, 选择A1~A4这4种粗糙图, 均采用5种不同初始化种子数, 计算分类准确率, 结果如图6所示.由图可看出, 不同的初始化种子数对粗糙图分类准确率存在一定影响, 但粗糙图A4的分类准确率始终最高, 这表明本文构造粗糙图选取的6个评价指标是合理的.
本节选择西南大学纵向成像多模态(SLIM)脑部数据集[30], 包括494名健康受试者(年龄范围为19岁~80岁, 187名男性, 308名女性)的脑部rs-fMRI图像.脑部rs-fMRI图像为受试者的成像数据, 非成像数据包括年龄、惯用手等基本人口统计信息和对不同扫描图像的质量评估措施.
本次实验采用的平台、参数设计、评估属性与3.2节相同.不同的是, 3.3节是对受试者是否患病进行分类, 这里是对受试者的性别进行分类.
各对比算法在SLIM数据集上的指标值对比结果如表4所示, 表中黑体数字表示最优值.由表可看出, RG-GCN在ACC、SEN、NPV、BAC上优于其它算法, 由此验证RG-GCN的有效性.
| 表4 各算法在SLIM数据集上的指标值对比结果 Table 4 Index value comparison of different algorithms on SLIM dataset % |
因为现实生活中具有很多不确定性关系, 本文考虑这种不确定性关系, 结合粗糙集理论和图卷积神经网络, 提出基于粗糙图的图卷积神经网络算法(RG-GCN).首先, 结合传统拓扑图的边理论与粗糙集的上下近似理论, 将表示确定关系的边转换成表示不确定关系的粗糙边, 利用表型属性的不同含义分别刻画上近似边和下近似边, 从而得到粗糙图.然后, 引入粗糙权重系数, 利用粗糙权重系数训练本文构造的粗糙图, 解决GCN只能训练确定性图这一问题, 以此提高分类准确度.在ABIDE数据集上的实验表明, RG-GCN可有效将节点标签信息传播到未标记的节点, 合理处理不确定性关系, 较准确地分类节点, 得到较高的分类准确率.今后会进一步考虑将粗糙集理论融入GCN的卷积层中, 处理节点特征中不确定、不精确信息.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|
| [19] |
|
| [20] |
|
| [21] |
|
| [22] |
|
| [23] |
|
| [24] |
|
| [25] |
|
| [26] |
|
| [27] |
|
| [28] |
|
| [29] |
|
| [30] |
|