引用本文
张所娟, 余晓晗, 陈恩红, 沈双宏, 郑雨, 黄松. 融合知识交互关系的认知诊断深度模型. 模式识别与人工智能, 2023,36(1): 22-33
ZHANG Suojuan, YU Xiaohan, CHEN Enhong, SHEN Shuanghong, ZHENG Yu, HUANG Song. A Concept Interaction-Based Cognitive Diagnosis Deep Model. PATTERN RECOGNITION AND ARTIFICIAL INTELLIGENCE, 2023,36(1): 22-33.  
Doi: 10.16451/j.cnki.issn1003-6059.202301002
Permissions
Copyright©2023, 《模式识别与人工智能》编辑部
《模式识别与人工智能》编辑部
融合知识交互关系的认知诊断深度模型
张所娟1,2, 余晓晗1, 陈恩红2, 沈双宏2, 郑雨1, 黄松1
1.中国人民解放军陆军工程大学 指挥控制工程学院 南京 210007
2.中国科学技术大学 计算机科学与技术学院 大数据分析与应用安徽省重点实验室 合肥 230027
通讯作者:

黄 松,博士,教授,主要研究方向为软件测试、数据挖掘.E-mail:huangsong@aeu.edu.cn.

作者简介:

张所娟,博士,副教授,主要研究方向为教育数据挖掘、认知诊断.E-mail:suojuanzhang@aeu.edu.cn.

余晓晗,博士,副教授,主要研究方向为人工智能.E-mail:yuxh@aeu.edu.cn.

陈恩红,博士,教授,主要研究方向为机器学习、数据挖掘、教育大数据分析、个性化推荐等.E-mail:cheneh@ustc.edu.cn.

沈双宏,博士研究生,主要研究方向为数据挖掘、学生建模、知识追踪.E-mail:closer@mail.ustc.edu.cn.

郑 雨,硕士,助教,主要研究方向为信息检索、自然语言处理.E-mail:zhengyu89@outlook.com.

收稿日期: 2022-11-07 接受日期: 2023-01-09
资助项目: 国家自然科学基金项目(No.62207031,U20A20229)资助
摘要

认知诊断是基于学习数据挖掘学习者潜在认知状态的一种智能评测技术.当前大多数认知诊断模型将学习任务中的知识视为同等重要,未考虑知识间的交互关系,从而影响诊断的准确性,同时也缺乏可解释性.针对上述问题,文中提出融合知识交互关系的认知诊断深度模型,实现学习者认知状态与知识权重的统一表达.同时,实现基于Choquet积分的理想作答反应计算算法.最后提出模糊测度的深度神经网络,预测学习者的作答表现.大量实验表明,文中模型不仅取得较好的预测结果,还能为预测结果提供知识交互层面的解释,具有一定的优越性.

关键词: 认知诊断; 知识交互; 模糊积分; 知识权重
中图分类号:G434
A Concept Interaction-Based Cognitive Diagnosis Deep Model
ZHANG Suojuan1,2, YU Xiaohan1, CHEN Enhong2, SHEN Shuanghong2, ZHENG Yu1, HUANG Song1
1. College of Command and Control Engineering, Army Engineering University of PLA, Nanjing 210007
2. Anhui Province Key Laboratory of Big Data Analysis and Application, School of Computer Science and Technology, University of Science and Technology of China, Hefei 230027
Corresponding author:
HUANG Song,Ph.D., professor. His research interests include software testing and data mining.

About Author:
ZHANG Suojuan, Ph.D., associate professor.Her research interests include educational data mining and cognitive diagnosis.
YU Xiaohan, Ph.D., associate professor. His research interests include artificial intelligence.
CHEN Enhong, Ph.D., professor. His research interests include machine learning, data mining, education big data analysis and personalized recommendation system.
SHEN Shuanghong, Ph.D. candidate. His research interests include data mining, student modeling and knowledge tracing.
ZHENG Yu, master, teaching assistant. Her research interests include information retrieval and natural language processing.

Fund:Supported by National Natural Science Foundation of China(No.62207031,U20A20229)
Abstract

Cognitive diagnosis is an intelligent assessment technique of mining learners' cognitive state based on learning data. Concepts in learning tasks are regarded as equally important by most cognitive diagnosis deep model. Without the consideration of the interaction between concepts, diagnosis accuracy is affected and interpretability is insufficient. To solve the problems, a concept interaction-based cognitive diagnosis deep model is proposed to realize the unified representation of students' cognitive state and concept weights. In the meanwhile, an algorithm of ideal response calculation based on the Choquet integral is implemented. Finally, a deep neural network based on fuzzy measures is proposed to predict learners' response performance. Experiments show that the proposed model holds advantages in prediction results and the explanation at the concept interaction level provided for prediction results.

Key words: Cognitive Diagnosis; Concept Interaction; Fuzzy Integral; Concept Weights

随着大数据、人工智能技术与教育的深度融合, 以及各类在线学习平台的广泛应用, 大量的在线学习数据被积累, 为实现更智能的个性化学习提供支撑.而实现个性化学习的基础是认知诊断, 即通过可观测的学习行为数据揭示学习者的认知状态(知识的掌握水平)[1].在学习者在线学习过程中, 完成学习任务时产生作答行为记录(作答得分), 根据学习任务对应的知识, 通过认知诊断模型获取学习者在各个知识上的掌握水平.认知诊断作为许多相关教育场景应用的基础任务[2], 在学习者的学习表现预测、学习资源个性化推荐、在线教育自适应学习、试题合理组卷等应用中发挥重要作用.

认知诊断研究源于心理与教育学理论[3], 通过传统计量方法建立学习者作答反应数据与知识掌握水平之间的关系, 由此设计开发一系列适应不同学习场景的认知诊断模型, 包括经典的IRT(Item Response Theory)[4]、DINA(Deterministic Inputs, Noisy "and" Gate)等[5], 并在此基础上发展一系列拓展模型, 如MIRT(Multidimensional IRT)[6]、G-DINA(Generalized DINA)[7].

随着学习数据的积累和计算能力的发展, 基于机器学习的方法逐步被引入诊断领域, 将作答反应模式转换为分类问题.认知诊断研究由依赖于人工方式的统计测量方法, 逐步向利用智能技术捕捉学习者、试题和知识间复杂关系能力的方向发展[8].学者们结合智能技术, 从数据驱动的角度提出不同的认知诊断模型, 如针对不同试题类型的FuzzyCDF(Fuzzy Cognitive Diagnosis Framework)[9]、结合神经网络的NeuralCD (Neural Cognitive Diagnosis)[10]、定量表达练习与知识之间的外显关系和内隐关系的QRCDM(Quantitative Relationship Cognitive Diagnosis Model)[11]等.

在学习场景中, 知识之间并不孤立[12, 13], 知识的交互关系普遍存在.随着研究的深入, 知识间的交互关系也受到更多的关注[14, 15].目前知识交互关系建模工作多集中于遵循学科规律表达知识的结构关系[16].在这种情况下, 知识交互关系可看作是相对静态、稳定的, 如知识层级结构[17, 18]、先决关系[19]等.

认知诊断模型对知识建模时, 通常将各个知识视为同等重要.然而同一学习任务中不同知识的重要性存在差异, 而这种差异由学习任务中多个知识间存在的交互关系产生.若忽视学习任务(本文中的学习任务特指包含多个知识的试题)中多知识间的交互关系带来的不同权重, 会影响诊断结果[20, 21, 22].例如, 编程实现两个城市之间最快路线的算法并打印输出距离, 完成该任务考察最短路径算法实现、打印输出及基本语法结构等知识, 其中最短路径算法这一知识的重要性明显高于其它知识.

在实际应用中, 面向学习任务的知识交互关系带来不同的知识权重.若学习者在更重要的知识上掌握得更好, 则可能作答成绩也更好, 答对的概率也更高.此外, 知识交互关系不仅是存在于两两知识之间的关系, 知识集合之间也存在交互作用[23].由于现有的认知诊断模型未考虑知识间的交互关系, 知识交互信息很难直接嵌入已有的认知诊断模型中.

针对上述问题, 本文提出融合知识交互的认知诊断深度模型(A Concept Interaction-Based Cognitive Diagnosis Deep Model, CI-CDM), 将知识及知识集合间的交互关系融入认知诊断的过程中, 实现学习者认知状态及面向学习任务的知识权重的统一学习.首先构建认知诊断模型框架.再提出基于多个学习任务的知识权重学习算法, 用于表征知识交互关系.然后, 提出模糊测度的深度神经网络(Deep Neural Network Based on Fuzzy Measures, FM-Net), 预测学习者作答表现, 实现融合知识交互的认知诊断深度模型构建.最后, 在公开数据集和真实数据集上进行学习者的学习表现预测实验, 验证模型效果, 并结合实际学习任务进行案例分析.

1 问题描述

本节介绍必要的假设及认知诊断的问题描述定义, 并阐明本文使用的数学符号的具体含义.

假设1 一个学习任务对应多个知识, 知识或知识集合之间存在不同的交互关系.

假设2 考虑学习任务中知识及知识集合存在的交互关系, 知识集合对于学习任务达成的支持力度不同, 称为知识权重.

假定有I个学习者构成学习者集合

S={si|i=1, 2, …, I},

在J项学习任务上完成作答, 构成学习任务集合

T={tj|j=1, 2, …, J}.

J项学习任务考察的知识

X={xk|k=1, 2, …, K},

其中K表示知识数量.同时由领域专家给定的矩阵

Q=[q1, q2, …, qJ]

建立学习任务与其考察知识的关系.知识权重

V=[v1, v2…, vJ],

其中vj表示第j项学习任务的知识权重向量.得分矩阵R= (rij)I×J, rij表示第i个学习者在第j项学习任务上的得分.学习者i在学习任务tj上形成的作答记录可表示为一个四元组{si, tj, qj, rij}, 其中, si∈ S, tj∈ T, rij表示R中元素, qj表示Q矩阵中第j个列向量.

认知诊断过程具体包含如下3个流程.

1)模型输入.输入学习者作答记录的四元组历史学习数据, 对于学习者si, 输入数据

log={(si, tj, qj, rij)|i=1, 2, …, I, j=1, 2, …, J}.

2)模型构建.基于Choquet积分提出融合知识交互关系的认知诊断深度模型(CI-CDM).

3)模型应用.将CI-CDM应用于如下3个任务:学习者表现预测、认知状态诊断及知识交互表征.

为了更清晰地说明, 表1列举本文重要的数学符号.

表1 本文中的重要符号 Table 1 Description of important symbols in this paper
2 融合知识交互关系的认知诊断深度模型

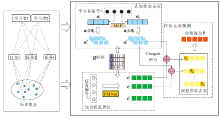
本节基于认知诊断的一般流程, 提出融合知识交互关系的认知诊断深度模型(CI-CDM), 框架如图1所示.该模型建模学习者作答时与学习任务交互的过程并输出作答结果预测值(如答对的概率).模型框架的构建分别从学习者、学习任务及知识聚合三方面实现学习者认知状态表征、面向学习任务的知识权重表征及融合知识权重的作答表现预测这三个模块, 最终实现CI-CDM.

图1 CI-CDM框架Fig.1 Structure of CI-CDM

2.1 学习者认知状态表征

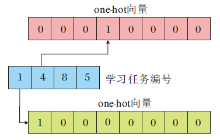
认知诊断的核心目标在于挖掘学习者潜在的认知状态, 沿用DINA的建模思路, 将学习者的认知状态(即各知识上的掌握水平α i)作为CI-CDM中的学习者特征向量.在CI-CDM中, 首先将学习者集合

S={si|i=1, 2, …, I}

作为输入, 通过多层融合网络模型学习获得相同维度的知识掌握水平.学习者知识掌握水平矩阵为:

A= [α1, α2, …, αK]T,

其中,

α i=[α 1, α 2…, α K]

对应学习者si在K个知识上的掌握水平, K表示输入模型的所有学习任务考察知识的数量.例如, 多个学习任务共考察4个知识, 学习者s1的知识掌握水平

α 1=[0.9, 0.6, 0.3, 0.1]

表示该学习者对知识x1的掌握水平最高为0.9, 但在知识x3上的掌握水平较低, 只有0.3, 对知识x4的掌握水平最低, 只有0.1.模型实现时, 可将学习者si的知识掌握水平表达为

α L= αL0* M,

其中, αL0表示读取log数据中L个学习者的样本数据, 对应学习者编号si生成知识掌握水平初始表征向量, M表示一个可训练的矩阵.通过多层神经网络获得L个学习者的知识掌握水平向量α L∈ RL× K.由于每项任务考察的知识并不相同, 进一步根据Q矩阵获得学习者在J项学习任务上对应知识的掌握水平表征向量:

αL(J)=α L[index],

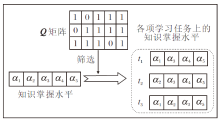
其中, index表示将二值的Q矩阵(取值为0或1)进行维度扩展, 通过index筛选学习者在各项任务上的知识掌握水平,

αL(J)∈ [0, 1]L× J× K', K'≤ K.

例如, 若3个学习任务共考察5个知识, 每个任务考察其中的4个知识, 如学习任务t1考察知识x1、x3、x4、x5.对于一个学习者而言, 其知识掌握水平被划分为对应3个学习任务的知识掌握水平向量:

α (1)=[α 1, α 3, α 4, α 5],
α (2)=[α 2, α 3, α 4, α 5],
α (3)=[α 1, α 2, α 3, α 5].

具体如图2所示.

图2 Q矩阵筛选学习任务对应的知识掌握水平Fig.2 Mastery of concepts selected by Q Matrix in learning tasks

2.2 面向学习任务的知识权重表征

每项学习任务考察的知识不同, 不同任务中知识集合间存在不同的交互关系.每个知识在特定学习任务中的重要程度不同.相应地, 同个知识在不同任务中的权重也不同.因此, 对于每项学习任务, 都需要建立一个知识权重表征向量.学习任务对应的知识权重表示为V=[v1, v2, …, vJ], vj表示第j项学习任务的知识权重向量.

本文充分考虑知识集合间的交互关系, 采用模糊测度表征知识权重.例如, 知识x1的权重表示为v(A)∈ [0, 1], A={x1}.根据模糊测度的定义[24], 知识权重集合的元素数量为知识的幂集, v(Ø )=0不影响计算结果, 则第j项学习任务的知识权重向量vj∈ R1×(2Kj-1), 其中Kj表示学习任务tj考察的知识数量.

例如, 学习任务t1考察3个知识, 对应如下的知识权重向量:

v1=[v({x1}), v({x2}), v({x3}), v({x1, x2}), v({x1, x3}), v({x2, x3}), v({x1, x2, x3})].

这里学习任务t1的知识权重数量为

23-1=7个.

知识权重向量的维度由知识的个数确定.需要说明的是, 本文仅针对等量知识的学习任务讨论, 即每项任务考察的知识点数目相等.

为了方便计算, 建立知识集合A⊆X与整数集I={1, 2, …, 2Kj-1}之间的一一映射关系, 从而建立知识权重向量中的模糊测度v(A)的索引编码.具体编码方式如下.

1)取整数集I中的集合元素转化为二进制表示.例如, 元素i=4, 对应的二进制表示为

i=4⇔ 100.

2)对于学习任务tj, 定义索引表征向量c∈ {0, 1}Kj.

若知识xi∈ A, cKj-i+1=1, 否则 cKj-i+1=0.其中, 知识集合

A⊆Xj={x1, x2, …, xKj},

|Xj|=Kj表示学习任务tj考察的知识个数为Kj.

3)根据索引表征向量c确定v(A)在整数集I中位置.

举例来说, 学习任务tj考察的知识Kj=3个.当知识集合A={x1}时, 索引表征向量c=(0, 0, 1).相应地, v(A)对应整数集I的元素

i=1(i=1⇔ 001), v({x1})=v1.

当知识集合A={x1, x3}时, 索引表征向量c=(1, 0, 1), 此时v(A)对应整数集I的元素

i=5(i=5⇔ 101), v({x1, x3})=v5.

以知识集合X={x1, x2, x3}为例, 按照表2的二进制编码方式, 进而确定知识集合模糊测度的位置, 最后实现知识权重度向量vj的有序排列.

表2 知识权重二进制编码方式 Table 2 Binary encoding of concept weights

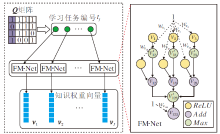
本文基于模糊测度的深度神经网络FM-Net训练参数, 获得知识权重的表征.为了方便表达, 简化如下.将知识x1构成的单点知识集合的权重v({x1})记作v1, 将知识集合{x1, x3}的权重v({x1, x3})记作v13, 以此类推, v({x1, x2, x3})记作v123.由于知识交互关系随学习任务不同而变化, 需要对应学习任务的神经网络以学习知识权重对应的参数.具体的参数学习过程如图3所示.

图3 FM-Net参数学习过程Fig.3 Parameters in learning process of FM-Net

FM-Net的构建采用文献[24]中的参数学习的基本思想, 初始化模糊测度学习深度神经网络参数矩阵W=( wvA)∈ RJ×(2K-1), 对应于具体学习任务的知识权重生成一个相应的网络权重参数.对于∀ A⊆X, A≠ Ø , 初始化参数统一赋值如下:

wvA= 1ρ-1, ρ = 2Kj-1,

其中Kj表示FM-Net对应的学习任务tj考察的知识数量.由此可见, FM-Net的初始参数取值与知识数量相关.具体分为如下2种情况, 计算学习任务tj中的知识权重.

1)单知识集合的模糊测度表征 vj(s)∈ [0, 1].单个知识集合的模糊测度不受单调性的约束, 因此网络权重参数直接通过ReLU函数获得, 具体定义如下:

if|A|=1, v(A)=ReLU( wvA).

例如, 知识x1的权重

v1=v({x1})= wv1,

知识x2的权重

v2=v({x2})= wv2.

2)知识集合的模糊测度表征

vj(m)∈ [0, 1]2Kj-1-Kj, 1< m< |X|.

根据模糊测度性质中的单调性约束, 若A⊆X, B⊆X, 同时B⊆A, 则v(A)≤ v(B).这意味着知识子集的权重取值应符合该约束条件.具体定义如下:

(1)

由式(1)可得, v(A)≥ v(B), 由此保证v(A)取值的单调性.例如, 知识集合A={x1, x2}, 则该知识集合的权重表示为

v12=max{v1, v2}+ReLU( wv12).

上述两类知识集合涵盖单项学习任务中所有知识集合的模糊测度.按索引编码的顺序依次拼接后, 获得该学习任务的知识权重向量:

vj= [vj(s), vj(m)]T.

2.3 融合知识权重的作答表现预测

由于学习者的知识掌握水平属于内隐状态, 现有数据集中的知识掌握水平未被标记, 无法直接评价从认知诊断模型计算知识掌握水平的准确性.但是, 学习者的作答表现(如作答分数)可基于知识掌握水平进行预测, 并且实际的作答分数在数据集上已标记.因此, 本文利用认知诊断模型获取作答表现的预测结果, 以反映认知诊断结果的有效性.学习任务涉及多个知识, 学习者的作答反应由该学习者在各个知识上的掌握水平及特定学习任务中的知识权重共同决定.考虑将反映知识交互关系的知识集合权重通过模糊积分的方式嵌入认知诊断过程中, 在充分考虑模糊测度的约束条件基础上学习获得知识权重的表征向量vj, 通过模糊积分神经网络实现融合知识权重的聚合方法.

模糊积分(Fuzzy Integral)以模糊测度为核心建立聚合函数, 能利用信息源之间丰富的相互作用.模糊测度可建模集合元素之间的交互作用, 通常被描述为重要性、可靠性、满意度等相似的概念.Choquet积分作为模糊积分中广泛使用的方法之一, 在分类[25]、模式识别[26], MCDM(Multiple Criteria Decision-Making)[27]等多个领域得到应用.

关于模糊测度m和输入X, Choquet积分可表示为

Cm(X)= ∑i=1n[x(i)-x(i-1)]m(Hi), (2)

其中, x(i)表示对输入XZ={x(1), x(2), …, x(n)}非递减排列后对应的元素, 即

x(1)≤ x(2)≤ …≤ x(n).Hi={(i), (i+1), …, (n)}

表示前n-i+1个最大元素对应下标构成的集合.这里选择广泛性较好的Choquet积分作为知识聚合函数, 预测学习者的作答反应.换个角度来看, 式(2)中Choquet积分可看作是关于知识权重向量的线性函数.为了构建适合于神经网络的表达形式, 可将Choquet积分转换为

Cm= ∑A⊆Xm(A)gA(α ), (3)

其中, m(A)表示知识权重, gA(α )表示关于知识掌握水平的函数.经文献[28]证明, 式(2)与式(3)等价.

本文采用Choquet积分聚合知识权重和认知状态, 构建融合知识交互关系的认知诊断深度模型, 实现学习者认知状态和学习任务知识权重的统一表达.结合认知诊断应用场景, 学习者si在学习任务tj中的理想作答表现为:

η ij= ∑A⊆Xvj(A)TgA(α i), (4)

其中, vj(A)表示学习任务tj的知识权重向量, gA(α i)表示学习者si关于知识掌握水平α i的函数.由式(4)可知, Choquet积分中知识权重向量vj的取值会影响该学习者在学习任务tj的作答表现.

具体地, 对于每个知识集合A⊆X, 令

gA(α i)=max(0, mink∈Aα (ik)- maxk∈X\Aα (ik)), (5)

其中α (ik)表示对α ik进行递减排序后的结果, 即

α (i1)≥ α (i2)≥ …≥ α (iK).

为了方便描述, 可将gA(α i)简写为gA.

需要注意的是, 集合A是知识掌握水平α i中前k个最大元素对应下标构成集合的子集, 即

A⊂{x(1), x(2), …, x(k)}, gA=0.

例如,

A={x(1), x(2), …, x(k-1)},

则

gA=max(0, α (i(k-1))-α (ik))=0.

举例来说, 学习任务t1涉及3个知识, 即X={x1, x2, x3}, 若学习者s2的知识掌握水平分别为

α (21)=0.5, α (22)=0.4, α (23)=0.7,

将知识掌握水平按照从大到小顺序排列, 可得α (21)=0.7, 对应知识x3.同理,

α (22)=0.5, α (23)=0.4,

分别对应知识x1和x2.计算过程如下:

g123=max(min(α (21), α (22), α (23))-0)=0.4,
g13max(0, min(α (21), α (22))-α (23))=0.1,
g3=max(0, α (21)-max(α (22), α (23)))=0.2,
g1=g2=g12=g23=0.

代入式(4)、式(5)计算理想作答反应, 可得

η ij= ∑A⊆Xv(A)TgA(α )= v({x1, x2, x3})g123+v({x1, x3})g13+v({x3})g3.

CI-CDM的目标是通过学习者知识掌握水平向量α (j)和基于知识交互的知识权重向量vj生成聚合结果, 预测学习者的作答表现.将学习者编号生成的嵌入向量输入多层神经网络后得到知识掌握水平α , 根据Q矩阵, 获得学习任务tj的知识掌握水平向量α (j).经过一系列变换后(如式(5)所示), 得到需要的知识掌握水平表征形式gA(α ), 由此获得作答预测模块的其中一个输入.另一方面, 将模糊测度深度神经网络输出的表征向量vj(第j项任务的知识权重向量)作为第2个输入, 经Choquet积分的聚合后, 计算得到理想作答表现N= (ηij)I×J.基于Choquet积分的理想作答反应计算实现过程见如下算法.

算法 基于Choquet积分的理想作答反应计算

实现过程

输入 学习者si知识掌握水平α i,

学习任务tj的知识权重向量vj

输出 学习者si在学习任务tj上的理想作答反应

η ij

step 1 初始化知识掌握水平向量函数

gA(α i)∈ {0}1×(2K-1).

step 2 对知识掌握水平α i∈ R1× K递减排序, 得到知识掌握水平α (i)及序号sort_id扩展知识掌握水平向量α (i)的维度, 增加全0列向量, 可得α '(i)∈ R1×(Kj+1), 其中Kj表示学习任务tj的知识数量.

step 3 获取差值向量:

Δ α =α '(i)[0∶ Kj]-α '(i)[1∶ Kj].

step 4 取2sort_id按列求和, 获得定位loc, 将Δ α 按定位赋值给gA(α i)[loc]=Δ α .

step 5 理想作答反应计算:

η ij= ∑A⊆Xvj(A)TgA(α ).

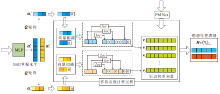
融合知识权重的理想作答表现预测过程如图4所示, 最后将输出的理想作答表现N作为输入连接多层神经网络, 通过Sigmoid函数保证最终预测作答得分 ŷ∈ [0, 1]I× J.

图4 融合知识权重的作答表现预测过程Fig.4 Prediction process of response performance based on concept weights

需要特别说明的是, 对于学习者i的知识掌握水平α i, 对应J项学习任务生成J个知识掌握水平向量 αi(j).模型在训练时, 相应输出学习者si在J项学习任务上的预测得分 ŷi∈ [0, 1]J× 1.这里根据当前学习者对应的任务编号进行one-hot编码(如图5所示), 用于提取当前学习者在某一项任务的预测得分, 再对比真实标签, 并计算损失函数.

图5 预测得分的one-hot 向量Fig.5 One-hot vector of predicted score

神经网络的损失函数是输出 ŷi(预测值)和真实标签yi(真实得分)之间的交叉熵, 目标函数定义如下:

L=- ∑iyi ln ŷi.

联合知识掌握水平和知识权重向量, 通过Choquet积分获得理想作答反应, 同时连接多层神经网络, 预测最终的作答表现.

3 实验及结果分析
3.1 实验设置

为了验证CI-CDM的有效性, 分别在公开数据集和真实数据集上进行实验.由于本文讨论的认知诊断模型考虑面向学习任务的知识交互关系, 因此学习任务与知识一一对应的映射关系的数据集不适合于CI-CDM的应用场景.因此, 本文采用知识交互较多的公开数据集Math1和Math2(http://staff.ustc.edu.cn/~qiliuql/data/math2015.rar).

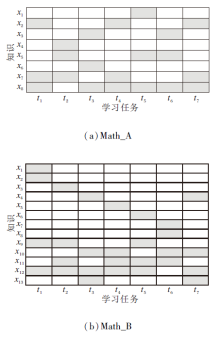
由于CI-CDM面向具有等量知识的学习任务, 预处理阶段根据Q矩阵筛选数据集上知识数目相同的学习任务, 生成Math_A、Math_B数据集, 如图6所示.Math_A数据集为Math1数据集筛选后的结果, 每项任务均包含3个知识(每项任务可能对应不同的3个知识).例如, 学习任务t5包含知识x1、x5和 x8.Math2数据集选择考察4个知识的学习任务后构成Math_B数据集.例如, 学习任务t1包含知识x1、x2、x9和 x12.

图6 筛选后的数据集Q矩阵示例Fig.6 Examples of Q Matrices from selected datasets

同时选取编程学习平台产生的真实数据集(Program数据集).平台允许学习者多次重复作答, 在本文实验场景中, 作答数据仅记录学习者前两次作答的记录以保证公平性.在预处理环节, 选取考察3个知识的学习任务, 包含22个学习任务, 共涉及30个知识, 123 750条作答记录.

各数据集基本情况如表3所示.

表3 实验数据集统计信息 Table 3 Statistical information of experimental datasets

学习者的作答数据以json格式文件读入模型, 每条学生作答记录包括学生编号、任务编号、任务得分、考察的知识这4个属性.

本文基于Pytorch深度学习框架实现CI-CDM.为了保证实验的公平性, 所有对比模型参数均调整至最优性能.在知识掌握水平的多层网络中, 网络参数维度分别设置为128, 256, 1.同时将ReLU作为中间层的激活函数.

为了保证知识掌握水平的范围在[0, 1]区间, 输出层采用Sigmoid激活函数.在初始化网络参数阶段, 使用Xavier初始化参数[29], 根据N(0, std2)采样随机值填充权重.在模糊测度神经网络中网络层数取决于学习的模糊测度个数.单个知识对应的模糊测度为第1层, 两个知识组合的知识集合对应第2层, 以此类推.Choquet积分计算结果输入全连接层, 维度分别设置为256, 128, 1.

为了防止过拟合情况发生, 在全连接层的每一层加入Dropout机制(p=0.5), 并同样采用ReLU作为激活函数, 输出层采用Sigmoid激活函数.最后使用交叉熵作为损失函数训练CI-CDM(https://github.com/kathy-sj/CI-CDM.)

为了验证CI-CDM的有效性, 本文选取如下基准模型预测学习者的学习表现.

1)NeuralCD[10].具有较好泛化性的深度学习认知诊断模型, 通过神经网络实现复杂的交互函数, 实现认知诊断.

2)IRT[4].认知诊断方法, 通过线性函数对学习者的潜在特质和任务特征参数(如难度与区分度)建模, 实现认知诊断.

3)MIRT(Multidimensional Item Response Theo-ry)[6].作为IRT的多维扩展, 对学习者和学习任务的多维度知识的熟练程度进行建模.

4)概率矩阵分解(Probabilistic Matrix Factoriza-tion, PMF)[30].通过分解学习者得分矩阵, 得到学习者和学习任务的潜在特征向量.

3.2 实验结果对比

为了衡量CI-CDM的性能, 从回归和分类的角度采用AUC(Area Under Curve)、F1-score、 MAE(Mean Absolute Error)指标.

首先, 将数据集作答数据中80%的记录划分为训练集, 其余部分平均划分为验证集和测试集.

实验对比CI-CDM和基准模型的预测表现, 各模型在学习者表现预测上的总体性能如表4所示, 表中黑体数字表示最优的预测结果.由表可得如下结论.

表4 各模型在学习者表现预测上的性能对比 Table 4 Performance comparison of learner performance prediction among different models

1)在Math_A数据集上, 相比NCD, CI-CDM的MAE值下降2.86%, 同时AUC和F1-score值均有提升.同时, 相比IRT、MIRT和PMF, CI-CDM更具有明显优势.这表明, 融合知识交互关系的CI-CDM对于学习者的学习表现预测任务是有效的, 可获得更准确诊断结果, 提高预测精度.

2)在Math_B数据集上, CI-CDM的预测表现几乎都优于不考虑知识交互的基准模型.CI-CDM的F1-score值略低于NCD, 但相比RT、MIRT和PMF, CI-CDM仍具有一定的优势.这可能与Math_B数据集上知识本身的特征有关, 部分学习任务中知识之间存在的交互关系较弱 (如掌握概率论和等差数列的能力之间是相对独立的).因此, 是否融合知识交互关系进行学习预测对结果影响并不明显.但同时也可说明CI-CDM对认知诊断工作的适用性, 在知识交互关系较弱的学习场景下, CI-CDM同样具有相对较优的性能.

3)在Program数据集上CI-CDM的性能明显优于其它模型.由此可知在编程学习领域, CI-CDM同样具有较好的适用性.编程学习强调综合运用多个知识解决问题, 知识间的关联关系更显著, 因此使用融合知识交互关系的认知诊断模型在处理这一类学习场景时更具有优势.

3.3 案例分析

案例分析1 面向学习任务的知识全局重要度及交互指标

CI-CDM可得到每个学习任务的知识权重向量, 进而可得出知识的全局重要度和交互指标[31].这里的知识全局重要度是综合考虑各知识自身的权重及包含该知识的集合权重, 也就是充分利用知识交互关系后得出的全局重要度.交互指标反映两两知识点在整个知识集合中的交互作用.若两个知识点之间的交互指标越高, 说明这两个知识点间的互补性越强.

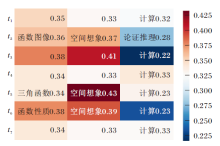
Math_A数据集上的知识全局重要度如图7所示.由图可知, 学习任务知识 “ 计算” 出现在6项学习任务中, 可看作这6项学习任务共同的知识基础.从考察目标上看, “ 计算” 必然不是学习任务重点关注的一个知识, 因此它在各项学习任务中的重要程度是最低的, 这也符合图7的结果.

图7 Math_A数据集上的知识全局重要度Fig.7 Global importance of concept on Math_A dataset

同时可知, Math_A数据集上学习任务t2考察的知识包括函数图像(x4)、空间想象(x5)和推理论证(x7), 学习任务t5考察的知识包括三角函数(x1)、空间想象(x5)和计算(x8), 学习任务t6考察的知识包括函数性质(x3)、空间想象(x5)和计算(x8).知识空间想象(x5)出现在3项学习任务中, 即t2、t5和t6.t2任务中知识x5对应的重要度

ϕ (x5)=0.37,

在t5任务中知识x5对应的重要度

ϕ (x5)=0.43,

而在任务t6中知识x5对应的重要度

ϕ (x5)=0.39.

由此可看出, 同个知识在不同的学习任务中, 重要程度随学习任务的不同而不同.

再看交互指标, 以Math_B数据集上的学习任务t6为例, 该任务涉及4个知识:线性规划(x1)、算法定义(x2)、空间想象(x3)及推理论证(x4).根据CI-CDM可获得知识权重如表5所示.

表5 CI-CDM学习获得的知识权重 Table 5 Concept weights learned from CI-CDM

由表5可得如下结论:

v({x1})+v({x2})=v({x1, x2}),
v({x1})+v({x3})=v({x1, x3}),
v({x2, x3, x4})=v({x2, x4})+v({x3}).

根据研究[22]可知该任务中各个知识及知识集合之间为独立关系.同时各知识的交互指标应接近于0(如图8所示), 表示各个知识之间相对独立.

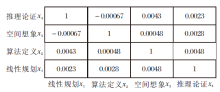图8 Math_B数据集上第6项学习任务的知识交互指标Fig.8 Concept interaction index of the 6th learning task on Math_B dataset

综上可知, 实验结果符合学科的一般认知规律, 同时也印证Math_B数据集上知识交互关系较弱, 结论具有一定的可解释性.根据CI-CDM得到的知识权重可获得知识全局重要度和交互指标, 有利于较好地理解学习任务特征.

案例分析2 学习者的认知状态诊断结果

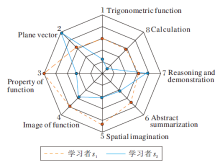
两个学习者s1、s2对于Math_A数据集上8个知识的掌握水平如图9所示.

图9 学习者知识掌握水平示例Fig.9 Example for concept mastery of learners

由图9可看出:学习者s1对知识3的掌握程度较高, 对其它知识的掌握程度较平均; 学习者s2对知识2的掌握程度很高, 而在知识8上的知识掌握水平较低.学习者的知识掌握水平通过认知诊断方法诊断获得, 展现学习者潜在的认知状态可视化.

案例分析3 知识交互关系分析

在Program数据集编程学习的立体几何计算任务上, 要求使用Scanf输入数据(指定为double型浮点数), 输出圆柱体积的计算结果, 输出时取小数点后两位数字.任务考察3个知识:输入输出函数x1、浮点数x2、乘法运算x3.从任务描述中可知重点考察的知识是输入输出函数x1和浮点数x2.从CI-CDM获得知识权重, 可得

v({x1})=0.12, v({x2})=0.2, v({x3})=0.13.

同时, 可知

v({x1, x2})=0.78, v({x2, x3})=0.3,

这样就可以计算得出知识间的关联关系及强度[23].例如,

v({x1, x2})> v({x1})+v({x2}),
v({x2, x3})< v({x2})+v({x3}),

可推出知识x1、x2存在协同增强关系, 交互强度为0.46.知识x2、x3存在负协同关系, 接近独立关系.同时计算全局重要度, 可得

ϕ (x1)=0.465, ϕ (x2)=0.308, ϕ (x3)=0.227.

从重要度的排序结果来看,

ϕ (x1)> ϕ (x2)> ϕ (x3),

即输入输出函数x1、浮点数x2均较重要, 而乘法运算x3对于完成该任务的重要度相对较弱.这与任务的考察重点一致, 能较准确地表征知识交互关系.

4 结束语

本文面向学习任务, 提出融合知识交互关系的认知诊断深度模型(CI-CDM), 实现学习者认知状态与知识交互关系的统一表达.针对知识数量相同的学习任务场景, 提出多个学习任务的知识权重学习算法, 反映知识交互关系.最后, 提出模糊测度的深度神经网络(FM-Net), 实现对学习者作答反应的预测, 在刻画知识交互关系的基础上构建认知诊断深度模型.本文进行学习者的学习表现预测实验, 在公开数据集和真实数据集上验证模型效果, 并结合CI-CDM的实验结果, 从学习任务的知识交互关系和知识掌握水平诊断结果两方面进行案例分析.

然而实际场景中学习任务的知识数量在大多数情况下并不相同, 本文的研究仅针对相同知识数量的学习任务进行诊断, 尚未解决多学习任务中知识数量不同的情况.下一步将进行优化以拓展CI-CDM的应用范围.学习任务涉及的知识数目不同, 知识权重表征向量的长度也相应变化.每个知识子集对应的索引位置也不相同, 这为模糊积分计算带来挑战.另一方面, 由于知识掌握程度的取值影响知识权重变量被访问的次数, 因此无法确定数据支持哪些知识权重变量.随着知识点数目的增加, 知识权重变量被访问的次数通常会变得更稀疏, 如何对这部分变量进行学习更新, 同样也是困难的.因此, 如何更准确地表征学习知识权重以应对学习任务的复杂场景同样值得深入研究.

本文责任编委 欧阳丹彤

Recommended by Associate Editor OUYANG Dantong

参考文献
[1] 罗照盛. 认知诊断评价理论基础. 北京: 北京师范大学出版社, 2019.
(LUO Z S. Fundamentals of Cognitive Diagnostic Assessment. Beijing, China: Beijing Normal University Press, 2019. ) [本文引用:1]
[2] CHEN S, JOACHIMS T. Predicting Matchups and Preferences in Con-text // Proc of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York, USA: ACM, 2016: 775-784. [本文引用:1]
[3] 涂冬波, 蔡艳, 高旭亮, 等. 高级认知诊断. 北京: 北京师范大学出版社, 2019.
(TU D B, CAI Y, GAO X L, et al. Advanced Cognitive Diagnosis. Beijing, China: Beijing Normal University Press, 2019. ) [本文引用:1]
[4] EMBRETSON S E, REISE S P. Item Response Theory. Hove, UK: Psychology Press, 2000. [本文引用:2]
[5] DE LA TORRE J. DINA Model and Parameter Estimation: A Didactic. Journal of Educational and Behavioral Statistics, 2009, 34(1): 115-130. [本文引用:1]
[6] RECKASE M D. The Past and Future of Multidimensional Item Response Theory. Applied Psychological Measurement, 1997, 21(1): 25-36. [本文引用:2]
[7] DE LA TORRE J. The Generalized DINA Model Framework. Psychometrika, 2011, 76(2): 179-199. [本文引用:1]
[8] LIU Q. Towards a New Generation of Cognitive Diagnosis // Proc of the 13th International Joint Conference on Artificial Intelligence. San Francisco, USA: IJCAI, 2021: 4961-4964. [本文引用:1]
[9] LIU Q, WU R Z, CHEN E H, et al. Fuzzy Cognitive Diagnosis for Modelling Examinee Performance. ACM Transactions on Intelligent Systems and Technology, 2018, 9(4). DOI: DOI:10.1145/3168361. [本文引用:1]
[10] WANG F, LIU Q, CHEN E H, et al. Neural Cognitive Diagnosis for Intelligent Education Systems. Proceedings of the AAAI Confe-rence on Artificial Intelligence, 2020, 34(4): 6153-6161. [本文引用:2]
[11] YANG H W, QI T L, LI J, et al. A Novel Quantitative Relationship Neural Network for Explainable Cognitive Diagnosis Model. Knowledge-Based Systems, 2022, 250. DOI: DOI:10.1016/j.knosys.2022.109156. [本文引用:1]
[12] 钟卓, 唐烨伟, 钟绍春, 等. 人工智能支持下教育知识图谱模型构建研究. 电化教育研究, 2020, 41(4): 62-70.
(ZHONG Z, TANG Y W, ZHONG S C, et al. Research on Constructing Model of Educational Knowledge Map Supported by Artificial Intelligence. e-Education Research, 2020, 41(4): 62-70. ) [本文引用:1]
[13] PIAGET J. . The Equilibration of Cognitive Structures: The Central Problem of Intellectual Development. BROWN T, THAMPY K J, trans. Chicago, USA: University of Chicago Press, 1985. [本文引用:1]
[14] GAO W B, LIU Q, HUANG Z Y, et al. RCD: Relation Map Dri-ven Cognitive Diagnosis for Intelligent Education Systems // Proc of the 44th International ACM SIGIR Conference on Research and Development in Information Retrieval. New York, USA: ACM, 2021: 501-510. [本文引用:1]
[15] GAO L N, ZHAO Z Y, LI C, et al. Deep Cognitive Diagnosis Model for Predicting Students' Performance. Future Generation Computer Systems, 2022, 126: 252-262. [本文引用:1]
[16] MENG L L, ZHANG M X, ZHANG W X, et al. CS-BKT: Introducing Item Relationship to the Bayesian Knowledge Tracing Mo-del. Interactive Learning Environments, 2019, 29(8): 1393-1403. [本文引用:1]
[17] LEIGHTON J P, GIERL M J, HUNKA S M. The Attribute Hierarchy Method for Cognitive Assessment: A Variation on Tatsuoka's Rule-Space Approach. Journal of Educational Measurement, 2004, 41(3): 205-237. [本文引用:1]
[18] GIERL M J, LEIGHTON J P, HUNKA S M. Using the Attribute Hierarchy Method to Make Diagnostic Inferences About Examinees' Cognitive Skills // LEIGHTON J, GIERL M, eds. Cognitive Diagnostic Assessment for Education: Theory and Applications. Cambridge, USA: Cambridge University Press, 2007: 242-274. [本文引用:1]
[19] YANG Y M, LIU H X, CARBONELL J, et al. Concept Graph Learning from Educational Data // Proc of the 8th ACM International Conference on Web Search and Data Mining. New York, USA: ACM, 2015: 159-168. [本文引用:1]
[20] TATSUOKA K K. Boolean Algebra Applied to Determination of Universal Set of Knowledge States. Technical Report, RR-91-44-ONR. Princeton, USA: Educational Testing Service, 1991. [本文引用:1]
[21] GUO L, BAO Y, WANG Z R, et al. Cognitive Diagnostic Assessment with Different Weight for Attribute: Based on the Dina Mo-del. Psychological Reports, 2014, 114(3): 802-822. [本文引用:1]
[22] ZHANG S J, HUANG S, YU X H, et al. A Generalized Multi-skill Aggregation Method for Cognitive Diagnosis. World Wide Web, 2022. DOI: DOI:10.1007/s11280-021-00990-4. [本文引用:2]
[23] 张所娟, 黄松, 余晓晗, 等. 基于模糊测度的知识关联性建模方法. 模式识别与人工智能, 2022, 35(2): 95-105.
(ZHANG S J, HUANG S, YU X H, et al. Modeling Method of Knowledge Relevance Based on Fuzzy Measures. Pattern Recognition and Artificial Intelligence, 2022, 35(2): 95-105. ) [本文引用:2]
[24] ISLAM M A, ANDERSON D T, PINAR A J, et al. Enabling Explainable Fusion in Deep Learning with Fuzzy Integral Neural Net-works. IEEE Transactions on Fuzzy Systems, 2020, 28(7): 1291-1300. [本文引用:2]
[25] ISLAM M A, ANDERSON D T, PINAR A J, et al. Data-Driven Compression and Efficient Learning of the Choquet Integral. IEEE Transactions on Fuzzy Systems, 2018, 26(4): 1908-1922. [本文引用:1]
[26] BELIAKOV G, DIVAKOV D. Fitting Sugeno Integral for Learning Fuzzy Measures Using PAVA Isotone Regression. International Journal of Intelligent Systems, 2019, 34(11): 2863-2871. [本文引用:1]
[27] YANG R, WANG Z Y, HENG P A, et al. Classification of Hetero-geneous Fuzzy Data by Choquet Integral with Fuzzy-Valued Integrand . IEEE Transactions on Fuzzy Systems, 2007, 15(5): 931-942. [本文引用:1]
[28] JIN L S, KALINA M, MESIAR R, et al. Discrete Choquet Integrals for Riemann Integrable Inputs with Some Applications. IEEE Transactions on Fuzzy Systems, 2018, 26(5): 3164-3169. [本文引用:1]
[29] GLOROT X, BENGIO Y. Understand ing the Difficulty of Training Deep Feedforward Neural Networks // Proc of the 13th Internatio-nal Conference on Artificial Intelligence and Statistics. San Diego, USA: JMLR, 2010: 249-256. [本文引用:1]
[30] SALAKHUTDINOV R, MNIH A. Probabilistic Matrix Factorization // Proc of the 21st International Conference on Neural Information Processing Systems. Cambridge, USA: MIT Press, 2007: 1257-1264. [本文引用:1]
[31] GRABISCH M. The Representation of Importance and Interaction of Features by Fuzzy Measures. Pattern Recognition Letters, 1996, 17(6): 567-575. [本文引用:1]