
林国平,博士,教授,主要研究方向为粒计算、人工智能.E-mail:guoplin@163.com.
作者简介:

张庐婧,硕士研究生,主要研究方向为粒计算、粗糙集理论.E-mail:zhangjdp@163.com.

林艺东,博士,副教授,主要研究方向为不确定性理论及其应用.E-mail:yidong_lin@yeah.net.

寇 毅,硕士研究生,主要研究方向为粒计算、机器学习.E-mail:ky20eku@163.com.
多尺度决策信息系统的特征子集选择是处理多尺度分类问题的一种有效的数据预处理方法.在实际应用中, 数据类型往往多样混合,现有的多尺度模型无法有效处理这类数据.针对该问题,文中面向多源异构多尺度数据,提出多尺度邻域半径的形式化定义,构造多尺度邻域信息粒并讨论其相关性质.在此基础上,探讨特征的重要度,提出可同步进行最优尺度选择和特征选择的特征子集选择算法.改进原有的Wu-Leung模型,在一定程度上扩展其在实际问题上应用的范围.最后,在UCI数据集上验证模型和算法的可行性和有效性.
LIN Guoping,professor. Her research interests include granular computing and artificial intelligence.
About Author:
ZHANG Lujing, master student. Her research interests include granular computing and rough set theory.
LIN Yidong, Ph.D., associate professor. His research interests include uncertain theories and application.
KOU Yi, master student. His research interests include granular computing and machine learning.
Feature subset selection for multi-scale decision information system is an effective data preprocessing method for multi-scale classification problems. However, data types are often diverse and mixed in real application. The existing multi-scale models cannot handle these data effectively. To solve this problem, a formal definition of multi-scale neighborhood radius for multi-source heterogeneous multi-scale data is proposed in this paper. Multi-scale neighborhood information granule is constructed and its related properties are studied. Attribute significance is discussed, and a feature subset selection algorithm is proposed. Optimal scale selection and feature selection are conducted synchronously. By improving the Wu-Leung model, the scope of its application in practical problems is expanded to some extent. Finally, the feasibility and effectiveness of the proposed model and algorithm are verified on UCI datasets.
粒计算[1, 2]是知识发现和数据挖掘的重要方法之一, 源自Zadeh[3]在模糊集理论背景下提出的“ 信息粒度” .而后Pawlak[4]提出经典粗糙集理论, 便于分析和处理语义型的数据, 尤其善于处理不确定问题.
然而经典粗糙集仅适用于处理语义型数据, 并不适用于实际生活中广泛存在的异构数据.因此, 胡清华等[5]利用拓扑空间中的球形邻域概念构造邻域粗糙集, 用于研究数值型数据.此后, Hu等[6]通过邻域粗糙集模型解决异构特征选择的问题.Chen等[7]提出基于优势关系的邻域粗糙集模型, 并设计并行的特征选择算法.Hu等[8]为了挖掘特征与决策之间的相关性, 在邻域关系中引入权重的概念, 构造加权邻域粗糙集模型.
上述研究均为单尺度决策表, 即仅研究特征在单一尺度下的取值问题, 而实际生活中存在的信息大多需要从多个尺度进行研究.针对该问题, Wu等[9]提出多尺度信息系统, 描述不同尺度下信息粒之间的关系, 并针对不一致的多尺度决策系统提出知识获取算法[10], 进一步分析多尺度决策系统的最优尺度选择问题[11].She等[12]研究局部规则归纳法.Wu等[13]提出不完备信息系统的规则获取方法.Li等[14]以Wu-Leung研究的特殊案例为例, 研究不同特征在不同尺度等级下的多尺度决策系统, 提出补模型和格模型.吴伟志团队[15, 16, 17, 18, 19, 20]利用D-S理论, 提出一系列多尺度决策系统的扩展模型.牛东苒等[21]基于对偶概率粗糙集模型讨论广义多尺度决策系统中的最优尺度组合选择问题.Huang等[22, 23]研究具有多尺度决策属性的广义多尺度决策系统, 将划分扩展到覆盖, 建立多尺度覆盖数据分析模型.Li等[24]在多尺度覆盖的基础上研究邻域算子和近似算子的一些性质, 建立基于多尺度覆盖的粗糙集模型.Zheng等[25]研究基于优势关系的多尺度序决策系统.Wang等[26]构造基于多粒度的多尺度决策系统扩展模型, 用于知识发现.
近年来, Li等[27, 28, 29]研究动态多尺度决策系统的最优尺度选择问题.陈应生等[30]构造多尺度集值信息系统, 讨论协调和不协调情况下的最优尺度选择问题.陈应生等[31]又采用布尔矩阵方法研究多尺度覆盖决策信息系统.Huang等[32, 33]研究基于优势关系的多尺度IF决策表.之后Huang等[34]又提出多尺度模糊决策系统, 用于研究多尺度粗糙集的模糊泛化及其在数值数据特征选择中的应用.杨璇等[35]将模糊相似关系引入多尺度决策系统, 拓展模糊决策粗糙集模型的应用.但是, 目前针对适用于研究多源异构多尺度数据的多尺度决策信息系统模型仍较少见.
随着大数据时代的到来, 数据表现形式多样化.例如, 同一部电影在不同平台的评价体系拥有多个评价方式, 评分可记录为0~10之间的数值型数据, 也可用0~5颗星星数进行评价, 再或是留言评价等.值得注意的是, 数据来源于多个平台, 并且每个平台的评分细则是多尺度的.与此同时, 这类多源异构多尺度数据集不仅包含语义型数据, 同时也包含数值型数据.在此情况下, 无法使用现有的一些模型进行有效处理.为此, 本文针对这一类型数据集构建多尺度邻域决策信息系统, 便于实际生活中多源异构多尺度数据集的研究, 并讨论模型的相关性质.
定义1[5] 给定非空有限集合
U={x1, x2, …, xn},
A为描述U的特征集, D为决策特征, 若A生成论域上的一族邻域关系, 则称NDT=< U, A, D> 为一个邻域决策系统.对于U上的任意对象xi, 定义由xi生成的δ 邻域信息粒:
δ (xi)={x|x∈ U, Δ (x, xi)≤ δ },
其中, δ ≥ 0, Δ 为RN上的一个度量, 满足自反性、对称性和三角不等性.
定义2[5] 给定一个邻域决策系统NDT=< U, A, D> , 根据决策特征D可将U划分为N个等价类{X1, X2, …, XN}, ∀ B⊆A, 定义决策D关于B的下近似和上近似:
其中,
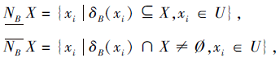
δ B(xi)为样本xi在特征子集B中的邻域信息粒.
决策的边界定义为
BN(D)=
决策D的下近似也称为决策正域, 记为POSB(D).决策特征D对条件特征B的依赖度定义为
γ B(D)=
定义3[11] 多尺度信息系统可表示为
(U, {
其中
即
其中
性质1[11] 给定一个多尺度信息系统
(U, {
对于B⊆A, k∈ {1, 2, …, I}, 有
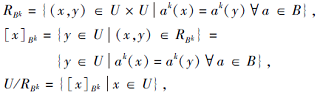
则
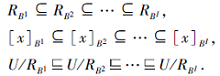
定义4[11] 给定一个系统
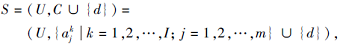
为多尺度决策系统, 其中
(U, {
为一个多尺度信息系统, d∶ U→ Vd称为决策.
定义5[11] 给定一个多尺度决策系统
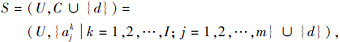
S称为协调的决策系统当且仅当最细尺度等级下的决策系统S1为协调的.若Sk为协调的, 但Sk+1为不协调的, 则称S的第k尺度等级为最优尺度.
在经典的多尺度信息系统[9]中, 每个特征在不同尺度下的特征值不一致, 但约束每个特征的尺度等级个数相同, 本文仍保持此假定.
定义6 称(U, A∪ {d}, δ )为一个多尺度邻域信息系统, 其中U={x1, x2, …, xn}为一个非空有限对象集, A={a1, a2, …, am}为U的条件特征集, d为决策特征, δ ={δ 1, δ 2, …, δ m}为邻域半径集, 其中δ j={
S=(U, A∪ {d}, {
当t≤ h时,
定义7 给定一个多尺度邻域决策信息系统
S=(U, A∪ {d}, {
对于邻域半径δ 关于特征子集B的多尺度邻域相似关系定义如下:
其中, 当特征值
|
当I=1时, 多尺度邻域相似关系退化为经典的邻域相似关系.因此, 多尺度邻域相似关系可视为邻域相似关系的推广.
邻域半径δ 的选取是影响多尺度邻域相似关系的关键因素之一, 本文参考文献[36]中利用标准差的方法, 改进后得到更适用于本文的邻域半径δ 的定义.
定义8 给定一个多尺度邻域决策信息系统
S=(U, A∪ {d}, {
对于∀ B⊆A, 定义邻域半径:
δ B=
其中, k=1, 2, …, I; j=1, 2, …, m.当B中只包含一个特征
其中, STD(
例1 给定一个多尺度邻域决策信息系统,
S=(U, A∪ {d}, {
其中U为对象集, 表示不同的电影,
表示电影在不同平台上对应的不同评价标准, 第一尺度等级为每部电影在该平台上评分的标准化数据, 第二尺度等级为观众在该平台上的留言评价, 即
V2={1, 2, 3}={不好看, 一般, 好看},
第三个尺度等级为该平台上专业影评的评价, 即
V3={1, 2}={不喜欢, 喜欢},
决策d为电影的最终评价分类.多尺度邻域决策信息系统如表1所示.
| 表1 多尺度邻域决策信息系统 Table 1 Multi-scale neighborhood decision information system |
根据定义8, α =1/3, μ =0.4, 计算得到每个特征在不同尺度下的邻域半径分别为

性质2 给定一个多尺度邻域决策信息系统,
S=(U, A∪ {d}, {
对于特征子集B的多尺度邻域相似关系
1)自反性.若x∈ U, 则(x, x)∈
2)对称性.若(x, y)∈
证明 先证明1).若x∈ U, 对于(x, x), 有
可得(x, x)∈
再证明2).若(x, y)∈
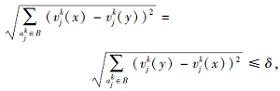
可得(y, x)∈
定义9 给定一个多尺度邻域决策信息系统
S=(U, A∪ {d}, {
假设对于每个特征
L={(l1, l2, …, lm)|lj∈ {1, 2, …, I}, j={1, 2, …, m}},
表示为多尺度组合全体.若
K1={l1, l2, …, lm}, K2={k1, k2, …, km},
且
lj≤ kj, j=1, 2, …, m,
则表示K1细于K2, 记为K1 ⪯K2; 若
lj< kj, j=1, 2, …, m,
则表示K1严格细于K2, 记为K1≺K2.
定义10 给定一个多尺度邻域决策信息系统
S=(U, A∪ {d}, {
对于邻域相似关系
R
而对于K=(k1, k2, …, km)∈ L, 对应多尺度邻域相似关系族
R
性质3 对于
∀ K1=(k1, k2, …, km)∈ L, K2=(l1, l2, …, lm)∈ L,
x∈ U, 对应的多尺度邻域相似关系族及多尺度邻域信息粒有如下性质:
1)若δ 1≤ δ 2, 则
2)若K1⪯K2, 则
3)若δ 1≤ δ 2, 则R
4)若K1⪯K2, 则R
证明 先证明1).若δ 1≤ δ 2, 由于
可得
再证明2).由于
设
K1=(k1, k2, …, km)∈ L, K2=(l1, l2, …, lm)∈ L,
对于K1⪯K2, ∀ 1≤ j≤ m, 有kj≤ lj, 可得
再证明3).由1)可得:若δ 1≤ δ 2, 有
R
可得
R
最后证明4).由2)可得:若K1⪯K2, 有
又
R
可得
R
定义11 给定一个多尺度邻域决策信息系统
S=(U, A∪ {d}, {
对于
K=(k1, k2, …, km)∈ L, U/
可得关于决策类Di对于
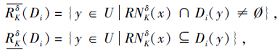
则对决策集d关于
PO
性质4 对于∀ K=(k1, k2, …, km)∈ L, 决策类Di关于
1)若δ 1≤ δ 2, Di∈ U/
2)若δ 1≤ δ 2, 则PO
3)若K1⪯K2, Di∈ U/
4)若K1⪯K2, 则PO
证明 先证明1).根据性质3中3)可得, 若δ 1≤ δ 2, 则
R
对∀ y∈ U, Di∈
R
可得
再证明2).由1) 根据性质3中3)可得, 若δ 1≤ δ 2, 则
R
对∀ y∈ U, 可得, 若δ 1≤ δ 2, 则
又
PO
可得
PO
再证明3).根据性质3中4)可得, 若K1⪯K2, 则
R
对∀ y∈ U, Di∈
R
可得
最后证明4).根据3)可得, 若K1⪯K2, 则
又
PO
可得
PO
定义12 给定一个多尺度邻域决策信息系统
S=(U, A∪ {d}, {
K=(k1, k2, …, km)∈ L,
在决策集d中对于邻域相似关系全体
因此可得, 对于
则可称对应的特征
则可称对应的特征
性质5 对于K=(k1, k2, …, km)∈ L, 在决策集d中, 邻域相似关系族
1)若δ 1≤ δ 2, 则
2)若K1⪯K2, 则
证明 先证明1).由性质4中2)可得, 若δ 1≤ δ 2, 则
PO
又
可得
再证明2).由性质4中4)可得, 若K1⪯K2, 则
PO
又
可得
现有的关于多尺度决策信息系统特征子集选择的研究多数采用首先选出最优尺度再进行特征选择的方式.与之不同的是, 本文采用特征选择和最优尺度选择结合的方式对多尺度邻域决策信息系统进行特征子集选择.面对多尺度模型中最优尺度选择时间复杂度过大的问题, 文献[37]中提出逐步最优尺度算法, 相比格模型[14], 可有效减少最优尺度选择的时间成本.受逐步最优尺度算法[37]启发, 本文引入特征重要度阈值λ 进行特征子集选择.
定义13 给定一个多尺度邻域决策信息系统
S=(U, A∪ {d}, {
K0=(1, 1, …, 1)∈ L, K=(k1, k2, …, km)∈ L,
若邻域相似关系族
定义14 给定一个多尺度邻域决策信息系统
S=(U, A∪ {d}, {
K=(1, 1, …, kj, …, 1)∈ L,
在决策集d中关于
sig(
因此, 根据定义14可得
0< sig(
并且对于特征aj的重要度采用加权和的方式进行定义, 即
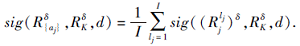
由此根据定义14给出的特征子集选择算法.首先基于最细的尺度组合计算每个特征在不同尺度下特征的重要度, 采用加权和的方式计算每个特征的重要度.由于重要度较小的特征对分类的影响较小, 根据设定的阈值λ , 删除重要度小于阈值λ 的特征, 对于其余特征, 根据特征的重要度由小到大排序, 根据所得的排序依次对每个特征进行选择最优尺度, 得到特征子集.具体算法步骤如下.
算法1 多尺度邻域决策信息系统的特征子集选择
算法
输入 多尺度邻域决策信息系统
S=(U, A∪ {d},
阈值λ
输出 特征子集 X
初始化 X=[], S'=[]
For k=1∶ Im//Im为每个特征的最粗尺度
令K← (1; 1; …; k; …; 1)
计算 sig(
计算 sig(
For aj∈ A(j=1, 2, …, m)
If sig(
令S'← S'∪ {aj}
End
End
End
For ap∈ S'(j=1, 2, …, q)
根据特征的重要度sig(
特征进行排序, 得到τ
For ap in τ
For k=Ip∶ 1
令 K'(p)← k∥K'(p)表示中的第p个元素
If
得到特征子集选择后的最优尺度组合 K'
End
End
End
得到特征子集 X
End
特征子集选择算法的时间复杂度为
O(max(|U|2
因此, 本文算法同时进行最优尺度选择和特征选择, 减少搜索最优尺度组合的遍历次数, 有效提高特征子集选择的效率.
例2(续例1) 根据定义14得到每个特征在每个尺度下的重要度:
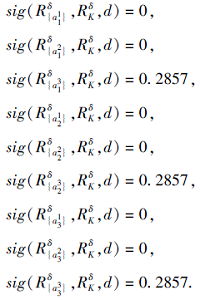
进而得到每个特征的重要度:
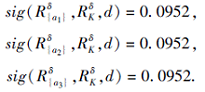
由于每个特征的重要度一致, 设λ =0.根据特征的重要度排序得到τ =123,
1)考虑特征a1.当K1=(3, 1, 1)时, 计算得到
即
2)考虑特征a2.当K2=(3, 3, 1)时, 计算得到
即
即
3)考虑特征a3.当K4=(3, 2, 3)时, 计算得到
即
即
K'=(3, 2, 1).
由例2可得每个特征均不为冗余特征, 即可得特征子集X={
对于本文提出的多尺度邻域决策信息系统模型及对应的特征子集选择算法, 本节通过实验分析验证其可行性和有效性.所有实验硬件环境配置为Inter(R)Core(TM)i5-8250U CPU@1.60 GHz和4 GB内存的个人计算机, 算法运行的软件环境为Matlab R2021a.
实验数据集选择UCI数据库上的7个数据集, 具体如表2所示.由于均为相应的单尺度决策表, 因此需要进行预处理, 构建相应的多尺度邻域决策表.
| 表2 实验数据集 Table 2 Experimental datasets |
通过文献[14]中方法类比得到多源异构多尺度数据集.鉴于语义型数据需转化为整数的数值型数据进行实验, 故后续数据获取均用整数表示.
1)若对象的某一特征值缺失, 删除该对象.
2)设σ a为标准差, ma为最小值, a(x)表示原始数据的特征值, 则多尺度邻域决策信息表中第一尺度的对象x的特征值为
a1(x)=roundn(
根据特征值a1(x)得到相应的特征值, 若对象的某一特征值为0, 删除该对象, 得到第一尺度的特征值.
3)利用定义8中的邻域半径定义求取第一尺度的邻域相似类的平均值, 并保留两位小数作为第二尺度对应的特征值a2(x), 删除特征值为0所在的对象, 其中对应δ 中的a1的取值为决策类的个数d.以此类推, ak的取值递减, 直到k的取值为d/3-1, 即
ak=d-
其中d为决策类的个数.
4)从k=d/3开始, 求取前一个尺度级别的邻域相似类的平均值后取整.对于后续尺度等级的获取, 将在前一个尺度级别的基础上, 通过从上到下的方式合并某个值, 直到某个特征的当前尺度级别中的等价类数量不超过3个.
对于所得特征子集结果, 采用十折交叉验证法分别在SVM和KNN两个分类器上进行分类性能评估.将本文算法得到的特征子集(简记为Opt)分类精度与原始数据集(简记为Raw)、最细尺度数据集(简记为Fin)、最粗尺度数据集(简记为Coa)在分类器上的分类精度进行对比, 详情如表3和表4所示, 表中参数设置为α =0.1, μ =0.8.从实验结果可知, 通过本文的模型与算法, 可获得较好的特征子集, 分类精度近似于原始数据集在分类器上的分类精度, 且绝大多数分类精度优于最细尺度数据集和最粗尺度数据集.由此说明本文的模型与算法是有效的.
| 表3 在分类器SVM上的分类精度对比 Table 3 Comparison of classification accuracy with classifier SVM % |
| 表4 在分类器KNN(K=2)上的分类精度 Table 4 Comparison of classification accuracy with classifier KNN(K=2) % |
本文针对多源异构多尺度数据进行研究, 通过构造多尺度邻域信息粒, 提出多尺度邻域决策信息系统模型, 给出多尺度邻域半径的形式化定义, 对多尺度邻域相似关系及上下近似的相关定义进行理论分析.最后, 给出基于特征重要度的多尺度邻域决策系统的特征子集选择算法, 并通过实验验证算法的有效性.今后将进一步探索多尺度信息系统在多源异构多尺度数据上的研究, 着重考虑大型数据集的多尺度邻域决策信息系统的知识表示、规则提取等问题.
本文责任编委 张燕平
Recommended by Associate Editor ZHANG Yanping
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|
| [19] |
|
| [20] |
|
| [21] |
|
| [22] |
|
| [23] |
|
| [24] |
|
| [25] |
|
| [26] |
|
| [27] |
|
| [28] |
|
| [29] |
|
| [30] |
|
| [31] |
|
| [32] |
|
| [33] |
|
| [34] |
|
| [35] |
|
| [36] |
|
| [37] |
|


