为了平衡性能与效率, 实体检索通常分为召回和重排序两个阶段.在召回阶段, 传统方法是基于BM25^[13]或实体别名表^[18]的启发式检索方法.然而此类方法依赖于实体名与查询的精确匹配, 当无法精确匹配时, 召回率较低.近年来, 神经网络被应用于实体检索任务, 取得比启发式方法更优的检索性能.在召回阶段, 常用基于稠密向量的检索模型.此类模型将查询、实体独立编码为稠密向量, 再通过简单的向量相似度函数(如点积、L2), 使用精确K近邻或近似K近邻算法召回K个最相似的实体.

基于稠密向量的检索模型按实体向量的表示方式不同, 大致可分为3类:基于描述的方法、基于上下文的方法、混合式方法.基于描述的方法以BLINK为代表, 使用BERT(Bidirectional Encoder Representa-tions from Transformers)^[19]将实体描述文本直接编码为向量.基于上下文的方法以LUKE为代表, 从海量上下文中利用实体与其它单词、实体的共现关系, 抽取实体的分布语义向量.混合式方法以MGAD为代表, 利用分布语义模型LUKE蒸馏实体描述编码器, 得到的实体向量同时具备描述和上下文的语义.

BLINK、LUKE、MGAD为当前性能较优的三个稠密向量实体检索方法, 分别适合在实体描述丰富、实体上下文丰富、实体描述和实体上下文都丰富的场景下训练实体向量.相比传统方法, 稠密向量模型的语义匹配能力更强, 召回率更高, 但缺点是时间复杂度和空间复杂度也更高.

二值检索是使用0、1或± 1的离散二值向量表示查询与实体, 然后使用汉明相似度检索的方法, 在图像检索和文本检索中都有应用.按照训练方式划分, 二值检索可分为两类:联合优化方法和后处理方法.在联合优化方法中, 二值化是与向量的学习过程一起训练的, 以文本检索任务的BPR(Binary Passage Retriever)^[20]为代表.BPR在训练过程中, 使用可微的tanh函数近似sign函数, 训练接近二值向量的浮点值向量, 在推断时直接使用sign函数二值化.后处理方法直接使用其它模型训练好的浮点值向量, 对浮点向量进行一些简单变换后再二值化, 以图像检索任务的HE-WGC(Hamming Embedding and Weak Geometric Consistency)^[21]和ITQ(Iterative Quantiza-tion)^[22]为代表.在使用sign函数二值化前, HE-WGC对稠密向量进行随机旋转, ITQ通过迭代计算将稠密向量旋转至量化误差最小的方向上, 但是两者并未给出理论上的解释.在这两类二值检索方法中, 联合优化方法的检索效果更优, 但训练代价高昂.后处理方法的检索效果略差于联合优化方法, 但不需要重新训练模型, 可直接在训练好的模型上应用, 泛用性更好.

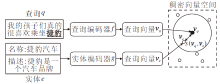
基于稠密向量的实体检索模型结构如图1所示, 首先使用两个独立的编码器将查询、实体分别编码为稠密向量, 再召回与查询向量最相似的K个候选实体.

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 基于稠密向量的实体检索模型结构图Fig.1 Structure of entity retrieval model based on dense vector

对于查询q和实体e, 对应的稠密向量分别为:

v_q=f(q), v_e=g(e),

其中f、g表示两个互相独立的编码器.以BLINK为例, f、g都采用BERT, 将文本编码为向量.关于查询、实体编码器的更多细节, 请参考BLINK、LUKE、MGAD的相关文献^{[13, 14, 15]}.

召回过程是利用KNN召回与查询向量v_q相似度最大或距离最小的K个候选实体.记s(· , · )为计算2个向量相似度的函数, KNN召回过程形式化表述为

KNN(v_q)=arg topkes(v_q, v_e).

常用的相似度函数s(· , · )有点乘相似度、余弦相似度、L2相似度(L2距离取反)等.本文与BLINK、LUKE、MGAD一样, 采用点乘相似度.

稠密向量检索模型可利用神经网络建模v_q、v_e的语义相似性, 因此召回率超过传统的精确匹配模型.但是, 由于v_q、v_e通常都是高维浮点值向量, 且v_e需要预先计算并存储, 当实体数量很多时, 大规模浮点向量的存储及相似度计算的开销很大.为了解决该问题, 本文提出二值化的实体检索方法.

二值化的实体检索方法(简称二值检索)简化使用浮点值的稠密向量实体检索(简称浮点值检索), 可压缩向量存储空间, 加快相似度计算.二值检索示意图如图2所示.

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 二值检索示意图Fig.2 Sketch map of binary retrieval

对于n维浮点值向量v_q∈ Rⁿ, v_e∈ Rⁿ, 首先利用符号函数

sign(x)= 1, x≥0-1, x< 0

获取每个浮点值的正负号, 得到n维二值向量

b_q∈ {1, -1}ⁿ, b_e∈ {1, -1}ⁿ.

假设原本每个浮点值需要使用m bit表示(m通常为32或64), 而± 1使用1 bit即可表示, 因此存储n维浮点向量需要n× m bit, 而二值向量只需要n bit, 二值化可将存储压缩至1/m.

之后可利用汉明相似度s_Ham计算二值向量b_q、b_e的相似度.定义汉明距离H(b₁, b₂)为b₁∈ {1, -1}ⁿ, b₂∈ {1, -1}ⁿ中不相同的bit的数量, 则二值向量的汉明相似度s_Ham、L2相似度s_L2、点乘相似度s_dot、余弦相似度s_cos四者都可从汉明距离H计算得到, 即

(1)

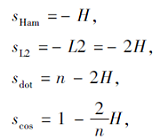容易看出, 4个相似度是等价的, 因此实践中使用汉明相似度即可.对于现代CPU, 汉明距离H可仅用两条指令计算:

H(b₁, b₂)=POPCOUNT(XOR(b₁, b₂)),

其中, XOR为按位异或, POPCOUNT(· )为统计值为1的bit数量.这两条指令都是简单的布尔运算, 计算速度快于复杂的浮点运算.

首先介绍PQ检索的原理.PQ检索首先将高维向量空间划分为多个低维子空间, 对每个子空间上的实体向量集合通过K-means聚类生成k个聚类中心, 使用每个子空间上最近的聚类中心代替原本的实体向量(称为量化).之后分别在每个子空间上, 使用查询向量到实体聚类中心的距离, 最后组合这些子空间上的距离, 得到一个查询向量到实体向量的近似距离(称为量化距离), 其中最重要的是K-means聚类与量化距离的计算.

给定n维实体向量的集合{v_e}⊆Rⁿ, 先将v_e 切分为多段独立的m维子向量的笛卡尔积:

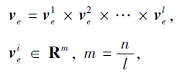
再在每个m维子空间上, 将子向量使用K-means聚为k个簇, 并使用最近的聚类中心代替原本的 vei.分配最近聚类中心的量化函数Q可形式化为

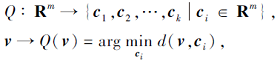
其中, d(· , · )为某种距离函数, 如L2距离, c_i为使用K-means聚类后的第i个聚类中心.

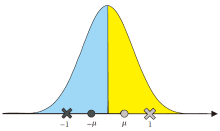
当各维度是均值为0的对称分布时, sign函数二值化等价于m=1, k=2的K-means聚类量化.这种K-means聚类的结果如图3所示.记左右两半的均值为± μ , 则{c₁, c₂}=± μ 就是K-means收敛时的聚类中心.若使用符号函数sign代替量化函数Q, 则等价于指定聚类中心{c₁, c₂}=± 1, 此时左右两簇的划分结果, 与以± μ 为聚类中心是相同的.

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 m=1, k=2的K-means聚类结果Fig.3 Clustering result of K-means with m=1 and k=2

当满足可使用sign函数代替量化函数Q的条件时, 汉明距离与对称的量化距离等价.对称的量化距离d_Q, 即对查询向量v_q、实体向量v_e都量化后计算的距离定义为

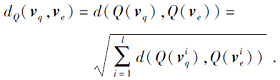
当Q(· )为sign函数, 距离d(· , · )为L2距离时, 由式(1)有d_Q=2H, H为汉明距离, 因此d_Q与汉明距离等价.

本节将从理论上分析汉明相似度与L2相似度在Rⁿ上大概率是保序的, 所以二值检索与浮点值的检索性能相差不大.

首先定义相似度之间的保序性.保序性的含义为:在一种相似度s下更相似的两点, 在另一种相似度 ŝ下依然更相似.形式化定义为:对于点x∈ Rⁿ, y₁∈ Rⁿ, y₂∈ Rⁿ, 记

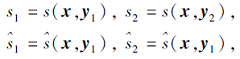
若满足

s₁> s₂⇒ ŝ1> ŝ2,

则称从s到 ŝ严格保序, 如式(1)中, 4种相似度彼此都严格保序.放宽限制, 定义概率意义上的保序, 若满足

P( ŝ1≤ ŝ2|s₁> s₂)→ 0, (2)

或

P( ŝ1> ŝ2|s₁> s₂)> P( ŝ1≤ ŝ2|s₁> s₂),

则称从s到 ŝ大概率保序(即保序概率大于不保序).对于L2距离与汉明距离, 记L2距离

l₁=L2(x, y₁), l₂=L2(x, y₂),

记汉明距离

h₁=H(x, y₁), h₂=H(x, y₂).

由于汉明距离等于汉明相似度取反(L2距离同理), 于是条件(2)等价于

P(l₁≥ l₂|h₁< h₂)→ 0. (3)

利用条件概率,

(4)

说明条件(3)成立.

对于汉明距离, 给定x、 y₁, 假设满足h₁< h₂的点y₂存在, 则y₂所在象限必须比y₁的象限离x更远, 而这样的象限数量是有限、离散的, 因此P(h₁< h₂)是(0, 1)内的常数c.

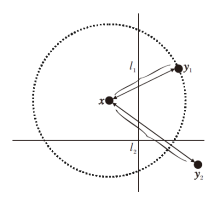
对于L2距离, 能满足条件l₁≥ l₂的点y₂必须落在以x为球心、|x-y₁|为半径的球里.以图4的二维空间为例, 相比无限的二维空间, 落在球内的概率趋近于0, 因此有

P(l₁≥ l₂)→ 0.

回到式(4), 由于左边

P(h₁< h₂)=c∈ (0, 1),

右边

P(h₁< h₂|l₁≥ l₂)< 1, P(l₁≥ l₂)→ 0,

于是必须有

P(l₁≥ l₂|h₁< h₂)→ 0,

式(4)得证, 因此汉明相似度到L2相似度大概率保序.

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 P(l1≥ l2)→ 0示意图Fig.4 Sketch map of P(l1≥ l2)→ 0

本节通过实验验证sign函数+汉明距离的二值检索方案可在检索性能损失不大时, 压缩实体向量存储, 加快相似度计算.

在实体链接的基准数据集AIDA^[17]上进行实验.除了BLINK、LUKE、MGAD, 还对比如下2个传统的启发式检索模型:1)Alias Table^[18], 可预先通过维基百科锚文本收集; 2)BM25, 使用实体名称构建索引^[13].

每个基于稠密向量的模型分为浮点值、二值化两种版本.浮点值模型是按官方超参数在AIDA-train数据集上微调的原版模型, 采用点乘相似度.二值化模型直接使用sign函数对浮点值模型的稠密向量二值化, 并使用汉明相似度检索, 该过程不需要训练.为公平起见, 所有模型的实体库统一限定为LUKE编码的约50万英文维基实体.

在AIDA-testB数据集上测试模型的检索性能、计算速度、存储空间.检索性能指标包括:MRR(Mean Reciprocal Rank)、Recall@K(K=1, 10, 30, 100), 后者简记为R@K.

实验平台的硬件配置如下:Intel(R) Xeon(R) Gold 5117 CPU @2.00 GHz, Tesla K80 GPU, 12 GB显存.

各模型检索性能如表1所示, 其中-b表示二值检索.由表可观察到, MGAD、BLINK、LUKE的浮点值模型效果优于Alias Table和BM25, 这显示稠密向量模型强大的语义匹配能力, 并且在3种稠密向量中, 使用上下文语义的MGAD和LUKE, 效果优于完全使用实体描述编码稠密向量的BLINK.由表还可发现, 二值化的BLINK和MGAD都可以保持较高的召回率, 其中MGAD在R@10上只损失0.8%, BLINK在R@30上只损失0.9%, 这两个模型二值化后依然性能优于启发式方法, 且二值化MGAD性能甚至优于浮点值BLINK.但是, 二值化的LUKE性能下降非常严重, 甚至差于启发式检索.总之, 对于部分神经检索模型, 二值化检索可保持较高的检索性能.

表1

Table 1

表1(Table 1)

表1 各模型检索性能对比 Table 1 Retrieval performance comparison of different models % 模型 MRR R@1 R@10 R@30 R@100 Alias Table 74.0 62.9 90.2 95.7 97.7 BM25 48.1 40.4 60.2 68.7 75.6 MGAD 94.7 91.6 99.0 99.8 99.8 MGAD-b 92.7 88.9 98.2 99.2 99.7 BLINK 91.7 87.8 98.0 98.9 99.5 BLINK-b 88.3 83.8 96.0 98.0 98.9 LUKE 94.5 90.7 99.3 99.5 99.8 LUKE-b 23.2 17.1 35.3 45.9 57.6

表1 各模型检索性能对比 Table 1 Retrieval performance comparison of different models %

对于维度最高且二值检索性能最优的MGAD, 在AIDA数据集上测试其实体向量的存储空间及相似度计算速度, 结果如表2所示.对于32位浮点的实体向量, 二值化存储可减至1/32, 在CPU+内存的配置下, 相似度计算可加速约1.5倍, 甚至快于GPU+显存的浮点值模型.因此二值检索可大幅压缩存储、加快计算, 适合在低资源设备上部署.

表2

Table 2

表2(Table 2)

表2 AIDA数据集上MGAD的效率 Table 2 Efficiency of MGAD on AIDA dataset 设置 存储 速度/s GPU+显存+浮点值 1.9 GB 98 CPU+内存+浮点值 1.9 GB 125 CPU+内存+二值化 61.0 MB 85

表2 AIDA数据集上MGAD的效率 Table 2 Efficiency of MGAD on AIDA dataset

4.2.1 定性分析

本节定性分析BLINK、LUKE、MGAD这3个稠密向量检索模型中实体向量的分布特点, 以及如何利用这些特点实现二值化检索.

分析三者预训练好的实体向量.三者的实体都来自英文维基, 但编码的实体数量不同, 最少的LUKE只编码最高频约10%实体, 最多的BLINK编码全部实体.此外3种实体向量的维度不同, BLINK为1 024维, MGAD为1 024维, LUKE为256维.本文发现如下2个特点, 并基于这2个特点提出二值检索方法.

特点1 实体向量分布在互不相同的象限里

使用sign函数提取浮点向量v每维的正负符号, 得到n维± 1向量b, 表示v在n维直角坐标系中所在的象限(n维空间有2ⁿ个象限).统计每个模型的实体向量分布在多少个象限里, 统计结果如表3所示, 表中all表示全量英文维基实体, top表示最高频的约10%实体.由表可发现:1)尽管3个模型编码实体向量的方法不同, 但对于高频实体, 每个实体向量都分布在不同象限里; 2)对于编码全部实体的BLINK, 只有很少的情况下多个实体会出现在同个象限里, 即每个象限里几乎最多只有一个实体.

表3

Table 3

表3(Table 3)

表3 各模型的实体数量和向量象限数量 Table 3 Entity number and vector quadrant number of different models 模型 实体数量 向量象限数量 LUKE top 499509 499509 MGAD top 499509 499509 BLINK top 499509 499509 BLINK all 5903527 5903023

表3 各模型的实体数量和向量象限数量 Table 3 Entity number and vector quadrant number of different models

本文发现, 只有在实体描述过于相似的情况下, 才会出现一个象限中不止一个实体的现象.具体而言, 这种实体可细分为3类:1)维基消歧页; 2)只有名字没有描述; 3)使用一套描述模板批量编写的实体.这3类罕见情况属于实体库的噪声.此外, 实体向量确实都分布在互不相同的象限里, 且高维空间本身的象限数远多于实体数.例如:256维的LUKE共有2²⁵⁶≈ 10⁷⁷个象限, 远多于全量英文维基实体数(约10⁶), 而对于1 024维的BLINK和MGAD, 其 21024≈ 10³⁰⁸个象限甚至远超过全宇宙的原子数(约10⁸⁰).因此对于这些高维稠密向量检索模型, 即使每个象限只有一个实体, 容量依然足够大.

该特点说明使用浮点数的稠密向量存在大量信息冗余, 仅保留象限(通过sign函数得到的二值向量)就可代替原本的浮点向量, 从而压缩存储空间.

特点2 语义相似的实体向量所在象限也更近

进一步分析发现, 语义相近的实体会分布在更近的象限里(如象限(1, -1, 1)离(-1, -1, 1)更近, 离(-1, 1, 1)更远).下面通过一个可视化的例子加以说明.

本文选择两个实体:Java (programming language)和Switzerland, 并从MGAD的浮点实体向量中分别选择3个离它们距离最近的实体向量, 得到两组实体:

{Python(programming language), Java(software platform), Lua(programming language)}, {Switzerland football team, Swiss people, Switzerland in the Roman era}.

可看出, 每个实体都和自己组内的实体语义更相似, 和另一组实体的语义较远.

再将这两组实体向量二值化, 可视化效果如图5所示, 图中每行表示一个1 024维的二值化实体向量(深灰色为1, 浅灰色为-1), 每列的维度一一对应.± 1在各维度上的分布产生“ 条纹” , 2个二值向量的条纹越相似, 汉明距离也越小, 即象限离得越近.由图可看出, 组内语义较近的实体, 向量更相似(汉明相似度更大, 象限更近), 组间语义较远的实体, 向量更不相似(汉明相似度更小, 象限更远).

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 语义相似实体向量二值化的可视化效果Fig.5 Visualization for binarization of semantically similar entity vectors

基于此特点, 可使用计算速度更快的汉明相似度, 衡量二值化后实体之间的语义相似度, 从而替换原本的浮点值相似度.

4.2.2 定量分析

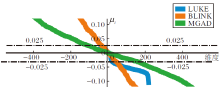
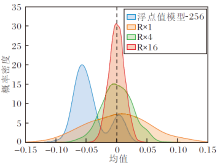
首先验证各模型是否满足二值化的理论前提, 即“ 各维度是均值为0的对称分布” , 发现对称分布基本成立(呈现为单峰对称分布), 但均值为0并不总成立.各模型各维度的均值(去除超过± 0.15的值)如图6所示.由图可发现, 只有部分维度的均值在0附近(图中± 0.025内), 这些维度与理论较符合.考虑到高维向量本身的冗余性, 及二值化的MGAD与BLINK召回性能并不差, 本文认为, 只要“ 均值接近0的维度足够多” , 就能抵消其余维度的负面影响.

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 各模型的各维度均值Fig.6 Mean of each dimension in different models

再验证依据理论推导的结论, 即相似度的保序性.随机采样1 000个实体, 使用第1种相似度召回k近邻后, 计算有多少邻居在第2种相似度上保序.取k=3、10、100, 并测试汉明相似度(简记为Ham)、L2相似度(简记为L2)、余弦相似度(简记为cos)、点乘相似度(简记为dot), 保序性的实验结果如表4所示.由表可发现, 相似度保序的概率

MGAD > BLINK > LUKE,

platform), Lua( programming language)},

{Switzerland football team, Swiss people, Switzerland in

the Roman era}

表4

Table 4

表4(Table 4)

表4 各模型相似度的保序概率 Table 4 Order-preserving probability of similarities for different models % 模型 相似度 top3 top10 top100 MGAD Ham→ L2 Ham→ cos Ham→ dot L2→ Ham cos→ Ham dot→ Ham 93.7 93.7 93.7 95.7 95.7 95.0 79.1 79.1 78.9 79.8 79.9 79.2 71.3 71.3 70.8 72.2 72.2 71.7 BLINK Ham→ L2 Ham→ cos Ham→ dot L2→ Ham cos→ Ham dot→ Ham 88.3 88.3 88.7 91.0 90.7 87.0 75.5 75.0 69.9 74.7 74.9 70.8 69.5 69.9 65.9 70.3 70.3 65.4 LUKE Ham→ L2 Ham→ cos Ham→ dot L2→ Ham cos→ Ham dot→ Ham 84.3 84.0 84.0 88.7 88.7 85.7 65.1 64.3 60.8 67.0 67.4 65.0 55.9 56.9 55.0 56.7 56.2 54.2

表4 各模型相似度的保序概率 Table 4 Order-preserving probability of similarities for different models %

该排序与图6中均值接近0的维度数量排序以及表5中二值化后的性能损失排序是一致的.此外以保序性最好的MGAD为例, 还可发现除了汉明相似度到L2相似度之外, 汉明相似度到余弦相似度、点乘相似度也是大概率保序的, 反之余弦相似度、点乘相似度到汉明相似度也大概率保序.

表5

Table 5

表5(Table 5)

表5 各模型二值化后的性能损失 Table 5 Performance loss after binarization of different models % 模型 Δ R@3 Δ R@10 Δ R@100 MGAD -1.5 -0.8 -0.1 BLINK -3.4 -2 -0.6 LUKE -72.9 -64 -42.2

表5 各模型二值化后的性能损失 Table 5 Performance loss after binarization of different models %

由此通过实验验证理论的正确性, 得到一个更宽松的结论:当各维度是对称分布时, 只要有足够多维度的均值接近0, 汉明相似度就大概率与L2相似度、余弦相似度、点乘相似度保序, 从而保证二值检索性能损失不大.进一步地, 均值接近0的维度越多, 保序性越优, 检索性能损失越小.

从4.1节和4.2节实验中发现, LUKE由于不能较好满足“ 有足够多的维度均值接近0” 的理论前提, 导致二值化后相似度保序性较差, 因此二值检索效果不佳.受HE-WGC在图像检索任务中应用随机旋转的启发, 发现对稠密向量随机升维旋转, 可以让更多维度均值接近0, 提高二值检索性能.

给定向量v∈ Rⁿ, 随机升维旋转即对v右乘一个随机正交阵M∈ R^{n× m}, 其中m≥ n(当m=n时只旋转不升维).旋转可保证稠密向量的内积相似度、L2相似度、点乘相似度都不变, 而随机的升维可让各维度均值更接近0(作为对比, 虽然中心化也能令均值为0, 但这是一种平移变换, 无法保证点乘相似度、余弦相似度不变).具体而言, 设稠密向量集合的均值向量为μ , 随机升维旋转不改变μ 的模长, 且变换后的μ 均匀分布在半径为|μ |的m维球面上, 即

μ ²= ∑i=1mμi2,

其中μ _i为μ 的第i维分量, 也是变换后第i维的均值.由于各μ _i同分布, 于是 μi2的期望为

Expect( μi2)= μ2m, (5)

维度m越大, μ _i的期望越接近0.

本节通过实验验证随机升维旋转确实可改善LUKE的二值化检索性能, 具体结果如表6所示, 表中b-R× n表示维度乘以n倍的随机升维旋转并二值化.除了浮点值模型以外, 其它行的数值是相对浮点值模型的性能损失.由表可发现:1)即使不升维, 只随机旋转(b-R× 1), 也可提高二值检索性能; 2)升维的倍数越大, 二值化检索效果越接近浮点值LUKE, 升维16倍时各项指标损失不到1%, 已非常接近浮点值模型(由于二值化可压缩至1/32, 即使升维16倍, 总存储空间依然能减半).

表6

Table 6

表6(Table 6)

表6 对LUKE随机升维旋转后的二值检索效果 Table 6 Binary retrieval results of LUKE after random dimension increase and rotation % 模型 MRR R@1 R@10 R@30 浮点值模型 94.5 90.7 99.3 99.5 直接二值化 -71.3 -73.6 -64.0 -53.6 b-R× 1 -39.6 -45.4 -25.8 -17.1 b-R× 2 -17.3 -21.9 -8.0 -4.7 b-R× 4 -5.1 -6.5 -2.0 -0.8 b-R× 8 -2.1 -2.4 -0.7 -0.1 b-R× 16 -0.9 -0.9 -0.3 -0.0 b-R× 32 -0.4 -0.3 -0.2 -0.0

表6 对LUKE随机升维旋转后的二值检索效果 Table 6 Binary retrieval results of LUKE after random dimension increase and rotation %

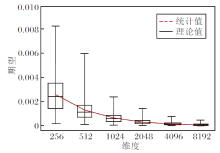
进一步绘制随机升维旋转后LUKE各维度的均值μ _i分布图, 如图7所示.期望Expect( μi2)的理论值与统计值如图8所示.由图7和图8可发现, 变换后维度越高, 均值越接近0.随机升维旋转同时也进一步佐证在有足够多维度的均值接近0时, 二值检索的性能损失较小.

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 LUKE随机升维旋转后均值分布Fig.7 Mean distribution of LUKE after random dimension increase and rotation

图8

Fig.8

	Figure Option ViewDownloadNew Window
	图8 期望Expect( μi2)的理论值与统计值Fig.8 Statistical and theoretical values of expectation Expect( μi2)