李永强,博士,副教授,主要研究方向为人工智能、强化学习、博弈论.E-mail:yqli@zjut.edu.cn.
作者简介:

周键,硕士研究生,主要研究方向为强化学习、马尔科夫博弈.E-mail:jzhou.xc@qq.com.

冯 宇,博士,教授,主要研究方向为人工智能、强化学习、博弈论.E-mail:yfeng@zjut.edu.cn.

冯远静,博士,教授,主要研究方向为人工智能、图像处理、智能优化.E-mail:fyjing@zjut.edu.cn.
在两方零和马尔科夫博弈中,由于玩家策略会受到另一个玩家策略的影响,传统的策略梯度定理只适用于交替训练两个玩家的策略.为了实现同时训练两个玩家的策略,文中给出两方零和马尔科夫博弈下的策略梯度定理.然后,基于该策略梯度定理,提出基于额外梯度的REINFORCE算法,可使玩家的联合策略收敛到近似纳什均衡.文中从多个维度分析算法的优越性.首先,在同时移动博弈游戏上的对比实验表明,文中算法的收敛性和收敛速度较优.其次,分析文中算法得到的联合策略的特点,并验证这些联合策略达到近似纳什均衡.最后,在不同难度等级的同时移动博弈游戏上的对比实验表明,文中算法在更大的难度等级下仍能保持不错的收敛速度.
LI Yongqiang,Ph.D., associate professor. His research interests include artificial intelligence, reinforcement learning and game theory.
About Author:
ZHOU Jian, master student. His research interests include reinforcement learning and markov game.
FENG Yu, Ph.D., professor. His research interests include artificial intelligence, reinforcement learning and game theory.
FENG Yuanjing, Ph.D., professor. His research interests include artificial intelligence, image processing and intelligent optimization.
In two-player zero-sum Markov games, the traditional policy gradient theorem is only applied to alternate training of two players due to the influence of one player's policy on the other player's policy. To train two players at the same time, the policy gradient theorem in two-player zero-sum Markov games is proposed. Then, based on the policy gradient theorem, an extra-gradient based REINFORCE algorithm is proposed to achieve approximate Nash convergence of the joint policy of two players. The superiority of the proposed algorithm is analyzed in multiple dimensions. Firstly, the comparative experiments on simultaneous-move game show that the convergence and convergence speed of the proposed algorithm are better. Secondly, the characteristics of the joint policy obtained by the proposed algorithm are analyzed and these joint policies are verified to achieve approximate Nash equilibrium. Finally, the comparative experiments on simultaneous-move game with different difficulty levels show that the proposed algorithm holds a good convergence speed at higher difficulty levels.
博弈问题是实际应用中的常见问题, 如围棋、象棋、扑克游戏、对抗类电子游戏等.近年来, 在模型未知的情况下, 利用多智能体强化学习求解博弈问题受到广泛关注[1, 2, 3, 4, 5, 6].在现有文献中, 通常利用如下两类框架描述多步博弈问题:扩展形式博弈(Extensive-Form Games)和马尔科夫博弈(Markov Games).
扩展形式博弈适用于描述不完全信息、回合制博弈问题, 如扑克游戏.回合制是指参与博弈的玩家在每步决策时, 知道已行动玩家采取的动作.例如, 在扑克游戏中, 参与的玩家轮流出牌或下注, 当前行动的玩家可看到已行动玩家出的牌或下的注.为了解决生活中流行的扩展形式博弈问题, 学者们提出大量基于策略梯度的多智能体强化学习算法, 如基于虚拟自博弈(Fictitious Self-Play)的方法[7, 8, 9, 10]和基于反事实遗憾(Counter factual Regret)的方法[11, 12, 13, 14].
马尔科夫博弈适用于描述完全信息、同时移动博弈问题.同时移动博弈问题是指在每步决策时, 所有参与的玩家同时选择动作, 玩家在决策时并不知道另一玩家会采取的动作, 如军事对抗博弈问题.
马尔科夫博弈拓宽马尔科夫决策过程(Markov Decision Process, MDP)只能有一个智能体的限制, 马尔科夫博弈可包含多个智能体.在使用多智能体强化学习方法求解博弈问题时, 强化学习中的术语“ 智能体” 一般称为“ 玩家” , 本文也保持这个习惯.这些玩家可以有各自的利益目标.两方零和马尔科夫博弈(Two-Player Zero-Sum Markov Games, TZMG)为马尔科夫博弈的一种特殊情况, 特殊之处是参与博弈的两个玩家的利益完全相反.
针对TZMG的多智能体强化学习算法可分为两类:值函数方法和策略梯度方法.现有文献中大部分方法都是值函数方法.Littman[15]提出Minimax-Q, 可找到纳什均衡策略, 但是由于每次更新Q函数需要构建线性规划以求解每个状态阶段博弈的纳什均衡策略, 计算量巨大.为了解决Minimax-Q的计算效率问题, Gran-Moya等[16]提出Soft Q-Learning, 计算熵正则化条件下闭合形式的软最优策略, 从而避免使用线性规划更新Q函数.然而, 由于固定的正则化条件, 策略可能无法达到纳什均衡.为了在保持计算效率的同时保证策略收敛到纳什均衡, Guan等[17]提出SNQ2L(Soft Nash Q2-Learning).值函数方法由于算法本身的限制并不适合动作空间大的环境.对于MDP, 策略梯度方法比值函数方法更容易扩展到大动作空间, 通常收敛速度更快.
策略梯度方法在许多领域具有较优性能[18, 19].但是, 对于TZMG, 策略梯度方法的研究结果依然很少.Daskalakis等[20]提出双时间尺度的策略梯度算法, 解决TZMG问题, 主要思想是两个玩家采用快慢学习率交替进行训练, 本质上还是单智能体强化学习, 并且训练过程比同时训练玩家的策略更繁琐.
本文致力于实现同时训练并更新玩家的策略, 围绕这个目标, 首先将策略梯度定理扩展到TZMG, 给出针对TZMG的策略梯度定理的严格证明.该定理是利用采样数据估计TZMG的玩家策略梯度的理论基础.本文采用类似于单智能体REINFORCE[21]的思路估计TZMG下的玩家策略梯度, 即利用完整采样轨迹的回报均值估计期望回报.得到玩家策略梯度的估计之后, 可利用基于梯度的方法求解TZMG的等价问题, 即最大最小化问题.由此, 本文提出基于额外梯度的REINFORCE算法(Extra-Gradient Based REINFORCE, EG-R), 求解最大最小化问题, 解决直接使用梯度上升下降算法时, 玩家的联合策略无法达到近似纳什均衡的问题.
马尔科夫决策过程(MDP)可用一个五元组( 
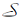
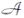
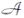
P(s', r|s, a)∶ 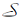
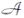
表示在任意动作a∈ 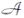
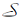
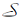
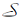
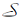
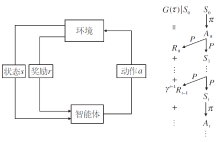
MDP下的智能体与环境的交互如图1所示, 环境根据初始状态的概率分布ρ 生成初始状态S0.在每个时刻t, 智能体按照随机策略
π (· |St)∶ S→ Δ ( 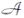
在当前状态St下选择动作, 得到的动作记为At.环境对动作At做出相应响应, 然后根据状态转移及奖励生成的概率分布P将状态从St转移到St+1, 并给出奖励Rt, 即
St+1, Rt~P(· , · |St, At).
智能体和环境如此交互直至终止时刻T.每局交互产生一条轨迹:
τ ∶ =(S0, A0, R0, S1, …, ST-1, AT-1, RT-1, ST).
获得的回报大小体现智能体在这局交互中的表现, 回报定义为累计折扣奖励:
G(τ )∶ =
对于MDP, 只有一个智能体与环境交互, 训练智能体的目的就是找到一个最优策略, 使智能体在与环境交互的过程中获得最大的期望回报.初始状态为s时的期望回报定义为
Vs(π )∶ =Eπ [G(τ )|S0=s]. (1)
由于初始状态s服从概率分布ρ , 期望回报也可定义为
Vρ (π )∶ =Es~ρ [Vs(π )]=Eπ [G(τ )], (2)
则最优策略满足
Vρ (π * )=
两方零和马尔科夫博弈(TZMG)可用一个六元组( 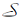
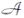
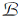
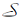
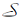
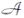
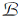
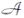
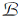
P(s', r|s, a, b)∶ 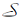
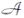
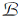
表示在任意联合动作(a, b)∈ 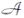
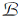
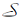
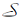
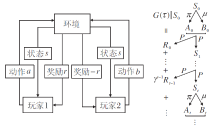
TZMG下的玩家与环境的交互如图2所示, 一轮博弈开始时, 环境根据初始状态的概率分布ρ 生成初始状态S0.在每个时刻t, 玩家1按照随机策略
π (· |St)∶ 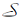
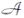
在当前状态St下选择动作, 得到的动作记为At.同时, 玩家2按照随机策略
μ (· |St)∶ 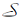
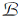
在当前状态St下选择动作, 得到的动作记为Bt.联合动作(At, Bt)送入环境中执行, 环境根据状态转移及奖励生成的概率分布P将环境状态从St转移到St+1, 并给出奖励Rt, 即
St+1, Rt~P(· , · |St, At, Bt).
如此直至本轮博弈的终止时刻T.每轮博弈都会产生一条轨迹
τ ∶ =(S0, A0, B0, R0, S1, …, ST-1, AT-1, BT-1, RT-1, ST).
玩家1的回报定义为累积折扣奖励:
G(τ )∶ =
由于是零和博弈, 玩家2的回报为-G(τ ).
对于TZMG, 有两个玩家同时与环境交互, 相比式(1)和式(2), 期望回报发生改变, 初始状态为s时的期望回报定义为
Vs(π , μ )∶ =Eπ , μ [G(τ )|S0=s],
由于初始状态s服从概率分布ρ , 期望回报可定义为
Vρ (π , μ )∶ =Es~ρ [Vs(π , μ )]=Eπ , μ [G(τ )]. (3)
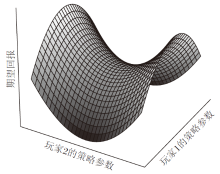
由式(3)可知, 期望回报Vρ (π , μ )不仅与己方策略有关, 也与对方策略有关, 即双方的联合策略(π , μ )共同确定Vρ (π , μ )的值.因此, TZMG的最优策略为达到纳什均衡时的联合策略, 此时的期望回报正好处于图3中的鞍点处.所以, 对于TZMG, 训练玩家的目的就是找到一个纳什均衡的联合策略.由于两个玩家的策略对期望回报的影响不同, 为了找到纳什均衡的联合策略, 两个玩家的目标也不同.玩家1的目标是:对任意玩家2的策略μ , 寻找最优策略π * 最大化期望回报Vρ (π , μ ).如图3所示, 玩家1的策略参数更新方向应为期望回报增大的方向.玩家2的目标是:对任意玩家1的策略π , 寻找最优策略μ * 最小化期望回报Vρ (π , μ ).如图3所示, 玩家2的策略参数更新方向应为期望回报减小的方向.
文献[22]证明TZMG满足最大最小化定理, 即对任意的TZMG, 一定存在一个纳什均衡的联合策略(π * , μ * ), 使
Vρ (π , μ * )≤ Vρ (π * , μ * )≤ Vρ (π * , μ ), ∀ π , μ . (4)
式(4)也称为鞍点不等式, 由式(4)可知, 纳什均衡的联合策略(π * , μ * )满足
Vρ (π * , μ * )=
TZMG可能存在多个纳什均衡的联合策略, 但是所有纳什均衡的联合策略的期望回报Vρ (π * , μ * )是相等的[20].
一方面, 如图1和图2所示, 根据MDP和TZMG的定义, MDP的状态转移和奖励生成只跟环境状态和一个智能体选择的动作有关, 而TZMG的状态转移和奖励生成跟环境状态, 及玩家1和玩家2各自选择的动作有关.由于两个玩家同时选择动作, 每个玩家并不知道对方选择的动作, 因此, 有必要研究MDP下的策略梯度定理对于TZMG是否适用.
另一方面, TZMG求解的是一个最大最小化问题
最优策略为期望回报处于鞍点时的联合策略.而MDP求解的是一个最大化问题
最优策略为期望回报最大时的策略.最大化问题只要使用梯度上升算法, 一定可找到一个局部极大值, 而最大最小化问题更复杂, 直接使用梯度上升下降算法不一定能收敛到鞍点.为了解决这个问题, 本文使用额外梯度算法求解鞍点.
考虑参数化的策略π θ 和μ ϕ , 其中θ ∈ Rd和ϕ ∈ Rd为可调参数.将联合策略(π θ , μ ϕ )代入期望回报Vρ (π , μ ), 结合式(3), 得到关于参数θ 和ϕ 的性能指标函数:
J(θ , ϕ )=Vρ (π θ , μ ϕ )=
由式(5)可知, TZMG问题可转化为最大最小化问题:
采用基于梯度的方法(如梯度上升下降算法、额外梯度算法等)求解最大最小化问题(7)的前提是:在状态转移及奖励生成的概率分布和初始状态的概率分布未知时, 实现用玩家与环境交互的采样数据估计指标函数J(θ , ϕ )关于参数θ 和ϕ 的梯度
文献[20]将对方策略看作环境不确定性的一部分, 进而给出关于己方策略参数的策略梯度估计方法, 这本质上还是基于MDP的策略梯度定理.本文给出针对TZMG的策略梯度定理的理论证明, 该定理是利用采样数据估计策略梯度的理论基础.
定理1 对于两方零和马尔科夫博弈问题和参数化的联合随机策略(π θ , μ ϕ ), 式(6)定义的指标函数J(θ , ϕ )关于参数θ 和ϕ 的梯度分别为
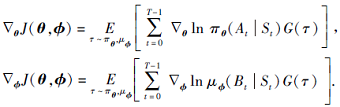 |
证明 由式(6)可得
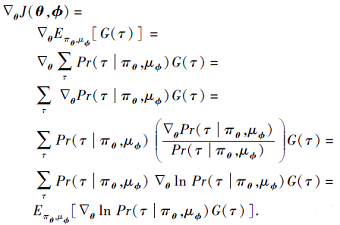 |
给定玩家的联合策略(π θ , μ ϕ ), 产生轨迹τ 的概率为
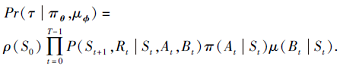 |
由式(10)可得
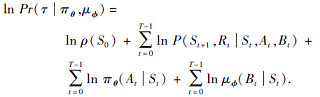
在上式中, ρ (S0)、P(St+1, Rt|St, At, Bt)、μ ϕ (Bt|St)都与参数θ 无关, 因此
将上式代入式(9), 可得
同理可得
证毕.
注意到式(8)求期望的部分并不包含状态转移及奖励生成的概率分布P和初始状态的概率分布ρ , 因此可使用采样数据的均值估计期望.假设收集到一个轨迹集合
D∶ =
其中每条轨迹都是在当前参数(θ , ϕ )确定的策略(π θ , μ ϕ )下采样得到, 那么指标函数J(θ , ϕ )关于参数θ 和ϕ 的梯度
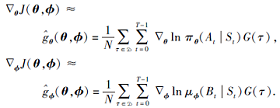
得到J(θ , ϕ )关于参数θ 和ϕ 的梯度估计后, 就可利用基于梯度的方法求解最大最小化问题.简单的方法为梯度上升下降算法, 即每次更新参数时, 沿着梯度
然而, 即使对于简单的最大最小化问题— — 凸凹最大最小化问题(指标函数是关于最大化参数的凸函数, 关于最小化参数的凹函数), 梯度上升下降算法也无法保证能收敛到指标函数的鞍点.例如, 考虑最大最小化问题
其中x∈ Rd, y∈ Rd, 显然中心处的原点是该问题的鞍点.利用梯度上升下降算法, (x, y)的轨迹是发散的, 如图4(a)所示, 图中的“ 五角星” 为轨迹的起点.而利用额外梯度算法, 能收敛到该问题的鞍点, 如图4(b)所示.相比梯度上升下降算法, 每次迭代, 额外梯度算法增加一步外推(Extrapolation)点的计算, 使用外推点的梯度完成当前参数的更新.
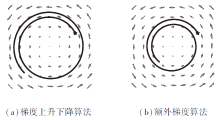 | 图4 |
额外梯度算法求解最大最小化问题(7)的参数更新为
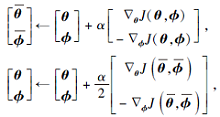 |
其中α 为更新步长.
如果J(θ , ϕ )是关于θ 的凸函数且关于ϕ 的凹函数, 额外梯度算法(式(11))可收敛到J(θ , ϕ )的鞍点[23].如果J(θ , ϕ )是非凸非凹的, 且满足Minty变分不等式, 那么额外梯度算法(式(11))也可收敛到J(θ , ϕ )的鞍点[24].但是最大最小化问题(7)的解在什么条件下满足Minty变分不等式目前依然是一个未解决的问题.
另外, 由于策略梯度
基于额外梯度的REINFORCE算法的伪代码见算法1.尽管该算法的收敛性目前没有理论上的严格证明, 但是第5节的仿真实验表明该算法可求解得到近似纳什均衡的联合策略.
算法1 EG-R
输入 初始策略参数θ , ϕ
for i=1, 2, …I do
在策略(π θ , μ ϕ )下, 收集博弈轨迹集合
D∶ =
计算策略梯度

更新策略参数
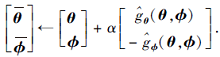
在策略(
D∶ =
计算策略梯度
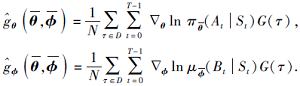
更新策略参数θ 和ϕ
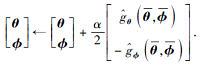
end for
本文采用DeepMind开发的open_spiel平台上的两玩家同时移动博弈游戏Oshi_Zumo验证EG-R算法.这款游戏是完全信息同时移动的零和博弈游戏, 一轮博弈往往需要经过多步博弈才能分出胜负.游戏规则如下:有2K+1个格子一维排列, 编号1, 2, …, 2K+1, 在第K+1个格子上有一面旗帜, 一轮博弈中玩家1和玩家2的每步博弈结果会控制旗帜的移动.玩家1和玩家2初始时各有N枚硬币, 每一步玩家1和玩家2同时出硬币, 记为M1和M2, 然后对比M1和M2的大小.若M1> M2, 旗帜向右移动一个格子; 若M1< M2, 旗帜向左移动一个格子; 若M1=M2, 旗帜不移动.当旗帜从左被移出第1个格子, 游戏结束, 玩家2最终获胜; 当旗帜从右被移出第2K+1个格子, 游戏结束, 玩家1最终获胜.当两个玩家的硬币都耗尽, 游戏结束, 若旗帜位于第K+1个格子的左侧, 玩家2最终获胜, 若旗帜位于第K+1个格子的右侧, 玩家1最终获胜.奖励规则为:仅当博弈结束后才有奖励, 玩家1获胜奖励为1; 玩家2获胜奖励为-1; 平局奖励为0.
Oshi-Zumo游戏的状态由3部分组成:玩家1的剩余硬币数、玩家2的剩余硬币数、旗帜的位置.旗帜的位置由格子的编号表示, 当从左移出第1个格子后, 旗帜位置为0, 当从右移出第2K+1个格子后, 旗帜位置为2K+2.玩家的动作就是出币数.Oshi-Zumo游戏在参数确定情况下, 初始状态是确定的.在本文的仿真研究中, Oshi-Zumo游戏的参数设置如下:初始币数N=6, 格子规模K=1, 最小出币数为0.
本文选择2个对比算法:基于值函数的算法(Minimax-Q)和基于策略梯度的算法(梯度上升下降算法).这两个对比算法和本文的EG-R超参数设置保持一致, 更新次数设为50 000, 每次更新的采样局数设为300, 学习率α 设为0.9.折扣因子λ 设为1.
梯度上升下降算法和EG-R都是基于策略梯度的算法, 玩家的策略采用直接参数化的方式.玩家在状态s下的策略参数θ s∈ 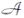
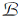
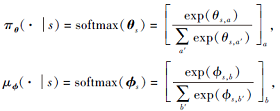 |
其中, [· ]a表示在状态s下的所有合法动作依次按照方括号内的公式计算得到的向量, θ 和ϕ 的初始值全为0, 即初始策略服从均匀分布.
Minimax-Q是基于值函数的算法, Q值函数采用直接参数化的方式.Q值函数在状态s下的参数q(s, · , · )∈
value[q(s, · , · )]=
式(13)可采用线性规划方法求解.求解式(13)可得到策略参数θ s、ϕ s、value[q(s, · , · )], 再通过式(12)得到玩家在状态s下的策略.Q值函数的更新公式如下:
q(St, At, Bt)=(1-α )q(St, At, Bt)+ α (Rt+λ · value[q(St+1, · , · )]).
本文采用常用的纳什收敛指标评价联合策略的性能.给定联合策略(π , μ ), 纳什收敛指标为[25]:
NashConv(π , μ )=Vρ (π b, μ )+Vρ (π , μ b).
其中, π b表示玩家1在给定玩家2策略μ 情况下的最佳响应策略, μ b同理.本文求解的是近似最佳响应策略, 固定对手的策略, 对玩家进行训练, 直到玩家的胜率达到95%或策略参数的更新次数达到5 000次.给定对手玩家策略下, 最佳响应策略保证玩家的回报最大, 需要注意的是, 最佳响应策略并不是唯一的.当
NashConv(π , μ )=0
时, 联合策略(π , μ )达到纳什均衡; 当
NashConv(π , μ )< ε , ∀ ε > 0
时, 联合策略为近似纳什均衡.
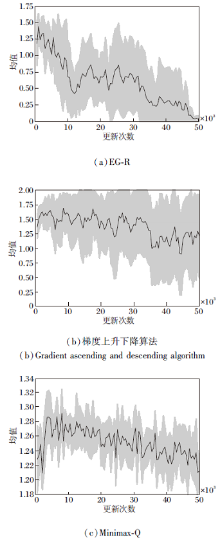
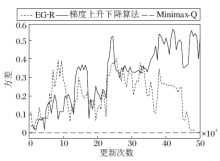
3种算法均收集10组实验的评估数据, 10组实验的纳什收敛指标均值如图5所示, 图中阴影部分表示10组实验纳什收敛指标的离散程度, 阴影的上下界分别由均值加减标准差得到.这3种算法纳什收敛指标的方差如图6所示.
由图5(a)可看出, 随着更新次数的增加, EG-R纳什收敛指标的均值整体呈下降趋势, 当更新次数达到50 000次左右时, 纳什收敛指标的均值接近于0, 此时联合策略达到近似纳什均衡.由于使用REINFORCE, 所以不同实验组的方差较大, 由图6可知, EG-R的最大方差为0.403, 在40 000次更新之前, 方差的波动较大, 但在40 000次更新之后, 方差开始明显减小, 并最终趋向于0.
由图5(b)可看出, 梯度上升下降算法的纳什收敛指标的均值在1.0~1.7之间, 无明显的下降趋势, 由此可见, 梯度上升下降算法无法得到近似纳什均衡的联合策略.梯度上升下降算法使用的也是REINFORCE, 由图6可知, 不同实验组的方差很大, 呈现增大的趋势, 最大方差为0.56.
从图6可看出Minimax-Q的方差很小, 波动也很小, 最大方差为0.002, 同时从图5(c)可看出, Minimax-Q的纳什收敛指标有轻微的下降趋势, 但在50 000次更新下, 距离下降到0还很遥远.由此可见, 在限定更新次数的条件下, Minimax-Q无法得到近似纳什均衡的联合策略.
分析3种算法的纳什收敛指标的均值和方差的变化趋势可看出, EG-R具有显著的优越性, 具体体现在EG-R可在更少的更新次数下得到近似纳什均衡的联合策略, 方差在后期明显趋向于0.
EG-R在训练过程中的方差较大, 是因为使用REINFORCE.对于MDP, REINFORCE的方差也较大, 广泛认可的一种解决方案是使用带基线的RE-INFORCE.沿着这个思路, 本文认为对于TZMG, 带基线的EG-R的方差也会小于EG-R.为此进行如下预实验:使用带基线的EG-R和EG-R分别进行10组实验, 游戏参数和算法超参数的设置见4.1节.然后, 选取其中5个检查点(检查点的更新次数为10 000次更新的整数倍)的联合策略进行评估, 得到这两种算法的纳什收敛指标的均值和方差, 如图7所示.需要注意的是, EG-R的基线可以是任意函数, 但不能和玩家的策略相关, 本文选取的基线是历史轨迹回报的滑动平均.
由图7可看出, 带基线的EG-R在前4个检查点处的方差小于EG-R, 而在第5个检查点处略大于EG-R.由图5(a)可知, EG-R的纳什收敛指标越接近0, 方差也越接近0.在第5个检查点处, 带基线的EG-R的纳什收敛指标均值在0.2左右, 而EG-R的纳什收敛指标均值在0左右, 所以在第5个检查点处带基线的EG-R的方差略大于EG-R.总之, 带基线的EG-R确实可减小方差.
EG-R的10组实验得到的联合策略都达到近似纳什均衡, 但会收敛到两个不同的近似纳什均衡解(记为NE解1和NE解2).限于篇幅, 本文仅给出NE解1和NE解2的联合策略在10个状态上的表现, 展示这两种不同联合策略的差异, 具体如表1和表2所示.表中第2行的数字0~6表示玩家的动作, 即玩家投出的硬币数, 第1列表示状态, 计算玩家在该状态下选择对应动作的概率, -表示在该状态下该玩家的合法动作不包括该动作.在一个状态下, 玩家选择合法动作的概率之和为1, 这些概率就是玩家在该状态下的策略.
| 表1 部分状态下NE解1的联合策略 Table 1 Joint policy of NE solution 1 in partial state |
| 表2 部分状态下NE解2的联合策略 Table 2 Joint policy of NE solution 2 in partial state |
使用NE解1和NE解2的联合策略各自进行多次博弈, 发现NE解1的联合策略的博弈结果几乎全是平局, 输局和赢局很少.而NE解2的联合策略的博弈结果几乎全是输局和赢局, 平局很少, 且输赢局数几乎相等.
虽然NE解1和NE解2的联合策略的博弈结果不同, 但是期望回报几乎相等.NE解1和NE解2的玩家策略都是混合策略, 即玩家在某个状态下以某个概率分布选择动作, 若在某个状态下确定性地选择某个动作, 为纯策略.混合策略的近似纳什均衡相对不稳定, 因为它可转换为它的混合均衡策略中任意正概率的策略, 即纯策略, 也可转换为这些纯策略的任意概率组合[26].因此, 相对纯策略, 混合策略的求解更困难.
为了进一步验证EG-R训练得到的联合策略是近似纳什均衡策略, 设计12组实验, 游戏参数和算法超参数的设置见4.1节.
在每组实验中, 玩家1和玩家2以选定的策略进行1 000局博弈, 记录每局的回报, 然后使用1 000局回报的均值作为期望回报的估计值.玩家可选择的策略有4种:EG-R训练得到的NE解1和NE解2的联合策略、两种随机策略(高斯分布策略和均匀分布策略).高斯分布策略表示在每个状态下玩家选取合法动作的概率服从标准正态分布.均匀分布策略表示在每个状态下玩家选取动作的概率服从均匀分布, 即在每个状态下, 玩家等概率选择合法动作.
4种策略交叉博弈的回报均值如表3所示.由表可看出, 当玩家1和玩家2都使用NE解1的策略时, 回报均值为0.当玩家1使用NE解1的策略, 玩家2使用均匀分布策略或高斯分布策略时, 回报均值大于0.当玩家1使用均匀分布策略或高斯分布策略, 玩家2使用NE解1的策略时, 回报均值小于0.根据鞍点不等式(4)可知, NE解1的联合策略达到近似纳什均衡.同理可知, NE解2的联合策略也达到近似纳什均衡.当玩家1和玩家2分别选择NE解1或NE解2的策略进行博弈时, 回报均值都在0附近, 这说明虽然NE解1和NE解2的联合策略不同, 但是期望回报几乎相等.
| 表3 4种策略交叉博弈的回报均值 Table 3 Average return of cross game of 4 policies |
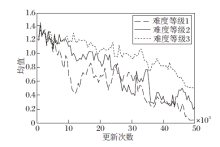
为了验证EG-R的鲁棒性, 本文选择3种不同难度等级的Oshi-Zumo游戏进行实验.不同难度等级的区别体现在:难度等级越高, 游戏的状态空间和玩家的动作空间越大, 玩家的联合策略越难收敛.不同难度等级的Oshi-Zumo游戏参数如表4所示, EG-R的超参数设置见4.1节.
| 表4 3种难度等级的Oshi-Zumo游戏参数 Table 4 Game parameters of Oshi-Zumo with 3 difficulty levels |
EG-R在3种游戏难度等级上的纳什收敛指标如图8所示.由图可看出, 在难度等级1上, 纳什收敛指标的均值接近于0, 联合策略达到近似纳什均衡.在难度等级2和难度等级3上, 纳什收敛指标的均值都呈现明显的下降趋势, 但是限于更新次数还未下降到0.综上所述, EG-R在更大的状态空间和动作空间下, 也可取得较好的效果.
为了在TZMG下实现同时训练并更新玩家的策略, 本文首先将策略梯度定理推广到TZMG, 然后提出基于额外梯度的REINFORCE算法(EG-R).在Oshi-Zumo游戏中, 对比分析EG-R的优越性, 并进一步在不同难度等级的Oshi-Zumo游戏中验证EG-R的鲁棒性.但是, 由于REINFORCE本身的缺点, 不同实验组的方差较大, 如何改进算法以减小方差是今后的一个研究方向.借鉴在MDP下的经验, 优化基线函数或引入行动家-评论家框架会是优先考虑的解决方案.另外将着重于EG-R收敛性的理论证明.
本文责任编委 兰旭光
Recommended by Associate Editor LAN Xuguang
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|
| [19] |
|
| [20] |
|
| [21] |
|
| [22] |
|
| [23] |
|
| [24] |
|
| [25] |
|
| [26] |
|