基于概念分解的显隐空间协同多视图聚类算法

引用本文

胡素婷, 沈宗鑫, 黄倩倩, 黄雁勇. 基于概念分解的显隐空间协同多视图聚类算法. 模式识别与人工智能, 2023,36(2): 160-173
HU Suting, SHEN Zongxin, HUANG Qianqian, HUANG Yanyong. Concept Factorization-Based Collaborative Multi-view Clustering Algorithm in Visible and Latent Spaces. PATTERN RECOGNITION AND ARTIFICIAL INTELLIGENCE, 2023,36(2): 160-173. 复制到剪切板

Doi: 10.16451/j.cnki.issn1003-6059.202302005
Permissions

《模式识别与人工智能》编辑部

基于概念分解的显隐空间协同多视图聚类算法

胡素婷¹, 沈宗鑫¹, 黄倩倩^2,³, 黄雁勇¹

1.西南财经大学统计学院成都 611130

2.西南交通大学计算机与人工智能学院成都 611756

3.西南民族大学计算机科学与工程学院成都 610041

通讯作者:

黄雁勇,博士,教授,主要研究方向为机器学习、数据挖掘.E-mail: huangyy@swufe.edu.cn.

作者简介:

胡素婷,硕士研究生,主要研究方向为机器学习、数据挖掘.E-mail:HST1101STU@163.com.

沈宗鑫,博士研究生,主要研究方向为数据挖掘、模式识别.E-mail:zxshen@smail.swufe.edu.cn.

黄倩倩,博士,讲师,主要研究方向为数据挖掘、粒计算、粗糙集.E-mail:huangqnqn@126.com

收稿日期: 2022-08-23 接受日期: 2023-02-26

资助项目: 教育部人文社会科学研究青年基金项目(No.21YJCZH045)资助

摘要

多视图聚类通过整合不同视图的特征以提升聚类性能.现有的多视图聚类更多地关注数据不同的低维表示方式和其在隐式空间的几何结构,而忽略数据样本在不同空间的结构关系,未同时考虑不同空间的聚类.为此,文中提出基于概念分解的显隐空间协同多视图聚类算法.首先,通过概念分解获取不同视图在隐式空间中的一个共同的低维特征表示,并利用图拉普拉斯正则化约束保持原始数据的局部结构不变.然后,将数据在显式空间中的聚类和隐式空间中的聚类整合到一个共同的框架中,进行协同学习和优化,得到最终的聚类结果.在8个真实数据集上的实验表明文中算法性能较优.

关键词: 多视图聚类; 协同训练; 概念分解; 拉普拉斯正则化

中图分类号:TP391

Concept Factorization-Based Collaborative Multi-view Clustering Algorithm in Visible and Latent Spaces

HU Suting¹, SHEN Zongxin¹, HUANG Qianqian^2,³, HUANG Yanyong¹

1.School of Statistics, Southwestern University of Finance and Economics, Chengdu 611130

2.School of Computing and Artificial Intelligence, Southwest Jiaotong University, Chengdu 611756

3.School of Computer Science and Technology, Southwest Minzu University, Chengdu 610041

Corresponding author:
HUANG Yanyong, Ph.D., professor. His research interests include machine learning and data mining.

About Author:
HU Suting,master student. Her research interests include machine learning and data mining.
SHEN Zongxin, Ph.D. candidate. His research interests include data mining and pa-ttern recognition.
HUANG Qianqian, Ph.D., lecturer. Her research interests include data mining, granular computing and rough sets.

Fund:Youth Fund Project of Humanities and Social Science Foundation of Ministry of Education(No.21YJCZH045)

Abstract

Multi-view clustering effectively improves the clustering performance by integrating the features derived from different views. The existing multi-view clustering methods more focus on different low-dimensional representations of data and their geometrical structures in latent space, while ignoring the structural relations of data in different spaces and the clustering of different spaces. To address this issue, a concept factorization-based collaborative multi-view clustering algorithm in visible and latent spaces is proposed in this paper. Firstly, common low-dimensional feature representation of different views in latent space is extracted through concept factorization. Besides, the local structure of the original data is preserved by means of graph Laplacian regularization. Then, the data clustering in visible and latent spaces are integrated into a unified framework for collaborative learning and optimizing to obtain the final clustering results. Experimental results on eight real datasets show the superiority of the proposed method.

Key words: Multi-view Clustering; Co-training; Concept Factorization; Laplacian Regularization

文章图片

随着信息技术的蓬勃发展, 数据来源与数据处理方式变得更加复杂多样.例如:不同新闻机构以各自的方式报道同一篇新闻; 一个网页可分别使用文本和超链接表示; 由音、视频组成的多媒体内容.这些数据在不同的特征空间中, 从不同的角度揭示事物不同的属性, 称为多视图数据.随着多视图数据的爆炸式增长, 多视图聚类成为大数据挖掘中一个重要的研究方向.

多视图聚类最优整合不同视图之间的特征信息, 将每条数据聚到不同的簇中.近年来, 学者们相继提出多种多视图聚类算法, 大致可分为三类:多视图协同聚类算法(Co-training Clustering)、多视图多核聚类算法(Multiple Kernel Clustering)和多视图子空间聚类算法(Multi-view Subspace Clustering).

多视图协同聚类算法采用协同训练的策略处理多视图数据.Cleuziou等^[1]提出CoFKM, 基于FKM(Fuzzy K-means, FKM), 采用协同聚类的思想同时最小化每个视图的模糊划分, 同时假定无论视图如何, 每个数据最终都会被分配到同一个集群中.Kumar等^[2]采用协同训练的思想, 在谱聚类的框架中使用来自彼此的信息引导不同视图的聚类, 最终得到多视图聚类结果.

多视图多核聚类算法利用核方法将数据的原始特征映射到更高维空间中进行聚类.Tzortzis 等^[3]提出基于核的多视图聚类算法, 每个视图都被表示为一个给定的核, 所有的核都被加权组合.Huang等^[4]在核空间中学习相似关系, 并为每个视图自动分配权重.Ren等^[5]提出LLMKL(Local Structural Graph and Low-Rank Consensus Multiple Kernel Learning), 引入共识核矩阵的低秩替代和稀疏误差矩阵, 探究Hilbert特征空间潜在的全局结构, 同时基于谱图理论保持样本之间的局部结构.

多视图子空间聚类算法将高维数据投影到低维子空间中, 然后在潜在的子空间中对数据点进行聚类划分.此类算法可保持数据的内在特性, 减少无关特征的影响.

近年来, 由于非负矩阵分解(Nonnegative Matrix Factorization, NMF)^[6]在处理高维数据上的优势和可解释性, 基于NMF的多视图子空间聚类算法获得研究者们的注意力.Liu等^[7]将NMF拓展到多视图聚类的情况, 提出MultiNMF(Multi-view NMF), 通过NMF探索每个视图的底层聚类结构, 并学习一个共同的聚类指示矩阵, 使每个视图的聚类结构保持一致.Tan等^[8]在低维空间上引入相关约束, 学习不同视图共享的一种隐式表示.Zong等^[9]提出MM- NMF(Multi-manifold Regularized NMF Framework), 在每个视图上进行NMF, 线性组合的一致流形和一致系数矩阵与多流形正则化结合, 保留多个隐式空间的局部几何结构.Liu等^[10]提出RMNMF(Robust Multi-view NMF), 考虑特征之间的高阶关系, 使用一阶关系和二阶关系获得最优的邻域结构.

上述基于NMF的多视图聚类算法虽然从保持多视图数据局部结构的角度出发, 获得良好的聚类性能, 却将多视图数据在显式空间和隐式空间中的聚类看作是两个相互独立的过程.由于在多视图聚类中, 每个视图包含的判别性信息和所有视图潜在的一致性信息对于聚类来说都是至关重要的, 因此, 如何有效结合多视图数据在隐式空间中的一致性信息和显示空间中的判别性信息是一个具有挑战性的问题.为此, Deng等^[11]提出MV-Co-VH(Multi-view Clustering Algorithm with the Cooperation of Visible and Hidden Views), 同时探索多视图数据在显式空间和隐式空间中的信息, 将隐式空间中的聚类与显式空间中的聚类整合到一个协同训练框架中, 获得最终的聚类结果.然而, 该方法未能充分考虑多视图数据的内在几何结构, 性能受到一定限制.此外, NMF的前提假设是输入样本数据是非负的, 这在现实场景中往往不能被满足, 因此利用NMF提取隐空间信息的方法在现实应用中存在局限性^[12].

为了解决上述问题, 本文基于协同训练和子空间聚类的思想, 提出基于概念分解(Concept Factori- zation, CF)的显隐空间协同多视图聚类算法(CF-Based Collaborative Multi-view Clustering Algorithm in Visible and Latent Spaces, Co-MVCF).具体地, Co-MVCF引入CF, 避免NMF只能处理非负数据的局限性, 同时综合考虑数据样本在显式空间和隐式空间的关系, 在保持数据局部结构关系的同时, 将数据样本在显式空间中的聚类和隐式空间中的聚类整合到一个协同训练框架中.此外, Co-MVCF基于极大熵的思想实现视图权重的自适应学习.最后, 为了验证Co-MVCF的有效性, 在8个真实世界的数据集上进行实验, 结果表明Co-MVCF的性能较优.

1 基础知识

1.1 非负矩阵分解

矩阵分解在聚类中被广泛应用, 常见的是NMF^[6].NMF将一个原始的非负数据矩阵分解成两个非负子矩阵.

对于任意给定的一个非负数据矩阵

X=[X₁, X₂, …, X_n]∈ R^d^×ⁿ,

X的每列表示一个数据样本, 一共有n个样本, 每个样本由d维特征组成.通过NMF将其分解为维数相对较低的基矩阵U∈ R^d^×^r和系数矩阵V∈ Rⁿ^×^r, 使得

X≈ UV^T, X≥ 0, U≥ 0, V≥ 0.

分解之后的特征维度为r, 远小于d和n.NMF的损失函数相当于解决如下最小化残差问题:

$\min_{U, V}$ ‖ X-UV^T $‖_{F}^{2}$ , s.t. U≥ 0, V≥ 0,

其中矩阵的‖ · ‖ _F表示Frobenius范数.更新迭代规则如下:

u_ir=u_ir $\frac{{(XV)}_{ir}}{(U V^{T} {V)}_{ir}}$ , vj_r₌vj_r $\frac{(X^{T} {U)}_{jr}}{(V U^{T} {U)}_{jr}}$

数据的每个样本点x_j可近似表示为U每个列向量的加权线性组合:

x_j≈ $\overset{r}{\sum_{l}}$ u_lv_jl, (1)

其中u_l为矩阵U的第l列.

1.2 概念分解

在现实应用中, 数据往往不能被保证是非负的.Xu等^[13]在NMF的基础上进行拓展, 提出概念分解(CF)算法, 解决上述问题, 使算法可以作用在任何数据空间.在概念分解算法中, 每个样本数据点表示成聚类中心的线性组合, 同时聚类中心又表示成各个聚类数据点的线性组合.NMF的基向量u_l(在概念分解中称为概念向量)可表示为每个样本数据x_j的非负线性组合,

G=[g_jl]∈ Rⁿ^×^r,

g_jl为关联权重, 则

u_l= $\overset{n}{\sum_{j}}$ x_jg_jl.(2)

式(2)表示样本数据点x_j和概念u_l的关联程度.结合式(1), 得到概念分解对应的优化问题:

$\min_{G, V}$ ‖ X-XGV^T‖ ², (3)

利用乘法更新法则求解式(3), 得

g_ir← g_ir $\frac{{(KV)}_{ir}}{(KG V^{T} {V)}_{ir}}$ , vj_r_←vj_r $\frac{{(KG)}_{jr}}{(V G^{T} {KG)}_{jr}}$

其中K=X^TX.

2 基于概念分解的显隐空间协同多视图聚类算法

本文提出基于概念分解的显隐空间协同多视图聚类算法(Co-MVCF), 不仅利用数据样本显式空间的所有视图信息, 还利用降维之后隐式空间的信息.基于高维相似, 低维也相似的基本假设^[14], Co-MVCF在显式空间和隐式空间中协同聚类, 最终得到一个聚类的共识.同时, 在各个视图上引入熵加权的策略, 使算法能够有效降低聚类特性较差的视图对迭代优化的干扰, 得到更理想的视图权重划分, 从而提升算法的有效性和鲁棒性.

2.1 模型构建

任意给定的一个多视图数据集

X={X¹, X², …, X^K} ,

第k个视图下的数据矩阵

X^k=[ $x_{1}^{k}$ , $x_{2}^{k}$ , …, $x_{n}^{k}$ ]∈ $R^{d_{k} \times N}$ ,

其中, d_k为第k个视图下的数据特征维度, N为数据集中数据样本的数目, K为视图总数.

多视图数据不同视图之间存在一致性信息和互补性信息.根据高维相似, 低维也相似的基本假设, 通过合理的方式将多视图数据从高维空间映射到低维特征空间时可以有效保留这些信息.那么, 可在映射过程中直接得到多个视图之间的一致性信息.

传统的多视图概念分解方法^[15]以矩阵的形式将数据映射到低维空间, 对于每个视图, 数据样本X^k被分解为该视图对应的关联矩阵G^k∈ Rⁿ^×^r和系数矩阵V^k∈ R^r^×ⁿ, 使得

X^k≈ X^kG^kV^k.

然而, 这样的分解方式将数据在每个视图下的分解独立, 孤立各个视图的关系, 忽略各个视图之间存在的一致性信息.为了利用不同视图之间的一致性信息, 在提取隐式空间的同时捕获一个共识的特征表示.具体地, 结合概念分解误差式(3), 重构多视图概念分解误差项, 在多个视图之间得到一个共识的低维特征表示V, 即

V¹=V²=…=V^k=V,

表达式为

min‖ X^k-X^kG^kV $‖_{F}^{2}$ ,

其中, 关联矩阵G^k∈ Rⁿ^×^r, 投影矩阵V∈ R^r^×ⁿ为数据样本在基向量上的投影值, 所在的空间表示为隐式空间.

在提取隐式空间时, 保持相似结构可以使提取的隐式空间更大程度地保留显式空间中的有用信息.基于流形假设, 对投影矩阵加入图拉普拉斯正则项约束, 保持样本数据在隐式空间中的局部几何结构近似不变.原始数据样本在隐式空间的特征表示应该是近似的, 即

J_manifold= $\underset{j = 1}{\overset{n}{\sum_{i}}}$ (‖ v_i-v_j‖ ²S_ij)=tr(VDVT⁾-tr(VSVT⁾=tr(VLVT)^,

其中, L=D-S为拉普拉斯矩阵,

(D)₍_jj₎= $\sum_{i}$ S_i_,_j∈ Rⁿ^×ⁿ

为对角矩阵, S为原始数据样本的亲和矩阵.因此, 多视图概念分解如下:

min $\overset{K}{\sum_{k}}$ w_k‖ X^k-X^kG^kV $‖_{F}^{2}$ +tr(VLV^T).(4)

为了充分考虑多视图数据中各个特征的影响, 本文对显式空间的各个视图的特征进行串联拼接, 构造数据样本的亲和矩阵S.

单视图K-means算法的基本思想是最小化数据集到所属类中心的误差平方和.在数据样本的显式空间中使用多视图K-means聚类可表示为

min $\overset{K}{\sum_{k}}$ w_k $\overset{c}{\sum_{i}} \overset{n}{\sum_{j}}$ p_ij‖ $x_{j}^{k}$ - $z_{i}^{k}$ ‖ ², (5)

其中, $x_{j}^{k}$ 为第k个视图下的第j个样本数据, $z_{i}^{k}$ 为显式空间中第k个视图下的第i个聚类中心, w_k为第k个视图的视图权重.

如果第k个视图下的数据 $x_{j}^{k}$ 属于第i个类, 那么p_ij=1, 否则p_ij=0.

在隐式空间中使用单视图K-means聚类可表示为

min $\overset{c}{\sum_{i}} \overset{n}{\sum_{j}}$ p_ij‖ v_j- ${\tilde{z}}_{i}$ ‖ ², (6)

其中 ${\tilde{z}}_{i}$ 为隐式空间中的第i个聚类中心.

综合式(4)~式(6), 在保持局部几何结构不变的同时考虑多视图数据在显、隐空间的结构关系, 协同训练得到一个共同的聚类表示:

J=α $\overset{K}{\sum_{k}}$ w_k‖ X^k-X^kG^kV $‖_{F}^{2}$ +γ tr(VLV^T)+β $\overset{c}{\sum_{i}} \overset{n}{\sum_{j}}$ p_ij‖ v_j- ${\tilde{z}}_{i}$ ‖ ²+(1-β ) $\overset{K}{\sum_{k}}$ w_k $\overset{c}{\sum_{i}} \overset{n}{\sum_{j}}$ p_ij‖ $x_{j}^{k}$ - $z_{i}^{k}$ ‖ ², s.t. p_ij∈ {0, 1}, $\overset{c}{\sum_{i}}$ p_ij=1, ∀ j=1, 2, …, n. (7)

真实数据中各个视图的重要性不一样, 有的视图因为有更显著的作用, 所以应该被赋予更高的权重.但是人为给定每个视图的权重, 不仅使视图分配具有很大的主观性, 而且增加工作量.于是, 考虑基于信息熵的加权策略, 通过熵的最大化, 在迭代优化过程自动为每个视图分配权重.将视图权重系数

W=[w₁, w₂, …, w_k]^T

看作概率分布, 则加权项表示为

f(k)=η $\overset{K}{\sum_{k}}$ w_kln w_k, (8)

其中,

$\overset{K}{\sum_{k}}$ w_k=1, 0≤ w_k≤ 1,

η ≥ 0, 控制视图加权的力度.

在式(7)达到最优的同时, 使信息熵(式(8))尽可能地大, 得到最终的目标函数:

$\begin{array}{ll} J_{\mathrm{Co-MVCF}} & (\boldsymbol{P}, \widetilde{\boldsymbol{Z}}, \boldsymbol{Z}, \boldsymbol{G}, \boldsymbol{V}, \boldsymbol{W})= \\ & \alpha \sum_{k=1}^{K} w_{k}\left\|\boldsymbol{X}^{k}-\boldsymbol{X}^{k} \boldsymbol{G}^{k} \boldsymbol{V}\right\|_{\mathrm{F}}^{2}+ \\ & \beta \sum_{i=1}^{c} \sum_{j=1}^{n} p_{i j}\left\|\boldsymbol{v}_{j}-\tilde{z}_{i}\right\|^{2}+ \\ & (1-\beta) \sum_{k=1}^{K} w_{k} \sum_{i=1}^{c} \sum_{j=1}^{n} p_{i j}\left\|\boldsymbol{x}_{j}^{k}-z_{i}^{k}\right\|^{2}+ \\ & \gamma \operatorname{tr}\left(\boldsymbol{V} \boldsymbol{L} \boldsymbol{V}^{\mathrm{T}}\right)+\eta \sum_{k=1}^{K} w_{k} \ln w_{k}, \\ \text { s. t. } & \sum_{k=1}^{k} w_{k}=1,0 \leqslant w_{k} \leqslant 1, \\ & p_{i j} \in\{0,1\}, \sum_{i=1}^{c} p_{i j}=1, \forall j=1,2, \cdots, n . \end{array}$ (9)

2.2 模型优化

目标函数式(9)中J_Co-MVCF有6个变量需要求解.单独求解每个变量的子优化问题的过程如下.

1)固定P和V, 求解 ${\tilde{z}}_{i}$ 和 $z_{i}^{k}$ .当其它变量固定时, 目标函数J_Co-MVCF分别关于聚类中心 ${\tilde{z}}_{i}$ 和 $z_{i}^{k}$ 求偏导, 令结果为0, 得

$z_{i}^{k}$ = $\frac{\overset{n}{\sum_{j}} p_{ij} x_{j}^{k}}{\overset{n}{\sum_{j}} p_{ij}}$ , ${\tilde{z}}_{i}$ = $\frac{\overset{n}{\sum_{j}} p_{ij} v_{j}}{\overset{n}{\sum_{j}} p_{ij}}$ .(10)

2)固定G, V, W, $\dot{Z}$ 和Z, 求解P.当其它变量固定时, 寻找显式空间中原始数据样本和隐式空间中共享的低维特征表示矩阵分别到各自聚类中心的加权距离最小值的和:

arg $\min_{p_{ij}}$ β $\overset{c}{\sum_{i}} \overset{n}{\sum_{j}}$ (d_ij)²+(1-β ) $\overset{K}{\sum_{k}}$ w_k $\overset{c}{\sum_{i}} \overset{n}{\sum_{j}}$ ( $d_{ij}^{k}$ )², (11)

其中,

$\begin{array}{ll}& d_{ij}=\parallel\nu_j-\tilde{z}_i\parallel, \\ & d_{ij}^k=\parallel\boldsymbol{x}_j^k-z_i^k\parallel.\end{array}$

如果第j(∀ j=1, 2, …, n)个样本数据属于第i(1≤ i≤ c)类, 则隶属度p_ij=1, 否则p_ij=0.

3)固定P, W, $\dot{Z}$ 和Z, 求解G和V.当固定P, W, $\dot{Z}$ 和Z时, 提取与G和V有关的项, 目标函数J_Co-MVCF等价于:

$\begin{aligned}J_{1}(\boldsymbol{G},\boldsymbol{V})=\beta\sum_{i=1}^{c}\sum_{j=1}^{n}p_{j}\|\boldsymbol{v}_{j}-\tilde{z}_{i}\|^{2}+\\ \alpha\sum_{k=1}^{K}w_{k}\|X^{k}-X^{k}G^{k}\boldsymbol{V}\|_{F}^{2}+\mathrm{tr}(\boldsymbol{VL}\boldsymbol{V}^{T}).\end{aligned}$.(12)

根据矩阵性质, 对式(12)进行求迹的转化, 表示为

$\begin{array}{l} J_{1}(\boldsymbol{G}, \boldsymbol{V})=\beta \sum_{i=1}^{c} \sum_{j=1}^{n} \boldsymbol{p}_{i j}\left\|v_{j}-\tilde{z}_{i}^{\mathrm{T}}\right\|^{2}+ \\ \quad \alpha \sum_{k=1}^{K} w_{k} \operatorname{tr}\left(\left(\boldsymbol{X}^{k}-\boldsymbol{X}^{k} \boldsymbol{G}^{k} \boldsymbol{V}\right)^{\mathrm{T}}\left(\boldsymbol{X}^{k}-\boldsymbol{X}^{k} \boldsymbol{G}^{k} \boldsymbol{V}\right)\right)+ \\ \quad \gamma \operatorname{tr}\left(\boldsymbol{V} \boldsymbol{L} \boldsymbol{V}^{\mathrm{T}}\right) . \end{array}$ (13)

当固定G或V时, J₁(G, V)对于另外一个变量是凸的, 因此可以采用迭代更新的方法求解.分别引入拉格朗日乘子Φ ∈ Rⁿ^×^r, Ψ ∈ R^r^×ⁿ , 则J₁(G, V)的拉格朗日函数为

L₁(G, V)=J₁(G, V)+tr(Φ (G^k)^T)+tr(Ψ V^T).

L₁(G, V)对G求偏导:

$\frac{\partial L_{1} (G, V)}{\partial G^{k}}$ =2α w_k(X^k)^TX^kG^kVV^T-2α wk₍Xk⁾T^Xk^VT⁺Φ .

L₁(G, V)对V求偏导:

$\frac{\partial L_{1} (G, V)}{\partial v_{bd}}$ =2β $\overset{c}{\sum_{i}}$ p_idv_bd-2β $\overset{c}{\sum_{i}}$ p_id ${\tilde{z}}_{bi}$ -2α $\overset{K}{\sum_{k}}$ w_k((G^k)^T(X^k)^TX^k)_bd+2α $\overset{K}{\sum_{k}}$ w_k((G^k)^T(X^k)^TX^kG^kV)_bd-2γ $\overset{n}{\sum_{j}}$ v_bjS_jd+2γ $\overset{n}{\sum_{j}}$ v_bdS_jd+Ψ _bd.

使用KKT(Karush-Kuhn-Tucker)条件, 有

Φ ☉G^k=0, Ψ ☉V=0,

其中☉(Hadamard Product)表示对应位置元素相乘.最终得到G和V的更新公式:

$\boldsymbol{\mathbf{G}}^k\leftarrow\boldsymbol{G}^k\odot\left\lbrace\dfrac{\left(\boldsymbol{X}^k\right)^{\text{T}}\boldsymbol{X}^{\boldsymbol{k}}\boldsymbol{V}^{\text{T}}}{\left(\boldsymbol{X^k}\right)^\text{T}\boldsymbol{X}^\boldsymbol{k}\boldsymbol{G}^\text{k}\boldsymbol{V}\boldsymbol{V}^\text{T}}\right\rbrace, $ (14)

$v_{bd}\leftarrow v_{id}\odot\left\{\dfrac{\beta\sum_{i=1}^c p_{id}z_{bi}+A+\gamma\sum_{j=1}^n v_{ij}S_{jd}}{\beta\sum_{t=1}^c\rho_{id}v_{bd}+B+\gamma\sum\limits_{j=1}^nv_{bd}D_{jd}}\right\},$(15)

其中, 在V的更新公式(14)中记

A=α $\overset{K}{\sum_{k}}$ w_k((G^k)^T(X^k)^TX^k)_bd, B=α $\overset{K}{\sum_{k}}$ k₍(Gk⁾T⁽Xk⁾T^Xk^Gk^V)b_d.

4)固定P, G, V, $\dot{Z}$ 和Z, 求解W.当其它变量固定时, 根据约束条件

$\overset{k}{\sum_{k}}$ w_k=1,

可建立拉格朗日函数:

$\begin{aligned}L_2(\textbf{W})& =(1-\beta)\sum_{k=1}^k w_k\sum_{i=1}^k\sum_{j=1}^n p_j\parallel\textbf{x}_j^k-z_i^k\parallel^2+\\ & \alpha\sum_{k=1}^{k}w_k\parallel\textbf{X}^k-X^k\textbf{Q}^k\textbf{V}\parallel_k^2+\\ & \eta\sum_{k=1}^K w_k\ln w_k+\lambda\left(\sum_{k=1}^kw_k-1\right).\end{aligned}$

L₂(W)对w_k求偏导, 结果为0, 得

w_k= $\frac{\exp (\frac{β - 1}{η} \overset{c}{\sum_{i}} \overset{n}{\sum_{j}} p_{ij} (d_{ij}^{k})^{2} - \frac{α}{η} D^{k})}{\overset{K}{\sum_{k}} (\exp (\frac{β - 1}{η} \overset{c}{\sum_{i}} \overset{n}{\sum_{j}} p_{ij} (d_{ij}^{k})^{2} - \frac{α}{η} D^{k}))}$ , (16)

其中

D^k=‖ X^k-X^kG^kV $‖_{F}^{2}$ .

基于上述求解过程, Co-MVCF的详细步骤如算法1所示.

算法1 Co-MVCF

输入多视图数据集X={X¹, X², …, X^K},

收敛阈值ε , 最大迭代次数maxiter,

聚类数c(2≤ c≤ n), 参数α , β , η , γ ,

低维特征表示矩阵维度参数r

输出根据指示矩阵P得到最终聚类结果

step 1 将X各视图特征串联拼接, 构造亲和矩阵S.

step 2 初始化聚类指示矩阵P, 随机初始化G, V, 0≤ W≤ 1.

step 3 对每个视图X^k, 执行step 4~step 8.

step 4 根据式(10)更新 ${\tilde{z}}_{i}$ 和 $z_{i}^{k}$ .

step 5 根据式(11)更新P.

step 6 根据式(14)更新G.

step 7 根据式(15)更新V.

step 8 根据式(16)更新W.

step 9 当目标函数

‖ Obj(t+1)-Obj(t+1)‖ < ε

或迭代次数达到最大迭代次数maxiter时, 停止迭代, 否则, 执行step 3~step 8.

2.3 收敛性与时间复杂度分析

算法1的收敛性取决于5个迭代子步骤.具体地, 在更新 ${\tilde{z}}_{i}$ 、 $z_{i}^{k}$ 、W、P时, 其对应的每个子问题都是凸的, 并且本文得到每个子问题的闭式解, 因此可以保证它们的收敛性.此外, 与文献[16]类似, 在更新G和V时, 容易利用二阶泰勒近似得到式(13)的辅助函数, 然后证明其收敛性.

综上所述, 虽然本文提出的目标函数不是关于所有变量的联合凸函数, 但本文采用的迭代优化算法能保证其收敛.在实验部分, 本文将在真实数据集上绘制优化过程中目标函数的收敛曲线, 进一步说明算法1的收敛性.

令数据视图个数为k, 样本数为n, 特征数为d, 子空间维度为r, 聚类数为c.那么:更新 ${\tilde{z}}_{i}$ 和 $z_{i}^{k}$ 的计算复杂度分别为Ο (ncr)和Ο (ncdk); 更新P的计算复杂度为Ο (nck); 更新G^k的计算复杂度为

O(dn²+n²r+r²n);

更新V的计算复杂度为

O(nrc+n²r+k(n²d+n²r+nr²));

更新W的计算复杂度为

O(nck+ndr).

则Co-MVCF总的计算复杂度为

O(ncr+ncdk+ndr+k(n²d+n²r+nr²)).

3 实验及结果分析

3.1 实验设置

3.1.1 实验数据集

本文实验采用11个真实世界的多视图数据集, 数据集的详细信息如表1所示.

表1 数据集的统计信息 Table 1 Statistical information of datasets

本文在mfeat、handwrittenRnsp、Caltech101-7、20newsgroups、ORL、HW2sources、3Sources和MSRC-v1数据集上进行对比实验, 验证Co-MVCF的有效性.具体地, mfeat、handwrittenRnsp数据集是手写数据集Multiple Features的子集, mfeat数据集由视图profile correlations和pixel averages in 2× 3 win-dows构成, 而handwrittenRnsp数据集由视图pixel averages in 2× 3 windows和Fourier coefficients of the character shapes构成.Caltech101-7数据集是图像数据集Caltech101的一个子集, 包含1 474个实例与7个类别.20newsgroups数据集是一组包含2万条新闻文档的数据集, 本文提取其中部分数据进行实验.ORL数据集是一个包含400幅图像的人脸数据集, 所有图像为经过归一化处理的灰度图像.HW2sources数据集是来自MNIST Handwritten Digits(0~9)数据集和USPS Handwritten Digits(0~9)的手写数据集.3Sources数据集是关于新闻的文本数据集, 由英国广播公司(BBC)、路透社(Reuters)和卫报(The Guardian)三个机构共同报道的169篇新闻组成.MSRC-v1数据集来自Microsoft Research in Cambridge, 包含210幅图像, 常用于进行场景分割, 每幅图像包含7个不同类别的目标.

此外, 为了验证Co-MVCF能够有效克服NMF只能处理非负数据的局限性, 在ToyData、syn500、MNIST-10k这3个具有负值的数据集上进行对比实验.

3.1.2 基线算法

为了验证本文算法的有效性, 选择如下9种基线算法进行对比.

1)K-means.单视图聚类算法, 首先拼接所有视图的样本, 再对拼接后的数据矩阵执行K-means算法, 获得聚类结果.

2)CoFKM^[1].多视图模糊聚类算法, 结合三种视图融合策略:串联策略、分布式策略和集中策略.

3)MV-Co-VH^[11].将矩阵分解和聚类分成两步进行.第1步利用NMF得到隐式空间的表达, 第2步融合显式视图和隐式视图的信息至一个模糊聚类框架中, 实现多视图数据可见视图和隐藏视图的协同学习.

4)MVCF(Multiview Concept Factorization)^[17].基于概念分解的多视图聚类算法, 并以自适应的方式关联所有视图的亲和矩阵.

5)FMR(Flexible Multi-view Representation)^[18].基于灵活多视图表征学习进行的子空间聚类算法, 避免使用部分信息进行数据重构, 使潜在表示能够更好地适应子空间聚类.

6)Co-FW-MVFCM(Collaborative Feature Weighted Multi-view Fuzzy C-means)^[19].包含如下两个步骤:局部步骤是一个单视图分区过程, 在每个视图中产生局部分区集群; 协作步骤是在不同视图之间共享成员关系信息.

7)CoMSC(Multiview Subspace Clustering via Co-training Robust Data Representation)^[20].将如下两个过程进行协同训练:对数据样本进行分组并去除原始数据的冗余信息; 通过特征分解得到鲁棒的低冗余数据表示.

8)COMVSC(Consensus One-Step Multi-view Sub- space Clustering)^[21].在一个框架中同时学习亲和矩阵、共识表示和最终聚类标签.在多视图数据的每个视图下都获得一个子空间表示, 通过模糊融合得到跨多视图的共识矩阵.

9)PLCMF(Pseudo-Label Guided Collective Ma-trix Factorization)^[22].利用聚类在每个视图上生成的伪标签指导矩阵分解过程, 学习一个共识的隐藏表示, 直接得到聚类结果.

3.1.3 评估指标

本文采用标准化互信息(Normalized Mutual Information, NMI)、准确率(Accuracy, ACC)和调整兰德系数(Adjusted Rand Index, ARI)这3种聚类指标评估所有聚类算法的性能.

NMI用于度量聚类标签与真实标签的相似度, 具体定义如下:

NMI= $\frac{\overset{c}{\sum_{i}} \overset{c}{\sum_{j}} N_{i, j} lo g_{2} (\frac{N N_{i, j}}{N_{i} N_{j}})}{\sqrt[]{(\overset{c}{\sum_{i}} N_{i} lo g_{2} (\frac{N_{i}}{N})) (\overset{c}{\sum_{j}} N_{j} lo g_{2} (\frac{N_{j}}{N}))}}$ ,

其中, N_i_,_j表示类i样本被分至第j类的数目, N_j表示第j类聚类包含的聚类个数, N_i表示类i包含的样本数目, N表示数据集的样本量.NMI取值范围在0~1之间, 值越大, 表示对应的聚类算法性能越优.

令p_i和q_i分别表示第i个数据样本x_i的聚类标签和真实标签, 则

ACC= $\frac{1}{n} \overset{n}{\sum_{i}}$ δ (q_i, map(p_i)).

其中:map(· )表示排列映射函数, 将聚类标签映射为真实标签; δ (· , · )表示δ 函数, 当x=y时, δ (x, y)=1, 否则δ (x, y)=0.ACC取值范围在0~1之间, 值越大, 表示对应的聚类算法的性能越优.

ARI衡量真实标签和聚类标签分布的吻合程度.定义a为在真实类簇Q中被划分为同一类, 在聚类算法聚类簇P中被划分为同一簇的实例对数量.定义b为在Q中被划分为不同类别, 在P中也被划分为不同簇的实例对数量.定义

ARI= $\frac{RI - E [RI]}{\max (RI) + E [RI]}$ ,

其中,

RI= $\frac{a + b}{C_{n}^{2}}$ , $C_{n}^{2} = \frac{n (n - 1)}{2}$

n 表示数据集的样本量.ARI取值范围为[-1, 1], 值越大, 表示对应的聚类算法的性能越优.

3.1.4 参数设置

Co-MVCF有α , β , η , γ 这4个可调节超参数.本文使用网格搜索进行参数调节.正则化参数α 的搜索范围为

α =10^-6, 10^-5, 10^-4, 10^-3, 10^-2, 10^-1, 1, 10, 10².

协同学习参数

β =0, 0.1, 0.2, …, 1.0,

在[0, 1]区间以步长0.1进行搜索.正则化参数γ 的搜索范围为

γ =1, 10, 10², 10³, 10⁴, 10⁵, 10⁶.

熵正则化参数η 的搜索范围为

η =1, 10, 10², 10³, 10⁴, 10⁵, 10⁶.

其余对比算法的参数按照对应文献中给出的参数范围进行调节, 以获得最优结果.

3.2 实验结果

3.2.1 聚类性能分析

各对比算法在8个基准数据集上的聚类结果如表2~表4所示, 表中黑体数字表示最优值, 斜体数字表示次优值, 数字后标记●/⚪表示在显著性水平为5%时, Co-MVCF是否在统计学意义上显著/不显著于其它算法, → 0表示标准差非常接近于0.

表2 各聚类算法在多视图数据集上的NMI值 Table 2 NMI of different clustering algorithms on multi-view datasets

表3 各聚类算法在多视图数据集上的ACC值 Table 3 ACC of different clustering algorithms on multi-view datasets

表4 各聚类算法在多视图数据集上的ARI值 Table 4 ARI of different clustering algorithms on multi-view datasets

为了避免实验的偶然性, 所有聚类算法重复执行30次, 记录均值和标准差.Co-FW-MVFCM引入阈值(式(14))排除不重要的特征, 在3sources数据集上由于特征权重都小于阈值而丢弃所有特征, 从而得不到有效结果.

由表2~表4可以看到, Co-MVCF几乎在所有数据集上取得最优值或次优值.就NMI而言, Co-MVCF在所有数据集上取得最优值, 比次优算法获得4%左右的提升.就ACC而言, Co-MVCF在mfeat、ORL、HW2sources、3sources数据集上取得最优值, 在Caltech101-7、20newsgroups、MSRC-v1数据集上取得次优值, 比最优算法降低5%左右.就ARI而言, Co-MVCF在mfeat、handwrittenRnsp、20newsgroups、HW2sources、3sources、MSRC-v1数据集上取得最优值, 比次优算法获得3.5%左右的提升.Co-MVCF在Caltech101-7、ORL数据集上取得次优性能, 比最优方法降低6.5%左右.

实验结果充分表明Co-MVCF的有效性.在多视图数据中, 各个视图提供的差异性信息以及视图之间隐藏的一致性信息对多视图聚类来说都至关重要.然而, 现存的大多数多视图聚类算法都只考虑其中一点, 因此性能受到限制.Co-MVCF不仅利用显式空间中各视图之间的差异性信息, 而且通过概念分解充分探索隐式空间中不同视图隐藏的一致性信息.通过显隐空间的协同聚类, 获得优异的性能.此外, Co-MVCF使用概念分解的方式提取隐式空间的特征信息, 从理论上克服NMF只能处理非负数据的局限性.

为了证实Co-MVCF有效性, 在ToyData、syn500、MNIST-10k这3个具有负值的多视图数据集上进行聚类性能的对比实验, 基线算法是基础的MultiNMF^[6]和使用的MV-Co-VH^10].3种对比算法具体的聚类实验结果如表5所示, 表中黑体数字表示最优值.此外, 由于MultiNMF和MV-Co-VH采用NMF, 不能直接将含有负值的数据作为输入.为此, 首先将数据进行归一化处理, 映射至0~1范围内, 再输入模型当中.

表5 各算法在含有负值数据集上的聚类结果 Table 5 Clustering results of different algorithms on datasets containing negative values

由表5可看出, Co-MVCF在所有数据集上的性能都显著高于MultiNMF和MV-Co-VH.具体地, CO-MVCF在ToyData、syn500、MNIST-10k数据集上分别比次优方法提升4.39%、12.66%和9.02%.因此, 实验结果表明, Co-MVCF能够有效克服NMF只能处理非负数据的局限性.

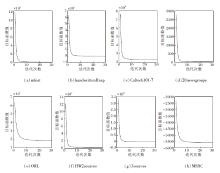
3.2.2 收敛性分析

Co-MVCF采用交替迭代更新的方式最小化目标函数, 在8个数据集上的目标函数值随迭代次数变化情况如图1所示.

	Figure Option View Download New Window
	图1 Co-MVCF在8个数据集上的收敛曲线Fig.1 Convergence curves of Co-MVCF on 8 datasets

由图1可看出, Co-MVCF收敛速度非常快, 通常在30次迭代内就可以收敛到稳定状态.在迭代开始时, 损失值减少, 聚类性能快速提高, 通常在15次左右收敛.

3.2.3 参数敏感性分析

Co-MVCF具有α , β , η , γ 这4个超参数.为了进一步验证Co-MVCF的性能, 本文分析其参数敏感性.当分析α 、β 、η 、γ 中的一个超参数时, 固定其它参数不变, 然后展示Co-MVCF随着该参数变化时的性能变化情况.

由于页面空间的限制, 只展示在mfeat、Calte- ch101-7数据集上的实验结果, 如图2和图3所示.

	Figure Option View Download New Window
	图2 mfeat数据集上聚类效果随α , β , η , γ 的变化情况Fig.2 Clustering results changing with parameters α , β , η and γ on mfeat dataset

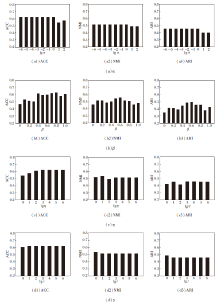	Figure Option View Download New Window
	图3 Caltech101-7数据集上聚类效果随α , β , η , γ 的变化情况Fig.3 Clustering results changing with parameters α , β , η and γ on Caltech101-7 dataset

分析α 时设置

β =0.7, η =1 000, γ =100;

分析β 时设置

α =0.01, η =1 000, γ =100;

分析η 时设置

α =0.01, β =0.7, γ =100;

分析γ 时设置

α =0.01, β =0.7, η =1 000.

β 权衡算法在显式空间和隐式空间中的聚类程度, 当固定α 、η 、γ 时, β 的变化对聚类性能的影响较大, 通常来说, β 较大时, 聚类性能较优.当正则化参数α 、η 、γ 变化时, Co-MVCF相对稳定, 在较大的参数范围内都能获得较优的聚类性能.因此, Co-MVCF对适当范围内的正则化参数不敏感.

3.2.4 消融实验

Co-MVCF引入图拉普拉斯正则项, 保留多视图数据的一致性局部几何结构, 本节通过消融实验验证该部分的有效性.为此, 在Co-MVCF基础上移除图拉普拉斯正则项, 得到退化模型Co-MVCF-N, 如下所示:

J=α $\overset{K}{\sum_{k}}$ w_k‖ X^k-X^kG^kV $‖_{F}^{2}$ +β $\overset{c}{\sum_{i}} \overset{n}{\sum_{j}}$ p_ij‖ v_j- ${\tilde{z}}_{i}$ ‖ ²+(1-β ) $\overset{K}{\sum_{k}}$ w_k $\overset{c}{\sum_{i}} \overset{n}{\sum_{j}}$ p_ij‖ $x_{j}^{k}$ - $z_{i}^{k}$ ‖ ²+η $\overset{K}{\sum_{k}}$ w_kln w_k, s.t. $\overset{k}{\sum_{k}}$ w_k=1, 0≤ w_k≤ 1, p_ij∈ {0, 1}, $\overset{c}{\sum_{i}}$ p_ij=1, ∀ j=1, 2, …, n.

Co-MVCF和Co-MVCF-N的消融实验结果如表6所示, 表中黑体数字表示最优值.由表可看出, Co-MVCF在所有数据集上都具有最优性能, 并且相比Co-MVCF-N, Co-MVCF在每个数据集上都获得超过5%的性能提升.特别地, 相比Co-MVCF-N, Co-MVCF在ORL数据集上的性能提高45%左右, 在3sources数据集上的性能提高50%左右.实验结果表明, 图拉普拉斯正则项有助于保留多视图数据的一致性局部几何结构, 可显著提升Co-MVCF性能.

表6 Co-MVCF和Co-MVCF-N的消融实验结果 Table 6 Ablation experiment results of Co-MVCF and Co-MVCF-N

4 结束语

本文提出基于概念分解的显隐空间协同多视图聚类算法(Co-MVCF).利用多视图数据的一致性特性, 通过概念分解得到多个视图之间的一个共识的低维特征矩阵, 用于代表数据的隐式空间.在保持数据局部结构关系的同时, 协同学习数据样本在显式空间和隐式空间的聚类, 从而得到多个视图之间统一的聚类结果.此外, 考虑到各视图数据重要程度的差异, 采用熵加权的策略, 在迭代更新的过程中为各个视图自动分配权重.确切地说, Co-MVCF充分利用多视图数据不同角度的信息以提高最终的聚类性能.与其它9种聚类算法在图像、文本、场景、手写数字等8个基准数据集上的实验验证Co-MVCF的有效性和可靠性.

当然, Co-MVCF也存在一定的局限性, 在未来的工作中, 还有如下问题需要进一步研究:1)寻找合适的方式初始化K-means聚类中心, 使算法性能更有效和鲁棒; 2)在Co-MVCF中需要调节四个参数, 因此可进一步考虑使用自适应策略降低调节参数的个数, 提高算法的可适用性和确定性.

本文责任编委陈恩红

Recommended by Associate Editor CHEN Enhong

参考文献

文献选项

[1]	CLEUZIOU G, EXBRAYAT M, MARTIN L, et al. CoFKM: A Centralized Method for Multiple-View Clustering // Proc of the 9th IEEE International Conference on Data Mining. Washington USA: IEEE, 2009: 752-757. [本文引用:2]
[2]	KUMAR A, DAUMÉ III H. A Co-training Approach for Multi-view Spectral Clustering // Proc of the 28th International Conference on Machine Learning. New York USA: ACM, 2011: 393-400. [本文引用:1]
[3]	TZORTZIS G, LIKAS A. Kernel-Based Weighted Multi-view Clu-stering // Proc of the IEEE 12th International Conference on Data Mi-ning. Washington USA: IEEE, 2012: 675-684. [本文引用:1]
[4]	HUANG S D, KANG Z, TSANG I W, et al. Auto-Weighted Multi-view Clustering via Kernelized Graph Learning. Pattern Recognition, 2019, 88: 174-184. [本文引用:1]
[5]	REN Z W, LI H R, YANG C, et al. Multiple Kernel Subspace Clustering with Local Structural Graph and Low-Rank Consensus Kernel Learning. Knowledge-Based Systems, 2020, 188. DOI: 10.1016/j.knosys.2019.105040. [本文引用:1]
[6]	LEE D D, SEUNG H S. Algorithms for Non-negative Matrix Factorization // Proc of the 13th International Conference on Neural Information Processing Systems. Cambridge, USA: MIT Press, 2000: 535-541. [本文引用:3]
[7]	LIU J L, WANG C, GAO J, et al. Multi-view Clustering via Joint Nonnegative Matrix Factorization // Proc of the SIAM International Conference on Data Mining. Philadelphia USA: SIAM, 2013: 252-260. [本文引用:1]
[8]	TAN Y, OU W H, LONG F, et al. Multi-view Clustering via Co-regularized Nonnegative Matrix Factorization with Correlation Constraint // Proc of the 7th International Conference on Cloud Computing and Big Data. Washington USA: IEEE, 2016: 1-6. [本文引用:1]
[9]	ZONG L L, ZHANG X C, ZHAO L, et al. Multi-view Clustering via Multi-manifold Regularized Non-negative Matrix Factorization. Neural Networks, 2017, 88: 74-89. [本文引用:1]
[10]	LIU X Y, SONG P, SHENG C, et al. Robust Multi-view Non-ne-gative Matrix Factorization for Clustering. Digital Signal Processing, 2022, 123. DOI: 10.1016/j.dsp.2022.103447. [本文引用:2]
[11]	DENG Z H, LIU R X, XU P, et al. Multi-view Clustering with the Cooperation of Visible and Hidden Views. IEEE Transactions on Knowledge and Data Engineering, 2020, 34(2): 803-815. [本文引用:2]
[12]	CAI D, HE X F, HAN J W. Locally Consistent Concept Factorization for Document Clustering. IEEE Transactions on Knowledge and Data Engineering, 2011, 23(6): 902-913. [本文引用:1]
[13]	XU W, GONG Y H. Document Clustering by Concept Factorization // Proc of the 27th Annual International ACM SIGIR Conference on Research and Development in Information Retrieval. New York USA: ACM, 2004: 202-209. [本文引用:1]
[14]	HINTON G E, ROWEIS S. Stochastic Neighbor Embedding // Proc of the 15th International Conference on Neural Information Proce-ssing Systems. Cambridge, USA: MIT Press, 2002: 857-864. [本文引用:1]
[15]	ZHAN K, SHI J H, WANG J, et al. Graph-Regularized Concept Factorization for Multi-view Document Clustering. Journal of Visual Communication and Image Representation, 2017, 48: 411-418. [本文引用:1]
[16]	CHANG S, HU J, LI T R, et al. Multi-view Clustering via Deep Concept Factorization. Knowledge-Based Systems, 2021, 217. DOI: 10.1016/j.knosys.2021.106807. [本文引用:1]
[17]	ZHAN K, SHI J H, WANG J, et al. Adaptive Structure Concept Factorization for Multi-view Clustering. Neural Computation, 2018, 30(4): 1080-1103. [本文引用:1]
[18]	LI R H, ZHANG C Q, HU Q H, et al. Flexible Multi-view Representation Learning for Subspace Clustering // Proc of the 28th International Joint Conference on Artificial Intelligence. San Francisco USA: IJCAI, 2019: 2916-2922. [本文引用:1]
[19]	YANG M S, SINAGA K P. Collaborative Feature-Weighted Multi-view Fuzzy C-means Clustering. Pattern Recognition, 2021, 119. DOI: 10.1016/j.patcog.2021.108064. [本文引用:1]
[20]	LIU J Y, LIU X W, YANG Y X, et al. Multiview Subspace Clustering via Co-training Robust Data Representation. IEEE Transactions on Neural Networks and Learning Systems, 2022, 33(10): 5177-5189. [本文引用:1]
[21]	ZHANG P, LIU X W, XIONG J, et al. Consensus One-Step Multi-view Subspace Clustering. IEEE Transactions on Knowledge and Data Engineering, 2022, 34(10): 4676-4689. [本文引用:1]
[22]	WANG D, HAN S W, WANG Q, et al. Pseudo-Label Guided Co-llective Matrix Factorization for Multiview Clustering. IEEE Tran-sactions on Cybernetics, 2022, 52(9): 8681-8691. [本文引用:1]

2009

0.0

... Cleuziou等^[1]提出CoFKM,基于FKM(Fuzzy K-means, FKM),采用协同聚类的思想同时最小化每个视图的模糊划分,同时假定无论视图如何,每个数据最终都会被分配到同一个集群中 ...

... 2)CoFKM^[1] ...

2011

0.0

... Kumar等^[2]采用协同训练的思想,在谱聚类的框架中使用来自彼此的信息引导不同视图的聚类,最终得到多视图聚类结果 ...

2012

0.0

... Tzortzis 等^[3]提出基于核的多视图聚类算法,每个视图都被表示为一个给定的核,所有的核都被加权组合 ...

2019

0.0

... Huang等^[4]在核空间中学习相似关系,并为每个视图自动分配权重 ...

2020

0.0

... Ren等^[5]提出LLMKL(Local Structural Graph and Low-Rank Consensus Multiple Kernel Learning),引入共识核矩阵的低秩替代和稀疏误差矩阵,探究Hilbert特征空间潜在的全局结构,同时基于谱图理论保持样本之间的局部结构 ...

2000

0.0

... 近年来,由于非负矩阵分解(Nonnegative Matrix Factorization, NMF)^[6]在处理高维数据上的优势和可解释性,基于NMF的多视图子空间聚类算法获得研究者们的注意力 ...

... 1 非负矩阵分解矩阵分解在聚类中被广泛应用,常见的是NMF^[6] ...

... 为了证实Co-MVCF有效性,在ToyData、syn500、MNIST-10k这3个具有负值的多视图数据集上进行聚类性能的对比实验,基线算法是基础的MultiNMF^[6]和使用的MV-Co-VH^10] ...

2013

0.0

... Liu等^[7]将NMF拓展到多视图聚类的情况,提出MultiNMF(Multi-view NMF),通过NMF探索每个视图的底层聚类结构,并学习一个共同的聚类指示矩阵,使每个视图的聚类结构保持一致 ...

2016

0.0

... Tan等^[8]在低维空间上引入相关约束,学习不同视图共享的一种隐式表示 ...

2017

0.0

... Zong等^[9]提出MM- NMF(Multi-manifold Regularized NMF Framework),在每个视图上进行NMF,线性组合的一致流形和一致系数矩阵与多流形正则化结合,保留多个隐式空间的局部几何结构 ...

2022

0.0

... Liu等^[10]提出RMNMF(Robust Multi-view NMF),考虑特征之间的高阶关系,使用一阶关系和二阶关系获得最优的邻域结构 ...

2020

0.0

... 为此,Deng等^[11]提出MV-Co-VH(Multi-view Clustering Algorithm with the Cooperation of Visible and Hidden Views),同时探索多视图数据在显式空间和隐式空间中的信息,将隐式空间中的聚类与显式空间中的聚类整合到一个协同训练框架中,获得最终的聚类结果 ...

... 3)MV-Co-VH^[11] ...

2011

0.0

... 此外,NMF的前提假设是输入样本数据是非负的,这在现实场景中往往不能被满足,因此利用NMF提取隐空间信息的方法在现实应用中存在局限性^[12] ...

2004

0.0

... Xu等^[13]在NMF的基础上进行拓展,提出概念分解(CF)算法,解决上述问题,使算法可以作用在任何数据空间 ...

2002

0.0

... 基于高维相似,低维也相似的基本假设^[14],Co-MVCF在显式空间和隐式空间中协同聚类,最终得到一个聚类的共识 ...

2017

0.0

... 传统的多视图概念分解方法^[15]以矩阵的形式将数据映射到低维空间,对于每个视图,数据样本X^k被分解为该视图对应的关联矩阵G^k#cod#x02208 ...

2021

0.0

... 此外,与文献[16]类似,在更新G和V时,容易利用二阶泰勒近似得到式(13)的辅助函数,然后证明其收敛性 ...

2018

0.0

... 4)MVCF(Multiview Concept Factorization)^[17] ...

2019

0.0

... 5)FMR(Flexible Multi-view Representation)^[18] ...

2021

0.0

... 6)Co-FW-MVFCM(Collaborative Feature Weighted Multi-view Fuzzy C-means)^[19] ...

2022

0.0

... 7)CoMSC(Multiview Subspace Clustering via Co-training Robust Data Representation)^[20] ...

2022

0.0

... 8)COMVSC(Consensus One-Step Multi-view Sub- space Clustering)^[21] ...

2022

0.0

... 9)PLCMF(Pseudo-Label Guided Collective Ma-trix Factorization)^[22] ...