王士同,硕士,教授,主要研究方向为人工智能、模式识别.E-mail:wxwangst@aliyun.com.
作者简介:

卞则康,博士,讲师,主要研究方向为人工智能、模式识别.E-mail:bianzekang@163.com.

张 进,博士研究生,主要研究方向为人工智能、模式识别.E-mail:jin.zhang.1991@foxmail.com.
为了进一步提升Takagi-Sugeno-Kang(TSK)模糊分类器在不平衡数据集上的泛化能力和保持其较好的语义可解释性,受集成学习的启发,提出面向不平衡数据的深度TSK模糊分类器(A Deep TSK Fuzzy Classifier for Imbalanced Data, ID-TSK-FC).ID-TSK-FC主要由一个不平衡全局线性回归子分类器(Imbalanced Global Linear Regression Sub-Classifier, IGLRc)和多个不平衡TSK模糊子分类器(Imbalanced TSK Fuzzy Sub-Classifier, I-TSK-FC)组成.根据人类“从全局粗糙到局部精细”的认知行为和栈式叠加泛化原理,ID-TSK-FC首先在所有原始训练样本上训练一个IGLRc,获得全局粗糙的分类结果.然后根据IGLRc的输出,识别原始训练样本中的非线性分布训练样本.在非线性分布训练样本上,以栈式深度结构生成多个局部I-TSK-FC,获得局部精细的结果.最后,对于栈式堆叠IGLRc和所有I-TSK-FC的输出,使用基于最小距离投票原理,得到ID-TSK-FC的最终输出.实验表明,ID-TSK-FC不仅具有基于特征重要性的可解释性,而且具有至少相当的泛化性能和语义可解释性.
WANG Shitong, master, professor. His research interests include artificial intelligence and pattern recognition.
About Author:
BIAN Zekang, Ph.D., lecturer. His research interests include artificial intelligence and pattern recognition
ZHANG Jin, Ph.D. candidate. His research interests include artificial intelligence and pattern recognition.
Inspired by ensemble learning, a deep Takagi-Sugeno-Kang fuzzy classifier for imbalanced data(ID-TSK-FC) is proposed to enhance the generalization capability and maintain good linguistic interpretability of TSK fuzzy classifier on imbalanced data. ID-TSK-FC is composed of an imbalanced global linear regression sub-classifier(IGLRc) and several imbalanced TSK fuzzy sub-classifiers(I-TSK-FCs). According to the human cognitive behavior "from wholly coarse to locally fine" and the stacked generalization principle, ID-TSK-FC firstly trains an IGLRc on all training samples to obtain a wholly coarse classification result. Then, the nonlinear training samples in the original training samples are classified according to the output of IGLRc. Next, several I-TSK-FCs are generated using a stacked depth structure on the nonlinear training samples to achieve a locally fine result. Finally, the minimum distance voting principle is applied on the outputs of stacked IGLRc and all I-TSK-FCs to obtain the final output of ID-TSK-FC. The experimental results confirm that ID-TSK-FC not only holds interpretability based on feature importance, but also holds at least comparable generalization capability and linguistic interpretability.
不平衡模糊分类器是一种特殊的模糊分类器[1, 2].它结合模糊集理论和不平衡学习方法, 不仅能够处理模糊性和不确定性数据集, 而且能够提升分类器在不平衡数据集上的泛化性能.更重要的是, 不平衡模糊分类器能够提供模糊可解释性, 如语义可解释性.
依据是否使用模糊规则, 可将不平衡模糊分类器分为:无模糊规则不平衡模糊分类器和基于模糊规则的不平衡模糊分类器.
无模糊规则不平衡模糊分类器主要使用模糊集理论以减少数据集的类间不平衡性.Ramentol等[3]提出IFROWANN(Imbalanced Fuzzy Rough Ordered Weighted Average Nearest Neighbor), 基于模糊粗糙集理论和有序加权平均策略构建一个权矢量, 能够有效消除数据集的类间不平衡性.Zhang等[4]提出IFSVM(Improved Fuzzy Support Vector Machine), 增加一个自适应不平衡正则项, 减少数据集的类间不平衡性.
与无模糊规则不平衡模糊分类器不同, 基于模糊规则的不平衡模糊分类器不仅能够取得较好的泛化性能, 而且其决策过程具有语义可解释性.Xu等[5]提出改进的模糊分类器, 结合归一化支持度量和归一化置信度量, 处理不平衡数据集, 提升分类器的不平衡处理能力.Villar等[6]提出基于模糊规则的不平衡模糊分类器, 联合多目标遗传算法和粒度学习, 减少数据集的不平衡性.Mahdizadeh等[7]提出基于模糊规则的不平衡模糊分类器, 分别使用减法聚类方法和多基因遗传规划生成模糊规则的前件和后件.Leski等[8]提出Fuzzy Ordered C-means Clus-tering, 分别通过模糊有序C-means算法和最小角度回归算法生成模糊规则的前件和后件.Sanz等[9]基于带调整和规则选择的区间值模糊规则分类系统以及短模糊规则, 提出紧凑的进化区间值模糊分类器, 能够同时取得较好的泛化性能和较高可解释性.Gu等[10]提出IB-TSK-FC(Imbalanced Takagi-Sugeno-Kang Fuzzy Classifier), 采用贝叶斯概率模型生成短模糊规则的可解释前件, 再采用不平衡学习方法生成规则的后件, 从而提升模型的泛化性能和可解释性.尽管上述基于模糊规则的不平衡模糊分类器可以在不平衡数据集上实现增强的泛化性能和较好的可解释性, 但常常受到由“ 维度诅咒” 导致的“ 规则爆炸” 的困扰.
为了解决上述“ 规则爆炸” 问题, 受到深度学习[11, 12, 13]的启发, Wang等[14]提出IDE-TSK-FC(Deep-Ensemble-Level-Based Takagi-Sugeno-Kang Fuzzy Cla-ssifier), 依据栈式堆叠泛化理论[15], 栈式集成一个全局TSK模糊分类器和多个局部TSK模糊分类器, 基于数据集的不平衡区域生成每个局部分类器.此外, IDE-TSK-FC中每个0阶TSK模糊子分类器从五个固定的高斯隶属函数中随机选择一个作为短模糊规则的前件, 并采用最小学习机(Least Learning Machine, LLM)[16, 17]作为短模糊规则的后件.由于每个子分类器采用短模糊规则, IDE-TSK-FC缓解“ 规则爆炸” 问题, 同时在不平衡数据集上实现增强的泛化能力和较好的可解释性.
基于集成结构的TSK(Takagi-Sugeno-Kang)模糊分类器可能是不平衡数据集的完美选择.这是因为使用深度或宽集结构和短模糊规则, 可以保证集成分类器的强泛化能力和较好的语义可解释性[18, 19, 20, 21].然而, 由于较好的非线性拟合能力和高可解释性, 这些深度或宽TSK模糊分类器仅采用TSK模糊分类作为其子分类器, 这可能会影响其它类型样本的识别效率, 如不平衡数据集上的线性分布样本.并且TSK模糊分类器只提供语义的可解释性.此外, 这些深度或宽TSK模糊分类器的每个子分类器都是在所有原始不平衡数据集上生成的, 增加集成分类器的训练时间.
为了解决上述问题, 本文尝试从如下两方面考虑.
1)集成模型的组成应该多样化.文献[22]指出“ 简单线性回归模型通常不仅优于多元线性回归, 而且优于最先进的回归模型, 尤其是在小训练集上.” .文献[14]也指出, “ 值得注意的是, 一些研究人员认为, 如果少数类和多数类可以线性分离, 学习算法仍然可以从不平衡数据集中充分学习.” .由此, 本文可以合理推断出:不平衡数据集的有效集成分类器应该由线性模型和非线性模型组成, 线性模型应该是基本模型.
2)集成模型的训练方法应遵循人类“ 从整体粗糙到局部精细” 的认知行为.具体而言, 应在所有训练样本上快速生成全局线性回归模型, 以获得完全粗糙的结果, 并识别不平衡数据集上非线性分布训练样本.为了实现较快的运行速度和局部精细的结果, 根据栈式堆叠泛化原理中的残差算子[15], 将非线性分布训练样本的输出残差在其实际标签和全局线性回归模型的相应输出之间进行划分, 分为多个区域.通过这种划分, 划分的区域很可能变得不平衡, 然后在相应的区域上生成若干局部非线性模型(即TSK模糊分类器).叠加线性回归模型和几个TSK模糊分类器, 输出采取多数投票或平均策略[14], 可以获得最终输出.此外, 线性回归模型可以提供基于特征重要性的可解释性[23, 24], TSK模糊分类器可以提供基于语义的可解释性.因此, 最终的集成分类器应该同时具有基于特征重要性的可解释性和语义可解释性.
基于上述考虑, 也为了更好地处理同时具有线性分布和非线性分布的不平衡数据集, 本文提出面向不平衡数据的深度TSK模糊分类器(Deep TSK Fuzzy Classifier for Imbalanced Data, ID-TSK-FC), 栈式堆叠一个不平衡全局回归子分类器(Imbalanced Global Linear Regression Sub-Classifier, IGLRc)和多个不平衡TSK模糊子分类器(Imbalanced TSK Fuzzy Sub-Classifier, I-TSK-FC), 生成深度集成分类器.此外, 提出一种训练算法训练ID-TSK-FC.具体地, 首先在所有训练样本上快速学习一个IGLRc, 得到全局粗糙的结果, 同时识别不平衡数据集上的非线性分布训练样本.为了提高分类器在非线性分布样本上的分类性能, 使用栈式堆叠多个I-TSK-FC, 取得局部精细的结果.最后, 提出基于最小距离的投票策略代替常用的主投票或者平均策略, 获得ID-TSK-FC最终的输出.实验表明, ID-TSK-FC具有与所有对比算法相当的泛化能力.除了额外的基于特征重要性的可解释性之外, ID-TSK-FC采用较少的模糊规则和较小的模型复杂度, 也具有较好的可解释性.
基于稀疏表示的线性回归模型[24, 25, 26]不仅能够取得较好的分类性能, 而且能够识别每个特征对分类结果的重要性, 即具有基于特征重要性的可解释性.常见的基于稀疏表示的线性回归模型[24]的目标函数如下:
$\begin{aligned} & \min _{\boldsymbol{v}}\left\lgroup\frac{1}{2 n}\|\boldsymbol{X} \boldsymbol{v}-\boldsymbol{Y}\|^2+\lambda_1\|\boldsymbol{v}\|_1+\frac{\lambda_2}{2}\|\boldsymbol{v}\|^2\right\rgroup \text {, } \\ & \end{aligned}$ (1)
其中, X表示训练样本集, Y表示标签向量, v∈ Rd× 1表示稀疏表示向量, n表示训练样本的总数, λ 1、λ 2分别控制两个正则项的权重.
式(1)中目标函数主要用于学习一个最优的稀疏表示向量v, 文献[24]通过ASSPN(Accelerated Proximal Subsampled Newton Method)求解式(1), 不仅具有较快的求解速度, 而且从v中可以看出不同的特征对于分类结果的重要性, 即优化得到的稀疏表示v具有基于特征重要性的可解释性.
作为一种常用的可解释模糊分类器, TSK模糊分类器具有良好的泛化能力和较高的可解释性.经典0阶TSK模糊分类器的第k条模糊规则定义为
Rulek:IF x1 is
THEN fk(x)=
其中, x=[x1, x2, …, xd]表示d维特征的输入样本, ∧ 表示模糊连接算子,
y(x)=
其中, μk(x)和
μk(x)=
$\begin{aligned} & \mu_{A_i^k}\left(x_i\right)=\exp \left(-\frac{1}{2}\left(\frac{x_i-c_i^k}{\sigma_i^k}\right)^2\right) \\ & \end{aligned}$
h表示人为给定的尺度参数, ujk表示第j个特征属于第k个中心的隶属度, n表示输入样本总数.
之后, 对于输入的样本x, 0阶TSK模糊分类器的所有K条模糊规则的前件可以表示为如下形式:
因此, 对于所有的训练集X, 0阶TSK模糊分类器的所有K条模糊规则的前件可以表示为
Φ =
然后, 基于给定的训练样本的标签Y, K条模糊规则的后件, 即
a=
可以通过优化如下的线性回归模型
$Y_{tr}= \boldsymbol{\Phi a } $ (2)
得到.依据文献[18]~文献[20]中的优化方法, 使用LLM优化式(2), 得到最优结果:
$\boldsymbol{a}=\left(\frac{1}{2 C} \boldsymbol{I}+\boldsymbol{\Phi}^{\mathrm{T}} \boldsymbol{\Phi}\right)^{-1} \boldsymbol{\Phi}^{\mathrm{T}} \boldsymbol{Y}_{\mathrm{tr}}$
近年来, 随着深度学习的发展, 研究者们开始研究TSK模糊分类器的深度集成结构, 其中基于栈式堆叠的深度TSK模糊分类器以其增强的泛化性能以及较高的可解释性受到越来越多的关注.依据栈式堆叠泛化原理[15], Zhou等[27]提出D-TSK-FC(Deep TSK Fuzzy Classifier).相比传统TSK模糊分类器, D-TSK-FC以深度栈式的形式集成多个TSK模糊子分类器, 具体地, 当前TSK模糊子分类器的输入由前一个TSK模糊子分类的输出残差加上原始输入样本组成, 因此D-TSK-FC具有增强的泛化性能和较好的可解释性.Zhang等[20]提出另一种深度TSK模糊分类器, 即HID-TSK-FC(Highly Interpretable Deep TSK Fuzzy Classifier), 共享不同层TSK模糊子分类器的模糊规则, 提高集成分类器的可解释性, 同时, 深度栈式结构保证HID-TSK-FC的高泛化性能.Gu等[19]提出DSA-FC(Stacked Adversarial TSK Fuzzy Classifiers), 基于对抗输出信息和平滑梯度信息, 能够取得增强的泛化性能和高可解释性.
综上所述, 以深度栈式方式集成多个TSK模糊分类器, 能够有效增强分类器的泛化性能, 同时具有较好的可解释性.
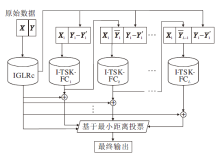
本文提出面向不平衡数据的深度TSK模糊分类器(ID-TSK-FC), 结构如图1所示.ID-TSK-FC总共包含L+1个子分类器, 即1个不平衡全局线性回归子分类器(IGLRc)和L个不平衡TSK模糊子分类器(I-TSK-FC).
下面详细介绍两种子分类器的训练过程.在训练阶段, 首先在原始训练数据集X及其标签向量Y上, 训练一个IGLRc.再识别X, 得到非线性分布样本集X1及其标签向量Y1, 并得到X1的IGLRc的输出Y'1.然后, 在非线性分布样本集X1及其输出残差Y1- Y'1上, 以栈式堆叠的方式训练L个I-TSK-FC.具体地, 在X1和Y1-Y'1上训练第1个TSK子分类器I-TSK-FC1, 将得到的输出
从图1的结构可以看出, 叠加泛化原理保证ID-TSK-FC增强的泛化能力.同时, 由于非线性分布样本集的数量远小于原始总样本, 因此ID-TSK-FC同时具有较快的运行速度.此外, ID-TSK-FC可以提供基于特征重要性和基于语义的可解释性.
总之, ID-TSK-FC包含两个主要过程:训练和测试.下面将分别详细介绍训练阶段和测试阶段.
ID-TSK-FC的训练阶段可分为两个部分:训练IGLRc和训练多个I-TSK-FC.
首先, 基于全部原始训练数据集X及其相应的标签向量Y, 训练IGLRc, 考虑到原始数据集上存在不平衡数据, 因此, 定义IGLRc的目标函数:
$\begin{aligned} & \min _{\boldsymbol{v}}\left\lgroup\frac{1}{2 n}\|\boldsymbol{X}^{* }(w1^{T}))v-\boldsymbol{Y}\|^2+\lambda_1\|\boldsymbol{v}\|_1+\frac{\lambda_2}{2}\|\boldsymbol{v}\|^2\right\rgroup \text {, } \\ & \end{aligned}$ (3)
其中, * 表示点乘运算符,
1=[1, 1, …, 1]T∈ Rn× 1,
w=
表示权重向量, wi=
从式(3)可以看出, 为每个训练样本施加不同的权重, 可有效减少不平衡的数据对于最终结果的影响.与1.1节相同, 对于式(3)的优化, 同样使用ASSPN进行求解.
优化式(3), 构建IGLRc.再使用构建好的IGLRc分类所有的训练样本X, 对于每个训练样本xi (i=1, 2, …, n), 分类公式
显然, 通过式(4)得到是回归结果而不是分类结果.因此, 需要对回归结果进行处理.根据文献[4]、文献[18]~文献[20]中的操作, 对于二分类问题, 设置数据集类别为正类和负类, 观察sign(xiv)的值将xi划分为正类或负类.对于多分类问题, 设置数据集类别为{1, 2, …, cl}, 其中cl表示数据集的总类别数, 通过观察xiv距离最近的整数, 将xi归于最近的整数类(即|c'-xiv|最小), c'∈ {1, 2, …, cl}表示划分的类别.上述这种分类策略, 称为基于最小距离的投票策略.
使用上述的方法, 在所有训练样本上训练IGLRc, 然后利用IGLRc预测所有训练样本, 使用基于最小距离的投票策略, 可以将训练样本集X划分为两部分:分类正确的训练样本集和分类不正确的训练样本.分类正确的训练样本集为线性分布训练样本, 分类不正确的训练样本为非线性分布训练样本.
由于IGLRc为线性分类器, 不能正确识别非线性分布训练样本, 因此, 需要使用非线性分类器对其正确识别.假设由IGLRc识别得到的非线性分布训练样本集
X1=
和标签向量
Y1=
其中n1表示非线性分布训练样本的总数,
Y'1=
表示非线性分布训练样本X1的IGLRc的输出回归值.
在上述非线性分布训练样本上, 使用深度栈式结构训练L个I-TSK-FC.具体过程如下.
首先, 基于非线性分布训练样本X1及其残差向量Y1-Y'1, 训练第1个I-TSK-FC1.
与IGLRc类似, I-TSK-FC1为不同的训练样本施加一个权重, 以减少不平衡数据集的影响.假设第1个I-TSK-FC1的规则数为K1, 由1.2节可知, 对于X1中任何一个训练样本xi(i=1, 2, …, n1), K1条规则的前件可表示为
其中,
ω 'i=
表示施加在训练样本xi上的权重,
对于X1中所有样本, K1条规则的前件可以表示为
Φ 1=
参考1.2节中的推导过程, 可以得到I-TSK-FC1所有的后件:
$\begin{aligned} & \boldsymbol{a}^1= \left[a_0^1, a_0^2, \cdots, a_0^{K^1}\right]^{\mathrm{T}}= \left\lgroup\frac{1}{2 C} \boldsymbol{I}+\left(\boldsymbol{\Phi}^1\right)^{\mathrm{T}} \boldsymbol{\Phi}^{\mathbf{1}}\right\rgroup \boldsymbol{\Phi}^{-1}\left(\boldsymbol{\Phi}^1\right)^{\mathrm{T}}\left(\boldsymbol{Y}_1-\boldsymbol{Y}_1^{\prime}\right) . \\ & \end{aligned}$ (7)
然后, 对于非线性分布训练样本集X1, I-TSK-FC1的输出向量为:
其中, 每个元素
上述为第1个TSK子分类器(即I-TSK-FC1)的全部训练过程.由于使用深度栈式结构训练L个I-TSK-FC, 所以依据栈式堆叠泛化原理中的残差算子[15], 从第2个TSK子分类器(即I-TSK-FC2)开始, 需要借助前一个分类器的输出作为当前分类器的输入, 即第l(2≤ l≤ L)个TSK子分类器(I-TSK-FCl)的输入为新的训练样本集
$\begin{aligned} & X_1^{\prime}=\left[X_1, \bar{Y}_{l-1}\right] \in \mathbf{R}^{n_1 \times d} \\ & \end{aligned}$
及其残差向量Y1-Y'1, 其中
与上述I-TSK-FC1的推导过程类似, 对于新的训练样本集X'1中每个新的训练样本x'i=[xi,
其中ω 'i与式(5)的定义一致.因此, X'1的Kl条规则前件可以表示为
Φ l=[
最终, 可以得到I-TSK-FCl的后件:
$\begin{aligned} & \boldsymbol{a}^l=\left[a_0^1, a_0^2, \cdots, a_0^{K^l}\right]^{\mathrm{T}}= \left(\frac{1}{2 C} \boldsymbol{I}+\left(\boldsymbol{\Phi}^l\right)^{\mathrm{T}} \boldsymbol{\Phi}^l\right)^{-1}\left(\boldsymbol{\Phi}^l\right)^{\mathrm{T}}\left(\boldsymbol{Y}_1-\boldsymbol{Y}_1^{\prime}\right) . \\ & \end{aligned}$ (11)
然后, 对于X'1, I-TSK-FCl的输出定义为
其中
当L个I-TSK-FC训练完毕后, ID-TSK-FC的训练阶段结束.
训练阶段的输出主要包含两部分:1)X中的线性训练样本, 输出就是IGLRc的正确输出; 2)X中的非线性分布训练样本X1的输出, 首先栈式叠加IGLRc的输出与每个I-TSK-FC的输出, 即
{Y1,
然后使用基于最小距离的投票策略得到最后的输出.
总之, ID-TSK-FC的训练阶段如算法1所示.
算法1 ID-TSK-FC训练阶段
输入 训练样本集X, 标签向量Y, 参数λ 1, λ 2, L, L个I-TSK-FC规则数{K1, K2, …, KL}
输出 稀疏表示v,
L个I-TSK-FC后件{a1, a2, …, aL}
step 1 训练一个IGLRc并划分训练样本集.
step 1.1 利用ASSPN优化公式(3), 求解最优稀疏表示v.
step 1.2 利用式(4)计算X的输出, 得到非线性分布训练样本集X1∈
step 2 训练L个I-TSK-FC.
step 2.1 在X1和残差向量Y1-Y'1上训练第1个I-TSK-FC1.
step 2.1.1 通过式(6)求解K1条规则的前件Φ 1.
step 2.1.2 通过式(7)求解K1条规则的后件a1.
step 2.1.3 通过式(8)求解I-TSK-FC1的输出
step 2.2 当2≤ l≤ L时, 构建I-TSK-FCl.
step 2.2.1 构建新训练样本集X'1=[X1,
step 2.2.2 通过式(10)求解Kl条规则的前件Φ l.
step 2.2.3 通过式(11)求解Kl条规则的后件al.
step 2.2.4 通过式(12)求解I-TSK-FCl的输出
step 2.2.5 l=l+1.
step 3 在{Y1,
对于测试数据集Xte∈
其中v表示最优的稀疏表示.然后分别使用I-TSK-FCl(l=1, 2, …, L)对
最后, 在
{
上使用基于最小距离的投票策略得到最终的标签.
ID-TSK-FC的测试阶段如算法2所示.
算法2 ID-TSK-FC测试阶段
输入 测试样本集Xte∈
IGLRc的最优稀疏表示v,
L个I-TSK-FC的后件{a1, a2, …, aL}
输出 预测标签Y'te=
step 1 当1≤ i≤ nte时, 转入step 2.
step 2 对于测试样本
step 3 当1≤ l≤ L时
step 3.1 通过式(9)求解
step 3.2 通过式(14)求解I-TSK-FCl的输出
step 4 在{
step 5 i=i+1, 返回step 1.
ID-TSK-FC的时间复杂度主要从模型的计算复杂度上进行分析, 模型复杂度主要从模型的参数量进行量化分析, 包括模型的模糊规则数和特征数[19, 20, 28].
首先, 讨论ID-TSK-FC的计算复杂度.ID-TSK-FC训练阶段的计算复杂度主要集中分析算法1.
依据文献[24], 算法1中step 1.1的计算复杂度为
$\begin{aligned} & O\left\lgroup\left\lgroup\frac{\left(s r(\boldsymbol{B}) \log _2 d\right)^{\frac{1}{4}}}{n^{\frac{1}{8}}} \sqrt{t_{\text {avereage }}}\right\rgroup\left(d n^2+s^2 n+d^2 n t_{\text {avereage }}^{\prime}\right)\right\rgroup \\ & \end{aligned},$
其中, n表示训练样本的总数, d表示总特征数, s表示随机采样的总数, t'average表示ASSPN平均迭代次数, sr(B)表示矩阵B的稳定秩, 具体定义见文献[24].step 1.2的计算复杂度为O(nd).因此, step 1的计算复杂度约为
$\begin{aligned} & O\left\lgroup\left\lgroup\frac{\left(s r(\boldsymbol{B}) \log _2 d\right)^{\frac{1}{4}}}{n^{\frac{1}{8}}} \sqrt{t_{\text {average }}}\right\rgroup \left(d n^2+s^2 n+d^2 n t_{\text {avererge }}^{\prime}\right)\right\rgroup \text {. } \\ & \end{aligned}$
step 2.1主要是训练I-TSK-FC1.依据文献[14], 文献[18]~文献[20]中的分析, step 2.1.1的计算复杂度为O(5n1d2K1), step 2.1.2的计算复杂度为
O(
step 2.1.3的计算复杂度为O(n1K1), 其中n1表示非线性分布样本的总数.因此, step 2.1的计算复杂度约为
O(5n1d2K1+
step 2.2是训练L个I-TSK-FC, 与step 2.1不同的是, step 2.2的数据集特征数为d+1, 因此, step 2.2.2的计算复杂度为
O(5n1(d+1)2Kl),
step 2.2.3的计算复杂度为
O(
step 2.2.4的计算复杂度为O(n1Kl), 其中Kl表示I-TSK-FCl的总规则数.因此, I-TSK-FCl的总计算复杂度约为
O(5n1(d+1)2Kl+
所以step 2.2的总计算复杂度为
因此, step 2的总计算复杂度约为
O(5n1d2K1+
综上所述, ID-TSK-FC的训练总计算复杂度约为
$\begin{aligned} & O\left\lgroup \left\lgroup\frac{\left(s r(\boldsymbol{B}) \log _2 d\right)^{\frac{1}{4}}}{n^{\frac{1}{8}}} \sqrt{t_{\text {avererge }}}\right\rgroup\left(d n^2+s^2 n+d^2 n t_{\text {average }}^{\prime}\right)+ \\ 5 n_1 d^2 K^1+\left(K^1\right)^3+\sum_{l=2}^L\left(5 n_1(d+1)^2 K^l+\left(K^l\right)^3\right)\right\rgroup \\ & \end{aligned}.$
考虑到本文使用的数据集的样本量远大于特征数(n≥ d)和n> n1, 因此, ID-TSK-FC的训练总计算复杂度记为
O(dn2+s2n+
可知, ID-TSK-FC的训练时间主要受到数据集的样本总量n、维度d、取样量s和平均规则数Kl_ave的影响.
在测试阶段, ID-TSK-FC需要分别计算每个子分类器的输出, 即算法2, 算法2的计算消耗主要集中在step 2和step 3.step 2的计算复杂度约为O(nted).step 3的计算复杂度主要集中在step 3.1和step 3.2.参考对于训练复杂度的分析, 可得到step 3.1的计算复杂度约为
$\begin{aligned} & O\left\lgroup 5 n_{\mathrm{te}} d^2 K^1+\sum_{l=2}^L\left(5 n_{\mathrm{te}}(d+1)^2 K^l\right)\right\rgroup \\ & \end{aligned}$
step 3.2的计算复杂度约为
$\begin{aligned} & O\left\lgroup n_{\mathrm{te}} \sum_{l=1}^L K^l\right\rgroup \\ & \end{aligned}.$
所以ID-TSK-FC测试阶段的总计算复杂度约为
$\begin{aligned} & O\left\lgroup5 n_{\mathrm{te}} d^2 K^1+\sum_{l=2}^L\left(5 n_{\mathrm{te}}(d+1)^2 K^l\right)\right\rgroup . \end{aligned}$
设Kl_ave为平均规则数, 则测试阶段的计算复杂度简单记为
O(nte(d+1)2Kl_ave),
易知, ID-TSK-FC的测试时间主要受到测试样本量nte、特征数d和平均规则数Kl_ave的影响.
接下来讨论ID-TSK-FC的模型复杂度(Model Complexity, MC), 主要从模型训练时使用的参数量进行分析.依据文献[19]、文献[20]、文献[28]中的分析, 0阶TSK分类模型复杂度主要通过计算IF和Then两部分的参数总量决定, 计算公式如下:
MC=2dK+K(d+1),
其中, d表示特征数, K表示规则数.
由算法1的描述可知, I-TSK-FC1使用的特征数为d, 而I-TSK-FCl(2≤ l≤ L)使用的特征数为d+1, 因此在IF部分使用的参数总量为
2K1d+2(d+1)
在Then部分的参数总量为
K1(d+1)+(d+2)
考虑到ID-TSK-FC中还包含1个IGLRc, 需要的特征数为d.因此, ID-TSK-FC的总参数量约为
3K1d+2(d+1)
综上所述, ID-TSK-FC的时间复杂度和模型复杂度均受到模型使用的规则数Kl和特征数d的影响, 同时, 这些参数也影响ID-TSK-FC的泛化性能.
在本文实验中, 主要从算法的分类性能和可解释性评估ID-TSK-FC.
本文选取20个常用的不平衡数据集作为实验数据集, 包含10个小样本数据集(样本量少于1 000), 10个大样本数据集(样本量为1 000~70 000), 详细信息如表1所示.表中数据集的不平衡率是指数据集上最大类与最小类样本量的比例.
| 表1 实验数据集描述 Table 1 Description of experimental datasets |
在本文实验中, 为了验证ID-TSK-FC在不平衡数据集上的效果, 主要选取如下4种不平衡分类器作为对比算法.
1)W-zero-TSK(A Weighted Zero-Order TSK Fuzzy Classifier).本文改进0阶TSK模糊分类器, 提出W-zero-TSK, 为样本施加一个权重, 提升算法的不平衡处理能力.
2)DSA-FC[19].深度栈式集成的TSK模糊分类器, 通过栈式集成多个0阶TSK子分类器, 提升集成分类器的分类性能.
3)IB-TSK-FC[10].采用跨类贝叶斯模糊聚类算法, 提高TSK模糊分类器对不平衡数据集的性能和可解释性.
4)IDE-TSK-FC[14].不平衡深度混合TSK模糊分类器, 以逐层的方式栈式堆叠多个TSK模糊子分类器, 从第2层开始, 在采用KNN(K Nearest Neighbor)生成的相应不平衡区域上训练每个TSK模糊分类器.
接下来讨论本文的参数设置.首先, 讨论ID-TSK-FC的参数设置.ID-TSK-FC包含两种子分类器:IGLRc和L个0阶I-TSK-FC.从算法1中可以看出, IGLRc含有λ 1和λ 2这两个正则参数, 依据文献[24]中设置, 设置这两个正则参数的网格搜索范围都是{0.001, 0.01, 0.1, 1, 10, 100}.对于L个0阶I-TSK-FC, 需要设置每个子分类器的规则数及子分类器的个数.简单设置L的寻参范围是1~5, 步长为1.对于每个I-TSK-FC的规则数, 简单设置寻参范围为c~20c, 步长为round(c/2), 其中, round(· )表示取整, c表示数据集的总类别数.
对于所有对比算法, 需要设置每个TSK分类器的规则数.为了公平起见, 同样设置规则数寻参范围也是c~20c, 步长为round(c/2).对于DSA-FC、IB-TSK-FC和IDE-TSK-FC的其它参数, 请参照其相应文献中的参数设置.
在本文实验中, 使用Friedman's with Bonferroni-Dunn Statistical Test[29]评估算法之间的差异性.从文献[29]可以看出, 统计测试方法需要使用到两种统计测试参数:
$\begin{aligned} & \tau_F=\frac{\left(N_d-1\right) \zeta}{N_d\left(N_m-1\right)-\zeta}, \\ & C D=q_\alpha \sqrt{\frac{N_m\left(N_m+1\right)}{6 N_d}}, \end{aligned}$
其中,
$\begin{aligned} & \zeta=\frac{12 N_d}{N_m\left(N_m+1\right)}\left(\sum_{i=1}^{N_m} \operatorname{Rank}_i^2-\frac{N_m\left(N_m+1\right)^2}{4}\right), \end{aligned}$
Ranki表示第i个算法的平均排名值, Nm表示算法个数, Nd表示数据集的个数.依据文献[29]中设置, α=0.05, qα≈ 2.850.
F((Nm-1), (Nm-1)(Nd-1))
表示自由度为(Nm-1)和(Nm-1)(Nd-1)的F分布.依据统计测试结果, 如果
τ F> F((Nm-1), (Nm-1)(Nd-1)),
表示所有算法之间存在显著差异.如果
|Ranki-Rankj|> CD,
表示第i种算法和第j种算法之间存在明显差异.
在本文的实验中, 使用五重交叉验证作为主要的实验方法.为了评估各分类器的分类性能, 选取常用的算法精度(Accuracy, ACC)作为评估标准.为了进一步验证各分类器对于不平衡数据集的分类效果, 选取F1分数(F1-score)作为另一个评估标准.通过结合精度和F1分数, 评估各分类器在不平衡数据集上的分类性能.此外, 从算法的规则数以及模型复杂度方面评估分类器的可解释性.
首先对比各分类器在所有数据集上的ACC和F1-score, 然后使用统计分析方法分析ID-TSK-FC与对比分类器之间的差异性.表2列出各分类器在所有数据集上的平均训练精度和测试精度.表3列出各分类器在所有数据集上的平均训练F1分数和测试F1分数.表4列出对应表2的平均排名.请注意, 这里的排名是按照测试精度的高低而评定的, 即测试精度越高, 平均排名越低.表2~表4中黑体数字表示最优值.
| 表2 各分类器的平均训练精度和测试精度 Table 2 Average training ACC and testing ACC of different classifiers |
| 表3 各分类器的平均训练F1分数和测试F1分数 Table 3 Average training F1-score and testing F1-score of different classifiers |
| 表4 各分类器对应的平均排名 Table 4 Average ranking of different classifiers |
由表2和表3的实验结果可以看出, ID-TSK-FC在大部分数据集上的测试精度和F1分数均高于对比分类器.这是因为, ID-TSK-FC集成两种分类器, 即线性分类器和TSK分类器, 这有利于提升集成分类器的分类性能, 并且通过栈式堆叠所有子分类器的输出, 进一步提升集成分类器的泛化性能.此外, 实验结果同时表明, 在本文采取的实验数据集上, ID-TSK-FC在小规模和大规模不平衡数据集上具有较好的泛化性能.
下面使用Friedman's with Bonferroni-Dunn Stati-stical Test分析各分类器之间的差异性, 各分类器精度的排名结果如表4所示.由表中结果可以计算得到统计分析的参数结果如下:
τ F≈ 44.018, F(4, 44)≈ 2.59, CD≈ 1.925.
本文使用的统计测试方法分析各分类器之间的差异性需要分成两步:1)分析所有分类器之间是否存在明显差异性, 因为
τ F> F(4, 44),
从统计结果可以得出, 就分类器的测试精度而言, 本文实验使用的所有分类器之间存在明显差异.2)进一步分析ID-TSK-FC分别与对比分类器之间是否存在明显差异性.从表4可以得出, ID-TSK-FC分别与W-zero-TSK、DSA-FC、IB-TSK-FC和IDE-TSK-FC之间的平均排名差值的绝对值为:3.25, 2.15, 2.4, 0.7.结合CD的描述, 由统计分析结果可以看出, ID-TSK-FC与W-zero-TSK、DSA-FC和IB-TSK-FC之间存在明显的差异性, 因为3.25、2.15、2.4均大于CD(CD≈ 1.925).尽管从统计分析结果可以看出ID-TSK-FC与IDE-TSK-FC之间的差异性并不明显(因为CD> 0.7), 但是结合表2中测试精度和表3中F1分数可看出, ID-TSK-FC拥有比IDE-TSK-FC更优的分类性能.
本节分析各分类器的可解释性, 分别从算法使用的规则数以及模型的复杂度进行算法可解释性分析.另一方面, 通过一个实例展示ID-TSK-FC的可解释性.
首先, 从算法使用的规则数和模型复杂度对比算法的可解释性, 结果如表5所示.从表可以看出, 相比深度集成分类器DSA-FC和IDE-TSK-FC, 在大多数数据集上, ID-TSK-FC需要更少的模糊规则数以及更小的模型复杂度.这是因为相对于DSA-FC中每个子分类器都是基于所有训练样本训练而成, ID-TSK-FC首先在全部训练数据集上训练一个线性分类器, 然后在非线性数据集上生成多个TSK模糊分类器, 因此, ID-TSK-FC需要更少的规则数.
| 表5 各分类器的平均规则数及模型复杂度 Table 5 Average number of rules and model complexity of different classifiers |
另一方面, 尽管IDE-TSK-FC中的模糊子分类器也是基于训练数据集中的子集训练而成, 但是也需要首先在所有训练样本集上训练一个全局TSK分类器, 因此, 相比ID-TSK-FC, IDE-TSK-FC需要更多的模糊规则.相比W-zero-TSK和IB-TSK-FC, ID-TSK-FC需要更多的模糊规则, 这是因为W-zero-TSK和IB-TSK-FC是单一的分类器, 相比集成分类器, 需要更少的模糊规则, 但是它们的分类性能低于集成分类器.
综上所述, 相比集成的对比分类器, ID-TSK-FC具有更少的模糊规则以及更小的模型复杂度.
下面说明ID-TSK-FC的可解释性.在Yeast数据集上, 选取其中的两个样本作为测试样本:
x1=[0.2700, 0.4600, 0.5200, 0.1700, 0.5000, 0.0000, 0.4900, 0.4400],
x2=[0.3000, 0.5000, 0.3400, 0.2600, 0.5000, 0.0000, 0.5100, 0.2200].
实验中ID-TSK-FC中的参数L=2.为了描述方便, 定义Yeast数据集上8个特征分别为F1, F2, …, F8.执行完ID-TSK-FC的训练过程, 得到ID-TSK-FC中IGLRc的表达如下:
y=1.8164F1+1.7798F2-2.9763F3-1.8207F4+3.1074F5+2.9173F6+2.0946F7-0.0650F8.
在测试阶段, ID-TSK-FC中所有子分类器(IGLRc+I-TSK-FC1+I-TSK-FC2)对测试样本x1的输出分别为:2.0034, 2.5154, 3.4204.基于最小距离投票策略, 可以得到x1的类别最终是由IGLRc决定, 即为2.因此, 对于测试样本x1, 最终预测结果由IGLRc决定, 可以使用IGLRc对其分类结果进行解释.由IGLRc的表达式可知, 特征F5对“ x1为正” 的预测影响程度较大, 而特征F3和F8对“ x1为负” 有着影响, 且F3的影响程度大于F8(因为F3的权值绝对值较大).
相似地, 对于测试样本x2, ID-TSK-FC中所有子分类器(IGLRc+I-TSK-FC1+I-TSK-FC2)的输出分别是2.5571, 4.6247, 5.0683.基于最小距离投票策略可知, x2的最终类别被预测为5, 因此, 可以使用I-TSK-FC2对其预测结果进行解释.为了简单起见, 只列出其中五条规则对应的前件和后件, 具体如表6所示.
| 表6 Yeast数据集上I-TSK-FC2的规则前件和后件 Table 6 Antecedents and consequents of rules by I-TSK-FC2on Yeast dataset |
以第1条模糊规则为例, 可以解释为如下形式:
IF(F1 is H) AND (F2 is Me) AND (F3 is L) AND
(F4 is VL) AND (F5 is H) AND (F6 is H) AND
(F7 is Me) AND (F8 is VH)
THEN y=2.4412
显然, 容易解释和理解这样一个模糊规则.综上所述, ID-TSK-FC既具有基于特征重要性的可解释性, 也具有基于语义的可解释性.
针对不平衡数据集, 本文提出面向不平衡数据的深度TSK模糊分类器(ID-TSK-FC), 不同于传统的深度TSK模糊分类器, ID-TSK-FC通过深度栈式方式集成一个不平衡全局线性回归子分类器(IGLRc)和多个不平衡TSK模糊子分类器(I-TSK-FC).具体地, ID-TSK-FC首先在所有的训练样本上训练一个IGLRc, 得到一个全局粗糙的分类结果.再根据IGLRc的输出结果, 得到训练样本中的非线性分布样本, 并依据其输出残差, 将其划分为多个部分.然后, 在非线性分布样本上以深度栈式方式生成多个I-TSK-FC.最后, 基于ID-TSK-FC中所有子分类器的输出, 使用基于最小距离的投票策略得到最后的输出.实验表明, ID-TSK-FC不仅具有增强的泛化性能, 而且除了具有额外的基于特征重要性的可解释性, 同时也具有较好的语义可解释性, 即更少的模糊规则数和更小的模型复杂度.
今后的研究工作可能集中在如下两方面:1)由于本文采用深度栈式方式生成多个I-TSK-FC, 因此如何加快集成分类器的运行速度将是下一个研究方向.2)由于本文采用加权策略减少类别不平衡, 因此采用其它不平衡策略以提高分类性能也是一个重要的研究方向.
本文责任编委 于剑
Recommended by Associate Editor YU Jian
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|
| [19] |
|
| [20] |
|
| [21] |
|
| [22] |
|
| [23] |
|
| [24] |
|
| [25] |
|
| [26] |
|
| [27] |
|
| [28] |
|
| [29] |
|