基于拓扑信息和属性信息协同对比的自监督异质图神经网络模型

引用本文

李超, 孙国义, 闫页宇, 段华, 曾庆田. 基于拓扑信息和属性信息协同对比的自监督异质图神经网络模型. 模式识别与人工智能, 2023,36(4): 287-299
LI Chao, SUN Guoyi, YAN Yeyu, DUAN Hua, ZENG Qingtian. Self-Supervised Heterogeneous Graph Neural Network Model Based on Collaborative Contrastive Learning of Topology Information and Attribute Information. PATTERN RECOGNITION AND ARTIFICIAL INTELLIGENCE, 2023,36(4): 287-299. 复制到剪切板

Doi: 10.16451/j.cnki.issn1003-6059.202304001
Permissions

《模式识别与人工智能》编辑部

基于拓扑信息和属性信息协同对比的自监督异质图神经网络模型

李超¹, 孙国义¹, 闫页宇¹, 段华³, 曾庆田²

1.山东科技大学电子信息工程学院青岛 266590

2.山东科技大学数学与系统科学学院青岛 266590

3.山东科技大学计算机科学与工程学院青岛 266590

通信作者：

曾庆田,博士,教授,主要研究方向为大数据分析与挖掘、流程挖掘、物联网.E-mail:qtzeng@163.com.

作者简介：

李超,博士,副教授,主要研究方向为网络表示学习、社交网络分析、推荐算法.E-mail:1008lichao@163.com.

孙国义,硕士研究生,主要研究方向为机器学习、异质图神经网络.E-mail:1139457124@qq.com.

闫页宇,硕士研究生,主要研究方向为图表示学习、异质图神经网络.E-mail:yanyeyuwork@foxmail.com.

段华,博士,教授,主要研究方向为社交网络分析、数据挖掘、隐私保护.E-mail:huaduan59@163.com.

收稿日期: 2023-01-09 接受日期: 2023-03-29

资助项目: 科技创新2030——“新一代人工智能”重大项目(No.2022ZD0119500)、山东省自然科学基金项目(No.ZR2022MF268)资助

摘要

异质图神经网络模型能够充分挖掘异质图的复杂结构和丰富语义,但在模型构建过程中,属性信息和拓扑信息之间存在相互干扰,致使模型的表达能力减弱.因此,文中提出基于拓扑信息和属性信息协同对比的自监督异质图神经网络模型.首先,在拓扑视角和属性视角下分别学习目标节点的表示.然后,利用协同对比算法优化两个视角下的节点表示,降低拓扑信息和属性信息之间的相互干扰.同时,在模型的自监督训练过程中,提出元路径条数与节点拓扑相似度融合的正样本生成方法.在真实数据集上的实验表明,文中模型性能较优.具体模型代码见https://github.com/sun281210/HGTA.

关键词: 图神经网络; 异质图; 对比学习; 自监督学习

中图分类号:TP 391

Self-Supervised Heterogeneous Graph Neural Network Model Based on Collaborative Contrastive Learning of Topology Information and Attribute Information

LI Chao¹, SUN Guoyi¹, YAN Yeyu¹, DUAN Hua³, ZENG Qingtian²

1. College of Electronic and Information Engineering, Shandong University of Science and Technology, Qingdao 266590

2. College of Mathematics and Systems Science, Shandong University of Science and Technology, Qingdao 266590

3. College of Computer Science and Engineering, Shandong University of Science and Technology, Qingdao 266590

Corresponding author:
ZENG Qingtian, Ph.D., professor. His research interests include big data analysis and mining, process mining and internet of things.

About Author:
LI Chao, Ph.D., associate professor. His research interests include network representation learning, social network analysis and re-commendation algorithm.
SUN Guoyi, master student. His research interests include machine learning and heterogeneous graph neural network.
YAN Yeyu, master student. His research interests include graph representation learning and heterogeneous graph neural network.
DUAN Hua, Ph.D., professor. Her research interests include social network analysis, data mining and privacy preserving.

Fund:National Key R&D Program of China(No.2022ZD0119500), Natural Science Foundation of Shandong Province(No.ZR2022MF268)

Abstract

The complex structure and rich semantics of heterogeneous graphs can be fully explored by heterogeneous graph neural network models. However, there is mutual interference between attribute information and topology information in the model construction process, resulting in weakened expression capability. Therefore, a self-supervised heterogeneous graph neural network model based on collaborative contrastive learning of topology information and attribute information is proposed. Firstly, the representation of the target nodes is learned from both topological and attribute perspectives. Then, the collaborative contrastive algorithm is employed to optimize the node representation from both perspectives, reducing the interference between topology information and attribute information. Additionally, a positive sample generation method combining the number of meta-paths and node topology similarity is proposed in the self-supervised training process of the model. The experiments on real datasets demonstrate the superior performance of the proposed model. The model code can be found at https://github.com/sun281210/HGTA.

Key words: Graph Neural Network; Heterogeneous Graph; Contrastive Learning; Self-Supervised Learning

文章图片

图数据在现实生活中无处不在, 如社交网络^[1]、电子商务^[2]、蛋白质网络^[3]和交通网络^[4]等.针对现实世界交互系统的复杂性, 研究人员将现实场景建模为包含多种类型节点和边的特殊的图数据结构, 即异质图.异质图能够对图数据实现更加细致全面的描述.由于异质图神经网络^[5]可以充分挖掘异质图上的复杂结构和丰富语义, 目前已受到研究人员的极大关注.

早期的异质图神经网络主要应用于半监督学习模型^[6].Wang等^[7]提出HAN(Heterogeneous Graph Attention Network), 引入节点级注意力和语义级注意力, 聚集来自基于元路径的邻居信息.Fu等^[8]进一步改进HAN, 提出MAGNN(Metapath Aggregated Graph Neural Network), 涉及到HAN中未考虑的节点之间的中间节点.Yu等^[9]提出GTNs(Graph Trans-former Networks), 不再依赖人工定义的元路径, 而是设计方法自动学习节点之间的多跳关系, 再基于多跳关系聚合消息.

然而, 半监督学习往往需要大量的标注数据, 在现实场景中数据标注信息的获取存在一定的困难, 成本较高.为了解决标签较难获取的问题, 自监督学习^[10]成为图表示学习模型构建的新方向.作为无监督学习的子类, 自监督学习是从数据本身获取监督信息的一种有效学习范式.在自监督学习中, 模型由代理任务进行训练, 从而确保学习到的节点表示具有更好的性能和更佳的泛化性^[11].对比学习^[12]广泛应用于自监督图表示学习中, 基本思想是提供一组负样本和正样本生成方式, 通过最小化目标节点与正样本之间的距离、最大化与负样本之间的距离以优化模型.

Zhang等^[13]提出HetGNN(Heterogeneous Graph Neural Network), 采样固定大小的邻居, 并使用长短期记忆网络(Long Short-Term Memory, LSTM)融合其特征.Velič ković 等^[14]提出DGI(Deep Graph Infomax), 使用由原始图像生成的局部嵌入和全局嵌入作为正样本, 由特征扰乱图生成的局部嵌入和由正常图生成的全局嵌入作为负样本, 最大化局部嵌入与全局嵌入的互信息, 优化节点表示.Ren等^[15]进一步将DGI的思想扩展到异质图, 提出HDGI(Heterogeneous DGI), 同时考虑局部图结构和全局图结构.Jing等^[16]提出HDMI(High-Order Deep Multiplex Infomax), 将给定的多路复用网络分解成多个属性图, 混合同尺度和跨尺度对比学习.Park等^[17]提出DMGI(Deep Multiplex Graph Infomax), 在原始网络和被破坏网络上对每个单视图元路径进行对比学习.Zhu等^[18]提出GRACE(Deep Graph Contrastive Representation Learning), 删除边和掩蔽属性以创建视图, 并设计损失函数优化节点表示.You等^[19]在GRACE的基础上提出GraphCL(Graph Contrastive Learning), 针对边和节点属性进行自适应扩充.Qiu等^[20]提出GCC(Graph Contrastive Co-ding), 采样原始图的多个子图, 利用MoCo(Momen-tum Contrast)^[21]对比框架进行对比学习.Zhu等^[22]提出GCA(Graph Contrastive Learning with Adaptive Augmentation), 使用不同的图扩充策略, 并利用图对比损失函数优化节点表示.Wang等^[23]提出HeCo(Heterogeneous Graph Neural Network with Co-contrastive Learning), 使用网络模式和元路径两种视图, 通过元路径创建正样本和负样本, 再利用对比损失函数优化模型.Wang等^[24]提出HGCML(Hetero-geneous Graph Contrastive Multi-view Learning), 增强元路径, 生成多个子图作为多视图, 并提出一个对比目标, 最大化任何元路径诱导视图之间的互信息.Yu等^[25]提出MEOW(Heterogeneous Graph Contras-tive Learning Model), 利用元路径构建一个粗粒度的视图和一个细粒度的视图, 并进行对比.

大多数现有模型主要集成节点属性信息和拓扑信息, 并进行节点嵌入的学习.然而这种集成忽略拓扑信息和属性信息之间的干扰问题^[26].一方面, 拓扑结构会干扰属性信息的学习, 具体表现在: 属性信息通过邻域进行传播, 从而达到相连节点具有相似的向量化表示, 这种领域传播会使属性信息同化, 导致过平滑^[27].另一方面, 属性信息会扭曲网络的拓扑信息, 具体表现在: 具有相似拓扑信息的一些节点在变换后可能获得不同的表示, 导致拓扑信息丢失^[28].

因此, 拓扑信息和属性信息之间的干扰问题是图神经网络模型需要解决的关键问题之一.为了减轻学习过程中拓扑信息与属性信息相互干扰的问题, 需要在不同视角下分别学习拓扑信息和属性信息.此外, 为了获得更加丰富的节点表示, 还需要引入跨视角的对比学习, 通过最大化不同视图节点表示之间的互信息, 学习节点表示.

为了缓解拓扑信息和属性信息之间的干扰, 本文提出基于拓扑信息和属性信息协同对比的自监督异质图神经网络模型(Self-Supervised Heterogeneous Graph Neural Network Model Based on Collaborative Contrastive Learning of Topology Information and Attribute Information, HGTA).模型由拓扑视角节点编码器模块、属性视角节点编码器模块和协同对比优化模块组成.在拓扑视角节点编码器模块中, 基于原始图的拓扑信息, 引入节点类型特征, 区分异质图不同类型节点, 学习目标节点的拓扑信息.在属性视角节点编码器模块中, 引入节点级注意力机制和语义级注意力机制, 聚合相同元路径下的节点表示及不同元路径下的节点表示, 得到属性视角下目标节点的表示.最后, 通过协同对比优化算法模块, 实现拓扑信息与属性信息的协同对比学习.本文还提出基于元路径条数与节点拓扑相似度融合的正样本生成方法, 实现节点局部结构信息和全局结构信息的有效融合.在3个公共数据集上的大量对比实验表明, HGTA的性能优于对比的自监督异质图神经网络模型和部分半监督异质图神经网络模型.

1 问题定义

定义 1 异质图^[29] 异质图

G=(V, E, A, R, ϕ , φ ),

其中, V表示节点集合, E表示边集合, A表示节点类型集合, R表示边类型集合, |A+R|> 2.节点类型映射函数ϕ ∶ V→ A, 边类型映射函数φ ∶ E→ R.

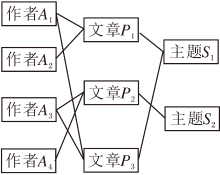
如图1所示, 一个由学术网络构建的异质图, 包含3种类型的节点(作者, 文章, 主题), 以及2种类型边的关系(作者-论文, 论文-主题).

	Figure Option View Download New Window
	图1 异质图Fig.1 Heterogeneous graph

定义 2 元路径^[30] 元路径是异质图中的一条路径:

$A_{1} \overset{R_{1}}{\to} A_{2} \overset{R_{2}}{\to} \dots \overset{R_{l}}{\to} A_{l + 1}$

表示A₁到A_l₊₁之间的一种复合连接关系

R=R₁$\circ$R₂$\circ$…$\circ$R_l,

其中$\circ$表示关系上的复合运算符.

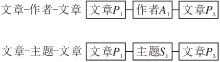
元路径描述异质图中两个节点的复合关系, 例如, 在图2中, 文章-作者-文章这条元路径描述两篇论文同属于一个作者, 文章-主题-文章描述两篇论文属于同一个主题.

	Figure Option View Download New Window
	图2 元路径Fig.2 Meta-path

定义 3 图的拓扑结构图的拓扑结构可以表示为它的邻接矩阵adj=[a_ij], 当且仅当节点i、 j存在边e_ij=(i, j), a_ij=1, 否则a_ij=0.具体拓扑结构示例如图3所示.

	Figure Option View Download New Window
	图3 拓扑结构Fig.3 Topology structure

给定一个异质图G=(V, E, A, R, ϕ , φ )作为输入, 生成多个子视图{G₁, G₂, …, G_n}, 生成视图中的嵌入分别为

${Z_{1} = f_{1} ({\tilde{X}}_{1}, {\tilde{A}}_{1}), Z_{2} = f_{2} ({\tilde{X}}_{2}, {\tilde{A}}_{2}) {, \dots, Z}_{n} = f_{n} ({\tilde{X}}_{n}, {\tilde{A}}_{n})}$

其中, ${\tilde{X}}_{}$ 表示视图的特征矩阵, ${\tilde{A}}_{i}$ 表示视图的邻接矩阵, 其目标是利用对比优化算法

Z=cont{Z₁, Z₂, …, Z_n},

优化并输出低维节点嵌入Z.

2 基于拓扑信息和属性信息协同对比的自监督异质图神经网络模型

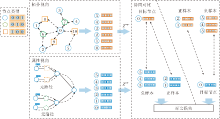
本文提出基于拓扑信息和属性信息协同对比的自监督异质图神经网络模型(HGTA), 总体框架如图4所示.HGTA从两种不同的视角融合异质图的拓扑信息和属性信息, 解决图神经网络中属性信息和拓扑信息在学习过程中互相干扰的问题.

	Figure Option View Download New Window
	图4 HGTA总体框架图Fig.4 Architecture of HGTA

HGTA由三部分组成: 拓扑视角节点编码器模块、属性视角节点编码器模块、协同对比优化模块.在拓扑视角编码过程中, 加入节点类型特征, 区分异质图不同类型节点.在属性视角编码过程中, 引入节点级注意力机制和语义级注意力机制.在拓扑视角和语义视角之间使用协同对比学习, 使这两个视角相互补充和监督.考虑到节点间的高相关性, 重新设计异质图中节点的正负样本选择方式.

2.1 拓扑视角节点嵌入编码器

异质图具有丰富的拓扑信息, 在节点表示学习过程中, 为了减少属性信息的干扰, HGTA将节点属性特征替换为单位阵, 并且为了更好地区分不同类型的节点, 加入节点类型特征, 以便更好地挖掘异质图的拓扑信息.

拓扑视角节点嵌入编码总体设计如下:首先, 将不同类型的节点特征(单位阵)以及节点类型特征投影到相同的公共空间, 并串联投影变换后的节点特征和节点类型特征作为节点初始表示.然后, 利用注意力机制计算不同邻居对于目标节点的重要性.最后, 对邻居节点嵌入进行加权求和, 得到拓扑视角下的节点嵌入.

在拓扑视角中, HGTA重点在于挖掘节点的拓扑信息, 因此节点特征被替换为单位矩阵f^e.此外, 为了区分不同类型的节点, 设计节点类型特征f^t, f^t在输入HGTA前被初始化为节点类型的单位阵.串联投影变换后的节点特征和节点类型特征, 作为节点的初始表示:

$h_{i}^{t} = σ [(w_{1}^{t} {f_{i}^{e}}_{} + b_{1}^{t}) | | (w_{2}^{t} f_{i}^{t} + b_{2}^{t})]$ ,

其中, σ 表示激活函数, ‖ 表示拼接节点特征和节点类型特征, $w_{1}^{t}$ 、 $w_{2}^{t}$ 表示类型转换参数, $b_{1}^{t}$ 、 $b_{2}^{t}$ 表示偏差.节点类型特征f^t的加入, 使模型可以更容易地区分不同类型节点.

对于一个节点对(i, j), 首先计算节点j对于目标节点i的注意力权重:

$e_{\overset{}{i}, j}^{t} = a_{t}^{T} (w_{α} h_{i}^{t} | | w_{α} h_{j}^{t})$ ,

其中, ${a^{T}}_{t}$ 表示参数化的注意力向量, $h_{i}^{t}$ 、 $h_{j}^{t}$ 表示节点i、 j投影后的特征.

然后通过softmax(·)实现对权重 $e_{i, j}^{t}$ 的归一化:

$\boldsymbol{\alpha}_{i, j}^{t}=\operatorname{softmax}\left(\boldsymbol{e}_{i, j}^{t}\right)=\frac{\exp \left(\boldsymbol{e}_{i, j}^{t}\right)}{\sum_{k \in N_{i}} \exp \left(\boldsymbol{e}_{i, k}^{t}\right)},$

其中N_i表示目标节点i的一阶邻域.

最后, 对邻居节点进行加权求和, 得到拓扑视角下节点的嵌入:

$z_{i}^{topo} = \begin{matrix} K \\ | | \\ k = 1 \end{matrix} σ (\sum_{j \in N i_{}} α_{i, j}^{t (l)} \cdot w_{}^{t (l)} h_{j}^{t (l - 1)})$ ,

其中, k表示注意力头数, 用于稳定学习过程和减少高方差.

2.2 属性视角节点嵌入编码器

本文首先将节点属性特征投影到相同空间, 利用节点级注意力计算相同元路径下节点邻居对于目标节点的重要性, 通过加权聚合邻居节点表示得到元路径下目标节点的嵌入.然后利用语义级注意力计算不同元路径下节点嵌入对于目标节点的重要性, 通过加权聚合不同元路径下的节点表示, 最终得到属性视角下节点的嵌入.

首先将不同类型的节点特征x_i投影变换到相同的空间中:

$h_{i}^{s}$ =σ ( $w_{i}^{s}$ x_i+ $b_{i}^{s}$ ).

假设存在M条元路径{p₁, p₂, …, p_M}, 对于元路径p_m下节点i的邻居 $j \in N_{i}^{p_{m}}$ , 重要性

$\boldsymbol{\beta}_{i, j}^{p_{m}}=\operatorname{softmax}\left(\boldsymbol{e}_{i, j}^{p_{m}}\right)=\frac{\exp \left(\boldsymbol{e}_{i, j}^{p_{m}}\right)}{\sum_{k \in N_{i}^{p_{m}}} \exp \left(\boldsymbol{e}_{i, k}^{p_{m}}\right)},$

其中

$e_{\overset{}{i}, j}^{p_{m}} = a_{p_{m}}^{T} (w_{α}^{p_{m}} h_{i}^{p_{m}} | | w_{α}^{p_{m}} h_{j}^{p_{m}})$

表示注意力系数.

最后, 加权聚合邻居节点信息, 得到同一元路径下节点的嵌入:

$z_{i}^{p_{m}} = σ (\sum_{j \in N i p_{m}} β_{i, j}^{p_{m}} \cdot w_{}^{p} h_{j}^{p_{m}})$

其中 $N_{i}^{p_{m}}$ 表示相同元路径下目标节点的邻域集合.

由此可以得到M条元路径下节点嵌入的集合{ $h_{i}^{p_{1}}$ , $h_{i}^{p_{2}}$ , …, $h_{i}^{p_{m}}$ }, 由于通过不同元路径构成的子图包含的语义信息不同, 因此还需要使用语义级注意力聚合不同元路径下的节点表示.

给定不同元路径下节点对p₍_i_,_j₎, $γ_{p_{i, j}}^{s}$ 用于衡量不同元路径下节点的嵌入对于目标节点的重要性:

${γ_{}}_{p_{i, j}}^{s} = softmax (e_{p_{i, j}}^{s}) = \frac{\exp (e_{p_{i, j}}^{s})}{\sum_{k \in M i}}$

其中

$e_{p_{i, j}}^{s} = \frac{1}{|V|} \sum_{i \in V} a_{p_{i, j}}^{T} \cdot \tanh (w^{s} z_{i}^{p_{m}} + b^{s})$

最后通过加权聚合不同元路径下的节点表示, 最终得到属性视角下节点的嵌入:

$z_{i}^{attr} = σ (\sum_{j \in M_{i}} {γ_{}}_{p_{i, j}}^{s} w^{s} z_{j}^{p_{m}})$

2.3 样本生成策略

对于正样本的选择, HGTA从节点的拓扑相似度和元路径条数两方面考虑.考虑到节点的拓扑相似度(图5中I、III部分), HGTA根据不同的元路径, 使用训练好的Metapath2vec(Scalable Representa-tion Learning for Heterogeneous Networks)^[30]得到不同元路径下的节点表示, 再构建不同元路径下的节点相似度矩阵, 并将不同元路径下的节点相似度矩阵求和, 得到节点的拓扑相似度矩阵.

	Figure Option View Download New Window
	图5 正负样本筛选框架图Fig.5 Framework of positive and negative samples screening

考虑到节点之间的元路径条数(图5中II部分), HGTA根据节点之间的元路径连接条数构建节点-元路径条数矩阵, 再将节点的拓扑相似度矩阵与元路径条数矩阵求和, 并根据得分对节点进行降序排列(图5中IV部分), 最终选择前K个节点作为目标节点的正样本, 其它节点作为负样本.

对于包含M种元路径{p₁, p₂, …, p_m}, 使用训练好的Metapath2vec, 得到嵌入

Z={ $Z_{p_{1}}$ , $Z_{p_{2}}$ , …, $Z_{p_{m}}$ }.

构建元路径p_m下的节点拓扑相似度矩阵:

$S_{p_{m}}$ = $Z_{p_{m}} {Z^{T}}_{p_{m}}$ .

每种元路径下的拓扑相似度矩阵表示不同节点间的相似度, 求和得到所有节点的拓扑相似度矩阵:

S^topo= $\frac{1}{M} \overset{M}{\sum_{m = 1}} S_{p_{m}}$ .

在元路径下, 由于节点之间是高度相关的, 节点之间如果有元路径连接, 那么这两个节点具有相关性, 如果两个节点通过多条元路径连接, 则它们具有更强的相关性.对于节点i、 j, 定义函数

C_i(j)= $\overset{M}{\sum_{n = 1}}$ θ ( j∈ N_i),

统计连接这两个节点的元路径条数, 其中θ (·)表示指向函数.然后构造C^meta, 表示所有节点之间的元路径条数矩阵.

将拓扑相似度矩阵S^topo与元路径条数矩阵C^meta进行归一化后相加, 得到节点之间的综合相似度.所有节点对节点i的综合相似度为:

D_i= $\frac{S_{i}^{topo}}{\overset{| V |}{\sum_{j = 1}} S_{i} (j)}$ + $\frac{C_{i}^{meta}}{\overset{| V |}{\sum_{j = 1}} C_{i} (j)}$ ,

其中S_i(j)表示节点j与节点i之间的拓扑相似度.根据D_i的得分对节点进行降序排列.

下面设置一个阈值K, 选择前Top-K个节点作为目标节点的正样本P_os, 其它节点为负样本N_eg.

2.4 协同对比优化

在获得拓扑视角下的嵌入 $z_{i}^{topo}$ 和属性视角下的嵌入 $z_{i}^{attr}$ 后, 映射到相同的对比损失空间:

$z_{i}^{topo}_pro j = w^{(2)} σ (w^{(1)} z_{i}^{topo} + b^{(1)}) + b^{(2)}$ ,

$z_{i}^{attr}_proj = w^{(2)} σ (w^{(1)} z_{i}^{attr} + b^{(1)}) + b^{(2)}$ ,

其中, σ 表示激活函数, 两个视角下共用一套可学习的参数w⁽¹⁾、w⁽²⁾、b⁽¹⁾、b⁽²⁾.在得到正样本集合P_os和负样本集合N_eg后, 计算拓扑视角下的损失:

$\begin{aligned}L_{i}^{\text {topo }} & = \\& -\ln \left(\frac{\sum_{j \in P_{\mathrm{os}}} \exp \left(\frac{\operatorname{sim}\left(\boldsymbol{z}_{i}^{\text {topo }}-p r o j, \boldsymbol{z}_{j}^{\text {attr }}-p r o j\right)}{\tau}\right)}{\sum_{k \in\left\{P_{\mathrm{os}} \cup N_{\mathrm{eg}}\right\}} \exp \left(\frac{\operatorname{sim}\left(\boldsymbol{z}_{i}^{\text {topo }}-p r o j, \boldsymbol{z}_{k}^{\text {attr }}-p r o j\right)}{\tau}\right)}\right), \end{aligned}$

其中, sim(· , ·)表示余弦相似度函数, τ 表示环境变量.在拓扑视角下, 目标嵌入 $z_{i}^{topo}$ _ proj来自拓扑视角, 而正负样本嵌入 $z_{k}^{attr}$ _ proj来自属性视角.

属性视角下的损失为:

$\begin{aligned} L_{i}^{\text {attr }} & = \\ & -\ln \left(\frac{\sum_{j \in P_{\mathrm{os}}} \exp \left(\frac{\operatorname{sim}\left(\boldsymbol{z}_{i}^{\text {attr }}-p r o j, \boldsymbol{z}_{j}^{\text {topo }}-p r o j\right)}{\tau}\right)}{\sum_{k \in\left\{P_{\mathrm{os}} \cup N_{\mathrm{eg}}\right\}} \exp \left(\frac{\operatorname{sim}\left(\boldsymbol{z}_{i}^{\text {attr }}-p r o j, \boldsymbol{z}_{k}^{\text {topo }}-p r o j\right)}{\tau}\right)}\right) . \end{aligned}$

与拓扑视角下损失函数不同的是, 目标嵌入 $z_{i}^{attr}$ _ proj来自属性视角, 而正负样本嵌入 $z_{k}^{topo}$ _ proj来自拓扑视角.

因此, 总损失函数为:

L= $\frac{1}{| V |} \sum_{i \in V}$ [λ $L_{i}^{topo}$ +(1-λ ) $L_{i}^{attr}$ ],

其中, λ 用于平衡两个视角下的损失, 并通过反向传播优化模型.最后, 使用z^topo执行下游任务.

3 实验及结果分析

3.1 实验数据集

为了验证HGTA的有效性, 本文使用3个真实世界的数据集, 具体信息如表1所示.

表1 实验数据集 Table 1 Experimental datasets

1)ACM数据集^[6].学术网络数据集, 目标节点为文章, 文章分为3类.数据集包含4 019篇文章、7 167位作者和60个主题.

2)DBLP数据集^[8].学术网络数据集, 目标节点为作者, 作者分为4类.数据集包含4 057位作者、14 328篇文章、20个会议和7 723个术语.

3)Freebase数据集^[31].电影信息网络数据集, 目标节点为电影, 电影分为3类.数据集包含3 492个电影、33 401位演员、2 502位导演和4 459位编辑.

3.2 基线模型

本文选择如下3类基线模型.

1)无监督同质图神经网络模型.

(1)GraphSAGE^[1].学习一个对邻居顶点进行聚合表示的函数, 生成目标顶点的节点表示.

(2)DGI^[14].训练一个编码模型, 最大化高阶全局表示和输入的局部表示之间的互信息.

2)无监督异质图神经网络模型.

(1)Metapath2vec^[30].利用基于元路径的随机游走构建节点的异质邻域, 通过skip-gram学习节点嵌入.

(2)HERec^[32].设计类型约束策略, 过滤节点序列, 并利用跳图学习异质图的节点表示.

(3)HDGI^[15].使用元路径对异质图中涉及语义的结构进行建模, 最大化局部表示和全局表示的互信息, 学习异质图中不同信息的节点表示.

(4)DMGI^[17].在每个单一视图上对原始网络和损坏网络进行对比学习, 设计共识正则化, 指导不同元路径下节点表示的融合.

(5)HeCo^[23].利用网络模式和元路径两个视图学习节点嵌入, 提出跨视图对比学习, 使两个视图能够相互协作监督, 并最终优化节点嵌入.

(6)MEOW^[25].利用元路径构建一个粗粒度的视图和一个细粒度的视图, 并进行对比.

(7)HGCML^[24].以元路径为扩展, 生成多个子图作为多视图, 提出对比目标, 即最大化任意一对元路径, 导出视图之间的互信息.

3)半监督异质图神经网络模型.HAN^[7].对基于元路径的邻域特征进行分层聚合, 生成节点嵌入.

3.3 参数设置

对于基于随机游走的方法(Metapath2vec和HERec), 将每个节点的游动次数设置为40, 游动长度设置为100, 窗口大小设置为5.对于GraphSAGE、Mp2vec、HERec、DGI, 测试它们所有的元路径, 并报告最佳性能.在其它参数方面, 遵循原始文献中的设置.对于所有模型, 嵌入维度设置为64, 随机运行10次, 计算平均结果.

3.4 节点分类实验

本节通过节点分类实验, 验证HGTA的性能.在ACM、DBLP、Freebase数据集上进行训练, 选择每类20、40、60个标记节点作为训练集, 并分别为每个数据集选择1 000个节点作为验证集, 1 000个节点作为测试集.

使用通用的评估指标:Macro-F1、Micro-F1和AUC(Area Under Curve).

各模型在3个数据集上的节点分类结果如表2~表4所示, 表中黑体数字表示最优结果, 斜体数字表示次优结果.

表2 各模型在ACM数据集上的节点分类结果 Table 2 Node classification results of different models on ACM dataset %

表3 各模型在DBLP数据集上的节点分类结果 Table 3 Node classification results of different models on DBLP dataset %

表4 各模型在Freebase数据集上的节点分类结果 Table 4 Node classification results of different models on Freebase dataset %

由表2可知, 在ACM数据集上, 相比无监督同质图神经网络模型(GraphSAGE和DGI).HGTA的Macro-F1值分别提升35%和31%, Micro-F1值分别提升3%和4%, 原因是GraphSAGE和DGI只能学到单条元路径下同质节点的信息, 而异质图拥有更加复杂的结构.HGTA是针对异质图的模型, 能够全面学到异质图更复杂的信息, 获得更好结果.

相比无监督异质图神经网络模型(Meta-path2vec, HERec, HDGI, DMGI和HeCo), HGTA也展现其优越性.相比Metapath2vec和HERec, HGTA的Macro-F1值分别提升30%和29%, Micro-F1值分别提升27%和26%.Metapath2vec和HERec虽然可适用于异质图, 但也仅能学习单条元路径下的信息.相比HDGI和DMGI, HGTA的Macro-F1值分别提升4%和4%, Micro-F1值分别提升3%和3%.虽然HDGI和DMGI保留最大化局部表示和全局表示间的互信息, 但都是单一视图的学习, 忽略不同视图下获得信息的能力不同, 也忽略异质节点的信息.相比HeCo, HGTA的Macro-F1和Micro-F1值分别提升5%和4%.HeCo虽然将两个视图进行对比学习, 但是在学习过程中, 未考虑节点属性信息和拓扑信息在学习过程中的干扰, 统一处理拓扑信息和节点属性信息, 并且也未考虑到高阶信息对目标节点的重要性.相比MEOW和HGCML, HGTA的Macro-F1值分别提升2%和1%, Micro-F1值分别提升1%和1%, 原因是MEOW和HGCML严重依赖元路径, 只学习目标节点的信息, 忽略异质节点的信息.

由表3可知, 在DBLP数据集上, 相比无监督同质图神经网络模型(GraphSAGE和DGI), HGTA的Macro-F1值分别提升21%和20%, Micro-F1值分别提升7%和5%.分析表明, GraphSAGE和DGI仅能学习单条元路径下目标节点作者(A)的信息, 忽略目标节点作者(A)的标签与会议节点(C)的依赖关系.

相比无监督异质图神经网络模型(Metapath2-vec, HERec, HDGI, DMGI和HeCo), HGTA的Macro-F1和Micro-F1值都有所提升.相比Metapath2vec和HERec, HGTA的Macro-F1值分别提升4%和4%, Micro-F1值分别提升27%和3%.分析表明, Meta-path2vec和HERec只学到单条元路径下目标节点作者(A)的信息.相比HDGI和DMGI, HGTA的Macro-F1值分别提升4%和3%, Micro-F1值分别提升5%和4%.相比MEOW和HGCML, HGTA的Macro-F1值分别提升1%和1%, Micro-F1值分别提升2%和2%.分析表明, HDGI、DMGI、MEOW和HGCML虽然可以通过元路径学习到多条元路径的信息, 但是仅限于同质节点, 也就是目标节点作者(A)的信息, 忽略异质节点的信息.相比HeCo, HGTA的Macro-F1和Micro-F1值分别提升3%和2%.原因是目标节点作者(A)的标签依赖节点会议(C), 因此元路径APCPA能够提供更多有效的信息, 而该路径的语义是:作者(A)将其文章(P)发表到会议(C).这与数据集的真实情况高度吻合.实际上, 作者(A)类型对象的真实类别标签是根据作者的文章(P)发表的会议(C)标记的, 然而HeCo只学到异质节点的属性信息, 忽略局部的拓扑信息.

由表4可知, 在Freebase数据集上, 虽然HGTA能够学到更高阶的拓扑信息, 但由于该数据集上节点没有特征, 因此两个视图学到的只有节点的拓扑信息, HGTA提升并不明显.

3.5 节点聚类实验

本文选择GraphSAGE、Metapath2vec、HERec、DGI、HDGI、DMGI、HeCo、MEOW、HGCML这9种无监督模型作为基线模型, 使用K-means算法学习所有节点的嵌入, 并采用归一化互信息(Normalized Mutual Information, NMI)和调整兰德指数(Adjusted Rand Index, ARI)评估聚类结果.重复该过程10次, 计算平均结果, 结果如表5所示, 表中黑体数字表示最优值.

表5 各模型在3个数据集上的节点聚类结果 Table 5 Node clustering results of different models on 3 datasets %

由表5可知, HGTA的节点聚类结果大部分优于对比模型, 并且多视图的对比学习优于单一视图.分析表明, 多视图模型充分考虑节点不同方面信息, 特别是HGTA充分考虑节点属性信息和拓扑信息在学习过程中的相互协同优化.

3.6 消融实验

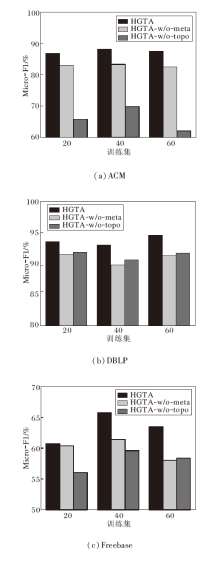
为了证实从节点的拓扑相似度和元路径条数联合筛选正样本节点更加可靠, 设计HGTA的两种变体:仅依据节点的拓扑相似度筛选正样本(HGTA-w/o-meta)、仅依据节点元路径条数筛选正样本(HGTA-w/o-topo).3种模型对比结果如图6所示.由图可知, 两种方式下共同筛选正样本要优于单一方式选择正样本.

	Figure Option View Download New Window
	图6 各模型在3个数据集上的消融实验结果Fig.6 Ablation experiment results of different models on 3 datasets

在ACM数据集上, HGTA-w/o-mata优于HGTA-w/o-topo, 原因是ACM数据集更加依赖元路径下的节点属性, 元路径能更好地捕捉节点间的相关性, HGTA-w/o-meta与目标节点具有更强的语义关系.

在DBLP数据集上, HGTA-w/o-topo优于HGTA-w/o-meta.原因是目标节点作者(A)的标签更加依赖会议节点(C), 而拓扑相似度忽略局部的连接信息, 使元路径条数筛选的正样本与目标节点的相关性大于拓扑相似度筛选的正样本.

在Freebase数据集上, 元路径条数能更好地捕捉节点的局部结构信息, 拓扑相似度可更好地捕捉节点的整体结构信息.

HGTA同时考虑节点的局部结构信息与整体结构信息, 利用元路径条数与拓扑相似度筛选正样本, 能达到更优的效果.

3.7 跨视图对比学习

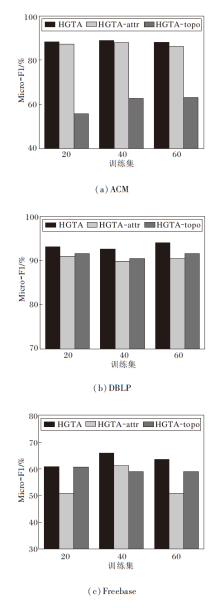
为了验证跨视图协同对比的重要性, 设计2个HGTA的变体:HGTA-attr和HGTA-topo, 具体结构如图7所示.在HGTA-topo中, 节点仅在拓扑视角下编码, 如(a)所示, 目标节点与正负样本的嵌入均来自拓扑视角.在HGTA-attr中, 节点仅在属性视角下编码, 如(b)所示, 目标节点与正负样本的嵌入均来自属性视角.

	Figure Option View Download New Window
	图7 HGTA变体的结构图Fig.7 Structure of HGTA variant

本文将这两种变体与HGTA对比, 结果如图8所示.由图可知, HGTA性能优于变体, 这说明跨视角学习可以学习到更多有用的信息, 节点的拓扑信息与属性信息互相补充.此外, 本文发现, 在ACM数据集上HGTA-attr优于HGTA-topo, 在DBLP数据集上HGTA-topo优于HGTA-attr, 说明不同的数据集在学习过程中拓扑信息和属性信息具有不同的重要性.

	Figure Option View Download New Window
	图8 各模型在3个数据集上不同视角对比结果Fig.8 Comparison of 3 models from different perspectives on 3 datasets

3.8 参数分析

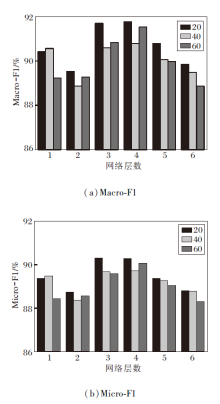
本文分析拓扑视角下的网络层数l对模型结果的影响, 在ACM数据集上不同网络层数的影响的对比结果如图9所示.由图可见, 在神经网络层数l达到两层以后, 随着神经网络层数的提高, 数据呈现上升的趋势, 到达四、五层以后, 随着网络层数的增加, 数据呈现下降趋势.在聚合邻居信息时, 各节点状态更新时一般只聚合一跳邻居信息, 因此, 网络层数就反映节点融合几跳内的邻居信息.当节点无标签时, 节点在浅层聚合过程中可能无法获取有效信息, 从而对分类性能造成不利影响.随着网络层数的增加, 节点获取更多的有效信息, 分类效果提升, 但网络层数到达某个数值以后, 整个网络的节点就会有相同特征, 出现过平滑现象, 导致性能下降.

	Figure Option View Download New Window
	图9 ACM数据集上l的参数敏感性分析Fig.9 Parameter sensitivity analysis of l on ACM dataset

4 结束语

本文提出基于拓扑信息和属性信息协同对比的自监督异质图神经网络模型(HGTA), 重点解决拓扑信息和属性信息之间的干扰问题.HGTA由拓扑视角节点编码器模块、属性视角节点编码器模块和协同对比优化模块组成.在拓扑视角中, 基于原始图的拓扑, 学习目标节点的拓扑信息, 并加入节点类型特征, 区分异质图不同类型的节点.在属性视角中, 利用元路径学习节点的属性信息, 在聚合相同元路径下的节点表示及不同元路径下的节点表示时分别加入节点级注意力机制和语义级注意力机制, 最终得到属性视角下目标节点的嵌入.通过协同对比优化算法, 实现拓扑信息与属性信息的协同对比学习.在正样本生成方面, 提出元路径条数与节点拓扑相似度融合的生成方法.在3个公共数据集上的对比实验表明, HGTA的性能较优.目前HGTA只考虑拓扑信息和属性信息在自监督异质图神经网络模型中的协同对比, 今后可从更多视角出发, 构建多视角系统的异质图神经网络模型.

本文责任编委陈松灿

Recommended by Associate Editor CHEN Songcan

参考文献

文献选项

[1]	HAMILTON W L, YING R, LESKOVEC J. Inductive Representation Learning on Large Graphs // Proc of the 31st International Conference on Neural Information Processing Systems. Cambridge, USA: MIT Press, 2017: 1025-1035. [本文引用:2]
[2]	GAO X Y, FENG F L, HUANG H Y, et al. Food Recommendation with Graph Convolutional Network. Information Sciences, 2022, 584: 170-183. [本文引用:1]
[3]	DAVIS A P, GRONDIN C J, JOHNSON R J, et al. The Comparative Toxicogenomics Database: Update 2019. Nucleic Acids Research, 2019, 47(D1): D948-D954. [本文引用:1]
[4]	WU Z H, PAN S R, LONG G D, et al. Graph Wavenet for Deep Spatial-Temporal Graph Modeling // Proc of the 28th International Joint Conference on Artificial Intelligence. San Francisco, USA: IJCAI, 2019: 1907-1913. [本文引用:1]
[5]	SUN Y Z, HAN J W. Mining Heterogeneous Information Networks: A Structural Analysis Approach. ACM SIGKDD Explorations Newsletter, 2012, 14(2): 20-28. [本文引用:1]
[6]	ZHAO J N, WANG X, SHI C, et al. Network Schema Preserving Heterogeneous Information Network Embedding // Proc of the 29th International Joint Conference on Artificial Intelligence. San Francisco, USA: IJCAI, 2021: 1366-1372. [本文引用:2]
[7]	WANG X, JI H Y, SHI C, et al. Heterogeneous Graph Attention Network // Proc of the World Wide Web Conference. New York, USA: ACM, 2019: 2022-2032. [本文引用:2]
[8]	FU X Y, ZHANG J N, MENG Z Q, et al. MAGNN: Metapath Aggregated Graph Neural Network for Heterogeneous Graph Embedding // Proc of the Web Conference. New York, USA: ACM, 2020: 2331-2341. [本文引用:2]
[9]	YUN S, JEONG M, KIM R, et al. Graph Transformer Networks // Proc of the 33rd International Conference on Neural Information Processing Systems. Cambridge, USA: MIT Press, 2019: 960-970. [本文引用:1]
[10]	LI C, YAN Y Y, FU J H, et al. HetReGAT-FC: Heterogeneous Residual Graph Attention Network via Feature Completion. Information Sciences, 2023, 632: 424-438. [本文引用:1]
[11]	HU W H, LIU B W, GOMES J, et al. Strategies for Pre-training Graph Neural Networks[C/OL]. [2022-12-10]. https://arxiv.org/pdf/1905.12265v3.pdf. [本文引用:1]
[12]	陈庆宇, 季繁繁, 袁晓彤. 基于伪孪生网络双层优化的对比学习. 模式识别与人工智能, 2022, 35(10): 928-938. (CHEN Q Y, JI F F, YUAN X T. Contrastive Learning Based on Bilevel Optimization of Pseudo Siamese Networks. Pattern Recognition and Artificial Intelligence, 2022, 35(10): 928-938.) [本文引用:1]
[13]	ZHANG C X, SONG D J, HUANG C, et al. Heterogeneous Graph Neural Network // Proc of the 25th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York, USA: ACM, 2019: 793-803. [本文引用:1]
[14]	VELIČKOVIĆ P, FEDUS W, HAMILTON W L, et al. Deep Graph Infomax[C/OL]. [2022-12-10]. https://arxiv.org/pdf/1209.10341.pdf. [本文引用:2]
[15]	REN Y X, LIU B, HUANG C, et al. Heterogeneous Deep Graph Infomax[C/OL]. [2022-12-10]. https://arxiv.org/pdf/1911.08538.pdf. [本文引用:2]
[16]	JING B Y, PARK C, TONG H H. HDMI: High-Order Deep Multi-plex Infomax // Proc of the World Wide Web Conference. New York, USA: ACM, 2021: 2414-2424. [本文引用:1]
[17]	PARK C, HAN J W, YU H. Deep Multiplex Graph Infomax: Atten-tive Multiplex Network Embedding Using Global Information. Knowledge-Based Systems, 2020, 197. DOI: DOI:10.1016/j.knosys.2020.105861. [本文引用:2]
[18]	ZHU Y Q, XU Y C, YU F, et al. Deep Graph Contrastive Representation Learning[C/OL]. [2022-12-10]. https://arxiv.org/pdf/2006.04131.pdf. [本文引用:1]
[19]	YOU Y N, CHEN T L, SUI Y D, et al. Graph Contrastive Lear-ning with Augmentations // Proc of the 34th International Confe-rence on Neural Information Processing Systems. Cambridge, USA: MIT Press, 2020: 5812-5823. [本文引用:1]
[20]	QIU J Z, CHEN Q B, DONG Y X, et al. GCC: Graph Contrastive Coding for Graph Neural Network Pre-training // Proc of the 26th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York, USA: ACM, 2020: 1150-1160. [本文引用:1]
[21]	HE K M, FAN H Q, WU Y X, et al. Momentum Contrast for Unsupervised Visual Representation Learning // Proc of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2020: 9726-9735. [本文引用:1]
[22]	ZHU Y Q, XU Y C, YU F, et al. Graph Contrastive Learning with Adaptive Augmentation // Proc of the Web Conference. New York, USA: ACM, 2021: 2069-2080. [本文引用:1]
[23]	WANG X, LIU N, HAN H, et al. Self-Supervised Heterogeneous Graph Neural Network with Co-contrastive Learning // Proc of the 27th ACM SIGKDD Conference on Knowledge Discovery and Data Mining. New York, USA: ACM, 2021: 1726-1736. [本文引用:2]
[24]	WANG Z H, LI Q, YU D H, et al. Heterogeneous Graph Contrastive Multi-view Learning[C/OL]. [2022-12-10]. https://arxiv.org/pdf/2210.00248.pdf. [本文引用:2]
[25]	YU J X, LI X. Heterogeneous Graph Contrastive Learning with Meta-Path Contexts and Weighted Negative Samples[C/OL]. [2022-12-10]. https://arxiv.org/pdf/2212.13847.pdf. [本文引用:2]
[26]	YANG L, CHEN Z Y, GU J H, et al. Dual Self-Paced Graph Convolutional Network: Towards Reducing Attribute Distortions Induced by Topology // Proc of the 28th International Joint Confe-rence on Artificial Intelligence. San Francisco, USA: IJCAI, 2019: 4062-4069. [本文引用:1]
[27]	YANG L, ZHOU W M, PENG W H, et al. Graph Neural Networks Beyond Compromise Between Attribute and Topology // Proc of the ACM Web Conference. New York, USA: ACM, 2022: 1127-1135. [本文引用:1]
[28]	JIN W, DERR T, WANG Y Q, et al. Node Similarity Preserving Graph Convolutional Networks // Proc of the 14th ACM International Conference on Web Search and Data Mining. New York, USA: ACM, 2021: 148-156. [本文引用:1]
[29]	SHI C, YU P S. Heterogeneous Information Network Analysis and Applications. Berlin, Germany: Springer, 2017. [本文引用:1]
[30]	DONG Y X, CHAWLA N V, SWAMI A. Metapath2vec: Scalable Representation Learning for Heterogeneous Networks // Proc of the 23rd ACM SIGKDD International Conference on Knowledge Disco-very and Data Mining. New York, USA: ACM, 2017: 135-144. [本文引用:3]
[31]	LI X, DING D H, KAO B, et al. Leveraging Meta-Path Contexts for Classification in Heterogeneous Information Networks // Proc of the IEEE 37th International Conference on Data Engineering. Washington, USA: IEEE, 2021: 912-923. [本文引用:1]
[32]	SHI C, HU B B, ZHAO W N, et al. Heterogeneous Information Network Embedding for Recommendation. IEEE Transactions on Knowledge and Data Engineering, 2019, 31(2): 357-370. [本文引用:1]

2017

0.0

... 图数据在现实生活中无处不在,如社交网络^[1]、电子商务^[2]、蛋白质网络^[3]和交通网络^[4]等 ...

... (1)GraphSAGE^[1] ...

2022

0.0

... 图数据在现实生活中无处不在,如社交网络^[1]、电子商务^[2]、蛋白质网络^[3]和交通网络^[4]等 ...

2019

0.0

... 图数据在现实生活中无处不在,如社交网络^[1]、电子商务^[2]、蛋白质网络^[3]和交通网络^[4]等 ...

2019

0.0

... 图数据在现实生活中无处不在,如社交网络^[1]、电子商务^[2]、蛋白质网络^[3]和交通网络^[4]等 ...

2012

0.0

... 由于异质图神经网络^[5]可以充分挖掘异质图上的复杂结构和丰富语义,目前已受到研究人员的极大关注 ...

2021

0.0

... 早期的异质图神经网络主要应用于半监督学习模型^[6] ...

... 1)ACM数据集^[6] ...

2019

0.0

... Wang等^[7]提出HAN(Heterogeneous Graph Attention Network),引入节点级注意力和语义级注意力,聚集来自基于元路径的邻居信息 ...

... HAN^[7] ...

2020

0.0

... Fu等^[8]进一步改进HAN,提出MAGNN(Metapath Aggregated Graph Neural Network),涉及到HAN中未考虑的节点之间的中间节点 ...

... 2)DBLP数据集^[8] ...

2019

0.0

... Yu等^[9]提出GTNs(Graph Trans-former Networks),不再依赖人工定义的元路径,而是设计方法自动学习节点之间的多跳关系,再基于多跳关系聚合消息 ...

2023

0.0

... 为了解决标签较难获取的问题,自监督学习^[10]成为图表示学习模型构建的新方向 ...

0.0

... 在自监督学习中,模型由代理任务进行训练,从而确保学习到的节点表示具有更好的性能和更佳的泛化性^[11] ...

2022

0.0

... 对比学习^[12]广泛应用于自监督图表示学习中,基本思想是提供一组负样本和正样本生成方式,通过最小化目标节点与正样本之间的距离、最大化与负样本之间的距离以优化模型 ...

2019

0.0

... Zhang等^[13]提出HetGNN(Heterogeneous Graph Neural Network),采样固定大小的邻居,并使用长短期记忆网络(Long Short-Term Memory, LSTM)融合其特征 ...

0.0

... 等^[14]提出DGI(Deep Graph Infomax),使用由原始图像生成的局部嵌入和全局嵌入作为正样本,由特征扰乱图生成的局部嵌入和由正常图生成的全局嵌入作为负样本,最大化局部嵌入与全局嵌入的互信息,优化节点表示 ...

... (2)DGI^[14] ...

0.0

... Ren等^[15]进一步将DGI的思想扩展到异质图,提出HDGI(Heterogeneous DGI),同时考虑局部图结构和全局图结构 ...

... (3)HDGI^[15] ...

2021

0.0

... Jing等^[16]提出HDMI(High-Order Deep Multiplex Infomax),将给定的多路复用网络分解成多个属性图,混合同尺度和跨尺度对比学习 ...

2020

0.0

... Park等^[17]提出DMGI(Deep Multiplex Graph Infomax),在原始网络和被破坏网络上对每个单视图元路径进行对比学习 ...

... (4)DMGI^[17] ...

0.0

... Zhu等^[18]提出GRACE(Deep Graph Contrastive Representation Learning),删除边和掩蔽属性以创建视图,并设计损失函数优化节点表示 ...

2020

0.0

... You等^[19]在GRACE的基础上提出GraphCL(Graph Contrastive Learning),针对边和节点属性进行自适应扩充 ...

2020

0.0

... Qiu等^[20]提出GCC(Graph Contrastive Co-ding),采样原始图的多个子图,利用MoCo(Momen-tum Contrast)^[21]对比框架进行对比学习 ...

2020

0.0

... Qiu等^[20]提出GCC(Graph Contrastive Co-ding),采样原始图的多个子图,利用MoCo(Momen-tum Contrast)^[21]对比框架进行对比学习 ...

2021

0.0

... Zhu等^[22]提出GCA(Graph Contrastive Learning with Adaptive Augmentation),使用不同的图扩充策略,并利用图对比损失函数优化节点表示 ...

2021

0.0

... Wang等^[23]提出HeCo(Heterogeneous Graph Neural Network with Co-contrastive Learning),使用网络模式和元路径两种视图,通过元路径创建正样本和负样本,再利用对比损失函数优化模型 ...

... (5)HeCo^[23] ...

0.0

... Wang等^[24]提出HGCML(Hetero-geneous Graph Contrastive Multi-view Learning),增强元路径,生成多个子图作为多视图,并提出一个对比目标,最大化任何元路径诱导视图之间的互信息 ...

... (7)HGCML^[24] ...

0.0

... Yu等^[25]提出MEOW(Heterogeneous Graph Contras-tive Learning Model),利用元路径构建一个粗粒度的视图和一个细粒度的视图,并进行对比 ...

... (6)MEOW^[25] ...

2019

0.0

... 然而这种集成忽略拓扑信息和属性信息之间的干扰问题^[26] ...

2022

0.0

... 一方面,拓扑结构会干扰属性信息的学习,具体表现在: 属性信息通过邻域进行传播,从而达到相连节点具有相似的向量化表示,这种领域传播会使属性信息同化,导致过平滑^[27] ...

2021

0.0

... 另一方面,属性信息会扭曲网络的拓扑信息,具体表现在: 具有相似拓扑信息的一些节点在变换后可能获得不同的表示,导致拓扑信息丢失^[28] ...

2017

0.0

... 1 问题定义定义 1 异质图^[29] 异质图 ...

2017

0.0

... 定义 2元路径^[30] 元路径是异质图中的一条路径: ...

... 考虑到节点的拓扑相似度(图5中I、III部分),HGTA根据不同的元路径,使用训练好的Metapath2vec(Scalable Representa-tion Learning for Heterogeneous Networks)^[30]得到不同元路径下的节点表示,再构建不同元路径下的节点相似度矩阵,并将不同元路径下的节点相似度矩阵求和,得到节点的拓扑相似度矩阵 ...

... (1)Metapath2vec^[30] ...

2021

0.0

... 3)Freebase数据集^[31] ...

2019

0.0

... (2)HERec^[32] ...