李进金,博士,教授,主要研究方向为信息技术、不确定性的数学理论与方法.E-mail:jinjinlimnu@126.com.
作者简介:
冯丹露,硕士研究生,主要研究方向为知识空间理论.E-mail:fengdanlu2020@163.com. 
李招文,博士,教授,主要研究方向为拓扑及其应用、粗糙集、模糊集、信息系统.E-mail:lizhaowen8846@126.com. 
周银凤,博士研究生,主要研究方向为知识空间理论.E-mail:j_jenifer@126.com. 
杨桃丽,硕士研究生,主要研究方向为知识空间理论.E-mail:yangtaoli2019@163.com.
模糊技能映射为构建知识结构提供一个途径,但将基本局部独立模式应用于前级(后级)知识结构中会呈现不可识别问题,因此,在模糊技能映射的前提下,文中主要解决两个问题:技能约简耗时过长、寻找前级(后级)知识结构的充要条件.首先,基于模糊技能背景,构造一对算子,通过算子确定的模糊技能概念格直接获取简单闭包空间,同时获得每个知识状态对应的最小技能熟练程度.然后,提出技能层约简的概念,利用标记技能约简对冗余技能层进行约简,并给出技能层约简算法.同时给出模糊技能映射诱导前级(后级)简单闭包空间的充分必要条件,并提供获取前级问题集和后级问题集的算法.最后,在5个UCI数据集上的对比实验验证文中算法的可行性和有效性,同时获取前级问题集和后级问题集.
LI Jinjin, Ph.D., professor. His research interests include information technology, mathematical theories and methods of uncertainty.
About Author:
FENG Danlu, master student. Her re-search interests include knowledge space theo-ry.
LI Zhaowen, Ph.D., professor. His research interests include topology and its applications, rough set, fuzzy set and information systems.
ZHOU Yinfeng, Ph.D. candidate. Her research interests include knowledge space theory.
YANG Taoli, master student. Her research interests include knowledge space theory.
Fuzzy skill mapping is a pathway to construct knowledge structure. However, applying the basic local independence model to the forward-graded(backward-graded) knowledge structure results in unrecognizable problem. Therefore, under the premise of fuzzy skill mapping, two problems are solved in this paper: excessive time consumption in skill reduction and searching for the necessary and sufficient conditions of the forward-graded(backward-graded) knowledge structure. Firstly, based on the fuzzy skill context, a pair of operators is constructed, and the simple closure space is acquired directly through the fuzzy skill concept lattice determined by the pair of operators. At the same time, the minimum skill proficiency corresponding to each knowledge state is obtained. Secondly, the concept of skill level reduction is proposed. Redundant skill level is reduced by label skill reduction, and the algorithm of skill level reduction is provided. In addition, the necessary and sufficient conditions for inducing forward-graded(backward-graded) simple closure space from fuzzy skill mapping are presented, along with an algorithm for obtaining the forward-graded problem set and the backward-graded problem set. Finally, comparative experiments on five UCI datasets verify the feasibility and effectiveness of the proposed algorithm, and the forward-graded problem set and the backward-graded problem set are obtained.
知识空间理论(Knowledge Space Theory, KST)[1, 2, 3]为开发基于计算机化的知识评估系统提供一个重要的数学心理框架.KST的核心概念是知识状态和知识结构.个体的知识状态K是在理想状态下能够正确回答的特定知识领域Q中的问题构成的集合.理想状态是指学生没有出现粗心致错和幸运蒙对的情况.知识结构(Q, K)是在总体中可以观察到的所有知识状态构成的集合.知识结构至少包含Ø 和Q, 通常直接使用K表示知识结构.
如何构建知识结构是KST的研究热点之一.最初, KST是在纯粹的行为视角下发展起来的.此时, 获取知识结构的方法主要有基于问询专家的Query[4, 5, 6]和Ps-Query[6].这两种方法只考虑专家的判断, 忽视不同个体可能具有不同的潜在认知能力.另外, 这两种方法要求个体对问题的解答要么完全正确要么完全错误, 最终只能给出个体的解答成绩, 无法更深层次地评估个体的认知能力.
FCA[8]是进行知识表示和数据处理的重要工具.FCA通过对象和属性的特定关系, 建立概念格, 将知识可视化[9].Rusch等[10]提出知识背景的概念, 给出由知识背景构建知识结构的方法, 首次建立KST和FCA之间的联系, 为研究KST提供一个新的途径.Spoto等[11]将KST运用到心理学中, 借助FCA的表征形式, 开发一种有效的适应性心理评估工具.李进金等[12]给出在形式背景中由知识基获取知识结构的方法.周银凤等[13]和Zhou等[14]基于形式背景的概念, 建立技能函数和多尺度形式背景的关系, 分别给出基于技能映射和技能函数构建知识结构的不同方法.上述方法借助概念获取的思想, 但只能单纯获得知识结构, 无法直接获得每个知识状态对应的技能掌握情况.另外, 周银凤等[15]借助面向对象(属性)概念, 进一步讨论技能函数下个体的表现水平和能力水平的一一对应条件, 但如需建立唯一的对应关系, 还需改进条件.
通过上述方法获取的知识结构是在理想状态下的所有知识状态构成的集合.在真实测试过程中, 个体在解决某个问题时可能处于一种不理想的状态, 即可能存在个体实际能解决某个问题, 但由于粗心错误导致该问题没有解决, 或存在个体实际没有能力解决某个问题, 但由于个体的幸运猜测而解决该问题, 导致得到的知识状态和知识结构不符合知识之间的逻辑性.因此, 如何获得准确的知识状态和知识结构受到学者的关注[18, 19, 20].为了更准确地评估个体的行为表现层次与真实认知能力的一致性, 将基本局部独立模型[18]引入KST中.
基本局部独立模型是对个体真实存在但未知的知识状态与个体在测评中的反应模式进行区分的概率模型.它将粗心错误和幸运猜测概率视为错误率, 从概率的角度评估一个知识结构对数据的拟合性.目前, 基本局部独立模型已应用于许多不同的环境中[18, 19, 20]但将基本局部独立模型应用于前级(For-ward-Graded)知识结构和后级(Backward-Graded)知识结构中会呈现不可识别的问题.事实上, 若知识结构在某个问题处是前级的, 说明知识结构对这个问题的幸运猜测恰好为0.若知识结构在某个问题处是后级的, 说明知识结构对这个问题的粗心误差恰好为0.因此, 近年来, 前级(后级)知识结构得到学者们的特别关注[21, 22, 23, 24, 25].Spoto等[21]给出技能映射在析取模型和合取模型下诱导的知识结构是前级和后级的充分条件.Spoto等[25]在充分条件的基础上进一步给出必要条件, 并给出技能映射在析取模型和合取模型下诱导的知识结构是后级和前级的充要条件.
上述对知识结构的获取、技能约简和前级(后级)知识结构的研究均是在技能映射下讨论的.对于技能映射, 个体想要解决某个问题必须要完全掌握某些技能, 否则将无法解决这个问题, 但个体学习技能的过程是循序渐进的.由于个体的接受水平和认知能力是有差异的, 在相同的学习环境中, 不同个体能达到的技能熟练程度是不同的.因此, Sun等[26]提出模糊技能映射的概念, 表示解决不同的问题需要的技能熟练程度不同, 并给出模糊技能映射在析取模型、合取模型和能力模型下诱导知识结构, 以及保持知识结构不变, 进行技能约简的方法.模糊技能映射更能体现个体的认知水平差异和个性化能力, 然而模糊技能映射诱导前级知识结构或后级知识结构的条件尚未得到研究.因此, 讨论如何快速获取模糊技能映射下诱导的知识结构, 以及给出快速判断模糊技能映射诱导的知识结构是前级和后级的条件具有重要意义.
受到FCA和KST之间联系的启发, 本文将模糊概念格思想[27, 28, 29, 30, 31, 32, 33]引入基于模糊技能映射的KST中.首先, 引入模糊技能背景的概念, 建立模糊技能映射和模糊技能背景的对应关系.构造一对算子, 生成模糊技能概念格.模糊技能概念格的外延集和内涵集分别对应模糊技能映射在合取模型下诱导的简单闭包空间和每个知识状态对应的最小技能熟练程度.因此, 模糊概念格可用于评估个体的认知水平和指导进一步的学习.然后, 提出技能层约简的概念, 建立模糊技能背景与标记技能背景的特定关系, 对技能层进行约简, 并设计技能层约简的算法.另外, 基于模糊技能背景, 讨论简单闭包空间是前级和后级的充要条件, 并给出相应的算法.最后, 在5个数据集上的数值实验验证本文算法的有效性.
本节回顾模糊形式概念分析与模糊技能映射的一些基本概念和性质.
定义1[34] 三元组(U, A, I)称为一个形式背景, 其中U={x1, x2, …, xn}为对象集, A={a1, a2, …, am} 为属性集, I⊆U× A为U和A之间的二元关系.若(x, a)∈ I, 称对象x具有属性a; 若(x, a)∉I, 称对象x不具有属性a.
定义2[34] 设(U, A, I)为形式背景, 对X⊆U和B⊆A, 分别定义运算:
${{X}^{\downarrow }}=\{a\in A|\forall x\in X, (x, a)\in I\}$,
${{B}^{\uparrow }}=\{x\in U|\forall a\in B, (x, a)\in I\}$.
若
X=B↑ , B=X↓ ,
称(X, B)为一个概念, 其中, X为概念的外延, B为概念的内涵.L(U, A, I)表示(U, A, I)的全体概念.
定义3[34] 设(U, A, I)为形式背景, 对
∀ (X1, B1)∈ L(U, A, I), (X2, B2)∈ L(U, A, I),
定义偏序关系:
(X1, B1)≤ (X2, B2)⇔ X1⊆X2⇔ B2⊆B1.
另外, 在L(U, A, I)上定义
(X1, B1)∨ (X2, B2)=((X1∪ X2)↓ ↑ , B1∩ B2),
(X1, B1)∧ (X2, B2)=(X1∩ X2, (B1⋃B2)↑ ↓ ),
则(L(U, A, I), ∨ , ∧ )为完备格, 称L(U, A, I)为(U, A, I)的概念格.
设U为一个有限非空集, P(U)表示U的所有子集构成的集合, F(U)表示U的所有模糊子集构成的集合.
定义4[35] 设P、Q为两个有序集, 给定映射
φ ∶ P→ Q, ψ ∶ Q→ P.
若映射对(φ , ψ )满足
φ (p)≤ q⇔ p≥ ψ (q),
称(φ , ψ )为P和Q之间的反序伽罗瓦连接.
定义5[36] 设P、Q为两个有序集, 给定映射
φ ∶ P→ Q, ψ ∶ Q→ P.
若映射对(φ , ψ )满足
φ (p)≤ q⇔ p≤ ψ (q),
称(φ , ψ )为P和Q之间的单调伽罗瓦连接.
三元组$(U, A, \tilde{I})$称为一个模糊形式背景, 其中U={x1, x2, …, xn}为对象集, A={a1, a2, …, am}为属性集, $\tilde{I}$∈ F(U× A)为关于U和A上的模糊二元关系.
定义6[28] 设$(U, A, \tilde{I})$为模糊形式背景.对B∈ P(U)和$\tilde{X}$∈ F(A), 定义算子
h∶ P(U)→ F(A), k∶ F(A)→ P(U)
如下:
$h(B)(x)=\underset{a\in B}{\mathop{\wedge }}\, \tilde{I}(x, a), \forall x\in U$,
$k(\tilde{X})=\{a\in A|\forall x\in U, \tilde{X}(x)\le \tilde{I}(x, a)\}$.
映射h和k形成P(U)和F(A)之间的反序伽罗瓦连接.若$B=k(\tilde{X})$且$\tilde{X}=h(B)$, 称$(B, \tilde{X})$为$(U, A, \tilde{I})$的一个经典-模糊概念, B和$\tilde{X}$分别称为经典-模糊概念的外延和内涵.
技能可以反映个体潜在的认知能力, 个体掌握一个技能的过程是循序渐进的.因此, 不同个体在同一时刻对技能的掌握程度可能是不同的.为了更好地评估个体对技能的掌握情况, Sun等[26]提出模糊技能映射的概念, 对不同问题赋予不同的技能熟练程度, 个体掌握技能的程度决定其能否解决相应的问题.
设S为非空技能集,
$\mathcal{F}(S)=\{\widetilde{X} \mid \widetilde{X}: S \rightarrow[0, 1]\}$
为S上所有模糊技能集构成的集族.记$\tilde{X}:S\to [0, 1]$为
$\tilde{X}=\{{{s}^{\tilde{X}(s\text{)}}}|s\in S\}\in \mathcal{F}(S)$,
其中$\tilde{X}(s)$表示技能s隶属于$\tilde{X}$的程度, 即若个体的技能掌握情况为$\tilde{X}$, 则其掌握技能s的程度为$\tilde{X}(s)$.若$\tilde{X}(s)=0$, 则忽略${{s}^{\tilde{X}(s\text{)}}}$.
定义7[26] 三元组(Q, S, τ )称为一个模糊技能映射, 其中Q={q1, q2, …, qn}为非空问题集, S={s1, s2, …, sm}为非空技能集, τ 为从Q到F(S)\Ø 的映射.对q∈ Q, 记τ q=τ (q)表示分配给问题q的所有模糊技能子集.τ q(s)≠ 0表示解决问题q至少需要掌握技能s的程度.若τ q(s)=0, 表示问题q的求解与技能s无关.
定义8[26] 设(Q, S, τ )为模糊技能映射, 对$\tilde{X}\in \mathcal{F}(S)$, 称
$K=\{q\in Q|{{\tau }_{q}}\subseteq \tilde{X}\}$
为(Q, S, τ )在合取模型下通过$\tilde{X}$诱导的知识状态.
合取模型表示个体至少需要达到解决问题q所需的每个技能的最小技能熟练程度.Sun等[26]将合取模型下诱导相同知识状态的所有模糊技能集视为等价的, 进而对F(S)内的模糊技能集进行分类.因此, 模糊技能映射(Q, S, τ )在合取模型下由F(S)内所有模糊技能集的等价类诱导的知识状态构成的集族K是一个知识结构.
引理1[26] 设(Q, S, τ )为模糊技能映射, K为(Q, S, τ )在合取模型下诱导的知识结构, 则K是一个简单闭包空间.
定义9[26] 设(Q, K)为简单闭包空间.若存在一个子集族K'⊆K, 使得对∀ K∈ K, 都存在一个子集族A⊆K', 使得K=∩ A成立, 则称K'为K的交式生成组.
交式生成组是能交成简单闭包空间的极小知识状态构成的集族.若求得极小交式生成组, 则可求得简单闭包空间.
在模糊形式背景中, 对象与属性之间存在模糊二元关系, 而模糊技能映射建立了解决问题与所需掌握技能程度的关系, 故可从模糊形式背景的角度思考与模糊技能映射相关的一些问题.
定义10 三元组$(Q, S, \tilde{I})$称为一个模糊技能背景, 其中, Q为非空问题集, S为非空技能集, $\tilde{I}\in \mathcal{F}(Q\times S)$为关于Q和S上的模糊二元关系.对q∈ Q, s∈ S, 若$\tilde{I}(q, s)\in (0, 1]$, $\tilde{I}(q, s)$表示解决问题q至少需要掌握技能s的程度; 若$\tilde{I}(q, s)=0$, 表示问题q的求解与技能s无关.
显然有
$\tilde{I}(q, s)\text{=}{{\tau }_{q}}(s)$,
即模糊技能背景与模糊技能映射具有一一对应的关系.故本文将模糊技能映射诱导的知识结构统一称为模糊技能背景诱导的知识结构.
技能可以反映个体不可观测的认知能力, 不同个体的潜在认知能力是不同的.KST观察个体对问题的解决情况, 评估个体潜在的认知能力水平, 进而指导个体下一步的学习.因此, 获得个体的知识状态与对应的技能掌握情况对评估个体知识和指导下一步的技能学习具有重要意义.
Sun等[26]给出模糊技能映射在合取模型下诱导简单闭包空间的方法, 但只能获得知识状态, 不能同时获得该知识状态对应的技能掌握情况.而通过概念格, 可将对象集和属性集的某些特定关系通过概念的内涵和外延进行反映.基于该思想, 本文构造一对算子, 通过其对应的概念反映知识状态和技能掌握情况的关系, 直接得到技能评估和学习路径图.考虑到模糊技能映射在合取模型下诱导的知识结构的特点, 基于模糊技能背景构造如下2个算子.
定义11 设$(Q, S, \tilde{I})$为模糊技能背景.对B∈ P(Q)和$\tilde{X}\in \mathcal{F}(S)$, 定义2个算子
f∶ P(Q)→ F(S), g∶ F(S)→ P(Q)
如下:
$f(B)(s)=\underset{q\in B}{\mathop{\vee }}\, \tilde{I}(q, s), \forall s\in S$,
$\text{g}(\tilde{X})=\{q\in Q|\forall s\in S, \tilde{X}(s)\ge \tilde{I}(q, s)\}$.
在合取模型下, 模糊技能集$\tilde{X}$诱导的知识状态为
$K=\{q\in Q|{{\tau }_{q}}\subseteq \tilde{X}\}$.
假设个体的技能掌握情况为$\tilde{X}$, 则个体只能解决包含于$\tilde{X}$的模糊技能集对应的问题.因为
$\tilde{I}(q, s)\text{=}{{\tau }_{q}}(s)$,
因此定义
$\text{g}(\tilde{X})=\{q\in Q|\forall s\in S, \tilde{X}(s)\ge \tilde{I}(q, s)\}$.
反之, 假设个体解决的问题集为B, 则个体至少已达到解决B中所有问题所需的最小技能熟练程度.因此定义
$f(B)(s)=\underset{q\in B}{\mathop{\vee }}\, \tilde{I}(q, s), \forall s\in S$.
另外, F(S)上的运算定义如下[37]:
${{\tilde{X}}_{1}}={{\tilde{X}}_{2}}\Leftrightarrow {{\tilde{X}}_{1}}(s)={{\tilde{X}}_{2}}(s), \forall s\in S$;
${{\tilde{X}}_{1}}\subseteq {{\tilde{X}}_{2}}\Leftrightarrow {{\tilde{X}}_{1}}(s)\le {{\tilde{X}}_{2}}(s), \forall s\in S$;
$({{\tilde{X}}_{1}}\vee {{\tilde{X}}_{2}})(s)\Leftrightarrow {{\tilde{X}}_{1}}(s)\vee {{\tilde{X}}_{2}}(s), \forall s\in S$;
$({{\tilde{X}}_{1}}\wedge {{\tilde{X}}_{2}})(s)\Leftrightarrow {{\tilde{X}}_{1}}(s)\wedge {{\tilde{X}}_{2}}(s), \forall s\in S$.
根据定义的映射$f\circ g$, 可得如下性质1.
性质1 设$(Q, S, \tilde{I})$为模糊技能背景.对B∈ P(Q), B1∈ P(Q), B2∈ P(Q), Bi∈ P(Q), $\tilde{X}\in \mathcal{F}(S)$, ${{\tilde{X}}_{1}}\in \mathcal{F}(S)$, ${{\tilde{X}}_{2}}\in \mathcal{F}(S)$, ${{\tilde{X}}_{i}}\in \mathcal{F}(S)$, i∈ J(J为一个指标集), 有如下性质成立:
1)${{\tilde{X}}_{1}}\subseteq {{\tilde{X}}_{2}}\Rightarrow g({{\tilde{X}}_{1}})\subseteq g({{\tilde{X}}_{2}})$, ${{B}_{1}}\subseteq {{B}_{2}}\Rightarrow f({{B}_{1}})\subseteq f({{B}_{2}})$;
2)$f\circ \text{g}(\tilde{X})\subseteq \tilde{X}$, B1⊆B2⇒ f(B1)⊆f(B2);
3)$f(B)\subseteq \tilde{X}\Leftrightarrow B\subseteq g(\tilde{X})$;
4)$f\circ \text{g}\circ f(B)=f(B)$, $\text{g}\circ f\circ \text{g}(\tilde{X})=\text{g}(\tilde{X})$;
5)$\underset{i\in J}{\mathop{\bigcap }}\, g({{\tilde{X}}_{i}})\text{=}g(\underset{i\in J}{\mathop{\wedge }}\, {{\tilde{X}}_{i}})$, $\underset{i\in J}{\mathop{\vee }}\, f({{B}_{i}})=f(\underset{i\in J}{\mathop{\bigcup }}\, {{B}_{i}})$.
证明 先证1).对$\forall q\in g({{\tilde{X}}_{1}})$, 满足对∀ s∈ S, 有
$\tilde{X}(\text{s})\ge \tilde{I}\left( q, s \right)$.
又因为${{\tilde{X}}_{1}}\subseteq {{\tilde{X}}_{2}}$, 故对∀ s∈ S, 有
${{\tilde{X}}_{1}}\left( s \right)\le {{\tilde{X}}_{2}}\left( s \right)$.
因此, 对∀ s∈ S, 有
${{\tilde{X}}_{2}}(\text{s})\ge \tilde{I}\left( q, s \right)$,
即$q\in g({{\tilde{X}}_{2}})$.从而
$g({{\tilde{X}}_{1}})\subseteq g({{\tilde{X}}_{2}})$.
同理可证
B1⊆B2⇒ f(B1)⊆f(B2).
再证2).假设$q\in g(\tilde{X})$, 则对∀ s∈ S, 有
$\tilde{X}(\text{s})\ge \tilde{I}\left( q, s \right)$,
故对∀ s∈ S, 有
$f(g(\tilde{X}))(s)\text{=}\underset{q\in g(\tilde{X})}{\mathop{\vee }}\, \tilde{I}(q, s)\le \tilde{X}(s)$,
从而
$f\circ \text{g}(\tilde{X})\subseteq \tilde{X}$.
此外, 因为对∀ q∈ B, s∈ S, 有
$\tilde{I}(q, s)\le \underset{q\in B}{\mathop{\vee }}\, \tilde{I}(q, s)=f(B)(s)$,
故$q\in g\circ f(B)$, 从而
$B\subseteq g\circ f(B)$.
再证3).假设$f(B)\subseteq \tilde{X}$, 由1)可得
$\text{g}\circ f(B)\subseteq g(\tilde{X})$,
又因为
$B\subseteq g\circ f(B)$,
故$B\subseteq g(\tilde{X})$.反之, 若$B\subseteq g(\tilde{X})$, 由1)可得
$f(B)\subseteq f\circ g(\tilde{X})$,
又因为
$f\circ \text{g}(\tilde{X})\subseteq \tilde{X}$,
故$f(B)\subseteq \tilde{X}$.从而
$f(B)\subseteq \tilde{X}\Leftrightarrow B\subseteq g(\tilde{X})$.
再证4).由2)有
$B\subseteq \text{g}\circ f(B)$,
又由1)可得
$f(B)\subseteq f\circ \text{g}\circ f(B)$.
因为
$f\circ \text{g}(\tilde{X})\subseteq \tilde{X}$,
故
$f\circ \text{g}\circ f(B)\subseteq f(B)$.
从而
$f\circ \text{g}\circ f(B)=f(B)$.
同理可证
$\text{g}\circ f\circ \text{g}(\tilde{X})=\text{g}(\tilde{X})$.
最后证5).对
$\forall q\in \underset{i\in J}{\mathop{\bigcap }}\, g({{\tilde{X}}_{i}})$,
满足对∀ i∈ J, s∈ S, 有
${{\tilde{X}}_{i}}(s)\ge \tilde{I}(q, s)$,
于是对∀ s∈ S, 有
$\underset{i\in J}{\mathop{\wedge }}\, {{\tilde{X}}_{i}}(s)\ge \tilde{I}(q, s)$
成立, 故
$q\in g(\underset{i\in J}{\mathop{\wedge }}\, {{\tilde{X}}_{i}})=\{q\in Q|\forall s\in S, \underset{i\in J}{\mathop{\wedge }}\, {{\tilde{X}}_{i}}(s)\ge \tilde{I}(q, s)\}$,
从而
$\underset{i\in J}{\mathop{\bigcap }}\, g({{\tilde{X}}_{i}})\subseteq g(\underset{i\in J}{\mathop{\wedge }}\, {{\tilde{X}}_{i}})$.
反之, 对
$\forall q\in g(\underset{i\in J}{\mathop{\wedge }}\, {{\tilde{X}}_{i}})$,
满足对∀ s∈ S, 有
$\underset{i\in J}{\mathop{\wedge }}\, {{\tilde{X}}_{i}}(s)\ge \tilde{I}(q, s)$,
于是对∀ i∈ J, s∈ S, 有
${{\tilde{X}}_{i}}(s)\ge \tilde{I}(q, s)$
成立, 故
$q\in \underset{i\in J}{\mathop{\bigcap }}\, g({{\tilde{X}}_{i}})$,
从而
$\underset{i\in J}{\mathop{\bigcap }}\, g({{\tilde{X}}_{i}})\supseteq g(\underset{i\in J}{\mathop{\wedge }}\, {{\tilde{X}}_{i}})$.
综上可得
$\underset{i\in J}{\mathop{\bigcap }}\, g({{\tilde{X}}_{i}})=g(\underset{i\in J}{\mathop{\wedge }}\, {{\tilde{X}}_{i}})$.
下证
$\underset{i\in J}{\mathop{\vee }}\, f({{B}_{i}})=f(\underset{i\in J}{\mathop{\bigcup }}\, {{B}_{i}})$.
由
$f(\underset{i\in J}{\mathop{\bigcup }}\, {{B}_{i}})={{\vee }_{a\in \underset{i\in J}{\mathop{\bigcup }}\, {{B}_{i}}}}\tilde{I}(q, s)=\underset{i\in J}{\mathop{\vee }}\, (\underset{a\in {{B}_{i}}}{\mathop{\vee }}\, \tilde{I}(q, s))=\underset{i\in J}{\mathop{\vee }}\, f({{B}_{i}})$
可证. 证毕
根据定义5, 性质1中3)说明映射对(f, g)形成(P(Q), ⊆)和(F(S), ⊆)之间的单调伽罗瓦连接.根据文献[38], 假设(f, g)形成集合X和Y之间的单调伽罗瓦连接.对映射对(h, k), 若对∀ A∈ 2X, B∈ 2Y, 有
h(A)=Y\f(A), k(B)=g(Y\B)
成立, 则(h, k)是一个反序伽罗瓦连接, 即通过该过程可建立反序伽罗瓦连接和单调伽罗瓦连接的双射.显然, 本文定义的映射$f\circ g$与定义6定义的映射$h\circ k$不符合这种双射关系.
若序对$(B, \tilde{X})$满足$B=g(\tilde{X})$且$\tilde{X}=f(B)$, 则称$(B, \tilde{X})$为$(Q, S, \tilde{I})$的一个模糊技能概念, B和$\tilde{X}$分别称为模糊技能概念的外延和内涵.将$(Q, S, \tilde{I})$的所有的模糊技能概念构成的集合记为$L(Q, S, \tilde{I})$.对于∀ B∈ P(Q), $\tilde{X}\in \mathcal{F}(S)$ , 由性质1中4), 易得$(g\circ f(B), f(B))$和$(g(\tilde{X}), f\circ g(\tilde{X}))$都是模糊技能概念.因此, 对∀ q∈ Q, $(g\circ f(q), f(q))$都是一个模糊技能概念.对
$\forall ({{B}_{1}}, {{\tilde{X}}_{1}})\in L(Q, S, \tilde{I}), ({{B}_{2}}, {{\tilde{X}}_{2}})\in L(Q, S, \tilde{I})$,
定义偏序关系:
$({{B}_{1}}, {{\tilde{X}}_{1}})\le ({{B}_{2}}, {{\tilde{X}}_{2}})\Leftrightarrow {{B}_{1}}\subseteq {{B}_{2}}({{\tilde{X}}_{1}}\subseteq {{\tilde{X}}_{2}})$.
定义12 设$(Q, S, \tilde{I})$为模糊技能背景, 对$\forall ({{B}_{1}}, {{\tilde{X}}_{1}})\in L(Q, S, \tilde{I}), ({{B}_{2}}, {{\tilde{X}}_{2}})\in L(Q, S, \tilde{I})$, 定义上确界和下确界如下:
$({{B}_{1}}, {{\tilde{X}}_{1}})\vee ({{B}_{2}}, {{\tilde{X}}_{2}})=(g\circ f({{B}_{1}}\bigcup {{B}_{2}}), {{\tilde{X}}_{1}}\vee {{\tilde{X}}_{2}}))=(g({{\tilde{X}}_{1}}\vee {{\tilde{X}}_{2}}), {{\tilde{X}}_{1}}\vee {{\tilde{X}}_{2}})$,
$({{B}_{1}}, {{\tilde{X}}_{1}})\wedge ({{B}_{2}}, {{\tilde{X}}_{2}})=({{B}_{1}}\bigcap {{B}_{2}}, f\circ g({{\tilde{X}}_{1}}\wedge {{\tilde{X}}_{2}}))=({{B}_{1}}\bigcap {{B}_{2}}, f({{B}_{1}}\bigcap {{B}_{2}}))$..
显然$(L(Q, S, \tilde{I}), \vee , \wedge )$是一个完备格, 称$L(Q, S, \tilde{I})$为$(Q, S, \tilde{I})$的模糊技能概念格.另外, 将$L(Q, S, \tilde{I})$的所有外延构成的集族记为${{L}_{Q}}(Q, S, \tilde{I})$.
推论1 设$(Q, S, \tilde{I})$为模糊技能背景, 对
$\forall (B, \tilde{X})\in L(Q, S, \tilde{I})$,
有
$(B, \tilde{X})=\underset{q\in B}{\mathop{\vee }}\, (g\circ f(q), f(q))$.
证明 由性质1中4)、5), 有
$\begin{matrix} & \underset{q\in B}{\mathop{\vee }}\, (g\circ f(q), f(q)) \\ & =(g\circ f(\underset{q\in B}{\mathop{\bigcup }}\, g\circ f(q)), \underset{q\in B}{\mathop{\vee }}\, f(q)) \\ & =(g(\underset{q\in B}{\mathop{\vee }}\, (f\circ g\circ f(q))), \underset{q\in B}{\mathop{\vee }}\, f(q)) \\ & =(g(\underset{q\in B}{\mathop{\vee }}\, f(q)), \underset{q\in B}{\mathop{\vee }}\, f(q)) \\ & =(g(f(B)), f(B))=(B, \tilde{X}). \\ \end{matrix}$ 证毕.
推论1表明, $L(Q, S, \tilde{I})$中的任意一个模糊技能概念都可以用集合
$\{(g\circ f(q), f(q))|q\in Q\}$
中的某些模糊技能概念的上确界表示.
推论2 设$(Q, S, \tilde{I})$为模糊技能背景.对${{\tilde{X}}_{i}}\in \mathcal{F}(S)$, i∈ J(J为一个指标集), 有
$\underset{i\in J}{\mathop{\bigcup }}\, g({{\tilde{X}}_{i}})\subseteq g(\underset{i\in J}{\mathop{\vee }}\, {{\tilde{X}}_{i}})$.
证明 对
$\forall q\in \underset{i\in J}{\mathop{\bigcup }}\, g({{\tilde{X}}_{i}})$,
满足存在i, 使得对∀ s∈ S, 有
${{\tilde{X}}_{i}}(s)\ge \tilde{I}(q, s)$
成立.因此, 对∀ s∈ S, 有
$\underset{i\in J}{\mathop{\vee }}\, {{\tilde{X}}_{i}}(s)\ge \tilde{I}(q, s)$,
故
$q\in g(\underset{i\in J}{\mathop{\vee }}\, {{\tilde{X}}_{i}})$.
从而
$\underset{i\in J}{\mathop{\bigcup }}\, g({{\tilde{X}}_{i}})\subseteq g(\underset{i\in J}{\mathop{\vee }}\, {{\tilde{X}}_{i}})$.证毕
定理1 设$(Q, S, \tilde{I})$为模糊技能背景.若对$\forall {{\tilde{X}}_{i}}\in \mathcal{F}(S)$, i∈ J(J为一个指标集), 满足存在B⊆Q, 使得对∀ s∈ S, 有
${{\tilde{X}}_{i}}(s)=\underset{q\in B}{\mathop{\vee }}\, \tilde{I}(q, s)$
成立, 则
$\underset{i\in J}{\mathop{\bigcup }}\, g({{\tilde{X}}_{i}})\text{=}g(\underset{i\in J}{\mathop{\vee }}\, {{\tilde{X}}_{i}})$
当且仅当
$\underset{i\in J}{\mathop{\bigcup }}\, g({{\tilde{X}}_{i}})\in {{L}_{Q}}(Q, S, \tilde{I})$.
证明 先证充分性.转证
$(\underset{i\in J}{\mathop{\bigcup }}\, g({{\tilde{X}}_{i}}), f(\underset{i\in J}{\mathop{\bigcup }}\, g({{\tilde{X}}_{i}}))\in L(Q, S, \tilde{I})$.
显然只需再证
$\underset{i\in J}{\mathop{\bigcup }}\, g({{\tilde{X}}_{i}})\text{=g}\circ f(\underset{i\in J}{\mathop{\bigcup }}\, g({{\tilde{X}}_{i}}))$.
由性质1中4)、5), 有
$\text{g}\circ f(\underset{i\in J}{\mathop{\bigcup }}\, g({{\tilde{X}}_{i}}))\text{=g}\circ f\circ \text{g(}\underset{i\in J}{\mathop{\vee }}\, {{\tilde{X}}_{i}}\text{)=g(}\underset{i\in J}{\mathop{\vee }}\, {{\tilde{X}}_{i}}\text{)}$,
又因为
$\underset{i\in J}{\mathop{\bigcup }}\, g({{\tilde{X}}_{i}})=\text{=}g(\underset{i\in J}{\mathop{\vee }}\, {{\tilde{X}}_{i}})$,
所以
$\text{g}\circ f(\underset{i\in J}{\mathop{\bigcup }}\, g({{\tilde{X}}_{i}}))=\underset{i\in J}{\mathop{\bigcup }}\, g({{\tilde{X}}_{i}})$.
从而, 有
$\underset{i\in J}{\mathop{\bigcup }}\, g({{\tilde{X}}_{i}})\in {{L}_{Q}}(Q, S, \tilde{I})$.
再证必要性.由推论2, 只需再证
$g(\underset{i\in J}{\mathop{\vee }}\, {{\tilde{X}}_{i}})\subseteq \underset{i\in J}{\mathop{\bigcup }}\, g({{\tilde{X}}_{i}})$.
对
$\forall q\in g(\underset{i\in J}{\mathop{\vee }}\, {{\tilde{X}}_{i}})$,
满足对∀ s∈ S, 有
$\underset{i\in J}{\mathop{\vee }}\, {{\tilde{X}}_{i}}(s)\ge \tilde{I}(q, s)$
成立.若对$\forall {{\tilde{X}}_{i}}\in \mathcal{F}(S)$, i∈ J, 满足存在B⊆Q, 使得对∀ s∈ S, 有
${{\tilde{X}}_{i}}(s)=\underset{q\in B}{\mathop{\vee }}\, \tilde{I}(q, s)$
成立, 又由性质1中4), 有
$f\circ \text{g}\circ f(B)=f(B)$,
故
$f\circ \text{g}({{\tilde{X}}_{i}})\text{=}{{\tilde{X}}_{i}}$.
所以对∀ s∈ S, 有
$\underset{i\in J}{\mathop{\vee }}\, f(g({{\tilde{X}}_{i}}))(s)\ge \tilde{I}(q, s)$.
另外, 由性质1中5), 对∀ s∈ S, 显然有
$f(\underset{i\in J}{\mathop{\bigcup }}\, g({{\tilde{X}}_{i}}))(s)=\underset{i\in J}{\mathop{\vee }}\, f(g({{\tilde{X}}_{i}}))(s)\ge \tilde{I}(q, s)$,
故
$q\in g(f(\underset{i\in J}{\mathop{\bigcup }}\, g({{\tilde{X}}_{i}})))$.
又因为
$\underset{i\in J}{\mathop{\bigcup }}\, g({{\tilde{X}}_{i}})\in {{L}_{Q}}(Q, S, \tilde{I})$,
所以
$\underset{i\in J}{\mathop{\bigcup }}\, g({{\tilde{X}}_{i}})\text{=}g(f(\underset{i\in J}{\mathop{\bigcup }}\, g({{\tilde{X}}_{i}})))$,
即
$q\in \underset{i\in J}{\mathop{\bigcup }}\, g({{\tilde{X}}_{i}})$,
故
$g(\underset{i\in J}{\mathop{\vee }}\, {{\tilde{X}}_{i}})\subseteq \underset{i\in J}{\mathop{\bigcup }}\, g({{\tilde{X}}_{i}})$.
从而
$\underset{i\in J}{\mathop{\bigcup }}\, g({{\tilde{X}}_{i}})\text{=}g(\underset{i\in J}{\mathop{\vee }}\, {{\tilde{X}}_{i}})$.证毕
定理2 设(Q, S, τ )为模糊技能映射, $(Q, S, \tilde{I})$为(Q, S, τ )对应的模糊技能背景.K为(Q, S, τ )在合取模型下诱导的简单闭包空间.对
$\forall (B, \tilde{X})\in L(Q, S, \tilde{I})$,
内涵$\tilde{X}$在合取模型下诱导的知识状态为外延B, 且所有外延B构成的集族等于K, 即
$\mathcal{K}={{L}_{Q}}(Q, S, \tilde{I})$.
证明 对∀ B∈ K, 存在$\tilde{X}\in \mathcal{F}(S)$, 使得对∀ q∈ B, s∈ S, 有
$\tilde{I}(q, s)={{\tau }_{q}}(s)\le \tilde{X}(s)$
成立, 故$B\in {{L}_{Q}}(Q, S, \tilde{I})$, 从而
$\mathcal{K}\subseteq {{L}_{Q}}(Q, S, \tilde{I})$.
对$\forall B\in {{L}_{Q}}(Q, S, \tilde{I})$, 存在$\tilde{X}\in \mathcal{F}(S)$, 使得对∀ q∈ B, s∈ S, 有
$\tilde{I}(q, s)\le \tilde{X}(s)$
成立.由
$\tilde{I}(q, s)={{\tau }_{q}}(s)$,
可得对∀ q∈ B, s∈ S, 有
${{\tau }_{q}}(s)\le \tilde{X}(s)$,
故模糊技能概念的外延B为模糊技能映射在合取模型下通过内涵$\tilde{X}$诱导的知识状态, 即B∈ K, 从而
${{L}_{Q}}(Q, \tilde{S}, \tilde{I})\subseteq \mathcal{K}$.
综上, 有
$\mathcal{K}={{L}_{Q}}(Q, S, \tilde{I})$.证毕
下面将${{L}_{Q}}(Q, S, \tilde{I})$称为模糊技能背景在合取模型下诱导的简单闭包空间.
注意到F(S)中的模糊集是无限的, 但在KST中, 模糊技能映射是给定的, 故在本文中, 基于模糊技能映射限制F(S).对s∈ S, 记
$W(s)=\{x\text{ }\!\!|\!\!\text{ }\forall q\in Q, x={{\tau }_{q}}(s)=\tilde{I}(q, s)\}$,
对
$\forall \tilde{X}=\{{{s}^{\tilde{X}(s\text{)}}}|s\in S\}\in \mathcal{F}(S)$,
满足对∀ s∈ S, 有$\tilde{X}(s)\in W(s)$成立, 即若给定模糊技能映射(Q, S, τ ), 模糊技能背景下的F(S)也随之确定.另外, 若$\tilde{X}(s)=0$, 忽略${{s}^{\tilde{X}(s\text{)}}}$.
为了简便表示模糊技能概念格, 在模糊技能概念格中统一使用数字序列表示问题集, 使用模糊技能序列表示模糊技能集.例如:使用1234表示{q1, q2, q3, q4}, 使用${{s}_{1}}^{x}{{s}_{2}}^{y}{{s}_{3}}^{z}{{s}_{4}}^{k}$表示$\text{ }\!\!\{\!\!\text{ }{{s}_{1}}^{x}, {{s}_{2}}^{y}, {{s}_{3}}^{z}, {{s}_{4}}^{k}\text{ }\!\!\}\!\!\text{ }$.
例1 设
Q={q1, q2, q3, q4, q5}, S={s1, s2, s3, s4, s5},
给定模糊技能映射(Q, S, τ ), 其中
${{\tau }_{{{q}_{1}}}}=\{{{s}_{1}}^{0.9}, {{s}_{3}}^{0.7}, {{s}_{4}}^{0.6}, {{s}_{5}}^{0.\text{8}}\}$,
${{\tau }_{{{q}_{2}}}}=\{{{s}_{3}}^{0.8}, {{s}_{\text{5}}}^{0.\text{8}}\}$,
${{\tau }_{{{q}_{3}}}}=\{{{s}_{1}}^{0.8}, {{s}_{2}}^{0.9}, {{s}_{4}}^{0.7}, {{s}_{\text{5}}}^{0.6}\}$,
${{\tau }_{{{q}_{4}}}}=\text{ }\!\!\{\!\!\text{ }{{s}_{1}}^{0.5}\text{ }\!\!\}\!\!\text{ }$,
${{\tau }_{{{q}_{5}}}}=\text{ }\!\!\{\!\!\text{ }{{s}_{1}}^{0.5}, {{s}_{3}}^{0.5}\}$.
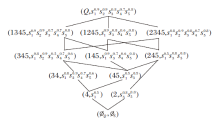
由$\tilde{I}(q, s)\text{=}{{\tau }_{q}}(s)$, 可得模糊技能映射(Q, S, τ )对应的模糊技能背景$(Q, S, \tilde{I})$, 如表1所示, $(Q, S, \tilde{I})$对应的模糊技能概念格$L(Q, S, \tilde{I})$如图1所示.
| 表1 模糊技能背景$(Q, S, \tilde{I})$ Table 1 Fuzzy skill context$(Q, S, \tilde{I})$ |
由定理2, 模糊技能背景$(Q, S, \tilde{I})$在合取模型下诱导的简单闭包空间为
$\begin{aligned}\mathscr{K}= & L_Q(Q, S, \tilde{I})= \\& \left\{\emptyset,\left\{q_2\right\},\left\{q_4\right\},\left\{q_3, q_4\right\},\left\{q_4, q_5\right\},\left\{q_1, q_4, q_5\right\},\right. \\& \left\{q_2, q_4, q_5\right\},\left\{q_3, q_4, q_5\right\},\left\{q_1, q_2, q_4, q_5\right\}, \\& \left.\left\{q_1, q_3, q_4, q_5\right\},\left\{q_2, q_3, q_4, q_5\right\}, Q\right\} .\end{aligned}$
通过模糊技能概念格能直观评估个体的技能掌握情况并指导下一步学习.例如, 对于图1, 若已知个体能解决的问题集为{q3, q4}, 则该个体分别掌握技能s1, s2, s4, s5的程度至少为0.8, 0.9, 0.7, 0.6, 且个体掌握技能s3的程度小于0.5.因为若个体掌握技能s3的程度大于等于0.5, 则个体能解决的问题集应为{q3, q4, q5}.此时, 下一步应该指导个体学习技能s3.若个体在学习之后通过测试能解决问题q5, 则此时个体掌握技能s3的程度要大于等于0.5.因此, 在模糊技能概念格中, 从(Ø Q, Ø S)到$(Q, s_{1}^{0.9}s_{2}^{0.9}s_{3}^{0.8}s_{4}^{0.7}s_{5}^{0.8})$的任意一条路径都是一条学习技能的路径.
接下来, 基于推论1给出获取模糊技能背景$(Q, S, \tilde{I})$的所有模糊技能概念的算法1.
算法1 获取模糊技能背景$(Q, S, \tilde{I})$的模糊技能概念集T
输入 模糊技能背景$(Q, S, \tilde{I})$
输出 模糊技能概念集T
step 1 令P=Ø , T=Ø .
step 2 对∀ q∈ Q, 计算f(q).
step 3 计算Q的幂集B=2Q.对∀ B'∈ B, 计算$X=\underset{q\in B'}{\mathop{\vee }}\, f(q)$.若X∉P, 则P← P∪ X.
step 4 对∀ X'∈ P, 计算g(X'), 获得$T\leftarrow T\bigcup (g({X}'), {X}')$.
step 5 输出模糊技能概念集T.
在算法1中, step 2、step 3的时间复杂度最大为$O(|{{2}^{Q}}|)$, step 4的时间复杂度最大为$O(|P||S|)$, 故算法1的时间复杂度最大为
$O(|{{2}^{Q}}|+(|P||S|))$.
在KST中, 技能约简是在保持知识结构不变的前提下, 删除冗余技能.技能约简能更简洁地表示问题与技能之间的关系, 从而有效提高生成知识结构的效率.Sun等[26]给出模糊技能映射下的技能约简的方法, 但在模糊技能映射的背景下, 不一定需要删除整个技能才能保持生成的知识结构不变.因此, 本文提出技能层约简的概念, 拓展KST的技能约简概念, 减少生成简单必包空间的时间.
定义13 设$(Q, S, \tilde{I})$为模糊技能背景.对s∈ S, 称
$W(s)=\{x|\forall q\in Q, x\text{=}\tilde{I}(q, s)\}$
为技能s在Q中的技能层集.x∈ W(s)称为技能s的一个技能层.
W(s)是解决Q中的问题需要掌握技能s的所有可能程度构成的集合.注意, 对∀ s∈ S, 下文使用∧ W(s)和∨ W(s)分别表示技能s在Q中的最小技能层和最大技能层.另外, 本文讨论的模糊技能背景$(Q, S, \tilde{I})$满足:对∀ s∈ S, 有$|W(s)|\ge 2$成立.
定义14 设$(Q, S, \tilde{I})$为模糊技能背景.对s∈ S,
$W(s)=\{x|\forall q\in Q, x\text{=}\tilde{I}(q, s)\}$.
若存在$(Q, {S}', {\tilde{I}}')$满足
$L(Q, {S}', {\tilde{I}}')\cong L(Q, S, \tilde{I})$,
其中S'⊆S, ${\tilde{I}}'\in \mathcal{F}(Q\times {S}')$ , 且${\tilde{I}}'$满足如下条件:
1)存在q∈ Q, s∈ S', 有
${\tilde{I}}'(q, s)\text{=}{{x}_{1}}\in W(s)< \tilde{I}(q, s)$
成立,
2)∀ q∈ Q, s∈ S', 有
${\tilde{I}}'(q, s)\text{=}{{x}_{1}}\in W(s)\le \tilde{I}(q, s)$
成立,
则称$(Q, {S}', {\tilde{I}}')$为$(Q, S, \tilde{I})$的一个极小技能层模糊技能背景.
定义15 设$(Q, S, \tilde{I})$为模糊技能背景, $(Q, {S}', {\tilde{I}}')$为$(Q, S, \tilde{I})$的一个极小技能层模糊技能背景.对s∈ S,
$W(s)=\{x|\forall q\in Q, x\text{=}\tilde{I}(q, s)\}$.
若对q∈ Q, s∈ S', 有
${\tilde{I}}'(q, s)\text{=}{{x}_{1}}\in W(s)< \tilde{I}(q, s)\text{=}x$
成立, 则称x为技能s的可约简技能层.
显然, 对于任意技能s∈ S的最小技能层∧ W(s), 已经不存在小于它的技能层, 故任意技能s∈ S的最小技能层∧ W(s)都不是可约简技能层.另外, 对每个技能s∈ S, 若至少存在一个x∈ W(s)且x≠ ∧ W(s), 使得x不是技能s的可约简技能层, 则有S'=S.
下面对极小技能层模糊技能背景赋予语义解析.定义14中条件1)说明, 若$(Q, {S}', {\tilde{I}}')$为$(Q, S, \tilde{I})$的一个极小技能层模糊技能背景, 则技能层模糊技能背景$(Q, S, \tilde{I})$中至少存在一个技能s∈ S的某个技能层x为可约简技能层.若技能s的技能层x可以被约简且s∈ S', 则在极小技能层模糊技能背景$(Q, {S}', {\tilde{I}}')$中s对应的技能层x会全部下降为W(s)中其它小于x的某个技能层, 这样问题与技能之间的模糊关系会更加简单化.条件2)表示对于技能s的技能层x不能被约简的情况, 则s对应的技能层x在极小技能层模糊技能背景$(Q, {S}', {\tilde{I}}')$中保持不变.另外, 若$\tilde{I}(q, s)=0$, 则${\tilde{I}}'(q, s)=0$成立, 说明若问题q的求解与技能s无关, 则对于技能层约简后得到的极小技能层模糊技能背景, 问题q的求解也与技能s无关.本文将获得模糊技能背景$(Q, S, \tilde{I})$的极小技能层模糊技能背景$(Q, {S}', {\tilde{I}}')$的过程称为技能层约简.
定义16 设$(Q, S, \tilde{I})$为模糊技能背景.若存在S'⊂S, 使得$(Q, {S}', {\tilde{I}}')$为$(Q, S, \tilde{I})$的一个极小技能层模糊技能背景, 则∀ s∈ S\{S'}称为一个可约简技能.
技能约简是对整个技能进行约简, 而技能层约简是通过降低某些技能的技能层进行约简.根据定义14和定义16, 技能层约简包含对整个技能进行约简的情形, 另外在不能删除整个技能的情形下还能约简某些技能层, 进而简化问题与技能的模糊关系.因此, 技能层约简是技能约简的拓展, 并且相对技能约简而言, 技能层约简可更有效降低获取简单闭包空间的时间, 进行技能层约简具有重要意义.下面讨论获取极小技能层模糊技能背景$(Q, {S}', {\tilde{I}}')$的技能层约简方法.
技能层约简的前提要保持${{L}_{Q}}(Q, S, \tilde{I})$不变, 但在模糊技能背景中直接考虑约简的问题是较复杂的.因此, 建立模糊技能背景与二分形式背景的特定关系, 借助二分形式背景考虑技能层约简问题.
定义17 设$(Q, S, \tilde{I})$为模糊技能背景.对s∈ S,
$W(s)=\{x|\forall q\in Q, x\text{=}\tilde{I}(q, s)\}$,
则称(Q, SX, I)为$(Q, S, \tilde{I})$对应的标记技能背景, 其中
${{S}^{X}}=\{{{s}^{x}}|\forall s\in s, X\in W(s)\}$
称为标记技能集, ∀ sx∈ SX称为一个标记技能, I⊆Q× SX定义为:对∀ q∈ Q, s∈ S, x∈ W(s), 有
$(q, {{s}^{x}})\in I\Leftrightarrow I(q, {{s}^{x}})\text{=}1\Leftrightarrow \tilde{I}(q, s)\le x$.
定义17建立模糊技能背景和标记技能背景的转换关系, 显然有如下推论.
推论3 设$(Q, S, \tilde{I})$为模糊技能背景, (Q, SX, I)为$(Q, S, \tilde{I})$对应的标记技能背景.对s∈ S,
$W(s)=\{x|\forall q\in Q, x\text{=}\tilde{I}(q, s)\}$.
对q∈ Q, s∈ S, 若对∀ x∈ W(s), 有(q, sx)∈ I成立, 则
$\tilde{I}(q, s)\text{=}\wedge W(s)$.
对于标记技能背景(Q, SX, I), 将每个标记技能sx∈ SX视为形式背景的一个属性, 通过定义2的映射$^{\uparrow }{{\circ }^{\downarrow }}$确定的概念格称为标记技能概念格, 记为L(Q, SX, I).另外, 记LQ(Q, SX, I)表示L(Q, SX, I)的所有外延构成的集族.
定理3 设$(Q, S, \tilde{I})$为模糊技能背景, (Q, SX, I)为$(Q, S, \tilde{I})$对应的标记技能背景.对s∈ S,
$W(s)=\{x|\forall q\in Q, x\text{=}\tilde{I}(q, s)\}$,
则(Q, SX, I)和$(Q, S, \tilde{I})$分别由映射$^{\uparrow }{{\circ }^{\downarrow }}$和$f\circ g$在2Q上得到的概念格同构, 即
${{L}_{Q}}(Q, {{S}^{X}}, I)={{L}_{Q}}(Q, S, \tilde{I})$.
证明 先证
${{L}_{Q}}(Q, {{S}^{X}}, I)\subseteq {{L}_{Q}}(Q, S, \tilde{I})$.
设存在B⊆Q, 使得B∈ LQ(Q, SX, I)成立, 则存在T⊆SX, 使B=T↑ 成立.对∀ s∈ S,
$T(s)=\{x\in W(s)|{{s}^{x}}\in T\}$.
另外, 对∀ s∈ S, 令
$\tilde{X}(s)=\wedge T(s)$,
下证
$B=g(\tilde{X})$.
设q∈ B=T↑ , 则对∀ sx∈ T, 有(q, sx)∈ I, 等价于对∀ s∈ S和x∈ T(s), 有
$\tilde{I}(q, s)\le x$,
等价于对∀ s∈ S, 有
$\tilde{I}(q, s)\le \wedge T(s)=\tilde{X}(s)$,
故
$q\in g(\tilde{X})\Leftrightarrow q\in {{T}^{\uparrow }}$,
从而
$B=g(\tilde{X})$.
再证
${{L}_{Q}}(Q, S, \tilde{I})\subseteq {{L}_{Q}}(Q, {{S}^{X}}, I)$.
设存在B⊆Q, 使得$B\in {{L}_{Q}}(Q, S, \tilde{I})$成立, 则存在$\tilde{X}\in \mathcal{F}(S)$, 使$B=g(\tilde{X})$成立.对∀ s∈ S, 存在T(s)⊆W(s), 满足
$\tilde{X}(s)=\wedge T(s)$.
令
$T=\underset{s\in S}{\mathop{\bigcup }}\, \{{{s}^{x}}|x\in T(s)\}$,
下证B= T↑ .对
$\forall q\in B=g(\tilde{X})$,
满足对∀ s∈ S, 有
$\tilde{I}(q, s)\le \tilde{X}(s)\text{=}\wedge T(s)$,
等价于对∀ s∈ S, x∈ T(s), 有
$\tilde{I}(q, s)\le x$,
等价于对∀ sx∈ T, 有(q, sx)∈ I, 故
$q\in g(\tilde{X})\Leftrightarrow q\in {{T}^{\uparrow }}$,
从而B=T↑ . 证毕
定理4 设$(Q, S, \tilde{I})$为模糊技能背景, (Q, SX, I)为$(Q, S, \tilde{I})$对应的标记技能背景, B⊆Q, $\tilde{X}\in \mathcal{F}(S)$.对s∈ S,
$W(s)=\{x|\forall q\in Q, x\text{=}\tilde{I}(q, s)\}$,
则其通过对应关系
$(B, \tilde{X})\mapsto (B, {{(\text{g}(\tilde{X}))}^{\downarrow }})=(B, \underset{s\in S}{\mathop{\bigcup }}\, \{{{s}^{x}}|\forall x\in W(s\text{)}, x\ge \tilde{X}(s) \})$
确定的概念格同构.
证明 由定理3, 映射$f\circ g$和$^{\uparrow }{{\circ }^{\downarrow }}$在2Q上得到的概念格同构, 则其通过对应关系
$(B, \tilde{X})\mapsto (B, {{(\text{g}(\tilde{X}))}^{\downarrow }})$
确定的概念格同构.只需再证
${{B}^{\downarrow }}=\underset{s\in S}{\mathop{\bigcup }}\, \{{{s}^{x}}|\forall x\in W(s\text{)}, x\ge \tilde{X}(s)\text{ }\!\!\}\!\!\text{ }$.
先证
$\underset{s\in S}{\mathop{\bigcup }}\, \{{{s}^{x}}|\forall x\in W(s\text{)}, x\ge \tilde{X}(s)\text{ }\!\!\}\!\!\text{ }\subseteq {{B}^{\downarrow }}$.
对
$\forall {{s}^{x}}\in \underset{s\in S}{\mathop{\bigcup }}\, \{{{s}^{x}}|\forall x\in W(s\text{)}, x\ge \tilde{X}(s)\}$,
因为
$B\text{=g(}\tilde{X})=\{q\in Q|\forall s\in S, \tilde{X}(s)\ge \tilde{I}(q, s)\}$,
故对∀ q∈ B, s∈ S, x∈ W(s), 有
$\tilde{I}(q, s)\le x$,
又因为
$\tilde{I}(q, s)\le x\Leftrightarrow (q, {{s}^{x}})\in I$,
从而sx∈ B↓ .
再证
${{B}^{\downarrow }}\subseteq \underset{s\in S}{\mathop{\bigcup }}\, \{{{s}^{x}}|\forall x\in W(s\text{)}, x\ge \tilde{X}(s)\text{ }\!\!\}\!\!\text{ }$.
假设存在s∈ S, x∈ W(s), 使
${{s}^{x}}\in {{B}^{\downarrow }}={{(g(\tilde{X}))}^{\downarrow }}$
成立, 即对∀ q∈ B, 有(q, sx)∈ I, 等价于对$\forall q\in g(\tilde{X})$, 有
$\tilde{I}(q, s)\le x$,
又因为
$\tilde{X}(s)\text{=}f(B)(s)=\underset{q\in B}{\mathop{\vee }}\, \tilde{I}(q, s)$,
故$\tilde{X}(s)$为
$\{\tilde{I}(q, s)|q\in B\text{=}g(\tilde{X})\}$
的上确界, 故$x\ge \tilde{X}(s)$, 则
${{s}^{x}}\in \underset{s\in S}{\mathop{\bigcup }}\, \{{{s}^{x}}|\forall x\in W(s\text{)}, x\ge \tilde{X}(s)\text{ }\!\!\}\!\!\text{ }$. 证毕
由于对∀ s∈ S, 当x=∨ W(s)时, 对∀ q∈ Q, 都有
$\tilde{I}(q, s)\le x=\vee W(s)$
恒成立, 即对∀ q∈ Q, s∈ S, 都有
$(q, {{s}^{\vee W(s)}})\in I\Leftrightarrow I(q, {{s}^{\vee W(s)}})\text{=1}$
恒成立.根据$^{\uparrow }{{\circ }^{\downarrow }}$的定义, ∀ s∈ S, s∨ W(s)都会出现在标记技能概念格L(Q, SX, I)的每个概念的内涵中.因此, 为了简便表示, 在标记技能概念格L(Q, SX, I)中, 除外延{Ø }对应的内涵以外, 其它所有外延对应的内涵中的s∨ W(s), ∀ s∈ S都忽略不写.
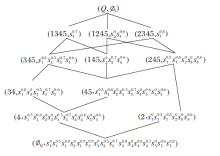
例2 对于表1的模糊技能背景$(Q, S, \tilde{I})$, 其对应的标记技能背景(Q, SX, I)如表2所示, (Q, SX, I)对应的标记技能概念格L(Q, SX, I)如图2所示.
| 表2 标记技能背景(Q, SX, I) Table 2 Marked skill context(Q, SX, I) |
下文将每个标记技能视为一个属性, 通过保持LQ(Q, SX, I)不变的标记技能约简方法解决保持${{L}_{Q}}(Q, S, \tilde{I})$不变的技能层约简的问题.
推论4 设$(Q, S, \tilde{I})$为模糊技能背景, (Q, SX, I)为$(Q, S, \tilde{I})$对应的标记技能背景.对∀ s∈ S, x∈ W(s), 令
${{s}^{x}}^{* }={{({{s}^{x}})}^{* }}=\{q\in Q|(q, {{s}^{x}})\in I\}$
表示与标记技能sx相关的问题集, 则$\{{{s}^{x}}^{* }|{{s}^{x}}\in {{S}^{X}}\}$为$(Q, S, \tilde{I})$通过合取模型诱导的简单闭包空间LQ(Q, SX, I)的一个交式生成组.
证明 对于标记技能背景(Q, SX, I), 因为
${{L}_{Q}}(Q, {{S}^{X}}, I)=\{{{T}^{\uparrow }}|\forall T\subseteq {{S}^{X}}, T={{T}^{\uparrow \downarrow }}\}$,
且对于任意一个标记技能集T⊆SX, 都有
${{T}^{\uparrow }}=\underset{{{s}^{x}}\in T}{\mathop{\bigcap }}\, {{s}^{x}}^{* }$,
故$\{{{s}^{x}}^{* }|{{s}^{x}}\in {{S}^{X}}\}$为LQ(Q, SX, I)的一个交式生成组. 证毕
保持LQ(Q, SX, I)不变的标记技能约简等价于保持LQ(Q, SX, I)的交式生成组不变的标记技能约简.对∀ s∈ S,
$W(s)=\{x|\forall q\in Q, x\text{=}\tilde{I}(q, s)\}$.
若x=∨ W(s), 因为对于∀ s∈ S, q∈ Q, 都有
$(q, {{s}^{\vee W(s)}})\in I$,
即对于∀ s∈ S, 有
${{s}^{\vee W(s)}}^{* }\text{=}Q$
恒成立, 故从交式生成组$\{{{s}^{x}}^{* }|{{s}^{x}}\in {{S}^{X}}\}$中删除${{s}^{\vee W(s)}}^{* }$并不影响$\{{{s}^{x}}^{* }|{{s}^{x}}\in {{S}^{X}}\}$生成${{L}_{Q}}(Q, S, \tilde{I})$中除全集Q之外的其它元素.因此, 为了减少标记技能约简的时间, 在讨论保持LQ(Q, SX, I)的交式生成组不变的标记技能约简的过程中, 考虑的交式生成组$\{{{s}^{x}}^{* }|{{s}^{x}}\in {{S}^{X}}\}$不包含任意s∈ S中的${{s}^{\vee W(s)}}^{* }$.因此, 后文讨论的模糊技能背景(Q, SX, I)对应的所有标记技能背景(Q, SX, I)均满足
${{S}^{X}}=\{{{s}^{x}}|s\in S, x\in W(s)且x\ne \vee W(s)\}$.
另外, 对sx∈ SX, 若存在t∈ S\{s}, y∈ W(t), 使得${{s}^{x}}^{\text{* }}={{t}^{y}}^{\text{* }}$, 说明标记技能sx和ty提供诱导简单闭包空间LQ(Q, SX, I)的作用是一样的.因此, 对sx∈ SX, 记
$[{{s}^{x}}]=\{{{t}^{y}}\in {{S}^{X}}|{{s}^{x}}^{* }={{t}^{y}}^{* }\}$
表示标记技能sx的等价类.
定义18 设$(Q, S, \tilde{I})$为模糊技能背景, (Q, SX, I)为$(Q, S, \tilde{I})$对应的标记技能背景.称$(Q, S_{1}^{{{X}_{1}}}, {{I}_{1}})$为(Q, SX, I)的一个极小标记技能背景, 若$(Q, S_{1}^{{{X}_{1}}}, {{I}_{1}})$满足:存在$S_{1}^{{{X}_{1}}}\subset {{S}^{X}}$, 满足
$L(Q, S_{1}^{{{X}_{1}}}, {{I}_{1}})\cong L(Q, {{S}^{X}}, I)$,
且对∀ q∈ Q, $s_{1}^{{{x}_{1}}}\in S_{1}^{{{X}_{1}}}$ , 有
${{I}_{1}}(q, s_{1}^{{{x}_{1}}}\text{)=}I(q, s_{1}^{{{x}_{1}}}\text{)}$.
另外, 称$S_{1}^{{{X}_{1}}}$为SX的一个极小标记技能集.记${{R}_{1}}={{S}^{X}}\backslash S_{1}^{{{X}_{1}}}$, 称R1为$S_{1}^{{{X}_{1}}}$对应的可约简标记技能集.对∀ sx∈ R1, 称sx为$S_{1}^{{{X}_{1}}}$对应的一个可约简标记技能.
显然, 极小标记技能集不唯一, 故极小标记技能背景$(Q, S_{1}^{{{X}_{1}}}, {{I}_{1}})$不唯一.记所有极小标记技能集对应的可约简标记技能集构成的集合为R, 称R为SX对应的可约简标记技能集.
下面将极小标记技能背景转化成一个新的模糊技能背景, 使其对应生成概念格同构.
定义19 设$(Q, S, \tilde{I})$为模糊技能背景, $(Q, {{S}^{X}}, \tilde{I})$为$(Q, S, \tilde{I})$对应的标记技能背景, $(Q, S_{1}^{{{X}_{1}}}, {{I}_{1}})$为(Q, SX, I)的一个极小标记技能背景.对s∈ S,
$W(s)=\{x|\forall q\in Q, x\text{=}\tilde{I}(q, s)\}$,
记
${{X}_{1}}(s)=\{x\in W(s)\text{ }\!\!|\!\!\text{ }{{s}^{x}}\in {{S}_{\text{1}}}^{{{X}_{1}}}\}$,
$X(s)=\{x\in W(s)|{{s}^{x}}\in {{S}^{X}}\}$,
称$(Q, {{S}_{1}}, {{\tilde{I}}_{1}})$为$(Q, S_{1}^{{{X}_{1}}}, {{I}_{1}})$对应的模糊技能背景, 其中
${{S}_{1}}=\{s\in S|{{X}_{1}}(s)\ne \varnothing \}$,
${{\tilde{I}}_{1}}$定义为:对q∈ Q, s∈ S,
${{\tilde{I}}_{1}}(q, s)={x}'\in W(s)$
满足
${x}'> \vee \{x\in {{X}_{1}}(s)|(q, {{s}^{x}})\notin {{I}_{1}}\}$,
且不存在x″∈ W(s), 使得
${x}'> {x}''> \vee \{x\in {{X}_{1}}(s)|(q, {{s}^{x}})\notin {{I}_{1}}\}$
成立.另外, 对q∈ Q, s∈ S, 若对∀ x∈ X1(s), 有(q, sx)∈ I1成立, 则
${{\tilde{I}}_{1}}(q, s)=\wedge X(s)$.
下面证明极小标记技能背景$(Q, S_{1}^{{{X}_{1}}}, {{I}_{1}})$对应的模糊技能背景$(Q, {{S}_{1}}, {{\tilde{I}}_{1}})$满足极小技能层模糊背景中的两个条件.
定理5 设$(Q, S, \tilde{I})$为模糊技能背景, (Q, SX, I)为$(Q, S, \tilde{I})$对应的标记技能背景, $(Q, S_{1}^{{{X}_{1}}}, {{I}_{1}})$为(Q, SX, I)的一个极小标记技能背景, $(Q, {{S}_{1}}, {{\tilde{I}}_{1}})$为$(Q, S_{1}^{{{X}_{1}}}, {{I}_{1}})$对应的模糊技能背景.对s∈ S,
$W(s)=\{x|\forall q\in Q, x\text{=}\tilde{I}(q, s)\}$,
$X(s)=\{x\in W(s)\text{ }\!\!|\!\!\text{ }{{s}^{x}}\in {{S}_{\text{1}}}^{{{X}_{1}}}\}$,
则
1)存在q∈ Q, s∈ S1, 有
${{\tilde{I}}_{1}}(q, s)\text{=}{{x}_{1}}\in W(s)< \tilde{I}(q, s)$
成立;
2)∀ q∈ Q, s∈ S1, 有
${{\tilde{I}}_{1}}(q, s)\text{=}{{x}_{1}}\in W(s)\le \tilde{I}(q, s)$
成立.
证明 由于$(Q, S_{1}^{{{X}_{1}}}, {{I}_{1}})$为(Q, SX, I)的一个极小标记技能背景, 故至少存在一个${{s}^{x}}\in {{S}^{X}}\backslash S_{1}^{{{X}_{1}}}$是可约简标记技能.对该技能s, 记
P(s)={x1, x2, …xn} ⊆X(s).
假设
${{s}^{P}}=\{{{s}^{x}}\text{ }\!\!|\!\!\text{ }x\in P(s)\}$
为s对应的所有可约简标记技能构成的集合, 若
P(s)={x1, x2, …xn}= X(s),
即$n=|X(s)|$, 则s∉S1.另外, 假设对∀ s'∈ S1\{s}, 都有$|P({s}')|\text{=}0$, 则由定义19, 显然对∀ q∈ Q, 有
${{\tilde{I}}_{1}}(q, {s}')\text{=}\tilde{I}(q, {s}')$.
由
${{L}_{Q}}(Q, {{S}_{1}}^{{{X}_{1}}}, {{I}_{1}})\text{=}{{L}_{Q}}(Q, {{S}_{1}}, {{\tilde{I}}_{1}})$,
显然不存在对∀ s'∈ S1\{s}, 都满足$n=|X({s}')|$的情形.因此, 只需再讨论
$P(s)\text{= }\!\!\{\!\!\text{ }{{x}_{1}}, {{x}_{2}}, \cdots , {{x}_{n}}\text{ }\!\!\}\!\!\text{ }\subset X(s), 1\le n< |X(s)|$
的情形.下证对该技能s, 满足对∀ q∈ Q, 有
${{\tilde{I}}_{1}}(q, s)\le \tilde{I}(q, s)$.
令
Y=(X(s)\P(s))∪ {∨ W(s)},
显然有$1\le |Y|< |X(s)|$.令
$M\text{= }\!\!\{\!\!\text{ }q\in Q|\tilde{I}\text{(}q\text{, }s\text{)=}\wedge X(s)\text{ }\!\!\}\!\!\text{ }$,
则对∀ q∈ M, x∈ X(s), 有(q, sx)∈ I.因此, 对∀ q∈ M, y∈ Y, 有(q, sy)∈ I1, 则由定义19, 对∀ q∈ M, 有
${{\tilde{I}}_{1}}(q, s)\text{=}\wedge X(s)$
成立.从而, 对∀ q∈ M, 有
${{\tilde{I}}_{1}}(q, s)\text{=}\tilde{I}(q, s)$.
将∀ xi∈ X(s), i=1, 2, …, $|X(s)|$ , 从小到大排序, 假设
${{x}_{1}}< \cdots < {{x}_{i}}< {{x}_{i+1}}< \cdots < {{x}_{|X(s)|}}$
成立.对∀ q∈ Q\{M}, 存在xi∈ X(s), $i\in \{1, 2, \cdots , |X(s)|\}$ , 有(q,
$\tilde{I}(q, s)\text{=}{{x}_{i+1}}$
成立.假设${{s}^{{{x}_{i}}}}$为一个可约简标记技能, 且
xi=∧ X(s),
则由定义19, 对∀ q∈ Q\{M}, 有
${{\tilde{I}}_{1}}(q, s)\text{=}\wedge X(s)$.
从而, 对∀ q∈ Q\{M}, 有
${{\tilde{I}}_{1}}(q, s)\text{}\tilde{I}(q, s)$.
假设${{s}^{{{x}_{i}}}}$为一个可约简标记技能, 且
xi≠ ∧ X(s),
记
$Y_{i}^{\le }=\{y\in Y\text{ }\!\!|\!\!\text{ }y\le {{x}_{i}}\}$,
$Y_{i}^{> }=\{{y}'\in Y\text{ }\!\!|\!\!\text{ }{y}'> {{x}_{i}}\}$,
则由定义19, 对∀ q∈ Q\{M}, 有
${{\tilde{I}}_{1}}(q, s)\text{=}\wedge Y_{i}^{\le }\text{=}{{x}_{i}}$.
从而, 对∀ q∈ Q\{M}, 有
${{\tilde{I}}_{1}}(q, s)\text{}\tilde{I}(q, s)$.
综上, 对该技能s, 存在q∈ Q, 有
${{\tilde{I}}_{1}}(q, s)\text{}\tilde{I}(q, s)$,
且对∀ q∈ Q, 有
${{\tilde{I}}_{1}}(q, s)\text{}\tilde{I}(q, s)$.
又因为对∀ s″∈ S1\{s}, 有上述类似结论成立, 故1)和2)成立. 证毕
由定理5和定义15, 显然有如下推论.
推论5 设$(Q, S, \tilde{I})$为模糊技能背景, (Q, SX, I)为$(Q, S, \tilde{I})$对应的标记技能背景, $(Q, S_{1}^{{{X}_{1}}}, {{I}_{1}})$为(Q, SX, I)的一个极小标记技能背景, $(Q, {{S}_{1}}, {{\tilde{I}}_{1}})$为$(Q, S_{1}^{{{X}_{1}}}, {{I}_{1}})$对应的模糊技能背景.对s∈ S,
$W(s)=\{x|\forall q\in Q, x\text{=}\tilde{I}(q, s)\}$,
对∀ xi∈ W(s), i=1, 2, …, m, $1\le m\le |W(s)|$ , 假设
x1< …< xu< xv< …< xm
成立.若
定理6 设$(Q, S, \tilde{I})$为模糊技能背景, (Q, SX, I)为$(Q, S, \tilde{I})$对应的标记技能背景, $(Q, S_{1}^{{{X}_{1}}}, {{I}_{1}})$为(Q, SX, I)的一个极小标记技能背景, $(Q, {{S}_{1}}, {{\tilde{I}}_{1}})$为$(Q, S_{1}^{{{X}_{1}}}, {{I}_{1}})$对应的模糊技能背景.对∀ q∈ Q, ${{s}^{x}}\in S_{1}^{{{X}_{1}}}$ , 有
$(q, {{s}^{x}})\notin {{I}_{1}}\Leftrightarrow {{\tilde{I}}_{1}}(q, s)> x$.
证明 先证充分性.假设(q, sx)∉I1, 由定义19, 有
${{\tilde{I}}_{1}}(q, s)> \vee \{x\in {{X}_{1}}(s)|(q, {{s}^{x}})\notin {{I}_{1}}\}\ge x$.
再证必要性.假设${{\tilde{I}}_{1}}(q, s)> x$, 由定理5, 有
${{\tilde{I}}_{1}}(q, s)\text{}\tilde{I}(q, s)$,
故$\tilde{I}(q, s)> x$, 等价于(q, sx)∉I, 又由定义18可得关系I1为关系I的限制, 故(q, sx)∉I1. 证毕
定理7 设$(Q, S, \tilde{I})$为模糊技能背景, (Q, SX, I)为$(Q, S, \tilde{I})$对应的标记技能背景, $(Q, S_{1}^{{{X}_{1}}}, {{I}_{1}})$为(Q, SX, I)的一个极小标记技能背景, $(Q, {{S}_{1}}, {{\tilde{I}}_{1}})$为$(Q, S_{1}^{{{X}_{1}}}, {{I}_{1}})$对应的模糊技能背景, 则$(Q, S_{1}^{{{X}_{1}}}, {{I}_{1}})$和$(Q, {{S}_{1}}, {{\tilde{I}}_{1}})$分别由映射$^{\uparrow }{{\circ }^{\downarrow }}$和$f\circ g$在2Q上得到的概念格同构, 即
${{L}_{Q}}(Q, {{S}_{1}}^{{{X}_{1}}}, {{I}_{1}})={{L}_{Q}}(Q, {{S}_{1}}, {{\tilde{I}}_{1}})$.
证明 先证
${{L}_{Q}}(Q, {{S}_{1}}^{{{X}_{1}}}, {{I}_{1}})={{L}_{Q}}(Q, {{S}_{1}}, {{\tilde{I}}_{1}})$.
设存在B⊆Q, 使得$B\in {{L}_{Q}}(Q, {{S}_{1}}^{{{X}_{1}}}, {{I}_{1}})$成立, 则存在$T\subseteq S_{1}^{{{X}_{1}}}$, 使得B=T↑ 成立.转证存在$\tilde{X}\in \mathcal{F}({{S}_{1}})$, 使得$B=g(\tilde{X})$成立.对∀ s∈ S1,
$T(s)=\{x\in {{X}_{1}}(s)|{{s}^{x}}\in T\}$.
另外, 对∀ s∈ S1, 令
$\tilde{X}(s)=\wedge T(s)$,
下证
$B=g(\tilde{X})$.
由定理6, 对∀ q∈ Q, s∈ S1, 满足对∀ sx∈ T, 有(q, sx)∈ I1, 等价于对∀ x∈ T(s), 有
${{\tilde{I}}_{1}}(q, s)\le x$,
等价于
$\tilde{X}(s)\ge {{\tilde{I}}_{1}}(q, s)$,
故
$\begin{align} & g(\tilde{X})=\{q\in Q|\forall s\in {{S}_{1}}, \tilde{X}(s)\ge {{{\tilde{I}}}_{1}}(q, s)\}\text{=} \\ & \{q\in Q|\forall s\in {{S}_{1}}, x\in T(s), {{{\tilde{I}}}_{1}}(q, s)\le x\}= \\ & \{q\in Q|\forall {{s}^{x}}\in T, (q, {{s}^{x}})\in {{I}_{1}}\}={{T}^{\uparrow }}=B, \\ \end{align}$
从而
${{L}_{Q}}(Q, {{S}_{1}}^{{{X}_{1}}}, {{I}_{1}})\subseteq {{L}_{Q}}(Q, {{S}_{1}}, {{\tilde{I}}_{1}})$.
再证
${{L}_{Q}}(Q, {{S}_{1}}, {{\tilde{I}}_{1}})\subseteq {{L}_{Q}}(Q, {{S}_{1}}^{{{X}_{1}}}, {{I}_{1}})$.
设存在B⊆ Q, 使$B\in {{L}_{Q}}(Q, {{S}_{1}}, {{\tilde{I}}_{1}})$成立, 则存在$\tilde{X}$∈ F(S1), 使$B=g(\tilde{X})$成立.转证存在$T\subseteq {{S}_{1}}^{{{X}_{1}}}$, 使得
$g(\tilde{X})={{T}^{\uparrow }}$
成立.对∀ s∈ S1, 存在T(s)⊆X1(s), 满足
$\tilde{X}(s)=\wedge T(s)$.
令
$T=\underset{s\in {{S}_{1}}}{\mathop{\bigcup }}\, \{{{s}^{x}}|x\in T(s)\}$,
下证$g(\tilde{X})={{T}^{\uparrow }}$.由定理6, 对∀ q∈ Q, s∈ S1, 有
$\tilde{X}(s)\ge {{\tilde{I}}_{1}}(q, s)$,
等价于对∀ x∈ T(s), 有
${{\tilde{I}}_{1}}(q, s)\le x$,
等价于对sx∈ T, 有(q, sx)∈ I1, 故
$g(\tilde{X})={{T}^{\uparrow }}$.
从而
${{L}_{Q}}(Q, {{S}_{1}}, {{\tilde{I}}_{1}})={{L}_{Q}}(Q, {{S}_{1}}^{{{X}_{1}}}, {{I}_{1}})$.证毕
定理8 设$(Q, S, \tilde{I})$为模糊技能背景, (Q, SX, I)为$(Q, S, \tilde{I})$对应的标记技能背景, $(Q, {{S}_{1}}^{{{X}_{1}}}, {{I}_{1}})$为(Q, SX, I)的一个极小标记技能背景, $(Q, {{S}_{1}}, {{\tilde{I}}_{1}})$为$(Q, {{S}_{1}}^{{{X}_{1}}}, {{I}_{1}})$对应的模糊技能背景, 则$(Q, {{S}_{1}}, {{\tilde{I}}_{1}})$为$(Q, S, \tilde{I})$的一个极小技能层模糊技能背景.
证明 由定理5, 只需再证
${{L}_{Q}}(Q, {{S}_{1}}, {{\tilde{I}}_{1}})={{L}_{Q}}(Q, {{S}_{1}}, \tilde{I})$.
由定理3有
${{L}_{Q}}(Q, S, \tilde{I})={{L}_{Q}}(Q, {{S}^{X}}, I)$,
由定义18有
${{L}_{Q}}(Q, {{S}^{X}}, I)\text{=}{{L}_{Q}}(Q, {{S}_{1}}^{{{X}_{1}}}, {{I}_{1}})$,
又由定理7, 有
${{L}_{Q}}(Q, {{S}_{1}}^{{{X}_{1}}}, {{I}_{1}})\text{=}{{L}_{Q}}(Q, {{S}_{1}}, {{\tilde{I}}_{1}})$,
故
${{L}_{Q}}(Q, {{S}_{1}}, {{\tilde{I}}_{1}})={{L}_{Q}}(Q, S, \tilde{I})$,
即
$L(Q, {{S}_{1}}, {{\tilde{I}}_{1}})\cong L(Q, S, \tilde{I})$.证毕
推论6 设$(Q, S, \tilde{I})$为模糊技能背景, (Q, SX, I)为$(Q, S, \tilde{I})$对应的标记技能背景, $(Q, {{S}_{1}}^{{{X}_{1}}}, {{I}_{1}})$为(Q, SX, I)的一个极小标记技能背景, $(Q, {{S}_{1}}, {{\tilde{I}}_{1}})$为$(Q, S, \tilde{I})$的一个极小技能层模糊技能背景.对s∈ S,
$W(s)=\{x\text{ }\!\!|\!\!\text{ }\forall q\in Q, x\text{=}\tilde{I}(q, s)\}$,
$X(s)=\{x\in W(s)|{{s}^{x}}\in {{S}^{X}}\}$.
若对s∈ S, 满足对∀ x∈ X(s), sx都是可约简标记技能, 则s为一个可约简技能.
证明 对s∈ S, 满足对∀ x∈ X(s), 都有sx可约简标记技能, 则s∉S1, 故s∈ S\{S1}为一个可约简技能. 证毕
下面, 给出获取标记技能背景(Q, SX, I)的极小标记技能背景$(Q, {{S}_{1}}^{{{X}_{1}}}, {{I}_{1}})$的算法, 具体见算法2中step 2~step 10.由定理8可得, 通过标记技能背景(Q, SX, I)的极小标记技能背景(Q,
算法2 获取极小技能层模糊技能背景$(Q, {{S}_{1}}, {{\tilde{I}}_{1}})$
输入 模糊技能背景$(Q, S, \tilde{I})$
输出 极小技能层模糊技能背景$(Q, {{S}_{1}}, {{\tilde{I}}_{1}})$
step 1 由
$(q, {{s}^{x}})\in I\Leftrightarrow \tilde{I}(q, s)\le x$,
${{S}^{X}}=\{{{s}^{x}}|\forall s\in S, x\in W(s)且x\ne \vee W(s)\}$
得到标记技能背景(Q, SX, I).
step 2 对∀ sx∈ SX, 计算
$\{{{s}^{x}}^{* }|{{s}^{x}}\in {{S}^{X}}\}, A=\{[{{s}^{x}}]|{{s}^{x}}\in {{S}^{X}}\}$.
step 3 在A中的每个元素[sx]中各取出一个代表元, 组成一个新的标记技能集SX'.
step 4 从$\{{{s}^{x}}^{* }|{{s}^{x}}\in {{S}^{X}}\}$找出$\{{{s}^{x}}^{* }|{{s}^{x}}\in {{S}^{X}}^{\prime }\}$, 并计算
$B=\{[{{s}^{x}}]|\forall {{s}^{x}}\in {{S}^{X}}^{\prime }, |[{{s}^{x}}]|> 1\}$.
step 5 令C=Ø , E=Ø , F=Ø , R=Ø .
step 6 将$\{{{s}^{x}}^{* }|{{s}^{x}}\in {{S}^{X}}^{\prime }\}$的
step 7 对∀ sx∈ SX', 若找到一个
${{s}^{x}}^{* }=\underset{{{t}^{y}}\in {{S}^{{{X}'}}}}{\mathop{\bigcap }}\, {{t}^{y}}^{* }$
成立, 则C← C∪ {sx}.
step 8 令D=SX'\C.对∀ sx∈ D, 若[sx]∈ B, 则E← E∪ [sx], 否则F← F∪ {sx}.
step 9 对E中的每个元素各取一个代表元进行组合, 所有可能的组合构成一个集合族G.
step 10 对E'∈ G, 令
${{S}_{1}}^{{{X}_{1}}}={E}'\bigcup F, {{I}_{1}}\subseteq Q\times {{S}_{1}}^{{{X}_{1}}}$,
获得一个极小标记技能背景$(Q, {{S}_{1}}^{{{X}_{1}}}, {{I}_{1}})$和${{S}_{1}}^{{{X}_{1}}}$对应的可约简标记技能集${{R}_{1}}\text{=}{{S}^{X}}\backslash S_{1}^{{{X}_{1}}}$.
step 11 由定义19将$(Q, {{S}_{1}}^{{{X}_{1}}}, {{I}_{1}})$转化成一个极小技能层模糊技能背景$(Q, {{S}_{1}}, {{\tilde{I}}_{1}})$.
step 12 根据推论5和推论6, 由${{R}_{1}}\text{=}{{S}^{X}}\backslash S_{1}^{{{X}_{1}}}$得到$(Q, {{S}_{1}}, {{\tilde{I}}_{1}})$对应的可约简技能层和可约简技能.
step 13 遍历G中元素, 重复step 10~step 12, 可获得所有的极小技能层模糊技能背景及其对应的可约简技能层和可约简技能.
对于算法2, step 2~step 4的时间复杂度最大为$O(|{{S}^{X}}|)$, step 6~step 13的时间复杂度最大为$O(|{{S}^{X}}||G|)$, 故算法2的时间复杂度最大为$O(|{{S}^{X}}||G|)$.
例3 针对表1的模糊技能背景$(Q, S, \tilde{I})$, 计算标记技能背景(Q, SX, I), 其中
${{S}^{X}}=\{{{s}^{x}}|\forall s\in S, x\in W(s)且x\ne \vee W(s)\}$.
根据算法2给出获取$(Q, S, \tilde{I})$的所有极小技能层模糊技能背景的过程如下.
1)由
$[{{s}^{x}}]=\{{{t}^{y}}\in {{S}^{X}}|{{s}^{x}}^{* }={{t}^{y}}^{* }\}$,
可得
$\begin{align} & [s_{1}^{0}]=\{s_{1}^{0}\}, [s_{1}^{0.5}]=[s_{4}^{0}]=\{s_{1}^{0.5}, s_{4}^{0}\}, \\ & [s_{1}^{0.8}]=\{s_{1}^{0.8}\}, [s_{2}^{0}]=\{s_{4}^{0.6}\}=\{s_{2}^{0}, s_{4}^{0.6}\}, \\ & [s_{3}^{0}]=\{s_{3}^{0}\}[s_{3}^{0.5}]=[s_{5}^{0.6}]=\{s_{3}^{0.5}, s_{5}^{0.6}\}, \\ & [s_{3}^{0.7}]=\{s_{3}^{0.7}\}, [s_{5}^{0}]=\{s_{5}^{0}\}. \\ \end{align}$
因此, 标记技能的所有等价类构成的集合如下所示:
$A=\{[s_{1}^{0}], [s_{1}^{0.5}], [s_{1}^{0.8}], [s_{2}^{0}], [s_{3}^{0}], [s_{3}^{0.5}], [s_{3}^{0.7}], [s_{5}^{0}]\}$.
2)从A中每个元素中任取一个代表元, 组成一个新的标记技能集SX'.假设
${{S}^{X}}^{\prime }=\{s_{1}^{0}, s_{1}^{0.5}, s_{1}^{0.8}, s_{2}^{0}, s_{3}^{0}, s_{3}^{0.5}, s_{3}^{0.7}, s_{5}^{0}\}$.
3)由于
$s_{1}^{0.5* }\text{=}s_{1}^{0.8* }\bigcap s_{2}^{0* }$,
$s_{3}^{0.5* }\text{=}s_{1}^{0.8* }\bigcap s_{3}^{0.7* }$,
$s_{5}^{0* }=s_{1}^{0.5* }\bigcap s_{3}^{0.5* }$,
故
$S_{1}^{{{X}_{1}}}=\{s_{1}^{0}, s_{1}^{0.8}, s_{2}^{0}, s_{3}^{0}, s_{3}^{0.7}\}$
为SX'的一个极小标记技能集, 即$S_{1}^{{{X}_{1}}}$为SX的一个极小标记技能集, 故
${{R}_{1}}\text{=}{{S}^{X}}\backslash S_{1}^{{{X}_{1}}}=\{s_{1}^{0.5}, s_{3}^{0.5}, s_{4}^{0}, s_{4}^{0.6}, s_{5}^{0}, s_{5}^{0.6}\}$
为对应$S_{1}^{{{X}_{1}}}$的可约简标记技能集.
4)由于
$[s_{1}^{0.5}]=\{s_{1}^{0.5}, s_{4}^{0}\}$,
$[s_{2}^{0}]=\{s_{2}^{0}, s_{4}^{0.6}\}$,
$[s_{3}^{0.5}]=\{s_{3}^{0.5}, s_{5}^{0.6}\}$,
且$s_{2}^{0}\in S_{1}^{{{X}_{1}}}$, 故SX只有2个极小标记技能集, 且SX的另外一个极小标记技能集为
$S_{2}^{{{X}_{2}}}=\{s_{1}^{0}, s_{1}^{0.8}, s_{3}^{0}, s_{3}^{0.7}, s_{4}^{0.6}\}$,
故
${{R}_{2}}\text{=}{{S}^{X}}\backslash S_{2}^{{{X}_{2}}}=\{s_{1}^{0.5}, s_{2}^{0}, s_{3}^{0.5}, s_{4}^{0}, s_{5}^{0}, s_{5}^{0.6}\}$
为对应$S_{2}^{{{X}_{2}}}$的可约简标记技能集.因此,
$R={{R}_{1}}\bigcup {{R}_{2}}\text{=}\{s_{1}^{0.5}, s_{2}^{0}, s_{3}^{0.5}, s_{4}^{0}, s_{4}^{0.6}, s_{5}^{0}, s_{5}^{0.6}\}$
为SX的可约简标记技能集.
5)由极小标记技能集$S_{1}^{{{X}_{1}}}$和$S_{2}^{{{X}_{2}}}$对应得到的极小标记技能背景$(Q, S_{1}^{{{X}_{1}}}, {{I}_{1}})$和$(Q, S_{2}^{{{X}_{2}}}, {{I}_{2}})$分别如表3和表4所示.
| 表3 极小标记技能背景$(Q, S_{1}^{{{X}_{1}}}, {{I}_{1}})$ Table 3 Minimally marked skill context $(Q, S_{1}^{{{X}_{1}}}, {{I}_{1}})$ |
| 表4 极小标记技能背景$(Q, S_{2}^{{{X}_{2}}}, {{I}_{2}})$ Table 4 Minimally marked skill context $(Q, S_{2}^{{{X}_{2}}}, {{I}_{2}})$ |
利用定义19, 将极小标记技能背景$(Q, S_{1}^{{{X}_{1}}}, I)$和$(Q, S_{2}^{{{X}_{2}}}, {{I}_{2}})$分别转化成极小技能层模糊技能背景$(Q, {{S}_{1}}, {{\tilde{I}}_{1}})$和$(Q, {{S}_{2}}, {{\tilde{I}}_{2}})$, 如表5和表6所示.
| 表5 极小技能层模糊技能背景$(Q, {{S}_{1}}, {{\tilde{I}}_{1}})$ Table 5 Fuzzy skill context with minimal skill level $(Q, {{S}_{1}}, {{\tilde{I}}_{1}})$ |
| 表6 极小技能层模糊技能背景 $(Q, {{S}_{2}}, {{\tilde{I}}_{2}})$ Table 6 Fuzzy skill context with minimal skill level $(Q, {{S}_{2}}, {{\tilde{I}}_{2}})$ |
对比表1, 在表5中, 技能s1的可约简技能层是0.8, 技能s3的可约简技能层是0.7, 技能s4和s5是$S_{1}^{{{X}_{1}}}$对应的可约简技能.在表6中, 技能s1的可约简技能层是0.8, 技能s3的可约简技能层是0.7, 技能s4的可约简技能层是0.6, 技能s2和s5是$S_{2}^{{{X}_{2}}}$对应的可约简技能.这与推论5和推论6一致.
第2节通过模糊技能概念格获得简单闭包空间, 第3节经过技能层约简提高获取简单闭包空间的效率, 但将基本局部独立模型应用于前级简单闭包空间和后级简单闭包空间将呈现出不可识别的问题, 导致无法评估个体的行为表现层次与真实认知能力的一致性.因此, 为了避免出现不可识别的问题, 下面给出判断模糊技能映射诱导前级(后级)简单闭包空间的充要条件.在充要条件的前提下, 只需判定模糊技能背景满足某些条件, 就可以确定诱导的简单闭包空间在某些问题中是否是前级的或后级的.
定理9 设(Q, S, τ )为模糊技能映射, $(Q, S, \tilde{I})$为(Q, S, τ )对应的模糊技能背景, $\mathcal{K}\text{=}{{L}_{Q}}(Q, S, \tilde{I})$为$(Q, S, \tilde{I})$在合取模型下诱导的简单闭包空间.K在问题q1∈ Q处是前级的当且仅当对∀ p∈ Q\{q1}, 满足如下两个条件:
1)存在s∈ S, 有$\tilde{I}(p, s)> \tilde{I}({{q}_{1}}, s)$;
2)对∀ K⊆Q\{q1, p}, 满足对∀ s∈ S, 若
$\tilde{I}(p, s)\le \underset{q\in K\bigcup \{{{q}_{1}}\}}{\mathop{\vee }}\, \tilde{I}(q, s)$,
则
$\tilde{I}(p, s)\le \underset{q\in K}{\mathop{\vee }}\, \tilde{I}(q, s)$.
证明 先证充分性.假设存在p∈ Q\{q1}, 对∀ s∈ S, 有
$\tilde{I}(p, s)> \tilde{I}({{q}_{1}}, s)$
成立, 则存在
${{\tilde{X}}_{1}}=f(\text{ }\!\!\{\!\!\text{ }{{q}_{1}}\text{ }\!\!\}\!\!\text{ })=\underset{q={{q}_{1}}}{\mathop{\vee }}\, \tilde{I}(q, s), \forall s\in S$,
${{\tilde{X}}_{2}}=f(\text{ }\!\!\{\!\!\text{ }{{q}_{1}}, p\text{ }\!\!\}\!\!\text{ })=\underset{q\in \{{{q}_{1}}, p\}}{\mathop{\vee }}\, \tilde{I}(q, s), \forall s\in S$,
使得
$({{\tilde{X}}_{1}})\text{=g}({{\tilde{X}}_{2}})\supseteq \text{ }\!\!\{\!\!\text{ }{{q}_{1}}, p\text{ }\!\!\}\!\!\text{ }$
成立.另外, 因为g(Ø )=Ø ∈ K, 故
$\text{g}(\varnothing \bigcup {{\tilde{X}}_{1}})=\text{g}({{\tilde{X}}_{1}})\supset \text{g}(\varnothing )\bigcup \{{{q}_{1}}\}\text{=}\{{{q}_{1}}\}$.
因此, 有
Ø ∪ {q1}∉K.
从而K在q1处不是前级的.故条件1)是必要的. 对K⊆Q\{q1, p}, 假设存在p∈ Q\{q1}, 使得存在
${{\tilde{X}}_{3}}=f(K\bigcup \{{{q}_{1}}\})=\underset{q\in K\bigcup \{{{q}_{1}}\}}{\mathop{\vee }}\, \tilde{I}(q, s), \forall s\in S$,
满足对∀ s∈ S, 有
$\tilde{I}(p, s)\le {{\tilde{X}}_{3}}(s)$,
且对
$\tilde{X}=f(K)=\underset{q\in K}{\mathop{\vee }}\, \tilde{I}(q, s), \forall s\in S$,
存在s∈ S, 有
$\tilde{I}(p, s)> \tilde{X}(s)$
成立.另外, 假设K⊆Q\{q1, p}非空, 且存在s∈ S, 有
$\tilde{I}({{q}_{1}}, s)> \tilde{X}(s)$
成立.因此, q1和p均属于$\text{g(}{{\tilde{X}}_{3}})$, 且q1和p均不属于$\text{g(}\tilde{X})$, 故对K∈ K, 有
K∪ {q1} ∉K.
从而K在q1处不是前级的.故条件2)是必要的.
再证必要性.假设K在q1∈ Q处不是前级的, 则存在K∈ K且q1∉K, 使得
K∪ {q1}∉K
成立.因此, 存在
$\tilde{X}=f(K)=\underset{q\in K}{\mathop{\vee }}\, \tilde{I}(q, s), \forall s\in S$,
有
$K\text{=g}(\tilde{X})=\{q\in Q|\forall s\in S, \tilde{X}(s)\ge \tilde{I}(q, s)\}$,
且存在s∈ S, 有
$\tilde{I}({{q}_{1}}, s)> \tilde{X}(s)$.
因为对∀ p∈ Q\{q1}, 存在s∈ S, 有
$\tilde{I}(p, s)\ge \tilde{I}({{q}_{1}}, s)$,
故存在
${{\tilde{X}}_{1}}=f(\text{ }\!\!\{\!\!\text{ }{{q}_{1}}\text{ }\!\!\}\!\!\text{ })=\underset{q\text{=}{{q}_{1}}}{\mathop{\vee }}\, \tilde{I}(q, s), \forall s\in S$,
满足
$\text{g}({{\tilde{X}}_{1}})\text{= }\!\!\{\!\!\text{ }{{q}_{1}}\text{ }\!\!\}\!\!\text{ }$.
又因为
K∪ {q1}∉K,
由定理1可得, 对
${{\tilde{X}}_{2}}=f(K\bigcup \{{{q}_{1}}\})=\underset{q\in K\bigcup \{{{q}_{1}}\}}{\mathop{\vee }}\, \tilde{I}(q, s), \forall s\in S$,
有
$\text{g}({{\tilde{X}}_{2}})\supset \text{g}(\tilde{X})\bigcup \text{g}({{\tilde{X}}_{1}})\text{=g}(\tilde{X})\bigcup \{{{q}_{1}}\}$,
故存在$p\in \text{g}({{\tilde{X}}_{2}})\backslash K$, 使得对∀ s∈ S, 有
$\tilde{I}(p, s)\le {{\tilde{X}}_{2}}(s)$
成立, 并且存在s∈ S, 有
$\tilde{I}(p, s)> \tilde{X}(s)$,
与条件2)矛盾. 证毕
注意到, 在条件2)中, 对q1∈ Q, p∈ Q\{q1}, 满足对∀ s∈ S, 有
$\tilde{I}(p, s)\le \underset{q\in K\bigcup \{{{q}_{1}}\}}{\mathop{\vee }}\, \tilde{I}(q, s)$
成立的K是很多的, 故为了更快地判定条件2)是否成立, 对满足条件2)的前提条件的那些K进行限制.
推论7 设(Q, S, τ )为模糊技能映射, $(Q, S, \tilde{I})$为(Q, S, τ )对应的模糊技能背景, q1∈ Q和p∈ Q\{q1}.记
$\mathcal{A}_{p}^{{{q}_{1}}}\text{= }\!\!\{\!\!\text{ }K\subseteq Q\backslash \{{{q}_{1}}, p\}|\forall s\in S, \tilde{I}(p, s)\le \underset{q\in K\bigcup \{{{q}_{1}}\}}{\mathop{\vee }}\, \tilde{I}(q, s)\text{ }\!\!\}\!\!\text{ }$,
且规定$\mathcal{A}_{p}^{{{q}_{1}}}$非空.记
$\mathcal{B}_{p}^{{{q}_{1}}}=\{K\in \mathcal{A}_{p}^{{{q}_{1}}}|不存在{K}'\in \mathcal{A}_{p}^{{{q}_{1}}}, 满足对\forall s\in S, 有\underset{q\in K}{\mathop{\vee }}\, \tilde{I}(q, s)> \underset{q\in {K}'}{\mathop{\vee }}\, \tilde{I}(q, s)\}$,
表示
1)若存在$K\in \text{B}_{p}^{{{q}_{1}}}$, 使得存在s∈ S, 有
$\tilde{I}(p, s)\le \underset{q\in K}{\mathop{\vee }}\, \tilde{I}(q, s)$
不成立, 则存在$K\in \text{A}_{p}^{{{q}_{1}}}$, 使得存在s∈ S, 有
$\tilde{I}(p, s)\le \underset{q\in K}{\mathop{\vee }}\, \tilde{I}(q, s)$
不成立.
2)若对$\forall K\in \text{B}_{p}^{{{q}_{1}}}$, 满足对∀ s∈ S, 有
$\tilde{I}(p, s)\le \underset{q\in K}{\mathop{\vee }}\, \tilde{I}(q, s)$
成立, 则对$\forall K\subseteq \text{A}_{p}^{{{q}_{1}}}$, 满足对∀ s∈ S, 有
$\tilde{I}(p, s)\le \underset{q\in K}{\mathop{\vee }}\, \tilde{I}(q, s)$
成立.
证明 1)是显然的.对于2), 因为对$\forall {K}''\in \mathcal{A}_{p}^{{{q}_{1}}}\backslash \mathcal{B}_{p}^{{{q}_{1}}}$, 都存在$K\in \mathcal{B}_{p}^{{{q}_{1}}}$, 满足对∀ s∈ S, 有
$\underset{q\in {K}''}{\mathop{\vee }}\, \tilde{I}(q, s)\ge \underset{q\in K}{\mathop{\vee }}\, \tilde{I}(q, s)$
成立, 故2)成立. 证毕
注意推论7规定$\mathcal{A}_{p}^{{{q}_{1}}}$非空, 因为若$\mathcal{A}_{p}^{{{q}_{1}}}$是空集, 说明对于q1和p, 条件2)的前提条件不成立.
例4 对于表1的模糊技能背景$(Q, S, \tilde{I})$, K为$(Q, S, \tilde{I})$在合取模型下诱导的简单闭包空间.对∀ q∈ Q, 利用定理9逐一验证K在q处是否是前级的.
对q1∈ Q, 存在
p=q4∈ Q\{q1},
使得对∀ s∈ S, 有
$\tilde{I}({{q}_{4}}, s)\le \tilde{I}({{q}_{1}}, s)$
成立, 故不满足条件1).故K在q1处不是前级的.
对q2∈ Q, 容易验证对∀ p∈ Q\{q2}, 都满足条件1).下面对每个p∈ Q\{q2}逐个验证条件2).容易验证, 当p=q1和p=q3时, 不满足条件2)的前提.对
p=q4∈ Q\{q2},
容易验证, 对
∀ K⊆Q\{q2, q4},
条件2)均成立.对
p=q5∈ Q\{q2},
存在
K={q4}⊆Q\{q2, q5},
使得对∀ s∈ S, 有
$\tilde{I}({{q}_{5}}, s)\le \underset{q\in \{{{q}_{2}}\text{ }\!\!\}\!\!\text{ }\bigcup \text{ }\!\!\{\!\!\text{ }{{q}_{4}}\}}{\mathop{\vee }}\, \tilde{I}(q, s)$
成立.但存在s3∈ S, 有
$\tilde{I}({{q}_{5}}, {{s}_{3}})> \underset{q={{q}_{4}}}{\mathop{\vee }}\, \tilde{I}(q, {{s}_{3}})$
成立, 故不满足条件2).因此, K在q2处不是前级的.
类似可验证K在q3, q4, q5处均不是前级的.
定理10 设(Q, S, τ )为模糊技能映射, $(Q, S, \tilde{I})$为(Q, S, τ )对应的模糊技能背景, $\mathcal{K}\text{=}{{L}_{Q}}(Q, S, \tilde{I})$为$(Q, S, \tilde{I})$在合取模型下诱导的简单闭包空间.K在问题q1∈ Q处是后级的当且仅当存在s∈ S, 对∀ p∈ Q\{q1}, 有
$\tilde{I}({{q}_{1}}, s)> \tilde{I}(p, s)$.
证明 先证充分性.已知Q∈ K, 因为K在问题 q1∈ Q处是后级的, 故
Q\{q1}∈ K.
因此, 存在
$\tilde{X}=f(Q\backslash \{{{q}_{1}}\text{ }\!\!\}\!\!\text{ })\text{=}\underset{q\in Q\backslash \{{{q}_{1}}\}}{\mathop{\vee }}\, \tilde{I}(q, s), \forall s\in S$,
有
$Q\backslash \{{{q}_{1}}\}\text{=}g(\tilde{X})=\{q=Q|\forall s\in S, \tilde{X}(s)\ge \tilde{I}(q, s)\}$
成立.但q1∉Q\{q1}, 所以存在s∈ S, 有
$\tilde{I}({{q}_{1}}, s)> \tilde{X}(s)$.
假设对∀ s∈ S, 存在p∈ Q\{q1}, 有
$\tilde{I}({{q}_{1}}, s)\le \tilde{I}(p, s)$,
则存在s∈ S, 有
$\tilde{I}(p, s)> \tilde{X}(s)$,
从而$p\notin \text{g}(\tilde{X})$, 与p∈ Q\{q1}矛盾.
再证必要性.对∀ K∈ K, 满足存在
$\tilde{X}=f(K)=\underset{q\in K}{\mathop{\vee }}\, \tilde{I}(q, s), \forall s\in S$,
有
$K\text{=g}(\tilde{X})=\{q\in Q|\forall s\in S, \tilde{X}(s)\ge \tilde{I}(q, s)\}$.
下证K\{q1}∈ K, 即证对
${{\tilde{X}}_{1}}=f(K\backslash \{{{q}_{1}}\text{ }\!\!\}\!\!\text{ })=\underset{q\in K\backslash \{{{q}_{1}}\}}{\mathop{\vee }}\, \tilde{I}(q, s), \forall s\in S$,
有
$K\backslash \{{{q}_{1}}\text{ }\!\!\}\!\!\text{ =g}({{\tilde{X}}_{1}})=\{q\in Q|\forall s\in S, {{\tilde{X}}_{1}}(s)\ge \tilde{I}(q, s)\}$
成立.先证
$\text{g}({{\tilde{X}}_{1}})\subseteq K\backslash \{{{q}_{1}}\text{ }\!\!\}\!\!\text{ }$.
对$\forall q\in \text{g}({{\tilde{X}}_{1}})$, 下证q∈ K\{q1}, 即证q∈ K且q≠ q1.对$\forall q\in \text{g}({{\tilde{X}}_{1}})$, 有q∈ K显然成立.假设q=q1, 因为存在s∈ S, 对∀ p∈ Q\{q1}, 有
$\tilde{I}({{q}_{1}}, s)> \tilde{I}(p, s)$,
与$q\in \text{g}({{\tilde{X}}_{1}})$矛盾, 故q≠ q1.再证
$K\backslash \{{{q}_{1}}\text{ }\!\!\}\!\!\text{ }\subseteq \text{g}({{\tilde{X}}_{1}})$.
假设{q1}∉K, 则
K\{q1}=K.
因此, 对∀ s∈ S, 有
${{\tilde{X}}_{1}}(s)=\tilde{X}(s)$,
故
$\text{g}({{\tilde{X}}_{1}})\text{=}K$.
从而
$K\backslash \{{{q}_{1}}\text{ }\!\!\}\!\!\text{ }\subseteq \text{g}({{\tilde{X}}_{1}})$
成立.假设{q1}∈ K, 则对∀ q∈ K\{q1}, 满足对∀ s∈ S, 有
${{\tilde{X}}_{1}}(s)\ge \tilde{I}(q, s)$
成立, 故$q\in \text{g}({{\tilde{X}}_{1}})$.从而
$K\backslash \{{{q}_{1}}\text{ }\!\!\}\!\!\text{ }\subseteq \text{g}({{\tilde{X}}_{1}})$.
综上, 有
$K\backslash \{{{q}_{1}}\text{ }\!\!\}\!\!\text{ }\subseteq \text{g}({{\tilde{X}}_{1}})$
成立. 证毕
例5 对表1的模糊技能背景$(Q, S, \tilde{I})$, K为$(Q, S, \tilde{I})$在合取模型下诱导的简单闭包空间.对∀ q∈ Q, 利用定理10逐一验证K在q处是否是后级的.
对q1∈ Q, 存在s1, 对∀ p∈ Q\{q1}, 满足
$\tilde{I}({{q}_{1}}, {{s}_{1}})\text{=}0.9\text{=}\vee W({{s}_{1}})> \tilde{I}(p, {{s}_{1}})$.
故K在q1处是后级的.类似可验证K在q2, q3处均是后级的.对q4∈ Q, 不存在s∈ S, 使得对∀ p∈ Q\{q4}, 有
$\tilde{I}({{q}_{4}}, s)> \tilde{I}(p, s)$
成立.故K在q4处不是后级的.类似, 易得K在q5处不是后级的.
将满足模糊技能背景$(Q, S, \tilde{I})$在合取模型下诱导的简单闭包空间在问题q∈ Q处是前级和后级的所有q构成的集合分别称为前级问题集(Forward-Graded Problem Set, FGS)和后级问题集(Backward-Graded Problem Set, BGS).下文基于定理9、推论7和定理10, 给出获取前级问题集和后级问题集的算法3.
算法3 获取前级问题集和后级问题集
输入 模糊技能背景$(Q, S, \tilde{I})$
输出 前级问题集和后级问题集
step 1 令FGS=Ø .对每个q∈ Q, 执行如下步骤.
step 1.1 对∀ p∈ Q\{q}, 如果不存在s∈ S, 满足
$\tilde{I}(p, s)> \tilde{I}({{q}_{1}}, s)$,
则返回step 1, 否则执行step 1.2.
step 1.2 对每个p∈ Q\{q}, 执行step 1.3.
step 1.3 逐一遍历Q\{q, p}的幂集A中的所有元素K.计算$\mathcal{A}_{p}^{q}$.若$\text{ }\!\!|\!\!\text{ }\mathcal{A}_{p}^{q}\text{ }\!\!|\!\!\text{ =}0$, 返回step 1.2, 否则执行step 1.4.
step 1.4 计算$\mathcal{B}_{p}^{q}$.若对$\forall K\in \mathcal{B}_{p}^{q}$, 都有∀ s∈ S,
$\tilde{I}(p, s)\le \underset{q\in K}{\mathop{\vee }}\, \tilde{I}(q, s)$
成立, 则
FGS← FGS∪ {q},
否则返回step 1.
step 2 令BGS=Ø .
step 3 对∀ s∈ S, 遍历Q中的所有问题q, 若只存在唯一一个q, 使得
$\tilde{I}(q, s)\text{=}\vee W(s)$
成立, 则
BGS← BGS∪ {q}.
step 4 输出前级问题集和后级问题集.
对于算法3, step 1的时间复杂度最大为
$O(|Q|(|Q|-1)|S|)$,
step 3的时间复杂度最大为$O(|Q||S|)$, 故算法3的时间复杂度最大为
$O(|Q|(|Q|-1)|S|)$.
本节在5个UCI数据上验证算法1~算法3的有效性.实验环境如下:Windows 10及Intel (R) Core (TM) i7-9700UCPU @3.00 GHz, 16.0 GB内存.数值实验所用软件为Python 3.8.
在UCI数据中选取Soybean_Small(简记为Soy-bean)、Stone Flakes、Daily Demand Forecasting Or-ders(简记为Daily)、Somerville Happiness Survey(简记为Somerville)、Algerian Forest Fires(简记为Fires)这5个数据集.通过min-max标准化处理原数据.将标准化后的每个数据集看作一个模糊技能背景$(Q, S, \tilde{I})$ (对象视作问题, 属性视作技能).Soybean原数据集有35个属性, 但预处理后有14个属性对应整列的信息值全为0, 故删除这14个属性.
对于标准化后的数据集, 存在大部分数据集技能对应的熟练程度过小或过细的问题, 导致生成知识结构的过程过于繁杂, 并且在实际教育背景中, 对技能熟练程度划分过小或过细会严格占用个体测试以及技能评估的时间.因此, 为了更贴切KST的教育背景, 将标准化后的信息值保留一位小数, 并根据不同的数据特点, 将Soybean、Stone Flakes、Daily、Fires数据集上分别小于等于0.4、0.6、0.6、0.5的信息值都替换成0, 并使用
$W(S)=\sum\limits_{s\in S}{|W(s)|}$
表示模糊技能背景中所有技能的技能层集的基数总和.数据预处理后的具体信息如表7所示.
| 表7 实验数据集 Table 7 Experimental datasets |
为了简洁表示文献[26]的算法, 使用算法A表示文献[26]中生成简单闭包空间的方法, 使用算法B表示文献[26]中保持简单闭包空间不变, 获取极小技能集M和冗余技能集R的方法(S\R=M).注意到由算法B得到的冗余技能集与技能的顺序有关, 所以冗余技能集不唯一.若要得到所有的冗余技能集, 需要对整个技能集S进行全排列, 重复执行算法B.考虑到算法对比的需要, 对于算法B, 本文不考虑对技能集S进行全排列, 只考虑技能集S的原始顺序这一种情形, 此时技能约简的结果是唯一的.
表8给出运用算法2进行技能层约简后得到的约简结果和运行时间, 另外给出运用算法B进行技能约简后得到的约简结果和运行时间.注意:为了简洁表示可约简技能层, 表中使用
| 表8 算法2和算法B约简结果与运行时间对比 Table 8 Comparison of reduction results and running time between algorithm 2 and algorithm B |
注意到由算法2得到的可约简技能层模糊技能背景不是唯一的, 故对应的可约简技能层和可约简技能也不唯一.因此, 表8的第2列只给出运行算法2得到的第一个可约简技能层模糊技能背景对应的可约简技能层和可约简技能.表中算法2的运行时间是获取所有可约简技能层模糊技能背景的时间.通过表8可以发现, 两种算法的约简结果是不同的, 并且算法2的运行时间远小于算法B.算法B只对技能集S的原始顺序执行一次, 由此说明算法2的有效性.
下文进一步说明技能层约简方法的高效性.首先对模糊技能背景$(Q, S, \tilde{I})$, 运用算法1获得模糊技能概念格${{L}_{Q}}(Q, S, \tilde{I})$, 对于$(Q, S, \tilde{I})$对应的模糊技能映射(Q, S, τ ), 运用算法A获得简单闭包空间K.取算法2得到的可约简技能层模糊技能背景, 再次运用算法1生成模糊技能概念格${{L}_{Q}}(Q, S, \tilde{I})$.
另外, 对于算法B约简后得到的极小技能集, 再次运用算法A生成简单闭包空间K.所得结果如表9所示, 其中, $|\mathcal{K}|$表示简单闭包空间K中的知识状态个数, 最后一行的求和表示对算法运行时间的求和.
| 表9 约简前后获取简单闭包空间的运行时间 Table 9 Running time for obtaining simple closure space before and after reduction |
通过表9可以发现, 技能层约简前运用算法1获取${{L}_{Q}}(Q, S, \tilde{I})$的运行时间少于算法A获取K的运行时间, 并且技能层约简后再次运用算法1获取${{L}_{Q}}(Q, S, \tilde{I})$的运行时间明显小于约简前的运行时间, 说明算法1比算法A更高效.
为了更直观地反映技能层约简以及技能约简前后算法1和算法A分别生成${{L}_{Q}}(Q, S, \tilde{I})$和K的运行时间受$|\mathcal{K}|$的影响, 以折线图的形式直观呈现它们之间的差距, 具体如图3所示.图中Algorithm_1_R表示经过技能层约简(算法2)后再运用算法1获得${{L}_{Q}}(Q, S, \tilde{I})$的运行时间, Algorithm_1_O表示对原始的模糊技能背景$(Q, S, \tilde{I})$运用算法1获得${{L}_{Q}}(Q, S, \tilde{I})$的运行时间, Algorithm_A_R表示经过技能约简(算法B)后再运用算法A获得K的运行时间, Algorithm_A_O表示对原始的模糊技能映射(Q, S, τ )运用算法A获得K的运行时间.
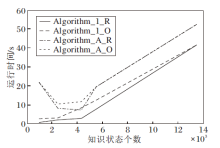 | 图3 算法1和算法A的运行时间随$|\mathcal{K}|$的变化Fig.3 Running time of algorithm 1 and algorithm A changing with $|\mathcal{K}|$ |
通过图3可以发现, 当简单闭包空间K中的知识状态的个数$|\mathcal{K}|$越大, 算法1和算法A运行耗时越多.Algorithm_1_R和Algorithm_A_R与Algorithm_A_O和Algorithm_1_O的运行时间差距是较大的, 说明经过约简后算法1和算法A的运行时间差距明显大于约简前.另外, 从表9的总运行时间可得:运用算法2进行技能层约简后, 再次运用算法1获取${{L}_{Q}}(Q, S, \tilde{I})$的总运行时间为55.237 5 s; 运用算法B进行技能约简后, 再次运用算法A获取K的总运行时间为109.310 3 s.由此说明算法2的约简大幅提升生成简单闭包空间的效率.因此算法1和算法2具有高效性.
针对表7的5个模糊技能背景$(Q, S, \tilde{I})$, 运用算法3计算$(Q, S, \tilde{I})$在合取模型下诱导的简单闭包空间的前级问题集和后级问题集, 结果如表10所示.
| 表10 简单闭包空间的前级(后级)问题集 Table 10 Forward-graded(backward-graded) problem sets of simple closure space |
本文基于模糊形式概念分析研究模糊技能映射.首先, 基于构造的算子计算模糊技能概念格, 通过外延集族获得模糊技能映射在合取模型下诱导的简单闭包空间, 通过内涵集族获得每个知识状态对应的最小技能熟练程度.再基于模糊技能背景, 提出技能层约简的概念, 使生成知识结构的效率更高.然后, 给出模糊技能映射诱导的简单闭包空间是前级和后级的充要条件.最后, 在5个UCI数据集中验证本文算法的有效性.本文建立模糊形式概念分析与知识空间理论的一些联系, 为研究知识空间理论提供另一种途径.今后将进一步考虑模糊技能映射在其它模型(析取模型和能力模型)下的技能层约简以及寻找前级和后级知识结构的充要条件.另外, 后续研究将考虑模糊技能映射下的技能评估和路径选择问题.
本文责任编委 张燕平
Recommended by Associate Editor ZHANG Yanping
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|
| [19] |
|
| [20] |
|
| [21] |
|
| [22] |
|
| [23] |
|
| [24] |
|
| [25] |
|
| [26] |
|
| [27] |
|
| [28] |
|
| [29] |
|
| [30] |
|
| [31] |
|
| [32] |
|
| [33] |
|
| [34] |
|
| [35] |
|
| [36] |
|
| [37] |
|
| [38] |
|