本文提出一个具有支持网络剪枝特性的搜索空间, 允许在搜索过程中对网络进行剪枝.

1.1.1 搜索空间与搜索网络

为了从源头上限制神经网络的参数和浮点计算, 考虑将更轻量级的卷积操作引入搜索空间中, 因此提出一个支持网络剪枝的搜索空间, 包含7个操作, 即GhostConv^[25]、3× 3 深度可分离卷积、3× 3 扩张卷积、3× 3 最大池化、3× 3 平均池化、恒等映射和零操作.其中GhostConv是一个便捷的卷积操作, 参数和FLOPs约为3× 3深度可分离卷积的一半.

NASNet^[26]和DARTS(Differentiable Architecture Search)^[27]在预定义的搜索空间中搜索两种类型的单元, 即正常单元和还原单元.正常单元用于返回相同维度的特征图, 而还原单元用于返回高度和宽度减少一半的特征图.本文可借鉴这一思想.

单元的拓扑结构是一个由n个节点组成的有向无环图(Directed Acyclic Graph, DAG), 按照规则有序连接.

具体来说, 每个节点N表示卷积网络的一个特征图.节点N_p和N_q连接, 形成单元的一条边E_{(p, q)}, 表示从搜索空间中选择的某种操作.每个节点和所有前驱节点连接, 并满足

${{N}_{p}}=\underset{q< p}{\mathop \sum }\, {{o}^{(p, q)}}{{N}_{q}}$,

其中, o^{(p, q)}表示从给定的操作集O中选择一个操作, 并应用于边E_{(p, q)}.为了使搜索空间连续化, 对离散操作选择进行连续松弛化:

${{\bar{o}}^{\left( p, q \right)}}\text{=}\underset{o\in O}{\mathop \sum }\, \left( \frac{\text{exp}\left( \alpha _{o} \ ^{\left( p, q \ \right)} \ \ \ \right)}{\mathop{\sum }_{o \ '\in O} \ \ \ \text{exp} \left( \alpha _{o \ '} \ ^{\left( p, q \right)} \ \ \ \right)} \right)o({{N}_{p}})$,

其中, $\alpha _{o \ '}^{\left( p, q \right)}$是$\left| O \right|$维向量α ^{(p, q)}的一个元素, 表示N_p和N_q之间的操作o'的权重.架构参数α 反映每个操作的重要性, 通过对架构参数进行更新, 得到单元的最终结构.

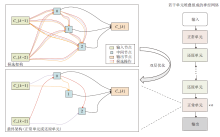
完整的神经网络由若干个正常单元和还原单元堆叠组成, 基本单元的搜索过程如图1所示.在网络总深度的1/3和2/3的位置为还原单元, 其余位置为正常单元, 这样的设置有利于为任何尺寸的输入图像构建可扩展的架构.

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 基本单元的搜索过程Fig.1 Search process of basic cell

1.1.2 掩码学习模块

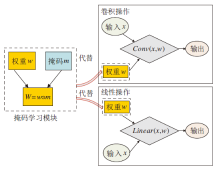
由于NAS的搜索过程中缺乏对网络剪枝的支持, 本文提出一个掩码学习模块, 结构如图2所示.模块包含一组与权重参数维度相同的二值掩码序列, 将其引入搜索空间的卷积和线性操作中, 为每个网络权重分配一个掩码.在搜索过程中, 根据设立的剪枝标准, 对网络性能贡献度低的权重进行掩码, 以便在后续的训练中删除该权重.

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 掩码学习模块结构图Fig.2 Structure of mask learning module

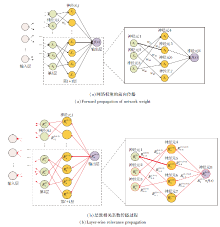
由于掩码是一组二进制参数, 直接更新具有挑战性, 因此引入层级相关系数传播(LRP)^[24], 协助掩码参数的更新, 同时作为剪枝标准.LRP最初被用于机器学习的可解释性, 计算每个输入特征对于网络输出的相对重要性, 分析神经网络的决策过程.LRP的计算是通过反向传播实现的, 具体如图3所示.

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 网络权重和层级相关性系数的传播过程Fig.3 Propagation process of network weight and layer-wise relevance score

在反向传播过程中, 通过对神经元激活的正向传播过程进行逆向传播, 计算每个网络单元(神经元或网络权重)对于输出的贡献, 并将这些贡献值分配给相应的网络单元.

传统的剪枝标准通常只考虑每个神经元的权重大小和梯度信息, 无法衡量每个神经元在网络中的作用.例如, 基于权重的剪枝标准可能删除网络中重要的神经元, 导致网络性能的衰退.

相比之下, LRP通过反向传播重要性考虑每个权重在网络中的作用, 从而更好地评估其重要性.此外, 使用LRP作为剪枝标准有助于保持网络的功能完整性.

因为可基于每个权重的贡献度进行剪枝, 所以剪枝后的网络仍然可以保持原有的功能, 而不会失去关键的权重.

为了确保所有重要性得到正确的分配和保存, LRP的重新分配遵守分层守恒原则:

$f(x)=\ldots =\underset{j\in l+1}{\mathop \sum }\, R_{j}^{l+1}=\underset{i\in l}{\mathop \sum }\, R_{i}^{l}=\ldots =\underset{d}{\mathop \sum }\, R_{d}^{1}$,

其中, $R_{j}^{l+1}$表示非线性网络中第l+1层中神经元j的相关系数, $R_{i}^{l}$表示第l层中神经元i的相关系数.

LRP与网络输出f(x)直接建立联系, 并在逐层分配中遵守分层守恒原则.即使在剪枝过程中神经网络隐藏层的大小以及神经元的数量发生变化, 分层守恒原则也能保证LRP的数量固定, 从而保证剪枝程序的平稳运行.

相关系数的分配是根据发送到前一层的神经元的信息获得的, 这种信息为R_{i← j}.在非线性网络中, 神经元的激活值z_j是x_j的非线性函数.当激活函数单调递增时, 如双曲切线和整流函数, 相关系数的分配基于局部和全局预激活的比率:

$R_{i\leftarrow j}^{\left( l, l+1 \right)}=\frac{{{z}_{ij}}}{{{z}_{j}}}\cdot R_{j}^{\left( l+1 \right)}$,

其中,

z_ij=x_iw_ij,

表示第l层的神经元i对第l+1层中神经元j的加权激活值,

$\underset{\text{k}\in \text{l}}{\mathop \sum }\, {{z}_{kj}}+b$,

表示第l层所有与第l+1层神经元j连接的神经元对j的加权激活值, b表示偏置项.

l+1层的某个神经元j的相关系数$R_{j}^{\left( l+1 \right)}$为l+1层的神经元j与l层相连接的神经元的相关系数之和, 即

${{z}_{j}}=\underset{i}{\mathop \sum }\, R_{i\leftarrow j}^{\left( l, l+1 \right)}=R_{j}^{\left( l+1 \right)}$.

当相关性被用作修剪标准时, 无论隐藏层的大小和每层迭代修剪的神经元数量如何变化, 这一特性都有助于保持逐层相关性守恒.根据相关系数R∈ (0, 1)^N学习用于剪枝的掩码参数m∈ {0, 1}^N, 其中N表示预训练网络权重的数量.根据剪枝的要求, 选择前k个最大的相关系数, 可以表述为第l层的神经元i与第l+1层中神经元j之间的权重w_ij分配的掩码值:

$m_{\left( i, j \right)}^{\left( l, l+1 \right)}=1(\left| R_{i\leftarrow j}^{\left( l, l+1 \right)} \right|\ge {{\left| {{R}^{\left( l, l+1 \right)}} \right|}_{k}})$,

其中, $R_{i}^{l}$表示第l层中神经元i的相关系数, ${{\left| {{R}^{\left( l, l+1 \right)}} \right|}_{k}}$表示第l层与第l+1层中第k个最大的相关系数值, 1(· )表示判别函数, 如果满足判别条件, 函数值赋为1, 否则赋为0.

将第l层与第l+1层中所有的相关系数按照从大到小的顺序排列, 如果神经元i与神经元j之间的权重对应的相关系数的绝对值

$\left| R_{i\leftarrow j}^{\left( l, l+1 \right)} \right|\ge {{\left| {{R}^{\left( l, l+1 \right)}} \right|}_{k}}$,

则将w_ij对应的掩码值$m_{\left( i, j \right)}^{\left( l, l+1 \right)}$设置为1, 在后续剪枝中保留该权重.

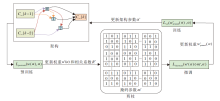
非结构化剪枝通常需要三个阶段:网络预训练、剪枝和微调, 流程如图4所示.为了训练有关剪枝权重的架构参数, 方法将网络权重和掩码参数的更新转化为双层优化中较低层次的优化问题, 使用基于梯度的方式与架构参数交替更新.UPNAS的搜索目标在于获得最优的架构参数α ^* , 使剪枝后网络的验证损失L_val(w_pruned(α ), α )最小, 即

${{\alpha }^{* }}=arg\underset{\alpha }{\mathop{\text{min}}}\, {{L}_{val}}({{w}_{pruned}}(\alpha ), \alpha )$,

$s.t.w{{* }^{(}}\alpha )=arg\underset{\text{w}}{\mathop{\text{min}}}\, {{L}_{p}}{{_{re}}_{-train}}(w(\alpha ), \alpha )$,

$R* =arg\underset{\text{R}}{\mathop{\text{min}}}\, {{L}_{pr}}{{_{e}}_{-train}}(w(\alpha ), \alpha )$,

${{w}_{pruned(}}_{\alpha )}=arg\underset{{{\text{w}}^{\text{* }}}\left( \text{ }\!\!\alpha\!\!\text{ } \right)}{\mathop{\text{min}}}\, {{L}_{\text{fine-tune}}}({{w}^{* }}(\alpha )m* , \alpha )$,

其中, w(α )表示预训练网络的权重参数, w_pruned(α )表示微调网络的权重参数.

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 非结构化剪枝方法流程图Fig.4 Flowchart of unstructured pruning method

UPNAS依次实现对w(α )、m、w_pruned(α )和α 的学习.首先, 给定一个初始化的搜索架构, 架构参数在预训练阶段保持不变, 而网络权重通过随机梯度下降法(Stochastic Gradient Descent, SGD)进行更新.根据LRP的传播规则, 相关系数采用类似于反向传播的方式进行更新.最小化预训练损失L_pre-train(w(α ), α )以更新权重w^* (α )与相关系数R^* .然后, 通过更新后的掩码参数m^* 删除网络中冗余的权重参数.在微调阶段, 对剪枝后的网络重新训练, 更新非零权重w_pruned(α )以达到最佳的网络精度.最后, 最小化验证损失L_val(w_pruned(α ), α ), 即可获得最优的架构参数α ^* .

本文在两个公开的分类数据集CIFAR-10^[28]和ImageNet^[29]上进行实验, 用于评估UPNAS的有效性.CIFAR-10数据集是一个分类数据集, 由60 000幅彩色图像组成, 平均分为10类, 训练图像50 000幅和测试图像10 000幅.ImageNet数据集共有1 000个类别, 14 197 122幅图像, 是一个用于分类的大型计算机视觉数据集, 每幅图像都经过手工标定.

将CIFAR-10数据集按照1∶ 1的比例划分为训练集和验证集, 便于在搜索过程中交替更新不同的参数.使用Top-1准确率和网络参数量作为评估指标.

本文使用SGD分别对预训练网络和微调网络进行训练, 历时60个迭代周期, 动量设置为0.9, 权重衰减为0.000 3, 每个训练批次由64幅图像组成.预训练和微调阶段的起始学习率分别设置为0.025和0.01, 使用余弦退火在每20个历时后衰减为原来的1/10.搜索网络由不同数量的单元堆叠构成, 网络中1/3和2/3的位置为还原单元, 其它为正常单元.

实验使用PyTorch框架在英伟达Tesla V100上进行训练和推理, 搜索过程累积花费2.1~2.8个GPU-day.

为了权衡网络的分类准确率和参数量, 将剪枝率设置为95%, 在CIFAR-10数据集上展开一组实验, 探究网络层数和初始通道数对剪枝网络的影响.分别取网络层数为14, 16, 18, 20, 初始通道数为36, 48, 64, 实验结果如表1所示, 表中黑体数字表示最优值.由表可以发现, 搜索的剪枝网络的参数量随着网络层数与通道数的增加而增大.而且, 当保持网络层数不变时, 增大网络的初始通道数有益于准确率的提升.但是, UPNAS在CIFAR-10数据集上取得的Top-1准确率与网络层数并未呈现正相关的关系.可以看出, 层数的加深导致网络复杂度的增加, 从而产生过拟合的现象, 阻碍UPNAS取得更佳的表现.

表1

Table 1

表1(Table 1)

表1 网络层数和初始通道数对算法的影响 Table 1 Effect of network layers and initial channels on algorithm performance 网络层数 初始通道数 Top-1准确率/% 参数量 14 36 93.95 0.124× 106 48 95.42 0.188× 106 64 96.35 0.367× 106 16 36 94.26 0.164× 106 48 94.78 0.283× 106 64 96.16 0.425× 106 18 36 93.78 0.225× 106 48 95.11 0.340× 106 64 95.83 0.479× 106 20 36 93.88 0.262× 106 48 94.73 0.383× 106 64 95.02 0.524× 106

表1 网络层数和初始通道数对算法的影响 Table 1 Effect of network layers and initial channels on algorithm performance

实验数据表明, 当网络层数设置为14, 初始通道数设置为64时, NPF取得最高的分类准确率, 为96.35%, 网络参数仅为0.367Í 10⁶个.PR-DARTS(Pruning-Based DARTS)^[30]也测试DARTS网络剪枝后的性能, 在相同的剪枝率下, 在CIFAR-10数据集上取得93.74%的Top-1准确率.相比之下, UPNAS在CIFAR-10数据集上的Top-1准确率提升2.61%.后续实验将在网络层数为14和初始通道数为64下搜索剪枝网络.

为了评估网络在极端剪枝率场景下的准确率衰减情况, 将网络剪枝率设置为99%, 在CIFAR-10数据集上进行实验.HYDRA^[15]作为目前先进的非结构化剪枝方法之一, 使用剪枝参数帮助掩码的更新, 能够为网络提供99%的剪枝率.因此, 使用HYDRA对MobileNetV2^[16]、DARTS^[26]、EfficientNet^[31]和ResNet-18^[32]进行剪枝, 并与UPNAS进行对比, 实验结果如表2所示, 表中黑体数字表示最优值.压缩比是以DARTS的参数量(3.3× 10⁶)为基准.

表2

Table 2

表2(Table 2)

表2 极端剪枝率下6种方法的结果对比 Table 2 Result comparison of 6 methods with extreme pruning rates 方法 Top-1准确率/% 参数量 压缩比 MobileNetV2(剪枝) 73.44 2.22× 104 148.65倍 EifficientNet(剪枝) 79.69 20.23× 104 16.31倍 ResNet-18(剪枝) 90.62 2.30× 104 29.57倍 DARTS(剪枝) 81.25 2.10× 104 157.14倍 PR-DARTS(Small) 89.06 1.70× 104 194.12倍 UPNAS 91.63 2.30× 104 143.48倍

表2 极端剪枝率下6种方法的结果对比 Table 2 Result comparison of 6 methods with extreme pruning rates

由表2可看出, 在极端剪枝率下, 不同网络架构的性能均出现退步, 相比在95%剪枝率的场景下, UPNAS在CIFAR-10数据集上的Top-1准确率下降4.72%, 但非剪枝场景设计的网络架构的性能下降得更快.例如, 相比剪枝前, 剪枝后的DARTS在CIFAR-10数据集上的准确率下降15.99%.这一结果也表明, 尽管先进的剪枝技术能够大幅削减网络权重参数量, 但由于人为设计的剪枝策略难以运用最优方式保留或删除网络权重, 因此导致网络在剪枝前后的泛化差距较高.UPNAS将剪枝集成在架构搜索过程中, 通过优化算法自动学习掩码参数m, 可避免此问题.

值得注意的是, 相比DARTS架构, PR-DARTS(Small)在保持89.06%的准确率的同时取得194.12倍的网络压缩率.PR-DARTS与UPNAS类似, 区别在于PR-DARTS在剪枝过程中遵从HYDRA提出的掩码学习方式, 而UPNAS使用层级相关系数^[27]作为剪枝标准, 能够衡量每个权重的重要性.相比PR-DARTS(Small), UPNAS取得2.57%的准确率提升, 网络参数量几乎相当.

本文选用如下3种压缩方法:1)神经网络架构搜索方法.TAS^[21]、ACGhostNet-B^[23]、ACGhostNet-C^[23].2)高效架构手工设计方法.ShuffleNet^[11]、MobileNetV2^[16].3)知识蒸馏方法.文献[33]方法、RKD(Relational Knowledge Distillation)^[34]、PU(Po-sitive-Unlabeled) Method^[35]、文献[36]方法、DFND(Data-Free Noisy Distillation)^[37].

在ImageNet数据集上重新训练UPNAS, 引入指

标A/P, 用于评估神经网络使用参数的效率.A/P结合模型的准确率和参数量, 公式如下:

A/P=Top-1准确率参数量.

可以看出, A/P值越大, 说明网络使用参数的效率越高^[38].

UPNAS和其它压缩方法在CIFAR-10、ImageNet数据集上的指标值对比如表3所示, 表中黑体数字表示最优值.由表可知, 相比其它方法, UPNAS性能最优.在CIFAR-10、ImageNet数据集上, UPNAS获得96.35%和73.60%的Top-1准确率, 相比MobileNetV2, 分别获得4.30%和1.60%的准确率提升, 网络参数量为0.367× 10⁶和0.480× 10⁶.相比ShuffleNet, UPNAS以10.34倍的A/P值在ImageNet数据集上获得相同的分类精度.相比ACGhostNet-C, UPNAS在CIFAR-10上获得1.25%的准确率提升, 两种方法在ImageNet数据集上获得相等的精度, 但UPNAS取得10.76倍的A/P值提升.此外, 相比文献[36]方法, UPNAS在两个数据集上的准确率分别提升1.69%和1.11%, 并取得262.53和152.33的A/P值.

表3

Table 3

表3(Table 3)

表3 UPNAS与其它压缩方法的指标值对比 Table 3 Index value comparison of UPNAS and other compression methods 方法 年份 CIFAR-10 ImageNet Top-1准确率/% 参数量 A/P Top-1准确率/% 参数量 A/P TAS 2022 91.94 2.40× 106 38.31 65.10 5.57× 106 11.69 ACGhostNet-B 2022 95.20 4.00× 106 23.80 73.40 5.20× 106 14.16 ACGhostNet-C 2022 95.10 4.00× 106 23.78 73.60 5.20× 106 14.15 ShuffleNet 2018 - - - 73.60 5.00× 106 14.72 MobileNetV2 2018 92.05 2.30× 106 40.02 72.00 3.40× 106 21.18 文献[33]方法 2019 94.30 0.69× 106 136.67 71.25 4.23× 106 16.84 RKD 2019 94.41 0.69× 106 136.83 71.32 4.23× 106 16.86 PU Method 2019 93.75 11.00× 106 8.52 61.92 12.00× 106 5.16 文献[36]方法 2021 94.66 0.69× 106 137.19 72.49 4.23× 106 17.14 DFND 2021 94.02 11.00× 106 8.55 61.75 12.00× 106 5.15 UPNAS - 96.35 0.367× 106 262.53 73.60 0.480× 106 152.33

表3 UPNAS与其它压缩方法的指标值对比 Table 3 Index value comparison of UPNAS and other compression methods

为了进一步探究UPNAS的有效性, 选择如下剪枝方法:WRN(Wide Residual Networks)^[7]、HRank(High Rank of Feature Maps)^[39]、GAL(Generative Adversarial Learning)-0.5^[40]、ABCPruner(A New Chan-nel Pruning Method Based on Artificial Bee Colony Algorithm)^[41]、PKP(Progressive Kernel Pruning)^[42]、FPGM(Filter Pruning via Geometric Median)^[43]、SFP(Soft Filter Pruning)^[44]、TAS(Transformable Archi-tecture Search)^[45].

各方法在CIFAR-10、ImageNet数据集上的实验结果如表4所示, 表中黑体数字表示最优值, 压缩率是根据使用GAL-0.5修剪后的网络参数量计算的.由表可知, 相比GAL-0.5, UPNAS在CIFAR-10、ImageNet数据集上获得3.80%和1.65%的准确率提升.以GAL-0.5的网络参数量为基准, UPNAS在CIFAR-10、ImageNet数据集上获得2.59倍和44.17倍的网络压缩率, 在CIFAR-10上取得最高的分类精度, 在ImageNet上的分类精度比ABCPruner降低0.26%, 但获得24.54倍的模型压缩率, 参数量大幅减少.可以看出, UPNAS不仅可以删除大量冗余的网络参数, 而且可以保持神经网络的泛化能力, 提高网络效率.

表4

Table 5

表4(Table 5)

表4 UPNAS与剪枝方法的指标值对比 Table 5 Index value comparison of UPNAS and other pruning methods 方法 年份 CIFAR-10 ImageNet Top-1准确率/% 参数量 压缩比 Top-1准确率/% 参数量 压缩比 HRank 2020 94.24 0.66× 106 1.44倍 71.98 13.77× 106 1.54倍 GAL-0.5 2019 92.55 0.95× 106 1倍 71.95 21.20× 106 1倍 ABCPruner 2020 93.58 0.56× 106 1.70倍 73.86 11.75× 106 1.80倍 WRN 2019 95.38 - - 72.65 4.59× 106 4.66倍 PKP 2021 93.82 - - 70.06 12.78× 106 1.66倍 FPGM 2019 92.31 0.269× 106 3.53倍 68.41 6.46× 106 3.28倍 SFP 2018 92.08 0.269× 106 3.53倍 67.10 6.46× 106 3.28倍 TAS 2019 93.16 0.106× 106 8.96倍 69.15 7.40× 106 2.86倍 UPNAS - 96.35 0.367× 106 2.59倍 73.60 0.480× 106 44.17倍

表4 UPNAS与剪枝方法的指标值对比 Table 5 Index value comparison of UPNAS and other pruning methods