引用本文
冯艳红, 王改革, 李明亮, 李晰. 基于自适应 ε约束处理法的改进蛾子搜索算法 . 模式识别与人工智能, 2023,36(6): 483-494
FENG Yanhong, WANG Gaige, LI Mingliang, LI Xi. Modified Moth Search Algorithm Based on Adaptive ε-Constrained Method . PATTERN RECOGNITION AND ARTIFICIAL INTELLIGENCE, 2023,36(6): 483-494.  
Doi: 10.16451/j.cnki.issn1003-6059.202306001
Permissions
Copyright©2023, 《模式识别与人工智能》编辑部
《模式识别与人工智能》编辑部
基于自适应 ε约束处理法的改进蛾子搜索算法
冯艳红1,2,3, 王改革4, 李明亮1,2, 李晰1
1.河北地质大学 信息工程学院 石家庄 050031
2.河北地质大学 河北省智能传感物联网技术工程研究中心石家庄 050031
3.河北地质大学 河北省光电信息与地球探测技术重点实验室 石家庄 050031
4.中国海洋大学 计算机科学与技术学院 青岛 266100
通讯作者：

王改革,博士,副教授,主要研究方向为进化计算、调度优化.E-mail:wgg@ouc.edu.cn.

作者简介:

冯艳红,硕士,教授,主要研究方向为进化计算、组合优化.E-mail:qinfyh@hgu.edu.cn.

李明亮,博士,教授,主要研究方向为物联网技术及应用.E-mail:li_mingliang@hgu.edu.cn.

李 晰,博士,副教授,主要研究方向为进化计算、机器学习.E-mail:lixi_sjz@foxmail.com.

收稿日期: 2023-04-10 接受日期: 2023-06-08
资助项目: 国家自然科学基金项目(No.61806069)、河北省重点研发计划项目(No.22375415D)、河北省高校科学技术研究项目(No.ZD2022083)资助
摘要

多需求多维背包问题包含相互冲突的两类不等式约束,对其可行域的搜索异常困难.因此,文中提出基于 ε约束处理法的改进蛾子搜索算法.在莱维飞行阶段,根据当前进化代数调节步长值.在直接飞行阶段,引入突变率,增加算法的种群多样性.最后,对整个种群应用均匀变异算子,提高算法的全局探索遍历性.采用空间映射方法实现搜索空间到问题空间的转换,采用自适应ε 约束处理法处理约束.在经典的96个测试用例上的验证实验表明:自适应莱维飞行算子、突变直接飞行算子、均匀变异算子对算法求解精度都具有显著效果,文中算法在求解绝大多数测试用例时的寻优精度较优.此外,文中应用正交实验方法分析参数对于ε约束处理法的影响.

关键词: 进化算法; 蛾子搜索算法(MS); 自适应ε约束处理法;; 多需求多维背包问题(MDMKP)
中图分类号:TP301.6
Modified Moth Search Algorithm Based on Adaptive ε-Constrained Method
FENG Yanhong1,2,3, WANG Gaige4, LI Mingliang1,2, LI Xi1
1. School of Information Engineering, Hebei GEO University, Shijiazhuang 050031
2. Intelligent Sensor Network Engineering Research Center of Hebei Province, Hebei GEO University, Shijiazhuang 050031
3. Hebei Key Laboratory of Optoelectronic Information and Geo-detection Technology, Hebei GEO University, Shijiazhuang 050031
4. School of Computer Science and Technology, Ocean University of China, Qingdao 266100
Corresponding author：
WANG Gaige, Ph.D., associate professor. His research interests include evolutionary computing and scheduling optimization.

About Author:
FENG Yanhong, master, professor. Her research interests include evolutionary computing and combinatorial optimization.
Li Mingliang, Ph.D., professor. His research interests include Internet of things technology and applications.
LI Xi, Ph.D., associate professor. Her research interests include evolutionary computing and machine learning.

Fund:National Natural Science Foundation of China(No.61806069), Key Research and Development Plan Project of Hebei Province(No.22375415D), Science and Technology Project of Hebei Education Department(No.ZD2022083)
Abstract

The multidemand multidimensional knapsack problem includes two types of inequality constraints with conflicts, making the search for the feasible solution region exceptionally difficult. Therefore, a modified moth search algorithm(MMS) based on adaptive ε-constrained method is proposed in this paper. In the Lévy flight phase, the step is adjusted according to the current iteration. In the straight flight phase, the mutation rate is introduced to increase the diversity of the population. Finally, the uniform mutation operator is applied to the whole population to improve the global search capability of the algorithm. The space mapping method is utilized to transfer the search space to the problem space, and the adaptive ε-constrained method is adopted. Experiments on classic 96 benchmark instances show that adaptive lévy flight operator, mutation straight flight operator and uniform mutation operator contribute significantly to the solution accuracy of the algorithm and the proposed algorithm performs better on the majority of instances. Furthermore, orthogonal experimental design method is utilized to analyze the influence of parameters on the ε-constrained method.

Key words: Key Words Evolutionary Algorithm; Moth Search Algorithm; Adaptive ε-Constrained Method;; Multidemand Multidimensional Knapsack Problem(MDMKP)

组合优化问题(Combinatorial Optimization Pro-blem, COP)的求解一直是运筹学领域重要的研究主题之一.典型的组合优化问题包括:作业车间调度问题(Job Shop Scheduling Problem, JSSP)[1, 2], 图着色问题(Graph Coloring Problem, GCP)[3], 车辆路径规划问题(Vehicle Routing Problem, VRP)[4], 旅行商问题(Travelling Salesman Problem, TSP)[5], 多维背包问题(Multidimensional Knapsack Problem, MKP)[6].

多需求多维背包问题(Multidemand MKP, MDMKP)[7]是MKP的一个重要扩展, 也被证明是一类复杂的NP-hard问题.相比MKP, MDMKP包含一组与背包约束冲突的需求约束, 是一类更难求解的多约束0-1规划问题.现实生活中的很多问题可以建模为MDMKP, 包括设备配置、选址方案设计、投资预算、证券选择等, 但是, MDMKP并未引起广大学者更多的关注.

目前, 针对MDMKP问题的求解分为两类:确切性算法(Exact Algorithm)和启发式算法(Heuristic Algorithm).Cappanera等[7]提出嵌套禁忌搜索启发式算法, 在标准禁忌搜索算法中增加扰动策略.Gortá zar等[8]介绍一种黑盒分散搜索算法, 特别提出一种静态罚函数法, 处理MDMKP问题的约束.Arntzen等[9]提出交替控制树搜索框架, 交替使用确切性算法和启发式算法求解问题.Lai等[10]提出高效的基于两阶段解的禁忌搜索算法.Al-Shihabi[11]提出基于核思想的优化框架, 更新28个已知最优解.因此, 寻找有效的方法解决MDMKP问题是有意义的.

群智能算法[12, 13]是利用群体智能高效求解优化问题的方法, 具有不依赖梯度信息、对待求解问题无需连续、可导等特点, 已被广泛应用于求解各类优化问题, 特别是组合优化问题.受蛾子趋光性和莱维飞行的启发, Wang[14]提出蛾子搜索算法(Moth Search, MS), 基于莱维飞行算子(Lé vy Flight Ope-rator, LFO)和直接飞行算子(Straight Flight Ope- rator, SFO)实现种群中个体的更新.目前, MS已在数值优化、约束优化、多目标优化、组合优化等诸多领域被广泛应用[15, 16].因此, 将MS应用到MDMKP问题, 无疑为该问题的求解提供一种新的方法.

因此, 本文提出改进蛾子搜索算法(Modified Moth Search, MMS), 用于求解MDMKP问题.主要思想是:引入突变概率, 设计突变直接飞行算子(Mutation SFO, MSFO), 增强MMS的搜索能力; 扩大参数α 的调节范围, 设计自适应莱维飞行算子(Adaptive LFO, ALFO), 帮助算法跳出局部最优; 增加均匀变异算子(Uniform Mutation Operator, UMO), 增强种群多样性.

本文方法的创新之处在于:1)采用自适应ε 约束处理法解决MDMKP中两组相互冲突的约束条件, 从而易于采用群智能算法求解; 2)对自适应ε 约束处理法的参数使用正交实验方法进行验证, 得到一组针对MDMKP问题的最适合参数; 3)基于空间转换思想, 设计应用连续型群智能算法求解离散优化问题的框架.

1 多需求多维背包问题模型

给定具有n个物品的集合V={1, 2, …, n}, MDMKP问题[10]可描述为:从集合V中选取一组满足所有问题约束的物品组合并使所选物品总价值最大.数学描述如下:

$\begin{aligned} \max & f(x)=\sum_{j=1}^{n} c_{j} x_{j}, \\ \text { s.t. } & \sum_{j=1}^{n} a_{i, j} x_{j} \leqslant b_{i}, \forall i \in\{1, 2, \cdots, m\} ; \\ & \sum_{j=1}^{n} a_{i, j} x_{j} \geqslant b_{i}, \forall i \in\{m+1, m+2, \cdots, m+q\} ; \\ & x_{j} \in\{0, 1\}, \forall j \in\{1, 2, \cdots, n\} .\end{aligned}$ (1)

其中, cj表示物品j的价值; xj表示物品是否被选中, xj=1表示物品被选择, xj=0表示物品未被选择; ai, j表示物品j对第i种资源的消耗量; bi表示第i种资源总量.特别地, 式(1)的小于等于约束称为背包约束, 大于等于约束称为需求约束.

不失一般性, 有如下假设:

$\begin{array}{l}b_{i}> 0, a_{i, j} \geqslant 0, \forall i \in\{1, 2, \cdots, m+q\}, \forall j \in\{1, 2, \cdots, n\}, \\ \sum_{j=1}^{n} a_{i, j}> b_{i}, \forall i \in\{1, 2, \cdots, m+q\}, \\ \max _{j}\left\{a_{i, j}\right\} \leqslant b_{i}, \forall i \in\{1, 2, \cdots, m\}, \\ \min _{i}\left\{a_{i, j}\right\}＜b_{i}, \forall i \in\{m+1, m+2, \cdots, m+q\} .\end{array}$

2 改进蛾子搜索算法求解多需求多维背包问题
2.1 基本蛾子搜索算法

在MS中, 假设待求解问题对应d维解空间, 随机初始化具有N个个体的种群

P={X1, X2, …, XN}

分布于此解空间, 第i个蛾子个体在解空间的位置向量

Xi=[xi, 1, xi, 2, …, xi, d]T.

显然, 每个个体位置对应目标问题的一个潜在解.MS按照适应度值升序排序后将种群等分为子种群1(SP1)和子种群2(SP2).子种群1中的个体依据LFO进行位置更新, 子种群2中的个体依据SFO进行位置更新.

1)LFO.SP1中的个体i位置更新公式如下:

$\begin{array}{l}x_{i}^{t+1}=x_{i}^{t}+\alpha L(s), \\ \alpha=\frac{S_{\max }}{t^{2}}, \\ L(s)=\frac{1}{\pi s^{\beta}}(\beta-1) \Gamma(\beta-1) \sin \left(\frac{\pi(\beta-1)}{2}\right), \end{array}$

其中, xit和 xit+1分别表示个体i在第t代和第t+1代的位置, smax表示最大飞行步长, α 表示比例因子, L(s)表示产生服从莱维分布的随机数, Γ (· )表示伽马函数.

2)SFO.SP2中的个体i位置更新公式如下:

xit+1= λ(xit+φ(xbestt-xit)), rand> 0.5λ(xit+1φ(xbestt-xit)), rand≤0.5

其中, λ 表示比例因子, φ 表示加速因子, xbestt表示在第t代的最优个体, λ 和rand表示在(0, 1)区间内服从均匀分布的随机数.

考虑最小优化问题, MS流程如算法1所示.

算法1 MS

输入 初始化所有参数, 适应度函数f(X),

随机初始化N个个体, 确定问题维度D,

最大迭代次数T

输出 最优蛾子个体的位置, 对应适应度函数值

step 1 WHILE未达到最大迭代次数或终止条件DO.

step 2 计算个体适应度值并进行升序排列, 记录最优个体信息.

step 3 种群划分.适应度值较小的N/2个体组成SP1, 余下个体组成SP2.

step 4 应用LFO更新SP1.

step 5 应用SFO更新SP2.

step 6 合并两个新生成子种群为一个种群.

step 7 判断终止条件是否满足.若未满足, t=t+1, 转step 2.

2.2 改进的蛾子搜索算法

一般而言, MS能够求得全局最优解.但是, 面对一些复杂的约束优化问题, 特别是问题的可行解介于可行域和不可行域边界之时, MS可能会陷入局部最优.

MDMKP问题是复杂的离散约束优化问题, 问题的可行域是离散的, 如何使搜索能穿梭于各个可行区域间, 是该问题的主要挑战.多种群可能是解决该问题的方案之一.MS是基于两个子种群进化的群智能算法, 为此, 提出如下改进策略.

1)自适应莱维飞行算子(ALFO).在LFO中, 参数α 控制蛾子飞行的步长, 该步长只与当前迭代次数有关, 忽略总迭代次数.受文献[17]启发, 将参数α 修改为

α =m Smaxt2, m= tmax-ttmax.

2)突变直接飞行算子(MSFO).在SFO中, 参数λ 是调节因子, 控制算法的收敛速度和种群多样性.在MS中, 参数λ ∈ U(0, 1), 为了使蛾子朝着当前最优个体飞去, 使用一个与最大迭代次数和当前迭代次数相关的突变率λ 对蛾子个体的局部搜索进行扰动.突变率

λ =0.9- 0.9(t-1)tmax-1.

显然:过高的突变率增加算法在搜索空间中搜索更多区域的概率, 防止种群收敛到任何最优解; 过小的突变率可能导致种群早熟收敛到局部最优.参数λ 从0.9线性递减到0, 突变率增加算法的搜索能力.

3)均匀变异算子(UMO).为了增加种群多样性, 对种群中每个个体的每个基因, 以较小的概率pm进行变异, 即更新当前基因为随机生成的(0, 1)内的随机实数.变异公式

xi, j=rand(), rand()≤ pm,

其中, xi, j 表示个体i的第j个分量, rand()是在(0, 1)内服从均匀分布的实数.

将上述3种策略应用到MS框架中, 得到MMS.

2.3 解的表示

MS的提出是用来求解连续优化问题, LFO和SFO在连续空间上的计算是封闭的, 而MDMKP问题

的每个潜在解对应一个二进制向量, 因此, 直接应用MS求解MDMKP问题是不可行的.

本文基于空间转换机制[18], 采用映射的方法, 将搜索空间的实值向量转换为问题空间的二进制向量.假设

Ω ={(x1, x2, …, xn)|Li≤ xi≤ Ui, 1≤ i≤ n}

为n维搜索空间,

Φ ={(y1, y2, …, yn)|yi∈ {0, 1}, 1≤ i≤ n}

为由所有可行解和不可行解组成的问题空间, 则可构建如下映射:

m:Ω → Φ . (2)

本文选取一种简单有效的映射函数m(x)=x, 映射方法

yi= 1, m(xi)≥00, m(xi)< 0

种群中的任何个体表示为一个二元组< X, Y> , 其中, X构成问题的搜索空间, Y形成问题的候选解空间.在本文中, X∈ [-5, 5]n, 则Y∈ {0, 1}n.

下面以n=10为例, 具体实值向量映射为二进制向量的映射过程如表1所示.

表1 实值向量映射为二进制向量 Table 1 Mapping process from real valued vectors to binary vectors
2.4 自适应ε 约束处理法

由式(1)可知, MDMKP包含m个小于等于不等式约束, q个大于等于不等式约束, 显然两组约束是对立的.采用传统的约束处理技术如罚函数法, 基于特定问题的不可行解修复法等很难对该约束进行处理.

因此, 本文采用自适应ε 约束处理法[19, 20, 21].该方法的核心思想是:基于人为设定的ε 值, 对个体的违约程度进行排序, 从而将个体划分为不同的区域.在不同的区域中, 可行解和不可行解采用不同的评价准则.此方法有效利用不可行域中目标函数值较好的不可行解信息, 具有更好的收敛性能.ε 水平控制方法如下:

ε (0)=ϕ (Xθ ),

ε (t)= ε(0)(1-tTc)cp, 0< t< Tc0, t≥Tc(3)

其中, Xθ 表示种群中个体按照约束违反程度升序排序后的第θ 个个体, Tc表示代数控制参数, cp在区间[2, 10]中取值.

设两个个体X1、X2 的目标函数值分别为f1、 f2, 约束违约度分别为ϕ 1、ϕ 2 , 则基于ε 水平的个体比较规则如下:

(f1, ϕ 1)< ε (f2, ϕ 2)⇔ f1< f2, ϕ1≤ε, ϕ2≤εf1< f2, ϕ1=ϕ2ϕ1< ϕ2, 其它

具体算法框架如算法2所示.

算法2 自适应约束处理法

输入 初始化所有参数, 初始种群, 当前代数t

输出 第t代的ε 值

step 1 对初始种群中所有个体的违约目标进行降序排列.

step 2 计算违约目标值第θ · N大的值, 记录ε (0).

step 3 如果 t≥ Tc 返回0值.

step 4 否则

step 4.1 计算当前代所有个体违约目标值.

step 4.2 如果违约目标值为0的个体个数大于等于ap· N, 返回0值.

step 4.3 否则基于式(3)的第1项计算ε (t).

step 5 输出ε (t).

2.5 求解算法框架

融合2.1节~2.4节的内容, 给出MMS求解MDMKP问题的流程, 如算法3所示.

算法3 MMS求解MDMKP框架

输入 初始化所有算法参数, 最大迭代次数T,

随机初始化N个个体, 适应度函数f(X),

问题实例I

输出 最优蛾子个体的位置,

对应的适应度函数值

step 1 WHILE未达到最大迭代次数或终止条件DO.

step 2 应用式(2)对个体编码为二元组< X, Y> .

step 3 基于自适应ε 约束处理法对个体进行排序, 记录最优个体信息.

step 4 种群划分.较优的N/2个体组成SP1, 余下个体组成SP2.

step 5 应用ALFO更新SP1.

step 6 应用MSFO更新SP2.

step 7 应用UMO更新SP1和SP2.

step 8 合并两个新生成子种群为一个种群.

step 9 判断终止条件是否满足.若未满足, t=t+1, 转step 2.

2.6 时间复杂度分析

应用MMS求解MDMKP问题主要由种群初始化、自适应ε 约束处理、ALFO、MSFO、UMO组成.设种群规模为N, 测试用例中物品个数为D, 则种群初始化时间复杂度为O(ND).

在迭代过程中, 对种群中所有个体按照自适应ε 约束处理, 时间复杂度为O(N), SP1应用ALFO进行位置更新, 时间复杂度为O(DN/2), SP2应用MSFO进行位置更新, 时间复杂度为O(ND/2), UMO的时间复杂度为O(ND).

因此, 每次迭代过程中算法的时间复杂度为

O(ND)+O(N)+O( ND2)+O( ND2)+O(ND)≈ O(ND),

与MS一致.

3 实验及结果分析

本节通过实验评价MMS的综合性能.实验包括如下3部分:1)考察自适应ε 约束处理法参数对算法性能的影响; 2)考察3种策略对算法性能的影响; 3)对比MMS与MS, 验证MMS的优越性.

3.1 测试函数与仿真环境

为了验证MMS的优化性能, 选取文献[10]中的两组测试用例与MS进行对比.每组包含48个测试用例, 表示为n-m-q-g-id.例如100-5-2-0-0表示该测试用例包含100个物品、5个背包约束、2个需求约束、第0组的第0个实例.第1组中n=100, 第2组中n=250, 两组实例其余参数设置如下:

m=5, 10, q=2, 5, 10, g=0, 1, id=0, 1, 2, 3, 4, 5.

与g=0组不同的是, g=1的组中项目对资源的消耗值可以为负值.具体实验数据可在https://grafo.etsii.urjc.es/optsicom/binaryss.html#instances下载.

为了确保实验的公平性, 依据文献[14], MS和MMS在所有测试用例上设置相同参数.种群规模为50, 迭代次数为1 000.算法参数设置如下:ϕ =0.618, MAXSTEP=1.0, λ 取值为在(0, 1)区间上服从均匀分布的随机数.此外, 为了消除随机性对算法性能的评估, 2种算法在所有96个测试用例上均进行30次独立实验.

本文采用最好目标值(Best)、平均目标值(Avg.)、最差目标值(Worst)这3个基本性能指标.同时, 为了对比最好目标值与已知最优值(BKV)之间的相对偏差, 引入Gap值考察算法逼近BKV的程度:

Gap= BKV-BestBKV× 100.

本文所有实验的硬件环境为:Intel(R) Core(TM) i5-2415M CPU 2.30 GHz、内存4.00 GB, 操作系统为Microsoft Windows 7.编程语言为Python, 解释器为Python3.9.

3.2 自适应ε 约束处理法参数分析

自适应ε 约束处理法包含3个主要参数:θ , cp, Tc.一般而言, 算法性能对参数设置具有敏感性.因此, 基于正交实验设计(Orthogonal Experimental Design, OED)[22]寻找一组较优的参数组合.实验包含3个因子, 每个因子包含3个水平, 设计具有9种组合的正交表.

选取100-5-2-0-0作为测试用例, 每组参数组合独立运行30次, 取平均值作为实验对比值, 则不同参数值的组合如表2所示.正交实验参数及实验结果如表3所示.因子分析如表4所示, 表中黑体数字表示最优值.

表2 不同参数值组合 Table 2 Combination of different parameter values
表3 正交实验参数及实验结果 Table 3 Parameters of orthogonal experiment and experimental results
表4 基于正交设计方法的因子分析 Table 4 Factor analysis based on orthogonal design method

从表4的标准差可以发现:Tc是3个参数中最重要的参数, 需要合理选择.基于上述OED, 分析最适合的参数组合为θ =0.2, cp=5, Tc=500.下面实验将采用这组参数.

3.3 改进策略有效性分析

为了验证3种策略对MMS性能的影响, 对比研究MS, 包括MS应用ALFO(简记为MS-I)、MS应用MSFO(简记为MS-II)、MS应用UMO(简记为MS-III)、融合3种策略的MMS.选取100-5-2-0-id和100-5-2-1-id形式的12个测试用例, 每种算法对每个测试用例均独自运行30次, 实验结果如表5所示, 表中黑体数字表示5种算法求解同个测试用例的最优值, total栏表示4种改进算法与MS相比取得更优值的个数.

表5 不同改进策略的实验结果 Table 5 Experimental results of different improvement strategies

由表5可知, ALFO和UMO均能在可行域复杂的情况下, 充分挖掘搜索空间, 对所有的12个测试用例的求解质量均有所提高.MSFO对9个测试用例的最优值有更高的精度, 说明MSFO可以有效增加种群多样性.同时, 融合3种策略的MMS的最优值和Gap值都优于单一改进策略的MS, 寻优性能显著, 表明MMS能够充分发挥不同改进策略的优点.

为了从统计意义上说明4种改进算法与MS是否有显著性差异, 采用Wilcoxon秩和检验验证MS的12个测试用例的Best值在α = 0.05的显著性水平下与其它算法的显著性差异.其中:p-value> 0.05, 表明接受原假设H0, 即认为两种优化算法之间无显著性差异, 算法寻优能力相当; p-value< 0.05, 拒绝原假设H0, 即两种算法存在显著性差异.由此可见, MS-I、MS-III、MMS与MS存在显著性差异, MS-II与MS无显著性差异.由表5还可以看出, 1)MMS在几乎所有的12个测试用例中, 取得的Best值均超过其它四种算法.说明三种策略的组合有益于提高算法求解性能.2)MS-I、MS-III在所有的12个测试用例上均优于MS, MS-II在绝大多数测试用例上优于MS, 说明三种改进策略均能够提高MS的优化性能.3)相比MS-I和MS-III, MS-II的改进效果不是很明显, 可能的原因是过高的突变率增加在搜索空间搜索更多可行域的概率, 延缓算法收敛速度, 太小的突变率导致算法早熟收敛.

3.4 MMS与MS对比

为了验证MMS对于MDMKP的求解能力, 与MS对96个测试用例进行对比, 实验结果如表6~表9所示, 表中黑体数字表示最优值.

表6 MS和MMS求解100-5-x-x-x测试用例的实验结果 Table 6 Experimental results of MS and MMS on test instances(100-5-x-x-x)
表7 MS和MMS求解100-10-x-x-x测试用例的实验结果 Table 7 Experimental results of MS and MMS on test instances(100-10-x-x-x)
表8 MS和MMS求解250-5-x-x-x测试用例的实验结果 Table 8 Experimental results of MS and MMS on test instances(250-5-x-x-x)
表9 MS和MMS求解250-10-x-x-x测试用例的实验结果 Table 9 Experimental results of MS and MMS on test instances (250-10-x-x-x)

由表6可以看出:1)就求得最优结果的总个数而言, MMS的Best指标、Avg.指标、Worst指标分别有20、24、20个优于MS; 2)就4种评价指标平均值而言, MMS均优于MS.

由表7可以看出, 除了Worst指标以外, MMS劣于MS.由此可以推断, MMS可能对于测试用例的属性具有敏感性.

由表8可以看出:1)就求得最优结果的总个数而言, MMS的Best指标、Avg.指标、Worst指标分别有20、8、6个优于MS; 2)就4种评价指标平均值而言, MMS均优于MS.

由表9可以看出, MMS的Avg.指标有12个优于MS, Worst指标有10个优于MS, Best指标有4个劣于MS.

从表6~表9的对比结果可以看出, 随着问题维数的增大, MMS优于MS的求解结果更加明显, 说明改进策略在搜索复杂的可行域时优势突显.

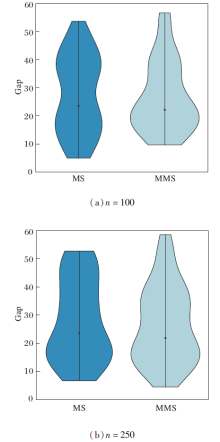
为了图形化显示MS和MMS求解n=100, 250两组实例的Gap指标分布情况, 图1给出小提琴图, 图中红点表示中位数, 黑色盒型表示最集中的50%区域.从图1可以看出:1)两种算法均存在较明显的离散值(上侧的须和下侧的须较长); 2)MS求解两组测试用例的Gap值分布相对集中, MMS的Gap值分布不太均匀.说明相比MS, MMS能够求得更优解, 但算法的稳定性需要进一步提高.

图1 2种算法求解两组测试用例的Gap值分布Fig.1 Gap value distribution of 2 algorithms on 2 sets of instances

3.5 测试用例属性对算法性能影响

在MDMKP的每一组测试用例中, n-m-q-g-0测试用例中背包中物品价值系数全部为正整数, n-m-q-g-1测试用例中背包中物品价值系数包含负整数.为了说明算法的求解性能是否与测试用例的特征具有相关性, 对MMS求得的两组测试用例(n=100, 250)的Gap值绘制散点图, 如图2所示.

图2 96个测试用例的Gap值分布散点图Fig.2 Scatter plot of Gap value distribution of 96 instances

从图2可以得出如下结论.

1)总体而言, Gap值的分布与测试用例的分组基本一致, 即同组的6个测试用例Gap值可以作为一组, 其中100-10-5-1、250-5-2-0、250-5-5-0、250-10- 10-1四组测试用例尤其明显, 说明测试用例的属性对算法的求解性能具有一定影响.

2)对于背包约束个数和需求约束个数相同的两组实例, 即g=0, 1, 组别为0的正系数测试用例求解效果明显优于组别为1的兼具正负系数的测试用例, 前者整体处于后者的底端, 说明收益可为正负值, 增加求解难度.

3)背包约束个数的增加使可行域的搜索变得困难, 解的质量变差, Gap值相对较大.然而, 需求约束个数增加, 求解效果影响不明显.可能的原因是约束条件比较宽泛.

4 结束语

MDMKP问题包含两组对立的约束条件, 使得该问题的求解非常困难.如果采用合适的方法, 处理好约束, 那么有可能降低问题的难度.本文提出基于ε 约束处理法的改进蛾子搜索算法(MMS), 用于求解该问题, 基于96个标准测试函数的实验表明, MMS比MS具有更高的寻优精度.实验分析表明3种改进策略对算法性能具有各自的影响:自适应莱维飞行算子(ALFO)扩大蛾子飞行步长的调节范围, 对个体进行局部扰动, 以更大概率跳出局部最优; 变异直接飞行算子(MSFO)引入合适的突变率, 防止种群过早收敛, 增加在搜索空间中搜索更多区域的概率; 均匀变异算子(UMO)以较小的概率更新种群中部分个体的基因, 增加种群多样性.同时, 本文还分析ε 约束处理法的3个主要参数对算法性能的影响.

本研究工作丰富现存的求解MDMKP问题的技术, 下一步将考虑应用不同约束处理方法, 如可行性法则、多目标优化法等.此外, 该框架也可应用于求解其它的多约束组合优化问题, 如凸可分背包问题、动态背包问题、多目标背包问题等.尽管MMS优于MS, 但解的质量还需要进一步提高.因此, 提出更好的策略在复杂的搜索空间中寻求高质量解将是下一步的研究工作.

本文责任编委 何清

Recommended by Associate Editor HE Qing

参考文献
[1] 姚友杰, 钱斌, 董钰明, 等. 基于EDA的绿色零等待作业车间调度问题求解. 电子学报, 2021, 49(2): 225-233.
(YAO Y J, QIAN B, DONG Y M, et al. EDA-Based for the Green No-wait Job Shop Scheduling Problem. Acta Electronica Sinica, 2021, 49(2): 225-232. ) [本文引用:1]
[2] 陈广锋, 韩玮. 基于最小负荷初始化的改进遗传算法求解柔性作业车间调度问题. 信息与控制, 2021, 50(3): 374-384.
(CHEN G F, HAN W. Improved Genetic Algorithm Based on Minimum-Load Initialization to Solve Flexible Job-Shop Scheduling Pro-blem. Information and Control, 2021, 50(3): 374-384. ) [本文引用:1]
[3] GOUDET O, GRELIER C, HAO J K. A Deep Learning Guided Memetic Framework for Graph Coloring Problems. Knowledge-Based Systems, 2022, 258(22). DOI: DOI:10.1016/j.knosys.2022.109986. [本文引用:1]
[4] 蒋华伟, 郭陶, 杨震. 车辆路径问题研究进展. 电子学报, 2022, 50(2): 480-492.
(JIANG H W, GUO T, YANG Z. Research Progress of Vehicle Routing Problem. Acta Electronica Sinica, 2022, 50(2): 480-492. ) [本文引用:1]
[5] 韩伟, 张子成. 求解旅行商问题的离散型贝壳漫步优化算法. 模式识别与人工智能, 2016, 29(7): 650-657.
(HAN W, ZHANG Z C. Discrete Mussels Wand ering Optimization Algorithm for Solving Traveling Salesman Problem. Pattern Recognition and Artificial Intelligence, 2016, 29(7): 650-657. ) [本文引用:1]
[6] WANG L, ZHENG X L, WANG S Y. A Novel Binary Fruit Fly Optimization Algorithm for Solving the Multidimensional Knapsack Problem. Knowledge-Based Systems, 2013, 48: 17-23. [本文引用:1]
[7] CAPPANERA P, TRUBIAN M. A Local-Search-Based Heuristic for the Demand -Constrained Multidimensional Knapsack Problem. INFORMS Journal on Computing, 2005, 17(1): 82-98. [本文引用:2]
[8] GORTÁZAR F, DUARTE A, LAGUNA M, et al. Black Box Scatter Search for General Classes of Binary Optimization Problems. Computers and Operations Research, 2010, 37(11): 1977-1986. [本文引用:1]
[9] ARNTZEN H, HVATTUM L M, LØKKETANGEN A. Adaptive Me-mory Search for Multidemand Multidimensional Knapsack Problems. Computers and Operations Research, 2006, 33(9): 2508-2525. [本文引用:1]
[10] LAI X J, HAO J K, YUE D. Two-Stage Solution-Based Tabu Search for the Multidemand Multidimensional Knapsack Problem. European Journal of Operational Research, 2019, 274(1): 35-48. [本文引用:3]
[11] AL-SHIHABI S. A Novel Core-Based Optimization Framework for Binary Integer Programs-The Multidemand Multidimensional Knapsack Problem as a Test Problem. Operations Research Perspectives, 2021, 8. DOI: DOI:10.1016/j.orp.2021.100182. [本文引用:1]
[12] 刘生建, 杨艳, 周永权. 一种群体智能算法——狮群算法. 模式识别与人工智能, 2018, 31(5): 431-441.
(LIU S J, YANG Y, ZHOU Y Q. A Swarm Intelligence Algorithm-Lion Swarm Optimization. Pattern Recognition and Artificial Intelligence, 2018, 31(5): 431-441. ) [本文引用:1]
[13] 刘宝, 张月, 杨金莹. 智能人工蜂群改进算法及其在油田注采优化中的应用. 信息与控制, 2023, 52(2): 245-256.
(LIU B, ZHANG Y, YANG J Y. Improved Intelligent Artificial Bee Colony Algorithm and Its Application to Optimization of Injection and Production in Oilfield. Information and Control, 2023, 52(2): 245-256. ) [本文引用:1]
[14] WANG G G. Moth Search Algorithm: A Bio-Inspired Metaheuristic Algorithm for Global Optimization Problems. Memetic Computing, 2018, 10(2): 151-164. [本文引用:2]
[15] LI J, YANG Y H, AN Q, et al. Moth Search: Variants, Hybrids, and Applications. Mathematics, 2022, 10(21). DOI: DOI:10.3390/math10214162. [本文引用:1]
[16] FENG Y H, WANG G G. A Binary Moth Search Algorithm Based on Self-Learning for Multidimensional Knapsack Problems. Future Generation Computer Systems, 2022, 126: 48-64. [本文引用:1]
[17] 孙林, 赵婧, 徐久成, 等. 基于邻域粗糙集和帝王蝶优化的特征选择算法. 计算机应用, 2022, 42(5): 1355-1366.
(SUN L, ZHAO J, XU J C, et al. Feature Selection Algorithm Based on Neighborhood Rough Set and Monarch Butterfly Optimization. Journal of Computer Applications, 2022, 42(5): 1355-1366. ) [本文引用:1]
[18] FENG Y H, AN H Z, GAO X Y. The Importance of Transfer Function in Solving Set-Union Knapsack Problem Based on Discrete Moth Search Algorithm. Mathematics, 2019, 7(1). DOI: DOI:10.3390/math7010017. [本文引用:1]
[19] 陈少淼, 陈瑞, 梁伟, 等. 面向复杂约束优化问题的进化算法综述. 软件学报, 2023, 34(2): 565-581.
(CHEN S M, CHEN R, LIANG W, et al. Overview of Evolutio-nary Algorithms for Complex Constrained Optimization Problems. Journal of Software, 2023, 34(2): 565-581. ) [本文引用:1]
[20] 李智勇, 黄滔, 陈少淼, 等. 约束优化进化算法综述. 软件学报, 2017, 28(6): 1529-1546.
(LI Z Y, HUANG T, CHEN S M, et al. Overview of Constrained Optimization Evolutionary Algorithms. Journal of Software, 2017, 28(6): 1529-1546. ) [本文引用:1]
[21] ZHANG C J, QIN A K, SHEN W M, et al. ε-Constrained Diffe-rential Evolution Using an Adaptive ε-Level Control Method. IEEE Transactions on Systems, Man, and Cybernetics(Systems), 2020, 52(2): 769-785. [本文引用:1]
[22] 龚文引, 蔡之华. 基于ε占优的正交多目标差分演化算法研究. 计算机研究与发展, 2009, 46(4): 655-666.
(GONG W Y, CAI Z H. Research on an ε-Domination Based Orthogonal Differential Evolution Algorithm for Multi-objective Opti-mization. Journal of Computer Research and Development, 2009, 46(4): 655-666. ) [本文引用:1]