基于熵的多尺度多重集值信息系统的最优尺度选择与属性约简

引用本文

王蕾晰, 吴伟志, 谢祯晃. 基于熵的多尺度多重集值信息系统的最优尺度选择与属性约简. 模式识别与人工智能, 2023,36(6): 495-510
WANG Leixi, WU Weizhi, XIE Zhenhuang. Optimal Scale Selection and Attribute Reduction of Multi-scale Multiset-Valued Information Systems Based on Entropy. PATTERN RECOGNITION AND ARTIFICIAL INTELLIGENCE, 2023,36(6): 495-510. 复制到剪切板

Doi: 10.16451/j.cnki.issn1003-6059.202306002
Permissions

《模式识别与人工智能》编辑部

基于熵的多尺度多重集值信息系统的最优尺度选择与属性约简

王蕾晰^1,², 吴伟志^1,², 谢祯晃^1,²

1.浙江海洋大学信息工程学院舟山 316022

2.浙江海洋大学浙江省海洋大数据挖掘与应用重点实验室舟山 316022

通讯作者：

吴伟志,博士,教授,主要研究方向为粗糙集、粒计算、数据挖掘、人工智能.E-mail:wuwz@zjou.edu.cn.

作者简介:

王蕾晰,硕士研究生,主要研究方向为粗糙集、粒计算.E-mail:wangleixi22@163.com.

谢祯晃,硕士研究生,主要研究方向为粗糙集、粒计算.E-mail:xiezh1120@163.com.

收稿日期: 2023-06-06 接受日期: 2023-06-30

资助项目: 国家自然科学基金项目(No.61976194,62076221)资助

摘要

针对现有的信息系统难以体现和处理数据融合时出现的数据重复问题,文中提出多尺度多重集值信息系统的概念,并讨论该系统的最优尺度选择和属性约简问题.首先,在多尺度多重集值信息系统的每个属性中,基于属性值域中多重集之间的海林格距离定义论域上的相似关系,获得由每个属性子集导出的论域中所有对象的相似类构成的信息粒.然后,引入多尺度多重集值信息系统中知识粗糙熵的概念,进一步给出多尺度多重集值信息系统中的最优尺度与熵最优尺度的概念,证明基于相似关系定义的最优尺度和基于知识粗糙熵定义的最优尺度是等价的.最后,在熵最优尺度的基础上提出系统中基于相似关系的约简和基于知识粗糙熵的约简的概念,并分别给出筛选熵最优尺度和熵约简的算法.

关键词: 属性约简; 知识粗糙熵; 多重集; 多尺度信息系统; 最优尺度

中图分类号:TP18

Optimal Scale Selection and Attribute Reduction of Multi-scale Multiset-Valued Information Systems Based on Entropy

WANG Leixi^1,², WU Weizhi^1,², XIE Zhenhuang^1,²

1. School of Information Engineering, Zhejiang Ocean University, Zhoushan 316022

2. Key Laboratory of Oceanograhic Big Data Mining and Application of Zhejiang Province, Zhejiang Ocean University, Zhoushan 316022

Corresponding author：
WU Weizhi, Ph.D., professor. His research interests include rough set, granular computing, data mining and artificial intelligence.

About Author:
WANG Leixi, master student. Her research interests include rough set and granular computing.
XIE Zhenhuang, master student. His research interests include rough set and granular computing.

Fund:National Natural Science Foundation of China(No.61976194,62076221)

Abstract

Existing information systems are difficult to reflect and deal with the data duplication in the process of data fusion. In this paper, the concept of multi-scale multiset-valued information systems is introduced and the optimal scale selection and attribute reduction in these systems are discussed. Firstly, a similarity relation on the universe of discourse from any attribute subset in a multi-scale multiset-valued information system is defined by employing the Hellinger distance on multi-sets of the domain of any attribute. Then, information granules in the form of similarity classes are constructed. Knowledge rough entropy is further introduced in the context of multi-scale multiset-valued information systems. Optimal scales based on the similarity relation and the knowledge rough entropy are defined in a multi-scale multiset-valued information system, respectively. It is examined that the optimal scale based on the similarity relation and entropy optimal scale are equivalent. Finally, reducts and entropy reducts based on the optimal scale are discussed in the multi-scale multiset-valued information system, and algorithms for calculating the entropy optimal scale and an entropy reduct are also designed in a multi-scale multiset-valued information system.

Key words: Key Words Attribute Reduction; Knowledge Rough Entropy; Multiset; Multi-scale Information Systems; Optimal Scale

文章图片

大数据时代下, 各行各业产生的数据具有不确定性和复杂性.高效处理数据, 挖掘数据背后的规律, 并运用于实际问题是数据挖掘的主要任务.粒计算^{[1, 2, 3]}是模拟人脑思维以处理数据不确定性和复杂性的一种方法, 源于Zadeh^[4]提出的“ 信息粒度” 概念.粒计算的核心思想是通过合适的粒化提取信息粒, 对信息粒进行处理和计算, 进而分析数据规律和解决实际问题^{[5, 6, 7]}.

在粒计算的研究和发展过程中, 粗糙集数据分析发挥重要的作用.粗糙集最早由Pawlak^[8]于1982年提出.粗糙集最初讨论的对象-属性取值多为数值或符号.随着数据挖掘的不断深入和实际应用的需要, 学者们研究数据类型日趋多样化, 如集值、区间值、区间集、模糊数、混合数据类型等.

多重集^{[9, 10, 11]}是一种元素可重复出现的集合, 元素在多重集中出现的次数称为该元素在多重集中的重数并且元素的顺序可以互换.多重集在组合数学^[12]、关系数据库理论^[13]、图论^[14]等领域都有重要应用.可以使用多重集描述决策分析中很多问题的数据.例如, 在专家评审系统中, 有4位专家参与评审, 专家评审结果可能存在重复, 如多重集{well, well, well, bad}中的元素分别为4位专家的评审结果.如果用经典集合{well, bad}则无法体现专家对评审对象的具体评价.此外, 多重集在模式识别^{[15, 16]}、多准则决策^[17]、医疗诊断^[18]等领域也有重要应用.

当信息系统的对象-属性取值为多重集时, 该系统称为多重集值信息系统, 多重集值信息系统是集值信息系统的推广.多重集值信息系统在决策分析^{[19, 20, 21]}、多源信息融合^{[22, 23]}等领域具有重要的研究价值.Zhao等^[19]在多重集值信息系统中建立决策理论粗糙集模型.王虹等^[20]结合多粒度粗糙集和模糊决策论, 研究在多重集值信息系统中乐观与悲观粗糙集的上、下近似的性质, 并讨论粗糙集精度与粗度等问题.Zhang等^[22]探索多重集值信息系统在多源信息融合领域的重要应用.Huang等^[23]利用多重集值信息系统, 解决在多源信息融合时产生的信息缺省问题, 从粒计算的角度给出多重集值信息系统中的信息结构, 并研究其在不确定度量中的应用.

众所周知, 经典粗糙集数据分析处理系统为单尺度信息系统, 即系统中每个对象在每个属性下只能取唯一的值.但在实际应用中, 对象属性的取值可以具有多种尺度的值, 如成绩的评定, 有百分制、五级记分制或二级记分制.生活中存在许多类似的多尺度属性的例子, 尺度过细会导致数据的存储代价过大, 而尺度过粗又会导致决策的准确性降低.因此, 在不同决策问题中可能会采用不同的属性尺度.针对类似问题, Wu等^[24]首次提出多尺度粗糙集数据分析模型, 处理的数据称为多尺度信息系统, 这种系统中每个属性对于同个对象具有不同尺度的取值, 并且在不同的尺度之间存在粒度变换的关系.

近年来, 多尺度粗糙集数据分析已成为粒计算领域的一个重要方向^{[25, 26, 27, 28, 29]}.陈应生等^[25]建立多尺度覆盖决策系统模型, 并使用布尔矩阵研究系统的粒描述.Zhan等^[26]利用多尺度信息系统与多专家群体决策系统的关系, 研究排序决策问题.陈艳等^[27]提出多尺度集值信息系统的概念, 给出系统在不同尺度下的粗糙近似.但多尺度集值信息系统无法处理属性的取值为多重集的情形.

信息熵是刻画信息系统不确定性的重要指标之一, 熵的概念最早来源于热力学理论, 由Shannon^[30]引入信息论中.信息熵越大, 系统的不确定程度越高.在保持信息熵不变的情况下, 即在保持系统不确定性不变的情况下找到原系统的最优尺度和属性约简, 是多尺度数据分析研究的一个重要问题^{[31, 32]}.张嘉宇^[31]研究条件熵和互补熵在多尺度信息系统中的最优尺度选择问题, 并类比两种方法的效果.郑嘉文等^[32]利用香农熵, 研究多尺度信息系统中的最优尺度选择问题, 并证明最优尺度与熵最优尺度的等价性, 但香农熵建立在由等价关系产生的划分上.Liang等^{[33, 34]}引入在相似关系下知识粗糙熵的概念, 并运用于不完备系统的知识表示与知识约简中.之后, Liang等^[35]讨论不完备信息系统中的信息熵、粗糙熵和知识粒化之间的关系.Sun等^[36]基于粗糙熵构造低计算复杂度的启发式算法.Ma等^[37]研究双论域上概率粗糙集的知识粒度和粗糙熵的不确定度量.邓切等^[38]讨论双论域覆盖空间中的粗糙熵与知识粒度等问题.

针对现有的信息系统难以体现和处理数据融合时出现的数据重复问题, 本文提出多尺度多重集值信息系统的概念, 并讨论该系统的最优尺度选择和属性约简问题.首先, 在多尺度多重集值信息系统的每个属性中, 基于属性值域中多重集之间的海林格距离(Hellinger Distance)定义论域上的相似关系, 并获得由每个属性子集导出的论域中所有对象的相似类构成的信息粒.然后, 引入多尺度多重集值信息系统中知识粗糙熵的概念, 并进一步给出多尺度多重集值信息系统中的最优尺度与熵最优尺度的概念, 证明基于相似关系定义的最优尺度和基于知识粗糙熵定义的最优尺度是等价的.最后, 在熵最优尺度的基础上提出系统中基于相似关系的约简和基于知识粗糙熵的约简的概念, 并分别给出筛选熵最优尺度和熵约简的算法.

1 基础知识

本节介绍相关的基础知识, 包括多重集、信息系统、多重集值信息系统、多尺度信息系统和熵的概念与基本性质.

定义1^[9] 设Z={z₁, z₂, …, z_o}为一个非空有限集合, N为自然数集合, 称M为集合Z上的一个多重集, 若Z中的元素z_i(z_i∈ Z)在M中重复出现k_i次, 即

$M = { \overset{k_{1}}{\overset{︷}{z_{1}, \dots, z_{1}}}, \dots, \overset{k_{o}}{\overset{︷}{z_{o}, \dots, z_{o}}}} .$

则M称为Z上的一个多重集.

由定义1可见, 一个多重集M可由函数C_M:Z→ N表示, 即

M={ $\frac{C_{M} (z)}{z}$ |z∈ Z},

其中

C_M(z_i)=k_i, z_i∈ Z.

由多重集的定义可知, 多重集中元素的顺序无关紧要.集合Z上所有多重集的集合记为M(Z), 若集合Z的幂集记为P(Z), 则

P(Z)⊆M(Z),

故多重集是经典集的推广.

一个多重集M的基数记为|M|, 定义如下:

|M|= $\overset{o}{\sum_{i = 1}}$ C_M(z_i).

例1 在专家评审系统中, 每篇论文的评审结果由3位专家共同给出.假设每位专家的意见只可能有2种情况— — 接受(a)和拒绝(r).那么所有评审结果M都是多重集, 且M∈ M(Z), 其中Z={a, r}.若3位专家中有2位专家给出接受的意见, 1位专家给出拒绝的意见, 则评审结果为

M={a, a, r},

也可以表示为

M={ $\frac{2}{a}$ , $\frac{1}{r}$ }.

文献[23]引入概率论中的海林格距离以定义多重集之间的距离.

定义2^[23] 对于Z={z₁, z₂, …, z_o}上的两个多重集M₁∈ M(Z), M₂∈ M(Z), M₁和M₂之间的海林格距离定义为

$H D (M_{1}, M_{2}) = \sqrt{1 - \sum_{i = 1}^{o} \sqrt{p_{i} q_{i}}}$

其中

p_i= $\frac{C_{M_{1}} (z_{i})}{|M_{1}|}$ , q_i= $\frac{C_{M_{2}} (z_{i})}{|M_{2}|}$ , i=1, 2, …, o.

有时, 一个多重集M也可以表示为

M={ $\frac{z_{1}, z_{2}, \dots, z_{o}}{p_{1}, p_{2}, \dots, p_{o}}$ },

其中

p_i= $\frac{C_{M} (z_{i})}{| M |}$ , i=1, 2, …, o.

例2 多重集

M₁={a, a, r, r}, M₂={a, r, r, r}

可以写成

M₁={ $\frac{a, r}{0.5, 0.5}$ }, M₂={ $\frac{a, r}{0.25, 0.75}$ },

而M₁和M₂之间的海林格距离

HD(M₁, M₂)= $\sqrt[]{1 - \overset{2}{\sum_{i = 1}} \sqrt[]{p_{i} q_{i}}}$ ≈ 0.1846.

定义3^[8] 称S=(U, A)为一个信息系统, 其中

U={x₁, x₂, …, x_n}

为非空有限对象集, 称为论域,

A={a₁, a₂, …, a_m}

为非空有限属性集, 对于

∀ a_j∈ A, a_j:U→ V_j,

其中V_j为属性a_j的值域.

若信息系统中存在对象有未知的或缺省的属性值, 则称该信息系统为不完备信息系统, 此时, 用符号* 表示不完备信息系统中的缺省值.

定义4^[19] 称S=(U, A)为一个多重集值信息系统, 其中

U={x₁, x₂, …, x_n}

为非空有限对象集, 称为论域,

A={a₁, a₂, …, a_m}

为非空有限属性集, 每个对象的属性取值都为多重集, 即

∀ a_j∈ A, a_j:U→ M(V_j),

其中V_j为属性a_j的值域.

针对对象的属性可能存在多种尺度的情况, Wu等^[24]首次提出多尺度信息系统的概念.

定义5^[24] 称S=(U, A)为一个多尺度信息系统, 其中

U={x₁, x₂, …, x_n}

为论域,

A={a₁, a₂, …, a_m}

为非空有限属性集, 每个属性都具有多尺度.假设所有属性的尺度个数都是I, 则一个多尺度信息系统可以表示为

(U, { $a_{j}^{k}$ |k=1, 2, …, I, j=1, 2, …, m}),

其中

∀ $a_{j}^{k}$ ∈ A, $a_{j}^{k}$ :U→ V $_{j}^{k}$ ,

V $_{j}^{k}$ 为属性a_j在第k个尺度标记下的值域, 对于k=1, 2, …, I-1, 存在一个满射

$g_{j}^{k, k + 1}$ :V $_{j}^{k}$ → V $_{j}^{k + 1}$ ,

使得

$a_{j}^{k + 1}$ = $g_{j}^{k, k + 1}$ $a_{j}^{k}$ ,

即

$a_{j}^{k + 1}$ (x)= $g_{j}^{k, k + 1}$ ( $a_{j}^{k}$ (x)), x∈ U,

称 $g_{j}^{k, k + 1}$ 为信息粒度变换.

对于k=1, 2, …, I, 记

A^k={ $a_{j}^{k}$ |j=1, 2, …, m},

则一个多尺度信息系统S=(U, A)可以分解为I个子信息系统

S^k=(U, A^k), k=1, 2, …, I.

定义6^[39] 称S=(U, A)为一个多尺度集值信息系统, 其中

U={x₁, x₂, …, x_n}

为论域,

A={a₁, a₂, …, a_m}

为非空有限属性集, 每个属性都具有多尺度, 且尺度个数都是I, 每个对象的属性取值都为集值.

非空有限集合U的幂集记为P(U), 设

C={C₁, C₂, …, C_e}⊆P(U),

若Ø ∉C, 且

$\overset{e}{⋃_{i = 1}}$ C_i=U,

则称C为U的一个覆盖.进一步, 若

$C_{i} \cap C_{j} = \emptyset (i \neq j)$ , $i, j \in { 1, 2, \dots, e}$

则称C为U的一个划分.

定义7^[40] 设U是非空有限集合,

X={X₁, X₂, …, X_t}, Y={Y₁, Y₂, …, Y_s}

为U上的两个覆盖, 若对于∀ X_i∈ X, 都存在Y_j∈ Y, 使得X_i⊆Y_j, 则称X细于Y, 或称Y粗于X, 记作X⪯Y.另外, 若进一步存在 $X_{i_{0}}$ ∈ X, $Y_{j_{0}}$ ∈ Y, 使得 $X_{i_{0}}$ ⊂ $Y_{j_{0}}$ , 则称X严格细于Y, 或称Y严格粗于X, 记作X≺Y.

定义8^[28] 设U为非空有限集合, 若

X={X₁, X₂, …, X_t}

为U上的一个划分, 则X的信息(香农)熵H(X)定义为

H(X)=- $\overset{t}{\sum_{i = 1}}$ P(X_i)log₂P(X_i),

其中

P(X_i)= $\frac{|X_{i}|}{| U |}$ , i=1, 2, …, t,

|· |表示集合的基数.

命题1^[41] 设U为非空有限集合, 对于U上两个划分X和Y, 若满足X⪯Y, 则H(X)≥ H(Y).

对于一个不完备信息系统(U, A), 由任一属性子集B产生的相似关系定义为

$\begin{array}{l} R_{B} = { (x, y) \in U \times U| a_{j} (x) = a_{j} (y) \lor \\ a_{j} (x) =' *' \lor a_{j} (y) =' *', \forall a_{j} \in B} . \end{array}$

相似关系R_B将论域U粒化为若干相似类

U/R_B={[x]_B|x∈ U},

其中

[x]_B={y∈ U|(x, y)∈ R_B}.

显然, 相似类全体U/R_B构成论域U的一个覆盖.

香农熵是定义在等价关系上的, 但在相似关系上并不适用.为此, Liang等^{[33, 34]}在不完备信息系统中提出在相似关系下的知识粗糙熵的概念.

定义9^[33] 设(U, A)为一个不完备信息系统, B⊆A, 属性集B的知识粗糙熵定义为

E(B)=- $\sum_{x \in U}$ ( $\frac{| {[x]}_{B} |}{| U |}$ log₂( $\frac{1}{| {[x]}_{B} |}$ )).

性质1^[33] 设(U, A)为一个不完备信息系统, B⊆A, C⊆A.若

U/R_B≺U/R_C,

则

E(B)< E(C).

性质2^[33] 设(U, A)为一个不完备信息系统, B⊆A, 则

U/R_B=U/R_A

当且仅当

E(B)=E(A).

2 多尺度多重集值信息系统

定义10 称S=(U, A)为一个多尺度多重集值信息系统, 其中

U={x₁, x₂, …, x_n}

为非空有限对象集, 称为论域,

A={a₁, a₂, …, a_m}

为非空有限属性集, 每个属性都具有多尺度且每个对象的属性取值都为多重集.假设所有属性的尺度个数都是I, 则一个多尺度多重集值信息系统可以表示为

(U, { $a_{j}^{k}$ |k=1, 2, …, I, j=1, 2, …, m}),

其中

∀ $a_{j}^{k}$ ∈ A, $a_{j}^{k}$ :U→ M(V $_{j}^{k}$ ), j=1, 2, …, m,

V $_{j}^{k}$ 为属性a_j在第k个尺度标记下的值域, 对于k=1, 2, …, I-1, 存在一个满射

$g_{j}^{k, k + 1}$ :V $_{j}^{k}$ → V $_{j}^{k + 1}$ ,

使得

$a_{j}^{k + 1}$ = $g_{j}^{k, k + 1}$ $a_{j}^{k}$ ,

即

$a_{j}^{k + 1}$ (x)= $g_{j}^{k, k + 1}$ ( $a_{j}^{k}$ (x)), x∈ U,

称 $g_{j}^{k, k + 1}$ 为信息粒度变换.

需要说明的是, 这里通过 $g_{j}^{k, k + 1}$ , 将对象x在属性a_j的第k个尺度标记下属性取值中的每个元素映射到第k+1个尺度标记下属性取值中, 并保持多重集 $a_{j}^{k + 1}$ (x)的基数与多重集 $a_{j}^{k}$ (x)的基数相同.

对于k=1, 2, …, I, 记

A^k={ $a_{j}^{k}$ |j=1, 2, …, m},

则一个多尺度多重集值信息系统S=(U, A)可以分解为I个多重集值信息系统

S^k=(U, A^k), k=1, 2, …, I.

在多源信息融合问题中, 数据来自于多个信息源, 其等级尺度和属性总量影响数据融合过程的效率和数据融合后信息系统的数据量, 因此筛选合适的属性尺度和属性在实际应用中具有研究意义.同时, 多重集值信息系统能够有效应对信息融合时容易出现的数据重复情况.

例3是一个手机质检问题, 也是多源信息融合问题.不同检测员表示不同信息源, 将对不同品牌手机的检测结果融合到一个信息系统中.

例3 设

U={x₁, x₂, …, x₈}

为论域, 分别表示8个手机品牌,

A={a₁, a₂, a₃}

为属性集, 多尺度多重集值信息系统如表1所示.

表1 一个多尺度多重集值信息系统 Table 1 A multi-scale multiset-valued information system

U	a₁		a₂		a₃
U	$a_{1}^{1}$	$a_{1}^{2}$	$a_{2}^{1}$	$a_{2}^{2}$	$a_{3}^{1}$	$a_{3}^{2}$
x₁	{6, 7, 7, 8}	{2, 2, 2, 2}	{ $\frac{2}{b}$ , $\frac{1}{m}$ , $\frac{1}{w}$ }	{ $\frac{2}{l}$ , $\frac{2}{s}$ }	{64%, 65%, 74%, 76%}	{6, 6, 7, 7}
x₂	{5, 6, 6, 7}	{1, 2, 2, 2}	{ $\frac{0}{b}$ , $\frac{3}{m}$ , $\frac{1}{w}$ }	{ $\frac{0}{l}$ , $\frac{4}{s}$ }	{74%, 74%, 84%, 89%}	{7, 7, 8, 8}
x₃	{8, 8, 9, 10}	{2, 2, 2, 2}	{ $\frac{0}{b}$ , $\frac{0}{m}$ , $\frac{4}{w}$ }	{ $\frac{0}{l}$ , $\frac{4}{s}$ }	{70%, 74%, 78%, 88%}	{7, 7, 7, 8}
x₄	{2, 3, 4, 4}	{1, 1, 1, 1}	${\frac{4}{b}$ , $\frac{0}{m}$ , $\frac{0}{w}$ }	{ $\frac{4}{l}$ , $\frac{0}{s}$ }	{17%, 20%, 24%, 29%}	{1, 2, 2, 2}
x₅	{3, 3, 4, 4}	{1, 1, 1, 1}	{ $\frac{3}{b}$ , $\frac{0}{m}$ , $\frac{1}{w}$ }	{ $\frac{3}{l}$ , $\frac{1}{s}$ }	{10%, 14%, 20%, 27%}	{1, 1, 2, 2}
x₆	{3, 4, 4, 5}	{1, 1, 1, 1}	{ $\frac{3}{b}$ , $\frac{1}{m}$ , $\frac{0}{w}$ }	{ $\frac{3}{l}$ , $\frac{1}{s}$ }	{12%, 14%, 17%, 20%}	{1, 1, 1, 2}
x₇	{5, 6, 6, 8}	{1, 2, 2, 2}	{ $\frac{2}{b}$ , $\frac{0}{m}$ , $\frac{2}{w}$ }	{ $\frac{2}{l}$ , $\frac{2}{s}$ }	{63%, 63%, 64%, 76%}	{6, 6, 6, 7}
x₈	{6, 6, 8, 7}	{2, 2, 2, 2}	{ $\frac{0}{b}$ , $\frac{4}{m}$ , $\frac{0}{w}$ }	{ $\frac{0}{l}$ , $\frac{4}{s}$ }	{61%, 64%, 68%, 72%}	{6, 6, 6, 7}

表1 一个多尺度多重集值信息系统 Table 1 A multi-scale multiset-valued information system

表1中, 属性a₁为4名检测员对抽检手机的处理器性能评分, 属性a₂为4名检测员对抽检手机的使用流畅度评分, 属性a₃为4名检测员使用抽检手机相同时间后所剩的电池容量, 每个属性的尺度个数都是2.

表1是一个多尺度多重集值信息系统

S=(U, { $a_{j}^{k}$ |k=1, 2, j=1, 2, 3}),

其属性在不同尺度标记之间的粒度变换为

$\begin{array}{l} g_{1}^{1, 2} (u) = { \begin{array}{l} 1, u \in { 1, 2, 3, 4, 5} , \\ 2, u \in { 6, 7, 8, 9, 10} , \end{array} \\ g_{2}^{1, 2} (v) = { \begin{array}{l} s, v = m or w, \\ l, v = b, \end{array} \\ g_{3}^{1, 2} (z) = r, z \in [10 % r, 10 % (r + 1)) . \end{array}$

根据定义2中的多重集之间的海林格距离, 定义多尺度多重集值信息系统上对象的属性值之间的相似度.

定义11 设

$S = (U, A) = (U, { a_{j}^{k} |k = 1, 2, \dots, I, j = 1, 2, \dots, m} )$

为一个多尺度多重集值信息系统, 对于∀ x∈ U, y∈ U, 在属性a_j的第k个尺度标记下的相似度为

SIM( $a_{j}^{k}$ (x), $a_{j}^{k}$ (y))=1-HD( $a_{j}^{k}$ (x), $a_{j}^{k}$ (y)).

命题2 定义11的相似性度量SIM满足如下性质, 对于∀ M∈ M(Z), M₁∈ M(Z), M₂∈ M(Z), 其中Z={z₁, z₂, …, z_o},

1)SIM(M, M)=1,

2)SIM(M₁, M₂)=SIM(M₂, M₁),

3)SIM(M₁, M₂)=1⇔ M₁=M₂.

证明 1)和2)显然成立, 只需证明3).充分性的证明是显然的, 下面证明必要性.

若

SIM(M₁, M₂)=1,

设

M₁={ $\frac{z_{1}, z_{2}, \dots, z_{o}}{p_{1}, p_{2}, \dots, p_{o}}$ }, M₂={ $\frac{z_{1}, z_{2}, \dots, z_{o}}{q_{1}, q_{2}, \dots, q_{o}}$ },

则

$\sqrt[]{1 - \overset{o}{\sum_{i = 1}} \sqrt[]{p_{i} q_{i}}}$ =0.

于是

$\overset{o}{\sum_{i = 1}} \sqrt[]{p_{i} q_{i}}$ =1.

由Hö lder不等式可知

$\overset{o}{\sum_{i = 1}} \sqrt[]{p_{i} q_{i}}$ ≤ ( $\overset{o}{\sum_{i = 1}}$ p_i) $^{\frac{1}{2}}$ ( $\overset{o}{\sum_{i = 1}}$ q_i) $^{\frac{1}{2}}$ ,

又

$\overset{o}{\sum_{i = 1}}$ p_i=1, $\overset{o}{\sum_{i = 1}}$ q_i=1,

故

$\overset{o}{\sum_{i = 1}} \sqrt[]{p_{i} q_{i}}$ =( $\overset{o}{\sum_{i = 1}}$ p_i) $^{\frac{1}{2}}$ ( $\overset{o}{\sum_{i = 1}}$ q_i) $^{\frac{1}{2}}$ .

由Hö lder不等式等号成立条件可得

p_i=q_i, i=1, 2, …, o,

即M₁=M₂. 证毕

命题3 设

$S = (U, A) = (U, { a_{j}^{k} |k = 1, 2, \dots, I, j = 1, 2, \dots, m} )$

为一个多尺度多重集值信息系统, 对于∀ x∈ U, y∈ U, 在属性a_j下的相似度关于尺度具有单调性, 即对于k∈ {1, 2, …, I-1}, 有

SIM( $a_{j}^{k}$ (x), $a_{j}^{k}$ (y))≤ SIM( $a_{j}^{k + 1}$ (x), $a_{j}^{k + 1}$ (y)).

证明对于∀ x∈ U, y∈ U, k∈ {1, 2, …, I-1}, 设属性 $a_{j}^{k}$ 的值域为

V $_{j}^{k}$ =Z^k,

其中

Z^k={ $z_{1}^{k}$ , $z_{2}^{k}$ , …, $z_{o}^{k}$ },

$Z^{k + 1} = { z_{1}^{k + 1}, z_{2}^{k + 1}, \dots, z_{l}^{k + 1}}$

设

$a_{j}^{k} (x) = { \frac{z_{1}^{k}, z_{2}^{k}, \dots, z_{o}^{k}}{p_{1}^{k}, p_{2}^{k}, \dots, p_{o}^{k}}}$ ,

$a_{j}^{k} (y) = { \frac{z_{1}^{k}, z_{2}^{k}, \dots, z_{o}^{k}}{q_{1}^{k}, q_{2}^{k}, \dots, q_{o}^{k}}}$

$a_{j}^{k + 1} (x) = { \frac{z_{1}^{k + 1}, z_{2}^{k + 1}, \dots, z_{l}^{k + 1}}{p_{1}^{k + 1}, p_{2}^{k + 1}, \dots, p_{l}^{k + 1}}}$ ,

$a_{j}^{k + 1} (y) = { \frac{z_{1}^{k + 1}, z_{2}^{k + 1}, \dots, z_{l}^{k + 1}}{q_{1}^{k + 1}, q_{2}^{k + 1}, \dots, q_{l}^{k + 1}}}$

由 $g_{j}^{k, k + 1}$ 是一个满射可知, 存在l+1个数

$\begin{array}{l}\tau_{1} \in\{1, 2, \cdots, o+1\}, \\ \tau_{2} \in\{1, 2, \cdots, o+1\}, \\ \vdots \\ \tau_{l+1} \in\{1, 2, \cdots, o+1\}, \end{array}$

其中

1=τ ₁< τ ₂< …< τ _l< τ _l₊₁=o+1,

使得

$g_{j}^{k, k + 1}$ ( $z_{λ}^{k}$ )= $z_{γ}^{k + 1}$ ,

其中

τ _γ≤ λ < τ _γ₊₁, γ =1, 2, …, l.

由此可得

$\sum_{τ_{γ} \leq λ < τ_{γ + 1}}$ $Δ_{λ}^{k}$ = $Δ_{γ}^{k + 1}$ , Δ =p, q.

由Hö lder不等式进一步可得

$\sum_{i=1}^{o} \sqrt{p_{i} q_{i}} \leqslant\left(\sum_{i=1}^{o} p_{i}\right)^{\frac{1}{2}}\left(\sum_{i=1}^{o} q_{i}\right)^{\frac{1}{2}}$

可知

$\overset{o}{\sum_{i = 1}} \sqrt[]{p_{i}^{k} q_{i}^{k}}$ ≤ $\overset{l}{\sum_{γ = 1}} \sqrt[]{p_{γ}^{k + 1} q_{γ}^{k + 1}}$ .

故

HD( $a_{j}^{k}$ (x), $a_{j}^{k}$ (y))≥ HD( $a_{j}^{k + 1}$ (x), $a_{j}^{k + 1}$ (y)),

得证

SIM( $a_{j}^{k}$ (x), $a_{j}^{k}$ (y))≤ SIM( $a_{j}^{k + 1}$ (x), $a_{j}^{k + 1}$ (y)).

证毕

例4 (续例3) 对于例3中的多尺度多重集值信息系统中的数据, 通过定义11给出的相似度, 可以计算每个属性在各个尺度标记下的相似度矩阵, 如表2~表7所示.

表2 属性a₁在第1个尺度标记下的相似度矩阵 Table 2 Similarity matrix of attribute a₁ under the first scale

$a_{1}^{1}$	x₁	x₂	x₃	x₄	x₅	x₆	x₇	x₈
x₁	1.00	0.46	0.20	0.00	0.00	0.00	0.37	0.79
x₂	0.46	1.00	0.00	0.00	0.00	0.13	0.50	0.50
x₃	0.20	0.00	1.00	0.00	0.00	0.00	0.20	0.20
x₄	0.00	0.00	0.00	1.00	0.62	0.50	0.00	0.00
x₅	0.00	0.00	0.00	0.62	1.00	0.62	0.00	0.00
x₆	0.00	0.13	0.00	0.50	0.62	1.00	0.13	0.00
x₇	0.37	0.50	0.20	0.00	0.00	0.13	1.00	0.50
x₈	0.79	0.50	0.20	0.00	0.00	0.00	0.50	1.00

表2 属性a₁在第1个尺度标记下的相似度矩阵 Table 2 Similarity matrix of attribute a₁ under the first scale

表3 属性a₁在第2个尺度标记下的相似度矩阵 Table 3 Similarity matrix of attribute a₁ under the second scale

$a_{1}^{2}$	x₁	x₂	x₃	x₄	x₅	x₆	x₇	x₈
x₁	1.00	0.63	1.00	0.00	0.00	0.00	0.63	1.00
x₂	0.63	1.00	0.63	0.29	0.29	0.29	1.00	0.63
x₃	1.00	0.63	1.00	0.00	0.00	0.00	0.63	1.00
x₄	0.00	0.29	0.00	1.00	1.00	1.00	0.29	0.00
x₅	0.00	0.29	0.00	1.00	1.00	1.00	0.29	0.00
x₆	0.00	0.29	0.00	1.00	1.00	1.00	0.29	0.00
x₇	0.63	1.00	0.63	0.29	0.29	0.29	1.00	0.63
x₈	1.00	0.63	1.00	0.00	0.00	0.00	0.63	1.00

表3 属性a₁在第2个尺度标记下的相似度矩阵 Table 3 Similarity matrix of attribute a₁ under the second scale

表4 属性a₂在第1个尺度标记下的相似度矩阵 Table 4 Similarity matrix of attribute a₂ under the first scale

$a_{2}^{1}$	x₁	x₂	x₃	x₄	x₅	x₆	x₇	x₈
x₁	1.00	0.44	0.29	0.46	0.63	0.63	0.62	0.29
x₂	0.44	1.00	0.29	0.00	0.13	0.25	0.20	0.63
x₃	0.29	0.29	1.00	0.00	0.29	0.00	0.46	0.00
x₄	0.46	0.00	0.00	1.00	0.63	0.63	0.46	0.00
x₅	0.63	0.13	0.29	0.63	1.00	0.50	0.82	0.00
x₆	0.63	0.25	0.00	0.63	0.50	1.00	0.38	0.29
x₇	0.62	0.20	0.46	0.46	0.82	0.38	1.00	0.00
x₈	0.29	0.63	0.00	0.00	0.00	0.29	0.00	1.00

表4 属性a₂在第1个尺度标记下的相似度矩阵 Table 4 Similarity matrix of attribute a₂ under the first scale

表5 属性a₂在第2个尺度标记下的相似度矩阵 Table 5 Similarity matrix of attribute a₂ under the second scale

$a_{2}^{2}$	x₁	x₂	x₃	x₄	x₅	x₆	x₇	x₈
x₁	1.00	0.46	0.46	0.46	0.82	0.82	1.00	0.46
x₂	0.46	1.00	1.00	0.00	0.29	0.29	0.46	1.00
x₃	0.46	1.00	1.00	0.00	0.29	0.29	0.46	1.00
x₄	0.46	0.00	0.00	1.00	0.63	0.63	0.46	0.00
x₅	0.82	0.29	0.29	0.63	1.00	1.00	0.82	0.29
x₆	0.82	0.29	0.29	0.63	1.00	1.00	0.82	0.29
x₇	1.00	0.46	0.46	0.46	0.82	0.82	1.00	0.46
x₈	0.46	1.00	1.00	0.00	0.29	0.29	0.46	1.00

表5 属性a₂在第2个尺度标记下的相似度矩阵 Table 5 Similarity matrix of attribute a₂ under the second scale

表6 属性a₃在第1个尺度标记下的相似度矩阵 Table 6 Similarity matrix of attribute a₃ under the first scale

$a_{3}^{1}$	x₁	x₂	x₃	x₄	x₅	x₆	x₇	x₈
x₁	1.00	0.20	0.13	0.00	0.00	0.00	0.29	0.13
x₂	0.20	1.00	0.20	0.00	0.00	0.00	0.00	0.00
x₃	0.13	0.20	1.00	0.00	0.00	0.00	0.00	0.00
x₄	0.00	0.00	0.00	1.00	0.13	0.29	0.00	0.00
x₅	0.00	0.00	0.00	0.13	1.00	0.29	0.00	0.00
x₆	0.00	0.00	0.00	0.29	0.29	1.00	0.00	0.00
x₇	0.29	0.00	0.00	0.00	0.00	0.00	1.00	0.13
x₈	0.13	0.00	0.00	0.00	0.00	0.00	0.13	1.00

表6 属性a₃在第1个尺度标记下的相似度矩阵 Table 6 Similarity matrix of attribute a₃ under the first scale

表7 属性a₃在第2个尺度标记下的相似度矩阵 Table 7 Similarity matrix of attribute a₃ under the second scale

$a_{3}^{2}$	x₁	x₂	x₃	x₄	x₅	x₆	x₇	x₈
x₁	1.00	0.29	0.38	0.00	0.00	0.00	0.82	0.82
x₂	0.29	1.00	0.82	0.00	0.00	0.00	0.20	0.20
x₃	0.38	0.82	1.00	0.00	0.00	0.00	0.25	0.25
x₄	0.00	0.00	0.00	1.00	0.82	0.63	0.00	0.00
x₅	0.00	0.00	0.00	0.82	1.00	0.82	0.00	0.00
x₆	0.00	0.00	0.00	0.63	0.82	1.00	0.00	0.00
x₇	0.82	0.20	0.25	0.00	0.00	0.00	1.00	1.00
x₈	0.82	0.20	0.25	0.00	0.00	0.00	1.00	1.00

表7 属性a₃在第2个尺度标记下的相似度矩阵 Table 7 Similarity matrix of attribute a₃ under the second scale

在一个多尺度多重集值信息系统S=(U, A)中, 当阈值α ∈ (0, 1]时, 属性a_j在第k个尺度标记下的相似关系定义为

$R_{a_{j}^{k}}^{α}$ ={(x, y)∈ U× U|SIM( $a_{j}^{k}$ (x), $a_{j}^{k}$ (y))≥ α }.

例5 (续例4) 当阈值α =0.95时, 属性a₁在第1个尺度标记下的相似关系:

$\begin{array}{l} R_{a_{1}^{1}}^{α} = { (x_{1}, x_{1}), (x_{2}, x_{2}), (x_{3}, x_{3}), (x_{4}, x_{4}), \\ (x_{5}, x_{5}), (x_{6}, x_{6}), (x_{7}, x_{7}), (x_{8}, x_{8})} . \end{array}$

属性a₁在第2个尺度标记下的相似关系:

$\begin{array}{l} R_{a_{1}^{2}}^{α} = { (x_{1}, x_{1}), (x_{1}, x_{3}), (x_{1}, x_{8}), (x_{2}, x_{2}), \\ (x_{2}, x_{7}), (x_{3}, x_{1}), (x_{3}, x_{3}), (x_{3}, x_{8}), \\ (x_{4}, x_{4}), (x_{4}, x_{5}), (x_{4}, x_{6}), (x_{5}, x_{4}), \\ (x_{5}, x_{5}), (x_{5}, x_{6}), (x_{6}, x_{4}), (x_{6}, x_{5}), \\ (x_{6}, x_{6}), (x_{7}, x_{2}), (x_{7}, x_{7}), (x_{8}, x_{1}), \\ (x_{8}, x_{3}), (x_{8}, x_{8})} . \end{array}$

属性a₂在第1个尺度标记下的相似关系:

$\begin{array}{l} R_{a_{2}^{1}}^{α} = { (x_{1}, x_{1}), (x_{2}, x_{2}), (x_{3}, x_{3}), (x_{4}, x_{4}), \\ (x_{5}, x_{5}), (x_{6}, x_{6}), (x_{7}, x_{7}), (x_{8}, x_{8})} . \end{array}$

属性a₂在第2个尺度标记下的相似关系:

$\begin{array}{l} R_{a_{2}^{2}}^{α} = { (x_{1}, x_{1}), (x_{1}, x_{7}), (x_{2}, x_{2}), (x_{2}, x_{3}), \\ (x_{2}, x_{8}), (x_{3}, x_{2}) ， (x_{3}, x_{3}), (x_{3}, x_{8}), \\ (x_{4}, x_{4}), (x_{5}, x_{5}), (x_{5}, x_{6}), (x_{6}, x_{5}), \\ (x_{6}, x_{6}), (x_{7}, x_{1}), (x_{7}, x_{7}), (x_{8}, x_{2}), \\ (x_{8}, x_{3}), (x_{8}, x_{8})} . \end{array}$

属性a₃在第1个尺度标记下的相似关系:

$\begin{array}{l} R_{a_{3}^{1}}^{α} = { (x_{1}, x_{1}), (x_{2}, x_{2}), (x_{3}, x_{3}), (x_{4}, x_{4}), \\ (x_{5}, x_{5}), (x_{6}, x_{6}), (x_{7}, x_{7}), (x_{8}, x_{8})} . \end{array}$

属性a₃在第2个尺度标记下的相似关系:

$\begin{array}{l} R_{a_{3}^{2}}^{α} = { (x_{1}, x_{1}), (x_{2}, x_{2}), (x_{3}, x_{3}), (x_{4}, x_{4}), \\ (x_{5}, x_{5}), (x_{6}, x_{6}), (x_{7}, x_{7}), (x_{7}, x_{8}), \\ (x_{8}, x_{7}), (x_{8}, x_{8})} . \end{array}$

命题4 设

$S = (U, A) = (U, { a_{j}^{k} |k = 1, 2, \dots, I, j = 1, 2, \dots, m} )$

为一个多尺度多重集值信息系统, 当阈值α ∈ (0, 1]时, 对于∀ a_j∈ A, k∈ {1, 2, …, I-1},

$R_{a_{j}^{k}}^{α}$ ⊆ $R_{a_{j}^{k + 1}}^{α}$

成立.

证明对于∀ a_j∈ A, k∈ {1, 2, …, I-1}, 若(x, y)∈ $R_{a_{j}^{k}}^{α}$ , 则

SIM( $a_{j}^{k}$ (x), $a_{j}^{k}$ (y))≥ α

成立.由命题3可知, 有

SIM( $a_{j}^{k}$ (x), $a_{j}^{k}$ (y))≤ SIM( $a_{j}^{k + 1}$ (x), $a_{j}^{k + 1}$ (y)).

因此得

SIM( $a_{j}^{k + 1}$ (x), $a_{j}^{k + 1}$ (y))≥ α ,

即

(x, y)∈ $R_{a_{j}^{k + 1}}^{α}$ ,

从而

$R_{a_{j}^{k}}^{α}$ ⊆ $R_{a_{j}^{k + 1}}^{α}$ .证毕

相似关系 $R_{a_{j}^{k}}^{α}$ 将论域U粒化为若干相似类:

U/ $R_{a_{j}^{k}}^{α}$ ={[x $]_{a_{j}^{k}}^{α}$ |x∈ U},

其中

[x $]_{a_{j}^{k}}^{α}$ ={y∈ U|(x, y)∈ $R_{a_{j}^{k}}^{α}$ },

且

$\cup_{x}^{\in}$ [x $]_{a_{j}^{k}}^{α}$ =U,

即相似类全体U/ $R_{a_{j}^{k}}^{α}$ 构成论域U的一个覆盖.

在一个多尺度多重集值信息系统S=(U, A)中, 当阈值α ∈ (0, 1]时, 属性子集B⊆A在第k个尺度标记下的相似关系定义为

$R_{B^{k}}^{α}$ ={(x, y)∈ U× U|SIM( $a_{j}^{k}$ (x), $a_{j}^{k}$ (y))≥ α , ∀ aj_∈B}.

显然

$R_{B^{k}}^{α}$ = $\cap_{a_{j}}^{\in} R_{a_{j}^{k}}^{α}$ , $R_{A^{k}}^{α}$ ⊆ $R_{B^{k}}^{α}$ .

同样相似关系 $R_{B^{k}}^{α}$ 可将论域U粒化为若干相似类:

U/ $R_{B^{k}}^{α}$ ={[x $]_{B^{k}}^{α}$ |x∈ U},

其中,

[x $]_{B^{k}}^{α}$ ={y∈ U|(x, y)∈ $R_{B^{k}}^{α}$ },

且

$\cup_{x}^{\in}$ [x $]_{B^{k}}^{α}$ =U,

即相似类全体U/ $R_{B^{k}}^{α}$ 也构成论域U的一个覆盖.

命题5 设

$S = (U, A) = (U, { a_{j}^{k} |k = 1, 2, \dots, I, j = 1, 2, \dots, m} )$

为一个多尺度多重集值信息系统, B⊆A, 当阈值α ∈ (0, 1]时,

$R_{B^{1}}^{α}$ ⊆ $R_{B^{2}}^{α}$ ⊆…⊆ $R_{B^{I}}^{α}$ .

证明只需要证明 $R_{B^{k}}^{α}$ ⊆ $R_{B^{k + 1}}^{α}$ , 对∀ k∈ {1, 2, …, I-1}都成立.对∀ k∈ {1, 2, …, I-1}, 由命题4可知, 对于∀ a_j∈ B, 有

$R_{a_{j}^{k}}^{α}$ ⊆ $R_{a_{j}^{k + 1}}^{α}$ .

从而对

∀ (x, y)∈ $\cap_{a_{j}}^{\in} R_{a_{j}^{k}}^{α}$ ,

有

(x, y)∈ $R_{a_{j}^{k}}^{α}$ , a_j∈ B.

又因为

$R_{a_{j}^{k}}^{α}$ ⊆ $R_{a_{j}^{k + 1}}^{α}$ ,

则

(x, y)∈ $R_{a_{j}^{k + 1}}^{α}$ , a_j∈ B,

所以

(x, y)∈ $\cap_{a_{j}}^{\in} R_{a_{j}^{k + 1}}^{α}$ .

因此

$\cap_{a_{j}}^{\in} R_{a_{j}^{k}}^{α}$ ⊆ $\cap_{a_{j}}^{\in} R_{a_{j}^{k + 1}}^{α}$ .

又由于

$R_{B^{k}}^{α}$ = $\cap_{a_{j}}^{\in} R_{a_{j}^{k}}^{α}$ ,

故得证 $R_{B^{k}}^{α}$ ⊆ $R_{B^{k + 1}}^{α}$ . 证毕

类比定义9中定义在不完备信息系统的相似关系下的知识粗糙熵, 本文在多尺度多重集值信息系统的相似关系下给出知识粗糙熵的定义.

定义12 设

$S = (U, A) = (U, { a_{j}^{k} |k = 1, 2, \dots, I, j = 1, 2, \dots, m} )$

为一个多尺度多重集值信息系统, B⊆A.当阈值α ∈ (0, 1]时, 对于k∈ {1, 2, …, I}, 属性集B在第k个尺度标记下的知识粗糙熵定义为

$E^{α} (B^{k}) = - \sum_{i = 1}^{|U|} \frac{|{[x_{i}]}_{B^{k}}^{α}|}{|U|} \log \frac{1}{|{[x_{i}]}_{B^{k}}^{α}|}$

性质3 设

$S = (U, A) = (U, { a_{j}^{k} |k = 1, 2, \dots, I, j = 1, 2, \dots, m} )$

为一个多尺度多重集值信息系统, B⊆A, C⊆A.当阈值α ∈ (0, 1]时, 对于k∈ {1, 2, …, I}, 若

U/ $R_{C^{k}}^{α}$ ⪯U/ $R_{B^{k}}^{α}$ ,

则

E^α(C^k)≤ E^α(B^k).

证明对于阈值α ∈ (0, 1], k∈ {1, 2, …, I}, 若

U/ $R_{C^{k}}^{α}$ ⪯U/ $R_{B^{k}}^{α}$ ,

则由定义7可知, 对于∀ x∈ U, 有

[x $]_{C^{k}}^{α}$ ⊆[x $]_{B^{k}}^{α}$ ,

于是

1≤ |[x $]_{C^{k}}^{α}$ |≤ |[x $]_{B^{k}}^{α}$ |

成立.由x log₂x在 $[1, + \infty)$ 有单调性, 有

$\begin{array}{l}\sum_{i=1}^{|U|}\left(\frac{\left|\left[x_{i}\right]_{C^{k}}^{\alpha}\right|}{|U|} \log _{2}\left(\left|\left[x_{i}\right]_{C^{k}}^{\alpha}\right|\right)\right) \leqslant \\ \sum_{i=1}^{|U|}\left(\frac{\left|\left[x_{i}\right]_{B^{k}}^{\alpha}\right|}{|U|} \log _{2}\left(\left|\left[x_{i}\right]_{B^{k}}^{\alpha}\right|\right)\right), \\\end{array}$

即

$\begin{aligned}-\sum_{i=1}^{|U|}( & \left.\frac{\left|\left[x_{i}\right]_{C^{k}}^{\alpha}\right|}{|U|} \log _{2}\left(\frac{1}{\left|\left[x_{i}\right]_{C^{k}}^{\alpha}\right|}\right)\right) \leqslant \\ & -\sum_{i=1}^{|U|}\left(\frac{\left|\left[x_{i}\right]_{B^{k}}^{\alpha}\right|}{|U|} \log _{2}\left(\frac{1}{\left|\left[x_{i}\right]_{B^{k}}^{\alpha}\right|}\right)\right) .\end{aligned}$

因此

E^α(C^k)≤ E^α(B^k).证毕

性质3说明在阈值α ∈ (0, 1]的情况下, 对于每个尺度标记, 若两个属性集生成的覆盖具有粗细关系, 则两个属性集对应的知识粗糙熵满足对应的大小关系.对应于覆盖越粗的属性集, 其知识粗糙熵越大.

推论1 设

$S = (U, A) = (U, { a_{j}^{k} |k = 1, 2, \dots, I, j = 1, 2, \dots, m} )$

为一个多尺度多重集值信息系统, B⊆A.当阈值α ∈ (0, 1]时, 对于k∈ {1, 2, …, I}, 则

E^α(A^k)≤ E^α(B^k).

性质4 设

$S = (U, A) = (U, { a_{j}^{k} |k = 1, 2, \dots, I, j = 1, 2, \dots, m} )$

为一个多尺度多重集值信息系统, B⊆A.当阈值α ∈ (0, 1]时, 对于k∈ {1, 2, …, I}, 则

U/ $R_{A^{k}}^{α}$ =U/ $R_{B^{k}}^{α}$

当且仅当

E^α(A^k)=E^α(B^k).

证明先证必要性, 对于阈值α ∈ (0, 1]和k∈ {1, 2, …, I}, 若

U/ $R_{A^{k}}^{α}$ =U/ $R_{B^{k}}^{α}$ ,

则

[x $]_{A^{k}}^{α}$ =[x $]_{B^{k}}^{α}$ , x∈ U.

由知识粗糙熵的定义可知

E^α(A^k)=E^α(B^k).

再证充分性.只需证明对于阈值α ∈ (0, 1]和k∈ {1, 2, …, I},

若

E^α(A^k)=E^α(B^k),

则

U/ $R_{A^{k}}^{α}$ =U/ $R_{B^{k}}^{α}$ .

对于阈值α ∈ (0, 1]和k∈ {1, 2, …, I}, 由

E^α(A^k)=E^α(B^k)

和知识粗糙熵的定义可知

$- \sum_{i = 1}^{|U|} \frac{|{[x_{i}]}_{B^{k}}^{α}|}{|U|} \log \frac{1}{|{[x_{i}]}_{B^{k}}^{α}|} = - \sum_{i = 1}^{|U|} \frac{|{[x_{i}]}_{B^{l}}^{α}|}{|U|} \log \frac{1}{|{[x_{i}]}_{B^{l}}^{α}|}$

可化简为

$\sum_{i = 1}^{|U|} |{[x_{i}]}_{B^{k}}^{α}| \log |{[x_{i}]}_{B^{k}}^{α}| = \sum_{i = 1}^{|U|} |{[x_{i}]}_{B^{l}}^{α}| \log |{[x_{i}]}_{B^{l}}^{α}|$

因为

$R_{A^{k}}^{α}$ ⊆ $R_{B^{k}}^{α}$ ,

即对于∀ x∈ U, 有

[x $]_{A^{k}}^{α}$ ⊆[x $]_{B^{k}}^{α}$ ,

从而相似类的基数满足

$1 \leqslant\left|[x]_{A^{k}}^{\alpha}\right| \leqslant\left|[x]_{B^{k}}^{\alpha}\right|$.

由函数x log₂x在[1, +¥ )上的单调性, 可得

$\left|[x]_{A^{k}}^{\alpha}\right| \log _{2}\left(\left|[x]_{A^{k}}^{\alpha}\right|\right) \leqslant\left|[x]_{B^{k}}^{\alpha}\right| \log _{2}\left(\left|[x]_{B^{k}}^{\alpha}\right|\right)$.

进而有

$\left|[x]_{A^{k}}^{\alpha}\right|=\left|[x]_{B^{k}}^{\alpha}\right|, \forall x \in U$,

否则

$\begin{array}{l} \sum_{x \in U}\left(\left|[x]_{A^{k}}^{\alpha}\right| \log _{2}\left(\left|[x]_{A^{k}}^{\alpha}\right|\right)\right)< \\ \sum_{x \in U}\left(\left|[x]_{B^{k}}^{\alpha}\right| \log _{2}\left(\left|[x]_{B^{k}}^{\alpha}\right|\right)\right), \end{array}$

矛盾.又因为

[x $]_{A^{k}}^{α}$ ⊆[x $]_{B^{k}}^{α}$ ,

故

[x $]_{A^{k}}^{α}$ =[x $]_{B^{k}}^{α}$ , x∈ U,

得证

U/ $R_{A^{k}}^{α}$ =U/ $R_{B^{k}}^{α}$ .证毕

性质5 设

$S = (U, A) = (U, { a_{j}^{k} |k = 1, 2, \dots, I, j = 1, 2, \dots, m} )$

为一个多尺度多重集值信息系统, B⊆A.当阈值α ∈ (0, 1]时, 则对于1≤ k≤ l≤ I, 有

E^α(B^k)≤ E^α(B^l).

证明由命题5可知, 对于阈值α ∈ (0, 1]和1≤ k≤ l≤ I, 有

$R_{B^{1}}^{α}$ ⊆ $R_{B^{2}}^{α}$ ⊆…⊆ $R_{B^{I}}^{α}$ ,

即

U/ $R_{B^{k}}^{α}$ ⪯U/ $R_{B^{l}}^{α}$ .

则由定义7可知, 对于∀ x∈ U, 有

[x $]_{B^{k}}^{α}$ ⊆[x $]_{B^{l}}^{α}$ ,

于是

$1 \leq |{[x]}_{B^{k}}^{α}| \leq |{[x]}_{B^{l}}^{α}|$

成立.由x log₂x在[1, +∞]有单调性, 故

$\begin{array}{l}\sum_{i=1}^{|U|}\left(\frac{\left|\left[x_{i}\right]_{B^{k}}^{\alpha}\right|}{|U|} \log _{2}\left(\left|\left[x_{i}\right]_{B^{k}}^{\alpha}\right|\right)\right) \leqslant \\ \sum_{i=1}^{|U|}\left(\frac{\left|\left[x_{i}\right]_{B^{l}}^{\alpha}\right|}{|U|} \log _{2}\left(\left|\left[x_{i}\right]_{B^{l}}^{\alpha}\right|\right)\right) \\\end{array}$

即

$\begin{aligned}-\sum_{i=1}^{|U|}( & \left.\frac{\left|\left[x_{i}\right]_{B^{k}}^{\alpha}\right|}{|U|} \log _{2}\left(\frac{1}{\left|\left[x_{i}\right]_{B^{k}}^{\alpha}\right|}\right)\right) \leqslant \\ & -\sum_{i=1}^{|U|}\left(\frac{\left|\left[x_{i}\right]_{B^{l}}^{\alpha}\right|}{|U|} \log _{2}\left(\frac{1}{\left|\left[x_{i}\right]_{B^{l}}^{\alpha}\right|}\right)\right) .\end{aligned}$

因此

E^α(B^k)≤ E^α(B^l)

成立. 证毕

性质6 设

$\begin{aligned} S= & (U, A)= \\ & \left(U, \left\{a_{j}^{k} \mid k=1, 2, \cdots, I, j=1, 2, \cdots, m\right\}\right)\end{aligned}$

为一个多尺度多重集值信息系统, B⊆A.当阈值α ∈ (0, 1]时, 对于1≤ k≤ l≤ I,

U/ $R_{B^{k}}^{α}$ =U/ $R_{B^{l}}^{α}$

当且仅当

E^α(B^k)=E^α(B^l).

证明先证必要性.对于阈值α ∈ (0, 1]和1≤ k≤ l≤ I, 若

U/ $R_{B^{k}}^{α}$ =U/ $R_{B^{l}}^{α}$ ,

则

[x $]_{B^{k}}^{α}$ =[x $]_{B^{l}}^{α}$ , x∈ U.

由知识粗糙熵的定义可知

E^α(B^k)=E^α(B^l).

再证充分性.只需证明对于阈值α ∈ (0, 1]和1≤ k≤ l≤ I, 若

E^α(B^k)=E^α(B^l),

则

U/ $R_{B^{k}}^{α}$ =U/ $R_{B^{l}}^{α}$ .

对于阈值α ∈ (0, 1]和1≤ k≤ l≤ I, 由

E^α(B^k)=E^α(B^l)

和知识粗糙熵的定义可知

$\begin{aligned}-\sum_{i=1}^{|U|} & \left(\frac{\left|\left[x_{i}\right]_{B^{k}}^{\alpha}\right|}{|U|} \log _{2}\left(\frac{1}{\left|\left[x_{i}\right]_{B^{k}}^{\alpha}\right|}\right)\right)= \\ & -\sum_{i=1}^{|U|}\left(\frac{\left|\left[x_{i}\right]_{B^{l}}^{\alpha}\right|}{|U|} \log _{2}\left(\frac{1}{\left|\left[x_{i}\right]_{B^{l}}^{\alpha}\right|}\right)\right) .\end{aligned}$

可化简为

$\begin{array}{l}\sum_{i=1}^{|U|}\left(\left|\left[x_{i}\right]_{B^{k}}^{\alpha}\right| \log _{2}\left(\left|\left[x_{i}\right]_{B^{k}}^{\alpha}\right|\right)\right)= \\ \sum_{i=1}^{|U|}\left(\left|\left[x_{i}\right]_{B^{l}}^{\alpha}\right| \log _{2}\left(\left|\left[x_{i}\right]_{B^{l}}^{\alpha}\right|\right)\right) .\end{array}$

由命题5可知, 对于1≤ k≤ l≤ I, 有

$R_{B^{k}}^{α}$ ⊆ $R_{B^{l}}^{α}$ ,

即对于∀ x∈ U, 有

[x $]_{B^{k}}^{α}$ ⊆[x $]_{B^{l}}^{α}$ .

从而

$1 \leqslant\left|[x]_{B^{k}}^{\alpha}\right| \leqslant\left|[x]_{B^{l}}^{\alpha}\right|$.

又由函数x log₂x在[1, +∞]上的单调性, 可得

$\left|[x]_{B^{k}}^{\alpha}\right| \log _{2}\left(\left|[x]_{B^{k}}^{\alpha}\right|\right) \leqslant\left|[x]_{B^{l}}^{\alpha}\right| \log _{2}\left(\left|[x]_{B^{l}}^{\alpha}\right|\right)$.

进而有

$\left|[x]_{B^{k}}^{\alpha}\right|=\left|[x]_{B^{l}}^{\alpha}\right|, x \in U, $

否则

$\begin{array}{l}\sum_{x \in U}\left(\left|[x]_{B^{k}}^{\alpha}\right| \log _{2}\left(\left|[x]_{B^{k}}^{\alpha}\right|\right)\right)＜ \\ \sum_{x \in U}\left(\left|[x]_{B^{l}}^{\alpha}\right| \log _{2}\left(\left|[x]_{B^{l}}^{\alpha}\right|\right)\right), \end{array}$

矛盾.又因为

[x $]_{B^{k}}^{α}$ ⊆[x $]_{B^{l}}^{α}$ ,

故

[x $]_{B^{k}}^{α}$ =[x $]_{B^{l}}^{α}$ , x∈ U,

得证

U/ $R_{B^{k}}^{α}$ =U/ $R_{B^{l}}^{α}$ .证毕

3 最优尺度选择和属性约简

本节主要讨论多尺度多重集值信息系统基于知识粗糙熵的熵最优尺度选择和熵约简的问题, 首先给出多尺度多重集值信息系统中最优尺度和熵最优尺度的概念, 再给出约简和熵约简的概念.

定义13 设

$\begin{aligned} S= & (U, A)= \\ & \left(U, \left\{a_{j}^{k} \mid k=1, 2, \cdots, I, j=1, 2, \cdots, m\right\}\right)\end{aligned}$

为一个多尺度多重集值信息系统, 对于阈值α ∈ (0, 1]和第k个尺度标记(k∈ {1, 2, …, I}), 若

$R_{A^{k}}^{α}$ = $R_{A^{1}}^{α}$ ,

则称S^k关于S是α -协调的.若进一步有

$R_{A^{k + 1}}^{α}$ ≠ $R_{A^{1}}^{α}$ , k+1≤ I,

则称k为S的α -最优尺度.

定义14 设

$\begin{aligned} S= & (U, A)= \\ & \left(U, \left\{a_{j}^{k} \mid k=1, 2, \cdots, I, j=1, 2, \cdots, m\right\}\right)\end{aligned}$

为一个多尺度多重集值信息系统, 对于阈值α ∈ (0, 1]和第k个尺度标记(k∈ {1, 2, …, I}), 若

E^α(A^k)=E^α(A¹),

则称S^k关于S是α -熵协调的.若进一步有

E^α(A^k⁺¹)≠ E^α(A¹), k+1≤ I,

则称k为S的α -熵最优尺度.

例6 (续例5) 当阈值α =0.95时,

$\begin{aligned} R_{A^{1}}^{\alpha}= & \left\{\left(x_{1}, x_{1}\right), \left(x_{2}, x_{2}\right), \left(x_{3}, x_{3}\right), \left(x_{4}, x_{4}\right), \right. \\ & \left.\left(x_{5}, x_{5}\right), \left(x_{6}, x_{6}\right), \left(x_{7}, x_{7}\right), \left(x_{8}, x_{8}\right)\right\}, \\ R_{A^{2}}^{\alpha}= & \left\{\left(x_{1}, x_{1}\right), \left(x_{2}, x_{2}\right), \left(x_{3}, x_{3}\right), \left(x_{4}, x_{4}\right), \right. \\ & \left.\left(x_{5}, x_{5}\right), \left(x_{6}, x_{6}\right), \left(x_{7}, x_{7}\right), \left(x_{8}, x_{8}\right)\right\}, \end{aligned}$

故

$R_{A^{2}}^{α}$ = $R_{A^{1}}^{α}$ ,

从而S²关于S是α -协调的.又由于

E^α(A¹)=0, E^α(A²)=0,

即

E^α(A²)=E^α(A¹),

因此S²关于S也是α -熵协调的.

当阈值α '=0.8时,

$\begin{aligned} R_{A^{1}}^{\alpha^{\prime}}= & \left\{\left(x_{1}, x_{1}\right), \left(x_{2}, x_{2}\right), \left(x_{3}, x_{3}\right), \left(x_{4}, x_{4}\right), \right. \\ & \left.\left(x_{5}, x_{5}\right), \left(x_{6}, x_{6}\right), \left(x_{7}, x_{7}\right), \left(x_{8}, x_{8}\right)\right\}, \\ R_{A^{2}}^{\alpha^{\prime}}= & \left\{\left(x_{1}, x_{1}\right), \left(x_{2}, x_{2}\right), \left(x_{3}, x_{3}\right), \left(x_{4}, x_{4}\right), \right. \\ & \left(x_{5}, x_{5}\right), \left(x_{5}, x_{6}\right), \left(x_{6}, x_{6}\right), \left(x_{6}, x_{5}\right), \\ & \left.\left(x_{7}, x_{7}\right), \left(x_{8}, x_{8}\right)\right\}, \end{aligned}$

故

$R_{A^{2}}^{α'}$ ≠ $R_{A^{1}}^{α'}$ ,

从而S²关于S不是α '-协调的.又由于

E^{α '}(A¹)=0, E^{α '}(A²)= $\frac{1}{2}$ ,

即

E^{α '}(A²)≠ E^{α '}(A¹),

因此S²关于S也不是α '-熵协调的.

综上所述, 当阈值α =0.95时, 系统S的α -最优尺度和α -熵最优尺度都为2, 但当阈值α '=0.8时, 系统S的α '-最优尺度和α '-熵最优尺度都为1.

定理1 设

$\begin{aligned} S= & (U, A)= \\ & \left(U, \left\{a_{j}^{k} \mid k=1, 2, \cdots, I, j=1, 2, \cdots, m\right\}\right)\end{aligned}$

为一个多尺度多重集值信息系统, 对于阈值α ∈ (0, 1]和k∈ {1, 2, …, I}, 则S^k关于S是α -协调的当且仅当S^k关于S是α -熵协调的.

证明根据定义13, 若S^k关于S是α -协调的, 则

$R_{A^{k}}^{α}$ = $R_{A^{1}}^{α}$

成立, 从而

U/ $R_{A^{k}}^{α}$ =U/ $R_{A^{1}}^{α}$ .

而由定义14和S^k关于S是α -熵协调的, 可知

E^α(A^k)=E^α(A¹).

因此, 只需证明

U/ $R_{A^{k}}^{α}$ =U/ $R_{A^{1}}^{α}$ , E^α(A^k)=E^α(A¹)

是等价的.由性质6可得两者的等价性成立, 即S^k关于S是α -协调的当且仅当S^k关于S是α -熵协调的.

证毕

定理1说明多尺度多重集值信息系统的α -协调和α -熵协调是等价的, 由定理1可直接得到定理2.

定理2 设

$\begin{aligned} S= & (U, A)= \\ & \left(U, \left\{a_{j}^{k} \mid k=1, 2, \cdots, I, j=1, 2, \cdots, m\right\}\right)\end{aligned}$

为一个多尺度多重集值信息系统, 对于阈值α ∈ (0, 1]和k∈ {1, 2, …, I}, 则k是S的α -最优尺度当且仅当k是S的α -熵最优尺度.

定义15 设

$\begin{aligned} S= & (U, A)= \\ & \left(U, \left\{a_{j}^{k} \mid k=1, 2, \cdots, I, j=1, 2, \cdots, m\right\}\right)\end{aligned}$

为一个多尺度多重集值信息系统, 对于阈值α ∈ (0, 1]和S的α -最优尺度k, 当B⊆A时, 若 $R_{B^{k}}^{α}$ = $R_{A^{1}}^{α}$ , 则称B是S在α -最优尺度k下的一个α -协调集.若进一步对于∀ b∈ B, 都有

$R_{B^{k} - {b^{k}}}^{α}$ ≠ $R_{A^{1}}^{α}$ ,

则称B是S在α -最优尺度k下的一个α -约简.

定义16 设

$\begin{aligned} S= & (U, A)= \\ & \left(U, \left\{a_{j}^{k} \mid k=1, 2, \cdots, I, j=1, 2, \cdots, m\right\}\right)\end{aligned}$

为一个多尺度多重集值信息系统, 对于阈值α ∈ (0, 1]和S的α -熵最优尺度k, 当B⊆A时, 若

E^α(B^k)=E^α(A¹),

则称B是S在α -熵最优尺度k下的一个α -熵协调集.若进一步对于∀ b∈ B, 都有

E^α(B^k-{b^k})≠ E^α(A¹),

则称B是S在α -熵最优尺度k下的一个α -熵约简.

例7(续例6) 当阈值α =0.95时, 在α -最优尺度2的情况下,

$\begin{aligned} R_{A^{2}-\left\{a_{1}^{2}\right\}}^{\alpha}= & \left\{\left(x_{1}, x_{1}\right), \left(x_{2}, x_{2}\right), \left(x_{3}, x_{3}\right), \left(x_{4}, x_{4}\right), \right. \\ & \left.\left(x_{5}, x_{5}\right), \left(x_{6}, x_{6}\right), \left(x_{7}, x_{7}\right), \left(x_{8}, x_{8}\right)\right\}, \end{aligned}$

$\begin{aligned} R_{A^{2}-\left\{a_{2}^{2}\right\}}^{\alpha}= & \left\{\left(x_{1}, x_{1}\right), \left(x_{2}, x_{2}\right), \left(x_{3}, x_{3}\right), \left(x_{4}, x_{4}\right), \right. \\ & \left.\left(x_{5}, x_{5}\right), \left(x_{6}, x_{6}\right), \left(x_{7}, x_{7}\right), \left(x_{8}, x_{8}\right)\right\}, \end{aligned}$

$\begin{aligned} R_{A^{2}-\left\{a_{3}^{2}\right\}}^{\alpha}= & \left\{\left(x_{1}, x_{1}\right), \left(x_{2}, x_{2}\right), \left(x_{3}, x_{3}\right), \left(x_{3}, x_{8}\right), \right. \\ & \left(x_{4}, x_{4}\right), \left(x_{5}, x_{5}\right), \left(x_{5}, x_{6}\right), \left(x_{6}, x_{6}\right), \\ & \left.\left(x_{6}, x_{5}\right), \left(x_{7}, x_{7}\right), \left(x_{8}, x_{3}\right), \left(x_{8}, x_{8}\right)\right\} .\end{aligned}$

显然有

$R_{A^{2}}^{α}$ = $R_{A^{2} - {a_{1}^{2}}}^{α}$ = $R_{A^{2} - {a_{2}^{2}}}^{α}$ ≠ $R_{A^{2} - {a_{3}^{2}}}^{α}$ ,

同时

$R_{A^{2}}^{α}$ ≠ $R_{a_{1}^{2}}^{α}$ , $R_{A^{2}}^{α}$ ≠ $R_{a_{2}^{2}}^{α}$ , $R_{A^{2}}^{α}$ ≠ $R_{a_{3}^{2}}^{α}$

成立.因此在α -最优尺度2下多尺度多重集值信息系统的α -约简为{a₂, a₃}和{a₁, a₃}.又因为

$\begin{array}{l}E^{\alpha}\left(A^{2}\right)=0, \\ E^{\alpha}\left(A^{2}-\left\{a_{1}^{2}\right\}\right)=0, \\ E^{\alpha}\left(A^{2}-\left\{a_{2}^{2}\right\}\right)=0, \\ E^{\alpha}\left(A^{2}-\left\{a_{3}^{2}\right\}\right)=1, \\ E^{\alpha}\left(a_{1}^{2}\right)=\frac{9}{4} \log _{2} 3+\frac{1}{2}, \\ E^{\alpha}\left(a_{2}^{2}\right)=\frac{9}{8} \log _{2} 3+1, \\ E^{\alpha}\left(a_{3}^{2}\right)=\frac{1}{2}, \end{array}$

因此, 在α -熵最优尺度2下多尺度多重集值信息系统的α -熵约简为{a₂, a₃}和{a₁, a₃}.

定理3 设

$\begin{aligned} S= & (U, A)= \\ & \left(U, \left\{a_{j}^{k} \mid k=1, 2, \cdots, I, j=1, 2, \cdots, m\right\}\right)\end{aligned}$

为一个多尺度多重集值信息系统, 对于阈值α , 当B⊆A时, 则B是S在α -最优尺度k下的一个α -约简当且仅当B是S在α -熵最优尺度k下的一个α -熵约简.

证明先证必要性.由于B是S在α -最优尺度k下的一个α -约简, 因此

$R_{B^{k}}^{α}$ = $R_{A^{1}}^{α}$ ,

且∀ b∈ B, 都有

$R_{B^{k} - {b^{k}}}^{α}$ ≠ $R_{A^{1}}^{α}$ .

对于阈值α 和S的α -最优尺度k, 由α -最优尺度的定义可知

$R_{A^{k}}^{α}$ = $R_{A^{1}}^{α}$ ,

从而

$R_{B^{k}}^{α}$ = $R_{A^{k}}^{α}$ .

又由性质4的证明可知, 有

E^α(B^k)=E^α(A^k).

同时由定理2得k也是α -熵最优尺度, 从而

E^α(A^k)=E^α(A¹),

因此

E^α(B^k)=E^α(A¹).

若对于∀ b∈ B, 都有

$R_{B^{k} - {b^{k}}}^{α}$ ≠ $R_{A^{1}}^{α}$ ,

则

U/ $R_{B^{k} - {b^{k}}}^{α}$ ≠ U/ $R_{A^{1}}^{α}$ .

由于k是α -最优尺度, 因此

U/ $R_{A^{1}}^{α}$ =U/ $R_{A^{k}}^{α}$ ,

即

U/ $R_{B^{k} - {b^{k}}}^{α}$ ≠ U/ $R_{A^{k}}^{α}$ .

由性质4的逆否命题可知

E^α(B^k-{b^k})≠ E^α(A^k).

同时由k也是α -熵最优尺度可知

E^α(A^k)=E^α(A¹),

从而

E^α(B^k-{b^k})≠ E^α(A¹).

故B是S在α -熵最优尺度k下的一个α -熵约简.

再证充分性.由于B是S在α -熵最优尺度k下的一个α -熵约简, 因此

E^α(B^k)=E^α(A¹),

且∀ b∈ B, 都有

E^α(B^k-{b^k})≠ E^α(A¹).

对于阈值α 和S的α -熵最优尺度k, 由α -熵最优尺度的定义可知

E^α(A^k)=E^α(A¹),

从而

E^α(B^k)=E^α(A^k).

又由性质4的证明可知, 有

$R_{B^{k}}^{α}$ = $R_{A^{k}}^{α}$ .

同时由定理2得k也是α -最优尺度, 从而

$R_{A^{k}}^{α}$ = $R_{A^{1}}^{α}$ ,

因此

$R_{B^{k}}^{α}$ = $R_{A^{1}}^{α}$ .

若对于∀ b∈ B, 都有

E^α(B^k-{b^k})≠ E^α(A¹)

成立, 由于k是α -熵最优尺度, 因此

E^α(A^k)=E^α(A¹),

即

E^α(B^k-{b^k})≠ E^α(A^k).

又由性质4的逆否命题可知

U/ $R_{B^{k} - {b^{k}}}^{α}$ ≠ U/ $R_{A^{k}}^{α}$ .

同时由k也是α -最优尺度可知

U/ $R_{A^{1}}^{α}$ =U/ $R_{A^{k}}^{α}$ ,

从而

U/ $R_{B^{k} - {b^{k}}}^{α}$ ≠ U/ $R_{A^{1}}^{α}$ ,

即

$R_{B^{k} - {b^{k}}}^{α}$ ≠ $R_{A^{1}}^{α}$ ,

故B是S在α -最优尺度k下的一个α -约简. 证毕

定理3说明多尺度多重集值信息系统的α -约简和α -熵约简是等价的.

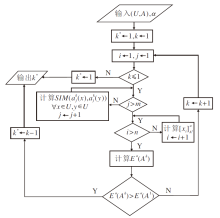
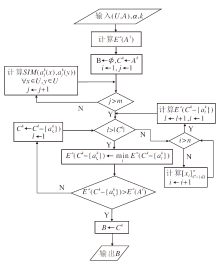
接下来, 基于知识粗糙熵给出计算α -熵最优尺度和α -熵约简的算法, 算法1是基于知识粗糙熵计算α -熵最优尺度的算法, 算法2是基于知识粗糙熵计算α -熵约简的算法.两种算法流程图如图1和图2所示.

	Figure Option View Download New Window
	图1 算法1流程图Fig.1 Flow chart of Algorithm 1

	Figure Option View Download New Window
	图2 算法2流程图Fig.2 Flow chart of Algorithm 2

算法1 基于知识粗糙熵的最优尺度算法

输入I个尺度的多尺度多重集值信息系统(U, A), 阈值α ∈ (0, 1]

输出α -熵最优尺度k^*

1.初始化k^*← 1, k← 1

2.while k≠ I do

3. for each $a_{j}^{k}$ ∈ A do

4. 计算对象两两之间的相似性

SIM( $a_{j}^{k}$ (x_s), $a_{j}^{k}$ (x_t))

5. end for

6. for each x∈ U do

7. 计算对象x的相似类[x $]_{A^{k}}^{α}$

8. end for

9. 求第k个尺度标记下的知识粗糙熵E^α(A^k)

10. if E^α(A^k)> E^α(A¹) then

11. k^*← k-1

12. break

13. end if

14. k← k+1

15.end while

在算法1中, 步骤3~5用于计算对象间的相似度, 时间复杂度为O(mn²), 其中m表示属性个数, n表示对象个数.步骤6~8用于计算每个对象的相似类, 时间复杂度为O(n).因为算法1最多需要考虑I个尺度, 因此算法1的时间复杂度为O(Imn²), 其中I表示系统的尺度标记个数.

算法2 基于知识粗糙熵的属性约简算法

输入I个尺度的多尺度多重集值信息系统(U, A), 阈值α ∈ (0, 1], α -熵最优尺度k

输出α -熵约简B

1.求最细尺度标记下知识粗糙熵E^α(A¹)

2.初始化B← Ø , C^k← A^k

3.for each $a_{j}^{k}$ ∈ A^k do

4. 计算对象两两之间的相似性

SIM( $a_{j}^{k}$ (x_s), $a_{j}^{k}$ (x_t))

5.end for

6.for each $a_{j}^{k}$ ∈ C^k do

7. for each x∈ U do

8. 计算对象x的相似类[x $]_{C^{k} - {a_{j}^{k}}}^{α}$

9. end for

10. 求属性集C^k-{ $a_{j}^{k}$ }的知识粗糙熵

E^α(C^k-{ $a_{j}^{k}$ })

11.end for

12.E^α(C^k-{ $a_{j_{0}}^{k}$ })← $\min_{j}$ E^α(C^k-{ $a_{j}^{k}$ })

13.if E^α(C^k-{ $a_{j_{0}}^{k}$ })> E^α(A¹) then

14. B← C^k

15.else

16. C^k← C^k-{ $a_{j_{0}}^{k}$ }

17. return 6

18.end if

在算法2中, 步骤3~5同样也用于计算对象间的相似度, 时间复杂度为O(mn²).步骤6~11用于计算属性集C^k-{ $a_{j}^{k}$ }的知识粗糙熵, 时间复杂度为O(rn), 其中r表示属性集C中的属性个数.若步骤13不满足条件, 则需要减少属性, 重新计算步骤6~11, 以求出属性约简, 最多需要考虑m次, 因此步骤6~18的时间复杂度为

$O\left(\frac{(1+m) m}{2} n\right)$

即为O(m²n).所以算法2的时间复杂度为

O(mn²+m²n).

4 结束语

多尺度信息系统中的最优尺度的选择和基于最优尺度的属性约简是多尺度数据分析研究的关键问题, 迄今尚未见到属性取值为多重集且具有多个尺度的信息系统的数据分析研究.本文将多重集引入多尺度信息系统, 提出多尺度多重集值信息系统的概念, 基于海林格距离的相似度在论域上构造对应于任一属性子集的相似类, 定义基于相似关系和基于知识粗糙熵的最优尺度概念, 并证明两者是等价的, 在最优尺度的基础上提出α -约简和α -熵约简的概念, 并给出计算α -熵最优尺度和α -熵约简算法.由于文中定义的相似度在处理尺度较细的属性时, 相似度变化不均匀, 影响模型的稳定性和鲁棒性, 因此所能应用的问题存在一定的局限性, 在后续的研究中需进一步改进.另外, 多尺度多重集值决策系统的最优尺度选择和知识获取是有待继续探讨的课题, 包括广义多尺度多重集值决策系统和不完备多尺度多重集值决策系统的知识获取问题.

本文责任编委苗夺谦

Recommended by Associate Editor MIAO Duoqian

参考文献

文献选项

[1]	LIN T Y. Granular Computing: Structures, Representations, and Applications // Proc of the 9th International Conference on Rough Sets, Fuzzy Sets, Data Mining, and Granular Computing. Berlin, Germany: Springer, 2003: 16-24. [本文引用:1]
[2]	PEDRYCZ W. Granular Computing: An Introduction // Proc of the Joint 9th IFSA World Congress and 20th NAFIPS International Conference. Washington, USA: IEEE, 2001: 1349-1354. [本文引用:1]
[3]	YAO J T, VASILAKOS A V, PEDRYCZ W. Granular Computing: Perspectives and Challenges. IEEE Transactions on Cybernetics, 2013, 43(6): 1977-1989. [本文引用:1]
[4]	ZADEH L A. Fuzzy Sets and Information Granularity // GUPTA M, RAGADE R, YAGER R, eds. Advances in Fuzzy Set Theory and Applications. Amsterdam, the Netherland : North-Holland Publi-shing, 1979: 3-18. [本文引用:1]
[5]	陈德刚, 徐伟华, 李金海, 等. 粒计算基础教程. 北京: 科学出版社, 2019. (CHEN D G, XU W H, LI J H, et al. Basic Course of Granular Computing. Beijing, China: Science Press, 2019. ) [本文引用:1]
[6]	NIU J J, CHEN D G, LI J H, et al. A Dynamic Rule-Based Classification Model Via Granular Computing. Information Sciences(An International Journal), 2022, 584: 325-341. [本文引用:1]
[7]	YANG X, LI T R, LIU D, et al. A Multilevel Neighborhood Sequential Decision Approach of Three-Way Granular Computing. Information Sciences, 2020, 538: 119-141. [本文引用:1]
[8]	PAWLAK Z. RoughSets. International Journal of Computer and Information Sciences, 1982, 11(5): 341-356. [本文引用:2]
[9]	MIYAMOTO S. Multisets and Fuzzy Multisets // LIU Z Q, MIYAMOTO S, eds. Soft Computing and Human-Centered Machines. Berlin, Germany: Springer, 2000: 9-33. [本文引用:2]
[10]	BLIZARD W D. Multiset Theory. Notre Dame Journal of Formal Logic, 1989, 30(1): 36-66. [本文引用:1]
[11]	YAGER R R. On the Theory of Bags. International Journal of Ge-neral System, 1986, 13(1): 23-37. [本文引用:1]
[12]	CHOPYUK Y, VASYLYSHYN T, ZAGORODNYUK A. Rings of Multisets and Integer Multinumbers. Mathematics, 2022, 10(5). DOI: DOI:10.3390/MOTH/0050778. [本文引用:1]
[13]	EISENBERG A, MELTON J, KULKARNI K, et al. SQL: 2003 Has Been Published. ACM SIGMOD Record, 2004, 33(1): 119-126. [本文引用:1]
[14]	D'AGOSTINO G, VISSER A. Finality Regained: A Coalgebraic Study of Scott-Sets and Multisets. Archive for Mathematical Logic, 2002, 41: 267-298. [本文引用:1]
[15]	赵前进, 平昕瑞, 苏树智, 等. 标签敏感的多重集正交相关特征融合方法. 电子与信息学报, 2022, 44(10): 3458-3464. (ZHAO Q J, PING X R, SU S Z, et al. Feature Fusion Method Based on Label-Sensitive Multi-set Orthogonal Correlation. Journal of Electronics & Information Technology, 2022, 44(10): 3458-3464. ) [本文引用:1]
[16]	LI Z W, YANG T L, LI J J. Semi-Supervised Attribute Reduction for Partially Labelled Multiset-Valued Data via a Prediction Label Strategy. Information Sciences, 2023, 634: 477-504. [本文引用:1]
[17]	DU C, YE J. Weighted Parameterized Correlation Coefficients of Indeterminacy Fuzzy Multisets and Their Multicriteria Group Decision Making Method with Different Decision Risks. Computer Mo-deling in Engineering and Sciences, 2021, 129(1): 341-354. [本文引用:1]
[18]	TÜRKARSLAN E, YE J, ÜNVER M, et al. Consistency Fuzzy Sets and a Cosine Similarity Measure in Fuzzy Multiset Setting and Application to Medical Diagnosis. Mathematical Problems in Engineering, 2021. DOI: DOI:10.1155/2021.9975983. [本文引用:1]
[19]	ZHAO X R, HU B Q. Three-Way Decisions with Decision-Theore-tic Rough Sets in Multiset-Valued Information Tables. Information Sciences, 2020, 507: 684-699. [本文引用:3]
[20]	王虹, 柴晓华. 多集值信息表中的多粒度模糊决策论粗糙集. 数学的实践与认识, 2020, 50(8): 141-148. (WANG H, CHAI X H. Multi-Granularity Fuzzy Decision Theory Rough Set in Multi-set-Valued Information Table. Mathematics in Practice and Theory, 2020, 50(8): 141-148. ) [本文引用:2]
[21]	陈跃, 李小南. 基于多重集值局势表的三支冲突分析. 模糊系统与数学, 2022, 36(2): 107-120. (CHEN Y, LI X N. Three-Way Conflict Analysis Based on Multiset-Valued Situation Tables. Fuzzy Systems and Mathematics, 2022, 36(2): 107-120. ) [本文引用:1]
[22]	ZHANG P F, LI T R, WANG G Q, et al. Multi-source Information Fusion Based on Rough Set Theory: A Review. Information Fusion, 2021, 68(1): 85-117. [本文引用:2]
[23]	HUANG D, LIN H, LI Z W. Information Structures in a Multiset-Valued Information System with Application to Uncertainty Mea-surement. Journal of Intelligent and Fuzzy Systems, 2022, 43(6): 7447-7469. [本文引用:4]
[24]	WU W Z, LEUNG Y. Theory and Applications of Granular Labelled Partitions in Multi-scale Decision Tables. Information Sciences, 2011, 181(18): 3878-3897. [本文引用:3]
[25]	陈应生, 李进金, 林荣德, 等. 多尺度覆盖决策信息系统的布尔矩阵方法. 模式识别与人工智能, 2020, 33(9): 776-785. (CHEN Y S, LI J J, LIN R D, et al. Boolean Matrix Approach for Multi-scale Covering Decision Information System. Pattern Recognition and Artificial Intelligence, 2020, 33(9): 776-785. ) [本文引用:2]
[26]	ZHAN J M, ZHANG K, WU W Z. An Investigation on Wu-Leung Multi-scale Information Systems and Multi-expert Group Decision-Making. Expert Systems with Applications, 2021, 170(1). DOI: DOI:10.1016/j.eswa.2020.114542. [本文引用:2]
[27]	陈艳, 胡军, 张清华, 等. 多尺度集值信息系统及其最优尺度选择. 山西大学学报(自然科学版), 2020, 43(4): 765-775. (CHEN Y, HU J, ZHANG Q H, et al. Multi-scale Set-Valued Information System and Its Optimal Scale Selection. Journal of Shanxi University(Natural Science Edition), 2020, 43(4): 765-775. ) [本文引用:2]
[28]	NEVEU P, TIREAU A, HILGERT N, et al. Dealing with Multi-source and Multi-scale Information in Plant Phenomics: The Onto-logy-Driven Phenotyping Hybrid Information System. The New Phytologist, 2019, 221(1): 588-601. [本文引用:2]
[29]	WANG H R, LI W T, ZHAN T, et al. Multi-granulation-Based Optimal Scale Selection in Multi-scale Information Systems. Computers and Electrical Engineering, 2021, 92. DOI: DOI:10.1016/j.compeleceng.2021.107107. [本文引用:1]
[30]	SHANNON C E. A Mathematical Theory of Communication. ACM SIGMOBILE Mobile Computing and Communications Review, 2001, 5(1): 3-55. [本文引用:1]
[31]	张嘉宇. 基于信息熵的多尺度决策表最优尺度选择. 硕士学位论文. 太原: 山西大学, 2020. (ZHANG J Y. Information Entropy Based Optimal Scale Selection in Multi-scale Decision Tables. Master Dissertation. Taiyuan, China: Shanxi University, 2020. ) [本文引用:2]
[32]	郑嘉文, 吴伟志, 包菡, 等. 基于熵的多尺度决策系统的最优尺度选择. 南京大学学报(自然科学), 2021, 57(1): 130-140. (ZHENG J W, WU W Z, BAO H, et al. Entropy Based Optimal Scale Selection for Multi-scale Decision Systems. Journal of Nanjing University(Natural Science), 2021, 57(1): 130-140. ) [本文引用:2]
[33]	LIANG J Y, XU Z B. Uncertainty Measures of Roughness of Know-ledge and Rough Sets in Incomplete Information Systems // Proc of the 3rd World Congress on Intelligent Control and Automation. Washington, USA: IEEE, 2000: 2526-2529. [本文引用:5]
[34]	LIANG J Y, XU Z B. The Algorithm on Knowledge Reduction in Incomplete Information Systems. International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems, 2002, 10(1): 95-103. [本文引用:2]
[35]	LIANG J Y, SHI Z Z, LI D Y, et al. Information Entropy, Rough Entropy and Knowledge Granulation in Incomplete Information Systems. International Journal of General Systems, 2006, 35(6): 641-654. [本文引用:1]
[36]	SUN L, XU J C, TIAN Y. Feature Selection Using Rough Entropy-Based Uncertainty Measures in Incomplete Decision Systems. Knowledge-Based Systems, 2012, 36: 206-216. [本文引用:1]
[37]	MA W M, SUN B Z. Probabilistic Rough Set over Two Universes and Rough Entropy. International Journal of Approximate Reaso-ning, 2012, 53(4): 608-619. [本文引用:1]
[38]	邓切, 张贤勇, 杨霁琳, 等. 基于双论域笛卡尔积的粗糙熵与知识粒度. 模式识别与人工智能, 2019, 32(11): 975-986. (DENG Q, ZHANG X Y, YANG J L, et al. Rough Entropy and Knowledge Granularity Based on Cartesian Product of Double Universes. Pattern Recognition and Artificial Intelligence, 2019, 32(11): 975-986. ) [本文引用:1]
[39]	陈艳. 多尺度集值信息系统及其应用研究. 硕士学位论文. 重庆: 重庆邮电大学, 2021. (CHEN Y. Research on Multi-scale Set-Valued Information System and Its Application. Master Dissertation. Chongqing, China: Chong-qing University of Posts and Telecommunications, 2021. ) [本文引用:1]
[40]	王金波, 吴伟志. 基于证据理论的广义多尺度覆盖决策系统的最优尺度组合. 模式识别与人工智能, 2022, 35(4): 291-305. (WANG J B, WU W Z. Evidence-Theory-Based Optimal Scale Combinations in Generalized Multi-scale Covering Decision Systems. Pattern Recognition and Artificial Intelligence, 2022, 35(4): 291-305. ) [本文引用:1]
[41]	苗夺谦, 王珏. 粗糙集理论中知识粗糙性与信息熵关系的讨论. 模式识别与人工智能, 1998, 11(1): 34-40. (MIAO D Q, WANG J. On the Relationships between Information Entropy and Roughness of Knowledge in Rough Set Theory. Pattern Recognition and Artificial Intelligence, 1998, 11(1): 34-40. ) [本文引用:1]

2003

0.0

... 粒计算^[1,2,3]是模拟人脑思维以处理数据不确定性和复杂性的一种方法,源于Zadeh^[4]提出的#cod#x0201c ...

2001

0.0

... 粒计算^[1,2,3]是模拟人脑思维以处理数据不确定性和复杂性的一种方法,源于Zadeh^[4]提出的#cod#x0201c ...

2013

0.0

... 粒计算^[1,2,3]是模拟人脑思维以处理数据不确定性和复杂性的一种方法,源于Zadeh^[4]提出的#cod#x0201c ...

1979

0.0

... 粒计算^[1,2,3]是模拟人脑思维以处理数据不确定性和复杂性的一种方法,源于Zadeh^[4]提出的#cod#x0201c ...

2019

0.0

... 粒计算的核心思想是通过合适的粒化提取信息粒,对信息粒进行处理和计算,进而分析数据规律和解决实际问题^[5,6,7] ...

2022

0.0

... 粒计算的核心思想是通过合适的粒化提取信息粒,对信息粒进行处理和计算,进而分析数据规律和解决实际问题^[5,6,7] ...

2020

0.0

... 粒计算的核心思想是通过合适的粒化提取信息粒,对信息粒进行处理和计算,进而分析数据规律和解决实际问题^[5,6,7] ...

1982

0.0

... 粗糙集最早由Pawlak^[8]于1982年提出 ...

... 定义3^[8] 称S=(U,A)为一个信息系统,其中 ...

2000

0.0

... 多重集^[9,10,11]是一种元素可重复出现的集合,元素在多重集中出现的次数称为该元素在多重集中的重数并且元素的顺序可以互换 ...

... 定义1^[9] 设Z={z₁,z₂,…,z_o}为一个非空有限集合,N为自然数集合,称M为集合Z上的一个多重集,若Z中的元素z_i(z_i#cod#x02208 ...

1989

0.0

... 多重集^[9,10,11]是一种元素可重复出现的集合,元素在多重集中出现的次数称为该元素在多重集中的重数并且元素的顺序可以互换 ...

1986

0.0

... 多重集^[9,10,11]是一种元素可重复出现的集合,元素在多重集中出现的次数称为该元素在多重集中的重数并且元素的顺序可以互换 ...

2022

0.0

... 多重集在组合数学^[12]、关系数据库理论^[13]、图论^[14]等领域都有重要应用 ...

2004

0.0

... 多重集在组合数学^[12]、关系数据库理论^[13]、图论^[14]等领域都有重要应用 ...

2002

0.0

... 多重集在组合数学^[12]、关系数据库理论^[13]、图论^[14]等领域都有重要应用 ...

2022

0.0

... 此外,多重集在模式识别^[15,16]、多准则决策^[17]、医疗诊断^[18]等领域也有重要应用 ...

2023

0.0

... 此外,多重集在模式识别^[15,16]、多准则决策^[17]、医疗诊断^[18]等领域也有重要应用 ...

2021

0.0

... 此外,多重集在模式识别^[15,16]、多准则决策^[17]、医疗诊断^[18]等领域也有重要应用 ...

2021

0.0

... 此外,多重集在模式识别^[15,16]、多准则决策^[17]、医疗诊断^[18]等领域也有重要应用 ...

2020

0.0

... 多重集值信息系统在决策分析^[19,20,21]、多源信息融合^[22,23]等领域具有重要的研究价值 ...

... Zhao等^[19]在多重集值信息系统中建立决策理论粗糙集模型 ...

... 定义4^[19] 称S=(U,A)为一个多重集值信息系统,其中 ...

2020

0.0

... 多重集值信息系统在决策分析^[19,20,21]、多源信息融合^[22,23]等领域具有重要的研究价值 ...

... 王虹等^[20]结合多粒度粗糙集和模糊决策论,研究在多重集值信息系统中乐观与悲观粗糙集的上、下近似的性质,并讨论粗糙集精度与粗度等问题 ...

2022

0.0

... 多重集值信息系统在决策分析^[19,20,21]、多源信息融合^[22,23]等领域具有重要的研究价值 ...

2021

0.0

... 多重集值信息系统在决策分析^[19,20,21]、多源信息融合^[22,23]等领域具有重要的研究价值 ...

... Zhang等^[22]探索多重集值信息系统在多源信息融合领域的重要应用 ...

2022

0.0

... 多重集值信息系统在决策分析^[19,20,21]、多源信息融合^[22,23]等领域具有重要的研究价值 ...

... Huang等^[23]利用多重集值信息系统,解决在多源信息融合时产生的信息缺省问题,从粒计算的角度给出多重集值信息系统中的信息结构,并研究其在不确定度量中的应用 ...

... 文献[23]引入概率论中的海林格距离以定义多重集之间的距离 ...

... 定义2^[23] 对于Z={z₁,z₂,…,z_o}上的两个多重集M₁#cod#x02208 ...

2011

0.0

... 针对类似问题,Wu等^[24]首次提出多尺度粗糙集数据分析模型,处理的数据称为多尺度信息系统,这种系统中每个属性对于同个对象具有不同尺度的取值,并且在不同的尺度之间存在粒度变换的关系 ...

... 针对对象的属性可能存在多种尺度的情况,Wu等^[24]首次提出多尺度信息系统的概念 ...

... 定义5^[24] 称S=(U,A)为一个多尺度信息系统,其中 ...

2020

0.0

... 近年来,多尺度粗糙集数据分析已成为粒计算领域的一个重要方向^{[25,26,27,28,29]} ...

... 陈应生等^[25]建立多尺度覆盖决策系统模型,并使用布尔矩阵研究系统的粒描述 ...

2021

0.0

... 近年来,多尺度粗糙集数据分析已成为粒计算领域的一个重要方向^{[25,26,27,28,29]} ...

... Zhan等^[26]利用多尺度信息系统与多专家群体决策系统的关系,研究排序决策问题 ...

2020

0.0

... 近年来,多尺度粗糙集数据分析已成为粒计算领域的一个重要方向^{[25,26,27,28,29]} ...

... 陈艳等^[27]提出多尺度集值信息系统的概念,给出系统在不同尺度下的粗糙近似 ...

2019

0.0

... 近年来,多尺度粗糙集数据分析已成为粒计算领域的一个重要方向^{[25,26,27,28,29]} ...

... 定义8^[28] 设U为非空有限集合,若 ...

2021

0.0

... 近年来,多尺度粗糙集数据分析已成为粒计算领域的一个重要方向^{[25,26,27,28,29]} ...

2001

0.0

... 信息熵是刻画信息系统不确定性的重要指标之一,熵的概念最早来源于热力学理论,由Shannon^[30]引入信息论中 ...

2020

0.0

... 在保持信息熵不变的情况下,即在保持系统不确定性不变的情况下找到原系统的最优尺度和属性约简,是多尺度数据分析研究的一个重要问题^[31,32] ...

... 张嘉宇^[31]研究条件熵和互补熵在多尺度信息系统中的最优尺度选择问题,并类比两种方法的效果 ...

2021

0.0

... 在保持信息熵不变的情况下,即在保持系统不确定性不变的情况下找到原系统的最优尺度和属性约简,是多尺度数据分析研究的一个重要问题^[31,32] ...

... 郑嘉文等^[32]利用香农熵,研究多尺度信息系统中的最优尺度选择问题,并证明最优尺度与熵最优尺度的等价性,但香农熵建立在由等价关系产生的划分上 ...

2000

0.0

... Liang等^[33,34]引入在相似关系下知识粗糙熵的概念,并运用于不完备系统的知识表示与知识约简中 ...

... 为此,Liang等^[33,34]在不完备信息系统中提出在相似关系下的知识粗糙熵的概念 ...

... 定义9^[33] 设(U,A)为一个不完备信息系统,B⊆A,属性集B的知识粗糙熵定义为 ...

... 性质1^[33] 设(U,A)为一个不完备信息系统,B⊆A,C⊆A ...

... 性质2^[33] 设(U,A)为一个不完备信息系统,B⊆A,则 ...

2002

0.0

... Liang等^[33,34]引入在相似关系下知识粗糙熵的概念,并运用于不完备系统的知识表示与知识约简中 ...

... 为此,Liang等^[33,34]在不完备信息系统中提出在相似关系下的知识粗糙熵的概念 ...

2006

0.0

... 之后,Liang等^[35]讨论不完备信息系统中的信息熵、粗糙熵和知识粒化之间的关系 ...

2012

0.0

... Sun等^[36]基于粗糙熵构造低计算复杂度的启发式算法 ...

2012

0.0

... Ma等^[37]研究双论域上概率粗糙集的知识粒度和粗糙熵的不确定度量 ...

2019

0.0

... 邓切等^[38]讨论双论域覆盖空间中的粗糙熵与知识粒度等问题 ...

2021

0.0

... 定义6^[39] 称S=(U,A)为一个多尺度集值信息系统,其中 ...

2022

0.0

... 定义7^[40] 设U是非空有限集合, ...

1998

0.0

... 命题1^[41] 设U为非空有限集合,对于U上两个划分X和Y,若满足X⪯Y,则H(X)#cod#x02265 ...