引用本文
冯夫健, 杨圆, 谭棉, 苟洪山, 梁椅辉, 王林. 基于微搜索的高分辨率图像前景遮罩提取算法. 模式识别与人工智能, 2023,36(6): 530-543
FENG Fujian, YANG Yuan, TAN Mian, GOU Hongshan, LIANG Yihui, WANG Lin. An Alpha Matting Algorithm Based on Micro-scale Searching for High-Resolution Images. PATTERN RECOGNITION AND ARTIFICIAL INTELLIGENCE, 2023,36(6): 530-543.  
Doi: 10.16451/j.cnki.issn1003-6059.202306004
Permissions
Copyright©2023, 《模式识别与人工智能》编辑部
《模式识别与人工智能》编辑部
基于微搜索的高分辨率图像前景遮罩提取算法
冯夫健1,2, 杨圆1,2, 谭棉1,2, 苟洪山1,2, 梁椅辉3, 王林1,2
1.贵州民族大学 数据科学与信息工程学院 贵阳 550025
2.贵州民族大学 贵州省模式识别与智能系统重点实验室 贵阳 550025
3.电子科技大学中山学院 计算机学院 中山 528400
通讯作者：

谭棉,硕士,副教授,主要研究方向为自然图像抠图、微计算.E-mail:tanmian@gzmu.edu.cn.

作者简介:

冯夫健,博士,教授,主要研究方向为进化计算、微计算.E-mail:fujian_feng@gzmu.edu.cn.

杨 圆,硕士研究生,主要研究方向为自然图像抠图.E-mail:380867698@qq.com.

苟洪山,硕士研究生,主要研究方向为前景遮罩值提取、图像处理.E-mail:hongshan_gou@yeah.net.

梁椅辉,博士,副教授,主要研究方向为图像抠图、图像处理.E-mail:yihuiliang@outlook.com.

王 林,博士,教授,主要研究方向为图像处理、模式识别.E-mail:wanglingz2008@qq.com.

收稿日期: 2023-02-27 接受日期: 2023-06-08
资助项目: 国家自然科学基金项目(No.62002053)、贵州省科技计划项目(No.黔科合基础-ZK[2022]一般195,黔科合基础-ZK[2023]一般143,黔科合平台人才-ZCKJ[2021]007)、贵州省青年科技人才成长项目(No.黔教合KY字[2021]104, 黔教合KY字[2021]111)、贵州省教育厅自然科学研究项目(No. 黔教技[2023]012号,黔教技[2022]015号,黔教技[2023]061号,黔教技[2023]062号)、贵州省深化新时代教育评价改革试点“教学过程质量评价”、广东省基础与应用基础研究基金项目(No.2019A1515111082)、广东省科学技术基金项目(No.2021A0101180005 )、中山市社会公益科技研究项目 (No.2019B2010,210714094038458)、中山市重点研发项目(No.2019A4018)资助
摘要

高分辨率图像抠图问题本质是前景背景像素对的大规模组合优化问题,目前相关研究成果较少.文中针对前景背景极相似时容易出现前景遮罩抠反的问题,设计决策集分解策略,实现高分辨率图像抠图问题的有效分解.此外,设计优化信息传递策略,获取子问题间的权重关系,建立图像抠图问题的优化序列.在优化信息传递策略的基础上,提出基于微搜索的前景遮罩提取算法.算法通过对有效决策子集的搜索代替对决策集的搜索,解决高分辨率图像抠图问题中的前景遮罩抠反问题,为大规模组合优化问题分析提供借鉴.选用alphamatting基准数据集作为测试数据,与典型的抠图优化算法对比分析,验证文中算法可以解决前景背景信息极为相似时的前景遮罩抠反问题,并且在高分辨率图像抠图问题维度显著降低的情况下,提高前景遮罩提取精度.

关键词: 高分辨率图像抠图; 前景遮罩; 微搜索; 有效决策子集; 等同关系
中图分类号:TP 391
An Alpha Matting Algorithm Based on Micro-scale Searching for High-Resolution Images
FENG Fujian1,2, YANG Yuan1,2, TAN Mian1,2, GOU Hongshan1,2, LIANG Yihui3, WANG Lin1,2
1. College of Data Science and Information Engineering, Guizhou Minzu University, Guiyang 550025
2. Key Laboratory of Pattern Recognition and Intelligent Systems of Guizhou Province, Guizhou Minzu University, Guiyang 550025
3. School of Computer Engineering, University of Electronic Science and Technology of China, Zhongshan Institute, Zhongshan 528400
Corresponding author：
TAN Mian, ma-ster, associate professor. Her research inte-rests include natural image matting and micro-computation.

About Author:
FENG Fujian, Ph.D., professor. His research interests include evolutionary computation and micro-computation.
YANG Yuan, master student. Her research interests include natural image matting.
GOU Hongshan, master student. His research interests include alpha matting and image processing.
LIANG Yihui, Ph.D., associate profe-ssor. His research interests include image matting and image processing.
WANG Lin, Ph.D., professor. His research interests include image processing and pattern recognition.

Fund:National Natural Science Foundation of China(No.62002053), the Science and Technology Program of Guizhou Province(No.QKH-Basic-ZK[2022]195,QKH-Basic-ZK[2023]143,QKH-Platform Talent-ZCKJ[2021]007), the Youth Science and Technology Talent Growth Project of Guizhou Province(No.QJH-KY[2021]104,QJH-KY[2021]111), the Natural Science Research Project of Education Department of Guizhou Province(No.QJJ2023012,QJJ2022015,QJJ2023061,QJJ2023062), the "Teaching Process Quality Evaluation" Pilot Project of Deepening Education Evaluation Reform in the New Era in Guizhou Province, Guangdong Basic and Applied Basic Research Foundation(No.2019A1515111082), the Science and Technology Foundation of Guangdong Province(No.2021A0101180005), the Social Welfare Science and Technology Research Project of Zhongshan City(No.2019B2010,210714094038458), the Key R&D Project of Zhongshan City(No.2019A4018)
Abstract

High-resolution image matting is essentially a large-scale combinatorial optimization for foreground/background pixel pairs. However, there is few research achievements on this issue. Alpha matte inverse extraction occurs when the foreground and the background in an image are highly similar. To address this problem, a decision set decomposition strategy is designed to effectively decompose high-resolution image matting problems. Moreover, a optimized information transmission strategy is designed, the weight relationship between sub-problems is obtained, and the optimization sequence of the image matting problem is established. Based on the optimized information transmission strategy, an alpha matting algorithm based on micro-scale searching(MS-AM) is proposed. MS-AM effectively solves the issue of alpha matte inverse extraction in high-resolution image matting problems by searching through effective decision subsets instead of the entire decision set, providing insights for the analysis of large-scale combinatorial optimization problems. The alphamatting benchmark dataset is selected as testing data, and MS-AM is compared with typical matting optimization algorithms. Results demonstrate that MS-AM can address alpha matte inverse extraction problem when the foreground is similar to the background and improve the alpha matting accuracy with significantly reduced dimension of high-resolution image matting problem.

Key words: Key Words High-Resolution Image Matting; Alpha Matte; Micro-scale Searching; Effective Decision Subset; Equivalence Relation

抠图作为图像处理中的重要技术之一, 广泛应用于图像合成、视频编辑、直播及影视特效等领域[1, 2, 3], 并且随着高分辨率以及超高分辨率图像的应用, 自然场景下的高分辨率图像抠图技术成为目前研究的一个热点问题[4].在图像抠图中, 前景遮罩值的提取精度决定合成图像质量的优劣.此外, 高分辨率图像局部区域中的颜色信息更细腻, 像素的前景信息和背景信息更相似, 这将导致前景遮罩提取过程中容易出现抠反的问题.前景遮罩值的抠反将直接影响抠图的质量.因此, 高分辨率图像前景遮罩提取过程中的抠反问题成为当前亟待解决的一个关键问题.

自Porter等[5]提出图像前景遮罩的概念后, 引入alpha通道, 构造图像前景遮罩提取模型.在该模型中, 任意像素点p的颜色值Ip可以由原始图像中的前景颜色Fp和背景颜色Bp线性表示, 即

Ip=α pFp+(1-α p)Bp, (1)

其中, α p表示像素点p的前景遮罩值, 物理意义为像素点p的不透明程度, 0≤ α p≤ 1.当α p=1时, 像素点p为完全不透明的前景像素信息, 当α p=0时, 像素点p为完全透明的背景像素信息, 当α p∈ (0, 1)时, 像素点p为半透明的前景和背景的混合像素信息.

对于一幅具有RGB三通道的彩色图像, Fp、Bp均为三维未知向量, α p为未知标量.因此, 该抠图模型是一个未知量个数大于方程数量的欠定问题[5].为了能精确求解α 值, Rhemann等[6]在抠图过程中引入三分图的概念, 将图像划分成已知前景F、已知背景B和未知区域U三个部分, 其中F、B、U分别对应α 为0、1、未知的区域.

近年来, 高分辨率图像前景遮罩提取问题已经引起计算机视觉领域研究人员的高度重视, 针对抠图问题已有一定的研究基础[7, 8].

在传统图像前景遮罩提取方面, 基于传播的方法[9]和基于采样的方法[10]利用前景遮罩取得不少的研究成果.Huang等[11]设计PDMS(Pixel-Level Discrete Multiobjective Sampling Method), 有效求解超像素采样方法中存在的采样空间不完整、最优样本丢失问题.在补丁图像抠图方法的基础上, Cao等[12]采用综合采样和随机游走算法以加速抠图模型, 提出基于补丁的高分辨率图像和视频自适应抠图算法, 将自适应框架扩展到视频抠图, 减少计算机内存的消耗.针对输入图像透明前景区域提取精度较低的问题, Zhu等[13]设计前景的透明度类型检测策略, 并根据其透明度类型提出ATPM(Adaptive Transparency-Based Propagation Matting).针对高分辨率图像抠图计算速度较慢的问题, Weng等[14]提出SSAM(Shared Sampling Alpha Matting), 与OpenMP(Open Multi-processing)进行并行运算, 在多核服务器平台上加快高分辨率图像抠图的计算速度.Tang等[15]提出基于学习的采样方法, 利用深度神经网络估计前景层、背景层的颜色, 进行分层采样, 从而提高前景遮罩值估计的性能.

此外, 针对输入图像局部复杂区域前景遮罩提取精度较低的问题, Feng等[16]设计WMGA(Weight Map Generation Algorithm), 测量输入图像与真实前景遮罩图像之间的局部差异, 提取局部复杂区域, 从而提高前景遮罩的精度.Aksoy等[9]通过已知透明度区域到未知区域以及未知区域内部的信息传递, 提高局部复杂区域的前景遮罩提取精度.

上述研究主要分析像素之间的相关性以及前景背景像素对的采样规则, 实现前景遮罩的提取.相对而言, 针对高分辨率图像中存在的局部前景背景信息相似时出现的抠反问题研究较少.

基于优化的前景遮罩提取方法将抠图问题建模成像素对优化问题, 为未知区域中的每个未知像素搜索最优的一组前景背景像素对.Liang等[17]将前景遮罩提取问题建模成基于前景、背景像素对的组合优化问题, 针对现有启发式算法求解过程中的过早收敛问题, 提出PSO-ACSC(Particle Swarm Optimi-zation-Adaptive Convergence Speed Controller).Liang等[18]针对计算资源和代价问题, 提出PMF(Pyramid Matting Framework), 利用图像金字塔, 将大规模像素对优化问题转化为多个不同尺度的子优化问题, 在不充足计算机资源情况下仍能提取较好的前景遮罩.针对大规模采样抠图的全局优化问题, Mohapatra等[19]提出NCSO(Novel Competitive Swarm Optimizer), 提高抠图精度.针对基于采样的抠图方法的不确定多准则优化问题, Liang等[20]提出FMCE(Fuzzy Multicriteria Evaluation)和MOEA-MCD(Multi-objective Evolutionary Algorithm Based on Multicriteria Decomposition).Wang等[21]针对人像抠图问题, 设计快速自动人像抠图方法, 利用多模型高斯过程回归对人像边缘区域进行检测, 提高人像抠图的精度.此外, 针对高清图像规模较大难以直接求解的问题, 冯夫健等[22]提出基于分组协同的群体竞争优化算法(Competitive Swarm Optimization Algorithm Based on Group Collaboration, GC-CSO), 对问题分解后同时估计每组的前景遮罩, 实现前景遮罩的并行提取.

综上所述, 虽然基于优化的前景遮罩提取方法在高清图像前景遮罩提取问题上取得一定成果, 但对于当前景背景信息极相似时容易出现抠反(前景像素抠成背景像素或背景像素抠成前景像素)的问题关注较少.因此, 针对高分辨率图像这一大规模组合优化问题中出现的抠反问题仍需要进一步的研究.

高分辨率图像抠图问题本质上是一个大规模的组合优化问题[17], 但当高分辨率图像中存在局部前景背景信息极相似时, 容易出现前景抠成背景、背景抠成前景的抠反问题.因此, 本文设计决策集分解策略, 将图像抠图这一大规模组合优化问题转化成多个小规模的子优化问题. 此外, 基于子问题之间的相似性, 设计优化信息传递策略, 获取子问题间的权重关系, 建立图像抠图问题的优化序列.受微尺度搜索思想[23]的启发, 结合决策集分解策略和优化信息传递策略, 提出基于微搜索的前景遮罩提取算法(Alpha Matting Algorithm Based on Micro-scale Sear-ching, MS-AM), 通过在有效决策子集中的搜索代替整个决策集的搜索, 有效解决高分辨率图像中局部前景背景信息抠反的问题, 提高高分辨率图像前景遮罩的提取精度.在alphamatting基准数据集[6]上进行实验验证, 结果表明, MS-AM可以解决局部前景背景信息极相似时出现的前景遮罩抠反问题, 并且在显著降低问题维度的情况下提高前景遮罩的精度.

1 相关知识

针对高分辨率图像的前景遮罩提取中局部前景背景信息极相似时容易出现的抠反问题, 从问题分解优化的思想出发, 引入均值偏移聚类算法的思想[24, 25, 26]作为高分辨率图像前景遮罩提取问题的分解工具, 将高分辨率大规模组合优化问题分解成多个小规模的子优化问题.

均值偏移聚类算法是一种常用的特征空间分析工具, 将数据点移向最高密度的数据点(即群集质心), 迭代地将数据点分配给群集, 从而实现群集数据的分类.本文采用均值偏移对高分辨率图像进行聚类分解, 根据像素点的空间位置和颜色信息计算同一带宽中的像素点, 并求取带宽内所有像素点的均值偏移向量mshift(pi), 实现未知区域像素的分类.具体计算方法如下:

$m_{\text {shift }}\left(\boldsymbol{p}_{i}\right)=\frac{\sum_{j=1}^{n} \boldsymbol{p}_{j} g\left(\left\|\frac{\boldsymbol{p}_{i}-\boldsymbol{p}_{j}}{h}\right\|_{2}\right)}{\sum_{j=1}^{n} g\left(\left\|\frac{\boldsymbol{p}_{i}-\boldsymbol{p}_{j}}{h}\right\|_{2}\right)}-\boldsymbol{p}_{i}, i=1, 2, \cdots, n(2)$

其中

g(α )=exp(− 12α )， α =pi− pjh2

mshift(pi)表示以像素点pi为窗口中心进行聚类之后, 同类中所有像素点的均值偏移向量, g(α )为一个以pi为窗口中心的单调递增函数, 窗口大小由带宽h决定, h> 0.

根据式(2)计算带宽h中所有像素点的均值偏移向量mshift(pi), 直到所有像素点的5维特征向量(R, G, B, x, y)收敛.具体聚类步骤如下.

1)设未知区域U的未知像素点数量为n, 其中, 任意一个像素pi, i=1, 2, …, n由5维特征向量(R, G, B, x, y)组成, 前三维表示像素点pi在RGB空间上的颜色值, 后两维表示pi在图像上的空间坐标.在未知区域中随机选择一个像素作为中心点.

2)记集合M为带宽h内所有像素点的信息.计算从中心像素点开始到集合M中每个元素的向量, 对得到的向量求和, 获取最终的偏移向量mshift(pi).

3)中心像素点向偏移向量mshift(pi)的方向移动, 设偏移向量的模长为像素点的移动步长.

4)重复上述操作, 直到所有像素点都归好类, 像素点个数小于ε 的类合并到相邻的类中, 最终产生η 个类.

根据均值偏移聚类算法, 高分辨率图像抠图这一大规模组合优化问题可以分解为多个小规模的子优化问题(高分辨率图像的未知区域被划分为多个子类).

2 问题描述与建模

高分辨率图像前景遮罩提取问题本质上是一个大规模组合优化问题, 当高分辨率图像中前景像素的颜色信息与背景像素的颜色信息极相似时, 容易出现前景像素抠成背景像素或背景像素抠成前景像素的抠反现象.前景遮罩值的抠反将会直接导致提取的前景遮罩精度较低, 影响抠图质量, 致使技术人员难以保证高分辨率图像抠图的精度.这成为当前亟需攻克的一个难点问题.

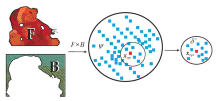
高分辨率图像局部相似像素点的规模较大, 相邻像素点之间RGB颜色信息具有很高的相似性.如图1所示, 图中绿色点表示抠反的像素点.(a)为具有前景背景交替的网状结构, 局部前景背景的颜色信息极相似, 对于更小单位的像素点而言, 颜色变化更加微小.因此, 在前景和背景相邻区域, 容易出现较多的抠反像素点, 大幅降低前景遮罩值的提取精度.

图1 前景遮罩抠反的可视化结果Fig.1 Visualization of inverted alpha matte

为了有效提高前景遮罩值的提取精度, 基于像素点之间的相似特性, 本文采用问题分解的思想将高分辨率图像抠图这一大规模组合优化问题进行降维.假设聚类后的同类像素之间可以共享像素点信息, 基于该假设, 本文通过均值偏移聚类的思想对等同关系[27]进行延伸定义, 具体如下.

定义1 等同关系 已知U为未知区域的未知像素点集合, 设 R˙⊆U× U, 对于未知区域中的任意两个像素点a∈ U, b∈ U(a, b均由像素点的5维特征组成), 若

(a-b)T(a-b)≤ h2,

且

$\begin{array}{l}m_{\text {shift }}(\boldsymbol{a})=\frac{\sum_{i=1}^{n} \boldsymbol{a}_{i} g\left(\left\|\frac{\boldsymbol{a}-\boldsymbol{a}_{i}}{h}\right\|_{2}\right)}{\sum_{i=1}^{n} g\left(\left\|\frac{\boldsymbol{a}-\boldsymbol{a}_{i}}{h}\right\|_{2}\right)}-\boldsymbol{a}, \\ m_{\text {shift }}(\boldsymbol{b})=\frac{\sum_{i=1}^{n} \boldsymbol{b}_{i} g\left(\left\|\frac{\boldsymbol{b}-\boldsymbol{b}_{i}}{h}\right\|_{2}\right)}{\sum_{i=1}^{n} g\left(\left\|\frac{\boldsymbol{b}-\boldsymbol{b}_{i}}{h}\right\|_{2}\right)}-\boldsymbol{b}, \end{array}$

满足

$\left|m_{\text {shift }}(\boldsymbol{a})-m_{\text {shift }}(\boldsymbol{b})\right| \rightarrow 0$

则称a等同于b, 记 aR⌢b, 也称 R˙为U上的等同关系.

根据定义1可知, 当未知区域像素点经过聚类分解后, 若像素点a、b间的欧氏距离满足在以h为带宽的圆内, 则认为a、b像素满足等同关系, 即两个像素点信息是相同的.因此, 若像素点之间满足等同关系, 则同时满足等价关系.下面给出等同关系是等价关系的定理.

定理1 等同关系是等价关系 已知U为未知区域的未知像素集合, 且 R˙为U上的等同关系, 那么 R˙是一个等价关系.

证明 1)自反性.对于∀ a∈ U, 有$a \widetilde{R} a$, 所以$\widetilde{R}$满足自反性.

2)对称性.对于∀ a∈ U, b∈ U, 根据定义1, 有$\boldsymbol{a} \widetilde{R} \boldsymbol{b} \Leftrightarrow \boldsymbol{b} \widetilde{R} \boldsymbol{a}$, 所以$\widetilde{R}$满足对称性.

3)传递性.对于∀ a∈ U, b∈ U, c∈ U, 当$a \widetilde{R} b$且$b \widetilde{R} a$时, 根据定义1, 有

$\boldsymbol{a} \widetilde{R} \boldsymbol{b} \wedge \boldsymbol{b} \widetilde{R} \boldsymbol{c} \Rightarrow \boldsymbol{a} \widetilde{c}$

所以$\widetilde{R}$满足传递性.因此, $\widetilde{R}$是一个等价关系.

由定理1可知, 未知区域经过聚类分解之后, 若同类中任意两个像素点a、b满足等同关系, 则a、b两个像素点为等价关系, 这为同类像素之间信息共享提供理论依据.

在高分辨率图像前景遮罩提取问题中, 假设通过共享像素信息可以解决高分辨率图像中前景与背景相似时出现的抠反问题.基于该假设, 本文设计前景区域像素信息共享的方法, 通过前景区域像素的颜色和位置信息对整个区域进行分解, 将高分辨率图像前景遮罩提取这一大规模组合优化问题划分为多个子优化问题, 从而实现问题分解.高分辨率图像前景遮罩提取问题可描述如下:

$\begin{array}{ll}\min & G(\boldsymbol{X}), \\ \text { s.t. } & G(\boldsymbol{X})=\left(G^{\prime}\left(\boldsymbol{X}_{1}\right), G^{\prime}\left(\boldsymbol{X}_{2}\right), \cdots, G^{\prime}\left(\boldsymbol{X}_{\eta}\right)\right), \\ & \boldsymbol{X}=\left(\boldsymbol{X}_{1}, \boldsymbol{X}_{2}, \cdots, \boldsymbol{X}_{\eta}\right), \\ & G^{\prime}\left(\boldsymbol{X}_{i}\right)=\sum_{k=1}^{\left|\eta_{i}\right|} m_{k}\left(\boldsymbol{x}_{k}\right), \\ & \boldsymbol{X}_{i}=\left(\boldsymbol{x}_{1}, \boldsymbol{x}_{2}, \cdots, \boldsymbol{x}_{\left|\eta_{i}\right|}\right), \\ & \boldsymbol{x}_{k}=\left(\boldsymbol{x}_{k}^{F}, \boldsymbol{x}_{k}^{B}\right) \in \eta_{i}, \\ & i=1, 2, \cdots, |\eta|, \boldsymbol{x}_{k}^{F} \in \boldsymbol{F}, \boldsymbol{x}_{k}^{B} \in \boldsymbol{B} .\end{array}$(3)

其中, X表示未知区域中所有未知像素的决策变量, G(X)表示未知区域所有未知像素对应前景背景像素对的目标函数, Xi表示第i类未知像素的决策变量, G'(Xi)表示未知区域中第i类未知像素对应前景背景像素对的目标函数, mk(xk)表示第i类中的第k个未知像素对应前景背景像素对的目标函数, η i表示第i类像素的集合, |η |表示未知区域的类数, xk表示第k个未知像素的决策变量, $x_{F}^{k}$表示属于前景F的前景像素, $x_{B}^{k}$表示属于背景B的背景像素.

由式(3)可知, 第k个未知像素对应的前景背景像素对的目标函数为:

gk( xkF, xkB)=fc( xkF, xkB)+fs( xkF)+fs( xkB), (4)

其中, fc(· )表示前景背景像素对( xkF, xkB)与第k个未知像素的颜色适应度函数, fs(· )表示已知前景、背景像素与第k个未知像素的空间距离适应度函数.

设I kU为第k个未知像素的RGB颜色, xkFi为已知前景区域第i个像素的RGB颜色, xkBj为已知背景区域第j个像素的RGB颜色, 则颜色适应度函数为:

fc( xkFi, xkBj)=‖ I kU-(α k xkFi+(1-α k) xkBj)‖ 2, (5)

其中

α k= (IkU-xkBj)(xkFi-xkBj)‖xkFi-xkBj‖22.

设I kUd表示第k个未知像素的空间坐标, xkFid表示已知前景区域中第i个像素的空间坐标, xkBjd表示已知背景区域中第j个像素的空间坐标, 则前景、背景像素与第k个未知像素的空间距离适应度函数为:

fs( xkFid)= ‖xkFid-IkUd‖2mint=1C‖xtFid-IkUd‖2, (6)

fs( xkBjd)= ‖xkBjd-IkUd‖2mint=1C‖xtBjd-IkUd‖2. (7)

通过式(4)给出的目标函数可以评估前景背景像素对的质量.式(5)主要用于评估前景背景像素对的颜色失真程度, 式(6)和式(7)分别用于评估前景背景像素与未知像素点的空间距离.

3 基于微搜索的前景遮罩提取算法
3.1 有效决策子集

由式(3)可知, 高分辨率图像前景遮罩提取问题是一个大规模组合优化问题.未知区域中的未知像素信息由前景背景组成的像素对信息决定, 导致高分辨率图像抠图问题的决策集维度较高, 直接求解计算复杂度较高.因此, 为了提高前景遮罩值的搜索效率, 假设未知区域的决策集可以分解为多个决策子集, 并且存在一个维度远小于决策集的有效决策子集(如图2所示), 那么通过对有效决策子集的搜索代替对决策集的搜索, 可以在降低计算时间复杂度的前提下保证求解效率[23], 解决高分辨率图像前景遮罩提取问题中的抠反问题.

图2 有效决策子集映射示意图Fig.2 Sketch map of effective decision subset mapping

定义2 决策子集 设ψ 为高分辨率图像前景遮罩提取问题P的决策集, 对问题P进行分解后的可行解集称为决策子集δ , δ ⊆ψ .

由定义2可知, 高分辨率图像前景遮罩提取问题的决策集ψ 可以分解为多个决策子集.假设在某个决策子集δ * 中存在最优解X* , 且在该决策子集δ * 中的搜索可以代替在决策集ψ 中的搜索, 则称该决策子集为有效决策子集.

定义3 有效决策子集 设δ * 为决策集ψ 的决策子集, 即δ * ⊆ψ .若存在最优解X* , 有X* ∈ δ * , 则称δ * 为问题P的有效决策子集.

根据定义2和定义3可知, 若决策子集δ * 中存在最优前景背景像素对, 则决策子集δ * 为有效决策子集.基于有效决策子集的概念, 本文设计决策集分解策略, 分解高分辨率图像抠图问题.

3.2 决策集分解策略

在定义有效决策子集的基础上, 假设根据图像的颜色信息和空间信息可以实现对高分辨率图像前景遮罩提取问题的分解(将决策集分解为多个决策子集).基于该假设, 本文设计决策集分解策略, 利用均值偏移的思想对未知区域像素的颜色信息与空间位置信息进行聚类降维, 从而将决策集分解为多个决策子集.

由式(3)可知, 未知区域像素集合U=(p1, p2, …, pn)中的每个未知像素对应决策集中一组前景背景像素对, 因此, 整个未知区域的决策集搜索维度为2n.在决策集分解策略的基础上, 假设高分辨率图像前景遮罩提取问题被分解成η 个子问题, 即有S=(S1, S2, …, Sη ), 每个子问题的未知像素个数为$|S_{i}|, i=1, 2, ..., η , $则此时每个子问题的决策子集维度为$2^{\left|S_{i}\right|} \ll 2^{n}$, 搜索的空间维度远小于整个决策集的维度.

因此, 根据决策集分解策略, 高分辨率图像这一大规模组合优化问题分解为多个小规模的子优化问题, 即决策集分解为多个决策子集, 那么, 通过对有效决策子集(分解的多个决策子集集合)的搜索代替对整个决策集的搜索, 能够求解每个子优化问题.本文的有效决策子集是分解后的决策子集的集合, 也是决策集的一个子集.设未知区域U中的像素点个数为n, U=(p1, p2, …, pn)为未知区域中未知像素点集合, η 为分解后的子问题个数, h表示带宽, ε 为每类中允许的最少像素点个数, M为带宽h内所有像素点的信息, mshiftnew(pi)为根据式(2)计算所得的偏移向量, 最优解X* 所在的决策子集被视为有效决策子集.决策集分解流程如算法1所示.

算法1 决策集分解策略

输入 高分辨率图像, 三分图

输出S=(S1, S2, …, Sη )

1.从未知区域U中随机选取一个像素点pi作为初始中心

2.//决策集分解过程

3.for i=1 to n do

4. while 未满足终止条件do

5. $M_{j}(\boldsymbol{p})=\left\{y \mid\left(\boldsymbol{p}-\boldsymbol{p}_{i}\right)^{\mathrm{T}}\left(\boldsymbol{p}-\boldsymbol{p}_{i}\right) \leqslant h^{2}\right\}$

6. S= Spi∈Mj∪ {p}

7. 利用式(2)计算偏移向量mshift(p)

8. pi=pi+mshift(p)

9. if| mshiftnew(p)-mshift(p)|→ 0 then

10. break

11. end if

12. end while

13. for j=1 to |S| do

14. if Sj中像素点个数小于ε then

15. Sj=Sj∪ Sj+1

16. else

17. j=j+1

18. end if

19. end for

20.end for

在算法1中, 高分辨率图像前景遮罩提取问题被分解成多个小规模的子优化问题.第4~6行计算中心像素点与其它像素点的距离, 得到同一带宽h中的像素点集合.第7~11行计算偏移向量之间的差值, 获取最终的偏移重心, 确定第i类像素点信息.第13~19行用于判断某一类中的像素点个数是否小于ε 个像素点, 若小于, 将该类别合并到相邻的类中, 最终产生η 个类, 得到S=(S1, S2, …, Sη ).

3.3 优化信息传递策略

在决策集分解策略的基础上, 高分辨率图像的前景遮罩提取问题分解为多个子优化问题.根据像素之间的相关性, 假设子问题(类)之间可以通过权重关系进行优化信息的传递.基于该假设, 设计优化信息传递策略, 计算子问题间的权重关系, 构建图像前景遮罩提取问题的优化序列, 将前一个类的最优解作为启发式信息传递到下一个类别中, 作为该类的初始解, 帮助该类搜寻到最优解.

定义4 类的权重 设 Siλ=( piR, piG, piB)为第i类中心像素的颜色值, Sid=( pix, piy)为第i类中心像素的坐标, 令

g(Sλ )= Siλ-Sλ¯σ(Sλ), g( Sid)= Sid-Sd¯σ(Sd),

则第i个类与第j个类之间的权重为:

$\begin{array}{c}\omega_{i, j}=\frac{1}{2}\left(\left\|g\left(\boldsymbol{S}_{i}^{\lambda}\right)-g\left(\boldsymbol{S}_{j}^{\lambda}\right)\right\|_{2}+\right. \\ \left.\left\|g\left(\boldsymbol{S}_{i}^{d}\right)-g\left(\boldsymbol{S}_{j}^{d}\right)\right\|_{2}\right) .\end{array}$

其中: Sλ¯、 Sd¯分别表示第i类中所有像素的颜色、坐标均值; σ (Sλ )、σ (Sd)分别表示第i类中所有像素的颜色、坐标标准差.

由定义4可知, 计算每个类中心像素点之间的权重值, 可以获取类与类之间的权重关系.假设权重值越小, 两个类之间相似程度越高, 在优化信息传递过程中优先进行传递.通过计算所有类别之间的权重值, 并按照权重大小对各类别进行排序, 从而获取优化信息的传递次序.设V=(V1, V2, …, Vη )表示对每个类进行排序之后的有序集合, W=(ω 1, ω 2, …, ω η )表示类之间的权重集合, η 表示类别个数.具体优化信息传递策略如算法2所示.

算法2 优化信息传递策略

输入 子优化问题S=(S1, S2, …, Sη )

输出V=(V1, V2, …, Vη )

1.利用式(8)计算所有类(子优化问题)之间的权重集合W=(ω 1, ω 2, …, ω η )

2.i=0

3.从集合S中随机选择第i个类Vi

4.while|V|≠ |S| do

5. for i=1 to η do

6. 从S和S-V中选择最小的权重ω i

7. i=i+1

8. Vi=Si, 其中Vi表示集合S中权重ω i对应的类

9. end for

10.end while

在算法2中, 针对高分辨率图像前景遮罩提取问题分解的η 个子优化问题, 首先根据式(8)计算所有类之间的权重集合.第5~11行对比类别之间的权重大小, 对各类进行排序, 得到最终的优化信息传递次序V=(V1, V2, …, Vη ).在决策集分解策略和优化信息传递策略的基础上, 本文提出基于微搜索的前景遮罩提取算法.

3.4 算法步骤

在决策集分解策略与优化信息传递策略的基础上, 针对高分辨率图像中局部前景背景信息极相似时容易出现前景遮罩抠反的问题, 本文提出基于微搜索的前景遮罩提取算法(MS-AM), 求解高分辨率图像中的抠反问题.MS-AM在决策集分解策略的基础上能够分解大规模问题, 并通过优化信息传递策略进行同类之间的信息共享.最后通过对有效决策子集(存在最优解的决策子集)的搜索替代整个决策集的搜索以寻找最优解, 在有效降低计算时间复杂度的同时避免前景背景极相似区域的抠反情况.设it为迭代次数, K为最大迭代次数, PSO(· )为采用PSO(Particle Swarm Optimization)[28]作为优化器搜寻最优解的过程, X* 为每个子问题优化后搜寻的最优解, Xmin为整个前景遮罩提取问题输出的最终解. MS-AM流程如算法3所示.

算法3 基于微搜索的前景遮罩提取算法

输入 高分辨率图像, 三分图

输出Xmin

1.//决策集分解策略部分

2.通过算法1, 将高分辨率图像抠图问题分解为多个子优化问题S=(S1, S2, …, Sη )

3.//优化信息传递策略部分

4.通过算法2, 利用类的权重关系对子优化问题进行排序, 获取优化信息传递次序V=(V1, V2, …, Vη )

5.//微搜索优化部分

6.θ =Vi, i=1

7.while i≤ η do

8. //优化子问题θ

9. if 存在候选解C then

10. PSO(X)更新最优解X*

11. Xmin=Xmin∪ X*

12. else

13. 随机初始化μ 个候选解C={c1, c2, …, cμ }

14. while it≤ K do

15. 利用式(5)~式(7)计算每个候选解cj(j=1, 2, …, μ )的颜色和空间适应值

16. 利用式(4)评估每个候选解的适应值

17. PSO(C)更新最优解X*

18. if X* 不需要更新then

19. Count = Count+1

20. else

21. Count=0

22. end if

23. end while

24. Xmin=Xmin∪ X*

25. θ =θ ∪ Vi

26. i=i+1

27. end if

28.end while

在算法3中, 选用PSO作为本文的优化器以求解优化目标, 在搜索最优解的过程中锁定有效决策子集的空间位置, 从而通过在有效决策子集中的搜索代替整个决策集的搜索.算法中的第1~2行为决策集分解策略部分, 实现高分辨图像大规模组合优化问题的有效分解.第3~4行为优化信息传递策略部分, 对子问题之间的权重大小进行排序, 获取优化信息的传递次序.第6~27行为微搜索优化部分, 其中, 第9~12行用于判断是否有从上一个类中传递下来的初始解.第13~22行用于对第i个类的最优解进行更新, 第23~25行实现最优解与问题的重组, 第27行将上一个类的最优解传递到下一个类别中作为初始解.

在MS-AM中, 假设未知区域对应的决策集为ψ , 则求解整个未知区域的计算时间复杂度为O(ψ ).由优化信息传递策略部分得到优化顺序(V1, V2, …, Vη ), 当MS-AM在求解第一个类V1时, 通过优化器搜索到的最优解并锁定有效决策子集的空间位置.假设该有效决策子集为 δV1* , 则对该有效决策子集搜索的计算时间复杂度为O( δV1* ), 其中, δV1* ≪ψ , 因此有O( δV1* )≪O(ψ ).此外, 根据优化信息传递次序V=(V1, V2, …, Vη ), 假设每个类对应的有效决策子集设为 δVi* , i=1, 2, …, η , 则对于∀ δVi* ∈ ψ , 都有O( δVi* )≪O(ψ ).因此有整个未知区域对应的计算时间复杂度为

O( δV1* )+O( δV2* )+…+O( δVη* )< O(ψ ),

即

O( δV1* + δV2* +…+ δVη* )< O(ψ ).

4 实验及结果分析

为了验证MS-AM在高分辨率图像前景遮罩提取问题中解决抠反问题的性能, 本节设置3组实验, 分别用于验证两个策略以及算法的有效性.

4.1 实验设置

本文选用的实验数据为Rhemann等[6]提出的alphamatting高分辨率基准数据集, 提供27幅用于训练的彩色图像及其对应的真实前景遮罩结果与三分图.

所有算法实现均在MATLAB 2018a环境下进行, 实验均使用Intel(R) Core(TM) i5-7500 3.4 GHz CPU及8 GB内存的服务器运行.

本文分别设置3组实验.

1)第1组实验.决策集分解策略的有效性分析, 主要验证决策集分解策略可以显著降低高分辨率图像前景遮罩提取问题的维度.

2)第2组实验.优化信息传递策略的有效性分析, 主要验证基于优化信息传递策略可以有助于MS-AM求解高分辨率图像抠图中的前景遮罩抠反问题.

3)第3组实验.MS-AM与目前典型的抠图优化方法对比分析.对比算法如下:VS-CCPSO(Vari-able-Size Cooperative Coevolutionary PSO Algori-thm)[29]、CC-DE-S(Cooperative Coevolution Diffe-rential Evolution Algorithm with a Scattered Stra-tegy)[30]、GC-CSO[22]、MOEA-MCD[20]、OIT-GOA[31]、文献[9]算法, 验证MS-AM在高分辨率图像前景遮罩提取问题上的性能与计算时间复杂性.

为了保证实验中不同算法实验结果的可对比性, 本文采用均方误差(Mean Square Error, MSE)作为评价指标.所有算法在每幅图像上分别运行30次, 以便对其性能进行统计分析.

4.2 决策集分解策略的有效性分析

为了验证决策集分解策略对高分辨率图像前景遮罩提取问题分解的有效性, 本文采用决策集分解策略对高分辨率图像的未知区域进行分解, 其中带宽h及每个类中允许最少像素点个数ε 的设置与文献[25]一致.

表1给出alphamatting数据集上27幅高分辨率图像降维前后的对比结果.在表中, X表示高分辨率图像前景遮罩提取问题决策变量的原始维度, X'表示高分辨率图像前景遮罩提取问题分解降维后的决策变量维度.在27幅图像的原始决策变量中, 维度均处于几十万维甚至上百万维, 由此可以看出, 本文优化的高分辨率图像前景遮罩提取问题属于超高维的优化问题.

表1 Alpha matting基准数据集上高分辨率图像降维前后的决策变量维度对比 Table 1 Comparison of decision variable dimensions before and after dimension reduction of high-resolution images on alphamatting benchmark dataset

由表1的分解结果可以看出, 除了决策变量原始维度均在百万维以上的GT04、GT08、GT11、GT13、GT26、GT27降维后的维度在1万维以上之外, 其余原始维度在几十万维以上的图像均降维到几千维, 降维效果十分明显, 因此该算法有效降低高分辨率图像前景遮罩提取问题的维度.根据每幅图像对应的降维效果发现, 高分辨率图像中相似区域越多, 降维效果越明显.

4.3 优化信息传递策略的有效性分析

为了验证优化信息传递策略在求解高分辨率图像中局部前景遮罩抠反问题的有效性, 本节对比分析基于优化信息传递策略的MS-AM与PSO, MS-AM的优化器参数设置与文献[28]一致.

实验采用alphamatting基准数据集上27幅高分辨率彩色图像及对应的三分图作为训练数据, 以其中提供的真实遮罩图作为实验结果的评价标准.根据文献[20]、文献[22]、文献[29]~文献[31]中设置的迭代次数, 本文将求解高分辨率图像前景遮罩的最大评估次数设置为5× 103.分别针对MS-AM和PSO求解的高分辨率图像前景遮罩值计算各自的MSE, 并给出27幅图像的MSE对比, 具体如表2所示, 表中黑体数字表示最优值.

表2 MS-AM和PSO的MSE对比结果 Table 2 MSE comparison between MS-AM and PSO

由表2可知, MS-AM在27幅图像中有23幅图像的MSE值低于PSO, 其余4幅图像的MSE值略高于PSO.MSE值越低, 表明前景遮罩的精度越高.实验表明, 在优化信息传递策略的基础上, MS-AM利用子问题之间的信息传递, 可以解决高分辨率图像前景遮罩提取问题中的抠反问题, 提高高分辨率图像的前景遮罩的提取精度.

为了进一步验证MS-AM在求解抠反问题上的性能, MS-AM与PSO的抠反可视化对比结果如图3所示, 图中绿色点为抠反像素点.由图中抠反结果的局部放大图可以看出, PSO的结果主要以局部区域前景遮罩抠反为主, 而由MS-AM的结果可知, MS-AM求解的高分辨率图像前景遮罩噪声更小, 前景物体的轮廓更清晰, 具有更优的视觉效果.

图3 MS-AM和PSO提取的高分辨率图像前景遮罩结果对比Fig.3 Alpha matting comparison between MS-AM and PSO

因此, 相比PSO, 基于优化信息传递策略的MS-AM在解决高分辨率图像抠图中的抠反问题上更具有优势, 有效提高前景遮罩的精度.因此, 优化信息传递策略有助于MS-AM的性能.这主要是由于优化信息传递策略通过共享同类中的像素信息, 有效求解前景遮罩值的抠反, 其次通过将前一个类的最优解作为下一个类的初始解, 有效提高优化器搜索最优解的准确性.

表2和图3的实验结果表明, 针对高分辨率图像前景遮罩提取中由于局部前景遮罩抠反而导致的前景遮罩提取精度较低的问题, 相比PSO, 基于优化信息传递策略的MS-AM具有明显的优势, 进一步验证优化信息传递策略通过子问题之间的优化信息传递以及子问题内部的信息共享, 有助于MS-AM求解局部前景遮罩抠反问题, 从而提高高分辨率图像前景遮罩的提取精度.

4.4 对比实验

MS-AM通过分解问题, 将高分辨率图像大规模的组合优化问题转化成多个小规模的子优化问题.因此, 为了验证在高分辨率图像前景遮罩提取问题上的性能, 本节进行对比实验.

为了保证实验的公平性, 每种算法在alpha-matting数据集上独立运行30次, 最大评估次数设置为5× 103.为了便于分析, 利用MSE作为各算法前景遮罩提取精度的评价指标.

MS-AM、MOEA-MCD、GC-CSO、文献[9]算法、OIT-GOA、VS-CCPSO的MSE对比结果如表3所示, 表中黑体数字表示最优值.

表3 各算法的MSE值对比 Table 3 MSE comparison of different algorithms

由表3可见, 在27幅训练图像中, MS-AM有22幅图像的MSE值低于MEOA-MCD, 24幅图像的MSE值低于GC-CSO, 20幅图像的MSE值低于OIT-GOA, 27幅图像的MSE值低于IF、CC-DE-S、VS-CCPSO, 即MS-AM的前景遮罩提取精度最优.对于MS-AM中提取精度略低的几幅图像, 其主要原因在于MS-AM在对问题进行分解时, 同一子问题中的像素信息为等价关系(即像素之间信息共享), 未考虑像素点之间本身存在的细微变化, 导致最终的MSE值略高于对比算法.

为了进一步验证MS-AM的计算时间复杂性, 统计MS-AM与VS-CCPSO、MOEA-MCD、GC-CSO、文献[9]算法的计算时间, 结果如表4所示, 表中黑体数字表示最优值.由表可见, MS-AM的计算时间明显优于VS-CCPSO、MOEA-MCD, 与GC-CSO的计算时间差异较小, 并且每幅图像的计算时间相近.计算时间最短的为文献[9]算法, 时间分布较均匀, 但该算法的前景遮罩提取精度明显低于MS-AM.在记录不同算法的计算时间过程中, 由于CC-DE-S在计算超过24 h之后仍无法求解最终的前景遮罩值, 因此结束算法计算.实验结果表明, MS-AM通过对有效决策子集的搜索有效降低计算时间复杂度. 此外, 实验也进一步验证决策集分解策略有助于MS-AM提升高分辨率图像前景遮罩提取问题的求解速度.

表4 各算法的计算时间对比 Table 4 Computational time comparison of different algorithms s

综合分析进一步验证MS-AM在对决策集分解的基础上, 通过对有效决策子集的搜索代替整个决策集的搜索, 不仅降低算法的计算时间复杂度, 同时提高前景遮罩的提取精度.因此, 相比文献[9]算法、VS-CCPSO、GC-CSO、CC-DE-S、MOEA-MCD, 在高分辨率图像前景遮罩抠反问题上, MS-AM更具优势.

5 结束语

本文针对高分辨率图像中前景信息与背景信息极相似时容易出现前景遮罩抠反的问题, 提出基于微搜索的前景遮罩提取算法(MS-AM).实验表明, MS-AM能够有效解决高分辨率图像中的抠反问题.此外, 设计决策集分解策略, 将高分辨率图像前景遮罩提取问题分解为多个独立的子优化问题, 显著降低问题的原始维度.基于子问题之间可以通过权重关系进行信息传递的假设, 设计优化信息传递策略, 获取子问题间的权重关系, 建立图像抠图问题的优化信息传递序列.实验表明, 优化信息传递策略有助于MS-AM求解高分辨率图像前景遮罩提取问题中的抠反问题.在决策集分解策略和优化信息传递策略的基础上, 本文提出MS-AM, 通过对有效决策子集中的搜索代替整个决策集的搜索, 在有效降低计算时间复杂度的同时提高前景遮罩的提取精度.实验表明, 通过典型抠图优化算法的对比分析, 验证MS-AM可以解决高分辨率图像中局部前景背景信息极相似时的前景遮罩抠反问题, 并且在高分辨率前景遮罩提取问题维度显著降低的情况下, 提高前景遮罩提取精度.

虽然MS-AM能有效解决高分辨率图像中局部前景背景相似时出现的抠反问题, 但在优化过程中仍存在部分前景遮罩值抠反的现象.因此, 后续的工作将集中在如下两点:1)探索决策集与决策子集间的拓扑关系, 设计更加高效的微搜索算法; 2)从理论的角度证明MS-AM的有效性.

本文责任编委 叶东毅

Recommended by Associate Editor YE Dongyi

参考文献
[1] LIN S C, YANG L J, SALEEMI I, et al. Robust High-Resolution Video Matting with Temporal Guidance // Proc of the IEEE/CVF Winter Conference on Applications of Computer Vision. Washington, USA: IEEE, 2022: 238-247. [本文引用:1]
[2] DING H H, ZHANG H, LIU C, et al. Deep Interactive Image Ma-tting with Feature Propagation. IEEE Transactions on Image Processing, 2022, 31: 2421-2432. [本文引用:1]
[3] GONG M L, QIAN Y M, CHENG L. Integrated Foreground Segmentation and Boundary Matting for Live Videos. IEEE Transactions on Image Processing, 2015, 24(4): 1356-1370. [本文引用:1]
[4] SUN Y N, TANG C K, TAI Y W. Semantic Image Matting // Proc of the IEEE/CVF Conference on Computer Vision and Pattern Re-cognition. Washington, USA: IEEE, 2021: 11115-11124. [本文引用:1]
[5] PORTER T, DUFF T. Compositing Digital Images. ACM SIGGRAPH Computer Graphics, 1984, 18(3): 253-259. [本文引用:2]
[6] RHEMANN C, ROTHER C, WANG J, et al. A Perceptually Motivated Online Benchmark for Image Matting // Proc of the IEEE Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2009: 1826-1833. [本文引用:3]
[7] 梁椅辉, 黄翰, 蔡昭权, 等. 自然图像抠图技术综述. 计算机应用研究, 2021, 38(5): 1294-1301.
(LIANG Y H, HUANG H, CAI Z Q, et al. Survey of Natural Image Matting. Application Research of Computers, 2021, 38(5): 1294-1301. ) [本文引用:1]
[8] LI X Q, LI J D, LU H. A Survey on Natural Image Matting with Closed-Form Solutions. IEEE Access, 2019, 7: 136658-136675. [本文引用:1]
[9] AKSOY Y, AYDIN T O, POLLEFEYS M. Designing Effective Inter-Pixel Information Flow for Natural Image Matting // Proc of the IEEE Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2017: 29-37. [本文引用:7]
[10] LIANG Y H. GOU H S, FENG F J, et al. Natural Image Matting Based on Surrogate Model. Applied Soft Computing, 2023. DOI: DOI:10.1016/j.asoc.2023.110407. [本文引用:1]
[11] HUANG H, LIANG Y H, YANG X W, et al. Pixel-Level Discrete Multiobjective Sampling for Image Matting. IEEE Transactions on Image Processing, 2019, 28(8): 3739-3751. [本文引用:1]
[12] CAO G Y, LI J W, CHEN X W, et al. Patch-Based Self-Adaptive Matting for High-Resolution Image and Video. The Visual Compu-ter, 2019, 35(1): 133-147. [本文引用:1]
[13] ZHU X Y, WANG P, HUANG Z H. Adaptive Propagation Matting Based on Transparency of Image. Multimedia Tools and Applications, 2018, 77(15): 19089-19112. [本文引用:1]
[14] WENG T H, LI K C, YANG Z L, et al. On the Code Modernization of Shared Sampling Alpha Matting with OpenMP. Future Generation Computer Systems, 2020, 107: 177-191. [本文引用:1]
[15] TANG J W, AKSOY Y, OZTIRELI C, et al. Learning-Based Sampling for Natural Image Matting // Proc of the IEEE/CVF Confe-rence on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2019: 3055-3063. [本文引用:1]
[16] FENG F J, HUANG H, LIU D, et al. Local Complexity Difference Matting Based on Weight Map and Alpha Mattes. Multimedia Tools and Applications, 2022, 81: 43357-43372. [本文引用:1]
[17] LIANG Y H, HUANG H, CAI Z Q. PSO-ACSC: A Large-Scale Evolutionary Algorithm for Image Matting. Frontiers in Computer Science, 2020, 14(6). DOI: DOI:10.1007/s11704-019-8441-5. [本文引用:2]
[18] LIANG Y H, FENG F J, CAI Z Q. Pyramid Matting: A Resource-Adaptive Multi-scale Pixel Pair Optimization Framework for Image Matting. IEEE Access, 2020, 8: 93487-93498. [本文引用:1]
[19] MOHAPATRA P, DAS K N, ROY S. Novel Competitive Swarm Optimizer for Sampling-Based Image Matting Problem // ELÇI A, SA P K, MODI C N, et al. , eds. Smart Computing Paradigms: New Progresses and Challenges. Berlin, Germany: Springer, 2020: 109-120. [本文引用:1]
[20] LIANG Y H, HUANG H, CAI Z Q, et al. Multiobjective Evolutionary Optimization Based on Fuzzy Multicriteria Evaluation and Decomposition for Image Matting. IEEE Transactions on Fuzzy Systems, 2019, 27(5): 1100-1111. [本文引用:3]
[21] WANG X F, LI S J, SUI L S, et al. Quick Automatic Head Image Matting Method Based on Segmentation and Propagation. Pattern Recognition Letters, 2020, 130: 30-37. [本文引用:1]
[22] 冯夫健, 黄翰, 吴秋霞, 等. 基于群体协同优化的高清图像前景遮罩提取算法. 中国科学(信息科学), 2020, 50(3): 424-437.
(FENG F J, HUANG H, WU Q X, et al. An Alpha Matting Algorithm Based on Collaborative Swarm Optimization for High-Resolution Images. Chinese Science(Information Science), 2020, 50(3): 424-437. ) [本文引用:3]
[23] HUANG H, FENG F J, HUANG S Q, et al. Microscale Sear-ching Algorithm for Coupling Matrix Optimization of Automated Microwave Filter Tuning. IEEE Transactions on Cybernetics, 2023, 53(5): 2829-2840. [本文引用:2]
[24] KUMAH C, ZHANG N, RAJI R K, et al. Unsupervised Segmentation of Printed Fabric Patterns Based on Mean Shift Algorithm. The Journal of the Textile Institute, 2022, 113(1). DOI: DOI:10.1080/00405000.2020.1867413. [本文引用:1]
[25] COMANICIU D, MEER P. Mean Shift: A Robust Approach Toward Feature Space Analysis. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2002, 24(5): 603-619. [本文引用:2]
[26] RYOYA Y, TOSHIYUKI T. Properties of Mean Shift. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2020, 42(9): 2273-2286. [本文引用:1]
[27] 冯夫健, 黄翰, 张宇山, 等. 基于等同关系模型的演化算法期望首达时间对比分析. 计算机学报, 2019, 42(10): 2297-2308.
(FENG F J, HUANG H, ZHANG Y S, et al. Comparative Analysis for First Hitting Time of Evolutionary Algorithms Based on Equal-in-Time Model. Chinese Journal of Computers, 2019, 42(10): 2297-2308. ) [本文引用:1]
[28] EBERHART R, KENNEDY J. A New Optimizer Using Particle Swarm Theory // Proc of the 6th International Symposium on Micro Machine and Human Science. Washington, USA: IEEE, 1995: 39-43. [本文引用:2]
[29] SONG X F, ZHANG Y, GUO Y N, et al. Variable-Size Cooperative Coevolutionary Particle Swarm Optimization for Feature Selection on High-Dimensional Data. IEEE Transactions on Evolutionary Computation, 2020, 24(5): 882-895. [本文引用:2]
[30] CAI I Q, LÜ L, HUANG H, et al. Improving Sampling-Based Image Matting with Cooperative Coevolution Differential Evolution Algorithm. Soft Computing, 2017, 21: 4417-4430. [本文引用:1]
[31] FENG F J, HUANG H, LIANG Y H. Graph-Order Optimization Algorithm Based on Equal-in-Space Distance Model for High-Resolution Image Matting // Proc of the IEEE 7th International Confe-rence on Cloud Computing and Intelligent Systems. Washington, USA: IEEE, 2021: 122-127. [本文引用:2]