本文采用流形学习中拉普拉斯特征映射^[16]进行图矩阵的构造, 拉普拉斯特征映射是一种非线性降维方法, 能够从高维数据中发现低维流形结构, 得到高维数据和低维数据之间的映射关系.

拉普拉斯特征映射算法在高维空间中通常使用K-近邻图描述局部数据点之间的结构.若数据点x_i与数据点x_j互为近邻, 则采用高斯核函数

si, j=exp( -xi-xj22δ2)

定义不同数据点之间的相似性, 其中δ 表示一个比例参数.若数据点x_i与数据点x_j不是近邻点, 则s_{i, j}=0.

设降维后的矩阵为

Y=[Y₁, Y₂, …, Y_n]∈ R^k,

n表示数据点, k表示降维后低维空间的维数.为了表示数据映射到低维空间中时依然可以保留在高维空间中的结构, 设目标函数:

tr(Y^TLY) = 12minS∑i=1nj=1yi-yj2s_{i, j}, s.t. si_{, i=}0, si_{, j≥} 0,

其中, y_i、y_j表示降维后的数据点, s_{i, j}表示数据点x_i和x_j之间的相似性, S表示邻接矩阵.

设

D=diag(d₁, d₂, …, d_n)

为度矩阵, 其中

d_ii= ∑j=1ns_{i, j}

表示数据点i的度,

L=D-S

表示拉普拉斯矩阵, 为了使最终所有节点的嵌入向量能够尽可能填充降维后的空间, 添加约束条件

Y^TDY=I,

其中I表示单位矩阵.根据拉普拉斯矩阵的性质, 有

tr(Y^TLY)= 12minS∑i=1nj=1yi-yj2s_{i, j}, s.t. si_{, i=}0, si_{, j≥} 0, YT^DY=I.

求解上式, 转化为广义特征值分解的问题:

D^-1LY=λ Y.

对上式中D^-1L进行特征值分解, 根据拉普拉斯矩阵最小特征值为0时, 对应的特征向量为全1单位向量的性质.因此, 取m个最小的非零特征值对应的特征向量组成降维后的矩阵Y.

非负矩阵分解(NMF)^[17]将一个非负矩阵分解成两个低秩的非负矩阵的乘积, 可以提取数据内部特征并实现降维, 从而节省存储空间和计算资源.NMF可表示为

minW≥0, H≥0V-WH2.

其中:V∈ R^{n× m}表示原始数据矩阵, 具有非负性; W∈ R^{n× k}、H∈ R^{k× m}表示分解后的低秩矩阵, 约束为非负矩阵, W表示基础矩阵, H表示系数矩阵, n表示数据点的个数, m表示原始数据点的维数, k表示分解后数据点的维数, 一般情况下, k≪m.

2.1.1 多视图流形学习谱嵌入矩阵

设X₁, X₂, …, X_v为v个视图的数据矩阵,

X_v=[ x1v, x2v, …, xnv]∈ Rn×dv

为第v个视图的数据矩阵, 其中, n表示数据点的个数, d^v表示第v个视图的维数.降维后的数据矩阵为Y₁, Y₂, …, Y_v,

Y_v=[ y1v, y2v, …, ynv]∈ Rn×mv

为第v个视图降维后的数据矩阵, 其中m^v表示第v个视图降维后的维数.则多视图流形学习的目标函数可表示为

tr((Y^v)^TL^vY^v)= 12minS∑v=1V∑i=1nj=1yiv-yjv2si, jv,

s.t. (Y^v)^TD^vY^v=I, (1)

其中, si, jv表示高维空间中每个视图不同数据点之间的相似性, S为邻接矩阵.设D^v为度矩阵,

L^v=D^v-S^v

为拉普拉斯矩阵, 将式(1)转化为求解广义特征值分解的问题:

(D^v)^-1L^vY^v=λ Y^v.(2)

对式(2)中的(D^v)^-1L^v进行特征值分解, 取m个最小的非零特征值对应的特征向量组成每个视图的谱嵌入矩阵Y^v, m表示降维后低维空间的维度.

2.1.2 谱嵌入矩阵的谱结构融合

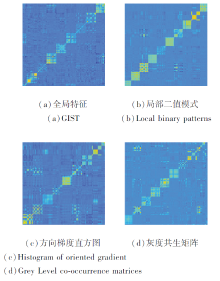
考虑到不同视图经过非线性降维后数据之间的结构会有差异, 若在此阶段直接将不同视图的谱嵌入矩阵Y^v融合为一致性图矩阵, 会造成数据信息受损, 不能真实反映数据间的关系, 而每个视图谱嵌入矩阵的谱块结构Y^v(Y^v)^T为严格的块对角矩阵.图1表示从ORL数据集的4个视图上得到每个视图的谱块结构Y^v(Y^v)^T.

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 ORL数据集上4个视图的谱块结构Fig.1 Spectrum block structure of 4 views on ORL dataset

由图1可以看出, 每个视图的谱块结构大致相同, 由谱块结构可以挖掘不同视图间潜在的一致类簇结构.因此, 在学习一致性图矩阵之前构建每个视图谱嵌入矩阵的谱块结构是必要的.本文通过最小化每个视图的谱块结构Y^v(Y^v)^T与一致性图矩阵S之间的差值实现谱结构的融合.目标函数如下:

$\begin{array}{ll}\min _{S} \sum_{v=1}^{V}\left\|\boldsymbol{S}-\boldsymbol{Y}^{v}\left(\boldsymbol{Y}^{v}\right)^{\mathrm{T}}\right\|_{\mathrm{F}}^{2}, \\ \text { s.t. } & s_{i, j} \geqslant 0, \mathbf{1}^{\mathrm{T}} \boldsymbol{s}_{i}=1, \left(\boldsymbol{Y}^{v}\right)^{\mathrm{T}} \boldsymbol{Y}^{v}=\boldsymbol{I} .\end{array}$ (3)

2.1.3 自适应权重一致性图矩阵生成

由图1可以看出, 不同视图的重要性存在差异, 因此应为每个视图设计自适应权值δ ^v(v=1, 2, …, V).视图中包含的有用信息越多, 赋予的权值越大, 反之, 赋予越小的权值.通过最小化一致性图矩阵S与不同视图谱结构块Y^v(Y^v)^T之间的距离差值学习一致性图矩阵S, 目标函数可以表示为

$\begin{aligned} \min _{S} & \sum_{v=1}^{V} \delta^{v}\left\|\boldsymbol{S}-\boldsymbol{Y}^{v}\left(\boldsymbol{Y}^{v}\right)^{\mathrm{T}}\right\|_{\mathrm{F}}^{2}, \\ \text { s.t. } & \boldsymbol{\delta}^{\mathrm{T}} \mathbf{1}=1, 0 \leqslant \delta^{v} \leqslant 1, s_{i, j} \geqslant 0, \\ & \mathbf{1}^{\mathrm{T}} \boldsymbol{s}_{i}=1, \left(\boldsymbol{Y}^{v}\right)^{\mathrm{T}} \boldsymbol{Y}^{v}=\boldsymbol{I} .\end{aligned}$(4)

其中:δ ^v表示每个视图的权值, δ ^T1=1, 0≤ δ ^v≤ 1为自适应权值δ ^v的约束条件, δ 表示元素为所有视图权值的列向量, 1表示元素全为1的列向量; s_{i, j}表示s_i的第j个元素; s_i∈ R^{n× 1}表示列向量; S表示一致性图矩阵.

视图的自适应权值δ ^v由一致性图矩阵S与不同视图谱结构块Y^v(Y^v)^T的距离差值动态获取:差值越小, 表明两者之间越相似, 应赋予越大的权值; 反之, 赋予越小的权值.因此, 自适应权值δ ^v可以定义为

$\delta^{v}=\frac{1}{2 \sqrt{\left\|\boldsymbol{S}-\boldsymbol{Y}^{v}\left(\boldsymbol{Y}^{v}\right)^{\mathrm{T}}\right\|_{\mathrm{F}}^{2}}}$ (5)

如果权值δ ^v被固定为式(5), 求解问题(4)可以等价于求解如下问题:

$\begin{array}{l}\min _{S} \sum_{v=1}^{V} \sqrt{\left\|\boldsymbol{S}-\boldsymbol{Y}^{v}\left(\boldsymbol{Y}^{v}\right)^{\mathrm{T}}\right\|_{\mathrm{F}}^{2}}, \\ \text { s. t. } \boldsymbol{S} \geqslant \mathbf{0}, \mathbf{1}^{\mathrm{T}} \boldsymbol{s}_{i}=1, \left(\boldsymbol{Y}^{v}\right)^{\mathrm{T}} \boldsymbol{Y}^{v}=\boldsymbol{I} .\end{array}$ (6)

式(6)的拉格朗日函数为

$\sum_{v=1}^{V} \sqrt{\left\|\boldsymbol{S}-\boldsymbol{Y}^{v}\left(\boldsymbol{Y}^{v}\right)^{\mathrm{T}}\right\|_{\mathrm{F}}^{2}}+\theta(\Lambda, \boldsymbol{S})$, (7)

其中, θ (Λ , S)表示由约束S≥ 0, 1^Ts_i=1导出的形式化术语, Λ 表示拉格朗日乘子.

对式(7)中的变量S求导, 将导数设为0, 可表示为

$\sum_{v=1}^{V} \delta^{v}\left(\frac{\partial\left\|\boldsymbol{S}-\boldsymbol{Y}^{v}\left(\boldsymbol{Y}^{v}\right)^{\mathrm{T}}\right\|_{\mathrm{F}}^{2}}{\partial \boldsymbol{S}}\right)+\frac{\partial \theta(\Lambda, \boldsymbol{S})}{\partial \boldsymbol{S}}=0$ (8)

其中δ ^v可由式(5)表示.

如果对式(4)的拉格朗日函数求导, 同样可得到式(8), 因此式(4)等价于式(6).式(5)中每个视图的权值由一致性图矩阵S与不同视图谱结构块Y^v(Y^v)^T之间的距离误差动态获取, 使每个视图的权重可以自动分配.

2.1.4 一致性图矩阵聚类

由于NMF约束输入矩阵和输出矩阵均为非负矩阵, 存在一定的局限性, Ding等^[11]提出单侧正交NMF的概念, 将一个数据矩阵分解为两个因子矩阵, 对分解后的矩阵分别施加正交约束和非负约束.分解后的正交矩阵可以保证解的唯一性, 非负矩阵具有聚类可解释性, 可作为聚类指标矩阵.单侧正交NMF可表示为

minH≥0, FFT=IX-HFT2,

其中, X∈ R^{n× m}表示原始数据矩阵, H∈ R^{n× k}表示非负矩阵, F∈ R^{m× k}表示正交矩阵, n表示数据点的个数, m表示原始数据点的维数, k表示分解后数据点的维数, 一般情况下, k≪m.

由式(4)得到一致性图矩阵后, 对其进行单侧正交NMF, 直接揭示聚类结果, 避免后处理带来的不确定性.结合式(4), 结合一致性图矩阵学习和非负正交矩阵分解的目标, 对生成的一致性图矩阵分解, 最终的目标函数为:

$\begin{array}{l}\min _{\boldsymbol{S}, \boldsymbol{H}, \boldsymbol{F}} \sum_{v=1}^{V} \delta^{v}\left\|\boldsymbol{S}-\boldsymbol{Y}^{v}\left(\boldsymbol{Y}^{v}\right)^{\mathrm{T}}\right\|_{\mathrm{F}}^{2}+\left\|\boldsymbol{S}-\boldsymbol{H} \boldsymbol{F}^{\mathrm{T}}\right\|_{\mathrm{F}}^{2}, \\ \text { s.t. } \boldsymbol{S} \geqslant \boldsymbol{0}, \left(\boldsymbol{Y}^{v}\right)^{\mathrm{T}} \boldsymbol{Y}^{v}=\boldsymbol{I}, \boldsymbol{H} \geqslant \boldsymbol{0}, \boldsymbol{F} \boldsymbol{F}^{\mathrm{T}}=\boldsymbol{I} \text {. } \\\end{array}$ (9)

其中:S表示由式(4)得到的一致性图矩阵; F表示矩阵分解后得到的正交矩阵, 每列表示一个基本向量; H表示矩阵分解后得到的非负矩阵, 具有可解释性, 故最终的聚类结果由非负矩阵直接获得; I表示单位矩阵.

目标函数(9)中第一部分首先构建每个视图谱嵌入矩阵的谱块结构Y^v(Y^v)^T, 然后将不同视图谱嵌入矩阵的谱块结构通过设计的自适应权重学习到具有一致性图矩阵S中.第二部分对一致性图矩阵进行非负正交分解, 通过非负正交约束重新构造一致性图矩阵, 最终获得的非负矩阵作为聚类指标矩阵, 直接得到聚类结果, 进而获得图像分割结果.通过最小化目标函数的这两部分, 使两部分相互学习, 避免以往谱聚类后处理中聚类结果会受到初始一致性相似矩阵质量影响的问题.

目标函数(9)中有3个变量.由于该目标函数具有非凸性, 很难直接求解.因此, 采用固定其它变量以更新一个变量的方法, 求解该目标函数的最优解.优化算法主要过程如下.

1)固定变量S和F, 更新变量H.当固定一致性图矩阵S和正交矩阵F时, 目标函数(9)可以简化为

minH≥0S-HFTF2.

由于正交矩阵F具有正交性, FF^T=I, 上式可以等价为

minH≥0SF-HF2,

则变量H的解可以表示为

H=max(SF, 0).(10)

2) 固定变量S和H, 更新变量F.当固定一致性图矩阵S和非负矩阵H时, 目标函数(9)可以简化为

minFFT=IS-HFTF2.

将上式转化为矩阵迹的形式:

minFFT=Itr(S^TS-2F^TS^TH+H^TH).

去掉多项式中全部为固定变量的项, 可以转化为

maxFFT=Itr(F^TS^TH), (11)

其中S^T、H为固定变量, 因此令

Q=S^TH,

则式(11)可以表示为

maxFFT=Itr(F^TQ).

在上式中, 设矩阵Q的左奇异值U∈ R^{n× c}和右奇异值V∈ R^{c× c}, 若给定一个矩阵M∈ R^{n× c}, 那么问题

maxWWT(W^TM)

中变量W的最优解为

W= U︿V︿^T,

其中, U︿∈ R^{n× c}表示矩阵M的左奇异值, V︿∈ R^{c× c}表示矩阵M的右奇异值^[18].由此可得变量F的最优解:

F=UV^T.(12)

3)固定H和F, 更新变量S.当固定非负矩阵H和正交矩阵F时, 目标函数(9)可以表示为

minS≥0∑v=1VS-Yv(Yv)TF2δ ^v+ S-HFTF2,

将上式表述为矩阵迹的形式:

$\begin{aligned} \min _{S \geqslant \mathbf{0}} & \sum_{v=1}^{V} \operatorname{tr}\left(\left(\boldsymbol{S}^{\mathrm{T}} \boldsymbol{S}-2 \boldsymbol{S}^{\mathrm{T}} \boldsymbol{Y}^{v}\left(\boldsymbol{Y}^{v}\right)^{\mathrm{T}}+\right.\right. \\ & \left.\boldsymbol{Y}^{v}\left(\boldsymbol{Y}^{v}\right)^{\mathrm{T}} \boldsymbol{Y}^{v}\left(\boldsymbol{Y}^{v}\right)^{\mathrm{T}}\right) \delta^{v}+ \\ & \left.\boldsymbol{S}^{\mathrm{T}} \boldsymbol{S}-2 \boldsymbol{S}^{\mathrm{T}} \boldsymbol{H} \boldsymbol{F}^{\mathrm{T}}+\boldsymbol{F} \boldsymbol{H}^{\mathrm{T}} \boldsymbol{H} \boldsymbol{F}^{\mathrm{T}}\right) .\end{aligned}$

去掉多项式中全部为固定变量的项, 可以转化为

minS≥0∑v=1Vtr((S^TS-2S^TY^v(Y^v)^T)δ ^v+ (ST^S-2ST^HFT⁾).

合并同类项, 上式可以转化为

$\begin{aligned} \min _{S \geqslant \mathbf{0}} \operatorname{tr}\left(\boldsymbol{S}^{\mathrm{T}} \boldsymbol{S}\left(\sum_{v=1}^{V} \delta^{v}+1\right)-\right. \\ \left.2 \boldsymbol{S}^{\mathrm{T}}\left(\sum_{v=1}^{V} \boldsymbol{Y}^{v}\left(\boldsymbol{Y}^{v}\right)^{\mathrm{T}} \boldsymbol{\delta}^{v}+\boldsymbol{H} \boldsymbol{F}^{\mathrm{T}}\right)\right), \end{aligned}$

继续转化为

$\min _{S \geqslant \mathbf{0}}\left\|\boldsymbol{S}-\frac{\sum_{v=1}^{V} \boldsymbol{Y}^{v}\left(\boldsymbol{Y}^{v}\right)^{\mathrm{T}} \delta^{v}+\boldsymbol{H} \boldsymbol{F}^{\mathrm{T}}}{\sum_{v=1}^{V} \delta^{v}+1}\right\|_{\mathrm{F}}^{2}$,

则获得变量S的最优解:

$\boldsymbol{S}=\max \left(\frac{\sum_{v=1}^{V} \boldsymbol{Y}^{v}\left(\boldsymbol{Y}^{v}\right)^{\mathrm{T}} \delta^{v}+\boldsymbol{H} \boldsymbol{F}^{\mathrm{T}}}{\sum_{v=1}^{V} \delta^{v}+1}, \mathbf{0}\right)$ (13)

NOMF-MVC根据像素特征数据之间的相似性分类, 将像素特征数据划分为不同的组.为此, 先将图像划分为多个超像素块^[19], 提取每个超像素块的多个不同视图特征, 再进行多视图聚类和图像分割.NOMF-MVC具体步骤如下.

算法1 NOMF-MVC

输入 待分割图像, 超像素个数n

输出 分割后的图像

step 1 将图像划分为n个超像素.

step 2 提取超像素的多个不同视图特征作为多视图数据矩阵X^v(v=1, 2, …, V).

step 3 根据式(1)和式(2)计算非线性降维后的谱嵌入矩阵Y^v.

step 4 计算每个视图谱嵌入矩阵的谱块结构Y^v(Y^v)^T.

step 5 根据式(3)和式(4)得到融合不同视图谱块结构后的一致性图矩阵S.

step 6 根据式(9)得到非负矩阵H和正交矩阵F.

step 7 判断是否满足收敛条件.若满足, 转step 12; 否则, 转step 8.

step 8 通过式(10)更新非负矩阵H.

step 9 通过式(12)更新正交矩阵F.

step 10 通过式(13)更新一致性矩阵S.

step 11 转step 7.

step 12 由非负矩阵H同行不同列的最大值索引得到聚类结果.

step 13 将聚类结果映射到超像素中.

step 14 输出分割结果图.

算法1中的时间复杂度主要在step 3中计算变量Y^v和step 9中更新变量F, step 3中对(D^v)^-1L^v进行特征值分解的时间复杂度为O(n³), step 9中对矩阵S^TH进行奇异值分解的时间复杂度为O(n³), 其中n表示数据量.因此, NOMF-MVC总的时间复杂度为O(2tn³), 其中t表示迭代次数.

本文实验在安装Windows 10, CPU 2.40 GHz, 16 GB RAM的计算机上通过 Matlab 2021a实现.

3.1.1 实验数据集

本文在多视图数据集COIL20、Outdoor Scene、ORL和图像数据集Berkeley、COCO上分别进行多视图聚类实验和图像分割对比实验, 验证NOMF-MVC的聚类性能和图像分割效果.

COIL20数据集包含1 440幅图像, 分成20组, 每组有72幅图像.Outdoor Scene数据集包含2 688幅图像, 分成8组.ORL数据集包含10组400幅图像.Berkeley数据集包括500幅图像, 大小为481× 321或321× 481.COCO数据集包含328 000个影像和2 500 000个标注.

3.1.2 基线算法

为了验证本文算法的性能, 选择如下7种算法进行对比.

1)NESE^[9].将非负嵌入和谱嵌入集成到统一框架中的多视图聚类算法.

2)S-MVSC(Sparse Multi-view Spectral Clus-tering)^[20].从多个视图中学习具有稀疏结构的一致相似矩阵的多视图聚类算法.

3)SMVSC(Scalable Multi-view Subspace Clus-tering with Unified Anchors)^[21].将锚学习和图构建结合到一个统一的优化框架中的大规模多视图聚类.

4)UOMVSC(Unified One-Step Multi-view Spec-tral Clustering)^[22].集成光谱嵌入和k-means进入统一的框架, 直接获得离散聚类标签的多视图聚类算法.

5)SFFCM(Superpixel-Based Fast Fuzzy c-means)^[23].基于超像素的快速FCM聚类的图像分割算法.

6)RSSFCA(Robust Self-Sparse Fuzzy Clus-tering Algorithm)^[24].用于图像分割的鲁棒自稀疏模糊聚类算法.

7)Mask2Former(Masked-Attention Mask Trans-former)^[25].能够处理多种图像分割任务(全景、实例或语义)的基于深度学习的图像分割算法.

3.1.3 评价指标

为了验证算法的有效性, 本文采用边缘召回率(Boundary Recall, BR)、F1、分割精度(Segmenta-tion Accuracy, SA)^[24]、交并比(Intersection Over Union, IOU)、边缘位移误差(Boundary Displace-ment Error, BDE)^[26]和运行时间这6个评价指标进行验证.另外, 为了验证本文算法的抗噪鲁棒性, 选取峰值信噪比(Peak Signal to Noise Ratio, PSNR)作为量化指标.

BR为衡量真值边界和算法生成边界之间一致性程度的指标.BR 值越高, 生成的分割边界与真实边界越接近.

F1是召回率(Recall)和精确率(Precision)的加权调和平均, 综合召回率和准确率的结果, 值越大, 实验结果越优.

SA指正确分类的像素点占总分割像素点的百分比, SA 值越高, 分割效果越优.

IOU指分割结果与真值之间交集与并集的比值.IOU值越大, 分割结果越接近真实分割.

PSNR作为评价聚类算法抗噪性能强弱的指标, 定义为

PSNR=10lg( 2552MSE),

其中, 均方误差

$M S E=\frac{1}{m n} \sum_{i=1}^{m} \sum_{j=1}^{n}\left\|I_{i j}-K_{i j}\right\|^{2}$,

I_ij表示无噪声干扰图像分割结果的像素值, K_ij表示噪声干扰图像分割结果的像素值, m× n表示图像大小.PSNR值越大表明聚类分割算法抗噪性能越优, 对噪声抑制能力越强.

为了更直观地表现本文算法的聚类性能, 在COIL20数据集上, 分别给出由本文算法构造的3个单视图相似矩阵可视化结果和NESE、UOMVSC、NOMF-MVC多视图融合后的相似矩阵可视化结果.具体如图2所示, 图中对角线块表示数据的相似性, 对角线块结构越清晰, 表明聚类性能越优.

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 相似矩阵可视化结果Fig.2 Similarity matrix visualization

由图2(a)~(c)可见, 对角线块结构较分散, (b)的对角线块结构比(a)更清晰, 表明视图2的性能优于视图1, 也体现出不同视图之间存在重要性差异.(d)~(f)中对角线块结构明显清晰, 表明多视图可以探索出各视图间的互补信息.对比(d)~(f), 发现(f)的对角线块最清晰, 表明NOMF-MVC能够探索出各个视图之间的相关性, 获得最佳的聚类结果.

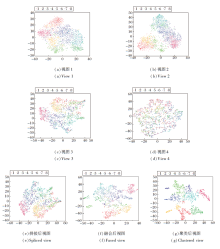
在多视图数据集Outdoor Scene上, 应用t-SNE(t-Distributed Stochastic Neighbor Embedding)非线性降维技术将高维空间中的数据映射到二维坐标轴上, 实现视图可视化.图3为降维后的可视化视图, 其中, (a)~(d)为4个单视图的可视化视图.将4个单视图拼接为一个长向量, (e)为拼接后的可视化视图.(f)为NOMF-MVC多个视图融合后的可视化视图.(g)为NOMF-MVC聚类后的可视化视图.由图3可见, 相比(a)~(d)中的单视图, (f)中相同颜色的数据点分布在一定区域内相对集中, 表明NOMF-MVC融合后的视图是基于每个单视图相似性获取的.相比(e), (f)中具有相同颜色的数据点分布更集中, 表明NOMF-MVC优于传统的拼接方法.相比(f), (g)中具有相同颜色的数据点基本分布在同一个区域内, 表明NOMF-MVC具有良好的聚类性能.

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 降维后的可视化视图Fig.3 Reduced-dimension visual view

为了在视觉上直观地对比各算法的分割效果, 在Berkeley、COCO数据集上分别选取部分图像进行图像分割实验, 8种算法的图像分割结果如图4所示.

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 各算法的图像分割结果对比Fig.4 Comparison of image segmentation results of different algorithms

由图4可见, S-MVSC和SMVSC需要后处理, 聚类结果容易受到初始图质量的影响, 导致在图像分割时图像前景轮廓容易受到背景干扰, 出现误分割和过分割的现象.NESE忽略特定视图嵌入矩阵的信息, 只考虑指标矩阵的非负性, 聚类性能受到限制, 导致在图像分割中表现不稳定, 如在图像80273上出现误分割现象.UOMVSC整体分割效果较优, 但在保留原始数据框架时受噪声影响, 会出现少量的误分割现象.RSSFCA考虑到图像的局部空间信息, 能分割出图像的前景轮廓, 但在细节中信息丢失过多.SFFCM整体分割效果相对较优, 但仅提取直方图特征, 导致细节部分分割不理想, 如在图像23025上未分割出小女孩的脸部.Mask2Former在Transformer解码器中使用屏蔽注意力, 并使用多尺度高分辨率特征帮助模型分割小区域, 故分割效果较理想.

NOMF-MVC在目标和背景相对复杂的图像上, 均能分割出整体轮廓, 如图4(i)所示.黄色方块标记为表现较好的细节部分, 这是由于NOMF-MVC考虑到图像数据固有的流形结构, 挖掘出数据内部的局部几何结构, 故在细节分割上表现较优; 在数据融合阶段考虑到不同视图内部结构和重要性的差异, 故出现相对较少的细节丢失现象.

为了定量说明NOMF-MVC的有效性, 对上述图像在BR、F1、SA、IOU、BDE和运行时间上进行对比, 结果如表1所示.

表1

Table 1

表1(Table 1)

表1 各算法的性能指标评估结果对比 Table 1 Comparison of performance index evaluation of different algorithms 图像 评价指标 S-MVSC SMVSC NESE UOMVSC SFFCM RSSFCA Mask2former NOMF-MVC 3063 BR F1 SA IOU BDE 运行时间/s 0.399 0.378 0.761 0.101 8.363 4.643 0.372 0.421 0.772 0.115 7.611 4.459 0.410 0.410 0.835 0.112 7.356 1.017 0.400 0.412 0.784 0.115 7.757 3.277 0.311 0.407 0.856 0.093 10.651 1.013 0.396 0.413 0.807 0.082 7.247 105.982 0.385 0.417 0.874 0.082 12.769 1.11 0.413 0.428 0.924 0.122 6.915 0.938 23025 BR F1 SA IOU BDE 运行时间/s 0.316 0.376 0.794 0.108 10.463 3.308 0.170 0.227 0.756 0.071 11.775 4.497 0.397 0.450 0.864 0.124 7.972 1.401 0.394 0.441 0.912 0.124 8.509 3.442 0.263 0.412 0.828 0.120 9.294 1.068 0.214 0.294 0.885 0.072 9.972 107.625 0.511 0.656 0.890 0.174 2.273 1.08 0.398 0.432 0.912 0.129 7.619 0.925 227092 BR F1 SA IOU BDE 运行时间/s 0.298 0.391 0.873 0.085 10.290 3.757 0.290 0.383 0.781 0.105 11.649 4.927 0.325 0.426 0.873 0.106 5.774 1.070 0.247 0.352 0.775 0.102 11.644 2.764 0.233 0.341 0.683 0.074 10.005 0.850 0.278 0.389 0.753 0.066 6.427 112.810 0.386 0.549 0.801 0.144 5.092 1.15 0.342 0.435 0.883 0.108 5.518 0.666 80273 BR F1 SA IOU BDE 运行时间/s 0.566 0.428 0.869 0.098 17.200 3.129 0.637 0.540 0.957 0.129 7.247 3.676 0.575 0.413 0.944 0.097 15.289 1.816 0.616 0.503 0.967 0.117 13.293 2.398 0.413 0.504 0.975 0.111 30.559 1.076 0.492 0.389 0.935 0.039 24.576 224.758 0.715 0.777 0.848 0.133 1.799 1.14 0.614 0.540 0.977 0.133 8.665 0.895 482477 BR F1 SA IOU BDE 运行时间/s 0.508 0.346 0.944 0.073 20.094 3.342 0.530 0.379 0.977 0.080 9.640 3.446 0.511 0.350 0.944 0.073 19.087 1.878 0.512 0.326 0.977 0.069 15.845 6.142 0.461 0.380 0.971 0.081 8.587 1.821 0.359 0.203 0.978 0.029 22.498 308.246 0.438 0.521 0.874 0.115 2.865 1.20 0.532 0.387 0.975 0.083 11.404 0.450

表1 各算法的性能指标评估结果对比 Table 1 Comparison of performance index evaluation of different algorithms

由表1可以看出, NOMF-MVC的分割效果在总体上表现较优.在BR和F1上, NOMF-MVC次优于Mask2Former, 优于其它算法.在SA上, NOMF-MVC表现最优, 比Mask2Former提升4.73%, 比SMVSC提升10.14%, 表明NOMF-MVC在细节分割上具有较大优势, 这是由于本文应用非线性降维方法, 充分探索出数据的局部几何结构, 并通过谱块结构保留数据的局部特征.在BDE上, NOMF-MVC在部分图像上次优于Mask2Former和SFFCM, 但SFFCM不稳定, 如在80273这类图像上出现边缘位移误差较大的现象.在时间效率上, NOMF-MVC是其它算法的1到12倍, 表现最优, 这是由于本文的非线性降维方法去除数据冗余, 减小数据规模, 另外, 非负正交分解方法避免后处理, 节省时间成本, 故在保证分割精度最优的条件下提高时间效率.

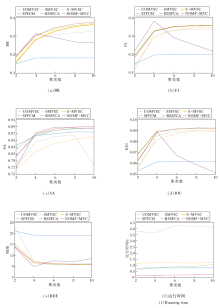
为了进一步验证NOMF-MVC的有效性, 对Berkeley 数据集上的全部500幅图像进行测试, 图5为各算法分别对500幅图像的6个评价指标取平均值后的结果对比.由图可以看出, NOMF-MVC在6个评价指标上均有良好的表现, 特别是在时间效率上有倍数级的提高.

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 各算法在Berkeley数据集上的评价指标平均值对比Fig.5 Average value comparison of evaluation indexes of different algorithms on Berkeley dataset

在Berkeley、COCO数据集上选取部分图像添加高斯噪声, 并选取分割效果较优的SFFCM和NESE与NOMF-MVC在原图和噪声图上进行图像分割实验, 分割结果如图6所示.

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 各算法对原图与噪声图的分割结果Fig.6 Segmentation results of different algorithms for original images and noisy images

图中第1列和第4列是各算法对原始图像的分割结果, 第2列和第5列是各算法对加入方差为0.01、均值为0.1高斯噪声图的分割结果, 第3列和第6列是各算法对加入方差为0.01、均值为0.2高斯噪声图的分割结果.

由图6可见, 各算法对噪声图分割时均会出现不同程度的误分割现象.SSFCM和NESE受噪声影响较大, 尤其是NESE, 噪声分割图的整体轮廓丢失.而NOMF-MVC受噪声影响较小, 这是因为NOMF-MVC通过非线性降维方式去除原始数据中噪声和冗余, 故抗噪鲁棒性较优.

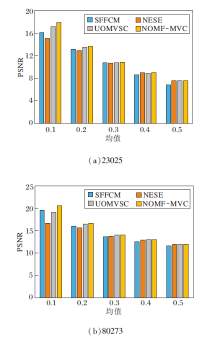
为了定量验证NOMF-MVC的抗噪鲁棒性, 分别为原始图像加入方差为0.01、均值为0.1~0.5的高斯噪声, 不同算法在不同噪声下的PSNR值如图7所示.

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 各算法在2个图像上的PSNR对比Fig.7 PSNR comparison of different algorithms on 2 images

由图7可以看出, 所有算法的PSNR值随着高斯噪声均值的增大而变小, 表明噪声越大, 聚类分割算法的抗噪性能越差.当高斯噪声的均值相同时, NOMF-MVC的PSNR值均大于其它算法, 表明其抗噪性能最优.

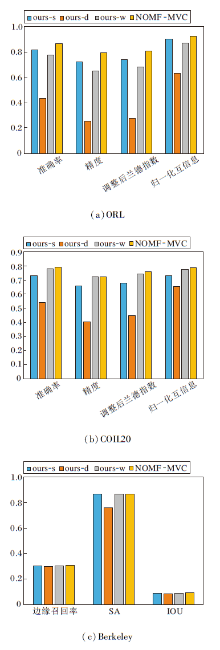
NOMF-MVC包括多视图、谱嵌入矩阵谱块结构和自适应学习不同视图权重三个关键部分.为了验证这三部分的重要性, 制定如下对比算法.1)ours-s.选取多视图中性能最优的单视图作为原始数据进行聚类分割.2)ours-d.将非线性降维后多个视图的谱嵌入矩阵直接学习到一致性图矩阵中, 去除构建谱块结构这一过程.3)ours-w.将每个视图的权重设为相同的值 1v, 其中v表示视图数.

各算法在ORL、COIL20两个多视图数据集和Berkeley 数据集上的评价指标对比如图8所示, 对Berkeley数据集上500幅图像的评价指标取平均值得到(c)的柱状图.

图8

Fig.8

	Figure Option ViewDownloadNew Window
	图8 各算法在3个数据集上的评价指标对比Fig.8 Evaluation index comparison of different algorithms on 3 datasets

由图8可以看出, 当去除NOMF-MVC中关键部分后, 聚类性能和分割效果均会下降, 这表明NOMF-MVC中的每个组成成分都是有效的.